1. Introduction
A nonlinear regression model refers to a regression model in which the relationship between variables is not linear. Nonlinear regression model has been widely used in various disciplines. For instance, Hong [
1] applied a nonlinear regression model to the economic system prediction; Wang et al. [
2] studied the application of nonlinear regression model in the detection of protein layer thickness; Chen et al. [
3] utilized a nonlinear regression model in the price estimation of surface-to-air missiles; Archontoulis and Miguez [
4] used a nonlinear regression model in agricultural research.
The principle of median-of-means (MOM) was firstly introduced by Alon, Matias, and Szegedy [
5] in order to approximate the frequency moment with space complexity. Lecu
and Lerasle [
6] proposed new estimators for robust machine learning based on MOM estimators of the mean of real-valued random variables. These estimators achieved optimal rates of convergence under minimal assumptions on the dataset. Lecu
et al. [
7] proposed MOM minimizers estimator based on MOM method. The MOM minimizers estimator is very effective when the instantaneous hypothesis may have been corrupted by some outliers. Zhang and Liu [
8] applied MOM method to estimate the parameters in multiple linear regression models and AR error models of repeated measurement data.
For unknown parameters of a nonlinear regression model, Radchenko [
9] proposed an estimator named nonlinear least square to approximate the unknown parameters. Ding [
10] introduced the empirical likelihood (EL) estimator of the parameter of the nonlinear regression model based on the empirical likelihood method. However, when there are outliers, the general methods are more sensitive and easily affected by the outliers based on Gao and Li [
11]. On the basis of the study of Zhang and Liu [
8], this paper applies the MOM method to estimate the parameters of the nonlinear regression models and receives more robust results.
The paper is organized as follows: In
Section 2, we review the definition of the nonlinear regression model and introduce the MOM method specifically. We prove the consistency and asymptotic properties of the MOM estimator. In
Section 3, we introduce a new test method based on the empirical likelihood method for the median.
Section 4 illustrates the superiority of the MOM method with simulation studies. A real application to GDP data is given in
Section 5, and the conclusion is discussed in the last section.
2. Median-of-Means Method Applies to Nonlinear Regression Model
We consider the following nonlinear regression model introduced by Wu [
12]
where
is a fixed
unknown parameter column vector.
is the
i-th “fixed” input vector with observation
.
is a known functional form (usually nonlinear).
are i.i.d errors with 0 mean and
unknown variance.
According to Zhang and Liu [
8], MOM estimator of
is produced by the following steps:
Step I: We seperate
into g groups. The number of observations in each group is
(Usually for the convenience of calculation, we assume that
T is always divisible by g). We discuss the choice of grouping number g. According to the suggestion by Emilien et al. [
13],
for any
, where
is the ceiling function. In fact, the structure of observations is always unknown, and the diagnosis of outliers is complicated. Therefore, we usually set
for some constant C regardless of outliers.
Step II: We estimate the parameter in each group by the nonlinear least square estimator .
Step III: The MOM estimator of is defined, where .
The asymptotic properties of
are summarized in the following theorems. Their proofs are postponed to
Appendix A.
Theorem 1. For some constant C and any positive integer g, we suppose the following:
(I) For certain and any , Θ
is is an open interval (finite or infinite) of the real axis . for if at least one of the points , is or ∞ ). . Suppose for some . For and sufficiently large positive ρ, c does not depend on n and ρ.
(II) , exist for all near , the true value is in the interior of , and (III) There exits as and . (IV) There exits a such thatfor all i = 1, …, n, where . According to conditions , for any fixed , we can get Theorem 1. (1) Suppose g is fixed and . Let , , …, be i.i.d standard normal random variables. When , (2) Suppose as and . Afterwards the following asymptotic normal holds 3. Empirical Likelihood Test Based on MOM Method
In
Section 2, this paper uses the MOM method to estimate the parameters of the nonlinear regression model. In this section, we consider the hypothesis test that
equals a given value parameter based on the empirical likelihood method.
Because different groups are disjoint,
,
are i.i.d. We treat them as a sample and apply empirical likelihood. For each j, we say
. Obviously,
. In fact,
(by the process of proof of Theorem in the
Appendix A. Given restrictive conditions, the empirical likelihood ratio of
is
Using the Lagrange multiplier to find the maximum point we obtained the following equation.
where
satisfies the equation
Theorem 3. According to Theorem 2 and Owen [14], as , we have Using the Theorem 3, the rejection region for the hypothesis with significance level
can be constructed as
where
is the upper
-th quantile of
.
4. Simulation Study
In this section, we use R software for simulation. Simulation experiments are carried out to compare the performance of the MOM estimator with the nonlinear least squares (NLS) estimator and the EL estimator under “no outliers” and “with outliers” cases in Examples 1–3. The definition of Mean Square Error (MSE) of
,
and
are as follows.
,
represent the estimated value of the parameter and the true value of the parameter Respectively in formula (8). D represents the total number of simulations, and in this article, D = 1000. The MSE results calculated in
Table 1,
Table 2 and
Table 3 are all multiplied by 100. The results are accurate to three decimal places. In Examples 4–6, we compare our proposed method with empirical likelihood inference proposed by Jiang [
15].
We report the empirical sizes and powers of the two methods, where size represents the probability of rejecting the null hypothesis provided it is true. In this paper, we set that the nominal significance level is 0.05. If the value is close to 0.05 it is good. Power represents the probability of rejecting the null hypothesis provided it is false. If the value of power is close to 1 it is good. Empirical size or power represents
, where
refers to the number of times the null hypothesis is rejected in D simulations. In
Table 4,
Table 5 and
Table 6 of this article, the size value refers to the empirical likelihood, and power refers to the empirical power. In fact, the empirical size is the estimated value of size, and the empirical power is the estimated value of power. We consider the following three forms of nonlinear regression models, which were also considered by Hong [
16].
In this paper, for convenience, we fix the number of groups in simulation. We find that the result is consistent with the calculation result according to the formula
which suggested by Emilien et al. [
13]. Throughout the paper, the distribution abbreviations B, U, N, P represent binomial distribution, uniform distribution, normal distribution respectively and Poisson distribution. N(0,1) represents the standard normal distribution. We set the number of repeated observations T to 100, 200, …, 1000.
Example 1. We consider model , For the observation data, the grouping is carried out according to the grouping principle. Taking the effect of the measures of dispersion in data sets into consideration (accuracy of the estimator may be affected by the dispersion in the data set). are generated from the , are generated from . The output variable has outliers. There are three cases of outliers. We choose outliers from , outliers from and outliers from , respectively. The results are shown in Table 1. Example 2. We consider model , are generated from the , are generated from . The output variable have outliers. There are three cases of outliers. We choose outliers from B(22,1/2), outliers from and outliers from , respectively. The results are shown in the Table 2. Example 3. We consider model , are generated from . are generated from . The output variable have outliers. There are three cases of outliers. We choose outliers from , outliers from and outliers from , respectively. The results are shown in the Table 3. - (1)
The MSE decrease for all estimators as T becomes large whether there are outliers.
- (2)
When there are no outliers, the MSE of , and are the same basically.
- (3)
When there are outliers, the MSE of
estimator is smaller than the MSE of
estimator and
estimator. From
Table 1 and
Table 3, the results show that they are no significant differences between the MSE of
estimator and
estimator as
T is large.
Example 4. We consider model , are generated from , are generated from , For the power, we use with as the alternative hypothesis. The results are shown in Table 4. MOMEL repersents empirical likelihood test based on MOM method, and EL represents hypothesis test based on the EL estimator. Example 5. We consider model , suppose are generated from , are generated from . For power, we use with as the alternative hypothesis. The results are shown in Table 5. Example 6. We consider model , are generated by , are generated by . For power, we use with as the alternative hypothesis. The results are shown in Table 6. From simulation results that are displayed in
Table 4,
Table 5 and
Table 6, we can see that the size of the proposed test is close to 0.05 and the power is close to 1 as T increases. Especially when N is small, the results of MOM are significantly better than EL’s. When T increases, the MOM also performs better in terms of size and power although the power of both methods tends to one. In summary, our method is better.
5. The Real Data Analysis
In this section, we apply the MOM method to analyze the top 50 data of GDP of China in 2019. Basing on the presentation of Zhu et al. [
17], there are many methods to test whether there are outliers in the data, such as the 4d test,
principle, the Chauvenet method, the t-test and the Grubbs test. Sun [
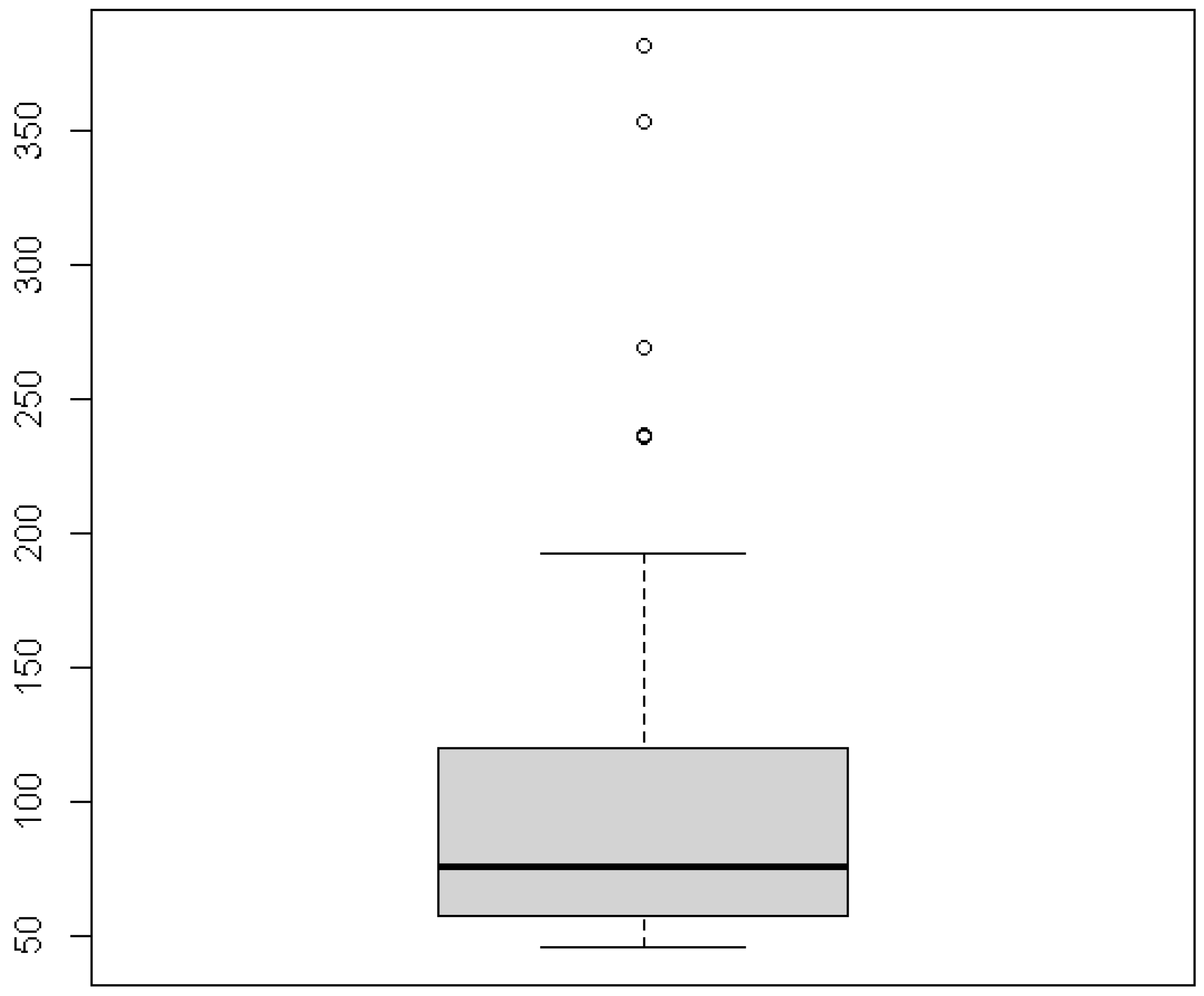
18] also introduced the box plot method. Different test methods will get different outliers. So we use the box plot as shown in
Figure 1 to confirm the existence of outliers in the actual data based on the suggestion of Sun et al. [
18]. The outliers are 381.55, 353.71, 269.27, and 236.28 (unit: ten billion RMB).
We also use a 3- principle to test whether there are outliers, and the result shows that the outliers are 381.55 and 353.71. Through the test of the above two methods, we can judge that there are outliers in this real data.
Yin and Du [
19] introduced a power-law distribution. For the purpose of predicting the GDP development trend of major cities accurately in China. We use the EL method, the MOM method and the NLS method to fit the curve respectively. Where
represents the sorting order of GDP of 50 cities in descending order. The dataset is from
www.askci.com (accessed on 15 February 2021).
The EL gives the nonlinear regression equation
The MOM gives the nonlinear regression equation
The NLS gives the nonlinear regression equation
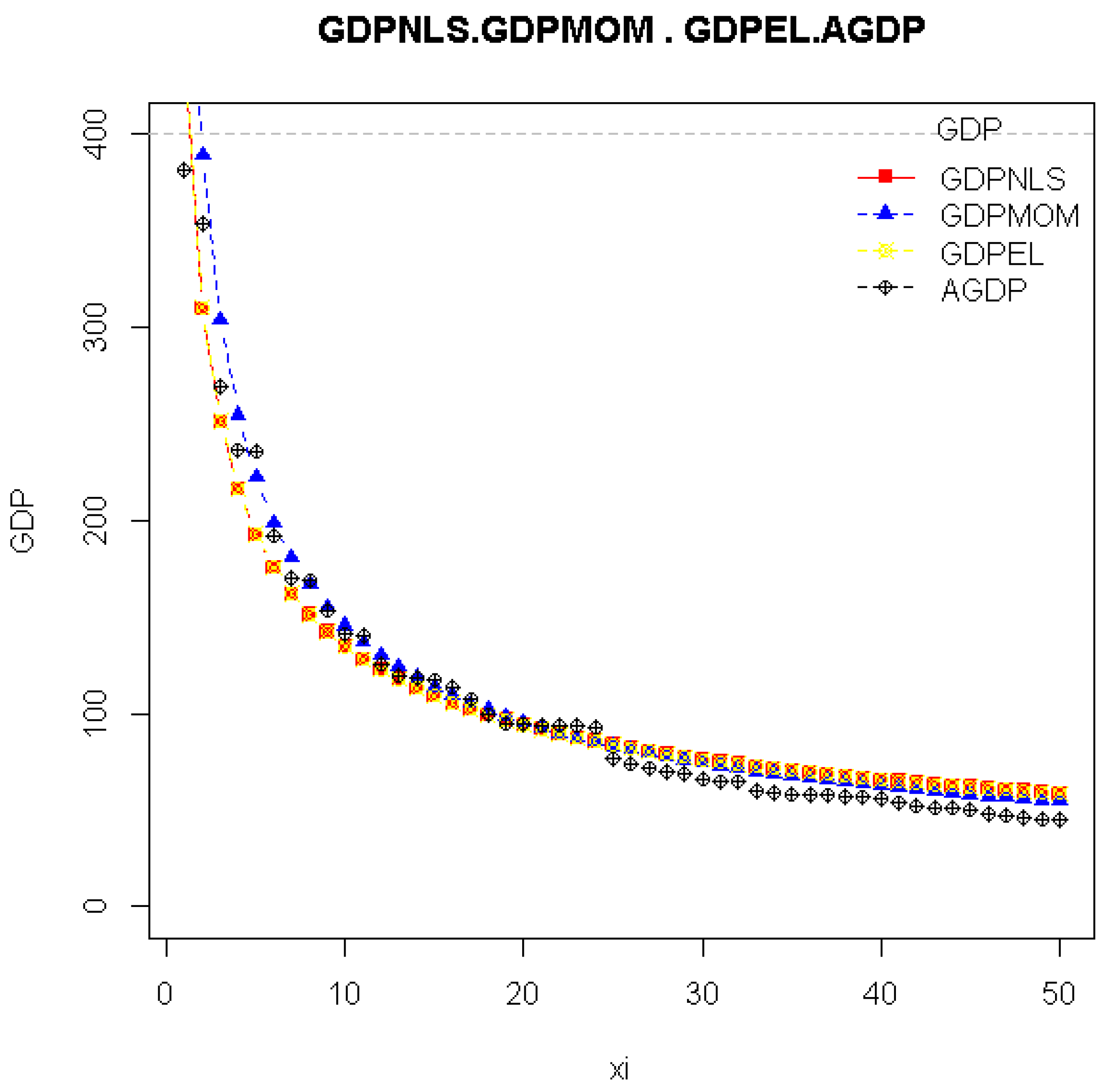
In
Figure 2, the red line represents the fitting result of NLS method, and the blue line represents the fitting result of MOM method. the black line represents the fitting result of EL method, and the yellow points represent the true value of GDP.
In actual data, the true values of parameters are really unknown, so we cannot calculate MSE of the parameter. MAE refers to the average value of the absolute error. The definition of Mean Absolute Error (MAE) is given below.
In the actual data, refers to the true value of GDP, and refers to the GDP value obtained from the fitted nonlinear regression model, so we calculated the MAE. MAE of the MOM method is 11.984. MAE of the NLS method is 12.024, MAE of the MOM method is 11.982. Cross-validations are taken to examine the accuracy of forecasting. Specifically, we take 40 data as experimental data and the other 10 as forecasting data randomly and the number of independent replications is 1000. The MAE of EL, ELS and MOM are 14.206, 14.271 and 12.242 respectively. These suggest that MOM is more plausible than NLS and EL.
6. Conclusions
It is shown that the NLS method is not robust to outliers based on the research of Gao and Li [
11]. So in this paper, firstly, we apply the MOM method to the nonlinear regression model and introduce its theory. We give the theoretical results of asymptotic normality and consistency of the MOM estimator. Secondly, we propose a new test method based on the empirical likelihood method. Thirdly, we use the MOM method to estimate the parameters of three forms of nonlinear regression models, and compare the MSE of
,
and
. The results show that the MSE of
is the smallest from
Table 1,
Table 2 and
Table 3 and the size and power prove the superiority of the MOM method from
Table 4,
Table 5 and
Table 6. Finally, the MOM method is applied to predict the GDP development of cities of China, the value of MAE shows that the prediction of the MOM method is better than the NLS method. All in all, the MOM method does not need to eliminate outliers. Regardless of whether there are outliers in the data, we will use the MOM method to get a robust estimation.
Author Contributions
Conceptualization, P.L.; methodology, P.L.; M.Z. and Q.Z.; software, R.Z.; writing—original draft, R.Z.; writing—review and editing, M.Z., R.Z. and Q.Z. All authors have read and agreed to the published version of the manuscript.
Funding
Pengfei Liu’s research is supported by the National Natural Science Foundation of China (NSFC11501261, NSFC52034007) and the State Scholarship funded by China Scholarship Council (CSC201808320107). Ru Zhang’s research is supported by the Project funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions. Qin Zhou’s research is supported by the National Natural Science Foundation of China (NSFC11671178).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Acknowledgments
Thank Shaochen Wang and Wang Zhou for their help. And thank the reviewers for their constructive comments.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
In this
Appendix A, we give the technical proofs of Theorems 1–3.
Lemma A1 (Chernoff’s inequality, cf. Vershynin [
20] Theorem 2.3.1).
Let is an independent Bernoulli random variable with the parameter . Consider sum and their mean , for any , we have Proof of Theorem 1. In accordance with the condition (I) of Theorem 1 and the Lemma 1 of Ivanov [
21], for
and sufficiently large positive
, c does not depend on n and
. We have
According to Wu [
22], we can get that the least square estimate of
is (
j = 1, …,
g)
According to Formula (2) and the conditions (II)(III)(IV). From the Theorem 5 of Wu [
12], we can know
According to Pinelis [
23],
is a constant, we can know
where
represent the cumulative distribution function of Standard normal distribution.
According to formula (A4), we have
For each
, suppose
, we have
for all
, according to the elementary inequality
where
for large n and fixed
, hence
Similarly, we can get
where
is a constant that depends on H but not n, so we have
It is easy to verify that
so we have the conclusion
Definite Bernoulli random variable
we have
by Formula (A9). It can be seen that event E occurs if and only if
is larger than
, hence
We have used Lemma 1 in the last step. This ends the proof of Theorem 1.
For any fixed x, we define i.i.d random variables
and suppose
according to Formula (A4)
for all real
x. The following lemma gives the central limit theorem for the partial sums of
. □
Lemma A2. Suppose as . We havefor the fixed x, as , Proof of Lemma 2. For convenience, we write
as
. By independence, for any real t and
, we have
through the Taylor’s expansion, we have
where we used the formula
, when
and
,
so the first conclusion of the Lemma 2 can get by formula (A13).
For the second conclusion, we find that the above calculations still hold if we replace
x with
and note the fact that
We can proof the formula (A15) by the virtue of Slutsky’s theorem. □
Proof of Theorem 2. (1) This follows immediately by formula (A4) and the continuous mapping theorem since the Median function is continuous.
We first assume g is odd and for any real
x, and we have
under the above lemma, it tends to
.
If g is even, we can know
and
The right hand sides of the above two inequalities tend to as . □
Proof of Theorem 3. Recall that
where
, so formula (6) is
set that
, and we have
Combining the constraint condition
, we can get that
, and
The last equality follows by formual (A20). So,
and according to Lemma 2,
, we can get
so
The final term in formula (A26) above has a norm bounded by
Therefore
where
.
Through formula (A26) and using Taylor expansion, we can find that
holds for some finite
,
,
as
and
.
This completes the proof. □
References
- Hong, Z. The application of nonlinear regression model to the economic system prediction. J. Jimei Inst. Navig. 1996, 4, 48–52. [Google Scholar]
- Wang, D.; Jiang, D.; Cheng, S. Application of nonlinear regression model to detectthe thickness of protein layer. J. Biophys. 2000, 16, 33–74. [Google Scholar]
- Chen, H.; Wang, J.; Zhang, H. Application of nonlinear regression analysis in establishing price model of ground-to-air missile. J. Abbr. 2005, 4, 77–79. [Google Scholar]
- Archontoulis, S.V.; Miguez, F.E. Nonlinear regression models and applications in agricultural research. Agron. J. 2015, 105, 1–13. [Google Scholar] [CrossRef]
- Alon, N.; Matias, Y.; Szegedy, M. The space complexity of approximating the frequency moment. J. Comput. Syst. Sci. 1999, 58, 137–147. [Google Scholar] [CrossRef]
- Lecué, G.; Lerasle, M. Robust machine learning by median-of-means: Theory and practice. Ann. Stat. 2017, 32, 4711–4759. [Google Scholar]
- Lecué, G.; Lerasle, M.; Mathieu, T. Robust classification via MOM minimization. Mach. Learn. 2018, 32, 1808–1837. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, P. Median-of-means approach for repeated measures data. Commun. Stat. Theory Methods 2020, 2020, 1–10. [Google Scholar] [CrossRef]
- Radchenko, P.P. Nonlinear least-squares estimation. J. Multivar. Anal. 2006, 97, 548–562. [Google Scholar]
- Ding, X.; Xu, L.; Lin, J. Empirical likelihood diagnosis of nonlinear regression model. Chin. J. Appl. Math. 2012, 4, 693–702. [Google Scholar]
- Gao, S.; Li, X. Analysis on the robustness of least squares method. Stat. Decis. 2006, 15, 125–126. [Google Scholar]
- Wu, C.-F. Asymptotic theory of nonlinear least squares estimation. Ann. Stat. 1981, 9, 501–513. [Google Scholar] [CrossRef]
- Emilien, J.; Gábor, L.; Roberto, I.O. Sub-Gaussian estimators of the mean of a random vector. Ann. Stat. 2017, 47, 440–451. [Google Scholar]
- Owen, A.B. Empirical likelihood ratio confidence intervals for a single functional. Biometrika 1988, 75, 237–249. [Google Scholar] [CrossRef]
- Jiang, Y. Empirical Likelihood Inference of Nonlinear Regression Model Parameters. Master’s Thesis, Beijing University of Technology, Beijing, China, 2005. [Google Scholar]
- Ratkowski, H.Z. Nonlinear Regression Model: A Unified Practical Method; Nanjing University Press: Nanjing, China, 1986; pp. 12–25. [Google Scholar]
- Zhu, J.; Bao, Y.; Li, C. Discussion on data outlier test and processing method. Univ. Chem. 2018, 33, 58–65. [Google Scholar] [CrossRef]
- Sun, X.; Liu, Y.; Chen, W.; Jia, Z.; Huang, B. The application of box and plot method in the outlier inspection of animal health data. China Anim. Quar. 2010, 27, 66–68. [Google Scholar]
- Yin, C.; Du, J. The collision theory reaction rate coefficient for power-law distributions. Phys. A Stat. Mech. Its Appl. 2014, 407, 119–127. [Google Scholar] [CrossRef]
- Vershynin, R. High-Dimensional Probability (An Introduction with Applications in Data Science); Cambridge University Press: Cambridge, UK, 2018; pp. 70–97. [Google Scholar]
- Ivanov, A.V. An asymptotic expansion for the Distribution of the Least Squares Estimator of the nonlinear regression parameter. Theory Probab. Appl. 1977, 21, 557–570. [Google Scholar] [CrossRef]
- Wu, Q. Asymptotic normality of least squares estimation in nonlinear models. J. Guilin Inst. Technol. 1998, 18, 394–400. [Google Scholar]
- Pinelis, I.; Molzon, R. Optimal-order bounds on the rate of convergence to normality in the multivariate delta method. Electron. J. Stat. 2016, 10, 1001–1063. [Google Scholar] [CrossRef]
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).