Lac Operon Boolean Models: Dynamical Robustness and Alternative Improvements
Abstract
1. Introduction
2. Mathematical Background
- Fixed point (or steady state): configuration such that .
- Limit cycle: sequence of configurations pairwise distinct such that , for all , and is a integer named the length of the limit cycle.
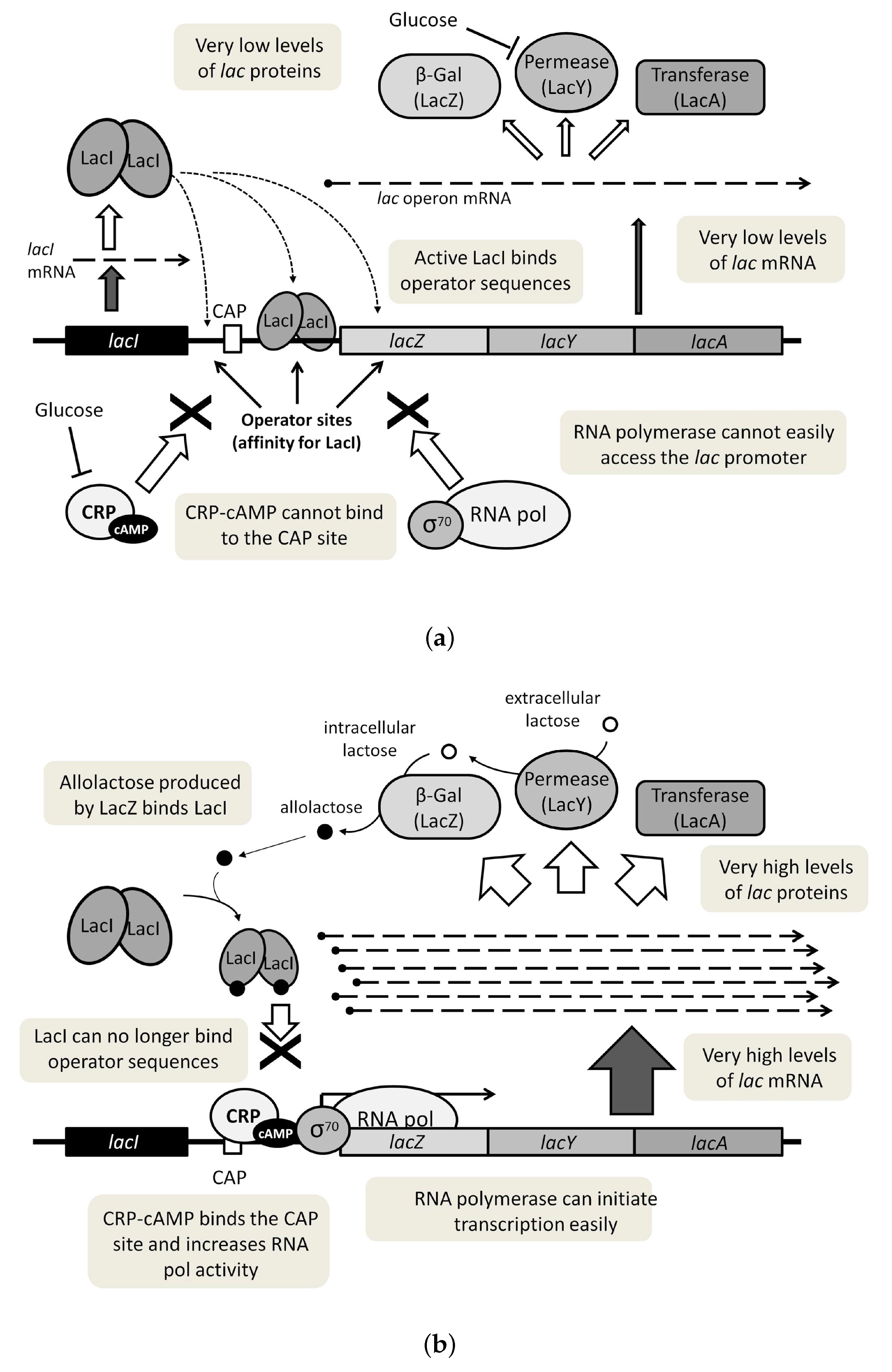
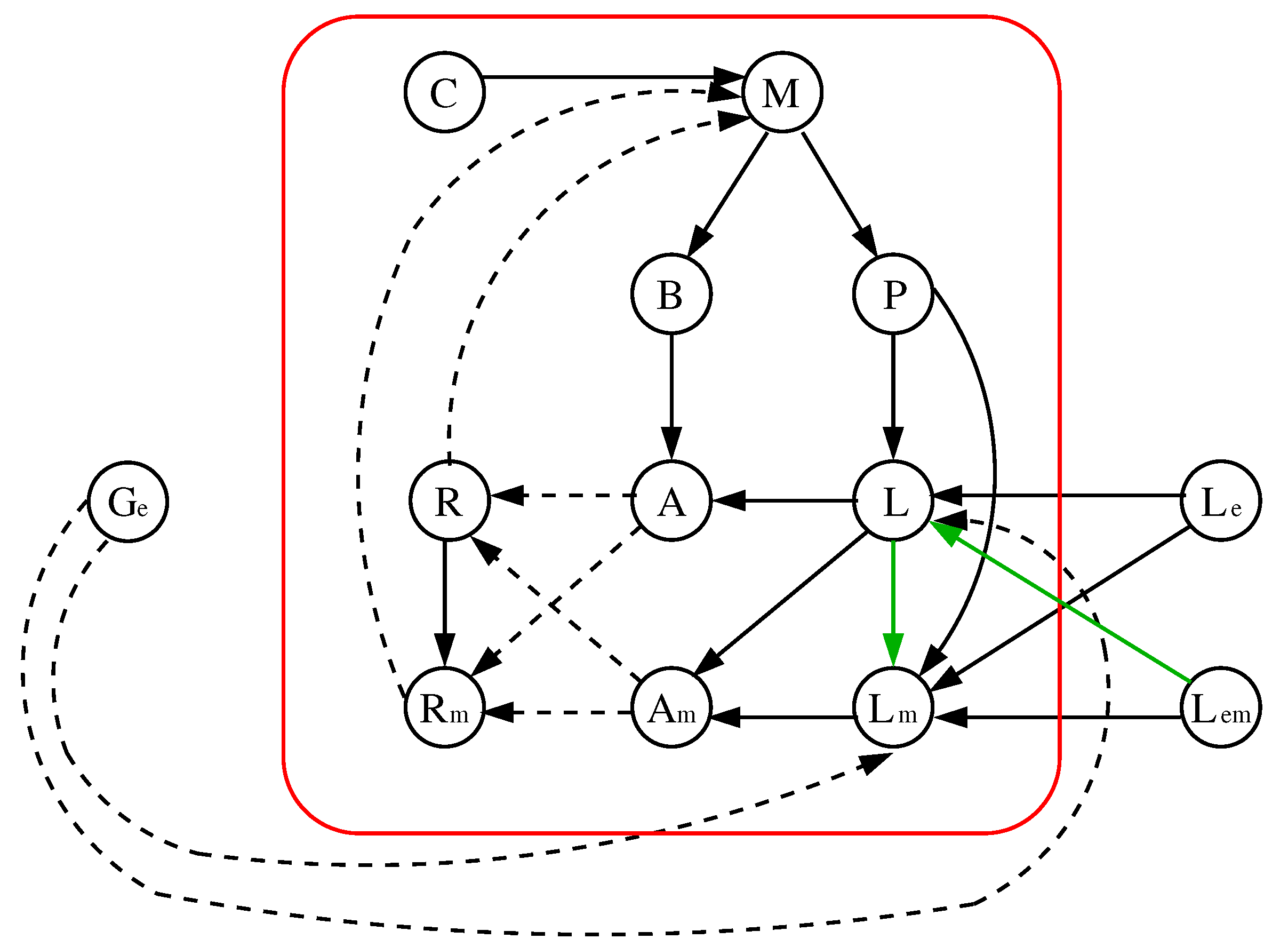
3. The lac Operon Boolean Models to Be Considered: Main Aspects and Choice Justification
- 1.
- All of them have qualitative behaviors that match very well with the experiments performed in [7].
- 2.
- The interaction digraph is composed by nodes that represent mRNA, proteins, and sugars. Its edges represent the type of interaction between the nodes (activation/inhibition).
- 3.
- The dynamic is obtained considering the parallel update schedule.
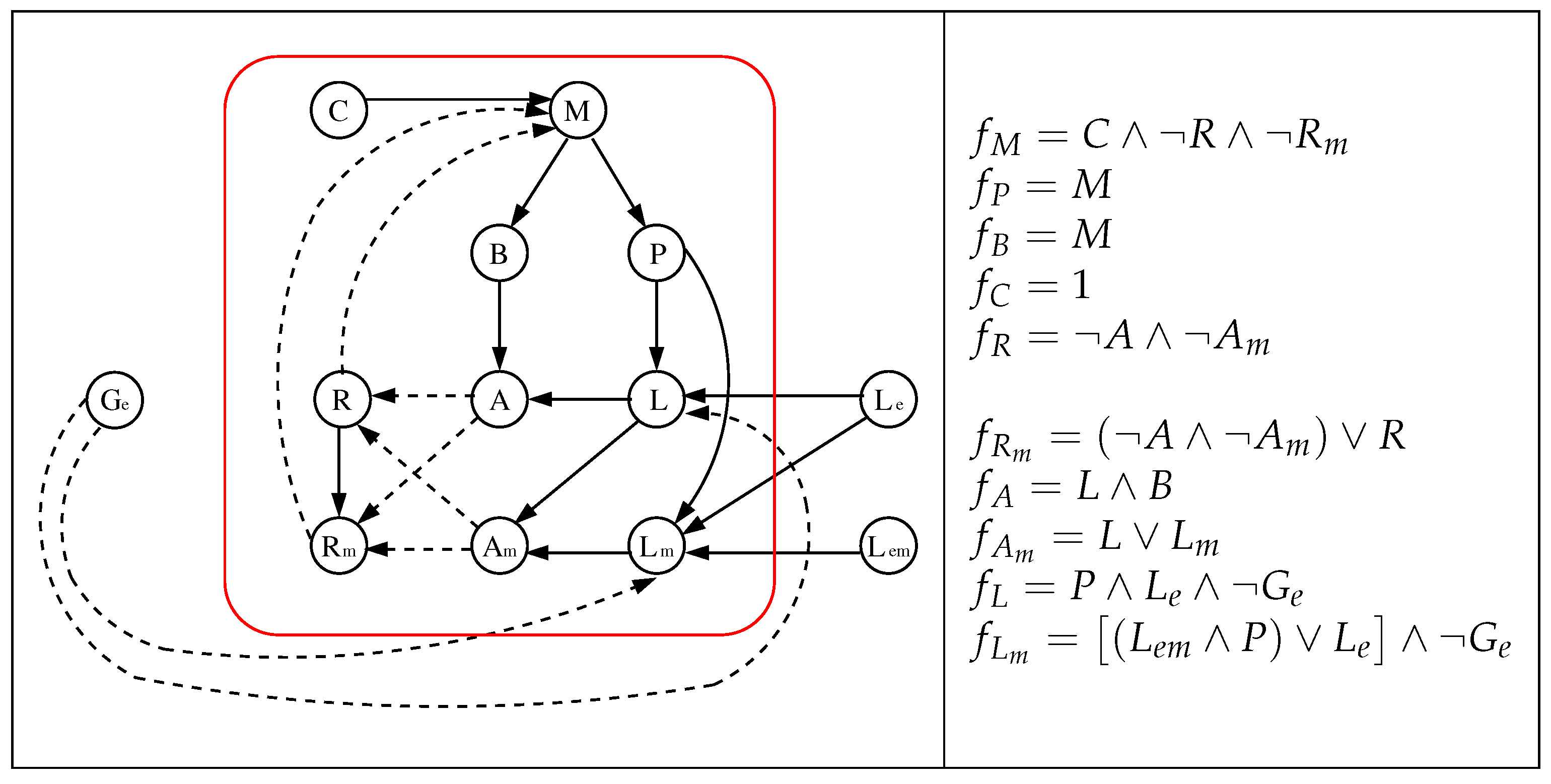
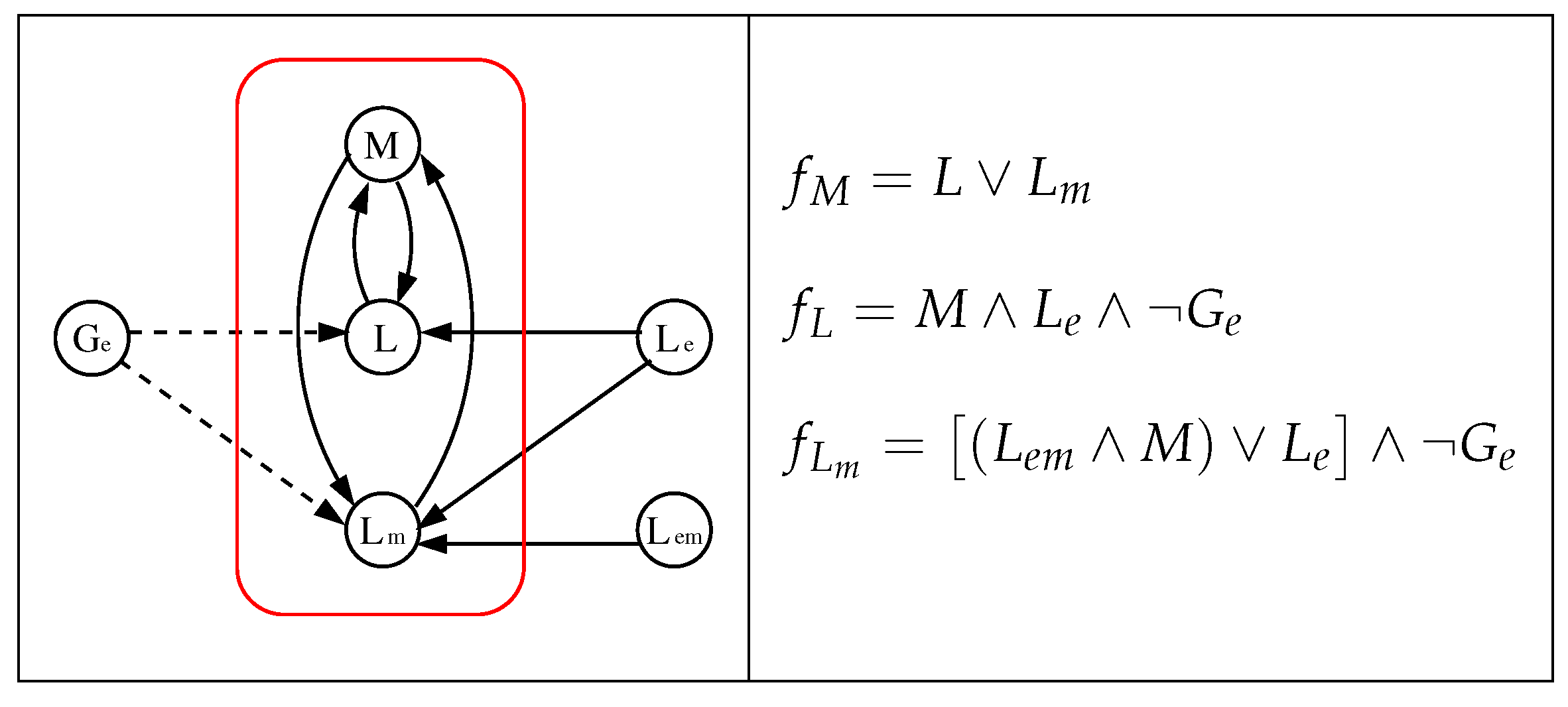
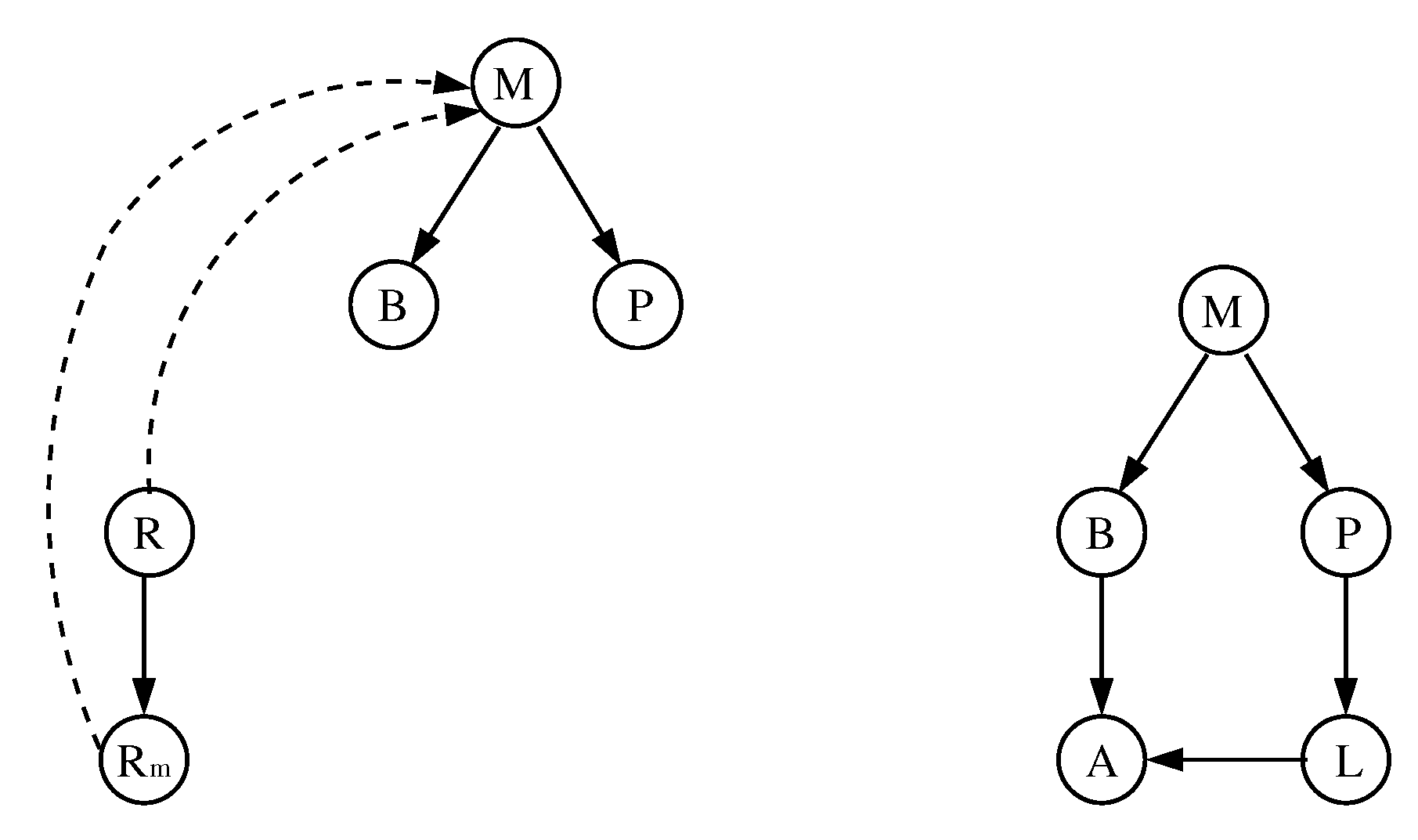
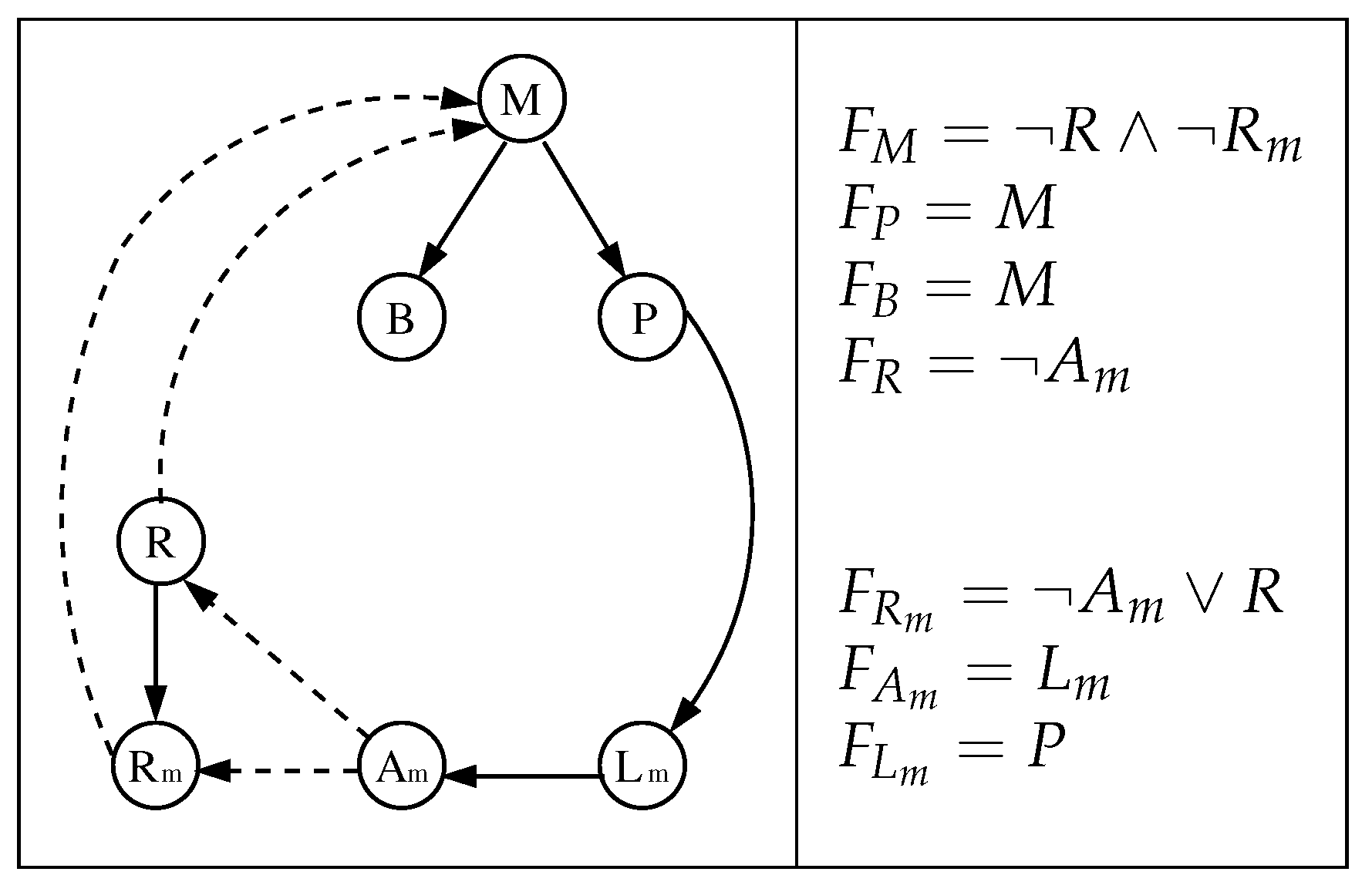
3.1. The Chosen Models of Veliz-Cuba and Stigler 2011: Those without Catabolite Repression
3.2. The Dynamics Produced by the Original and Reduced Models
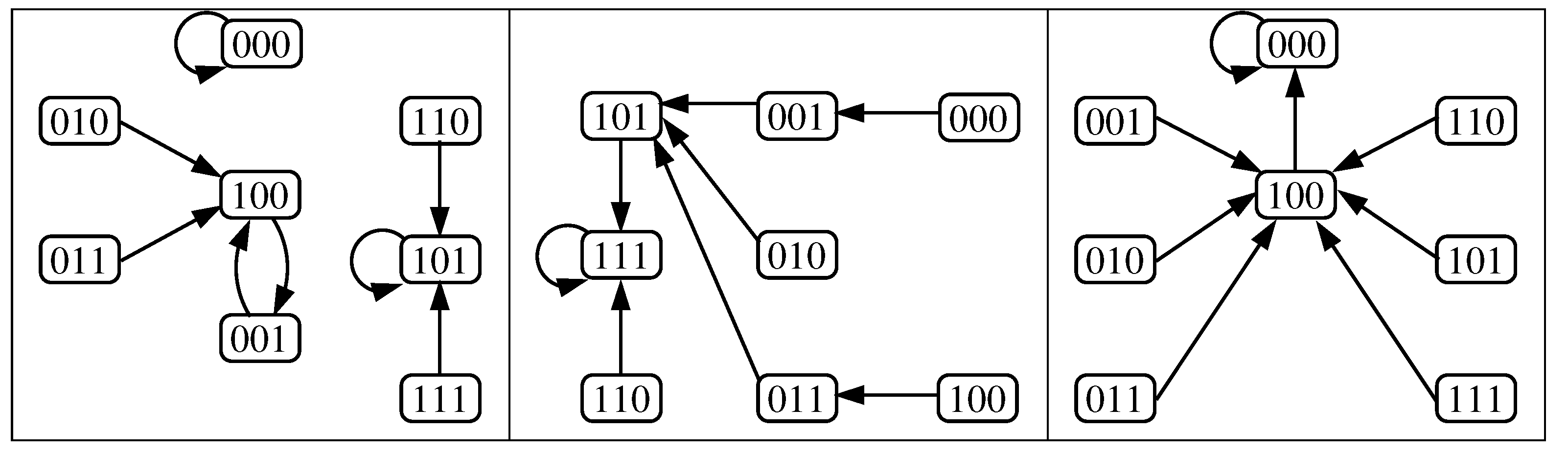
- Case 1:
- . Any configuration eventually converges to the unique fixed point OFF = .
- Case 2:
- . Any configuration eventually converges to the unique fixed point OFF .
- Case 3:
- . Any configuration eventually converges to the unique fixed point ON .
- Case 4:
- . Any configuration eventually converges to one of the two fixed points; OFF or ON , i.e., bistability is obtained.
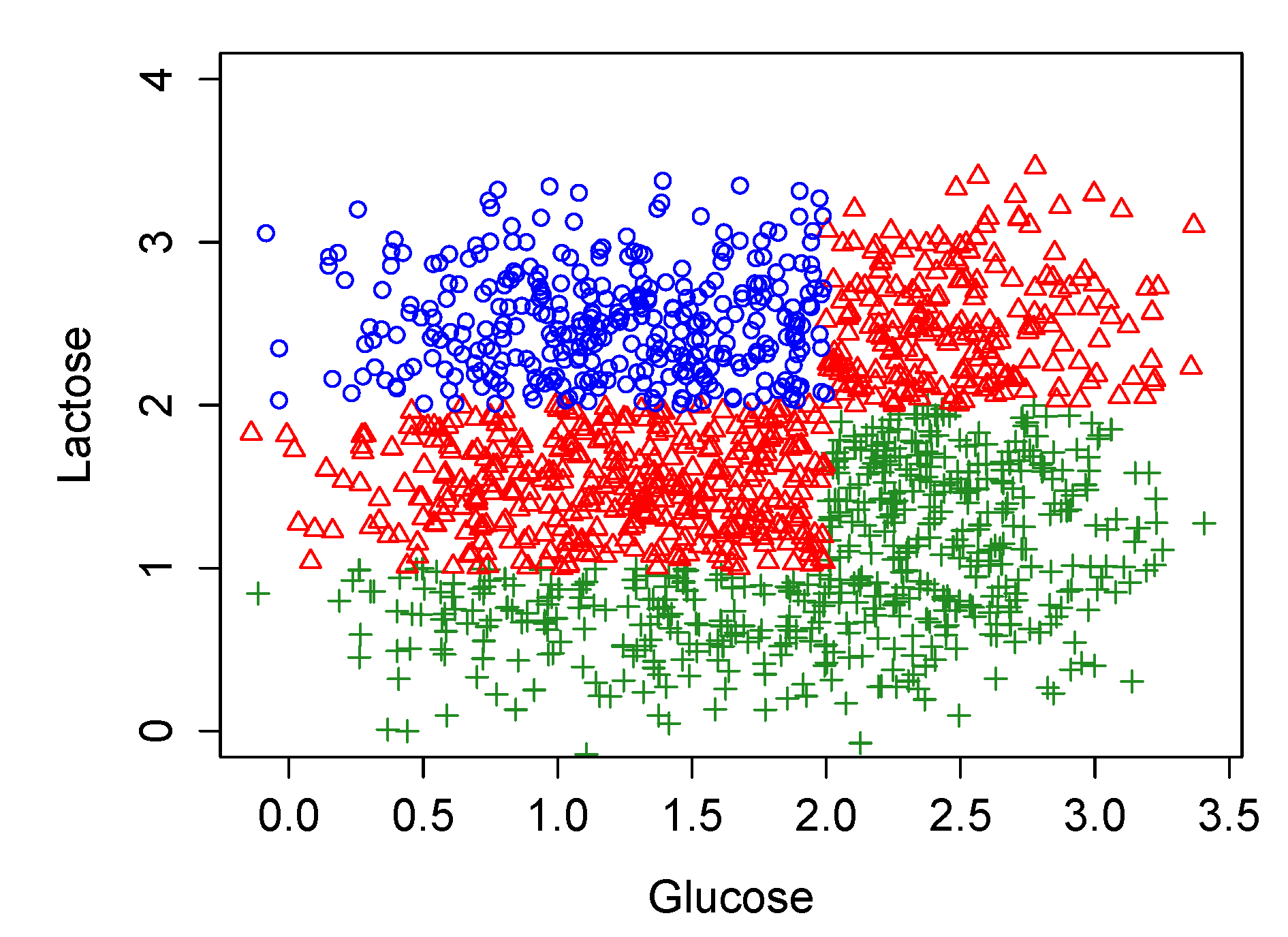
3.3. Stochastic Simulations in the Original Model Which Largely Coincide with the Biological Experiments of Ozbudak et al., 2004
- (1)
- Starting with the normal distribution for , to generate randomly a set of values for and calculate for each of them the corresponding value for the pair .
- (2)
- Assuming , to find which are the steady states of the dynamic obtained for each value of (1), it is simply one of the three possibilities showed in the second column of Table 1; OFF, bistable (i.e., OFF and ON) or ON.
- (3)
- To repeat (1) and (2) but for with .
3.4. Our Justification for the Choice of Models without Catabolite Repression
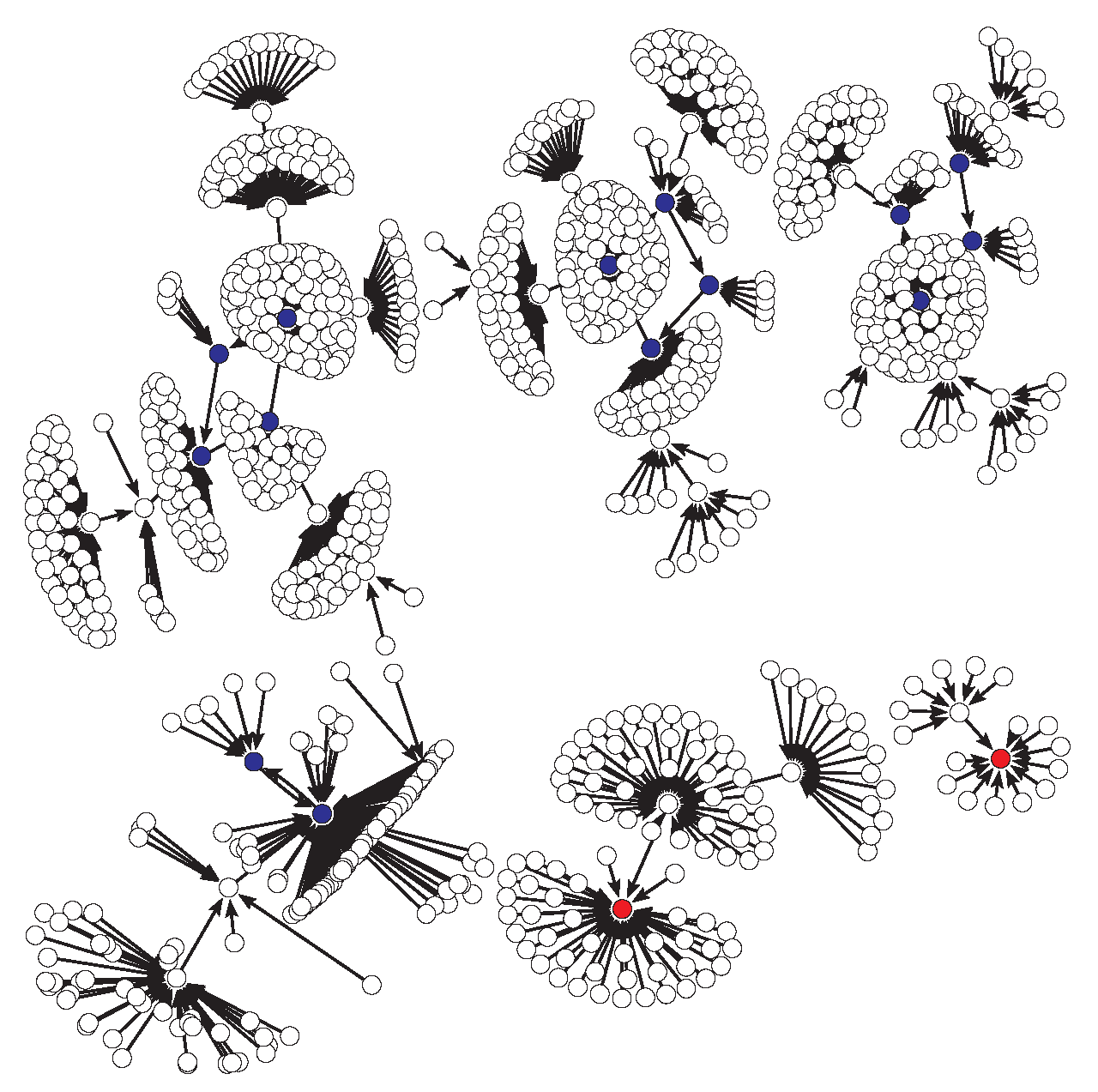
4. Results: Dynamical Robustness of the Original and Reduced Models
4.1. Dynamical Robustness of the Original Model
4.1.1. Cases 1, 2 and 3 for the Original Model
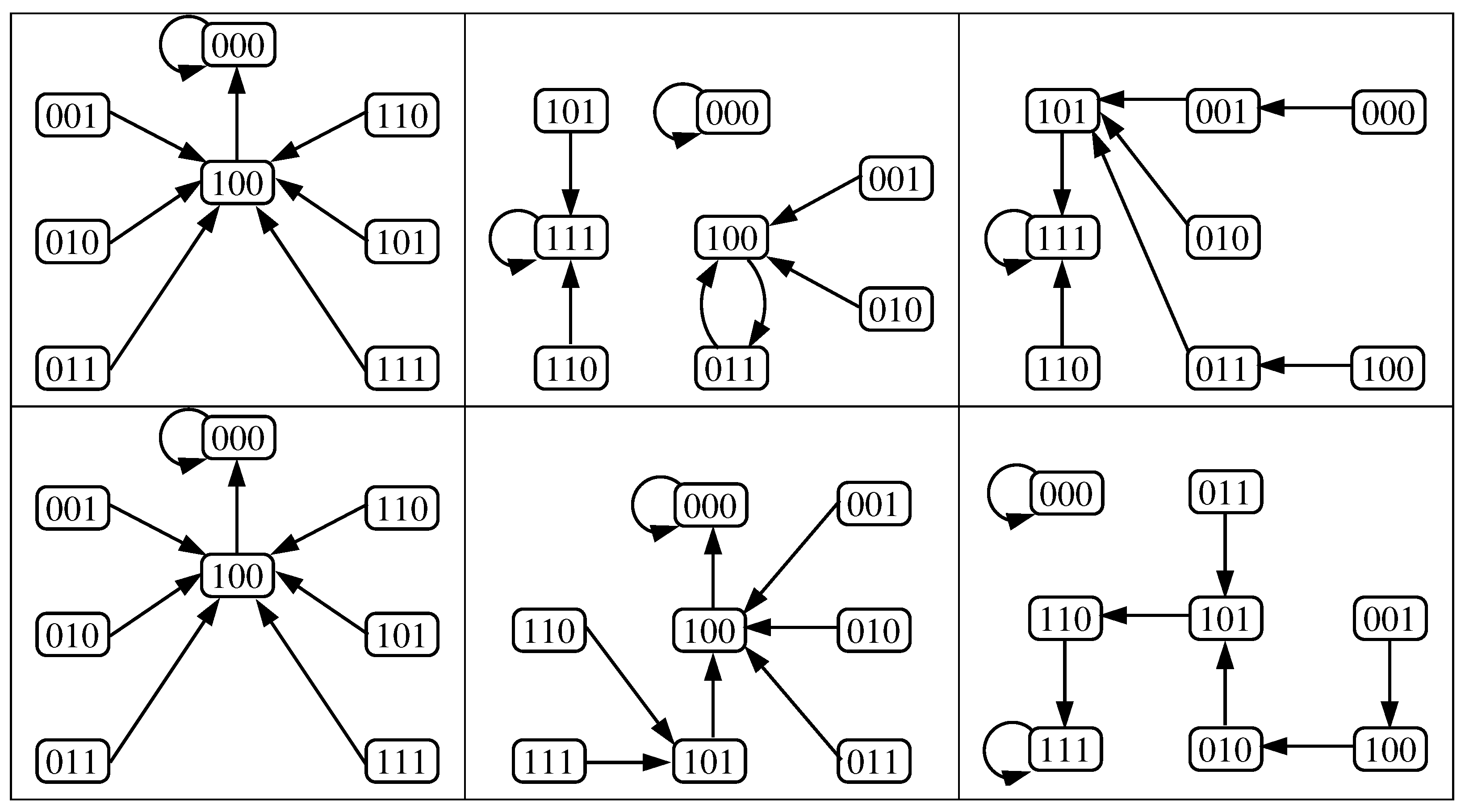
4.1.2. Case 4 for the Original Model
4.2. Dynamical Robustness of the Reduced Model
4.2.1. Cases 1, 2 and 3 for the Reduced Model
4.2.2. Case 4 for the Reduced Model
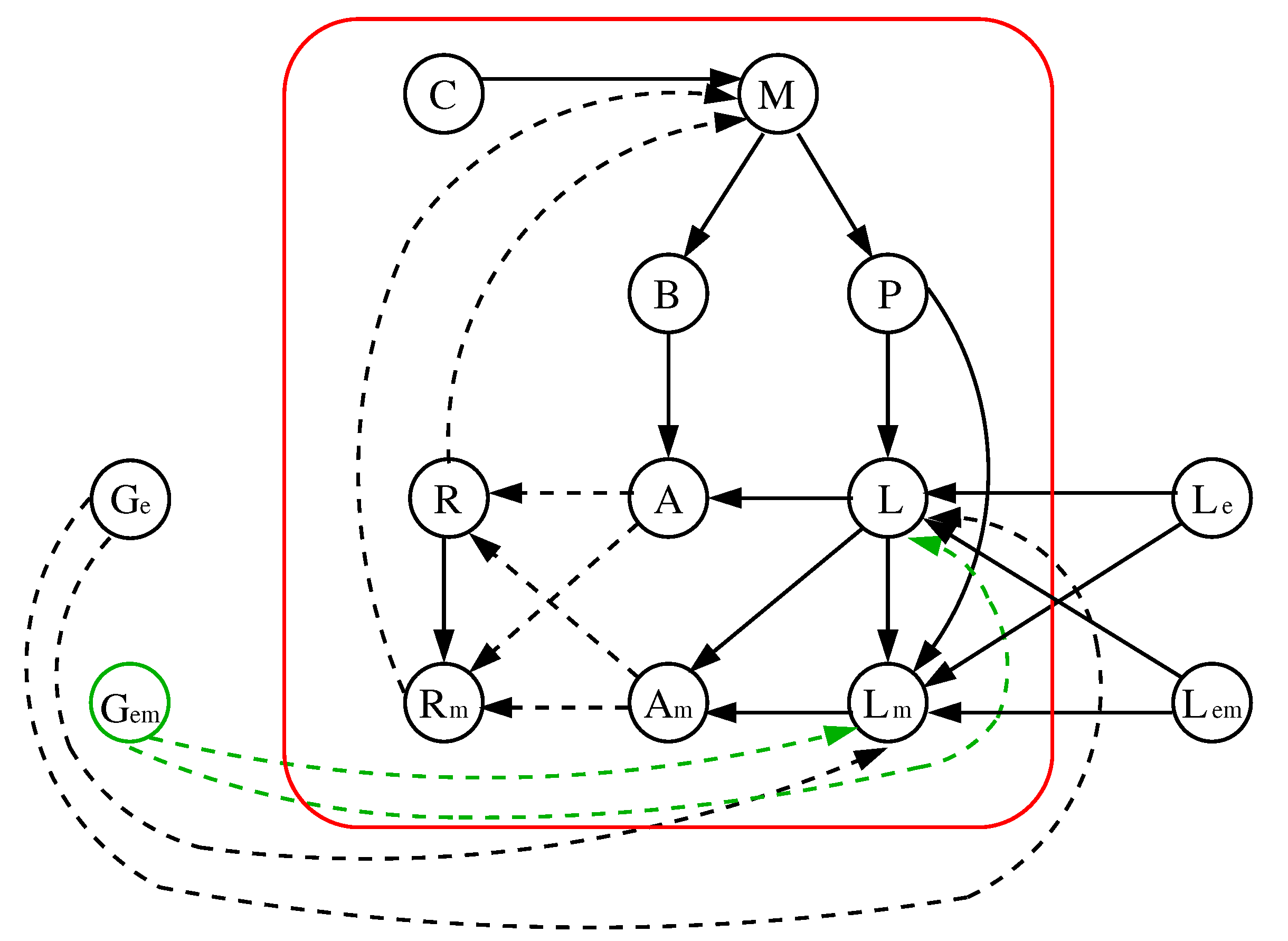
5. Alternative Improvements for the Studied Models
5.1. Improvement 1: The Original and Reduced Models Match in All 6 Parameter Combinations with Ozbudak et al., 2004
- (1)
- Bistability: when .
- (2)
- OFF: when .
- (3)
- ON: when .
5.2. Improvement 2: (Improved) Original Model Extended to 9 Parameters
6. Conclusions
- For the first 3 cases described in Section 3.2 and that included 5 of the 6 combinations of parameters allowed in the original and reduced models, we establish two Propositions proving the non-existence of any limit cycle, whatever the update schedule used.
- For the case 4, where bistability appears, we made an exhaustive analysis of all its possible dynamics generated with any update schedule. Here we detail for both models the average sizes of their attraction basins, the number of dynamics without limit cycles (i.e., only with fixed points) and the number of dynamics with limit cycles (being less than 30% in both models).
- Again in the case 4, its predominant attractor (those that have the bigger attraction basin), changes dramatically; OFF attraction basin being, in average, 8 times bigger than that of ON for the original model while that in the reduced one, the ON basin is almost 2 times bigger than that of OFF.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Novick, A.; Weiner, M. Enzyme induction as an all-or-none phenomenon. Proc. Natl. Acad. Sci. USA 1957, 43, 553. [Google Scholar] [CrossRef] [PubMed]
- Cohn, M.; Horibata, K. Inhibition by glucose of the induced synthesis of the β-galactoside-enzyme system of Escherichia coli. Analysis of maintenance. J. Bacteriol. 1959, 78, 601. [Google Scholar] [CrossRef] [PubMed]
- Jacob, F.; Monod, J. Genetic regulatory mechanisms in the synthesis of proteins. J. Mol. Biol. 1961, 3, 318–356. [Google Scholar] [CrossRef]
- Griffith, J. Mathematics of cellular control processes II. Positive feedback to one gene. J. Theor. Biol. 1968, 20, 209–216. [Google Scholar] [CrossRef]
- Monod, J.; Pappenheimer, A., Jr.; Cohen-Bazire, G. La cinétique de la biosynthèse de la β-galactosidáse chez E. coli considérée comme fonction de la croissance. Biochim. Biophys. Acta 1952, 9, 648–660. [Google Scholar] [CrossRef]
- Deutscher, J. The mechanisms of carbon catabolite repression in bacteria. Curr. Opin. Microbiol. 2008, 11, 87–93. [Google Scholar] [CrossRef]
- Ozbudak, E.M.; Thattai, M.; Lim, H.N.; Shraiman, B.I.; Van Oudenaarden, A. Multistability in the lactose utilization network of Escherichia coli. Nature 2004, 427, 737–740. [Google Scholar] [CrossRef] [PubMed]
- Jenkins, A.; Macauley, M. Bistability and Asynchrony in a Boolean Model of the L-arabinose Operon in Escherichia coli. Bull. Math. Biol. 2017, 79, 1778–1795. [Google Scholar] [CrossRef]
- De Jong, H. Modeling and simulation of genetic regulatory systems: A literature review. J. Comput. Biol. 2002, 9, 67–103. [Google Scholar] [CrossRef] [PubMed]
- Albert, R. Boolean modeling of genetic regulatory networks. In Complex Networks; Springer: Berlin/Heidelberg, Germay, 2004; pp. 459–481. [Google Scholar]
- Albert, R.; Othmer, H.G. The topology of the regulatory interactions predicts the expression pattern of the segment polarity genes in Drosophila melanogaster. J. Theor. Biol. 2003, 223, 1–18. [Google Scholar] [CrossRef]
- Mendoza, L.; Xenarios, I. A method for the generation of standardized qualitative dynamical systems of regulatory networks. Theor. Biol. Med. Model. 2006, 3, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.S.; Saadatpour, A.; Albert, R. Boolean modeling in systems biology: An overview of methodology and applications. Phys. Biol. 2012, 9, 055001. [Google Scholar] [CrossRef]
- Chaves, M.; de Jong, H. Qualitative Modeling, Analysis and Control of Synthetic Regulatory Circuits. In Synthetic Gene Circuits; Humana: New York, NY, USA, 2021; pp. 1–40. [Google Scholar]
- Silva-Rocha, R.; de Lorenzo, V. The TOL network of P seudomonas putida mt-2 processes multiple environmental inputs into a narrow response space. Environ. Microbiol. 2013, 15, 271–286. [Google Scholar] [CrossRef] [PubMed]
- Timmermann, T.; González, B.; Ruz, G.A. Reconstruction of a gene regulatory network of the induced systemic resistance defense response in Arabidopsis using boolean networks. BMC Bioinform. 2020, 21, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Offermann, B.; Knauer, S.; Singh, A.; Fernández-Cachón, M.L.; Klose, M.; Kowar, S.; Busch, H.; Boerries, M. Boolean modeling reveals the necessity of transcriptional regulation for bistability in PC12 cell differentiation. Front. Genet. 2016, 7, 44. [Google Scholar] [CrossRef]
- Richard, A.; Rossignol, G.; Comet, J.P.; Bernot, G.; Guespin-Michel, J.; Merieau, A. Boolean models of biosurfactants production in Pseudomonas fluorescens. PLoS ONE 2012, 7, e24651. [Google Scholar] [CrossRef] [PubMed]
- Kothamachu, V.B.; Feliu, E.; Cardelli, L.; Soyer, O.S. Unlimited multistability and Boolean logic in microbial signalling. J. R. Soc. Interface 2015, 12, 20150234. [Google Scholar] [CrossRef] [PubMed]
- Veliz-Cuba, A.; Stigler, B. Boolean models can explain bistability in the lac operon. J. Comput. Biol. 2011, 18, 783–794. [Google Scholar] [CrossRef] [PubMed]
- Aracena, J.; Demongeot, J.; Fanchon, E.; Montalva, M. On the number of update digraphs and its relation with the feedback arc sets and tournaments. Discret. Appl. Math. 2013, 161, 1345–1355. [Google Scholar] [CrossRef]
- Aracena, J.; Demongeot, J.; Fanchon, E.; Montalva, M. On the number of different dynamics in Boolean networks with deterministic update schedules. Math. Biosci. 2013, 242, 188–194. [Google Scholar] [CrossRef]
- Santillán, M.; Mackey, M.C. Influence of catabolite repression and inducer exclusion on the bistable behavior of the lac operon. Biophys. J. 2004, 86, 1282–1292. [Google Scholar] [CrossRef][Green Version]
- Cohn, M. Contributions of studies on the β-galactosidase of Escherichia coli to our understanding of enzyme synthesis. Bacteriol. Rev. 1957, 21, 140. [Google Scholar] [CrossRef] [PubMed]
- Görke, B.; Stülke, J. Carbon catabolite repression in bacteria: Many ways to make the most out of nutrients. Nat. Rev. Microbiol. 2008, 6, 613–624. [Google Scholar] [CrossRef] [PubMed]
- Narang, A. cAMP does not have an important role in carbon catabolite repression of the Escherichia coli lac operon. Nat. Rev. Microbiol. 2009, 7, 250. [Google Scholar] [CrossRef] [PubMed]
- Narang, A. Quantitative effect and regulatory function of cyclic adenosine 5’-phosphate in Escherichia coli. J. Biosci. 2009, 34, 445–463. [Google Scholar] [CrossRef] [PubMed]
- Crasnier-Mednansky, M. Is there any role for cAMP–CRP in carbon catabolite repression of the Escherichia coli lac operon? Nat. Rev. Microbiol. 2008, 6, 954. [Google Scholar] [CrossRef] [PubMed]
- Notley-McRobb, L.; Death, A.; Ferenci, T. The relationship between external glucose concentration and cAMP levels inside Escherichia coli: Implications for models of phosphotransferase-mediated regulation of adenylate cyclase. Microbiology 1997, 143, 1909–1918. [Google Scholar] [CrossRef][Green Version]
- Bettenbrock, K.; Sauter, T.; Jahreis, K.; Kremling, A.; Lengeler, J.W.; Gilles, E.D. Correlation between growth rates, EIIACrr phosphorylation, and intracellular cyclic AMP levels in Escherichia coli K-12. J. Bacteriol. 2007, 189, 6891–6900. [Google Scholar] [CrossRef]
- Wanner, B.L.; Kodaira, R.; Neidhardt, F.C. Regulation of lac operon expression: Reappraisal of the theory of catabolite repression. J. Bacteriol. 1978, 136, 947–954. [Google Scholar] [CrossRef]
- Inada, T.; Kimata, K.; Aiba, H. Mechanism responsible for glucose–lactose diauxie in Escherichia coli: Challenge to the cAMP model. Genes Cells 1996, 1, 293–301. [Google Scholar] [CrossRef]
- Kimata, K.; Takahashi, H.; Inada, T.; Postma, P.; Aiba, H. cAMP receptor protein–cAMP plays a crucial role in glucose–lactose diauxie by activating the major glucose transporter gene in Escherichia coli. Proc. Natl. Acad. Sci. USA 1997, 94, 12914–12919. [Google Scholar] [CrossRef] [PubMed]
- Goles, E.; Montalva, M.; Ruz, G.A. Deconstruction and dynamical robustness of regulatory networks: Application to the yeast cell cycle networks. Bull. Math. Biol. 2013, 75, 939–966. [Google Scholar] [CrossRef] [PubMed]
- Ruz, G.A.; Goles, E.; Montalva, M.; Fogel, G.B. Dynamical and topological robustness of the mammalian cell cycle network: A reverse engineering approach. Biosystems 2014, 115, 23–32. [Google Scholar] [CrossRef]
- Ruivo, E.L.; Montalva-Medel, M.; de Oliveira, P.P.; Perrot, K. Characterisation of the elementary cellular automata in terms of their maximum sensitivity to all possible asynchronous updates. Chaos Solitons Fractals 2018, 113, 209–220. [Google Scholar] [CrossRef]
- Perrot, K.; Montalva-Medel, M.; De Oliveira, P.P.; Ruivo, E.L. Maximum sensitivity to update schedules of elementary cellular automata over periodic configurations. Nat. Comput. 2020, 19, 51–90. [Google Scholar] [CrossRef]
- Ruivo, E.L.; Balbi, P.P.; Montalva-Medel, M.; Perrot, K. Maximum sensitivity to update schedules of elementary cellular automata over infinite configurations. Inf. Comput. 2020, 274, 104538. [Google Scholar] [CrossRef]
- Goles, E.; Montalva-Medel, M.; Maclean, S.; Mortveit, H. Block Invariance in a Family of Elementary Cellular Automata. J. Cell. Autom. 2018, 13, 15–32. [Google Scholar]
- Goles, E.; Montalva-Medel, M.; Mortveit, H.; Ramirez-Flandes, S. Block invariance in elementary cellular automata. J. Cell. Autom. 2015, 10, 119–135. [Google Scholar]
- MacLean, S.; Montalva-Medel, M.; Goles, E. Block invariance and reversibility of one dimensional linear cellular automata. Adv. Appl. Math. 2019, 105, 83–101. [Google Scholar] [CrossRef]
- Santillán, M. Bistable behavior in a model of the lac operon in Escherichia coli with variable growth rate. Biophys. J. 2008, 94, 2065–2081. [Google Scholar] [CrossRef]
- Santillán, M.; Mackey, M.C. Quantitative approaches to the study of bistability in the lac operon of Escherichia coli. J. R. Soc. Interface 2008, 5, S29–S39. [Google Scholar] [CrossRef] [PubMed]
- Veening, J.W.; Smits, W.K.; Kuipers, O.P. Bistability, epigenetics, and bet-hedging in bacteria. Annu. Rev. Microbiol. 2008, 62, 193–210. [Google Scholar] [CrossRef] [PubMed]
- Jack, J.; Wambaugh, J.F.; Shah, I. Simulating quantitative cellular responses using asynchronous threshold Boolean network ensembles. BMC Syst. Biol. 2011, 5, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Samaga, R.; Klamt, S. Modeling approaches for qualitative and semi-quantitative analysis of cellular signaling networks. Cell Commun. Signal. 2013, 11, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Wittmann, D.M.; Krumsiek, J.; Saez-Rodriguez, J.; Lauffenburger, D.A.; Klamt, S.; Theis, F.J. Transforming Boolean models to continuous models: Methodology and application to T-cell receptor signaling. BMC Syst. Biol. 2009, 3, 1–21. [Google Scholar] [CrossRef] [PubMed]


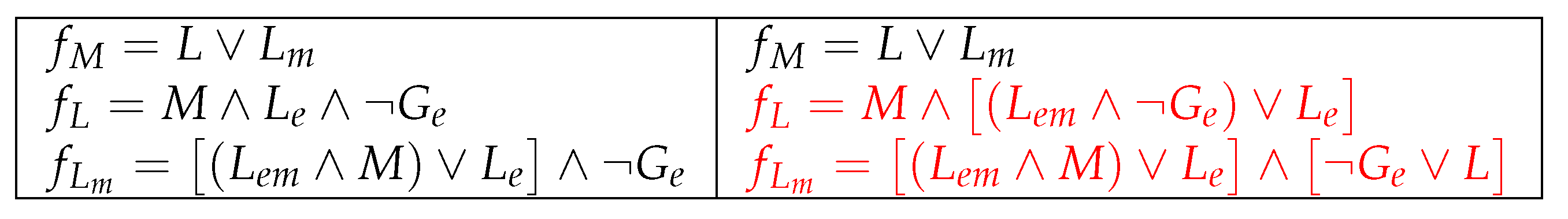

| Glucose | |||
|---|---|---|---|
| Lactose | |||
| Low: | |||
| Medium: | |||
| High: | |||
| Attractor | OFF | ON | |
|---|---|---|---|
| Case | |||
| 1: | 1024 | 0 | |
| 2: | 1024 | 0 | |
| 3: | 0 | 1024 | |
| Case 4: (Bistability) | |||
|---|---|---|---|
| Attractors | |||
| OFF | 684.7 | 908.9 | 153.7 |
| ON | 124.4 | 115.1 | 146.5 |
| Limit cycles | 214.9 | 0 | 723.8 |
| Total | 1024 | 1024 | 1024 |
| Attractor | OFF | ON | |
|---|---|---|---|
| Case | |||
| 1: | 8 | 0 | |
| 2: | 8 | 0 | |
| 3: | 0 | 8 | |
| Case 4: (Bistability) | |||
|---|---|---|---|
| Attractors | |||
| OFF | 2.5 | 2.8 | 1.3 |
| ON | 4.6 | 5.2 | 2.7 |
| Limit cycles | 0.9 | 0 | 4 |
| Glucose | |||
|---|---|---|---|
| Lactose | |||
| Low: | OFF | OFF | |
| Medium: | Bistability | OFF | |
| High: | ON | Bistability | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montalva-Medel, M.; Ledger, T.; Ruz, G.A.; Goles, E. Lac Operon Boolean Models: Dynamical Robustness and Alternative Improvements. Mathematics 2021, 9, 600. https://doi.org/10.3390/math9060600
Montalva-Medel M, Ledger T, Ruz GA, Goles E. Lac Operon Boolean Models: Dynamical Robustness and Alternative Improvements. Mathematics. 2021; 9(6):600. https://doi.org/10.3390/math9060600
Chicago/Turabian StyleMontalva-Medel, Marco, Thomas Ledger, Gonzalo A. Ruz, and Eric Goles. 2021. "Lac Operon Boolean Models: Dynamical Robustness and Alternative Improvements" Mathematics 9, no. 6: 600. https://doi.org/10.3390/math9060600
APA StyleMontalva-Medel, M., Ledger, T., Ruz, G. A., & Goles, E. (2021). Lac Operon Boolean Models: Dynamical Robustness and Alternative Improvements. Mathematics, 9(6), 600. https://doi.org/10.3390/math9060600






