1. Introduction
Statistical Inference with spatial data requires to take into consideration a strong possibility of spatial dependency. In case of observations corresponding to the realization of a point process, the available data can be either point spatial locations or counts of points in spatial units [
1,
2]. These authors developed the mathematical theory of point processes which are used in many areas for describing event occurrences, like earthquakes, accidents, pest infestations, disease appearances, neuronal spikes, and many other situations [
3,
4,
5,
6,
7]. Thus, a wide range of scientific applications can be cited, for example: ecology, epidemiology, geology, forestry, neurophysiology. De Oliveira [
8] described a class of models for geostatistical count data generalizing the class proposed by Diggle et al., in 1998 [
9]. Diggle [
10] discussed about different spatial and spatio-temporal point process models, along with marked and multivariate counting processes. Wakefield [
11] presented a critical review of spatial count data analysis methods for either disease mapping or spatial regression. He emphasizes the importance of the nature of variability in spatial risk and the fact that models must account for both spatial and non-spatial variability. Ickstadt and Wolpert [
12] introduced a class of Bayesian hierarchical spatial models taking into account dependence on unobserved or unreported covariates. Examples and illustrations of state-of-the art developments in statistics for spatial data are presented in Cressie [
13] with focus on lattice data, geostatistical data and point patterns. Sain and Cressie [
14] emphasize that incorporating general forms of correlation is important in building spatial models for lattice data. Our goal is to consider Gamma-distributed effects which are spatially correlated. Given this constraint of marginal Gamma distributions, joint laws allowing such marginal properties, along with spatial dependence, are rare. This is the reason why we use the copula theory which allows both marginal laws and spatial dependence or spatial effects [
15]. A spatial copula as defined in Durocher et al. [
16] provide a full probabilistic model. Conversely, a covariance function describes only the covariance between marginal distributions except in the case of a multivariate Gaussian distribution which is fully specified by its expectation and covariance matrix.
In this paper, we consider count observations from a doubly stochastic Poisson process also called Cox process [
8,
17,
18,
19,
20] on a measured space
and driven by a random measure
such that there exists a positive random field
verifying:
is the process intensity with respect to the reference measure
. Its state space is
and
denotes its intensity measure. For example,
can be the Lebesgue measure or a counting measure for individuals at risks.
The idea behind the model based on a Cox process is that environmental heterogeneity can generate overdispersion but also dependency. The counting measure
N associated with such a Cox process verifies:
which means that, conditionally to
, the count
follows the Poisson distribution with parameter
.
A well known result on doubly stochastic Poisson process is that stochasticity on
generates overdispersion: for any element
B of
such that
and
, the dispersion index is
If
is not a proper random variable or in other terms if
, then the dispersion index is equal to unity, what corresponds to a standard Poisson process. It is worth pointing out that modeling a Cox process is equivalent to modeling either its intensity
or its driving measure
. For example, Wolpert and Ickstadt [
21] constructed
as a linear combination of location-specific attributes and a kernel mixture measure associated with an independent-increment infinitely divisible random measure.
The general model studied in this paper is as follows. We assume that
has a finite
n-partition
and:
where
is a positive random variable, and
stands for the indicator function of
. We denote by
the random vector of
q covariates at point
x and by
the positive link function defined on
and parameterized by
. Therefore,
Z is a random field taking values in a
q-dimensional space and can not be observed entirely in practice. However we assume that for a given sampling unit, we have relevant summaries providing information on the Cox process. The unknown parameter
belongs to
with
and has to be estimated from observations of the Cox process and its
q covariate summaries. Our aim is to present tools for statistical inference with data from the counting measure associated with a Cox process which intensity function given by Equation (
3), along with partial observations of its spatial covariates. This inference is on
and also about the
parameters.
It should be noted that we consider count data derived from a stratified sampling procedure [
22], whereas, in the literature, for each stratum
, complete observations are available for the count measure and for the covariates [
11], particularly for disease mapping [
23]. We are, therefore, interested in a situation encountered in practice where the observations in each stratum are partial and carried out across sampling units. Furthermore, the spatial effects
are not necessarily mutually independent. Such a spatial correlation can be modeled by means of copula functions: Xue-Kun Song [
24] presented a class of multivariate dispersion models based on multivariate Gaussian copula, Masarotto [
25] identified Gaussian copula models for marginal regression analysis, Krupskii and Genton [
26] proposed copula models for spatial data repeatedly observed in time, and Lee [
27] developed a copula-based model for multisite precipitation occurrences.
In
Section 2, distributional properties of the counting measure
N are presented. A set of sampling units is considered in
Section 3 with general features met in practice: the units are disjoint and entirely included in one of the partition elements
. Firstly, the expressions of the likelihood conditional on the covariate field
Z and the effect
are provided. Following Wakefield [
11], spatially correlated log-normal effects are considered. This leads to observed counts in sampling units following the multivariate Poisson-log normal distribution [
28]. Secondly, we show that the joint distribution of counts in the sampling units for each
is negative multinomial when the effects are gamma-distributed, and also that correlated gamma-distributed effects lead to dependent negative multinomial counts. Spatial correlations between effects are taken into account by means of Gaussian copula associated with Gamma distributed margins. In
Section 4, the focus is on estimating the model parameters. In some situations, closed-form estimators may be obtained, but it is generally not the case. Likelihood inference can be performed when the effects are independent. Otherwise, a Markov chain Monte Carlo (MCMC) procedure is proposed in order to perform Bayesian inference [
29]. An illustration is provided in
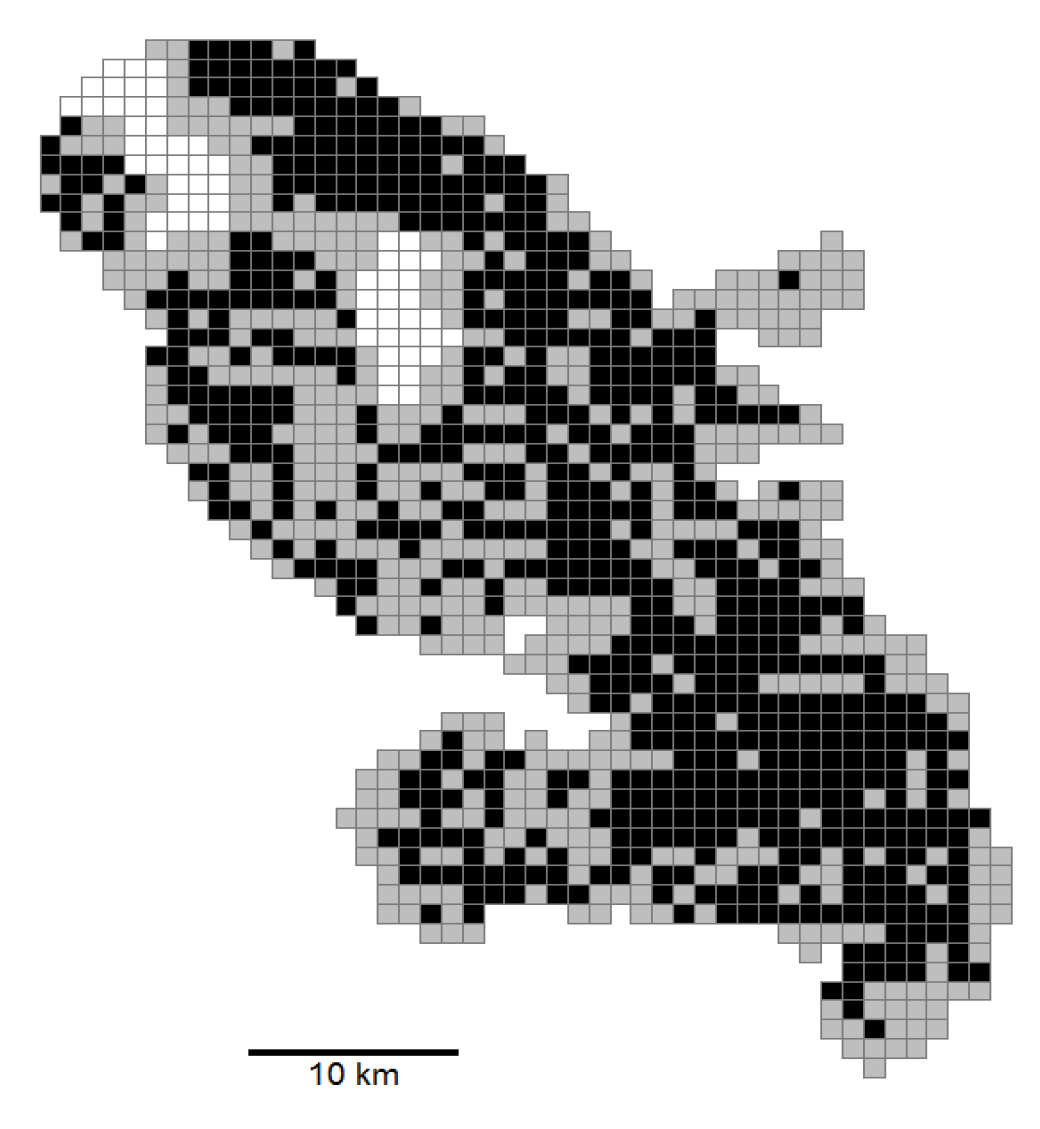
Section 5 from BLSD data collected in Martinique Island within a network coordinated by the DAAL (Direction de l’Alimentation, de l’Agriculture et de la Forêt) and the FREDON Martinique (Fédération REgionale de Défense contre les Organismes Nuisibles de la Martinique).
2. Distributional Properties
In this section, we present the distributional properties associated with the counting measure N. These properties conditional on covariate vector Z give an idea of the dependency between the different spatial zones considered.
For any
B in
, let us write
Here, the random measure depends on Z only through its restricted random field on B.
The following proposition gives the expected number of points conditional on Z and :
Proposition 1. Let N be the counting measure associated with the point process in which intensity is given by Equation (3); then, Proof of Proposition 1. For any element
B of
, we have
which shows (
5). □
We have the following results about count correlation:
Proposition 2. Consider the counting measure N associated with the point process defined by Equation (3). For any ( in , the following equality holds: Proof of Proposition 2. From the covariance decomposition formula, we get
Since
N is a Cox process, the second term of the right-hand side of the above equation is equal to zero so that Equation (
5) leads to
and also to the final result. □
Corollary 1. Consider the counting measure N associated with the point process defined by Equation (3) and assume the are independent conditionally to Z. For any couple in , Proof of Corollary 1. From Proposition 2 and conditional independence, whenever any distinct in J, we get , and the final result follows. □
Corollary 2. Consider the counting measure N associated with the point process defined by Equation (3) and assume the spatial effect variables are mutually independent. Let and be two elements of . If , with , and , then Proof of Corollary 2. From corollary 1, the result is straightforward. □
Corollary 3. Let and be two elements of . If there exists j in J, such that , then Proof of Corollary 3. Both and are subsets of . Therefore, Proposition 2 give us the final result. □
It is worth noticing that, in the case where is a non-degenerate random variable conditional on Z, then , which implies that .
3. Sampling Theory Results
In this section, we consider a set of sampling units such that:
(C1) ,
(C2) ,
(C3) .
Condition (C3) means that there is no overlapping sampling units. When these three conditions are verified, we have the following results about the likelihood from the model defined by Equation (
3).
Proposition 3. Let be a sample verifying conditions (C1), (C2), and (C3). For the model defined by Equation (3), if the joint distribution of admits a probability density function g parameterized by β, then the conditional likelihood on for with respect to the counting measure N and denoted by is equal toIt is worth noticing that this likelihood is conditional on Z. Proof of Proposition 3. Since condition (C2) is verified, then . Therefore, conditionally to and Z, the count is distributed according to the Poisson law . Furthermore, the are independent conditionally to the . □
The likelihood given in Proposition 3 is useful for Bayesian approach when prior information on are available, as well as sampling algorithms for augmented data. In practice, the are not observed. Consequently, the likelihood techniques are based on count observations only. The following corollary provides such a likelihood:
Corollary 4. Let be a sample verifying conditions (C1), (C2), and (C3), if the joint distribution of admits a probability density function g parameterized by β, then the unconditional likelihood for with respect to the counting measure N and denoted by is equal to Proof of Corollary 4. The result is straightforward from Proposition 3. □
Many distributions can be used for the joint probability law of
which has to be considered as a mixing distribution in the framework of Poisson mixtures [
30]. In the case where this joint probability law is a multivariate log-normal distribution
with
and
a square matrix or order
n, then the probability density function
g is such that:
where
and
n is the cardinality of
J.
Following Wakefield [
11], for any
j in
J, we can write
, where the
are independent identically distributed according to
corresponding to non spatial contribution to overdispersion. On the other hand, the
are spatial contributions associated with a distance
d on
such that
follows a multivariate normal distribution with
, where
and
are the centroids of
and
, respectively. Consequently,
so that parameter
stands for the correlation between
and
if
. We assume that
. Therefore, in Equation (
8),
is the null vector of
, and matrix
has each diagonal element equal to
, whereas element on line
j and column
k equal to
. In the case where the mixture distribution is a multivariate log-normal distribution, Equations (
7) and (
8) provide tools for statistical analysis of counts in sampling units similarly to Aitchison and Ho [
28].
An other choice of law for the effect
is the Gamma distribution with two parameters
and
, where
is its expectation, and
the shape parameter. Equation (
9) gives its density function. It is worth noticing that several parameterizations can be met in the literature. We have the following theorem:
Theorem 1. Let the random measurebe as in Equation (4). For any element j of J, andelements ofverifying conditions (C2) and (C3), if we assume thatfollows a Gamma distributionwith density functiongiven by:then: - (i)
follows a multinomial negative distribution,
- (ii)
- (iii)
For two distinct elements i andof, the following equality holds:
Proof of Theorem 1. Using the probability generating function of , along with the moment generating function of , leads us to the result.
In fact, for any
j in
J, if we write
, then the probability generating function of
conditionally to
and
Z at any point
of
is:
Therefore, the probability generating function of
conditional on
Z is such that:
where
stands for the moment generating function of
.
Since
, then
so that
conditional on
Z follows a multinomial negative distribution with parameters
.
and The first derivative of with respect to at point 1 gives us . The second derivatives of provide in a similar manner the second moments associated with . □
Proposition 4. Let be a sample verifying conditions (C1), (C2), and (C3). Assume the random variables are mutually independent and distributed according to as defined by Equation (9). Writing , then the likelihood for with respect to the counting measure N and is equal towith , and . Proof of Proposition 4. Let
be a random variable on probability space
. Let
be an element of
. Since the
are independent,
Moreover, each random variable
,
, follows a Gamma distribution. From (i) in Theorem 1,
follows a multinomial negative distribution, and we get
with
. □
In Proposition 4, we assume that the
are independent. Nevertheless, we can consider the case where
follows a multivariate Gamma distribution. We can refer to Kotz et al. [
31] (Chapter 48) for an overview of multivariate Gamma distributions. We can also refer to Rahayu et al. [
32] for statistical applications with multivariate Gamma distributions. In such a case of dependent univariate Gamma distributions, the result in Theorem 1 still holds so that we now have dependent negative multinomial counts. Thus, Equations (
6) and (
7) provide the conditional and unconditional likelihoods provided that we know the joint density function
g of the
. The following proposition provides a joint gamma distribution for the effects
taking into account their spatial correlation.
Proposition 5. Let be a sample verifying conditions (C1), (C2), and (C3). For the model defined by Equation (3), if follows a multivariate gamma distribution with joint density g parameterized by and spatial correlation given by a copula density c, then the conditional likelihood on , for with respect to the counting measure N and iswhere is the cumulative distribution function of , and is given by Equation (9). ρ stands for the copula density parameter. Proof of Proposition 5. The joint density g is the product of the marginal densities multiplied by the copula density c. Consequently, . Proposition 3 leads to the final result. □
In the case where the copula density is constant equal to 1, the
are independent and expression (
10) holds. In the sequel, we will use a multivariate gaussian copula [
24] so that the correlation
between two effects
and
depends on the distance
between centroids:
where
,
is the inverse of the standard normal probability distribution function, and
with .
The greater is, the higher the dependency between effects is. The greater the distance is between and , the lower is the dependency between effects and .
Note that Lee [
27] has shown that, in the case of a bivariate Gaussian copula with gamma margins,
cannot be resolved analytically but numerically.