Analytical Solutions of Upper Convected Maxwell Fluid with Exponential Dependence of Viscosity under the Influence of Pressure
Abstract
:1. Introduction
2. Presentation of the Problem
3. Exact Expressions for the Dimensionless Velocity and Shear Stress Fields
3.1. Calculation of the Velocity Field
3.2. Calculation of the Velocity Field
3.3. Calculation of the Shear Stress
3.4. Calculation of the Shear Stress
4. Limiting Cases
4.1. Case (Lower Plate Applies an Exponential Shear Stress to the Fluid)
4.2. Case (Flows of Ordinary Incompressible UCM Fluids)
4.3. Case (Flows of Incompressible Newtonian Fluids with Exponential Dependence of Viscosity on the Pressure)
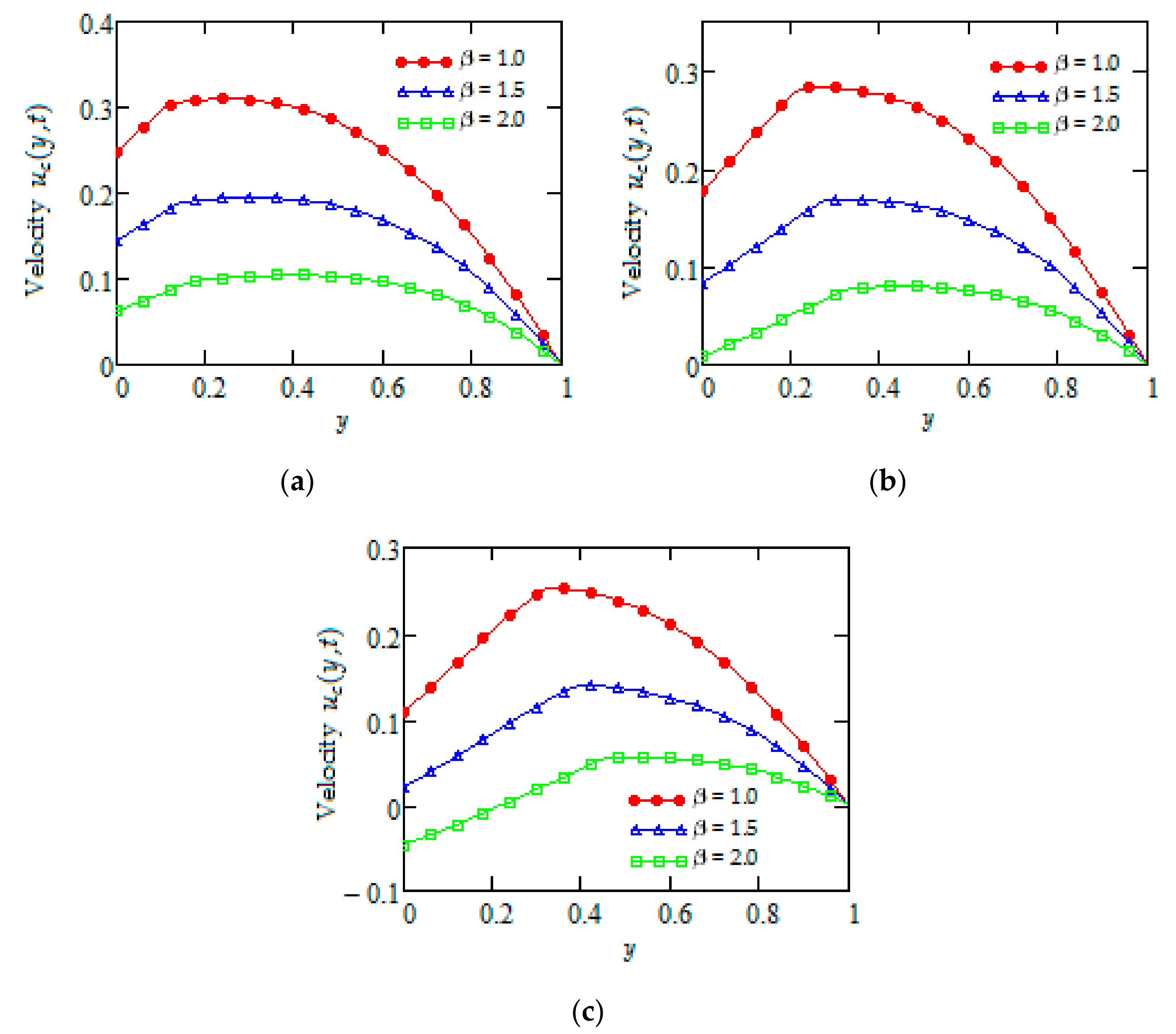
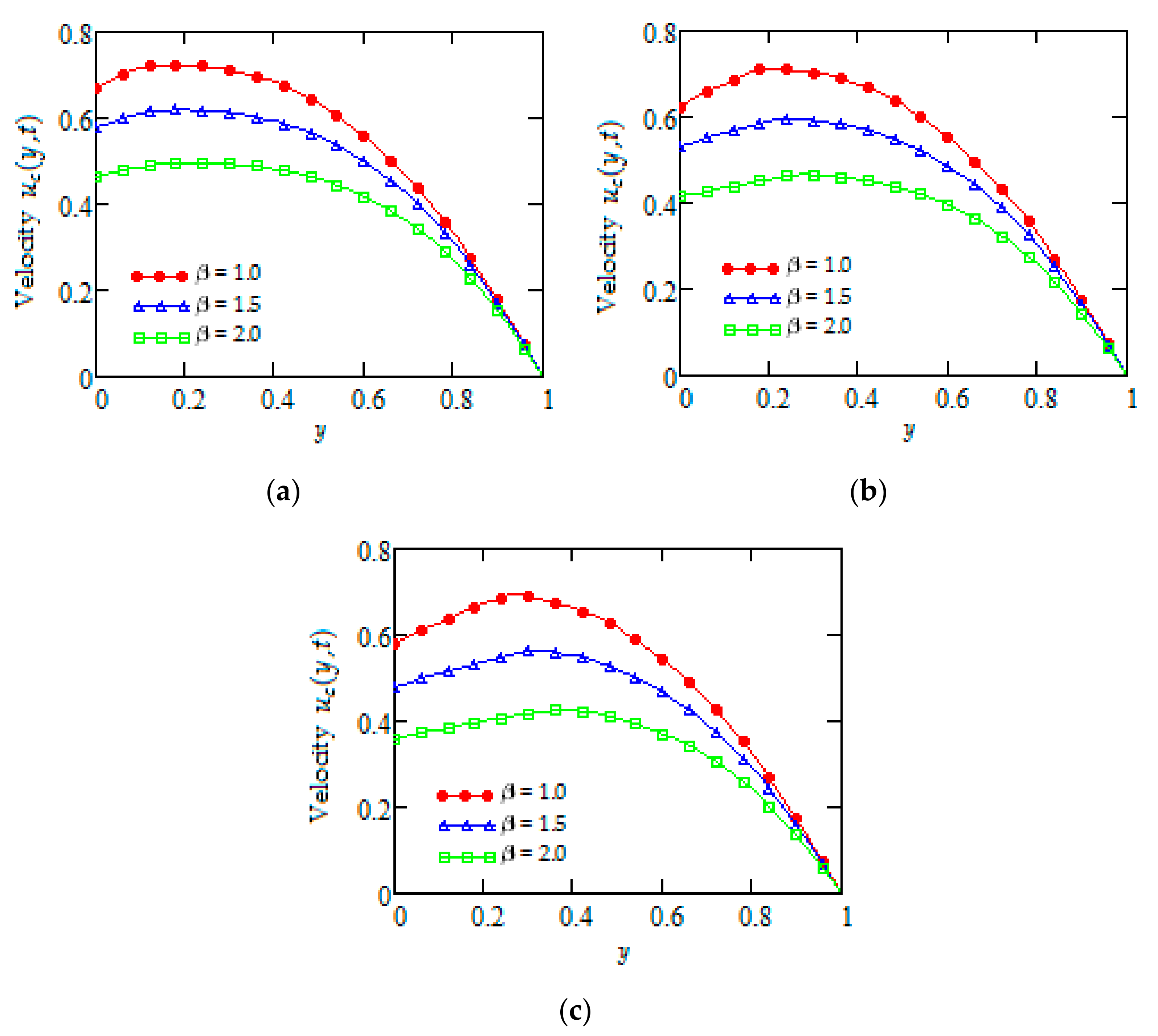
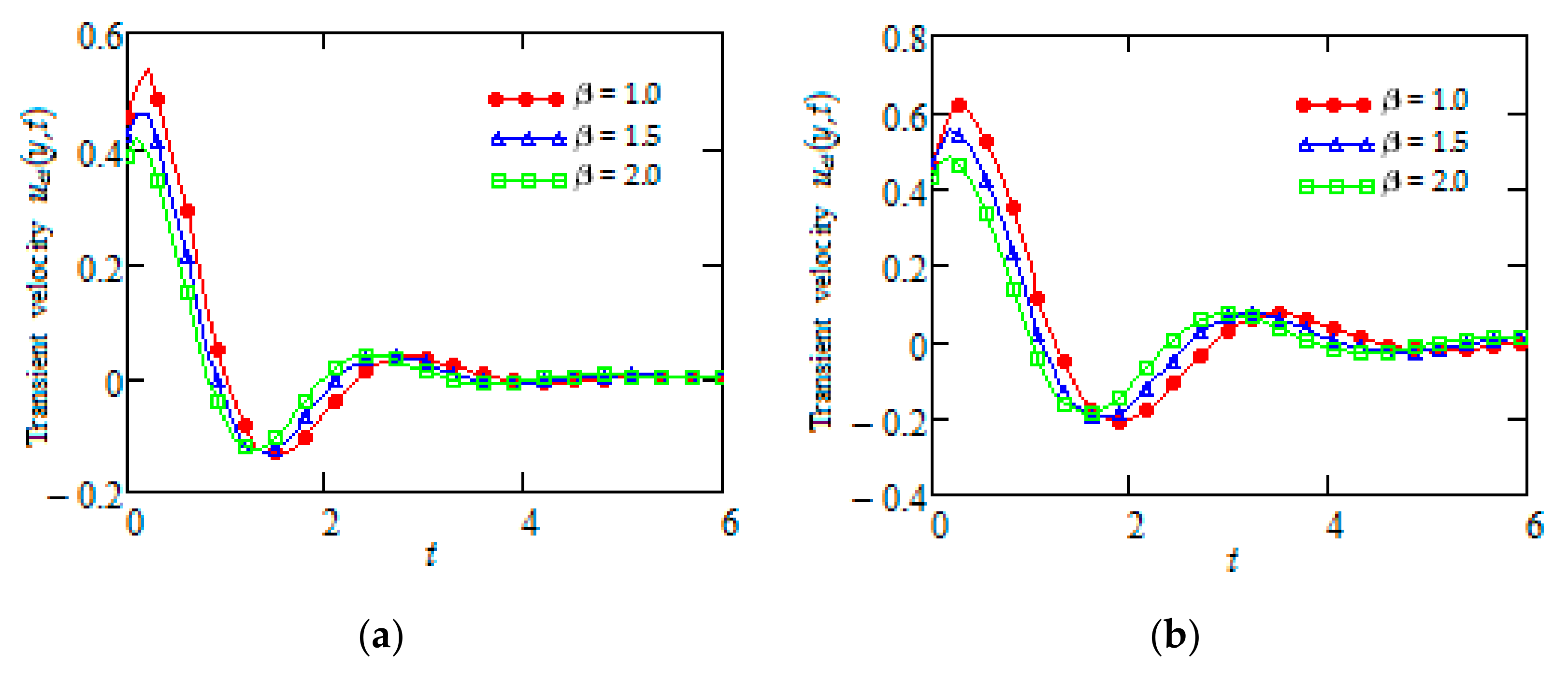
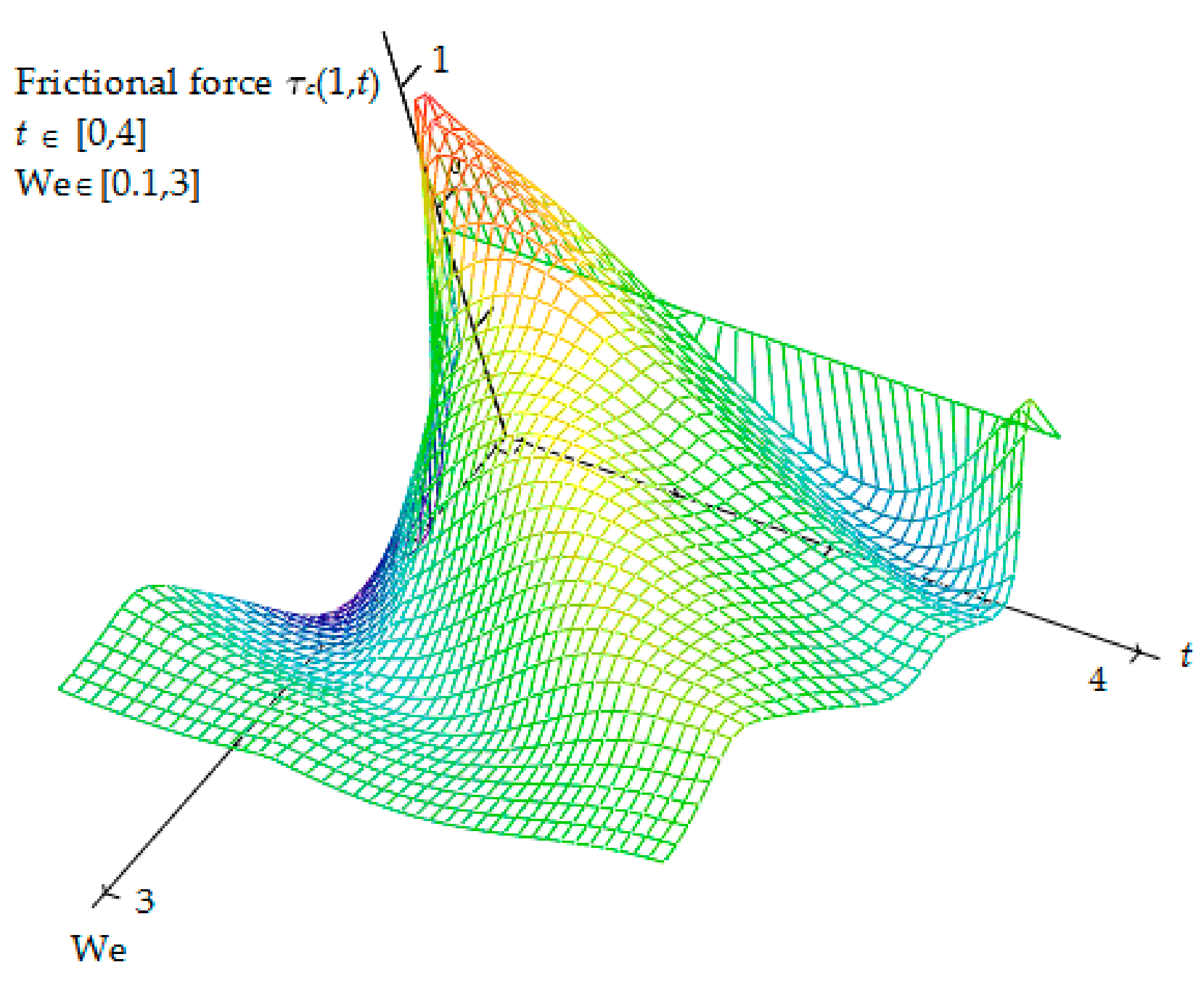
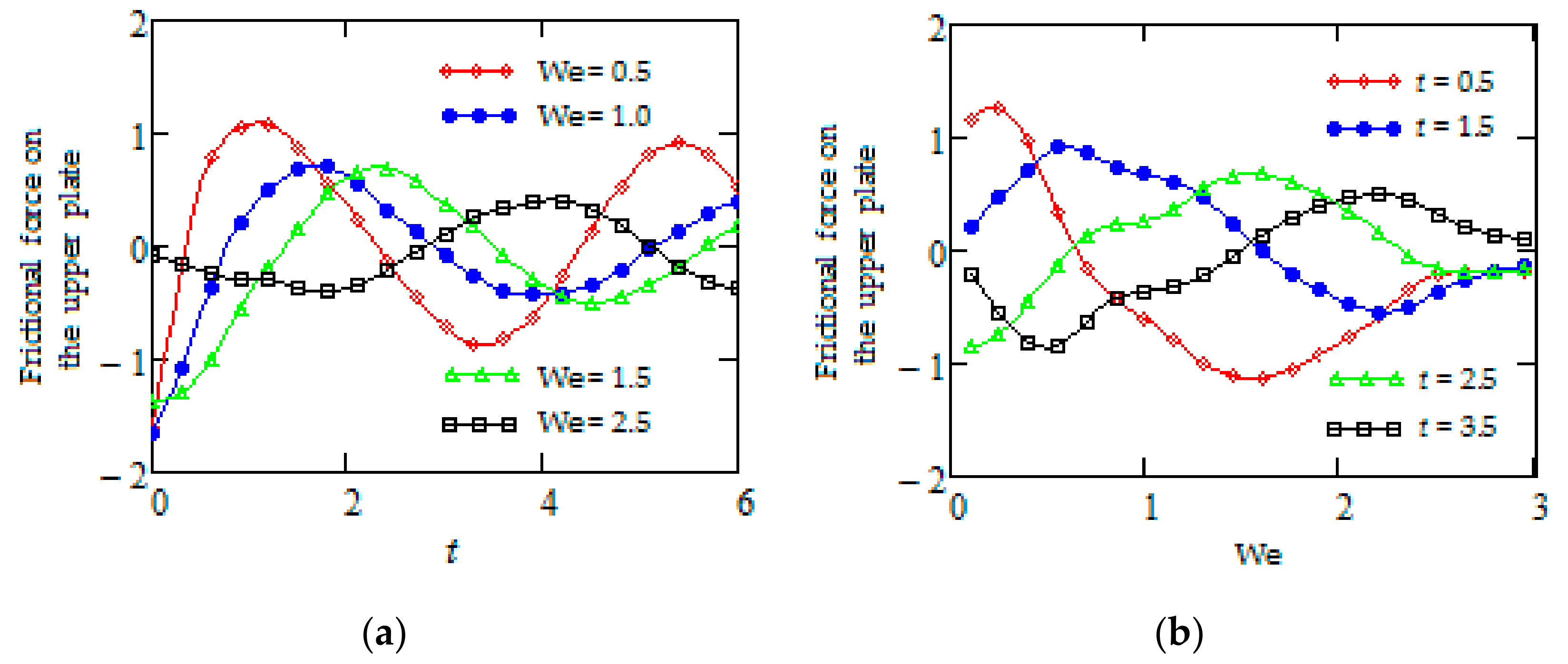
5. Some Numerical Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Cauchy stress tensor | Extra stress tensor | ||
| First Rivlin–Ericksen tensor | Velocity vector | ||
| L | The velocity gradient | u | Fluid velocity |
| p | Pressure | Cartesian coordinates | |
| Non-trivial shear stress | Non-trivial normal stress | ||
| t | Time | g | Gravitational acceleration |
| Relaxation time | Fluid density | ||
| Fluid viscosity at the reference pressure | Kinematic viscosity | ||
| Pressure–viscosity coefficient | S | Constant shear-stress | |
| d | Distance between plates | We | Weissenberg number |
Appendix A
References
- Stokes, G.G. On the theories of the internal friction of fluids in motion, and motion of elastic solids. Trans. Camb. Phil. Soc. 1845, 8, 287–305. [Google Scholar]
- Bridgman, P.W. The Physics of High Pressure; MacMillan Company: New York, NY, USA, 1931. [Google Scholar]
- Griest, E.M.; Webb, W.; Schiessler, R.W. Effect of pressure on viscosity of high hydrocarbons and their mixture. J. Chem. Phys. 1958, 29, 711–720. [Google Scholar] [CrossRef]
- Johnson, K.L.; Cameron, R. Shear behavior of elastohydrodynamic oil films at high rolling contact pressures. Proc. Inst. Mech. Eng. 1967, 182, 307–319. [Google Scholar] [CrossRef]
- Johnson, K.L.; Tevaarwerk, J.L. Shear behavior of elastohydrodynamic oil films. Proc. Roy. Soc. Lond. Ser. A 1977, 356, 215–236. [Google Scholar]
- Bair, S.; Jarzynski, J.; Winer, W.O. The temperature, pressure and time dependence of lubricant viscosity. Tribol. Inter. 2001, 34, 461–468. [Google Scholar] [CrossRef]
- Bair, S.; Kottke, P. Pressure-viscosity relationships for elastohydrodynamics. Tribol. Trans. 2003, 46, 289–295. [Google Scholar] [CrossRef]
- Prusa, V.; Srinivasan, S.; Rajagopal, K.R. Role of pressure dependent viscosity in measurements with falling cylinder viscometer. Int. J. Non Linear Mech. 2012, 47, 743–750. [Google Scholar] [CrossRef]
- Fusi, L. Unidirectional flows of a Herschel-Bulkley fluid with pressure-dependent rheological moduli. Eur. Phys. J. Plus 2020, 135, 544. [Google Scholar] [CrossRef]
- Barus, C. Note on the dependence of viscosity on pressure and temperature. Proc. Am. Acad. Arts. Sci. 1891, 27, 13–18. [Google Scholar] [CrossRef]
- Barus, C. Isothermals, isopiestics and isometrics relative to viscosity. Am. J. Sci. 1893, 45, 87–96. [Google Scholar] [CrossRef]
- Dowson, D.; Higginson, G.R. Elastohydrodynamic Lubrication: The Fundamentals of Roller and Gear Lubrication; Pergamon Press: Oxford, UK, 1966. [Google Scholar]
- Rajagopal, K.R. On implicit constitutive theories for fluids. J. Fluid Mech. 2006, 550, 243–249. [Google Scholar] [CrossRef]
- Hron, J.; Malek, J.; Rajagopal, K.R. Simple flows of fluids with pressure-dependent viscosities. Proc. R. Soc. Lond. A 2001, 457, 1603–1622. [Google Scholar] [CrossRef]
- Karra, S.; Prusa, V.; Rajagopal, K.R. On Maxwell fluids with relaxation time and viscosity depending on the pressure. Int. J. Non Linear Mech. 2011, 46, 819–827. [Google Scholar] [CrossRef] [Green Version]
- Renardy, M. Parallel shears flows of fluids with a pressure-dependent viscosity. J. Nonnewton. Fluid Mech. 2003, 114, 229–238. [Google Scholar] [CrossRef]
- Lord, H.A. Flow of polymers with pressure-dependent viscosity. Polym. Eng. Sci. 1979, 19, 469–473. [Google Scholar] [CrossRef]
- Denn, M.M. Polymer Melt Processing: Foundations in Fluid Mechanics and Heat Transfer; Cambridge University Press: New York, NY, USA, 2008. [Google Scholar]
- Szeri, A.Z. Fluid Film Lubrication; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Cui, H.H.; Silber-Li, Z.; Zhu, S. Flow characteristics of liquids in microtubes driven by a high pressure. Phys. Fluids 2004, 16, 1803–1810. [Google Scholar] [CrossRef] [Green Version]
- Martinez-Boza, F.J.; Martin-Alfonso, M.J.; Callegos, C.; Fernandez, M. High-pressure behavior of intermediate fuel oils. Energy Fuels 2011, 25, 5138–5144. [Google Scholar] [CrossRef]
- Stemmer, K.; Harder, H.; Hansen, U. A new method to stimulate convection with strong temperature and pressure-dependent viscosity in a spherical shell: Applications to the Earth’ mantle. Phys. Earth. Planet. Inter. 2006, 157, 223–249. [Google Scholar] [CrossRef]
- Goubert, A.; Vermant, J.; Moldenaers, P.; Göttfert, A.; Ernst, B. Comparison of measurement techniques for evaluating the pressure dependence of the viscosity. Appl. Rheol. 2001, 11, 26–37. [Google Scholar] [CrossRef]
- Park, H.E.; Lim, S.T.; Laun, H.M.; Dealy, J.M. Measurement of pressure coefficient of melt viscosity: Drag flow versus capillary flow. Rheol. Acta 2008, 47, 1023–1038. [Google Scholar] [CrossRef]
- Carreras, E.S.; Kissi, N.E.; Piau, J.M.; Toussaint, F.; Nigen, S. Pressure effects on viscosity and flow stability of polyethylene melts during extension. Rheol. Acta 2006, 45, 209–222. [Google Scholar] [CrossRef]
- Sorrentino, A.; Pantani, R. Pressure dependent viscosity and free volume of atactic and syndiotactic polystyrene. Rheol. Acta 2009, 48, 467–478. [Google Scholar] [CrossRef]
- Kottke, P.A.; Bair, S.S.; Winer, W.O. The measurement of viscosity of liquids under tension. Trans. ASME 2003, 125, 260–266. [Google Scholar] [CrossRef]
- Venner, C.H.; Lubrecht, A.A. Multilevel Methods in Lubrication; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Rajagopal, K.R. Couette flows of fluids with pressure dependent viscosity. J. Appl. Mech. Eng. 2004, 9, 573–585. [Google Scholar]
- Rajagopal, K.R. A semi-inverse problem of flows of fluids with pressure dependent viscosities. Inverse Probl. Sci. Eng. 2008, 16, 269–280. [Google Scholar] [CrossRef]
- Prusa, V. Revisiting Stokes first and second problems for fluids with pressure-dependent viscosities. Int. J. Eng. Sci. 2010, 48, 2054–2065. [Google Scholar] [CrossRef]
- Fetecau, C.; Bridges, C. Analytical solutions for some unsteady flows of fluids with linear dependence of viscosity on the pressure. Inverse Probl. Sci. Eng. 2020, 1–18. [Google Scholar] [CrossRef]
- Vieru, D.; Fetecau, C.; Bridges, C. Analytical solutions for a general mixed boundary value problem associated to motions of fluids with linear dependence of viscosity on the pressure. Int. J. Appl. Mech. Eng. 2020, 25, 181–197. [Google Scholar] [CrossRef]
- Fetecau, C.; Vieru, D. Exact solutions for unsteady motion between parallel plates of some fluids with power-law dependence of viscosity on the pressure. Appl. Eng. Sci. 2020, 1, 100003. [Google Scholar] [CrossRef]
- Rajagopal, K.R.; Saccomandi, G.; Vergori, L. Unsteady flows of fluids with pressure dependent viscosity. J. Math. Anal. Appl. 2013, 404, 362–372. [Google Scholar] [CrossRef]
- Akyildiz, F.T.; Siginer, D. A note on the steady flow of Newtonian fluids with pressure dependent viscosity in rectangular duct. Int. J. Eng. Sci. 2016, 104, 1–4. [Google Scholar] [CrossRef]
- Housiadas, K.D.; Georgiou, G.C. Analytical solution of the flow of a Newtonian fluid with pressure-dependent viscosity in a rectangular duct. Appl. Math. Comput. 2018, 322, 123–128. [Google Scholar] [CrossRef]
- Housiadas, K.D. An exact analytical solution for viscoelastic fluids with pressure-dependent viscosity. J. Nonnewton. Fluid Mech. 2015, 223, 147–156. [Google Scholar] [CrossRef]
- Housiadas, K.D. Internal viscoelastic flows for fluids with exponential type pressure-dependent viscosity and relaxation time. J. Rheol. 2015, 59, 769–791. [Google Scholar] [CrossRef]
- Housiadas, K.D. Viscoelastic fluids with pressure-dependent viscosity; exact analytical solutions and their singularities in Poiseuille flows. Int. J. Eng. Sci. 2020, 147, 103207. [Google Scholar] [CrossRef]
- Renardy, M. Some remarks on the Navier-Stokes equations with a pressure-dependent viscosity. Commun. Partial Differ. Equ. 1986, 11, 779–793. [Google Scholar] [CrossRef]
- Malek, J.; Necas, J.; Rajagopal, K.R. Global existence of solutions for flows of fluids with pressure and shear dependent viscosities. Appl. Math. Lett. 2002, 15, 961–967. [Google Scholar] [CrossRef] [Green Version]
- Malek, J.; Rajagopal, K.R.; Zabensky, J. On power-law fluids with the power-law index proportional to the pressure. Appl. Math. Lett. 2016, 62, 118–123. [Google Scholar] [CrossRef] [Green Version]
- Danish, G.A.; Imran, M.; Fetecau, C.; Vieru, D. First exact solutions for mixed boundary value problems concerning the motions of fluids with exponential dependence of viscosity on pressure. AIP Adv. 2020, 10, 065206. [Google Scholar] [CrossRef]
- Renardy, M. Inflow boundary condition for steady flow of viscoelastic fluids with differential constitutive laws. Rocky Mt. J. Math. 1988, 18, 445–453. [Google Scholar] [CrossRef]
- Renardy, M. An alternative approach to inflow boundary conditions for Maxwell fluids in three space dimensions. J. Nonnewton. Fluid Mech. 1990, 36, 419–425. [Google Scholar] [CrossRef]
- Baranovskii, E.S. Mixed initial-boundary value problem for equations of motion of Kelvin-Voight fluids. Comput. Math. Math. Phys. 2016, 56, 1363–1371. [Google Scholar] [CrossRef]
- Poole, R.J. The Deborah and Weissenberg numbers. The British Society of Rheology. Rheol. Bull. 2012, 53, 32–39. [Google Scholar]
- Fusi, L.; Farina, A.; Rosso, A.F. Mathematical models for fluids with pressure-dependent viscosity flowing in porous media. Int. J. Eng. Sci. 2015, 87, 110–118. [Google Scholar] [CrossRef]
- Ullah, H.; Lu, D.; Siddiqui, A.M.; Haroon, T.; Maqbool, K. Hydrodynamical study of creeping Maxwell fluid flow through a porous slit with uniform reabsorption and wall slip. Mathematics 2020, 8, 1852. [Google Scholar] [CrossRef]
- Fetecau, C.; Ellahi, R.; Sait, S.M. Mathematical analysis of Maxwell fluid flow through a porous plate channel induced by a constantly accelerating or oscillating wall. Mathematics 2021, 9, 90. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fetecau, C.; Vieru, D.; Abbas, T.; Ellahi, R. Analytical Solutions of Upper Convected Maxwell Fluid with Exponential Dependence of Viscosity under the Influence of Pressure. Mathematics 2021, 9, 334. https://doi.org/10.3390/math9040334
Fetecau C, Vieru D, Abbas T, Ellahi R. Analytical Solutions of Upper Convected Maxwell Fluid with Exponential Dependence of Viscosity under the Influence of Pressure. Mathematics. 2021; 9(4):334. https://doi.org/10.3390/math9040334
Chicago/Turabian StyleFetecau, Constantin, Dumitru Vieru, Tehseen Abbas, and Rahmat Ellahi. 2021. "Analytical Solutions of Upper Convected Maxwell Fluid with Exponential Dependence of Viscosity under the Influence of Pressure" Mathematics 9, no. 4: 334. https://doi.org/10.3390/math9040334
APA StyleFetecau, C., Vieru, D., Abbas, T., & Ellahi, R. (2021). Analytical Solutions of Upper Convected Maxwell Fluid with Exponential Dependence of Viscosity under the Influence of Pressure. Mathematics, 9(4), 334. https://doi.org/10.3390/math9040334






