On the Canonical Foliation of an Indefinite Locally Conformal Kähler Manifold with a Parallel Lee Form
Abstract
1. Reminder of l.c.K. Geometry and Statement of Main Results
2. Indefinite Hopf Manifolds
3. Conformally Flat Indefinite l.c.K. Manifolds
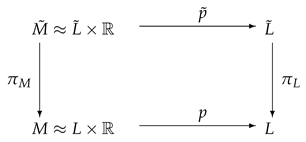 where , , p, are projections. Let be the indefinite Sasakian structure of L and its lift to . Then
where , , p, are projections. Let be the indefinite Sasakian structure of L and its lift to . Then
4. Conclusions and Open Problems
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Canonical Foliations with Lightlike Leaves
References
- Barros, M.; Romero, A. Indefinite Kähler manifolds. Math. Ann. 1982, 261, 55–62. [Google Scholar] [CrossRef]
- Libermann, P. Sur les structures presque complexes at autres structures infinitésimales réguliers. Bull. Soc. Math. 1955, 83, 195–224. [Google Scholar]
- Aubin, T. Variétés hermitiennes localment conformément Kählériennes. C. R. Acad. Sci. 1965, 261, 2427–2430. [Google Scholar]
- Vaisman, I. On locally conformal almost Kähler manifolds. Israel J. Math. 1976, 24, 338–351. [Google Scholar] [CrossRef]
- Dragomir, S.; Ornea, L. Locally Conformal Kähler Geometry; Progress in Mathematics; Birkhäuser: Berlin/Heidelberg, Germany; New York, NY, USA, 1998; Volume 155. [Google Scholar]
- Dragomir, S.; Duggal, K.L. Indefinite locally conformal Kähler manifolds. Differ. Geom. Its Appl. 2007, 25, 8–22. [Google Scholar] [CrossRef][Green Version]
- Dragomir, S.; Duggal, K.L. Indefinite extrinsic spheres. Tsukuba J. Math. 2008, 32, 335–348. [Google Scholar] [CrossRef]
- Lee, H.C. A kind of even dimensional geometry and its application to exterior calculus. Am. J. Math. 1943, 65, 433–438. [Google Scholar] [CrossRef]
- Vaisman, I. Generalized Hopf manifolds. Geom. Dedicata 1982, 13, 231–255. [Google Scholar] [CrossRef]
- O’Neill, B. Semi-Riemannian Geometry; Academic Press: New York, NY, USA; London, UK; Paris, France, 1983. [Google Scholar]
- Bejancu, A.; Duggal, K.L. Lightlike Submanifolds of Semi-Riemannian Manifolds and Applications; Kluwer Academic: Dordrecht, The Netherlands, 1996; Volume 364. [Google Scholar]
- Wu, H. On the de Rham decomposition theorem. Ill. J. Math. 1964, 8, 291–311. [Google Scholar] [CrossRef]
- Kobayashi, S.; Nomizu, K. Foundations of Differential Geometry; Interscience Publishers: New York, NY, USA, 1963; Volume I. [Google Scholar]
- Vaisman, I. Locally conformal Kähler manifolds with parallel Lee form. Rendiconti di Matematica e delle sue Applicazioni 1979, 12, 263–284. [Google Scholar]
- Boothby, W.M. Some fundamental formulas for Hermitian manifolds with non-vanishing torsion. Am. J. Math. 1954, 76, 509–534. [Google Scholar] [CrossRef]
- Berger, M.; Gauduchon, P.; Mazet, E. Le Spectre D’une Varieté Riemanniene; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1971; Volume 194. [Google Scholar]
- Blair, D.E. Contact Manifolds in Riemannian Geometry; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1976; Volume 509. [Google Scholar]
- Duggal, K.L. Space-time manifolds and contact structures. Int. J. Math. Math. Sci. 1990, 13, 545–554. [Google Scholar] [CrossRef]
- Takahashi, T. Sasakian manifolds with pseudo-Riemannian metric. Tohoku Math. J. 1969, 21, 271–290. [Google Scholar] [CrossRef]
- Wolf, J.A. Spaces of Constant Curvature; Publish or Perish, Inc.: Wilmington, DE, USA, 1984. [Google Scholar]
- Barletta, E.; Dragomir, S.; Duggal, K.L. Foliations in Cauchy-Riemann geometry. In Mathematical Surveys and Monographs; American Mathematical Society: Providence, RI, USA, 2007; Volume 140. [Google Scholar]
- Dragomir, S.; Tomassini, G. Differential Geometry and Analysis on CR Manifolds; Progress in Mathematics; Birkhäuser: Boston, MA, USA; Basel, Switzerland; Berlin, Germany, 2006; Volume 246. [Google Scholar]
- Barletta, E. On the pseudohermitian sectional curvature of a strictly pseudoconvex CR manifold. Differ. Geom. Its Appl. 2007, 25, 612–631. [Google Scholar] [CrossRef]
- Chern, S.S.; Moser, J.K. Real hypersurfaces in complex manifolds. Acta Math. 1974, 133, 219–271. [Google Scholar] [CrossRef]
- Gray, A.; Hervella, L.M. The sixteen classes of almost Hermitian manifolds and their linear invariants. Ann. Mat. Pura Appl. 1980, 123, 35–58. [Google Scholar] [CrossRef]
- Kirichenko, V. Conformally flat and locally conformal Kähler manifolds. Math. Notes 1992, 51, 462–468. [Google Scholar] [CrossRef]
- Wu, H. Decomposition of Riemannian manifolds. Bull. Am. math. Soc. 1964, 70, 610–617. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barletta, E.; Dragomir, S.; Esposito, F. On the Canonical Foliation of an Indefinite Locally Conformal Kähler Manifold with a Parallel Lee Form. Mathematics 2021, 9, 333. https://doi.org/10.3390/math9040333
Barletta E, Dragomir S, Esposito F. On the Canonical Foliation of an Indefinite Locally Conformal Kähler Manifold with a Parallel Lee Form. Mathematics. 2021; 9(4):333. https://doi.org/10.3390/math9040333
Chicago/Turabian StyleBarletta, Elisabetta, Sorin Dragomir, and Francesco Esposito. 2021. "On the Canonical Foliation of an Indefinite Locally Conformal Kähler Manifold with a Parallel Lee Form" Mathematics 9, no. 4: 333. https://doi.org/10.3390/math9040333
APA StyleBarletta, E., Dragomir, S., & Esposito, F. (2021). On the Canonical Foliation of an Indefinite Locally Conformal Kähler Manifold with a Parallel Lee Form. Mathematics, 9(4), 333. https://doi.org/10.3390/math9040333





