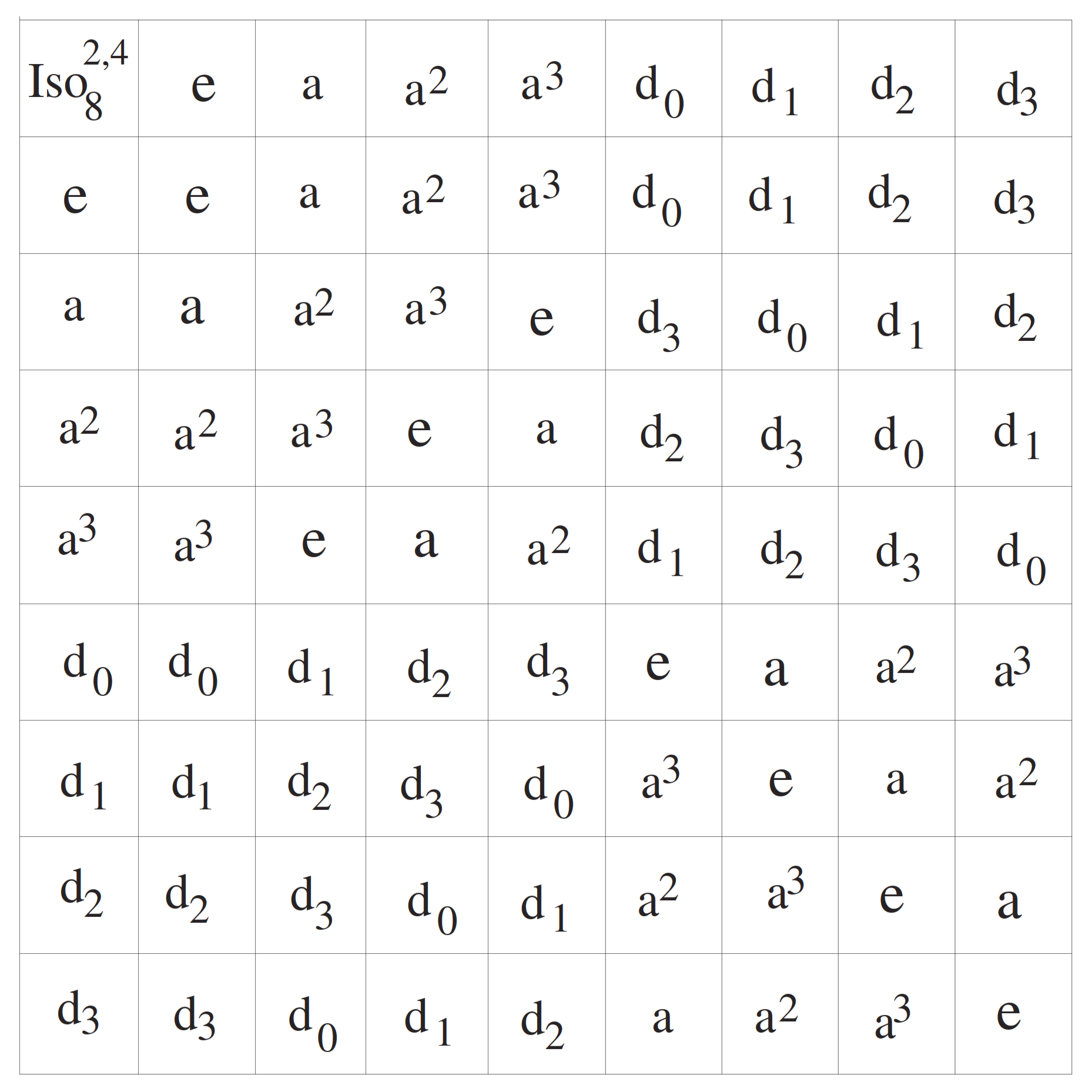Discrete Group Actions on Digital Objects and Fixed Point Sets by Iso_k(·)-Actions

Abstract

Given a digital image (or digital object) $(X,k),X\subset {\mathbb{Z}}^n$, this paper initially establishes a group structure of the set of self-k-isomorphisms of $(X,k)$ with the function composition, denoted by $Is{o}_k(X)$ or $Au{t}_k(X)$. In particular, let $C_k^{n,l}$ be a simple closed k-curve with l elements in ${\mathbb{Z}}^n$. Then, the group $Is{o}_k(C_k^{n,l})$ is proved to be isomorphic to the standard dihedral group $D_l$ with order l. The calculation of this quantity $Is{o}_k(C_k^{n,l})$ is a key step for obtaining many new results. Indeed, it is essential for exploring many features of $Is{o}_k(X)$. Furthermore, this quantity is proved to be a digital topological invariant. After proceeding with an $Is{o}_k(X)$-action on $(X,k)$, we investigate some properties of fixed point sets by this action. Finally, we explore various features of fixed point sets by this action from the viewpoint of digital k-curve theory. This paper only deals with k-connected digital images $(X,k)$ whose cardinality is equal to or greater than 2. Besides, we discuss some errors that have appeared in the lilterature.

1. Introduction

Let $\mathbb{Z}$ (resp.$\mathbb{N}$) represent the set of integers (resp. natural numbers), and ${\mathbb{Z}}^n$ be the n times Cartesian product of $\mathbb{Z}$, $n\in \mathbb{N}$. Besides, let ${\mathbb{N}}_0$ (resp.${\mathbb{N}}_1$) be the set of even (resp. odd) natural numbers. Digital geometry mainly deals with discrete objects in ${\mathbb{Z}}^n$ from the viewpoints of digital k-curve and digital k-surface theory, where the k-adjacency means the digital k-connectivity of ${\mathbb{Z}}^n$ (see (1) in Section 2). Indeed, a digital image $(X,k)$, $X\subset {\mathbb{Z}}^n$, can be considered to be a digital graph on ${\mathbb{Z}}^n$ with a certain k-adjacency of ${\mathbb{Z}}^n$ or a discrete topological subspace on ${\mathbb{Z}}^n$ with a k-adjacency relation of ${\mathbb{Z}}^n$ (for details see Section 2). They are indeed equivalent to each other. This kind of consideration facilitates our recognition of some discrete objects in a modern smart electronic device. For instance, a smart computer screen, being finite pixels, can be assumed to be a set followed from these two approaches among others. In addition, there are also further many types of approaches of studying digital objects in ${\mathbb{Z}}^n$. Hence, many works taking these approaches include the papers [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]. Besides, some studies related to nonlinearizable action of dihedral groups on affine space [20], free actions on $\mathbb{R}$-trees [21], and a group of paths in ${\mathbb{R}}^2$ [22] were done. In addition, there are some researches on the fixed point property related to two-dimensional polyhedra [23] and fixed point sets of circle action [24]. Hereinafter, for convenience, for $a,b\in \mathbb{Z}$ with $a<b$, we follow the notation ${[a,b]}_{\mathbb{Z}}:=\{n\in \mathbb{Z}|a\le n\le b\}$ [13]. Besides, in the present paper we call $(X,k)$ a digital image or a digital object in ${\mathbb{Z}}^n$.

Given a digital image (or digital object) $(X,k)$ in ${\mathbb{Z}}^n$, we assume (for more detail see Section 3, Section 4 and Section 5)

$\left\{\begin{array}{c}Is{o}_k(X):=Au{t}_k(X):=\left\{h\right|h:(X,k)\to (X,k)\mathrm{is}\mathrm{a}k-\mathrm{isomorphism}\},\mathrm{and}\hfill \\ Co{n}_k(X):=\left\{f\right|f:(X,k)\to (X,k)\mathrm{is}\mathrm{a}k-\mathrm{continuous}\mathrm{map}\}.\hfill \end{array}\right.$

One important thing to note is that the current approach in a digital topological setting plays an important role in applied mathematics as well as applied sciences. Hence, based on this approach, let ${\mathcal{D}}_k(X)\in \{Is{o}_k(X),Co{n}_k(X)\}$, the present paper explores some new structures and features associated with the fixed point sets by the ${\mathcal{D}}_k(X)$-actions on a digital image $(X,k)$ (see Definition 10) and further, examines if alignments of fixed point sets by the ${\mathcal{D}}_k(X)$-actions are 2-connected or perfect (see Definition 11). In particular, these actions include fixed point and fixed point free ones [25] and further, these are discrete groups or monoid ones.

The recent papers [7,8,26] studied the set of cardinalities of fixed point sets of all k-continuous self-maps of $(X,k)$, denoted by $F(Co{n}_k(X))$ in the present paper (or $F(X)$ in [26]). Motivated by this approach, this paper further investigates some more important features of ${\mathcal{D}}_k(X)$. The obtained results give us some big advantages of recognizing the sizes or volumes of the fixed points sets by the ${\mathcal{D}}_k(X)$-actions on $(X,k)$. The papers [7,8] also characterized the set $F(Co{n}_k(X))$ with 2-adjacency which is referred to as “an alignment of fixed point sets” (see Definition 10) [8]. Since the present paper indeed deals with two kinds of algebraic structures, $Is{o}_k(X)$ and $Co{n}_k(X)$, the usage of the notations $F(Is{o}_k(X))$ and $F(Co{n}_k(X))$ can finally avoid a certain possible confusion among fixed point sets derived from these two actions on $(X,k)$.

The algebraic structure of $Is{o}_k(X)$ is essential for exploring fixed point sets of the $Is{o}_k(X)$-actions on $(X,k)$ in a $DTC(k)$ setting, where $DTC(k)$ is a category consisting of the set of digital images (or digital objects) $(X,k)$ and the set of digitally k-continuous maps (for details see Section 2). Thus, they play important roles in studying fixed point theory [27] and group theory in a $DTC(k)$ setting. Using these structures, we further investigate some properties of the $Is{o}_k(X)$-action on $(X,k)$ and explore a certain condition that makes the alignment of fixed point sets by the $Co{n}_k(X)$-action perfect (for details see Definitions 10 and 11), where for a digital object $(X,k)$ we say that $F(Co{n}_k(X))$ is perfect if it is equal to ${[0,X^{♯}]}_{\mathbb{Z}}$ (see Definition 11). Papers [7,8] have also explored some alignments of fixed point sets that are 2-connected (or perfect). Since an existence of a perfect alignment of fixed point sets depends on the situation, we strongly need to examine if $F(Co{n}_k(X))$ is perfect, which can play an important role in digital topology and many areas of applied sciences [8]. Indeed, this kind of approach gives us to efficiently characterize the fixed point sets of $f\in Co{n}_k(X)$.

The present paper investigates various properties of $F(Is{o}_k(X))$ and $F(Co{n}_k(X))$ related to fixed point sets in the category $DTC(k)$ (for details see Section 5). Let $C_k^{n,l}$ be a simple closed k-curve with l elements in ${\mathbb{Z}}^n$ (for more details see the property (2)). Then, based on the minimal simple closed k-curve $C_k^{n,4}$ in ${\mathbb{Z}}^n$, it turns out that either $C_k^{n,5}$ or $C_k^{n,6}$ is the secondary to the minimal simple closed k-curve $C_k^{n,4}$ in ${\mathbb{Z}}^n$ depending on both the “k-adjacency” and the dimension “n” [8]. Naively, while there is $C_8^{2,6}$, neither $C_4^{2,6}$ nor $C_k^{2,5}$ exists, where $k\in \{4,8\}$. Meanwhile, $C_k^{n,5}$ exists if $3\le t\le n$ and $k:=k(t,n)$ (for more details see the property (2) in the present paper or the property of (2) of [8]). Considering a digital wedge $C_k^{n,l}\vee C_k^{n,4}$ whose digital k-fundamental group is an infinite cyclic group or a trivial group depending on the number l, a recent paper mentioned that in the case $l\in {\mathbb{N}}_0\backslash \left\{2\right\}$, $F(Co{n}_k(C_k^{n,l}\vee C_k^{n,4}))$ is 2-connected (or perfect) (see Definition 11) if and only if $l\in \{4,6,8,10\}$, where the term “perfect“ means that $F(Co{n}_k(C_k^{n,l}\vee C_k^{n,4}))={[0,l+3]}_{\mathbb{Z}}$. Besides, a recent paper further developed a certain condition of which $F(Co{n}_k(C_k^{n,l}\vee C_k^{n,6}\vee C_k^{n,4}))$ is perfect. In addition, in the case $5\le l\in {\mathbb{N}}_1$, the study of $F(Co{n}_k(C_k^{n,l}\vee C_k^{n,4}))$ was also proceeded [8]. This kind of study can be substantially helpful to study fixed point theory and k-homotopy theory in a digital topological setting. Since the present paper deals with many properties related to the digital topological property, let us recall the property in advance. Hereafter, as usual, we say that a digital topological invariant is a property of a digital image $(X,k)$ which is invariant under digital k-isomorphisms. In other words, a property of digital images is a digital topological property if whenever a digital image $(X,k)$ possesses that property every digital image k-isomorphic to $(X,k)$ has that property.

Based on this approach, we may pose the following queries.

(●1)

How can we characterize the group $Is{o}_k(X)$?

(●2)

Given $C_k^{n,l}$, what group is isomorphic to $Is{o}_k(C_k^{n,l})$ ?

(●3)

After proceeding with the $Is{o}_k(X)$-action on $(X,k)$, how can we characterize the fixed point sets by the $Is{o}_k(X)$-action ?

(●4)

What are the fixed point sets of an $Is{o}_k(C_k^{n,l_1}\vee C_k^{n,l_2})$-action on $C_k^{n,l_1}\vee C_k^{n,l_2}$ ?

(●5)

Given $C_k^{n,l_1}\vee C_k^{n,l_2}$ with a certain hypothesis, $l_1,l_2\in {\mathbb{N}}_0\backslash \left\{2\right\}$, how can we formulate $F(Co{n}_k(C_k^{n,l_1}\vee C_k^{n,l_2}))$ ?

After developing many new tools, we will address all of these issues in this paper.

The rest of the paper is organized as follows: Section 2 provides various concepts needed for this study and deals with some properties of them. Section 3 develops the group structure of $Is{o}_k(X)$. Besides, we prove that $Is{o}_k(C_k^{n,l})$ is isomorphic to the standard dihedral group $D_l$ with $2l$ elements. Section 4 deals with some fixed point sets of an $Is{o}_k(X)$-action on the given digital image $(X,k)$. Section 5 explores various properties of $F(Co{n}_k(C_k^{n,l_1}\vee C_k^{n,l_2}))$, where $l_1,l_2\in {\mathbb{N}}_0\backslash \left\{2\right\}$. Indeed, the study of this kind of a digital wedge remains open. Section 6 concludes the paper with some remarks and a further work. In this paper the notation “$:=$” is used for introducing a new terminology. In addition, we will use the notation $X^{♯}$ to indicate the cardinality of a set X.

2. Preliminaries

Rosenfeld [17,18] called the pair $(X,k)$ a digital image (or digital object), where $X\subset {\mathbb{Z}}^n$ with digital k-connectivity, $n\in \{1,2,3\}$. Motivated by these k-adjacency relations for low dimensional digital images, a paper [5] initially developed the generalized version of them for high dimensional digital images $X\subset {\mathbb{Z}}^n$, $n\in \mathbb{N}$. Indeed, this approach is essential for studying many digital objects from the viewpoint of digital topology such as digital products with normal adjacencies [5] and their applications [28,29]. More explicitly, the following k-adjacency relations of ${\mathbb{Z}}^n$ were taken in [5,28] for studying $X\subset {\mathbb{Z}}^n$.

For a natural number t, $1\le t\le n$, distinct points

$$p=(p_1,p_2,\dots ,p_n)\mathrm{and}q=(q_1,q_2,\dots ,q_n)\in {\mathbb{Z}}^n,$$

are $k(t,n)$-adjacent if at most t of their coordinates differ by $\pm 1$ and the others coincide. According to this statement, the $k(t,n)$-adjacency relations of ${\mathbb{Z}}^n,n\in \mathbb{N}$, were formulated [5,28]), as follows:

$$k:=k(t,n)=\sum _{i=1}^t{2}^i{C}_i^n,\mathrm{where}{C}_i^n=\frac{n!}{(n-i)!i!}.$$

(1)

Using a digital k-adjacency of ${\mathbb{Z}}^n,n\in \mathbb{N}$, it turns out that a digital image $(X,k)$ is a digital space [30]. In this paper $(X,k)$ is assumed in ${\mathbb{Z}}^n,n\in \mathbb{N}$, with one of the k-adjacency of (1). The following terminology and notions [5,7,17,18,29] will be often used later.

Given a digital image $(X,k)$ with $X^{♯}\ge 2$, by a k-path with $l+1$ elements in X, we mean the sequence ${(x_i)}_{i\in {[0,l]}_{\mathbb{Z}}}\subset X$ such that $x_i$ and $x_j$ are k-adjacent if $|i-j|=1$ [13]. Using this approach, we can also represent the concept of k-connectedness, as follows [13].

• We say that $(X,k)$ is k-connected if for any distinct points $x,y\in X$ there is a k-path ${(x_i)}_{i\in {[0,l]}_{\mathbb{Z}}}$ in X such that $x_0=x$ and $x_l=y$ (for more details see [7]).
• By a simple k-path, we mean a finite set ${(x_i)}_{i\in {[0,m]}_{\mathbb{Z}}}\subset {\mathbb{Z}}^n$ such that $x_i$ and $x_j$ are k-adjacent if and only if $|i-j|=1$[13]. In particular, if $x_0=x$ and $x_m=y$, then the length of this set ${(x_i)}_{i\in {[0,m]}_{\mathbb{Z}}}$ is denoted by $l_k(x,y):=m$.
• We say that a simple closed k-curve (or simple k-cycle) with l elements in ${\mathbb{Z}}^n,n\ge 2$, denoted by $S{C}_k^{n,l}$[5,13], $l\ge 4$, is a set ${(x_i)}_{i\in {[0,l-1]}_{\mathbb{Z}}}\subset {\mathbb{Z}}^n$ such that $x_i$ and $x_j$ are k-adjacent if and only if $|i-j|=\pm 1(\mathrm{mod}l)$. In particular, as mentioned in the previous part, in this paper we use the notation $C_k^{n,l}$ to abbreviate $S{C}_k^{n,l}$.

More precisely, for $l\in {\mathbb{N}}_1$, no $C_{2n}^{n,l}$ exists, according to the notion of $C_k^{n,l}$ (see also (2) below), we observe the following properties [8]. The number l of $C_k^{n,l}$ depends on the k-adjacency of ${\mathbb{Z}}^n$ in (1), i.e., $k:=k(t,n)$ of (1) (for more details, see the property (2) of [8] and several examples in Figure 1 and Figure 2).

$$\left\{\begin{array}{c}(1)\mathrm{in}\mathrm{the}\mathrm{case}k=2n(n\ge 2),\mathrm{we}\mathrm{have}l\in {\mathbb{N}}_0\backslash \left\{2\right\};\hfill \\ (2)\mathrm{in}\mathrm{the}\mathrm{case}k\ne 2n,\mathrm{the}\mathrm{number}l\mathrm{depends}\mathrm{on}\mathrm{the}\mathrm{dimension}\mathrm{of}n\hfill \\ (\mathrm{for}\mathrm{more}\mathrm{details},\mathrm{see}\mathrm{the}\mathrm{property}(2)\text{of [8]});\mathrm{and}\hfill \\ (3)\mathrm{in}\mathrm{the}\mathrm{case}k:=k(t,n),3\le t\le n,\mathrm{we}\mathrm{have}l\in \mathbb{N}\backslash \{1,2,3\}\hfill \\ (\mathrm{for}\mathrm{more}\mathrm{details},\mathrm{see}\mathrm{the}\mathrm{property}(2)\mathrm{of\; [8]}).\hfill \end{array}\right.$$

(2)

For instance, we can consider the following digital objects: $C_4^{2,4}$, $C_8^{2,4}$, $C_8^{2,7}$, $C_{18}^{3,9}$ and $C_{26}^{3,5}$. However, in ${\mathbb{Z}}^2$ neither $C_4^{2,5}$ nor $C_8^{2,5}$ exists. Besides, in ${\mathbb{Z}}^3$ neither $C_6^{2,5}$ nor $C_{18}^{2,5}$ exists.

• Given $(X,k)$, by the k-component of $x\in X$, we mean the maximal k-connected subset of $(X,k)$ containing the point x [13].

For a k-connected digital image $(X,k)$, the paper [5] already established a certain metric on $(X,k)$ (for more details see [5,7]). Thus, given a digital image $(X,k)$ on ${\mathbb{Z}}^n$, we obtain [5,29] that for a point $x_0\in (X,k)$,

$$N_k(x_0,1)=\{x\in X|x\mathrm{is}k-\mathrm{adjacent}\mathrm{to}{x}_0\}\cup \left\{x_0\right\}.$$

(3)

This set is called a digital k-neighborhood of $x_0$ with radius 1 [5]. As another approach for the digital k-neighborhood of $x_0$ with radius $\epsilon$ in (3) using a special kind of metric on $(X,k)$ was established in the papers [5,7]. The digital $(k_0,k_1)$-continuity of a map $f:(X,k_0)\to (Y,k_1)$ in [18] can be represented, as follows:

Proposition 1.

[4,6] A function $f:(X,k_0)\to (Y,k_1)$ is (digitally) $(k_0,k_1)$-continuous if and only if for every $x\in X$, $f(N_{k_0}(x,1))\subset N_{k_1}(f(x),1)$.

In Proposition 1, in the case $k:=k_0=k_1$, the map f is called a “k-continuous” map to abbreviate the $(k,k)$-continuity of Proposition 1. Using the presentation of the k-continuity from Proposition 1, let us recall the category DTC consisting of the following two pieces of data [5], called the digital topological category.

• The set of $(X,k)$, where $X\subset {\mathbb{Z}}^n$, as objects of DTC;
• for every ordered pair of objects $(X_i,k_i),i\in \{0,1\}$, the set of all $(k_0,k_1)$-continuous maps between them as morphisms of DTC.

In DTC, in the case $k:=k_0=k_1$, we will particularly use the notation DTC(k) [29].

The recent paper studied the following property of digital continuity of a set $X\in {\mathbb{Z}}^n$, which can play an important role in digital topology.

Theorem 1.

[8] Given a set $X\subset {\mathbb{Z}}^n$, let us consider the two digital connectivities of X such as $k(t_1,n)$ and $k(t_2,n)$ with $t_1<t_2$ (see the property of (1)). Naively, we can assume the two digital images $(X,k_1:=k(t_1,n))$ and $(X,k_2:=k(t_2,n))$. Further consider a $k_1$-continuous self-map of $(X,k_1)$ and a $k_2$-continuous self-map of $(X,k_2)$. Then, neither of them implies the other.

In order to discuss some errors in the literature written by L. Boxer [31], we need to recall the following. We say that a nonempty digital image $(X,k)$ has the almost fixed point property (AFPP for brevity) if every k-continuous self-map f of $(X,k)$ has a point $x\in X$ such that $f(x)=x$ or $f(x)$ is k-adjacent to x[18]. Then, a paper [18] proved that a digital screen $(X:={[a,b]}_{\mathbb{Z}}\times {[c,d]}_{\mathbb{Z}},8)$ has the AFPP. Motivated by this research, the paper [7] has generalized it as follows:

Theorem 2.

[7] For $n\in \mathbb{N}$, the n-dimensional digital cube with k-adjacency $(X:={[-1,1]}_{\mathbb{Z}}^n,k)$ on ${\mathbb{Z}}^n$ has the AFPP if and only if $k=3^n-1$.

Indeed, this assertion is correct. Moreover, this fact plays an important role in digital geometry. A paper [31] also agrees that this assertion holds. Despite this fact, Boxer [31] mentions that the proof of this theorem in [7] has some errors or unclear. However, it is clear that Boxer’s argument is false. More explicitly, let us set the false straightfoward more precisely, as follows:

• As for this comment on the page 362 of the paper [31], we now state that Boxer’s argument is false because he seems to read Han’s proof in [7] incorrectly.

  (1)

  The proof of this theorem in [7] is correct. More explicitly, as we can see the proof in [7] as well as Theorem 1 above, given a set X in ${\mathbb{Z}}^3$, Han [7] does not say that every 6-continuous map implies an 18-continuous map. As mentioned in Theorem 1, for instance, given a set X in ${\mathbb{Z}}^3$, assume a 6-continuous self-map of $(X,6)$ and an 18-continuous self-map of $(X,18)$. Then, in general, neither of them implies the other (for more details, see Figure 2 in [8]). Indeed, although every 6-continuous map need not imply 18-continuous, depending on the situation, a certain 6-continuous map can be an 18-continuous map. For instance, given the set $Y:={[-1,1]}_{\mathbb{Z}}^3$ and the given maps g of (7), h of (8), and r of (9) in [7], the composite $r\circ h\circ g:(Y,18)\to (Y,18)$ in the proof of Theorem 2 in [7] is clearly 18-continuous. Indeed, Example 3.1 of [31] is not related to Han’s assertion in [7] (for more details see the proof of [8] and Figure 2 of [8]).

  (2)

  Boxer [31] also incorrectly argues about Han’s second proof in [7] related to Theorem 2. Since the method of suggesting a counterexample againt a certain assertion is obviously a kind of typical proof, Han’s proof taken in [7] can be acceptable because the counterexample considered in ${\mathbb{Z}}^3$ can be enough to prove Theorem 2. Besides, a paper [7] further explains an n-dimensional case.

To classify digital images $(X,k)$ [6], we often use the notion of a $(k_0,k_1)$-isomorphism (or k-isomorphism) as in [6], as follows:

Definition 1.

[6] ($(k_0,k_1)$-homeomorphism in [32]) Consider two digital images $(Z,k_0)$ and $(W,k_1)$ in ${\mathbb{Z}}^{n_0}$ and ${\mathbb{Z}}^{n_1}$, respectively. Then, a map $h:Z\to W$ is called a $(k_0,k_1)$-isomorphism if h is a $(k_0,k_1)$-continuous bijection and further, $h^{-1}:W\to Z$ is $(k_1,k_0)$-continuous. Then, we use the notation $Z{\approx }_{(k_0,k_1)}W$. In the case $k:=k_0=k_1$, we use the notation $Z{\approx }_{k}W$ to abbreviate $Z{\approx }_{(k_0,k_1)}W$.

The notion of (strict) digital wedge (or one point union of two digital images was initially proposed in [5,33]. Given two digital images $(X,k)$ and $(Y,k)$, a digital wedge (or one point union of digital images), denoted by $(X\vee Y,k)$, is defined [5,33] as the union of the digital images $(X^{\prime },k)$ and $(Y^{\prime },k)$, where

(1)

$X^{\prime }\cap Y^{\prime }$ is a singleton, say $\left\{p\right\}$.

(2)

$X^{\prime }\backslash \left\{p\right\}$ and $Y^{\prime }\backslash \left\{p\right\}$ are not k-adjacent, where two subsets A and B of $(X,k)$ is k-adjacent if $A\cap B=\varnothing$ and there are at least two points $a\in A$ and $b\in B$ such that a is k-adjacent to b [13].

(3)

$(X^{\prime },k)$ is k-isomorphic to $(X,k)$ and $(Y^{\prime },k)$ is k-isomorphic to $(Y,k)$ (see Definition 1).

In view of this process, we may finally consider $(X\vee Y,k)$ to be a digital object $(X^{\prime }\vee Y^{\prime },k)$ using these $(X^{\prime },k)$ and $(Y^{\prime },k)$. In this paper we only deal with this digital wedge which is quite different from the typical one point union in classical topology [34].

In digital topology, we are strongly required to follow this digital wedge $(X\vee Y,k)$. If we do not follow this approach, we will get some big difficulties in proceeding with further works in digital topology. Meanwhile, in the case of $(X,k_0)$ and $(Y,k_1)$ such that $k_0\ne k_1$, the compatible k-adjacency of $(X\vee Y,k)$ was also established. More precisely, for $l\in {\mathbb{N}}_1$, since no $C_{2n}^{n,l}$ exists, given $C_k^{n,l_1}\vee C_k^{n,l_2}$ such that $l_1\in {\mathbb{N}}_1$ and $l_2\in {\mathbb{N}}_0$, depending on the numbers $l_i,i\in \{1,2\}$, we can consider many types of $C_k^{n,l_1}\vee C_k^{n,l_2}$ (for more details, see the property (4) of [8]).

Based on the pointed digital k-homotopy in [9,10,11] (see also [32]), the concept of k-homotopy relative to a subset $A\subset X$ is established, as follows:

Definition 2.

[5,32] Let $((X,A),k_0)$ and $(Y,k_1)$ be a digital image pair and a digital image in ${\mathbb{Z}}^{n_0}$ and ${\mathbb{Z}}^{n_1}$, respectively. Let $f,g:X\to Y$ be $(k_0,k_1)$-continuous functions. Suppose there exist $m\in \mathbb{N}$ and a function $H:X\times {[0,m]}_{\mathbb{Z}}\to Y$ such that

(●1)

for all $x\in X,H(x,0)=f(x)$ and $H(x,m)=g(x)$;

(●2)

for all $t\in {[0,m]}_{\mathbb{Z}}$, the induced function $H_t:X\to Y$ given by $H_t(x)=H(x,t)$ for all $x\in X$ is $(k_0,k_1)$-continuous;

(●3)

for all $x\in X$, the induced function $H_x:{[0,m]}_{\mathbb{Z}}\to Y$ given by $H_x(t)=H(x,t)$ for all $t\in {[0,m]}_{\mathbb{Z}}$ is $(2,k_1)$-continuous.

Then, H is said to be a $(k_0,k_1)$-homotopy between f and g [32].

(●4)

Furthermore, for all $t\in {[0,m]}_{\mathbb{Z}}$, $H_t(x)=f(x)=g(x)$ for all $x\in A$ and for all $t\in {[0,m]}_{\mathbb{Z}}$ [5].

Then, we call H a $(k_0,k_1)$-homotopy relative to A between f and g, and f and g are said to be $(k_0,k_1)$-homotopic relative to A in Y, $f{\simeq }_{(k_0,k_1)rel.A}g$ in symbols [29].

In Definition 2, in the case $k:=k_0=k_1$ and $n_0=n_1$, we call a k-homotopy to abbreviate $(k_0,k_1)$-homotopy. In addition, if $A=\left\{x_0\right\}\subset X$, then we say that F is a pointed $(k_0,k_1)$-homotopy at $\left\{x_0\right\}$ [32]. When f and g are pointed $(k_0,k_1)$-homotopic in Y, we use the notation $f{\simeq }_{(k_0,k_1)}g$. In the case $k:=k_0=k_1$ and $n_0=n_1$, f and g are said to be pointed k-homotopic in Y and we take the symbol $f{\simeq }_{k}g$ to abbreviate $f{\simeq }_{(k_0,k_1)}g$. If, for some $x_0\in X$, $1_X$ is k-homotopic to the constant map in the space X relative to $\left\{x_0\right\}$, then $(X,x_0)$ is said to be pointed k-contractible [32]. Indeed, taking this approach, the concept of strong k-deformation retract was developed in [29].

Based on this k-homotopy, the notion of digital homotopy equivalence firstly introduced in [35] (see also [36]), as follows:

Definition 3.

[35] (see also [36]) Given two digital images $(Z,k)$ and $(W,k)$, if there are k-continuous maps $h:Z\to W$ and $l:W\to Z$ such that the composite $l\circ h$ is k-homotopic to $1_Z$ and the composite $h\circ l$ is k-homotopic to $1_W$, then the map $h:Z\to W$ is called a k-homotopy equivalence and is denoted by $Z{\simeq }_{k·h·e}W$. Besides, $(Z,k)$ is said to be k-homotopy equivalent to $(W,k)$ or $(Z,k)$ is the same k-homotopy types with $(W,k)$. If the identity map $1_Z$ is k-homotopy equivalent to a certain constant map $c_{\left\{z_0\right\}},z_0\in Z$, we say that $(Z,k)$ is k-contractible.

Based on the several concepts such as a digital k-homotopy class [9,10,11], a Khalimsky operation of two k-homotopy classes [9], a trivial extension [32], the paper [32] defined the digital k-fundamental group, denoted by ${\pi }^k(X,x_0),x_0\in X$. Also, we have the following: If X is pointed k-contractible, then it is clear that ${\pi }^k(X,x_0)$ is a trivial group [32]. A recent paper written by the present author recently proposed the most simplified axiom for a digital covering space. Using the homotopy lifting theorem [4] and the unique digital lifting theorem [5] in digital covering theory [5], we obtain the following [5,29,33]:

Theorem 3.

(1) 

For a non-k-contractible $C_k^{n,l}$, ${\pi }^k(C_k^{n,l})$ is an infinite cyclic group [5].

(2) 

Given $C_k^{n,l}$, ${\pi }^k(C_k^{n,l})$ is trivial if and only if $l=4$ [5,32]. Namely, $C_k^{n,l}$ is k-contractible if and only if $l=4$.

(3) 

For non-k-contractible $C_k^{n,l_i},i\in \{1,2\}$, ${\pi }^k(C_k^{n,l_1}\vee C_k^{n,l_2})$ is a free group generated by two generators with infinite orders, i.e., ${\pi }^k(C_k^{n,l_1}\vee C_k^{n,l_2})$ is isomorphic to the free group $\mathbb{Z}*\mathbb{Z}$ [5].

This result is essential to characterizing an alignment of fixed point sets in Section 5. Regarding Theorem 3, for instance, $C_4^{2,4}$ has the trivial group and further, $C_{3^n-1}^{n,4}$ also has the trivial group, $n\ge 2$ [4,5,32]. Hence, we have ${\pi }^4(C_4^{2,8}\vee C_4^{2,8})$ and ${\pi }^8(C_8^{2,8}\vee C_8^{2,6})$ which are infinite free groups with two generators. In other words, ${\pi }^4(C_4^{2,8}\vee C_4^{2,4})$ is isomorphic to the infinite cyclic group $\mathbb{Z}$ and each ${\pi }^4(C_4^{2,8}\vee C_4^{2,8})$ and ${\pi }^8(C_8^{2,8}\vee C_8^{2,6})$ is isomorphic to the free group with two generators, $\mathbb{Z}*\mathbb{Z}$. In view of Theorem 3, we obtain the following:

Remark 1.

For a given $C_k^{2,l},k\in \{4,8\}$, we obtain the following:

(1) 

${\pi }^4(C_4^{2,l}\vee C_4^{2,4})$ is an infinite cyclic group with an infinite order if and only if $l\ge 8$.

(2) 

${\pi }^8(C_8^{2,l}\vee C_8^{2,4})$ is an infinite cyclic group with an infinite order if and only if $l\ge 6$.

Theorem 4.

[7] A k-isomorphism preserves a k-homotopy, k-contractibility, and a k-homotopy equivalence.

Corollary 1.

A $(k_1,k_2)$-isomorphism preserves a $(k_1,k_2)$-homotopy and a $(k_1,k_2)$-homotopy equivalence, and it transforms $k_1$-contractibility into $k_2$-contractibility.

3. Characterizations of $\mathit{I}\mathit{s}{\mathit{o}}_{\mathit{k}}(\mathbf{·})$: $\mathit{I}\mathit{s}{\mathit{o}}_{\mathit{k}}({\mathit{C}}_{\mathit{k}}^{\mathit{n}\mathbf{,}\mathit{l}})$ Is Isomorphic to the Dihedral Group ${\mathit{D}}_{\mathit{l}}$

This section focuses on characterizing a group of the set of all self-k-isomorphisms of $X:=(X,k)$, denoted by $Is{o}_k(X):=(Is{o}_k(X),\circ )$, i.e., an automorphism group of $(X,k)$ in a $DTC(k)$ setting. Given a digital image $X:=(X,k)$, the computation of $Is{o}_k(X)$ is a very important step for the self-k-isomorphisms classifications of digital images. Indeed, the group $Is{o}_k(X)$ is also essential for studying fixed points of continuous self-maps of digital images $X:=(X,k)$ (see Section 5).

Comparing with the group of the set of homeomorphisms for typical topological spaces, a digital topological analogue of it has its own features. Hence, motivated by the research of the group of the set of self-homeomorphisms of a topological space [37], given a finite digital image $X:=(X,k)$, we firstly need to characterize a group structure of the set of self-k-isomorphisms of X. Based on this work (see Remark 2 and Theorem 5), we further apply this structure to the fields of group theory, homotopy theory, fixed point theory (see Section 5) and applied sciences.

In particular, given $C_k^{n,l}$, we will intensively explore some properties of

$$Is{o}_k^{n,l}:=(Is{o}_k(C_k^{n,l}),\circ )\mathrm{or}Au{t}_k^{n,l}:=(Au{t}_k(C_k^{n,l}),\circ ).$$

Namely, we will prove that the group $Is{o}_k^{n,l}$ has two generators $\alpha$ and $\delta$ with orders l and 2, respectively, such that $\delta \alpha {\delta }^{-1}={\alpha }^{-1}$ (or ${(\alpha \delta )}^2=e$). After recognizing some strong relationships between $Is{o}_k^{n,l}$ and the standard dihedral group $D_l$ with respect to the multiplication tables and the sizes of them, we prove that they are isomorphic to each other.

Given a digital image $X:=(X,k)$, we define the following:

Definition 4.

For $X:=(X,k)$, let $Is{o}_k(X)$ be the set $\left\{f\right|f:X\to X\mathrm{is}\mathrm{a}k-\mathrm{isomorphism}.\}$. Consider the function composition, denoted by “$\circ$”, as a binary operation on $Is{o}_k(X)$.

Then, we obviously obtain the following:

Lemma 1.

$Is{o}_k(X):=(Is{o}_k(X),\circ )$ is a group.

Proof. 

It is obvious that $Is{o}_k(X)$ forms a group with the function composition for a group operation. Then, we clearly observe that the identity map $1_X$ is the identity element of the group. □

We will often use the notation ${\mathbb{Z}}_m:=\{0,1,\dots ,m-1\}$ instead of $({\mathbb{Z}}_m,+)$ which is the finite cyclic group with the operation “$+$”, as usual.

Remark 2.

Let $(X,k)$ be a simple k-path which is not a singleton. Then, $Is{o}_k(X)$ is isomorphic to the finite cyclic group ${\mathbb{Z}}_2$.

Proof. 

Let $(X:={(x_t)}_{t\in {[0,l-1]}_{\mathbb{Z}}},k)$ be a simple k-path on ${\mathbb{Z}}^n$ such that $X^{♯}=l,l\in \mathbb{N}\backslash \left\{1\right\}$. Then, we have the typical identity map $1_X$ and further, another self-k-isomorphism h of X such that $h(x_t)=x_{l-t-1},t\in {[0,l-1]}_{\mathbb{Z}}$, which completes the proof. □

It is important to recognize and understand certain key features of $Is{o}_k(C_k^{n,l})$. Hence, for any $C_k^{n,l}$, we now intensively explore some properties of $Is{o}_k^{n,l}:=Is{o}_k(C_k^{n,l})$. Before studying this issue, let us recall some properties of the dihedral group $D_l$ with $2l$ elements, $l\ge 4$. To be precise, $D_l$ indeed consists of two generators r and s with order l and 2, respectively, such that $sr{s}^{-1}=r^{-1}$. Indeed, $D_l$ is produced by $2l$ symmetries from a regular l-gon in ${\mathbb{R}}^2$ [38]. Namely, “$r$” and “$s$" represent the rotations and the reflections of this regular l-gon, respectively.

Based on this geometric definition of $D_l$, to make a good combination between this geometric definition for $D_l$ and that of $Is{o}_k^{n,l}$ with respect to relations of the two groups, $l\ge 4$, we recall $D_l$, as follows:

$$\left\{\begin{array}{c}{D}_l:=<r,s|r^l=e=s^2,sr{s}^{-1}=r^{-1}>\hfill \\ =\{r^i,s_i|s_i=r^i{s}_0,i\in {[0,l-1]}_{\mathbb{Z}}\},\mathrm{with}\mathrm{the}\mathrm{property}{r}^i\hfill \\ r^j=r^{i+j},r^i{s}_j=s_{i+j},s_i{r}^j=s_{i-j},\mathrm{and}{s}_i{s}_j=r^{i-j},\hfill \\ \mathrm{where}\mathrm{the}\mathrm{subscripts}\mathrm{and}\mathrm{the}\mathrm{superscripts}\mathrm{are}\mathrm{always}\mathrm{read}\mathrm{modulo}l.\hfill \end{array}\right\}$$

(4)

The relation “$sr{s}^{-1}=r^{-1}$” in (4) can be equivalently considered as “$rsr=s$”, “${(sr)}^2=e$”, or “$srs=r^{-1}$”. However, for convenience in the paper we will follow the relation taken in (4). Furthermore, the equation $s_i=r^i{s}_0$ has strong advantages in comparing $D_l$ and $Is{o}_k^{n,l}$, we certainly follow the equality. This presentation of (4) indeed plays an important role in making a good combination between $D_l$ and $Is{o}_k^{n,l}:=Is{o}_k(C_k^{n,l})$. Motivated by this approach, let us move onto the study of rotations and reflections of $C_k^{n,l}$ formulating $Is{o}_k^{n,l}$. 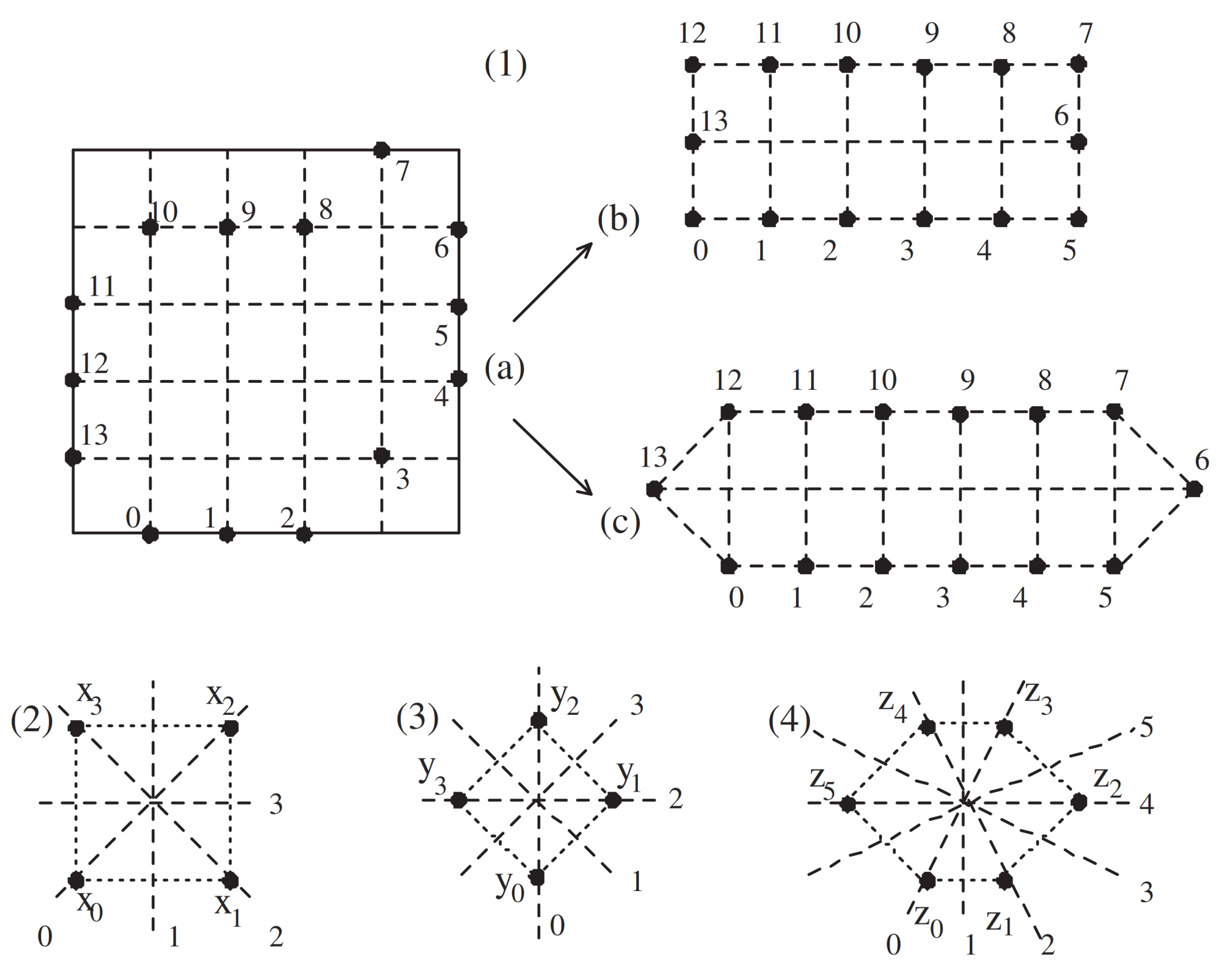For convenience, firstly reshape $C_k^{n,l}:={(x_i)}_{i\in {[0,l-1]}_{\mathbb{Z}}}$ into like a (digital) rectangle or a virtual l-gon (need not be regular) on ${\mathbb{Z}}^2$ up to k-isomorphism (see Figure 1(1) and Figure 2). One important thing to note is that this reshaped object need not be a regular l-gon. According to the number l of $C_k^{n,l}$, based on the reshaped object from $C_k^{n,l}$, we can efficiently consider special kinds of rotations and reflections (or symmetries, or diagonal like flips) of $C_k^{n,l}$ (see Figure 1(1) and Figure 2). Indeed, this kind of consideration can be acceptable because a digital $(k_1,k_2)$-isomorphism $h:C_{k_1}^{n_1,l}\to C_{k_2}^{n_2,l}$ induces a group isomorphism $h_{*}:Is{o}_{k_1}^{n_1,l}\to Is{o}_{k_2}^{n_2,l}$ (for details see Theorem 6 and Corollary 2). Furthermore, these rotations and symmetries are different from those related to a regular l-gon with some angle producing a traditional dihedral group $D_l$ as mentioned above (for details see Remark 3). Based on a self-k-isomorphism of $C_k^{n,l}$, $Is{o}_k(C_k^{n,l})$ is produced by l rotations of $C_k^{n,l}$ and l reflections of $C_k^{n,l}$. Hence, our work that is strongly involved in $Is{o}_k^{n,l}$ related to the presentation of $D_l$ in (4). Indeed, owing to a k-isomorphism of $C_k^{n,l}$ and the reshaped simple closed 4- or 8-curve with l elements in ${\mathbb{Z}}^2$, the current rotations should proceed with special types of rotations with some angles depending on the situation (see Figure 1(1)(a)–(c) and Figure 2) or special kinds of symmetries with some different angles depending on the situation (see Figure 1(4)).

The next theorem plays an important role in establishing many results later.

Theorem 5.

Given $C_k^{n,l},l\ge 4$, $Is{o}_k^{n,l}:=Is{o}_k(C_k^{n,l})$ is isomorphic to the dihedral group $D_l$.

When proving the assertion, we will count on both l rotational symmetries and l reflection symmetries which are slightly different from those associated with the typical dihedral group with respect to the angles associated with the rotations and the reflections (for details see Remark 3).

Proof. (Case 1) Let us consider the case $l\in {\mathbb{N}}_0\backslash \left\{2\right\}$.

(Case 1-1) [l rotational symmetries of $C_k^{n,l}$ with respect to the k-isomorphism of $C_k^{n,l}$]

Let us consider the following self-k-isomorphism of $C_k^{n,l}:={(x_t)}_{t\in {[0,l-1]}_{\mathbb{Z}}}$ as l rotational symmetries.

With $l\ge 4$, for $i\in {[0,l-1]}_{\mathbb{Z}}$, assume the map

$${\alpha }^i,\mathrm{such}\mathrm{that}{\alpha }^i(x_t)=x_{i+t(\mathrm{mod}l)},t\in {[0,l-1]}_{\mathbb{Z}}.$$

(5)

Based on (5), we obtain the set

$$A:=\left\{{\alpha }^i\right|{({\alpha }^i)}^l=e=1_{C_k^{n,l}},i\in {[0,l-1]}_{\mathbb{Z}}\}$$

(6)

Then, further consider the function composition for A as a binary operation on A, denoted by ∘. Next, we may consider the set A in (6) with the operation “∘” to be a cyclic group with a generator $\alpha$. Namely, using the following operation,

$$\alpha \circ {\alpha }^m:={\alpha }^{m+1(\mathrm{mod}l)}:=\alpha {\alpha }^m,m\in {[0,l-1]}_{\mathbb{Z}}\mathrm{with}{({\alpha }^m)}^l=e=1_{C_k^{n,l}},$$

we finally recognize that the pair $(A,\circ )$ is equivalent to the cyclic group $<\alpha >$ with degree l. Indeed, $<\alpha >$ is a cyclic subgroup of $Is{o}_k^{n,l}:=Is{o}_k(C_k^{n,l})$ such that ${\alpha }^l=e$.

(Case 1-2) [l reflection symmetries of $C_k^{n,l}$ with respect to the k-isomorphism of $C_k^{n,l}$]

Based on the reshaped digital-based rectangle or a virtual l-gon (see Figure 1(1)), according to the reflections (diagonal like flips with some angles) of $C_k^{n,l}$ up to k-isomorphism (see the picture in Figure 1(2)–(4)), we obviously have only l types of self-k-isomorphisms of $C_k^{n,l}$. For convenience, we may admit l types of certain reflection symmetries using some diagonal-like flips with some angles. These angles need not be constant, which is quite different from the geometric definition of $D_l$. Indeed, we only need take the reflections of $C_k^{n,l}$ as k-isomorphisms of $C_k^{n,l}$, as follows (see Figure 1(2)–(4)):

$$\left\{\begin{array}{c}{\delta }_0\mathrm{is}\mathrm{the}\mathrm{reflection}\hfill \\ \mathrm{based}\mathrm{on}\mathrm{the}\mathrm{axis}\mathrm{joining}\mathrm{the}\mathrm{two}\mathrm{points}{x}_0,x_{\frac{l}{2}};\hfill \\ {\delta }_1\mathrm{is}\mathrm{the}\mathrm{reflection}\mathrm{using}\mathrm{a}\mathrm{mirror}\mathrm{axis}\mathrm{in}\mathrm{bisection}\hfill \\ \mathrm{between}\mathrm{the}\mathrm{two}\mathrm{virtual}\mathrm{line}\mathrm{segments}\overline{x_0{x}_1}\mathrm{and}\overline{x_{\frac{l}{2}}{x}_{\frac{l}{2}+1}};\hfill \\ {\delta }_2\mathrm{is}\mathrm{the}\mathrm{reflection}\hfill \\ \mathrm{about}\mathrm{the}\mathrm{axis}\mathrm{formulated}\mathrm{by}\mathrm{the}\mathrm{two}\mathrm{points}{x}_1,x_{\frac{l}{2}+1};\hfill \\ \cdots \hfill \\ {\delta }_{l-2}\mathrm{is}\mathrm{the}\mathrm{reflection}\hfill \\ \mathrm{w}.\mathrm{r}.\mathrm{t}.\mathrm{the}\mathrm{axis}\mathrm{joining}\mathrm{the}\mathrm{two}\mathrm{points}{x}_{\frac{l}{2}-1},x_{l-1};\mathrm{and}\hfill \\ {\delta }_{l-1}\mathrm{is}\mathrm{the}\mathrm{reflection}\mathrm{using}\mathrm{a}\mathrm{mirror}\mathrm{axis}\mathrm{in}\mathrm{bisection}\hfill \\ \mathrm{between}\mathrm{the}\mathrm{two}\mathrm{virtual}\mathrm{line}\mathrm{segments}\overline{x_{\frac{l}{2}-1}{x}_{\frac{l}{2}}}\mathrm{and}\overline{x_{l-1}{x}_0}.\hfill \end{array}\right\}$$

(7)

Then, it is clear that the map ${\delta }_i$ in (7) is a self-k-isomorphism of $C_k^{n,l}$ because the generator $\delta \in Is{o}_k^{n,l}$ is termed by “diagonal flip”. Then, owing to the reflection ${\delta }_i$ from (7), we obtain the paired set $(B,\circ )$, where

$$B:=\left\{{\delta }_i\right|{\delta }_i^2=1_{C_k^{n,l}},\alpha {\delta }_i={\delta }_{i+1(\mathrm{mod}l)},i\in {[0,l-1]}_{\mathbb{Z}}\}.$$

(8)

Owing to (8), we observe the property

$${\delta }_i{\delta }_{i+1(\mathrm{mod}l)}\ne {\delta }_{i+1(\mathrm{mod}l)}{\delta }_i.$$

Besides, the cosets $<\alpha >$ and $<\alpha >{\delta }_i,i\in {[0,l-1]}_{\mathbb{Z}}$, exhaust all of the set $Is{o}_k^{n,l}=A\cup B$, $A\cap B=\varnothing$, and ${(Is{o}_k^{n,l})}^{♯}=2l$ (see the multiplication table for the elements of $Is{o}_8^{2,4}$ in Figure 3 and $Is{o}_8^{2,6}$ in Figure 4). Hence,. due to (6) and (8), it turns out that the elements $\alpha \in A$ and ${\delta }_0\in B$ are generators for the group $Is{o}_k^{n,l}$ with $2l$ elements because the element $\alpha$ has the order l and each ${\delta }_i$ has the order 2 and further, ${\delta }_i={\alpha }^i{\delta }_0,i\in {[0,l-1]}_{\mathbb{Z}}$. At the moment, let us explore the relation among elements of $Is{o}_k^{n,l}$ from (6) and (7) (see the multiplication tables for $Is{o}_8^{2,4}$ in Figure 3 and $Is{o}_8^{2,6}$ in Figure 4), as follows: For $i,j\in {[0,l-1]}_{\mathbb{Z}}$, the following properties are obtained (see Figure 3 and Figure 4).

$$\left\{\begin{array}{c}{\alpha }^l=e={\delta }_i^2={(\alpha {\delta }_i)}^2;\hfill \\ {\alpha }^i{\alpha }^j={\alpha }^{i+j(\mathrm{mod}l)};\hfill \\ {\alpha }^i{\delta }_j={\delta }_{i+j(\mathrm{mod}l)};\hfill \\ {\delta }_i{\alpha }^j={\delta }_{i-j(\mathrm{mod}l)};\hfill \\ {\delta }_i{\delta }_j={\alpha }^{i-j(\mathrm{mod}l)};\mathrm{and}\hfill \\ {\delta }_i{\delta }_{i+1(\mathrm{mod}l)}\ne {\delta }_{i+1(\mathrm{mod}l)}{\delta }_i.\hfill \end{array}\right.$$

(9)

The order of the elements of $Is{o}_k^{n,l}$ denoting the composition is right to left, as usual. Eventually, owing to the properties (9), the group $Is{o}_k^{n,l}:=(Is{o}_k^{n,l},\circ )$ has the following presentation.

$$\left\{\begin{array}{c}Is{o}_k^{n,l}:=<\alpha ,\delta |{\alpha }^l=e={\alpha }^0={\delta }^2,{(\alpha \delta )}^2=e>\hfill \\ =\{{\alpha }^i,{\delta }_j|{\delta }_i={\alpha }^i{\delta }_0,i,j\in {[0,l-1]}_{\mathbb{Z}}\},\hfill \\ \mathrm{with}\mathrm{the}\mathrm{following}\mathrm{property}:\hfill \\ {\alpha }^i{\alpha }^j={\alpha }^{i+j},{\alpha }^i{\delta }_j={\delta }_{i+j},{\delta }_i{\alpha }^j={\delta }_{i-j},\mathrm{and}{\delta }_i{\delta }_j={\alpha }^{i-j},\hfill \\ \mathrm{where}\mathrm{all}\mathrm{cases}\mathrm{of}\mathrm{subtractions}\mathrm{and}\mathrm{additions}\mathrm{of}\mathrm{subscripts}\mathrm{and}\hfill \\ \mathrm{superscripts}\mathrm{are}\mathrm{always}\mathrm{read}\mathrm{by}\mathrm{using}\mathrm{modular}\mathrm{arithmetic}\mathrm{with}\mathrm{modulo}l.\hfill \end{array}\right\}$$

(10)

Naively, it is clear that $Is{o}_k^{n,l}$ is a finite group whose degree is equal to $2l$. Comparing the properties of (4) and those of (10), it is obvious that they are equivalent. In view of the group presentation of $Is{o}_k^{n,l},l\ge 4$, owing to the property ${\delta }_i{\delta }_{i+1(\mathrm{mod}l)}\ne {\delta }_{i+1(\mathrm{mod}l)}{\delta }_i$, we see that $Is{o}_k^{n,l}$ is not abelian. Indeed, since $Is{o}_k^{n,l}$ has the property of (10) and $Is{o}_k^{n,l}$ has the same size as $D_l$ with respect to their multiplication tables (see the tables in Figure 3 and Figure 4), we can establish a homomorphism from $D_l$ to $Is{o}_k^{n,l}$ which leads to an isomorphism because they have the same order $2l$ and same numbers of generators with same orders. Writing down an explicit homomorphism from $D_l$ to $Is{o}_k^{n,l}$, we now prove an isomorphism between $D_l$ of (4) and $Is{o}_k^{n,l}$ of (10) in the following way: consider the map

$$h:D_l\to Is{o}_k^{n,l}$$

defined by

$$h(r)=\alpha ,h(s)=\delta \mathrm{so}\mathrm{that}h(r^i{s}_k)={\alpha }^i{\delta }_k,i,k\in {[0,l-1]}_{\mathbb{Z}},$$

(11)

which leads to a homomorphism from $D_l$ to $Is{o}_k^{n,l}$. Let us now check if h is surjective. Since each element of $Is{o}_k^{n,l}$ has the form ${\alpha }^i{\delta }_k$ which is mapped by the established-map h, this mapping of h is eventually a surjection to lead to an isomorphism between $D_l$ and $Is{o}_k^{n,l}$.

(Case 2) Let us consider the case $l\in {\mathbb{N}}_1\backslash \{1,3\}$.

(Case 2-1) [l rotational symmetries of $C_k^{n,l}$ with respect to the k-isomorphism of $C_k^{n,l}$]

Using the methods referred to in (5) and (6), given the assumption, we obtain l rotations of $C_k^{n,l}$ (see Figure 2(b)), which completes the proof.

(Case 2-2) [l reflection symmetries of $C_k^{n,l}$ with respect to the k-isomorphism of $C_k^{n,l}$]

Indeed, the l reflection symmetries of $C_k^{n,l}$, $l\in {\mathbb{N}}_1$, are similarly considered to those of $C_k^{n,l}$, $l\in {\mathbb{N}}_0$, as stated in (Case 1-2) (see (7)). However, as compared with the reflections referred to in (7), the current reflections are slightly different from the reflections referred to in (6) because of the odd number of l (compare Figure 1(2)–(4) and Figure 2(c)). □

Based on Theorem 5, let us now compare a geometric definition of $D_l$ and that of $Is{o}_k^{n,l}$.

Remark 3.

[Comparison a geometric definition of $Is{o}_k^{n,l}$ and that of $D_l$]

(1) 

As for the rotations r producing $D_l$, first of all, recall the geometric definition producing $D_l$ stated in (4). Meanwhile, as to the rotations of $Is{o}_k^{n,l}$, the element $\alpha \in Is{o}_k^{n,l}$(see (6)) is termed the rotation or the generator of the cyclic piece of $Is{o}_k^{n,l}$ (see (6)). However, there are some difference between $\alpha \in Is{o}_k^{n,l}$ and $r\in D_l$ with respect to the angles of the rotations. To be precise, let $P:=\left\{p_i\right|i\in {[0,l-1]}_{\mathbb{Z}}\}$ be a regular l-gon with vertex $p_i\in P$ on the plane. In the case $r^k\in D_l$, with P, the rotation r proceeds evenly over $\frac{2\pi k}{n}$ angle. Namely, each of the vertices $p_i$ on P is transformed in terms of the one click counterclockwise movement on P by a constant angle.

Meanwhile, in the case $\alpha :={\alpha }^i\in Is{o}_k^{n,l}$, the element α is a self-k-isomorphism of $C_k^{n,l}$ being mapped as in (5). Thus, we may recognize $\alpha \in Is{o}_k^{n,l}$ as one click movement of points of $C_k^{n,l}$ in the counterclockwise direction (see the map $f_1$ in (5) and Figure 2(b) as an example). However, in light of these rotations, $\alpha \in Is{o}_k^{n,l},\alpha \in \left\{{\alpha }^i\right|i\in {[1,l-1]}_{\mathbb{Z}}\}$, is equivalent (not equal) to $r\in D_l$ because ${\alpha }^l=e=r^l$. Meanwhile, unlike $r\in D_l$ (see (4)), the rotation α need not proceed evenly over a certain angle on the plane, which is a slightly different from the rotation r of $D_l$.

(2) 

Comparing $s_i\in D_l$ and ${\delta }_i\in Is{o}_k^{n,l}$, we see only one difference between them with respect to the reflection angle (see Figure 1 (4) and Figure 2(c)).

Example 1.

$Is{o}_8^{2,6}:=Is{o}_k(C_8^{2,6})$ is isomorphic to the dihedral group $D_6$.

(Case 1) [Rotation as an 8-isomorphism of $C_8^{2,6}$]

Let us consider the following self-map ${\alpha }^i$ of $C_8^{2,6}:={(z_t)}_{t\in {[0,5]}_{\mathbb{Z}}}$ defined in the following way (see Figure 1 (4)). For instance, consider six rotations of $C_8^{2,6}$ (see Figure 1 (4)), as follows: For $i\in {[0,5]}_{\mathbb{Z}}$,

$${\alpha }^i\mathrm{such}\mathrm{that}{\alpha }^i(z_t)=z_{t+i(\mathrm{mod}6)},t\in {[0,5]}_{\mathbb{Z}}.$$

(12)

Then, the map ${\alpha }^i$ of $(12)$ is a self-8-isomorphism of $C_8^{2,6}$. From (12), we obtain the pair $(A,\circ )$, where

$$A:=\left\{{\alpha }^i\right|e:={\alpha }^0=1_{C_8^{2,6}},i\in {[0,5]}_{\mathbb{Z}}\},$$

(13)

which makes $(A,\circ )$ the cyclic group $<\alpha >$ with ${({\alpha }^i)}^6=1_{C_8^{2,6}}$. Then, we clearly obtain $A^{♯}=6$.

(Case 2) [Some reflections (diagonal like flips) of $C_8^{2,6}$]

Based on the reshaped digital-based rectangle (see Figure 1(1)(a) → (b) or (c) as an example) according to the 8-isomorphism of $C_8^{2,6}$, we obviously have only six types of reflections as self-8-isomorphisms of $C_8^{2,6}$ (see the picture in Figure 1(4)). To be precise, we may represent these reflections more precisely in the following way (see Figure 1(4)).

$$\left\{\begin{array}{c}{\delta }_0\mathrm{is}\mathrm{the}\mathrm{reflection}\mathrm{about}\mathrm{the}\mathrm{diagonal}\mathrm{joining}\mathrm{the}\mathrm{points}{z}_0,z_3;\hfill \\ {\delta }_1\mathrm{is}\mathrm{the}\mathrm{reflection}\mathrm{using}\mathrm{a}\mathrm{mirror}\mathrm{axis}\mathrm{in}\mathrm{bisection}\hfill \\ \mathrm{between}\mathrm{the}\mathrm{two}\mathrm{virtual}\mathrm{line}\mathrm{segments}\overline{z_0{z}_1}\mathrm{and}\overline{z_3{z}_4}\hfill \\ (\mathrm{see}\mathrm{the}\mathrm{number}1:={\delta }_1\mathrm{in}\mathrm{Figure}(4));\hfill \\ {\delta }_2\mathrm{is}\mathrm{the}\mathrm{reflection}\mathrm{about}\mathrm{the}\mathrm{axis}\mathrm{joining}\mathrm{by}\mathrm{the}\mathrm{points}{z}_1,z_4;\hfill \\ {\delta }_3\mathrm{is}\mathrm{the}\mathrm{reflection}\mathrm{using}\mathrm{a}\mathrm{mirror}\mathrm{axis}\mathrm{in}\mathrm{bisection}\hfill \\ \mathrm{between}\mathrm{the}\mathrm{two}\mathrm{virtual}\mathrm{line}\mathrm{segments}\overline{z_1{z}_2}\mathrm{and}\overline{z_4{z}_5}\hfill \\ (\mathrm{see}\mathrm{the}\mathrm{number}3:={\delta }_3\mathrm{in}\mathrm{Figure}(4));\hfill \\ {\delta }_4\mathrm{is}\mathrm{the}\mathrm{reflection}\mathrm{about}\mathrm{the}\mathrm{axis}\mathrm{joining}\mathrm{the}\mathrm{points}{z}_2,z_5;\mathrm{and}\hfill \\ {\delta }_5\mathrm{is}\mathrm{the}\mathrm{reflection}\mathrm{using}\mathrm{a}\mathrm{mirror}\mathrm{axis}\mathrm{in}\mathrm{bisection}\hfill \\ \mathrm{between}\mathrm{the}\mathrm{two}\mathrm{virtual}\mathrm{line}\mathrm{segments}\overline{z_2{z}_3}\mathrm{and}\overline{z_5{z}_0}\hfill \\ (\mathrm{see}\mathrm{the}\mathrm{number}5:={\delta }_5\mathrm{in}\mathrm{Figure}(4)).\hfill \end{array}\right.$$

(14)

Then, it is clear that the maps ${\delta }_i,i\in {[0,5]}_{\mathbb{Z}}$ in $(14)$ are self-8-isomorphisms of $C_8^{2,6}$. Thereby, owing to (13) and (14), we obtain the pair $(B,\circ )$, where (see Figure 1(4))

$$B:=\left\{{\delta }_i\right|{\delta }_i^2=1_{C_8^{2,6}},{\delta }_i={\alpha }^i{\delta }_0,i\in {[0,5]}_{\mathbb{Z}}\}.$$

(15)

Then, it is clear that $B^{♯}=6$. Besides, owing to the partition of $Is{o}_8^{2,6}$ by the set $\{A,B\}$, we see that $Is{o}_8^{2,6}=A\cup B$. In particular, in $Is{o}_8^{2,6}$, after carefully examining the relationships among the elements of $Is{o}_8^{2,6}$, we observe the following: For $i,j\in {[0,5]}_{\mathbb{Z}}$,

$$\left\{\begin{array}{c}{\alpha }^6={\delta }_i^2=e={(\alpha {\delta }_i)}^2;\hfill \\ {\alpha }^i{\alpha }^j={\alpha }^{i+j(\mathrm{mod}l)};\hfill \\ {\alpha }^i{\delta }_j={\delta }_{i+j(\mathrm{mod}6)};\hfill \\ {\delta }_i{\alpha }^j={\delta }_{i-j(\mathrm{mod}6)};\hfill \\ {\delta }_i{\delta }_j={\alpha }^{i-j(\mathrm{mod}6)};\mathrm{and}\hfill \\ {\delta }_i{\delta }_{i+1(\mathrm{mod}6)}\ne {\delta }_{i+1(\mathrm{mod}6){\delta }_i}.\hfill \end{array}\right.$$

(16)

With the dihedral group $D_6$ of (4) in mind, using the properties in (16), using the properties from (13) and (15), we finally have the presentation, as follows:

$$Is{o}_8^{2,6}=<\alpha ,\delta |{\alpha }^6=e={\delta }^2,{(\alpha \delta )}^2=e>.$$

Comparing the relation of (4) and that of (16) and further, taking a look at the multiplication table in Figure 4, we conclude that $D_6$ is isomorphic to $Is{o}_8^{2,6}$. However, as already stated in the proof of Theorem 5, $D_6$ is not equal to $Is{o}_8^{2,6}$. More precisely, we now establish the following map

$$h(r)=\alpha ,h(s)=\delta ,\mathrm{so}\mathrm{that}h(r^i{s}_k)={\alpha }^i{\delta }_k,i,k\in {[0,5]}_{\mathbb{Z}},$$

(17)

as referred in the proof of Theorem 5. Indeed, since $Is{o}_8^{2,6}$ has two generators with the property (17) and it has the same size as $D_6$. By mapping $r\to \alpha$ and $s\to \delta$, we finally have an isomorphism between them (see the multiplication table in Figure 4).

Using a method similar to the process of Example 1, we obtain the following:

Example 2.

(1) $Is{o}_{26}^{3,5}:=Is{o}_k(C_{26}^{3,5})$ is isomorphic to the dihedral group $D_5$.

(2) $Is{o}_8^{2,7}:=Is{o}_k(C_8^{2,7})$ is isomorphic to the dihedral group $D_7$.

Theorem 6.

A k-isomorphism between $(X,k)$ and $(Y,k)$ implies an isomorphism between $Is{o}_k(X)$ and $Is{o}_k(Y)$.

Proof. 

Let $h:X:=(X,k)\to Y:=(Y,k)$ be a k-isomorphism.

Consider $f\in Is{o}_k(X)$. Then, we obtain the composite $h\circ f\circ h^{-1}\in Is{o}_k(Y)$. Thus, let us now define the map

$$h_{*}:Is{o}_k(X)\to Is{o}_k(Y)\mathrm{such}\mathrm{that}{h}_{*}(f)=h\circ f\circ h^{-1}.$$

(18)

Then, for any $f_2,f_1\in Is{o}_k(X)$, we clearly obtain $h_{*}(f_2\circ f_1)=h_{*}(f_2)\circ h_{*}(f_1)$ and further, using the property of (18), we observe that $h_{*}$ is a bijection, which completes the proof. □

By Theorem 6, we obtain the following because the identity $l_1=l_2$ obviously implies an isomorphism between $Is{o}_k(C_k^{n,l_1})$ and $Is{o}_k(C_k^{n,l_2})$, as follows:

Corollary 2.

In a $DTC(k)$ setting, $Is{o}_k(C_k^{n,l_1})$ is isomorphic to $Is{o}_k(C_k^{n,l_2})$ if and only if $l_1=l_2$.

According to Theorems 5 and 6, it is clear that $Is{o}_k(C_k^{n,l})$ depends on the number l. Thus, for a $(k_1,k_2)$-isomorphism between $C_{k_1}^{n_1,l_1}$ and $C_{k_2}^{n_2,l_2}$ we obtain the following:

Corollary 3.

Given two digital images $C_{k_i}^{n_i,l_i},i\in \{1,2\}$, $Is{o}_{k_1}(C_{k_1}^{n_1,l_1})$ is isomorphic to $Is{o}_{k_2}(C_{k_2}^{n_2,l_2})$ if and only if $l_1=l_2$.

4. Fixed Points Sets of an $\mathit{I}\mathit{s}{\mathit{o}}_{\mathit{k}}({\mathit{C}}_{\mathit{k}}^{\mathit{n},\mathit{l}})$-Action on ${\mathit{C}}_{\mathit{k}}^{\mathit{n},\mathit{l}}$ and an $\mathit{I}\mathit{s}{\mathit{o}}_{\mathit{k}}({\mathit{C}}_{\mathit{k}}^{\mathit{n},{\mathit{l}}_{\mathbf{1}}}\mathbf{\vee }{\mathit{C}}_{\mathit{k}}^{\mathit{n},{\mathit{l}}_{\mathbf{2}}})$-Action on ${\mathit{C}}_{\mathit{k}}^{\mathit{n},{\mathit{l}}_{\mathbf{1}}}\mathbf{\vee }{\mathit{C}}_{\mathit{k}}^{\mathit{n},{\mathit{l}}_{\mathbf{2}}}$

Given a digital image $(X,k)$ and ${\mathcal{D}}_k(X)\in \{Is{o}_k(X),Co{n}_k(X)\}$, for $f\in {\mathcal{D}}_k(X)$, we use the notation $Fix(f):=\{x\in X|f(x)=x\}$, where $Co{n}_k(X)$ is the set of self-k-continuous maps of $(X,k)$.

Definition 5.

Given a digital image $(X,k)$, we use the notation

$$F(Is{o}_k(X)):=\left\{Fix{(f)}^{♯}\right|f\in Is{o}_k(X)\}.$$

Let us now prove that $F(Is{o}_k(X))$ is a digital topological invariant, as follows:

Proposition 2.

In a $DTC(k)$ setting, $F(Is{o}_k(X))$ is a digital topological invariant.

Proof. 

Let $h:(X,k)\to (Y,k)$ be a k-isomorphism. Then, it suffices to prove that $F(Is{o}_k(X))$ is equal to $F(Is{o}_k(Y))$. More explicitly, consider an arbitrary $t\in F(Is{o}_k(X))$. Then there is a set $C\subset X$ such that $C^{♯}=t$, where for any $x\in C$ and a certain $f\in Is{o}_k(X)$ we have the property $f(x)=x$. Then we need to prove that the number t belongs to $F(Is{o}_k(Y))$. Furthermore, using a method similar to this approach above, we need to prove that any element s in $F(Is{o}_k(Y))$ also belongs to $F(Is{o}_k(X))$.

As mentioned above, given a number $t\in F(Is{o}_k(X))$, take the set $C\subset X$ such that $C^{♯}=t$, where for a certain $f\in Is{o}_k(X)$ we obtain that any $x\in C$ has the property $f(x)=x$. Since h is a k-isomorphism, we have $h{(C)}^{♯}=C^{♯}$. By (18), take $g:=h\circ f\circ h^{-1}$. Then, we clearly obtain $g\in Is{o}_k(Y)$. Then, for $y^{\prime }\in h(C)$, let $x^{\prime }=h^{-1}(y^{\prime })$. Since we obtain

$$g(y^{\prime })=h\circ f\circ h^{-1}(y^{\prime })=h\circ f(x^{\prime })=h(x^{\prime })=y^{\prime }.$$

(19)

Let us now put $D:=Fix(g)$, which implies that $h(C)\subset D$ so that

$$C^{♯}\le D^{♯}.$$

(20)

Similarly, for any $y^{″}\in D$, let us put $x^{″}:=h^{-1}(y^{″})$. Then, using a method similar to the process of (19), for any $g\in Is{o}_k(Y)$, after putting $f:=h^{-1}\circ g\circ h$, we obtain

$$f(x^{″})=x^{″}\mathrm{so}\mathrm{that}{h}^{-1}(D)\subset C$$

which implies that

$$D^{♯}\le C^{♯}.$$

(21)

Due to the properties of (20) and (21), we obtain that $F(Is{o}_k(Y))$ is equal to $F(Is{o}_k(X))$. □

By Theorem 6 and Proposition 2, we obtain the following:

Corollary 4.

Consider two digital images $(X,k_1),(Y,k_2)$ which are $(k_1,k_2)$-isomorphic. Then $F(Is{o}_{k_1}(X))$ is equal to $F(Is{o}_{k_2}(Y))$.

Since both $C_k^{n,l}$ and $C_k^{n,l_1}\vee C_k^{n,l_2}$ play important roles in digital geometry, let us characterize the set of cardinalities of the fixed sets of self-k-continuous maps of them.

Lemma 2.

Given $C_k^{n,l}$ with $4\le l\in {\mathbb{N}}_0$, $F(Is{o}_k(C_k^{n,l}))=\{0,2,l\}$.

Proof. 

With the hypothesis, consider $f\in Is{o}_k(C_k^{n,l})$. By Theorem 5, it is clear that $f\in A$ in (6) or $f\in B$ in (8) (see Figure 1).

(Case 1) Assume $f=1_{C_k^{n,l}}\in A$ in (6). Then we obtain $Fix{(f)}^{♯}=l$.

(Case 2) Assume $f\in \left\{{\alpha }_i\right|i\in {[1,l-1]}_{\mathbb{Z}}\}\subset A$ in (6). Then we have $Fix{(f)}^{♯}=0$.

(Case 3) Assume $f\in B$ in (8). Then we obtain $Fix{(f)}^{♯}\in \{0,2\}$. □

Unlike the above case of $4\le l\in {\mathbb{N}}_0$, for an odd number $5\le l\in {\mathbb{N}}_1$ (see also the property (2)), we obtain the following:

Lemma 3.

Given $C_k^{n,l}$ with $5\le l\in {\mathbb{N}}_1$, $F(Is{o}_k(C_k^{n,l}))=\{0,1,l\}$.

Proof. 

In the case of $5\le l\in {\mathbb{N}}_1$, the proof of $\{0,l\}\subset F(Is{o}_k(C_k^{n,l}))$ is proceeded by using a method similar to the proofs of the Cases 1 and 2 stated in the proof of Lemma 2. However, unlike the Case 3 referred to in the proof of Lemma 2, in the case that f is a reflection of $C_k^{n,l},l\in {\mathbb{N}}_1$, as shown in Figure 2(c), we obtain $Fix{(f)}^{♯}=1$. □

Based on the properties from Lemmas 2 and 3, we obtain the following:

Theorem 7.

Given $(C_k^{n,l_1}\vee C_k^{n,l_2},k)$ with $l_1=l_2\in {\mathbb{N}}_0$, $F(Is{o}_k(C_k^{n,l_1}\vee C_k^{n,l_2}))=$$\{l_1+l_2-1,l_1+1,3,1\}$.

Proof. 

Using Theorem 5 and Lemmas 2 and 3, we need to consider the following several cases.

(Case 1) Making the part $C_k^{n,l_1}$ or $C_k^{n,l_2}$ of $C_k^{n,l_1}\vee C_k^{n,l_2}$ remained, we consider a certain symmetry of $C_k^{n,l_1}\vee C_k^{n,l_2}$ referred to in (6). More explicitly, we first consider $1_{C_k^{n,l_1}\vee C_k^{n,l_2}}$ to obtain $l_1+l_2-1\in F(Is{o}_k(C_k^{n,l_1}\vee C_k^{n,l_2}))$.

Second, as another case, after fixing $C_k^{n,l_1}$ (resp.$C_k^{n,l_2}$) of $C_k^{n,l_1}\vee C_k^{n,l_2}$, we further consider a certain symmetry of the part $C_k^{n,l_2}$ (resp.$C_k^{n,l_1}$) introduced in (8) to obtain $l_1+1\in F(Is{o}_k(C_k^{n,l_1}\vee C_k^{n,l_2}))$.

(Case 2) Fixing the point in $C_k^{n,l_1}\cap C_k^{n,l_2}$ and using the property (8), we further consider the reflection of both $C_k^{n,l_1}$ and $C_k^{n,l_2}$ on themselves respectively to obtain $3\in F(Is{o}_k(C_k^{n,l_1}\vee C_k^{n,l_2}))$.

(Case 3) Fixing the point in $C_k^{n,l_1}\cap C_k^{n,l_2}$ and exchanging the points of $C_k^{n,l_1}$ and those of $C_k^{n,l_2}$ under a k-isomorphism to obtain $1\in F(Is{o}_k(C_k^{n,l_1}\vee C_k^{n,l_2}))$. □

Unlike the case of $l_1=l_2\in {\mathbb{N}}_0$ of $(C_k^{n,l_1}\vee C_k^{n,l_2},k)$ stated in Theorem 7, using a method similar to the proof of Theorem 7, we obtain the following:

Corollary 5.

Given $(C_k^{n,l_1}\vee C_k^{n,l_2},k)$ with $l_1,l_2\in {\mathbb{N}}_0$ and $l_1\ne l_2$, $F(Is{o}_k(C_k^{n,l_1}\vee C_k^{n,l_2}))=\{l_1+l_2-1,l_1+1,l_2+1,3\}$.

Proof. 

The assertion of $\{l_1+l_2-1,l_1+1,l_2+1\}\subset F(Is{o}_k(C_k^{n,l_1}\vee C_k^{n,l_2}))$ is proved by using the methods referred to in the cases of Theorem 7. However, since $l_1\ne l_2$, we cannot further proceed with the process of Case 3 of the proof of Theorem 7. □

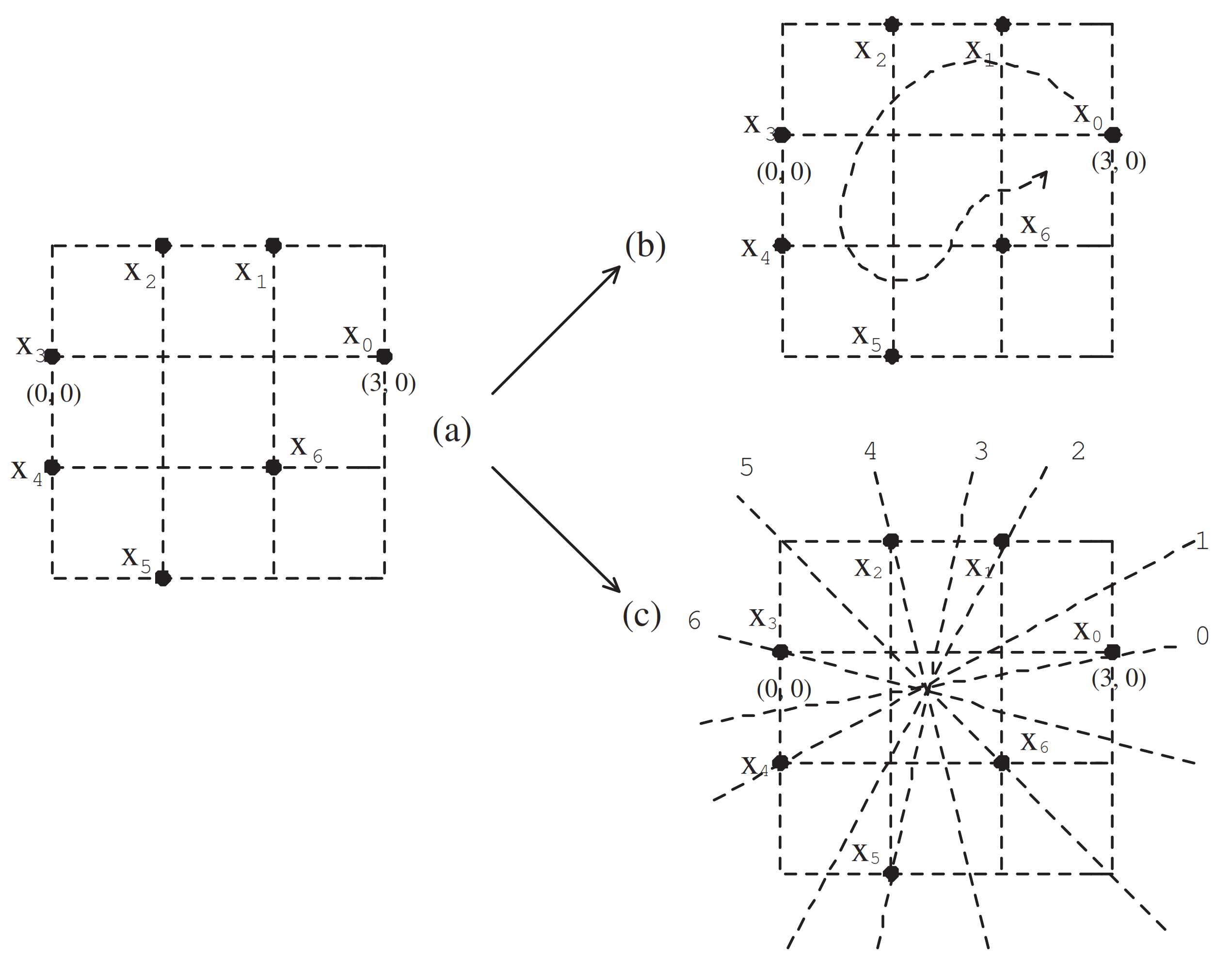
Let us now consider the cases $l_1\in {\mathbb{N}}_0,l_2\in {\mathbb{N}}_1$ or $l_2\in {\mathbb{N}}_0,l_1\in {\mathbb{N}}_1$. Without loss of generality, we may consider the case $l_1\in {\mathbb{N}}_0,l_2\in {\mathbb{N}}_1$ (see Figure 5b), as follows:

Theorem 8.

Given $(C_k^{n,l_1}\vee C_k^{n,l_2},k)$ with $l_1\in {\mathbb{N}}_0,l_2\in {\mathbb{N}}_1$, $F(Is{o}_k(C_k^{n,l_1}\vee C_k^{n,l_2}))=\{l_1+l_2-1,l_1,l_2+1,2\}$.

Proof. 

Using a method similar to the proof of Theorem 7, we complete the proof. To guarantee this approach, for instance, given $C_{26}^{3,5}\vee C_{26}^{3,6}$ in Figure 5b, we obtain $F_{26}(Is{o}_{26}(C_{26}^{3,5}\vee C_{26}^{3,6}))=\{10,6,2\}$. □

Let us now investigate $F(Is{o}_k(C_k^{n,l_1}\vee C_k^{n,l_2}))$ for the case of $l_1,l_2\in {\mathbb{N}}_1$.

Theorem 9.

Given $(C_k^{n,l_1}\vee C_k^{n,l_2},k)$ with $l_1,l_2\in {\mathbb{N}}_1$, we obtain the following:

(1) 

$F(Is{o}_k(C_k^{n,l_1}\vee C_k^{n,l_2}))=\{l_1+l_2-1,l_1,1\}$ if $l_1=l_2$.

(2) 

$F(Is{o}_k(C_k^{n,l_1}\vee C_k^{n,l_2}))=\{l_1+l_2-1,l_1,l_2\}$ if $l_1\ne l_2$.

Proof. 

Using Theorem 5 and Lemmas 2 and 3, we need to consider the following cases.

(1)

In the case of $l_1=l_2\in {\mathbb{N}}_1$, making the part $C_k^{n,l_1}$ of $C_k^{n,l_1}\vee C_k^{n,l_2}$ remained, we consider a certain symmetry of $C_k^{n,l_1}\vee C_k^{n,l_2}$ used in the Case 2 of the proof of Theorem 5. Then we first consider $1_{C_k^{n,l_1}\vee C_k^{n,l_2}}$ to obtain $l_1+l_2-1\in F(Is{o}_k(C_k^{n,l_1}\vee C_k^{n,l_2}))$.

Second, we can consider a certain symmetry of $C_k^{n,l_1}\vee C_k^{n,l_2}$ referred to in (8) to obtain $l_1\in F(Is{o}_k(C_k^{n,l_1}\vee C_k^{n,l_2}))$.

Third, making the point in $C_k^{n,l_1}\cap C_k^{n,l_2}$ fixed and using the property referred to in the Case 2 of the proof of Theorem 5 (see also the property (8)), we map the points of $C_k^{n,l_1}$ onto those of $C_k^{n,l_2}$ under a k-isomorphism to obtain $1\in F(Is{o}_k(C_k^{n,l_1}\vee C_k^{n,l_2}))$.

Fourth, making the point in $C_k^{n,l_1}\cap C_k^{n,l_2}$ fixed and exchanging the points of $C_k^{n,l_1}$ and those of $C_k^{n,l_2}$ under a k-isomorphism, we obtain $1\in F(Is{o}_k(C_k^{n,l_1}\vee C_k^{n,l_2}))$. To support this process, for instance, given $C_{26}^{3,5}\vee C_{26}^{3,5}$ in Figure 5a, we obtain $F_{26}(Is{o}_{26}(C_{26}^{3,5}\vee C_{26}^{3,5}))=\{9,5,1\}$.

(2)

In the case of $l_1\ne l_2\in {\mathbb{N}}_1$, using a method similar to the proof of the above Case 1 and the proof of Corollary 5, we complete the proof. For instance, we obtain $F(Is{o}_k(C_8^{2,7}\vee C_8^{2,9}))=\{15,9,7\}$.

□

Let us now recall the notion of digital $(k,k^{\prime })$-imbedding to study some generalized versions of Theorems 7–9 and Corollary 5.

Definition 6.

[39] Consider two digital images $(X,k:=k(t,n)),X\subset {\mathbb{Z}}^n$ and $(Y,k^{\prime }:=k(t^{\prime },n^{\prime })),Y\subset {\mathbb{Z}}^{n^{\prime }}$ such that there is an arbitrary $(k,k^{\prime })$-isomorphism $h:(X,k)\to (h(X),k^{\prime })\subset (Y,k^{\prime })$. Then, $(X,k)$ is said to be a digital topological imbedding into $(Y,k^{\prime })$ with respect to the $(k,k^{\prime })$-isomorphism h or the map h is called a digital topological $(k,k^{\prime })$-imbedding from $(X,k)$ into $(Y,k^{\prime })$.

Definition 7.

In Definition 6, as to $k:=k(t,n)$ for X and $k^{\prime }:=k(t^{\prime },n^{\prime })$ for Y, if $t=t^{\prime }$, then $(X,k)$ is said to be a strictly digital topological imbedding into $(Y,k^{\prime })$ with respect to the $(k,k^{\prime })$-isomorphism h. In particular, in the case $X\subset {\mathbb{Z}}^n$ with the same k-adjacency of both X and ${\mathbb{Z}}^n$, a digital topological imbedding is simply understood to be an inclusion $(X,k)\subset ({\mathbb{Z}}^n,k)$.

Based on the concept of the digital topological imbedding above, let us now make the digital wedge $(C_k^{n,l_1}\vee C_k^{n,l_2},k)$ more generalized, as follows:

Definition 8.

[39] Given two digital images $(X,k_1)$ in ${\mathbb{Z}}^{n_1}$ and $(Y,k_2)$ in ${\mathbb{Z}}^{n_2}$, where $k_1:=k(t_1,n_1)$ and $k_2:=k(t_2,n_2)$, take $n:=max\{n_1,n_2\}$ and $t:=max\{t_1,t_2\}$. Then, we define a digital wedge of $(X,k_1)$ and $(Y,k_2)$ in ${\mathbb{Z}}^n$ with a k-adjacency of ${\mathbb{Z}}^n$, where $k:=k(t,n)$, denoted by $(X\vee Y,k)$, as one point union of the certain digital images $(X^{\prime },k_1^{\prime }:=k(t_1,n))$ and $(Y^{\prime },k_2^{\prime }:=k(t_2,n))$ in ${\mathbb{Z}}^n$ satisfying the following properties.

(W1) 

There are the following digital topological imbeddings,

$$\left\{\begin{array}{c}f:(X,k_1)\to (X^{\prime },k_1^{\prime })withrespecttoa(k_1,k_1^{\prime })-isomorphismand\hfill \\ g:(Y,k_2)\to (Y^{\prime },k_2^{\prime })withrespecttoa(k_2,k_2^{\prime })-isomorphism,\hfill \end{array}\right.$$

such that the set $X^{\prime }\cup Y^{\prime }\subset {\mathbb{Z}}^n$ is assumed with the k-adjacency and further,

(W2) 

$X^{\prime }\cap Y^{\prime }$ is a singleton, say $\left\{p\right\}$,

(W3) 

$X^{\prime }\backslash \left\{p\right\}$ and $Y^{\prime }\backslash \left\{p\right\}$ are not k-adjacent, and

(W4) 

as for the subsets $(X^{\prime },k),(Y^{\prime },k)\subset (X^{\prime }\cup Y^{\prime },k)$, the following properties hold.

$$\left\{\begin{array}{c}{W}_{X^{\prime }}:(X^{\prime },k)\to (X,k_1)isa(k,k_1)-isomorphismand\hfill \\ W_{Y^{\prime }}:(Y^{\prime },k)\to (X,k_2)\mathrm{is}\mathrm{a}(k,k_2)-isomorphism.\hfill \end{array}\right.$$

In view of this feature, we may consider $(X\vee Y,k)$ to be $(X^{\prime }\vee Y^{\prime },k)$ which is one point union of $X^{\prime }$ and $Y^{\prime }$ with k-adjacency.

As mentioned in [39], given $C_{k_i}^{n_i,l_i},i\in \{1,2\}$, not every $C_{k_1}^{n_1,l_1}\vee C_{k_2}^{n_2,l_2}$ always exists in ${\mathbb{Z}}^n$ with a certain k-adjacency of ${\mathbb{Z}}^n$, where $n:=max\{n_1,n_2\}$. For instance, given $C_4^{2,8}$ and $C_8^{2,6}$, no $C_4^{2,8}\vee C_8^{2,6}$ exists in ${\mathbb{Z}}^2$ for any k-adjacency, where $k\in \{4,8\}$. However, given $C_{26}^{3,5}$ and $C_{18}^{3,6}$, we can consider $C_{26}^{3,5}\vee C_{18}^{3,6}$ in ${\mathbb{Z}}^3$ with 26-adjacency, i.e., $(C_{26}^{3,5}\vee C_{18}^{3,6},26)$ (see Figure 5b). Based on the generalized digital wedge from Definition 8, we obtain the following:

Theorem 10.

Given $(C_{k_1}^{n,l_1}\vee C_{k_2}^{n,l_2},k)$ with $l_1,l_2\in {\mathbb{N}}_0$, we obtain the following:

(1) 

$F(Is{o}_k(C_{k_1}^{n_1,l_1}\vee C_{k_2}^{n_2,l_2}))=\{l_1+l_2-1,l_1+1,3,1\}$ if $l_1=l_2$.

(2) 

$F(Is{o}_k(C_{k_1}^{n_1,l_1}\vee C_{k_2}^{n_2,l_2}))=\{l_1+l_2-1,l_1+1,l_2+1,3\}$ if $l_1\ne l_2$.

Proof. 

Using certain methods similar to the proofs of (1) and (2) of Theorem 7 and the proof of Corollary 5, we complete the proof. □

Theorem 11.

Given $(C_{k_1}^{n,l_1}\vee C_{k_2}^{n,l_2},k)$ with $l_1,l_2\in {\mathbb{N}}_1$, we obtain the following:

(1) 

$F(Is{o}_k(C_{k_1}^{n_1,l_1}\vee C_{k_2}^{n_2,l_2}))=\{l_1+l_2-1,l_1,1\}$ if $l_1=l_2$.

(2) 

$F(Is{o}_k(C_{k_1}^{n_1,l_1}\vee C_{k_2}^{n_2,l_2}))=\{l_1+l_2-1,l_1,l_2\}$ if $l_1\ne l_2$.

Proof. 

Using certain methods similar to the proofs of (1) and (2) of Theorem 9, we complete the proof. □

Theorem 12.

Given $(C_{k_1}^{n_1,l_1}\vee C_{k_2}^{n_2,l_2},k)$ with $l_1\in {\mathbb{N}}_0,l_2\in {\mathbb{N}}_1$, $F(Is{o}_k(C_{k_1}^{n_1,l_1}\vee C_{k_2}^{n_2,l_2}))=\{l_1+l_2-1,l_1,l_2+1,2\}$.

Proof. 

Using a certain method similar to the proof of Theorem 8, we complete the proof. □

Remark 4.

In view of Lemmas 2 and 3 and Theorems 7–10, and Corollary 5, for $X\in \{C_k^{n,l},C_k^{n,l_1}\vee C_k^{n,l_2},C_{k_1}^{n_1,l_1}\vee C_{k_2}^{n_2,l_2}\}$, we observe that each $F(Is{o}_k(X))$ depends on the numbers $l,l_i,i\in \{1,2\}$.

5. Conditions Being the Perfectness of $\mathit{F}(\mathit{C}\mathit{o}{\mathit{n}}_{\mathit{k}}({\mathit{C}}_{\mathit{k}}^{\mathit{n},{\mathit{l}}_{\mathbf{1}}}\vee {\mathit{C}}_{\mathit{k}}^{\mathit{n},{\mathit{l}}_{\mathbf{2}}})),{\mathit{l}}_{\mathbf{1}},{\mathit{l}}_{\mathbf{2}}\mathbf{\in }{\mathbb{N}}_{\mathbf{0}}$

As for the study of some properties of $F(Co{n}_k(C_k^{n,l_1}\vee C_k^{n,l_2}))$, we have recently studied the following cases, $l_i\in {\mathbb{N}}_1,i\in \{1,2\}$[39] and $l_1\in {\mathbb{N}}_0,l_2\in {\mathbb{N}}_1$ (or $l_1\in {\mathbb{N}}_1,l_2\in {\mathbb{N}}_0$) [39]. Thus, for the case of $l_i\in {\mathbb{N}}_0,i\in \{1,2\}$, the study of $F(Co{n}_k(C_k^{n,l_1}\vee C_k^{n,l_2}))$ still remains. This section explores certain conditions which make $F(Co{n}_k(C_k^{n,l_1}\vee C_k^{n,l_2}))$ perfect. Based on the study of $F(Co{n}_k(X))$ [8], and the property of (2), where $X\in \{C_k^{n,l}\vee C_k^{n,4},C_k^{n,l}\vee C_k^{n,4}\vee C_k^{n,4}\vee C_k^{n,4},C_k^{n,l}\vee C_k^{n,6},C_k^{n,l}\vee C_k^{n,6}\vee C_k^{n,6},C_k^{n,l}\vee C_k^{n,6}\vee C_k^{n,4}|l\in {\mathbb{N}}_0\}$, this section investigates some digital topological properties of $C_k^{n,l_1}\vee C_k^{n,l_2}$, where $l_i\in {\mathbb{N}}_0\backslash \left\{2\right\},i\in \{1,2\}$. Since $C_k^{n,l_1}\vee C_k^{n,l_2}$ is k-isomorphic to $C_k^{n,l_2}\vee C_k^{n,l_1}$ and an alignment of fixed point sets is a digital topological invariant (see Proposition 3), we obtain

$$F(Co{n}_k(C_k^{n,l_1}\vee C_k^{n,l_2}))=F(Co{n}_k(C_k^{n,l_2}\vee C_k^{n,l_1})).$$

(22)

Furthermore, given a digital image $(X,k)$, after studying $Co{n}_k(X)$-action on a digital object $(X,k)$, we investigate certain properties of fixed point sets of $(X,k)$ by the $Co{n}_k(X)$-action on $(X,k)$. Regarding this approach, we count on certain roles of $C_k^{n,6}$ and $C_k^{n,4}$ that are involved in the perfectness of $F(Co{n}_k(C_k^{n,l_1}\vee C_k^{n,l_2}))$ (see Definition 11). Indeed, the study of $F(Co{n}_k(C_k^{n,l_1}\vee C_k^{n,l_2}))$ still remains open. Up to now, it turns out that digital fundamental groups of $C_k^{n,l}\vee C_k^{n,4}$ and $C_k^{n,l}\vee C_k^{n,6}$ are strongly related to the digital topological features of alignments of fixed point sets of them (see Theorem 13). Given $f\in Co{n}_k(X)$, we use the notation $Fix(f):=\{x\in X|f(x)=x\}$.

Definition 9.

[26] Given a digital image $(X,k)$, we say

$$F(Co{n}_k(X)):=\left\{Fix{(f)}^{♯}\right|f\in Co{n}_k(X)\}.$$

Given ${\mathcal{D}}_k(X)\in \{Is{o}_k(X),Co{n}_k(X)\}$, for $f\in {\mathcal{D}}_k(X)$, we define $Fix(f):=\{x\in X|f(x)=x\}$. As a generalization of $F(Co{n}_k(X))$ [8,26], the following is defined.

Definition 10.

Given a digital object $(X,k)$, we say that the digital image

$$F({\mathcal{D}}_k(X)):=\left\{Fix{(f)}^{♯}\right|f\in {\mathcal{D}}_k(X)\}:=(F({\mathcal{D}}_k(X)),2)$$

is an alignment of the set of cardinalities of fixed point sets of maps in ${\mathcal{D}}_k(X)$, where ${\mathcal{D}}_k(X)\in \{Is{o}_k(X),Co{n}_k(X)\}$. Then, we call $(F({\mathcal{D}}_k(X)),2)$ (or $F({\mathcal{D}}_k(X))$ for brevity) an alignment of fixed point sets of $(X,k)$ according to ${\mathcal{D}}_k(X)$.

In view of Definition 10, it is clear that $(F(Co{n}_k(X)),2)$ is a special case of $(F({\mathcal{D}}_k(X)),2)$ stated in Definition 9. Using Lemma 4, we obtain the following:

Proposition 3.

[26] The quantity $F(Co{n}_k(X))$ is a digital topological invariant.

Definition 11.

[8] Given $(X,k)$, if $F(Co{n}_k(X))={[0,X^{♯}]}_{\mathbb{Z}}$, then $(F(Co{n}_k(X)),2)$ (or $F(Co{n}_k(X))$ for brevity) is said to be perfect.

Remark 5.

In view of Lemmas 2 and 3 and Theorems 7–12, we observe that each $F(Is{o}_k(X))$, $X\in \{C_k^{n,l},C_{k_1}^{n_1,l_1}\vee C_{k_2}^{n_2,l_2}\}$, is a proper subset of ${[0,X^{♯}]}_{\mathbb{Z}}$.

We now explore some conditions supporting perfectness of an alignment of fixed point sets.

Lemma 4.

(1) 

In the case $C_k^{n,l}$ is k-contractible, $F(Co{n}_k(C_k^{n,l}))$ is perfect [8].

(2) 

In the case $C_k^{n,l}$ is not k-contractible, $F(Co{n}_k(C_k^{n,l}))$ is not perfect [8].

(3) 

Given $C_k^{n,l},l\in {\mathbb{N}}_0$, $F(Co{n}_k(C_k^{n,l}))={[0,\frac{l}{2}+1]}_{\mathbb{Z}}\cup \left\{l\right\}$ [26].

Regarding Lemma 4, we also need to remind that not every k-contractible digital image $(X,k)$ has a perfect $F(Co{n}_k(X))$ [26]. However, by Lemma 4, it is clear that the k-contractibility of $C_k^{n,l}$ implies the perfectness of $F(Co{n}_k(C_k^{n,l}))$ and the converse also holds [8]. This section is based on the studies of some digital topological properties of $F(Co{n}_k(C_k^{n,l}\vee C_k^{n,4}))$ in [8] and the perfectness of it associated with the number l, where $l\ge 4$ [8]. One important thing to note is that we need to recall that the digital k-fundamental group of $C_k^{n,l}\vee C_k^{n,4}$ is trivial or an infinite cyclic group with an infinite order depending on the number l (see Theorem 3). For instance, $C_k^{n,4}\vee C_k^{n,4}$ is k-contractible [5], and if $l\ge 6$, then $C_k^{n,l}\vee C_k^{n,4}$ is not k-contractible [5] (see also Theorem 3).

In view of Theorems 3–5, since the number l of $C_k^{n,l}$ strongly influences some digital topological properties of $C_k^{n,l}$. In particular, depending on the number l (even or odd), many digital topological properties of $C_k^{n,l}$ are determined. A recent paper [26] only proposed the property referred to in Lemma 4(3). In view of the property of (2), we need the following result improving the assertion of [26] (see Lemma 4(3)).

Lemma 5.

[8] Given $C_k^{n,l}$ with $5\le l\in {\mathbb{N}}_1$, $F(Co{n}_k(C_k^{n,l}))={[0,\frac{l+1}{2}]}_{\mathbb{Z}}\cup \left\{l\right\}$.

Theorem 13.

Given $(C_k^{n,l_1}\vee C_k^{n,l_2},k)$, $l_i\in \mathbb{N}\backslash \{1,2,3\}$, if ${\pi }^k(C_k^{n,l_1}\vee C_k^{n,l_2})$ is isomorphic to an infinite cyclic group such that $|l_1-l_2|\le 6$ or trivial, then $F(Co{n}_k(C_k^{n,l_1}\vee C_k^{n,l_2}))$ is perfect.

Proof. (Case 1) Let us consider the case that ${\pi }^k(C_k^{n,l_1}\vee C_k^{n,l_2})$ is trivial. Then, by Theorem 3, owing to the k-homotopic property of $C_k^{n,l_1}\vee C_k^{n,l_2}$, by the properties $(•2)$ and $(•3)$ of Definition 2, it is clear that each $C_k^{n,l_1}$ and $C_k^{n,l_2}$ are k-contractible. Thus, by Theorem 3, we have only the case $C_k^{n,4}\vee C_k^{n,4}$. Then, by Lemma 4, we obtain

$$F(Co{n}_k(C_k^{n,4}\vee C_k^{n,4}))={[0,7]}_{\mathbb{Z}},$$

which proves the perfectness of $F(Co{n}_k(C_k^{n,4}\vee C_k^{n,4}))$.

(Case 2) Let us consider the case that ${\pi }^k(C_k^{n,l_1}\vee C_k^{n,l_2})$ is isomorphic to an infinite cyclic group. Then, without loss of generality we may replace $C_k^{n,l_1}\vee C_k^{n,l_2}$ by $C_k^{n,l}\vee C_k^{n,4}$ or $C_k^{n,4}\vee C_k^{n,l}$ (see (22)), where $l\ge 5$.

Without loss of generality, we may take $C_k^{n,l}\vee C_k^{n,4}$.

(Case 2-1) Let us assume $6\le l\in {\mathbb{N}}_0$. Owing to the part $C_k^{n,4}$ of $C_k^{n,l}\vee C_k^{n,4}$, if $l\le 10$, by Lemma 4(3), we obtain [8]

$$F(Co{n}_k(C_k^{n,l}\vee C_k^{n,4}))={[0,l+3]}_{\mathbb{Z}},$$

which implies the perfectness of $F(Co{n}_k(C_k^{n,l}\vee C_k^{n,4}))$ because ${(C_k^{n,l}\vee C_k^{n,4})}^{♯}=l+3$.

(Case 2-2) Let us assume $5\le l\in {\mathbb{N}}_1$. Owing to the part $C_k^{n,4}$ of $C_k^{n,l}\vee C_k^{n,4}$, if $l\le 9$, by Lemma 5, we obtain [8]

$$F(Co{n}_k(C_k^{n,l}\vee C_k^{n,4}))={[0,l+3]}_{\mathbb{Z}},$$

which implies the perfectness of $F(Co{n}_k(C_k^{n,l}\vee C_k^{n,4}))$ because ${(C_k^{n,l}\vee C_k^{n,4})}^{♯}=l+3$. □

Since the perfectness of $F(Co{n}_k(C_k^{n,l_1}\vee C_k^{n,l_2}))$ depends on the numbers $l_1$ and $l_2$, the paper [8] investigated various properties of $F(Co{n}_k(C_k^{n,l}\vee C_k^{n,4}))$, $F(Co{n}_k(C_k^{n,l}\vee C_k^{n,4}\vee C_k^{n,4}))$, $F(Co{n}_k(C_k^{n,l}\vee C_k^{n,6}))$, and so on.

As mentioned in the earlier part, sinc $C_k^{n,6}$ also plays a crucial role in digital and computational topology. Let us explore an alignment of fixed point sets of $C_k^{n,l}\vee C_k^{n,6}$. Let us now explore $F(Co{n}_k(C_k^{n,l}\vee C_k^{n,6}))$ for the case $l\ge 16$.

Theorem 14.

In the case $16\le l\in {\mathbb{N}}_0$, $F(Co{n}_k(C_k^{n,l}\vee C_k^{n,6}))$ has three 2-components. Namely, $F(Co{n}_k(C_k^{n,l}\vee C_k^{n,6}))={[0,l+5]}_{\mathbb{Z}}\backslash (\{l-1,l-2,\dots ,l-i\}\cup \{l+4\})$, where $i=\frac{l-14}{2}$.

Proof. 

Regarding $F(Co{n}_k(C_k^{n,l}\vee C_k^{n,6}))$, though there are several cases of self-k-continuous maps of $C_k^{n,l}\vee C_k^{n,6}$ we have the following four cases.

$$\left\{\begin{array}{c}{(a)f|}_{C_k^{n,6}}(x)=x;\mathrm{or}\hfill \\ (b)f{|}_{C_k^{n,l}}(x)=x;\mathrm{or}\hfill \\ (c)f(C_k^{n,l})⊊C_k^{n,l}\mathrm{and}f(C_k^{n,6})⊊C_k^{n,6};\mathrm{or}\hfill \\ (d)f\mathrm{does}\mathrm{not}\mathrm{have}\mathrm{any}\mathrm{fixed}\mathrm{point}.\hfill \end{array}\right.$$

First, from (a) we obtain the following:

$${[6,6+\frac{l}{2}]}_{\mathbb{Z}}\cup \{l+5\}\subset F(Co{n}_k(C_k^{n,l}\vee C_k^{n,6})).$$

Second, from (b) we have the following:

$${[l,l+3]}_{\mathbb{Z}}\subset F(Co{n}_k(C_k^{n,l}\vee C_k^{n,6})).$$

Third, from (c) and (d), the following is obtained.

$${[0,\frac{l}{2}+4]}_{\mathbb{Z}}\subset F(Co{n}_k(C_k^{n,l}\vee C_k^{n,6})).$$

Hence based on these three quantities as subsets of $F(Co{n}_k(C_k^{n,l}\vee C_k^{n,6}))$, we obtain

$$F(Co{n}_k(C_k^{n,l}\vee C_k^{n,6}))={[0,\frac{l}{2}+6]}_{\mathbb{Z}}\cup {[l,l+3]}_{\mathbb{Z}}\cup \{l+5\}.$$

(23)

For instance, in the case $l=16$, we obtain

$$F(Co{n}_k(C_k^{n,16}\vee C_k^{n,6}))={[0,14]}_{\mathbb{Z}}\cup {[16,19]}_{\mathbb{Z}}\cup \left\{21\right\}.$$

Thus, in view of these calculations and by the property in (23), in the case $l\ge 16$, we can conclude that $F(Co{n}_k(C_k^{n,l}\vee C_k^{n,6}))$ has three 2-components. Furthermore, we have the formula representing (23) in the following way. If $l\ge 16$, then we obtain

$$F(Co{n}_k(C_k^{n,l}\vee C_k^{n,6}))={[0,l+5]}_{\mathbb{Z}}\backslash (\{l-1,l-2,\dots ,l-i\}\cup \{l+4\}),$$

where $i=\frac{l-14}{2}$. □

Example 3.

$F(Co{n}_k(C_k^{n,22}\vee C_k^{n,6}))={[0,27]}_{\mathbb{Z}}\backslash (\{21,20,19,18\}\cup \left\{26\right\})$. Thus, we see that the alignment $(F(Co{n}_k(C_k^{n,22}\vee C_k^{n,6})),2)$ has three 2-components.

Based on Theorems 13 and 14, we obtain the following:

Theorem 15.

Assume $l_1\ge l_2(\ge 6)\in {\mathbb{N}}_0$. Then, $F(Co{n}_k(C_k^{n,l_1}\vee C_k^{n,l_2}))={[0,l_2+\frac{l_1}{2}]}_{\mathbb{Z}}\cup {[l_1,l_1+\frac{l_2}{2}]}_{\mathbb{Z}}\cup \{l_1+l_2-1\}$.

Proof. 

Using a method similar to the approach taken in (23), regarding $F(Co{n}_k(C_k^{n,l_1}\vee C_k^{n,l_2}))$, it is sufficient to consider the following k-continuous self-maps f of $C_k^{n,l_1}\vee C_k^{n,l_2}$ such that

$$\left\{\begin{array}{c}{(a)f|}_{C_k^{n,l_2}}(x)=x;\mathrm{or}\hfill \\ (b)f{|}_{C_k^{n,l_1}}(x)=x;\mathrm{or}\hfill \\ (c)f(C_k^{n,l_i})⊊C_k^{n,l_i},i\in \{1,2\};\mathrm{or}\hfill \\ (d)f\mathrm{does}\mathrm{not}\mathrm{have}\mathrm{any}\mathrm{fixed}\mathrm{point},\hfill \\ \mathrm{where}f|B\mathrm{means}\mathrm{the}\mathrm{restriction}\mathrm{function}f\mathrm{to}\mathrm{the}\mathrm{given}\mathrm{set}B.\hfill \end{array}\right.$$

(24)

First of all, from (a) above and Lemma 4, since $C_k^{n,l_1}\vee C_k^{n,l_2}$ has the cardinality $l_1+l_2-1$, we obtain

$${[l_2,l_2+\frac{l_1}{2}]}_{\mathbb{Z}}\cup \{l_1+l_2-1\}\subset F(Co{n}_k(C_k^{n,l_1}\vee C_k^{n,l_2})).$$

(25)

Second, from (b) above, we have

$${[l_1,l_1+\frac{l_2}{2}]}_{\mathbb{Z}}\cup \{l_1+l_2-1\}\subset F(Co{n}_k(C_k^{n,l_1}\vee C_k^{n,l_2})).$$

Third, from (c) and (d) above, we obtain

$${[0,\frac{l_1+l_2}{2}+1]}_{\mathbb{Z}}\subset F(Co{n}_k(C_k^{n,l_1}\vee C_k^{n,l_2})).$$

(26)

Owing to the hypothesis “$l_1\ge l_2$, $l_i\ge 6,i\in \{1,2\}$”, and the Properties (24)–(26), we conclude that

$$F(Co{n}_k(C_k^{n,l_1}\vee C_k^{n,l_2}))={[0,l_2+\frac{l_1}{2}]}_{\mathbb{Z}}\cup {[l_1,l_1+\frac{l_2}{2}]}_{\mathbb{Z}}\cup \{l_1+l_2-1\}$$

which completes the proof.

For instance, in the case $l_1=14$ and $l_2=6$, we obtain

$$F(Co{n}_k(C_k^{n,14}\vee C_k^{n,6}))={[0,17]}_{\mathbb{Z}}\cup \left\{19\right\}.$$

□

Example 4.(1) $F(Co{n}_8(C_8^{2,18}\vee C_8^{2,6}))={[0,15]}_{\mathbb{Z}}\cup {[18,21]}_{\mathbb{Z}}\cup \left\{23\right\}$.

(2) $F(Co{n}_8(C_8^{2,20}\vee C_8^{2,8}))={[0,18]}_{\mathbb{Z}}\cup {[20,24]}_{\mathbb{Z}}\cup \left\{27\right\}$.

As shown in (1) and (2) above, we observe that these alignments consist of three 2-components.

In view of Proposition 3, we obtain the following:

Corollary 6.

Given a digital image $(X,k)$, the perfectness of $F(Co{n}_k(X))$ is a digital topological invariant.

6. Conclusions

We have addressed five issues posed in Section 1, which can facilitate the studies of both digital topology and fixed point theory. One of the important things that comes from this paper is the development of group structures, $Is{o}_k^{n,l}$ which play crucial roles in studying digital images from the viewpoint of fixed point theory. Besides, we have explored various properties of fixed point sets of the $Is{o}_k^{n,l}(·)$-actions in a $DTC$ setting. On top of this, we have intensively studied the algebraic topological structures of $Is{o}_k^{n,l}(·)$ and $Co{n}_k(·)$. Furthermore, given a digital image $(X,k)$$Co{n}_k(X)$- and $Is{o}_k(X)$-action on $(X,k)$, we have studied some alignments of fixed point sets by these actions.

As a further work, we can study various properties of these actions from the aspect of digital geometry. The obtained results in the $DTC$ setting can be applied to the fields of chemistry, physics, computer sciences and so on. In particular, this approach can be extremely useful in the fields of classifying molecular structures, computer graphics, image processing, approximation theory, game theory, mathematical morphology, optimization theory, digitization, information processing, rough set theory, and so forth.