Mean Squared Variance Portfolio: A Mixed-Integer Linear Programming Formulation
Abstract
1. Introduction
- High concentration: MV-inspired portfolios are highly concentrated on a few securities with the "best: features [13,14]. Assets with either high expected returns or low expected variance will be overweighted, in this way losing the power of diversification that the theory is supposed to ensure [15].
- Instability: MV portfolios tend to drastically re-allocate resources when the asset features change slightly, regardless of transaction costs or data inaccuracy [16,17]. This mainly occurs because MV portfolios do not take estimation inaccuracy into account and concentrate on assets with "good" features.
- Maximize the expected return for a specified risk: the first possible formulation includes the maximization of the portfolio mean in the objective function of the problem and the maximum level of risk that an investor is able to assume as a constraint of the problem.
- Minimize the risk for a pre-determined expected return: the second alternative tries to minimize the risk and introduces the minimum level of the mean return as a constraint of the optimization.
- Minimize the risk and maximize the expected return combining both of the objectives through a user-defined risk aversion parameter.
2. The Proposed Method
2.1. Mathematical Formulation of the Model
2.2. Main Foundations of the Model
2.3. Mixed-Integer Linear Programming Reformulation
3. Experimental Framework
3.1. Out-Of-Sample Empirical Validation and Portfolio Problems Selected
3.2. Strategies Implemented
3.3. Performance Measures
- The out-of-sample mean returns (MR):
- The out-of-sample Sharpe ratio (SR), defined as the sample mean of out-of-sample excess returns, MR, divided by their corresponding sample standard deviation:
3.4. Hyper-Parameter Optimization
3.5. Statistical Hypothesis Testing
4. Results
- to compare the out-of-sample performance of the MSV portfolio with the performance provided by state-of-the-art MV-based strategies (Section 4.1); and,
- to analyse the diversification levels produced by the proposed MSV portfolio and the MV portfolio in problems with different dimensions (Section 4.2).
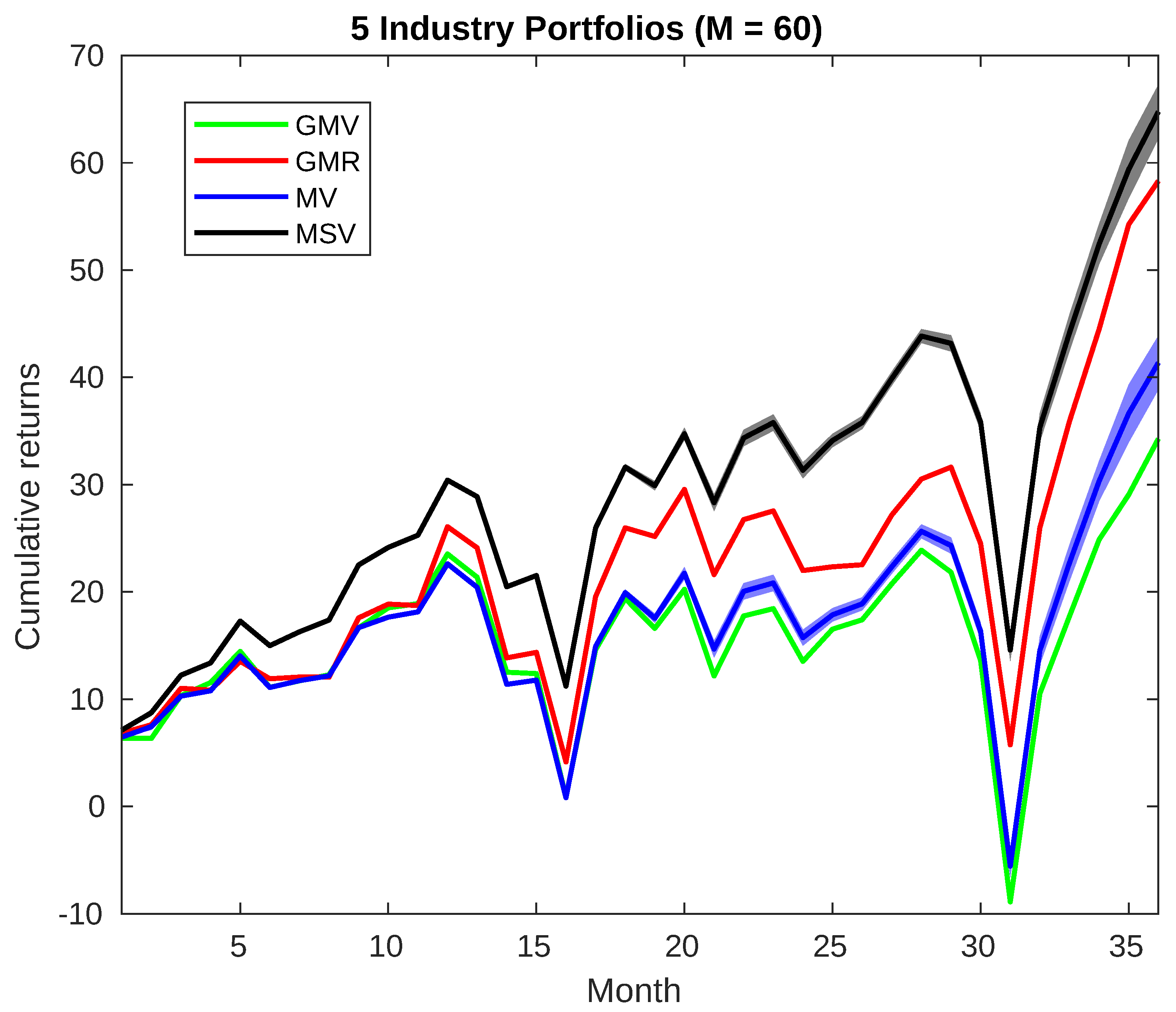
4.1. Performance Analysis
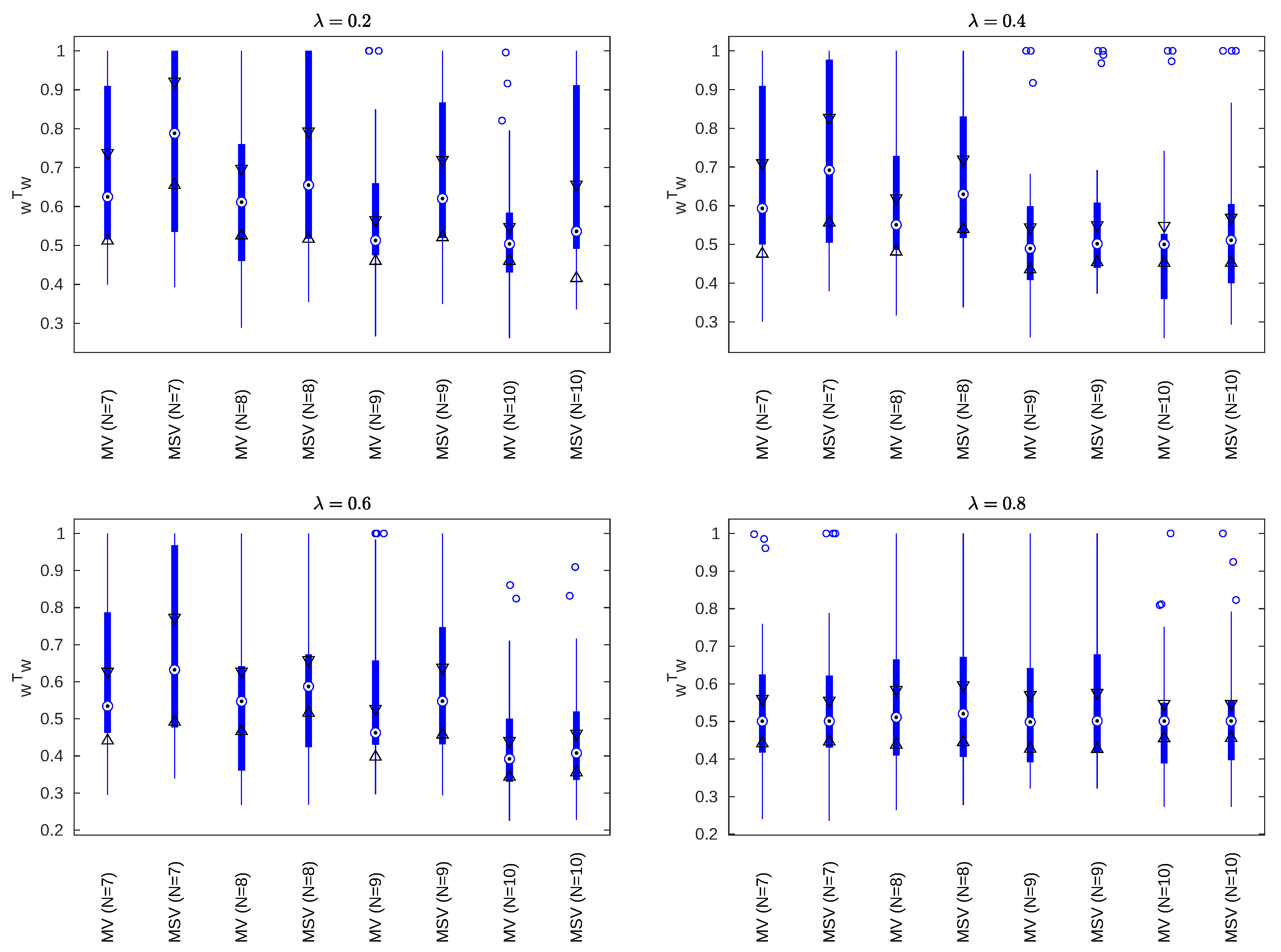
4.2. Diversification Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| BM | Book-to-market |
| GMR | Global maximum return |
| GMV | Global minimum variance |
| I | Investment |
| MILP | Mixed-integer linear programming |
| MR | Mean return |
| MSV | Mean squared variance |
| MV | Mean-variance |
| OP | Operating profitability |
| QP | Quadratic programming |
| SR | Sharpe ratio |
References
- Markowitz, H. Portfolio selection. J. Financ. 1952, 7, 77–91. [Google Scholar]
- Markowitz, H. Mean–variance approximations to expected utility. Eur. J. Oper. Res. 2014, 234, 346–355. [Google Scholar] [CrossRef]
- Zhou, R.; Palomar, D.P. Understanding the Quintile Portfolio. IEEE Trans. Signal Process. 2020, 68, 4030–4040. [Google Scholar] [CrossRef]
- Coqueret, G. Diversified minimum-variance portfolios. Ann. Financ. 2015, 11, 221–241. [Google Scholar] [CrossRef]
- Maillet, B.; Tokpavi, S.; Vaucher, B. Global minimum variance portfolio optimisation under some model risk: A robust regression-based approach. Eur. J. Oper. Res. 2015, 244, 289–299. [Google Scholar] [CrossRef]
- Bodnar, T.; Parolya, N.; Schmid, W. Estimation of the global minimum variance portfolio in high dimensions. Eur. J. Oper. Res. 2018, 266, 371–390. [Google Scholar] [CrossRef]
- Lim, A.E.; Zhou, X.Y. Mean-variance portfolio selection with random parameters in a complete market. Math. Oper. Res. 2002, 27, 101–120. [Google Scholar] [CrossRef]
- Yin, G.; Zhou, X.Y. Markowitz’s mean-variance portfolio selection with regime switching: From discrete-time models to their continuous-time limits. IEEE Trans. Autom. Control 2004, 49, 349–360. [Google Scholar] [CrossRef]
- Usta, I.; Kantar, Y.M. Mean-variance-skewness-entropy measures: A multi-objective approach for portfolio selection. Entropy 2011, 13, 117–133. [Google Scholar] [CrossRef]
- DeMiguel, V.; Garlappi, L.; Uppal, R. Optimal versus naive diversification: How inefficient is the 1/N portfolio strategy? Rev. Financ. Stud. 2009, 22, 1915–1953. [Google Scholar] [CrossRef]
- Tu, J.; Zhou, G. Markowitz meets Talmud: A combination of sophisticated and naive diversification strategies. J. Financ. Econ. 2011, 99, 204–215. [Google Scholar] [CrossRef]
- Li, H.; Huang, Q.; Wu, B. Improving the naive diversification: An enhanced indexation approach. Financ. Res. Lett. 2020, 101661. [Google Scholar] [CrossRef]
- Schmidt, A.B. Managing portfolio diversity within the mean variance theory. Ann. Oper. Res. 2019, 282, 315–329. [Google Scholar] [CrossRef]
- Cai, H.; Schmidt, A.B. Comparing mean–variance portfolios and equal-weight portfolios for major US equity indexes. J. Asset Manag. 2020, 21, 326–332. [Google Scholar] [CrossRef]
- Bird, R.; Tippett, M. Note—naive diversification and portfolio risk—A note. Manag. Sci. 1986, 32, 244–251. [Google Scholar] [CrossRef]
- Schreiner, J. Portfolio revision: A turnover-constrained approach. Financ. Manag. 1980, 9, 67–75. [Google Scholar] [CrossRef]
- Kourtis, A. A Stability Approach to Mean-Variance Optimization. Financ. Rev. 2015, 50, 301–330. [Google Scholar] [CrossRef]
- Best, M.J.; Grauer, R.R. On the sensitivity of mean-variance-efficient portfolios to changes in asset means: Some analytical and computational results. Rev. Financ. Stud. 1991, 4, 315–342. [Google Scholar] [CrossRef]
- Chopra, V.K.; Ziemba, W.T. The effect of errors in means, variances, and covariances on optimal portfolio choice. In Handbook of the Fundamentals of Financial Decision Making: Part I; World Scientific: London, UK, 2013; pp. 365–373. [Google Scholar]
- Palczewski, A.; Palczewski, J. Theoretical and empirical estimates of mean–variance portfolio sensitivity. Eur. J. Oper. Res. 2014, 234, 402–410. [Google Scholar] [CrossRef]
- Sharpe, W.F. Capital asset prices: A theory of market equilibrium under conditions of risk. J. Financ. 1964, 19, 425–442. [Google Scholar]
- Sharpe, W.F. Portfolio Theory and Capital Markets; McGraw-Hill College: New York, NY, USA, 1970. [Google Scholar]
- Bailey, D.H.; Lopez de Prado, M. The Sharpe ratio efficient frontier. J. Risk 2012, 15, 3–44. [Google Scholar] [CrossRef]
- Sharpe, W.F. The sharpe ratio. J. Portf. Manag. 1994, 21, 49–58. [Google Scholar] [CrossRef]
- Xia, W.; Vera, J.C.; Zuluaga, L.F. Globally solving nonconvex quadratic programs via linear integer programming techniques. INFORMS J. Comput. 2020, 32, 40–56. [Google Scholar] [CrossRef]
- Mockus, J. Bayesian Approach to Global Optimization: Theory and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 37. [Google Scholar]
- Giannessi, F.; Tomasin, E. Nonconvex quadratic programs, linear complementarity problems, and integer linear programs. In Proceedings of the IFIP Technical Conference on Optimization Techniques, Rome, Italy, 7–11 May 1973; Springer: Berlin/Heidelberg, Germany, 1973; pp. 437–449. [Google Scholar]
- Bergmeir, C.; Benítez, J.M. On the use of cross-validation for time series predictor evaluation. Inf. Sci. 2012, 191, 192–213. [Google Scholar] [CrossRef]
- Black, A.J.; McMillan, D.G. Non-linear predictability of value and growth stocks and economic activity. J. Bus. Financ. Account. 2004, 31, 439–474. [Google Scholar] [CrossRef]
- Swinkels, L.; Tjong-A-Tjoe, L. Can mutual funds time investment styles? J. Asset Manag. 2007, 8, 123–132. [Google Scholar] [CrossRef]
- Demšar, J. Statistical comparisons of classifiers over multiple data sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]
- Friedman, M. A comparison of alternative tests of significance for the problem of m rankings. Ann. Math. Stat. 1940, 11, 86–92. [Google Scholar] [CrossRef]
- Bender, J.; Briand, R.; Nielsen, F.; Stefek, D. Portfolio of risk premia: A new approach to diversification. J. Portf. Manag. 2010, 36, 17–25. [Google Scholar] [CrossRef]
- Liesiö, J.; Xu, P.; Kuosmanen, T. Portfolio Diversification based on Stochastic Dominance under Incomplete Probability Information. Eur. J. Oper. Res. 2020, 286, 755–768. [Google Scholar] [CrossRef]
- Cesarone, F.; Scozzari, A.; Tardella, F. An optimization–diversification approach to portfolio selection. J. Glob. Optim. 2020, 76, 245–265. [Google Scholar] [CrossRef]
| ID. | Dataset | M | T | N |
|---|---|---|---|---|
| Industry Portfolios | ||||
| 5 Industry Portfolios | 5 | |||
| 10 Industry Portfolios | 10 | |||
| Emerging Market Factors | ||||
| 6 Emerging Market Portfolios Formed on BM and OP | 6 | |||
| 6 Emerging Market Portfolios Formed on Size and BM | 6 | |||
| 6 Emerging Market Portfolios Formed on Size and OP | 6 | |||
| Bivariate sorts on Size, BM and I | ||||
| 6 Portfolios Formed on Size and BM | 6 | |||
| 6 Portfolios Formed on Size and I | 6 | |||
| Bivariate sorts on Size, BM and I | ||||
| 25 European Portfolios Formed on Size and BM | 25 | |||
| MR Metric | SR Metric | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| ID | GMV | GMR | MV | MSV | GMV | GMR | MV | MSV | ID |
| 1 | 0.9521 | 0.1330 | 1 | ||||||
| 2 | 1.4004 | 0.2825 | 2 | ||||||
| 3 | 1.3098 | 0.9897 | 0.2698 | 0.1748 | 3 | ||||
| 4 | 0.6058 | 0.1411 | 4 | ||||||
| 5 | 0.6324 | 0.1541 | 5 | ||||||
| 6 | 0.7234 | 0.1752 | 0.2079 | 6 | |||||
| 7 | 0.5404 | 0.5456 | 0.0960 | 7 | |||||
| 8 | 0.4494 | 0.0791 | 8 | ||||||
| 9 | −0.1094 | −0.0175 | 9 | ||||||
| 10 | 0.1898 | 0.6411 | 0.0324 | 0.1277 | 10 | ||||
| 11 | 0.4162 | 0.0742 | 11 | ||||||
| 12 | 0.3150 | 0.0306 | 12 | ||||||
| 13 | 0.1505 | 0.0262 | 13 | ||||||
| 14 | 0.2519 | 0.0444 | 14 | ||||||
| 15 | 0.1601 | 0.0283 | 15 | ||||||
| 16 | 1.1048 | 0.2017 | 16 | ||||||
| 17 | 1.4131 | 1.4092 | 0.2534 | 0.2600 | 17 | ||||
| 18 | 1.0582 | 0.1845 | 0.0276 | 18 | |||||
| 19 | 1.0294 | 1.4941 | 0.1948 | 0.2271 | 19 | ||||
| 20 | 1.0063 | 0.1908 | 0.1721 | 20 | |||||
| 21 | 0.0917 | 0.1488 | 0.0134 | 21 | |||||
| 22 | 0.4391 | 0.5806 | 0.1011 | 22 | |||||
| 23 | 0.7158 | 0.8431 | 0.1530 | 23 | |||||
| 24 | −0.2092 | −0.0347 | 24 | ||||||
| 0.6934 | 0.8196 | 0.1369 | 0.1452 | ||||||
| 3.2500 | 2.5208 | 3.0208 | 2.7292 | ||||||
| MR Analysis | |||||
|---|---|---|---|---|---|
| Method | z-statistic | p-value | |||
| 3.2500 | 4.0249 | 1 × 10 | 0.0333 | 0.0167 | |
| 2.5208 | 2.0683 | 0.0386 | 0.0500 | 0.0250 | |
| 1.9566 | 0.0504 | 0.1000 | 0.0500 | ||
| MSV | - | - | - | - | |
| SR Analysis | |||||
| Method | z-statistic | p-value | |||
| 3.0208 | 3.5218 | 4 × 10 | 0.0333 | 0.0167 | |
| 2.7292 | 2.7394 | 0.0062 | 0.0500 | 0.0250 | |
| 2.2362 | 0.0253 | 0.1000 | 0.0500 | ||
| MSV | - | - | - | - | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernández-Navarro, F.; Martínez-Nieto, L.; Carbonero-Ruz, M.; Montero-Romero, T. Mean Squared Variance Portfolio: A Mixed-Integer Linear Programming Formulation. Mathematics 2021, 9, 223. https://doi.org/10.3390/math9030223
Fernández-Navarro F, Martínez-Nieto L, Carbonero-Ruz M, Montero-Romero T. Mean Squared Variance Portfolio: A Mixed-Integer Linear Programming Formulation. Mathematics. 2021; 9(3):223. https://doi.org/10.3390/math9030223
Chicago/Turabian StyleFernández-Navarro, Francisco, Luisa Martínez-Nieto, Mariano Carbonero-Ruz, and Teresa Montero-Romero. 2021. "Mean Squared Variance Portfolio: A Mixed-Integer Linear Programming Formulation" Mathematics 9, no. 3: 223. https://doi.org/10.3390/math9030223
APA StyleFernández-Navarro, F., Martínez-Nieto, L., Carbonero-Ruz, M., & Montero-Romero, T. (2021). Mean Squared Variance Portfolio: A Mixed-Integer Linear Programming Formulation. Mathematics, 9(3), 223. https://doi.org/10.3390/math9030223








