3.1. The Fourier-Exponential Smooth Transition Autoregressive (ESTAR) Hybrid Data-Generating Processes (DGP)
We first investigate the empirical power of the tests by using the FKSS-DGP where the process is a stationary nonlinear adjustment around a smooth break. We construct the Fourier-ESTAR(1) model by:
where
and
and
are the parameters of the Fourier series and take the values
and
, respectively. We also consider the following parameter values: for
, for the transition speed,
,
and
. These simulation results for
are presented in
Table 2.
LNV state that the natural competitor of Model 1 (including the structural break in the intercept only) is the ADF test which includes both intercept and trend. Since the original KSS and ADF tests do not allow for a structural break, we include both terms in our power analysis. As readily seen from
Table 2, the power of the EL test dominates all other tests. This result is rather unexpected, because the power of the FKSS test is expected to dominate mostly under the current DGP, except for the parameter region where the transition parameter
is sufficiently high. A general finding by KSS and OY suggests that non-linear unit root tests are relatively more powerful when the slope parameter is relatively small regardless of the values of
. But, their power falls as the slope parameter rises. If the slope parameter is equal or greater, the power of the Dickey–Fuller test dominates other tests. Notice that as
grows large, the model becomes approximately linear, though
is not a scale-free parameter. KSS [
11] argue that the nonlinear tests would be more powerful than the linear tests in the region local to the null, where the series tends to be more persistent. They state that most economic time series are likely to be highly persistent or stay near unit root. Thus, we argue that the power results tabulated in
Table 2 are not in line with the findings by KSS and OY.
Enders and Lee [
1] claim that the LNV and KSS tests deal with smooth structural breaks in their unit root testing procedures, via LSTR and ESTR breaks, respectively. Notice however that the KSS test is a non-linear unit root test that imposes the ESTR non-linearity to the stochastic component of the series, but it does not deal with structural breaks directly. As argued by Becker et al. [
12], the presence of high-frequency components would reflect various forms of stochastic parameter instability. In this regard, we argue that the non-linearity embedded within the KSS test would be regarded as dealing with the stochastic parameter instability instead of smooth deterministic structural breaks.
Originally, the EL test was proposed for smooth structural break. EL argue that the low-frequency component of the Fourier function only captures the smooth structural break. However, the power analysis employed here with this hybrid data sheds light on the issue that the low-frequency component also captures non-linearity in the stochastic component which can be classified as stochastic parameter instability. As previously stated, the presence of high-frequency components would reflect various forms of stochastic parameter instability such as non-linearity in the slope parameter of the ESTAR type of unit root test. Therefore, using low-frequency component
it is not feasible to capture such a parameter’s instability. Notice that we consider the low-frequency (
) component only, in the power analyses reported in
Table 1. However, the EL test has the best-performing test in this DGP setting. Enders and Lee [
1,
2] probably recognise that the low frequency Fourier approximation (
) filters out structural breaks as well as other forms of non-linearity, as discussed in the Introduction. Due to this observation, they classify the KSS test as the alternative to their unit root test. In the current setting, two sources of non-linearity are imposed (smooth structural break and state-dependent non-linearity) and the EL test captures both of them. This result seems to be in contradiction with Becker et al. [
12] and Enders and Lee [
1]. Therefore, aggregating the results of power analysis tabulated in
Table 3 with the findings in the related literature, we can conclude that the low-frequency component of the Fourier function over-filters the hybrid DGPs or it can capture both smooth break and non-linearity in stochastic parts.
It may be useful to further prove the over-filtration problem of Fourier transforms in hybrid DGP by employing a newly designed simulation study.
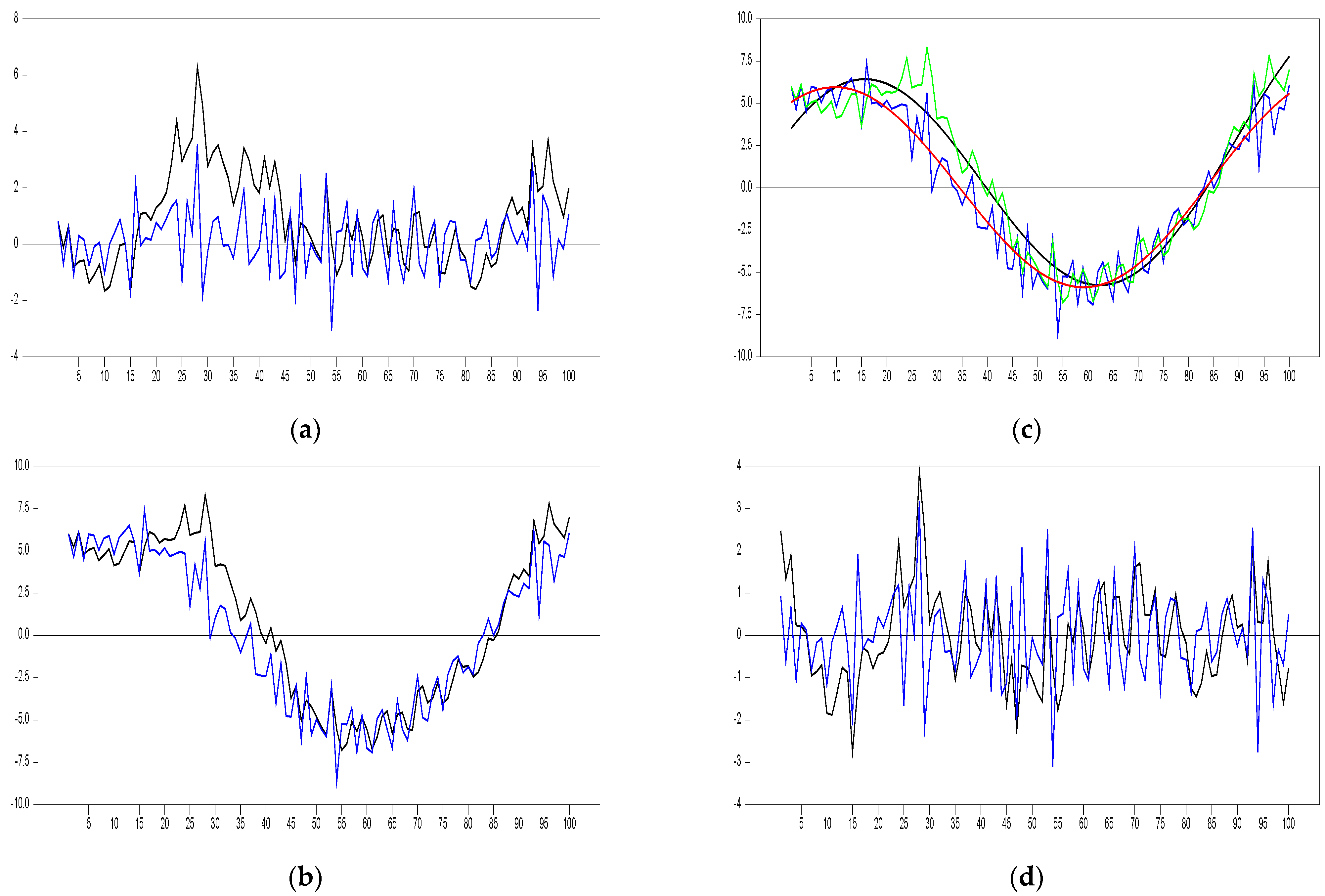
Figure 1 is generated under the two sets of DGP. The first is the linear
process with the AR parameter, 0.8 (light series), and the other is the KSS DGP with
and
(dark series). We can explicitly see the difference between linear and non-linear series in Panel (a) of
Figure 1. In Panel (b), the two DGPs augmented with the same Fourier series (
and
) are displayed; they are the
process (Fourier trend with
plus an
), and the
process, respectively. In Panel (c) the non-linear trends estimated using the Enders and Lee [
1,
2] methodology. Therefore, we expect to obtain the same Fourier trends from both series
. We obtained the same Fourier trend
from
DGP, however, the estimated Fourier trend from
is not equal to
. When we have obtained the residuals from de-trended series from
and
in Panel (d) of
Figure 1, we see that estimated Fourier trend from
is equal to the summation of two effects:
Therefore, when we de-trend by using the Fourier we are left an process with approximately the AR parameter, 0.8. (More specific, , KSS 2 nd DGP with ).
In
Figure 1, Panel (a), the blue series is an AR(1) stationary process while the black series is the stationary ESTAR (1) process. In Panel (b), the same Fourier function has been added to these two processes with the same colours. In Panel (c), trend functions were found using the grid search method described in Enders and Lee [
1] in these two series. The Red Fourier trend is obtained for AR (1)+Fourier and Black Fourier trend is obtained for ESTAR (1)+Fourier. Finally, we can see the nonlinear detrended ESTAR (1) process and AR(1) processes in
Figure 1, Panel (d). As can be seen from here, the Fourier de-trended stationary AR(1) process given in blue is the same as the Fourier de-trended ESTAR(1) process given in black, which has almost transformed into the same structure.
We now provide more explanations about the behaviour of the Fourier series. (The convergence of the Fourier transforms to a stochastic process is studied by Gallant [
5]. He argued that the norm measure shall be global and the Sobolov norm satisfies these requirements. See Technical Annex for more details, which is available upon request.) We first have the Dirichlet (1829) condition, stating that the Fourier series converge to a real-valued periodic function at every jump discontinuity from its midpoint [
17]. Furthermore, it is well-established that as the frequency component increases, the low frequencies capture the structural break or deterministic components of the series whilst the high-frequency components capture the other stochastic component (e.g., [
5,
12,
18,
19,
20]). These can be combined to explain unexpected findings in the power analysis observed in
Table 2. When estimating a stochastic process with Fourier series, the low-frequency estimates the mid-point of the highest jump discontinuity, which we call a structural break (see also [
1,
2]). This issue can also be traced from Figures 1 and 3 in [
13]. Therefore, the second series generated under the (
) leads to a bigger jump discontinuity in Panel (b). Thus, in the estimation phase in Panel (c) the Fourier function passes through the mid-point of this jump discontinuity, however this jump discontinuity is now obtained by two different sources (smooth structural break and state-dependent non-linearity). Therefore, in Panels (c) and (d), we see that the Fourier trend overreact to (
) DGP due to the Dirichlet condition where this result contradicts with [
1,
2,
5,
12,
18,
19,
20].
To further support our claim of the over-filtration of the Fourier transforms, we conduct the following simulation experiment. First, we construct the FKSS-DGP similarly to the power analysis conducted in
Table 2. Next, we estimate structural break by the Fourier function and then test the ESTAR non-linearity with the de-trended series. This simulation study can be used as the validation of the results in
Figure 1. Here we employ the linearity test proposed by [
14]. Notice that the KSS test is the linearized version of the first order Taylor approximation of the ESTAR non-linearity.
From the first row of
Table 3, we find that 180 out of 2000 (9%) simulated series exhibit non-linearity by the LM test. The simulated series are (
) series, therefore after removing the Fourier trend
, we expect to obtain ESTAR-type non-linearity from de-trended series. The LM test is employed to the de-trended series; however, the non-linearity obtained in these de-trended series does not exceed 17.5% which means that state-dependent non-linearity has disappeared.
This simulation experiments further confirm the power analysis in
Table 3 and explanation obtained from
Figure 1. Therefore, the estimated Fourier trends are as follows:
and
includes the features of
and the de-trended series are
process. Thus, we obtain very rare rejection of null hypothesis of linearity.
3.2. The Behaviour of the Fourier Function under the Exponential Smooth Transition DGP
As mentioned in the Introduction, the KSS test is one of the potential rivals of the EL test and our previous results (in
Table 2 and
Table 3, and
Figure 1) also support the claim of [
1,
2]. Therefore, it is interesting to see the power performance of the EL test under the KSS-DGP setting as that may increase our understanding of the behaviour of the Fourier function for state-dependent non-linearity in isolation. We now consider the following
process as a DGP:
where we use
and
. The power experiments obtained under this DGP with
are summarized in
Table 4.
We find from
Table 4 that the most powerful test appears to be the CL Test,
. This is rather an interesting result, considering the claim by Enders and Lee [
1] that “If a non-linear trend is absent from the DGP, a standard unit root test without a non-linear trend will be more powerful than our test.” Even in the region where the KSS test should be mostly powerful, we find that the CL test performs better than the KSS test. The KSS test is constructed after deriving the Taylor approximation to the original ESTAR process; hence some information inherent in the data may be lost. Thus, the Fourier function incorporated in the KSS test would make some adjustments for the remainder of the terms (
), thereby increasing the power of the CL test and showing why a non-linear unit root test including Fourier transforms displays better power even under the DGP without containing any structural breaks. On the other hand, the EL test has similar power to the KSS test as a second-best test. This result again supports the findings that we have found in the previous section and the claim of [
1,
2]. This result is also an indication of the over-filtration problem of the Fourier function, showing that the Fourier function can imitate any type of series behaviour even if it has a low-frequency component
while de-trending the series.
By using the KSS DGP, we have reached the conclusions given above, but the KSS DGP has its own limitation to show more information about the behaviour of the Fourier function. The transition speed is taken to be 0.1 and 1.0; these are of relatively smooth transition speed, hence for further investigation we have to increase the transition speed in order to see the behaviour of Fourier function. However, when we increase the greater than 1, the power results of all tests rapidly converge to 1.0. Therefore, there is no opportunity to compare the unit root test with each other and the behaviour of the Fourier function. Thus, for a moderate and sharp transition, it is better to select the DGP setting where we can provide these kinds of features. As mentioned earlier, the second potential rival test for the EL test is the LNV test. The LNV test is simply the logistic smooth transition counterpart of the EL test which is also proposed for detecting smooth structural breaks. Therefore, we proceed with the LNV-DGP in the next section in order to see the behaviour of the Fourier function in sharp transitions and/or sharp breaks.
3.3. The Behaviour of the Fourier Function under the Logistic Smooth Transition DGP
We proceed to conduct the power experiment under the DGP set-up by the LNV test, which is an important alternative to the EL test. This contains the logistic smooth transition function (LST), which has desirable features in determining the location of the structural break and speed of transition. The speed of transition parameter, determines the structure of breaks such that smooth and sharp breaks are dictated by low and high values, respectively.
We construct the following
DGP, in which there is a stationary nonlinear adjustment around a smooth transition from one constant to another:
Here,
is a logistic smooth transition function, and we consider of the following parameter values: for the speed of transition parameter,
, for the threshold parameter,
and for the structural break parameter,
(small, medium and large breaks), and for the autoregressive parameter,
. These results with
are provided in
Table 5.
In
Table 5, we consider three different cases depending on the magnitudes of the structural break parameter
. For the small break with
, the ADF test performs better than all the other tests, see also similar results documented in LNV, Sollis [
15] and OY. Surprisingly, however, the second-best test in this parameter region is the EL test, not the LNV. This may simply reflect that the Fourier form performs better in approximating the very smooth breaks. (The CL test is as good as the other test and better than the STR type analogous test LNVKSS (OY test). The FKSS test is better than the OY test, with the reason similar to the comparison of LNV and the EL test.) The power of all the tests is negatively associated with the
parameter. Furthermore, the threshold location parameter,
, also affects the power of the STR-type tests negatively. In particular, when the threshold is located at the beginning of the sample, the Fourier type tests tend to display better power, see [
12] for similar findings. They document that the power of the Fourier type structural break test (i.e. the
Trig-test) deteriorates as the break point moves to the end of the sample.
For the moderate structural break with , we obtain completely different results. For small slope parameters with the structural break dated at the beginning of the sample, () the ADF test outperforms all the other tests. As the slope parameter rises, the CL test becomes more powerful. This result is somewhat unexpected. On the other hand, when the structural break parameter is located in the middle of the sample (), the ADF test performs best for the low values of only. As expected, in the rest of the parameter region, the LNV test becomes more powerful than the other tests. Hence, we may conclude that the logistic smooth transition function is able to capture the sharper breaks.
The Fourier-type structural break unit root tests are shown to display better power performance when the structural break is located at the beginning of the sample. Thus, a unit root test such as the EL test, that includes Fourier transforms, is expected to perform better in this case. Surprisingly, however, we find that the CL test is the best performing even in the smooth structural parameter region.
Finally, when the structural break parameter is substantially large, both the ADF and KSS tests lose power, see LNV, Sollis [
15] and OY. Similar simulation results are also documented in the Technical Annex. The performance of the smooth transition type de-trending tests improves when the value of the structural break parameter increases. Therefore, in this region, the LNV test should become more powerful. By contrast, the EL test using only one frequency
fails to achieve decent power in the presence of sharp breaks. Enders and Lee [
1] notice that sharp breaks of short duration will not be approximated well by few low-frequency components. They also suggest adding a second frequency in estimating the non-linear trend in order to capture the sharp breaks. However, the negative effects of including cumulative frequencies were also discussed in the previous section as over-filtration problem using
and it is also documented in [
1,
2]. They have shown that there is no practical way of testing for selecting the cumulative frequency,
. Increasing the cumulative frequency, the sum of squares of the estimates continuously decreasing, hence any type of test continuously has achieved more significant results by these increments in
. Therefore, the limiting case or the most significant result can be obtained when
, which means that there is no way to select an optimal cumulative frequency. On the other hand, increasing the cumulative frequency, the high-frequency components of the Fourier function take place in the analysis which is detecting the stochastic parameter instabilities. Therefore, by using cumulative frequency it is not appropriate to detect sharp breaks.
Overall, we draw the following conclusions from these power experiments conducted under the LNV-DGP. First, the LNV test outperforms other tests for the cases with high structural breaks and high transition speeds. Second, the CL and EL tests become more powerful in the presence of smooth breaks, especially when the threshold parameter is located at the beginning of the sample. Their power increases as the structural breaks and transition speed parameters are weakened. Moreover, when the threshold is located at the beginning of the series, the power performance of the CL and EL tests further improved. Hence, the EL test, which is the main competitor of the LNV test, gains significant power boost in the case of very smooth transitions. On the other hand, such power gain disappears for sharp breaks. Furthermore, we notice that the CL test becomes the main competitor to the LNV test when the structural break parameter is located at the beginning of the series where the EL test is expected to be the competitor.
3.4. The Behaviour of the Fourier Function under a Hybrid DGP with Both a Logistic Smooth Transition Function of Structural Breaks and Regime-Dependent ESTAR Non-Linearity
Finally, we consider the DGP investigated by OY, who propose the LNVKSS (OY) test, which is the smooth transition counterpart of the CL test. We consider the following
model:
where
is defined earlier. We consider the following parameter values: two extreme values for
, two extreme values of
, and small, moderate and large structural break parameters,
. These simulation results with
are presented in
Table 6.
The power experiment results tabulated in
Table 6 are qualitatively similar to those obtained in
Table 5.
Overall, we can draw the stylized findings from all the simulations results as follows:
- (1)
While the tests using the Fourier form display better power performance in the presence of very smooth structural breaks, the tests with the logistic smooth transition will be more powerful in the presence of moderate and sharp breaks.
- (2)
While the tests using the Fourier approximation show better power performance when the threshold is located at the beginning of the sample, the tests with the logistic smooth transition achieves better power when the threshold is located in the middle of the sample.
- (3)
Testing procedures using Fourier approximation over-filters the data in the presence of both structural breaks and stochastic non-linearities. On the other hand, the logistic smooth transition function does not suffer from such a problem.
- (4)
Testing procedures that use more than one approximation (namely the Fourier and Taylor approximations) have better power performances than the other procedures.
- (5)
The KSS test employs the Taylor approximation to the original ESTAR process which renders some valuable information lost in the auxiliary testing equation. Thus, embedding the Fourier transforms within a test such as the CL test will make some adjustment for the remainder of the Taylor approximation, which helps to boost the power of the CL test over the KSS test.
- (6)
The EL test appears to be the third and fourth best performing test under the KSS- and LNV-DGPs. Their power performance worsens when the power analyses are conducted for the models with both intercept and trend. (We have conducted such analysis for the model with intercept and trend. These results are qualitatively similar to the simulation results reported for the models with the intercept only. These results are available upon request.) Therefore, we do not support the claim of Enders and Lee [
1] that the EL test is a potential rival for the KSS and LNV tests. Rather, we find that the CL test appears to be a potential rival of the LNV and KSS tests when considering all the simulation results (Under the LNV-DGP, the CL test becomes more powerful when the threshold is located at the beginning of the sample. Furthermore, the CL test is also the best-performing test under the KSS-DGP).
Theoretical articles that have recently focused on the problems we have obtained from power analysis can be found in [
21,
22,
23,
24,
25,
26,
27,
28]. In these studies, the authors propose theoretical approaches that try to solve the problems we mentioned in the power study of the Fourier and logistic smooth transition function. However, none of these studies explore a holistic comparison and they touch only on some of the problems that we obtained from power analysis. In terms of empirical research, studies which utilize the tests discussed to make the correct unit root test in line with the results of the power study, as well as try to identify which one of the tests is the best, are [
29,
30,
31,
32,
33]. These studies perform identification tests to determine whether the Fourier trend or the logistic trend fits the data better. Beyond that, they also explore which of the state-dependent, time-varying and hybrid tests is superior in these exercises. Although their findings are in line with the results of the simulation studies we have discussed, none of them theoretically produce data and achieve general results. More specifically, their decisions only come from within the characteristics of the available datasets. In this sense, our present study will shed light on the theoretical and empirical areas to be dealt with in the future.
In this paper, we discuss the integer form of the Fourier function. It may be beneficial to expand our research by taking into account the fractional frequency studies that have just started to become popular. Among others, we see the studies of Omay [
34] and Omay et al. [
26] on this subject in the literature. Their findings indicate that fractional frequency fits the data better than the integer frequency. However, since the results obtained here are valid within the fractional frequency, only how much the problem can be reduced will be explored. Accordingly, our investigation in this paper has general results that can give an insight into the issues of fractional frequency.