On the Quantitative Properties of Some Market Models Involving Fractional Derivatives
Abstract
:1. Introduction
1.1. Stock Returns and Tempered Stable Lévy Processes
1.2. Why Fractional Operators Arise
1.3. Pricing Contingent Claims
1.4. Contributions of the Paper
- -
- Review the various models in the tempered stable family that involve a fractional derivative in the space and/or time variable, and explain the link between order of fractional derivatives a model properties (state of randomness, time subordination, diffusion regime);
- -
- By analogy with the probabilistic approach, define the fundamental concepts needed for option pricing (convexity adjustement, risk-neutral expectation) in the context of a space-time diffusion;
- -
- Focus on a fractional diffusion model involving a Riesz time fractional derivative, and establish closed form expression for the convexity adjustment and the price of several options (European, digital, power, log). These formulas are new and come as a complement to the formulas previously obtained in the case of a Caputo time fractional derivative;
- -
- Derive closed form expression for at-the-money implied volatility and market sensitivities, and deduce some practical considerations for hedging policies and profit and loss of portfolios.
1.5. Structure of the Paper
2. Principles of Option Pricing with Exponential Lévy Motions
2.1. Basics of Lévy Processes
2.2. Exponential Lévy Markets
3. Tempered Stable Processes, Fractional Partial Differential Equations, and Measures of Randomness
3.1. Tempered Stable Densities and Subordination
3.2. CGMY Model, Riemann–Liouville Derivatives
3.3. FMLS Model, Riesz–Feller Derivative and the “States of Randomness”
- -
- For , the Lévy stable process degenerates into the centered Brownian motion of variance whatever the skewness , and all standardized moments (skewness, excess kurtosis) are null from . This situation, which underlies the BSM model, corresponds to a (proper) mild randomness state;
- -
- When , the scale factor becomes infinite for and one speaks of pre-wild randomness;
- -
- By far the most interesting situation from the point of view of financial modeling occurs for ; in this case, all moments for are infinite, but the mean () can be finite for some choice of asymmetry (see discussion below), a configuration known under the name of wild randomness. Note that stable distributions with the stability parameter in are said to be Paretian [59] and famously arose after Mandelbrot’s initial calibration giving for the cotton market [60];
- -
- If (Cauchy distribution) or is lower than 1, moments are infinite for all N, and we are in a case of extreme randomness. This situation, however, is not desirable for pricing purposes because this divergence prevents achieving finite option prices via the risk-neutral expectation (9).
- -
- It establishes a direct correspondence between order of the space fractional derivative and randomness of the model, as both are controlled by the parameter ;
- -
- It extends the traditional diffusion equation which is obtained for , thus recovering the heat Equation (8) in that case;
- -
- Note also that turns out to be the fractional calculus analogue to the probabilistic condition .
4. A Space-Time Fractional Diffusion Model for Option Pricing
4.1. Main Idea and Fundamental Analogies
- -
- By analogy with (26), we restrict ourselves to and we choose (maximal asymmetry hypothesis) and we denote the corresponding diffusion equation in that case by RFFD RFFD.
- -
- By analogy with the risk-neutral formula (10), we define the price at time t of a contingent claim delivering a payoff at its maturity T to be:where we have defined .
- -
- The convexity adjustment is defined by analogy with (5) as:
- -
- First, the order of the spatial derivative , that controls the kurtosis of the left fat tail of the distribution of returns, and the magnitude of the model’s randomness. When , the distribution decays according to a power law in when , and we are in a situation of wild randomness according to the terminology defined above. If then the Green function (30) degenerates into the normal distribution and one recovers the mild randomness configuration of the BSM model.
- -
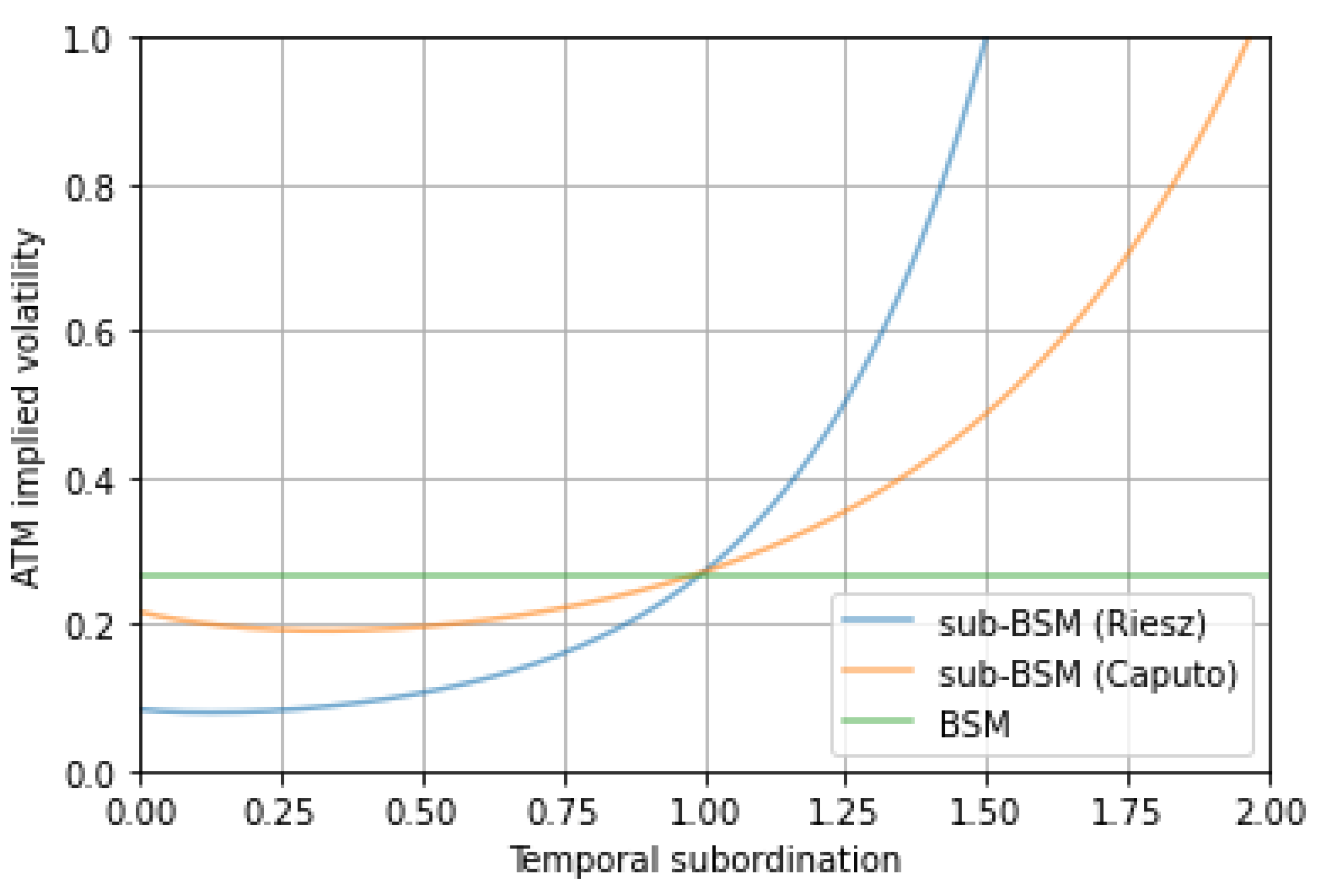
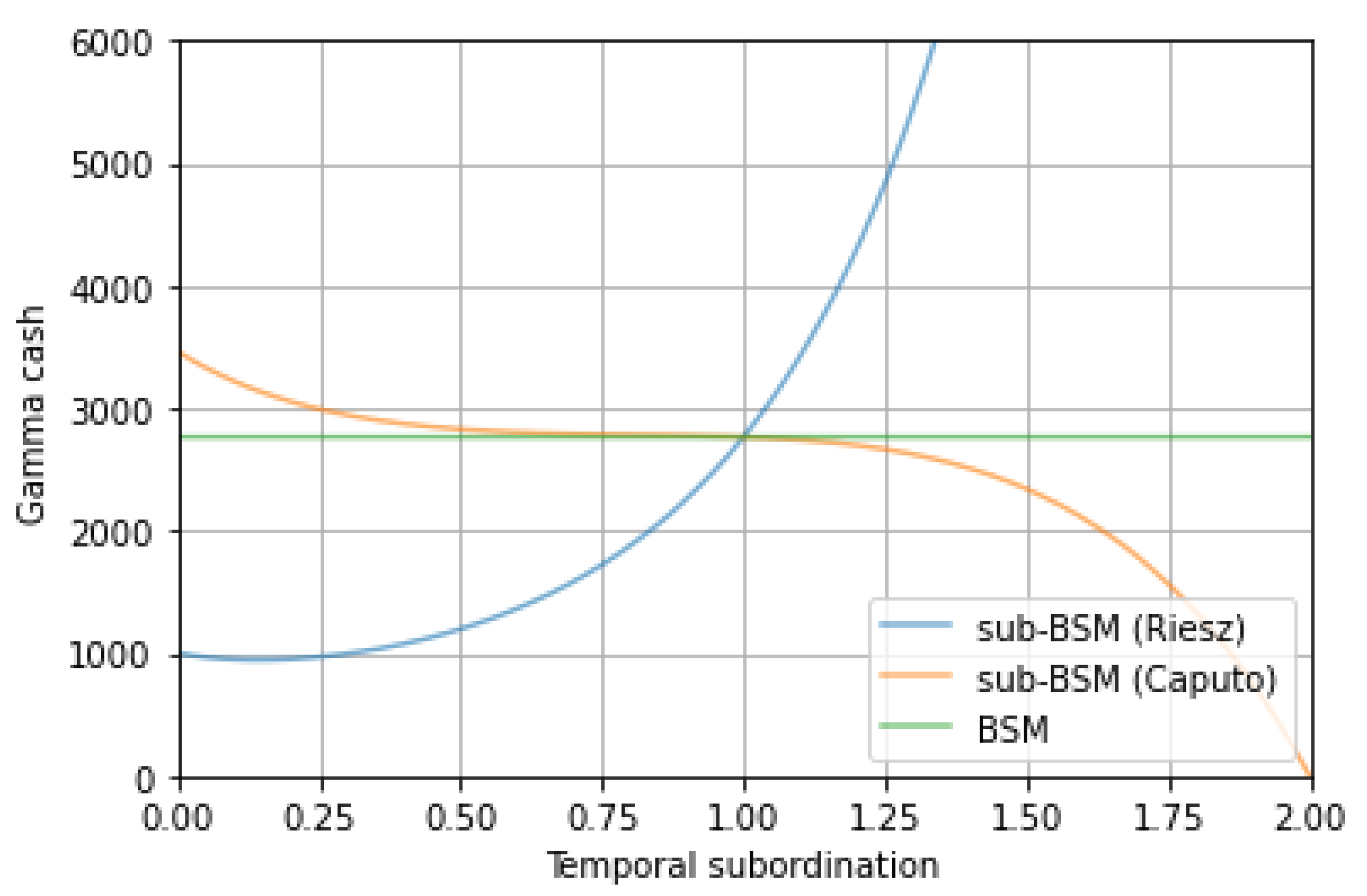
- Second, the order of the temporal derivative that acts as a fractional calculus analogue to the time subordination in the VG and NIG models. Variations of allow a switch between regimes ( is called the slow diffusion regime, and the fast diffusion regime) and a temporal redistribution of risk (typically, makes short-term options more expensive and long-term options cheaper, a situation that occur in case of market crash, sell off, or brutal price moves). For parameter calibration and further discussion, we refer to [31].
4.2. Particular Cases
- -
- Taking recovers the FMLS model [23]; in that case there is no temporal subordination, and only a (left) fat tail measured by the kurtosis parameter which coincides with the order of the Riesz–Feller space derivative;
- -
- Taking defines a “subordinated Black–Scholes model” sub-BSM, in the sense that there is no fat tail but a subordination parameter induced by the order of the Riesz time derivative. A similar model had already been introduced in [48] but in the case of a Caputo time derivative.
- -
- -
- Let us also mention that the case (or equivalently ) corresponds to the so-called neutral diffusion, but is only of limited financial interest.
4.3. Convexity Adjutment
4.4. Pricing Formula in the Mellin Space
5. Application to Vanilla and Exotic Path Independent Options
5.1. Digital
5.2. European
5.3. Power
5.4. Log
- -
- A simple pole in with residue:
- -
- A series of poles at every positive integer with residues:
6. Impact on Volatility Modeling and Hedging Policies
6.1. At the Money Forward Price and Volatility
6.2. Delta Hedging
6.3. Profit and Loss
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ATM | At the money |
| ATMF | At the money forward |
| BSM | Black-Scholes-Merton |
| ITM | In the money |
| BSM | Black-Scholes-Merton |
| sub-BSM | Subordinated Black-Scholes-Merton |
| OTM | Out of the money |
| P&L | Profit and loss |
| RFFD | Riesz-Feller fractional diffusion |
| VG | Variance Gamma |
Appendix A. Notations
Appendix B. Special Functions
Appendix B.1. Gamma Function
Appendix B.2. Wright M-Function
References
- Bachelier, L. Théorie de la spéculation. Ann. Sci. Éc. Norm. Supér. 1900, 3, 21–86. [Google Scholar] [CrossRef]
- Black, F.; Scholes, M. The Pricing of Options and Corporate Liabilities. J. Polit. Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef] [Green Version]
- Merton, R. Theory of Rational Option Pricing. Bell J. Econ. Manag. Sci. 1973, 4, 141–183. [Google Scholar] [CrossRef] [Green Version]
- Heston, S.L. A Closed-Form Solution for Options with Stochastic Volatility with Applications to Bond and Currency Options. Rev. Financ. Stud. 1993, 6, 327–343. [Google Scholar] [CrossRef] [Green Version]
- Cont, R.; Tankov, P. Financial Modelling with Jump Processes; Chapman & Hall: New York, NY, USA, 2004. [Google Scholar]
- Krawiecki, A.; Holyst, J.A.; Helbing, D. Volatility Clustering and Scaling for Financial Time Series due to Attractor Bubbling. Phys. Rev. Lett. 2000, 89, 158701. [Google Scholar] [CrossRef] [Green Version]
- Mandelbrot, B. Fractals and Scaling in Finance: Discontinuity, Concentration, Risk; Springer: New York, NY, USA, 1997. [Google Scholar]
- Calvet, L.; Fischer, A. Multifractal Volatility: Theory, Forecasting, and Pricing; Academic Press: Cambridge, UK, 2008. [Google Scholar]
- Chatterjee, A.; Yarlagadda, S.; Chakrabarti, B.K. Econophysics of Wealth Distributions; Springer: Milan, Italy, 2005. [Google Scholar]
- D’Arcangelis, A.M.; Rotundo, G. Complex networds in finance. In Complex Networks and Dynamics. Lecture Notes in Economics and Mathematical Systems; Commendatore, P., Matilla-García, M., Varela, L., Cánovas, J., Eds.; Springer: Cham, Switzerland, 2016; Volume 683. [Google Scholar]
- Mantegna, R.N.; Stanley, H.E. An Introduction to Econophysics: Correlations and Complexity in Finance; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Mantegna, R.N.; Stanley, H.E. Stochastic process with ultraslow convergence to a Gaussian: The truncated Lévy flight. Phys. Rev. Lett. 1994, 73, 2946. [Google Scholar] [CrossRef]
- Koponen, E. Analytic approach to the problem of convergence of truncated Lévy flights towards the Gaussian stochastic process. Phys. Rev. E 1995, 52, 1197–1199. [Google Scholar] [CrossRef]
- Carr, P.; Geman, H.; Madan, D.; Yor, M. The Fine Structure of Asset Returns: An Empirical Investigation. J. Bus. 2002, 75, 305–332. [Google Scholar] [CrossRef] [Green Version]
- Boyarchenko, S.; Levendorskii, S. Non Gaussian Black-Scholes-Merton Theory; World Scientific Publishing Co.: River Edge, NJ, USA, 2002. [Google Scholar]
- Rosinski, J. Tempering Stable Processes. Stoch. Process. Their Appl. 2007, 117, 677–707. [Google Scholar] [CrossRef] [Green Version]
- Madan, D.; Carr, P.; Chang, E. The Variance Gamma Process and Option Pricing. Eur. Financ. Rev. 1998, 2, 79–105. [Google Scholar] [CrossRef] [Green Version]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach: New York, NY, USA, 1993. [Google Scholar]
- Kochubei, A.; Luchko, Y. (Eds.) Handbook of Fractional Calculus with Applications. Volume 1: Basic Theory; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Kochubei, A.; Luchko, Y. (Eds.) Handbook of Fractional Calculus with Applications. Volume 2: Fractional Differential Equations; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Cartea, A.; Del-Castillo-Negrete, D. Fractional diffusion models of option prices in markets with jumps. Physica A 2007, 374, 749–763. [Google Scholar] [CrossRef] [Green Version]
- Carr, P.; Wu, L. The Finite Moment Log Stable Process and Option Pricing. J. Financ. 2003, 58, 753–777. [Google Scholar] [CrossRef] [Green Version]
- Feller, W. An Introduction to Probability Theory and Its Applications, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1971; Volume II. [Google Scholar]
- Gorenflo, R.; Mainardi, F. Random walk models for space-fractional diffusion processes. Fract. Calc. Appl. Anal. 1998, 1, 167–191. [Google Scholar]
- Carte, A. Derivatives pricing with marked point processes using tick-by-tick data. Quant. Financ. 2013, 13, 111–123. [Google Scholar] [CrossRef] [Green Version]
- Clark, P. A subordinated stochastic process model with fixed variance for speculative prices. Econometrica 1973, 41, 135–155. [Google Scholar] [CrossRef]
- Carr, P.; Wu, L. Time-changed Lévy processes and option pricing. J. Financ. Econ. 2004, 71, 113–141. [Google Scholar] [CrossRef] [Green Version]
- Gorenflo, R.; Mainardi, F.; Vivoli, A. Discrete and Continuous Random Walk Models for Space-Time Fractional Diffusion. J. Math. Sci. 2006, 132, 614–628. [Google Scholar] [CrossRef]
- Korbel, J.; Luchko, Y. Modeling of financial processes with a space-time fractional diffusion equation of varying order. Fract. Calc. Appl. Anal. 2016, 19, 1414–1433. [Google Scholar] [CrossRef]
- Kleinert, H.; Korbel, J. Option Pricing Beyond Black-Scholes Based on Double-Fractional Diffusion. Physica A 2016, 449, 200–214. [Google Scholar] [CrossRef] [Green Version]
- Tarasov, V.E.; Tarasova, V.V. Macroeconomic models with long dynamic memory: Fractional calculus approach. Appl. Math. Comput. 2018, 338, 466–486. [Google Scholar] [CrossRef]
- Tomovski, Z.; Dubbeldam, J.L.A.; Korbel, J. Applications of Hilfer-Prabhakar operator to option pricing financial model. Fract. Calc. Appl. Anal. 2020, 23, 996–1012. [Google Scholar] [CrossRef]
- Wilmott, P. Paul Wilmott on Quantitative Finance; Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Carr, P.; Madan, D. Option valuation using the Fast Fourier Transform. J. Comput. Financ. 1999, 2, 61–73. [Google Scholar] [CrossRef] [Green Version]
- Lewis, A. A Simple Option Formula for General Jump-Diffusion and Other Exponential Lévy Processes. SSRN 2001, SSRN 282110. Available online: https://ssrn.com/abstract=282110 (accessed on 10 November 2021). [CrossRef] [Green Version]
- Fang, F.; Oosterlee, C.W. A novel pricing method for European options based on Fourier cosine series expansions. SIAM J. Sci. Comput. 2008, 31, 826–848. [Google Scholar] [CrossRef] [Green Version]
- Kirkby, J.L. Efficient Option Pricing by Frame Duality with the Fast Fourier Transform. SIAM J. Financ. Math. 2015, 6, 713–747. [Google Scholar] [CrossRef]
- Du, Q.; Yang, J.; Zhou, Z. Time-Fractional Allen–Cahn Equations: Analysis and Numerical Methods. J. Sci. Comput. 2020, 85, 42. [Google Scholar] [CrossRef]
- Al-Maskari, M. and Karaa, S. The time-fractional Cahn–Hilliard equation: Analysis and approximation. IMA J. Numer. Anal. 2021, drab025. [Google Scholar] [CrossRef]
- Lin, J.; Feng, W.; Reutskiy, S.; Xu, H.; He, Y. A new semi-analytical method for solving a class of time fractional partial differential equations with variable coefficients. Appl. Math. Lett. 2021, 112, 106712. [Google Scholar] [CrossRef]
- Gottlieb, S.; Wang, C. Stability and Convergence Analysis of Fully Discrete Fourier Collocation Spectral Method for 3-D Viscous Burgers’ Equation. J. Sci. Comput. 2012, 53, 102–128. [Google Scholar] [CrossRef]
- Cheng, K.; Cheng, W.; Wise, S.; Yue, X. A Second-Order, Weakly Energy-Stable Pseudo-spectral Scheme for the Cahn–Hilliard Equation and Its Solution by the Homogeneous Linear Iteration Method. J. Sci. Comput. 2016, 69, 1083–1114. [Google Scholar] [CrossRef]
- Lin, J. Simulation of 2D and 3D inverse source problems of nonlinear time-fractional wave equation by the meshless homogenization function method. Eng. Comput. 2021. [Google Scholar] [CrossRef]
- Mainardi, F.; Luchko, Y.; Pagnini, G. The fundamental solution of the space-time fractional diffusion equation. Fract. Calc. Appl. Anal. 2001, 4, 153–192. [Google Scholar]
- Aguilar, J.-P.; Coste, C.; Korbel, J. Series representation of the pricing formula for the European option driven by space-time fractional diffusion. Fract. Calc. Appl. Anal. 2018, 21, 981–1004. [Google Scholar] [CrossRef] [Green Version]
- Luchko, Y.; Aguilar, J.-P.; Korbel, J. Applications of the Fractional Diffusion Equation to Option Pricing and Risk Calculations. Mathematics 2019, 7, 796. [Google Scholar]
- Aguilar, J.-P. Pricing Path-Independent Payoffs with Exotic Features in the Fractional Diffusion Model. Fractal Fract. 2020, 4, 16. [Google Scholar] [CrossRef] [Green Version]
- Aguilar, J.-P. Explicit option valuation in the exponential NIG model. Quant. Financ. 2020, 21, 1281–1299. [Google Scholar] [CrossRef]
- Bertoin, J. Lévy Processes; Cambridge University Press: Cambridge, UK; New York, NY, USA; Melbourne, Australia, 1996. [Google Scholar]
- Schoutens, W. Lévy Processes in Finance: Pricing Financial Derivatives; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Tankov, P. Pricing and Hedging in Exponential Lévy Models: Review of Recent Results; Paris-Princeton Lectures on Mathematical Finance; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Kou, S. A jump-diffusion model for option pricing. Manag. Sci. 2002, 48, 1086–1101. [Google Scholar] [CrossRef] [Green Version]
- Merton, R. Option pricing when underlying stock returns are discontinuous. J. Financ. Econ. 1976, 3, 125–144. [Google Scholar] [CrossRef] [Green Version]
- Barndorff-Nielsen, O.E. Normal Inverse Gaussian Distributions and Stochastic Volatility Modelling. Scand. J. Stat. 1997, 24, 1–13. [Google Scholar] [CrossRef]
- Madan, D.; Seneta, E. The Variance Gamma (V.G.) Model for Share Market Returns. J. Bus. 1990, 63, 511–524. [Google Scholar] [CrossRef]
- Geman, H. Stochastic Clock and Financial Markets. Handb. Numer. Anal. 2009, 15, 649–663. [Google Scholar]
- Barndorff-Nielsen, O.; Kent, J.; Sørensen, M. Normal Variance-Mean Mixtures and z Distributions. Int. Stat. Rev. 1982, 50, 145–159. [Google Scholar] [CrossRef]
- Mittnik, S.; Rachev, S. Stable Paretian Models in Finance; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Mandelbrot, B. The Variation of Certain Speculative Prices. J. Bus. 1963, 36, 384–419. [Google Scholar] [CrossRef]
- Samorodnitsky, G.; Taqqu, M.S. Stable Non-Gaussian Random Processes: Stochastic Models with Infinite Variance; Chapman & Hall: New York, NY, USA, 1994. [Google Scholar]
- Luchko, Y. Entropy Production Rates of the Multi-Dimensional Fractional Diffusion Processes. Entropy 2019, 21, 973. [Google Scholar] [CrossRef] [Green Version]
- Aguilar, J.-P.; Kirkby, J.L.; Korbel, J. Pricing, Risk and Volatility in Subordinated Market Models. Risks 2020, 8, 124. [Google Scholar] [CrossRef]
- Flajolet, P.; Gourdon, X.; Dumas, P. Mellin transform and asymptotics: Harmonic sums. Theor. Comput. Sci. 1995, 144, 3–58. [Google Scholar] [CrossRef] [Green Version]
- Mainardi, F.; Mura, A.; Pagnini, G. The M-Wright Function in Time-Fractional Diffusion Processes: A Tutorial Survey. Int. J. Differ. Equ. 2010, 2010, 104505. [Google Scholar] [CrossRef] [Green Version]
| Space Derivative | Time Derivative | |
|---|---|---|
| Randomness | Yes: Wild randomness if Mild randomness if | No |
| Regime | No | Yes: Slow diffusion if Fast diffusion if |
| ATM prices/volatility | Yes | Yes |
| Delta hedging | Yes: Long 1 stock Short α call options | No |
| Delta hedged P&L | Yes | Yes |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aguilar, J.-P.; Korbel, J.; Pesci, N. On the Quantitative Properties of Some Market Models Involving Fractional Derivatives. Mathematics 2021, 9, 3198. https://doi.org/10.3390/math9243198
Aguilar J-P, Korbel J, Pesci N. On the Quantitative Properties of Some Market Models Involving Fractional Derivatives. Mathematics. 2021; 9(24):3198. https://doi.org/10.3390/math9243198
Chicago/Turabian StyleAguilar, Jean-Philippe, Jan Korbel, and Nicolas Pesci. 2021. "On the Quantitative Properties of Some Market Models Involving Fractional Derivatives" Mathematics 9, no. 24: 3198. https://doi.org/10.3390/math9243198
APA StyleAguilar, J.-P., Korbel, J., & Pesci, N. (2021). On the Quantitative Properties of Some Market Models Involving Fractional Derivatives. Mathematics, 9(24), 3198. https://doi.org/10.3390/math9243198







