Heronian Mean Operators Based on Novel Complex Linear Diophantine Uncertain Linguistic Variables and Their Applications in Multi-Attribute Decision Making

Abstract

In this manuscript, we combine the notion of linear Diophantine fuzzy set (LDFS), uncertain linguistic set (ULS), and complex fuzzy set (CFS) to elaborate the notion of complex linear Diophantine uncertain linguistic set (CLDULS). CLDULS refers to truth, falsity, reference parameters, and their uncertain linguistic terms to handle problematic and challenging data in factual life impasses. By using the elaborated CLDULSs, some operational laws are also settled. Furthermore, by using the power Einstein (PE) aggregation operators based on CLDULS: the complex linear Diophantine uncertain linguistic PE averaging (CLDULPEA), complex linear Diophantine uncertain linguistic PE weighted averaging (CLDULPEWA), complex linear Diophantine uncertain linguistic PE Geometric (CLDULPEG), and complex linear Diophantine uncertain linguistic PE weighted geometric (CLDULPEWG) operators, and their useful results are elaborated with the help of some remarkable cases. Additionally, by utilizing the expounded works dependent on CLDULS, I propose a multi-attribute decision-making (MADM) issue. To decide the quality of the expounded works, some mathematical models are outlined. Finally, the incomparability and relative examination of the expounded approaches with the assistance of graphical articulations are evolved.

1. Introduction

MADM is the basic procedure of the dynamic issues whose point is to distinguish the amazingly productive choice(s) from the arrangement of potential ones. In genuine dynamic, the individual requirements to ascertain the offered decisions by different gatherings, such as solitary and time, of appraisal standards. By and by, in a few unsteady circumstances, it is often hard for the supervisor to convey their choices as a fresh number. To put together it, Zadeh [1] alluded the guideline of fuzzy sets (FSs), to deal with the concerns in the information, using the TG (“Truth grade”) to explain the agreement. Advancing this idea, Atanassov [2] stretched out FSs to the intuitionistic FSs (IFSs) by adding the FG (“Falsity grade”) alongside TG to signify the information. Later, researchers began to investigate it to determine MADM inconveniences [3,4,5,6]. Further, Yager [7] changed the IFS to the standard of Pythagorean FSs (PFSs) with the standard: ${\mathcal{T}}_{{ℂ}_{TG}}^2+{\mathcal{F}}_{{ℂ}_{FG}}^2\le 1$. Later, examiners began to break it down comprehensively and genuinely to determine MADM inconveniences [8,9,10,11,12,13,14]. In any case, the assortment of PFS information is slight, with the limitation that the squares of TG ${\mathcal{T}}_{{ℂ}_{TG}}$ and FG ${\mathcal{F}}_{{ℂ}_{FG}}$ ought not be better than one. To achieve the dynamic inconveniences explicitly, Yager [15] again changed the PFS, proposing the hypothesis of q-rung orthopair FSs (QROFSs) with the condition: ${\mathcal{T}}_{{ℂ}_{TG}}^q+{\mathcal{F}}_{{ℂ}_{FG}}^q\le 1$. Uncertainties and PFS are a sure instance of QROFS, and specialists have dissected the hypothesis of QROFSs in MADM inconveniences [16,17,18,19]. On the other hand, certain inadequacies in PFSs and QROFSs closely resemble the TG and FG. Common constraints show that there exist a few dependences among the assessments. To remove these limits, the rule of linear Diophantine FS (LDFS) was created by Riaz et al. [20], which covers the TG ${\mathcal{T}}_{{ℂ}_{LD}}$, FG ${\mathcal{F}}_{{ℂ}_{LD}}$, and reference parameters $\left({\mathfrak{U}}_{{ℂ}_{LD}}\left({\mathbb{𝕩}}_{EL}\right),{\mathfrak{B}}_{{ℂ}_{LD}}\left({\mathbb{𝕩}}_{EL}\right)\right)$, including $0\le {\mathcal{T}}_{{ℂ}_{LD}}\left({\mathbb{𝕩}}_{EL}\right){\mathfrak{U}}_{{ℂ}_{LD}}\left({\mathbb{𝕩}}_{EL}\right)+{\mathcal{F}}_{{ℂ}_{LD}}\left({\mathbb{𝕩}}_{EL}\right){\mathfrak{B}}_{{ℂ}_{LD}}\left({\mathbb{𝕩}}_{EL}\right)\le 1$, where $0\le {\mathfrak{U}}_{{ℂ}_{LD}}\left({\mathbb{𝕩}}_{EL}\right)+{\mathfrak{B}}_{{ℂ}_{LD}}\left({\mathbb{𝕩}}_{EL}\right)\le 1$. Later, researchers began to investigate it to determine MADM inconveniences [21,22].

Ramot et al. [23] described the perplexing state of FSs (CFSs). He used TG (“Truth grade”) to explain the confusion by looking like a complex number. As a result, Alkouri and Salleh [24] stretched out CFSs to complex IFSs (CIFSs) by adding FG (Falsity grade) alongside TG to imply the information. Later, researchers tried to determine MADM inconveniences [25,26,27,28,29]. However, the assortment of CIFS information is slight, with the limitation that TG ${\mathcal{T}}_{{ℂ}_{RP}}{e}^{i2\pi \left({\mathcal{T}}_{{ℂ}_{IP}}\right)}$ and FG ${\mathcal{F}}_{{ℂ}_{RP}}{e}^{i2\pi \left({\mathcal{F}}_{{ℂ}_{IP}}\right)}$ should not be superior to one. For this, Ullah et al. [30] elabrated the complex PFSs (CPFSs) with a well-known property ${\mathcal{T}}_{{ℂ}_{RP}}^2+{\mathcal{F}}_{{ℂ}_{RP}}^2\le 1,{\mathcal{T}}_{{ℂ}_{IP}}^2+{\mathcal{F}}_{{ℂ}_{IP}}^2\le 1$. CIFS is a sure instance of CPFS and subsequently CPFS can achieve mastery using fluffy regular habitat. Researchers began to examine it to determine MADM inconveniences [31]. In any case, the assortment of CPFS information is slight with the limitation that the squares of the pieces of TG ${\mathcal{T}}_{{ℂ}_{RP}}{e}^{i2\pi \left({\mathcal{T}}_{{ℂ}_{IP}}\right)}$ and FG ${\mathcal{F}}_{{ℂ}_{RP}}{e}^{i2\pi \left({\mathcal{F}}_{{ℂ}_{IP}}\right)}$ should not be superior to one. For this, Liu et al. [32,33] developed a complex QROFSs (CQROFSs) with ${\mathcal{T}}_{{ℂ}_{RP}}^q+{\mathcal{F}}_{{ℂ}_{RP}}^q\le 1,{\mathcal{T}}_{{ℂ}_{IP}}^q+{\mathcal{F}}_{{ℂ}_{IP}}^q\le 1$. CIFS is an example of CQROFS and thus CQROFS can improve with fluffy indigenous habitat. Researchers investigated it to determine MADM issues [34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51].

With a few genuine difficulties, it is not simple for leaders to give their contemplations in quantifiable translations. For example, when a counsel subterranean insect evaluates a petitioner’s convergence of explicit information, he might ponder additional appropriate or past agreements in utilizing semantic expressions, for example, “awesome”, “great”, or “medium”, to communicate their assessment. To deal with such stresses, Zadeh [42] tested the standard of linguistic variable (LV) to outline the tendencies of chiefs. Moreover, Herrera and Martinez proposed the rule of 2-tuple LV [43]. On the other hand, inadequacies in CPFSs and CQROFSs were undifferentiated from the TG and FG. Common limits show that there exists some reliance among the assessments. At the point when an individual produces data containing TG, FG, references boundaries, and ULT, then, at that point, the overall thoughts, for example, IFSs, CIFSs, PFSs, CPFSs, QROFSs, LDFSs, and their extraordinary cases cannot deal with it. To dispose of these limits, the guideline of CLDULV is set up in this manuscript, which covers ${\mathcal{T}}_{{ℂ}_{CLU}}\left({\mathbb{𝕩}}_{EL}\right)={\mathcal{T}}_{{ℂ}_{RP}}\left({\mathbb{𝕩}}_{EL}\right)e^{i2\pi \left({\mathcal{T}}_{{ℂ}_{IP}}\left({\mathbb{𝕩}}_{EL}\right)\right)},{\mathcal{F}}_{{ℂ}_{CLU}}\left({\mathbb{𝕩}}_{EL}\right)={\mathcal{F}}_{{ℂ}_{RP}}\left({\mathbb{𝕩}}_{EL}\right)e^{i2\pi \left({\mathcal{F}}_{{ℂ}_{IP}}\left({\mathbb{𝕩}}_{EL}\right)\right)},{\mathfrak{U}}_{{ℂ}_{CLU}}\left({\mathbb{𝕩}}_{EL}\right)={\mathfrak{U}}_{{ℂ}_{RP}}\left({\mathbb{𝕩}}_{EL}\right)e^{i2\pi \left({\mathfrak{U}}_{{ℂ}_{IP}}\left({\mathbb{𝕩}}_{EL}\right)\right)},{\mathfrak{B}}_{{ℂ}_{CLU}}\left({\mathbb{𝕩}}_{EL}\right)={\mathfrak{B}}_{{ℂ}_{RP}}\left({\mathbb{𝕩}}_{EL}\right)e^{i2\pi \left({\mathfrak{B}}_{{ℂ}_{IP}}\left({\mathbb{𝕩}}_{EL}\right)\right)}$, which express the grade of truth, falsity, and reference parameters with some rules: $0\le {\mathcal{T}}_{{ℂ}_{RP}}\left({\mathbb{𝕩}}_{EL}\right){\mathfrak{U}}_{{ℂ}_{RP}}\left({\mathbb{𝕩}}_{EL}\right)+{\mathcal{F}}_{{ℂ}_{RP}}\left({\mathbb{𝕩}}_{EL}\right){\mathfrak{B}}_{{ℂ}_{RP}}\left({\mathbb{𝕩}}_{EL}\right)\le 1.0\le {\mathcal{T}}_{{ℂ}_{RP}}\left({\mathbb{𝕩}}_{EL}\right){\mathfrak{U}}_{{ℂ}_{IP}}\left({\mathbb{𝕩}}_{EL}\right)+{\mathcal{F}}_{{ℂ}_{RP}}\left({\mathbb{𝕩}}_{EL}\right){\mathfrak{B}}_{{ℂ}_{IP}}\left({\mathbb{𝕩}}_{EL}\right)\le 1,0\le {\mathcal{T}}_{{ℂ}_{IP}}\left({\mathbb{𝕩}}_{EL}\right){\mathfrak{U}}_{{ℂ}_{RP}}\left({\mathbb{𝕩}}_{EL}\right)+{\mathcal{F}}_{{ℂ}_{IP}}\left({\mathbb{𝕩}}_{EL}\right){\mathfrak{B}}_{{ℂ}_{RP}}\left({\mathbb{𝕩}}_{EL}\right)\le 1$ and $0\le {\mathcal{T}}_{{ℂ}_{IP}}\left({\mathbb{𝕩}}_{EL}\right){\mathfrak{U}}_{{ℂ}_{IP}}\left({\mathbb{𝕩}}_{EL}\right)+{\mathcal{F}}_{{ℂ}_{IP}}\left({\mathbb{𝕩}}_{EL}\right){\mathfrak{B}}_{{ℂ}_{IP}}\left({\mathbb{𝕩}}_{EL}\right)\le 1$, where $0\le {\mathfrak{U}}_{{ℂ}_{RP}}\left({\mathbb{𝕩}}_{EL}\right)+{\mathfrak{B}}_{{ℂ}_{RP}}\left({\mathbb{𝕩}}_{EL}\right)\le 1$ and $0\le {\mathfrak{U}}_{{ℂ}_{IP}}\left({\mathbb{𝕩}}_{EL}\right)+{\mathfrak{B}}_{{ℂ}_{IP}}\left({\mathbb{𝕩}}_{EL}\right)\le 1$. Scholars have explained the time complexity of the presented MADM approach. The ideas of IFSs, CIFSs, PFSs, CPFSs, QROFSs, CQROFSs, LDFSs, LDULS, and CLDFSs have various applications in different fields; however, these hypotheses have their limitations, identified with the enrollment and non-participation grades. To annihilate these restrictions, we present the original idea of CLDULS with the expansion of reference boundaries and dubious semantic terms. The proposed model of CLDULS is effective and adaptable compared to other approaches because of the utilization of reference boundaries and ULVs. CLDULS additionally orders the information in MADM issues by changing the actual feeling of reference boundaries and ULVs. This set covers the spaces of existing constructions and augments the space for membership and non-enrollment levels with the assistance of reference boundaries looking like complex numbers who’s genuine and fanciful part having a place with unit span with ULVs. The inspiration of the proposed model is given bit by bit in the entire original copy. Presently we examine some significant targets of this paper.

•  For $\left(0.5e^{i2\pi \left(0.5\right)},0.6e^{i2\pi \left(0.6\right)}\right)$, based on the well-known characteristic of CIFSs, we obtained $0.5+0.6=1.1>1$, the principle of CIFS has been neglected. For this, the CLDULS is massive suitable to determine the solution of the above problem based on reference parameters $\left(0.1e^{i2\pi \left(0.1\right)},0.2e^{i2\pi \left(0.2\right)}\right)$, then $0.1\times 0.5+0.2\times 0.6=0.05+0.12=0.17<1$. The principle of CLDULS is suitable for every kind of dilemmas.
•  For $\left(0.8e^{i2\pi \left(0.8\right)},0.9e^{i2\pi \left(0.9\right)}\right)$, based on the well-known characteristic of CPFSs, we obtained ${0.8}^2+{0.9}^2=0.64+0.81=1.45>1$, the principle of CPFS has been neglected. For this, the CLDULS is massive suitable to determine the solution of the above problem based on reference parameters $\left(0.2e^{i2\pi \left(0.2\right)},0.2e^{i2\pi \left(0.2\right)}\right)$, then $0.2\times 0.8+0.2\times 0.9=0.16+0.18=0.34<1$. The principle of CLDULS is suitable for every kind of dilemmas.
•  For $\left(0.1e^{i2\pi \left(0.1\right)},0.1e^{i2\pi \left(0.1\right)}\right)$, based on the well-known characteristic of CQROFSs, we obtained $1+1=2>1$, the principle of CQROFS has been neglected. For this, the CLDULS is massive suitable to determine the solution of the above problem based on reference parameters $\left(0e^{i2\pi \left(0.0\right)},0.1e^{i2\pi \left(0.1\right)}\right)$, then $0.0\times 1+0.1\times 1=0+0.1=0.1<1$. The principle of CLDULS is suitable for every kind of dilemmas.

If we choose the information in the form of $\left(\left[s_1,s_2\right],\left(0.5e^{i2\pi \left(0.5\right)},0.3e^{i2\pi \left(0.3\right)}\right),\left(0.5e^{i2\pi \left(0.5\right)},0.4e^{i2\pi \left(0.4\right)}\right)\right)$, then, at that point, by utilizing the state of IFSs, CIFSs, PFSs, CPFSs, QROFSs, CQROFSs, LDFSs, and CLDFS have been fizzled, for adapting to such kinds of issues, the hypothesis of CLDULS is an extremely capable and solid method to determine it. From the above investigation, the hypothesis of IFSs, CIFSs, PFSs, CPFSs, QROFSs, CQROFSs, LDFSs, and CLDFSs is the uncommon instance of the proposed CLDULS.

By utilizing the upsides of the explained thoughts, the fundamental proposes of this manuscript are summed up are follows:

•  To elaborate the CLDULS and fostered their functional laws.
•  To investigate the Einstein functional laws and their connected tasks, for example, score and exactness esteems.
•  To use the force Einstein collection administrators dependent on CLDULS and discussed their extraordinary cases.
• To foster a MADM procedure by utilizing the explained administrators with CLDULNs to discover consistency and validness of the expounded approaches.
• To discover the incomparability and consistency of the explained administrators with the assistance of similar investigation and their graphical articulations.

The objective of this composition is following as: In Section 2, we momentarily appraisal some overall ideas like CFSs, LDFSs, ULSs, and their functional laws. The possibility of PEAO and Einstein functional laws are additionally reconsidered. In Section 3, to expound the guideline of CLDULS. CLDULS covers the grade of truth, deception, reference boundaries, and their uncertain etymological terms to achieve with off-kilter and complicated information in genuine life dilemmas. Some functional laws by utilizing the expounded CLDULSs are additionally settled. In Section 4, by utilizing the PEAOs dependent on CLDULS is to expand the CLDULPEA, CLDULPEWA, CLDULPEG, CLDULPEWG administrators, and their valuable outcomes are additionally expounded with the assistance of some astounding cases. In Section 5, by utilizing the explained administrators dependent on CLDULS, a MADM quandary. To decide the reasonableness and reliability of the expounded administrators, some mathematical models are represented. At last, the matchless quality and near investigation of the explained approaches with the assistance of graphical articulations are likewise evolved. In Section 6, we examined the finish of this composition.

2. Preliminaries

In this study, we briefly assessment some prevailing concepts like CFSs, LDFSs, ULSs, and their operational laws. The idea of PEAO and Einstein operational laws are also revised. All symbols which are used in this manuscript are discussed in the shape of

Table 1. Expressed the symbols.

Symbols	Meanings	Symbols	Meanings	Symbols	Meanings
${\mathbb{X}}^{\mathit{U}\mathit{N}\mathit{I}}$	Universal set	${\mathcal{T}}_{{ℂ}_{CF}}\left({\mathbb{𝕩}}_{EL}\right)$	Truth grade	${\mathcal{T}}_{{ℂ}_{RP}}\left({\mathbb{𝕩}}_{EL}\right)$	Real part of truth grade
${\mathbb{𝕩}}_{\mathit{EL}}$	Element of universal set	${\mathcal{F}}_{{ℂ}_{LD}}\left({\mathbb{𝕩}}_{EL}\right)$	Falsity grade	${\mathcal{T}}_{{ℂ}_{IP}}\left({\mathbb{𝕩}}_{EL}\right)$	Imaginary part of truth grade
${\mathfrak{U}}_{{ℂ}_{\mathit{L}\mathit{D}}}\left({\mathbb{𝕩}}_{\mathit{E}\mathit{L}}\right)$	Reference parameter for truth grade	${\mathfrak{B}}_{{ℂ}_{LD}}\left({\mathbb{𝕩}}_{EL}\right)$	Reference parameter for falsity grade	$\widehat{\Xi }=\left[{\Xi }_{\alpha },{\Xi }_{\beta }\right],{\Xi }_{\alpha },{\Xi }_{\beta }\in \stackrel{=}{\Xi }$	Uncertain linguistic terms

.

Definition 1 ([23]).

A CFS${ℂ}_{CF}$is initiated by:

$${ℂ}_{CF}=\left\{\left({\mathbb{𝕩}}_{EL},{\mathcal{T}}_{{ℂ}_{CF}}\left({\mathbb{𝕩}}_{EL}\right)\right):{\mathbb{𝕩}}_{EL}\in {\mathbb{X}}^{UNI}\right\}$$

(1)

where${\mathcal{T}}_{{ℂ}_{CF}}\left({\mathbb{𝕩}}_{EL}\right)={\mathcal{T}}_{{ℂ}_{RP}}\left({\mathbb{𝕩}}_{EL}\right)e^{i2\pi \left({\mathcal{T}}_{{ℂ}_{IP}}\left({\mathbb{𝕩}}_{EL}\right)\right)}$with a rule that is$0\le {\mathcal{T}}_{{ℂ}_{RP}}\left({\mathbb{𝕩}}_{EL}\right),{\mathcal{T}}_{{ℂ}_{IP}}\left({\mathbb{𝕩}}_{EL}\right)\le 1$. The complex fuzzy numbers (CFNs) are dented by${ℂ}_{CF-i}=\left({\mathbb{𝕩}}_{EL},{\mathcal{T}}_{{ℂ}_{RP-i}}\left({\mathbb{𝕩}}_{EL}\right)e^{i2\pi \left({\mathcal{T}}_{{ℂ}_{IP-i}}\left({\mathbb{𝕩}}_{EL}\right)\right)}\right),i=1,2,\dots ,{𝓃}_{NE}$. By using any two CFNs${ℂ}_{CF-1}=\left({\mathbb{𝕩}}_{EL},{\mathcal{T}}_{{ℂ}_{RP-1}}\left({\mathbb{𝕩}}_{EL}\right)e^{i2\pi \left({\mathcal{T}}_{{ℂ}_{IP-1}}\left({\mathbb{𝕩}}_{EL}\right)\right)}\right)$and${ℂ}_{CF-2}=\left({\mathbb{𝕩}}_{EL},{\mathcal{T}}_{{ℂ}_{RP-2}}\left({\mathbb{𝕩}}_{EL}\right)e^{i2\pi \left({\mathcal{T}}_{{ℂ}_{IP-2}}\left({\mathbb{𝕩}}_{EL}\right)\right)}\right)$, with constant${\delta }_{SC}$, then

$${ℂ}_{CF-1}\oplus {ℂ}_{CF-2}=\left({\mathbb{𝕩}}_{EL},\left(\begin{array}{c}{\mathcal{T}}_{{ℂ}_{RP-1}}\left({\mathbb{𝕩}}_{EL}\right)+{\mathcal{T}}_{{ℂ}_{RP-2}}\left({\mathbb{𝕩}}_{EL}\right)\\ -{\mathcal{T}}_{{ℂ}_{RP-1}}\left({\mathbb{𝕩}}_{EL}\right){\mathcal{T}}_{{ℂ}_{RP-2}}\left({\mathbb{𝕩}}_{EL}\right)\end{array}\right)e^{i2\pi \left(\begin{array}{c}{\mathcal{T}}_{{ℂ}_{IP-1}}\left({\mathbb{𝕩}}_{EL}\right)+{\mathcal{T}}_{{ℂ}_{IP-2}}\left({\mathbb{𝕩}}_{EL}\right)\\ -{\mathcal{T}}_{{ℂ}_{IP-1}}\left({\mathbb{𝕩}}_{EL}\right){\mathcal{T}}_{{ℂ}_{IP-2}}\left({\mathbb{𝕩}}_{EL}\right)\end{array}\right)}\right)$$

(2)

$${ℂ}_{CF-1}\otimes {ℂ}_{CF-2}=\left({\mathbb{𝕩}}_{EL},\left({\mathcal{T}}_{{ℂ}_{RP-1}}\left({\mathbb{𝕩}}_{EL}\right){\mathcal{T}}_{{ℂ}_{RP-2}}\left({\mathbb{𝕩}}_{EL}\right)\right)e^{i2\pi \left({\mathcal{T}}_{{ℂ}_{IP-1}}\left({\mathbb{𝕩}}_{EL}\right){\mathcal{T}}_{{ℂ}_{IP-2}}\left({\mathbb{𝕩}}_{EL}\right)\right)}\right)$$

(3)

$${\delta }_{SC}{ℂ}_{CF-1}=\left({\mathbb{𝕩}}_{EL},\left(1-{\left(1-{\mathcal{T}}_{{ℂ}_{RP-1}}\left({\mathbb{𝕩}}_{EL}\right)\right)}^{{\delta }_{SC}}\right)e^{i2\pi \left(1-{\left(1-{\mathcal{T}}_{{ℂ}_{IP-1}}\left({\mathbb{𝕩}}_{EL}\right)\right)}^{{\delta }_{SC}}\right)}\right)$$

(4)

$${ℂ}_{CF-1}^{{\delta }_{SC}}=\left({\mathbb{𝕩}}_{EL},{\mathcal{T}}_{{ℂ}_{RP-1}}^{{\delta }_{SC}}\left({\mathbb{𝕩}}_{EL}\right)e^{i2\pi \left({\mathcal{T}}_{{ℂ}_{IP-1}}^{{\delta }_{SC}}\left({\mathbb{𝕩}}_{EL}\right)\right)}\right)$$

(5)

Definition 2 ([20])

A LDFS ${ℂ}_{LD}$ is initiated by:

$${ℂ}_{LD}=\left\{\left({\mathbb{𝕩}}_{EL},\left({\mathcal{T}}_{{ℂ}_{LD}}\left({\mathbb{𝕩}}_{EL}\right),{\mathcal{F}}_{{ℂ}_{LD}}\left({\mathbb{𝕩}}_{EL}\right)\right),\left({\mathfrak{U}}_{{ℂ}_{LD}}\left({\mathbb{𝕩}}_{EL}\right),{\mathfrak{B}}_{{ℂ}_{LD}}\left({\mathbb{𝕩}}_{EL}\right)\right)\right):{\mathbb{𝕩}}_{EL}\in {\mathbb{𝕏}}^{UNI}\right\}$$

(6)

with a rule that is $0\le {\mathcal{T}}_{{ℂ}_{LD}}\left({\mathbb{𝕩}}_{EL}\right){\mathfrak{U}}_{{ℂ}_{LD}}\left({\mathbb{𝕩}}_{EL}\right)+{\mathcal{F}}_{{ℂ}_{LD}}\left({\mathbb{𝕩}}_{EL}\right){\mathfrak{B}}_{{ℂ}_{LD}}\left({\mathbb{𝕩}}_{EL}\right)\le 1$, where $0\le {\mathfrak{U}}_{{ℂ}_{LD}}\left({\mathbb{𝕩}}_{EL}\right)+{\mathfrak{B}}_{{ℂ}_{LD}}\left({\mathbb{𝕩}}_{EL}\right)\le 1$. The linear Diophantine fuzzy numbers (LDFNs) are dented by ${ℂ}_{LD-i}=\left(\left({\mathcal{T}}_{{ℂ}_{LD-i}},{\mathcal{F}}_{{ℂ}_{LD-i}}\right),\left({\mathfrak{U}}_{{ℂ}_{LD-i}},{\mathfrak{B}}_{{ℂ}_{LD-i}}\right)\right),i=1,2,\dots ,{𝓃}_{NE}$. By using any two LDFNs ${ℂ}_{CF-1}=\left(\left({\mathcal{T}}_{{ℂ}_{LD-1}},{\mathcal{F}}_{{ℂ}_{LD-1}}\right),\left({\mathfrak{U}}_{{ℂ}_{LD-1}},{\mathfrak{B}}_{{ℂ}_{LD-1}}\right)\right)$and ${ℂ}_{CF-2}=\left(\left({\mathcal{T}}_{{ℂ}_{LD-2}},{\mathcal{F}}_{{ℂ}_{LD-2}}\right),\left({\mathfrak{U}}_{{ℂ}_{LD-2}},{\mathfrak{B}}_{{ℂ}_{LD-2}}\right)\right)$, with constant ${\delta }_{SC}$, then

$${ℂ}_{LD-1}\oplus {ℂ}_{LD-2}=\left(\begin{array}{c}\left({\mathcal{T}}_{{ℂ}_{LD-1}}+{\mathcal{T}}_{{ℂ}_{LD-2}}-{\mathcal{T}}_{{ℂ}_{LD-1}}{\mathcal{T}}_{{ℂ}_{LD-2}},{\mathcal{F}}_{{ℂ}_{LD-1}}{\mathcal{F}}_{{ℂ}_{LD-2}}\right),\\ \left({\mathfrak{U}}_{{ℂ}_{LD-1}}+{\mathfrak{U}}_{{ℂ}_{LD-2}}-{\mathfrak{U}}_{{ℂ}_{LD-1}}{\mathfrak{U}}_{{ℂ}_{LD-2}},{\mathfrak{B}}_{{ℂ}_{LD-1}}{\mathfrak{B}}_{{ℂ}_{LD-2}}\right)\end{array}\right)$$

(7)

$${ℂ}_{LD-1}\otimes {ℂ}_{LD-2}=\left(\begin{array}{c}\left({\mathcal{T}}_{{ℂ}_{LD-1}}{\mathcal{T}}_{{ℂ}_{LD-2}},{\mathcal{F}}_{{ℂ}_{LD-1}}+{\mathcal{F}}_{{ℂ}_{LD-2}}-{\mathcal{F}}_{{ℂ}_{LD-1}}{\mathcal{F}}_{{ℂ}_{LD-2}}\right),\\ \left({\mathfrak{U}}_{{ℂ}_{LD-1}}{\mathfrak{U}}_{{ℂ}_{LD-2}},{\mathfrak{B}}_{{ℂ}_{LD-1}}+{\mathfrak{B}}_{{ℂ}_{LD-2}}-{\mathfrak{B}}_{{ℂ}_{LD-1}}{\mathfrak{B}}_{{ℂ}_{LD-2}}\right)\end{array}\right)$$

(8)

$${\delta }_{SC}{ℂ}_{LD-1}=\left(\left(\left(1-{\left(1-{\mathcal{T}}_{{ℂ}_{LD-1}}\right)}^{{\delta }_{SC}}\right),{\mathcal{F}}_{{ℂ}_{LD-1}}^{{\delta }_{SC}}\right),\left(\left(1-{\left(1-{\mathfrak{U}}_{{ℂ}_{LD-1}}\right)}^{{\delta }_{SC}}\right),{\mathfrak{B}}_{{ℂ}_{LD-1}}^{{\delta }_{SC}}\right)\right)$$

(9)

$${ℂ}_{LD-1}^{{\delta }_{SC}}=\left(\left({\mathcal{T}}_{{ℂ}_{LD-1}}^{{\delta }_{SC}},\left(1-{\left(1-{\mathcal{F}}_{{ℂ}_{LD-1}}\right)}^{{\delta }_{SC}}\right)\right),\left({\mathfrak{U}}_{{ℂ}_{LD-1}}^{{\delta }_{SC}},\left(1-{\left(1-{\mathfrak{B}}_{{ℂ}_{LD-1}}\right)}^{{\delta }_{SC}}\right)\right)\right)$$

(10)

By using any LDFN ${ℂ}_{\mathrm{CF}-1}=\left(\left({\mathcal{T}}_{{ℂ}_{\mathrm{LD}-1}},{\mathcal{F}}_{{ℂ}_{\mathrm{LD}-1}}\right),\left({\mathfrak{U}}_{{ℂ}_{\mathrm{LD}-1}},{\mathfrak{B}}_{{ℂ}_{\mathrm{LD}-1}}\right)\right)$, we have

$${\mathbb{S}}_{SV}\left({ℂ}_{CF-1}\right)=\frac{1}{2}\left(\left({\mathcal{T}}_{{ℂ}_{LD-1}}-{\mathcal{F}}_{{ℂ}_{LD-1}}\right),\left({\mathfrak{U}}_{{ℂ}_{LD-1}}-{\mathfrak{B}}_{{ℂ}_{LD-1}}\right)\right),{\mathbb{S}}_{SV}\left({ℂ}_{CF-1}\right)\in \left[-1,1\right]$$

(11)

$${ℍ}_{AV}\left({ℂ}_{CF-1}\right)=\frac{1}{2}\left(\left({\mathcal{T}}_{{ℂ}_{LD-1}}+{\mathcal{F}}_{{ℂ}_{LD-1}}\right),\left({\mathfrak{U}}_{{ℂ}_{LD-1}}+{\mathfrak{B}}_{{ℂ}_{LD-1}}\right)\right),{ℍ}_{SV}\left({ℂ}_{CF-1}\right)\in \left[0,1\right]$$

(12)

For Equations (11) and (12), we obtained some rules, such that

•  When ${\mathbb{S}}_{\mathrm{SV}}\left({ℂ}_{\mathrm{CF}-1}\right)>{\mathbb{S}}_{\mathrm{SV}}\left({ℂ}_{\mathrm{CF}-2}\right)\Rightarrow {ℂ}_{\mathrm{CF}-1}>{ℂ}_{\mathrm{CF}-2}$;
•  When ${\mathbb{S}}_{\mathrm{SV}}\left({ℂ}_{\mathrm{CF}-1}\right)<{\mathbb{S}}_{\mathrm{SV}}\left({ℂ}_{\mathrm{CF}-2}\right)\Rightarrow {ℂ}_{\mathrm{CF}-1}<{ℂ}_{\mathrm{CF}-2}$;
•  When ${\mathbb{S}}_{\mathrm{SV}}\left({ℂ}_{\mathrm{CF}-1}\right)={\mathbb{S}}_{\mathrm{SV}}\left({ℂ}_{\mathrm{CF}-2}\right)\Rightarrow$
  •  When ${ℍ}_{\mathrm{AV}}\left({ℂ}_{\mathrm{CF}-1}\right)>{ℍ}_{\mathrm{AV}}\left({ℂ}_{\mathrm{CF}-2}\right)\Rightarrow {ℂ}_{\mathrm{CF}-1}>{ℂ}_{\mathrm{CF}-2}$;
  •  When ${ℍ}_{\mathrm{AV}}\left({ℂ}_{\mathrm{CF}-1}\right)<{ℍ}_{\mathrm{AV}}\left({ℂ}_{\mathrm{CF}-2}\right)\Rightarrow {ℂ}_{\mathrm{CF}-1}<{ℂ}_{\mathrm{CF}-2}$;
  •  When ${ℍ}_{\mathrm{AV}}\left({ℂ}_{\mathrm{CF}-1}\right)={ℍ}_{\mathrm{AV}}\left({ℂ}_{\mathrm{CF}-2}\right)\Rightarrow {ℂ}_{\mathrm{CF}-1}={ℂ}_{\mathrm{CF}-2}$.

Definition 3 ([43]).

Let$\widehat{\Xi } =\left[{\Xi }_{\alpha },{\Xi }_{\beta }\right],{\Xi }_{\alpha },{\Xi }_{\beta }\in \stackrel{=}{\Xi }$, where $\stackrel{=}{\Xi }=\left\{{\Xi }_{\alpha }:\alpha \in R^{+}\right\}$ is called ULS. By using any two ULSs ${ \widehat{\Xi }}_1=\left[{\Xi }_{{\alpha }_1},{\Xi }_{{\beta }_1}\right]$ and ${\widehat{\Xi }}_2=\left[{\Xi }_{{\alpha }_2},{\Xi }_{{\beta }_2}\right]$, then

$${\widehat{\Xi }}_1\oplus {\widehat{\Xi }}_2=\left[{\Xi }_{{\alpha }_1},{\Xi }_{{\beta }_1}\right]\oplus \left[{\Xi }_{{\alpha }_2},{\Xi }_{{\beta }_2}\right]=\left[{\Xi }_{{\alpha }_1+{\alpha }_2},{\Xi }_{{\beta }_1+{\beta }_2}\right]$$

(13)

$${\widehat{\Xi }}_1\otimes {\widehat{\Xi }}_2=\left[{\Xi }_{{\alpha }_1},{\Xi }_{{\beta }_1}\right]\otimes \left[{\Xi }_{{\alpha }_2},{\Xi }_{{\beta }_2}\right]=\left[{\Xi }_{{\alpha }_1\ast {\alpha }_2},{\Xi }_{{\beta }_1\ast {\beta }_2}\right]$$

(14)

$${\delta }_{SC}{\widehat{\Xi }}_1={\delta }_{SC}\left[{\Xi }_{{\alpha }_1},{\Xi }_{{\beta }_1}\right]=\left[{\Xi }_{{\delta }_{SC}\ast {\alpha }_1},{\Xi }_{{\delta }_{SC}\ast {\beta }_1}\right]$$

(15)

$${\widehat{\Xi }}_1^{{\delta }_{SC}}={\left[{\Xi }_{{\alpha }_1},{\Xi }_{{\beta }_1}\right]}^{{\delta }_{SC}}=\left[{\Xi }_{{\alpha }_1^{{\delta }_{SC}}},{\Xi }_{{\beta }_1^{{\delta }_{SC}}}\right]$$

(16)

Definition 4 ([35]).

A PA is initiated by:

$$PA\left({ℂ}_{CF-1},{ℂ}_{CF-2},\dots ,{ℂ}_{CF-{𝓃}_{NE}}\right)=\frac{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CF-i}\right)\right){ℂ}_{CF-i}}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CF-i}\right)\right)}$$

(17)

where ${\mathbb{T}}^{\mathit{LD}}\left({ℂ}_{\mathit{CF}-\mathrm{i}}\right)={\displaystyle \sum }_{\mathrm{j}=1,\mathrm{i}\ne \mathrm{j}}^{{𝓃}_{\mathit{NE}}}\sup \left({ℂ}_{\mathit{CF}-\mathrm{i}},{ℂ}_{\mathit{CF}-\mathrm{j}}\right)$, where $\sup \left({ℂ}_{\mathrm{CF}-\mathrm{i}},{ℂ}_{\mathit{CF}-\mathrm{j}}\right)$ holds the following conditions:

• $\sup \left({ℂ}_{\mathit{CF}-\mathrm{i}},{ℂ}_{\mathit{CF}-\mathrm{j}}\right)=\sup \left({ℂ}_{\mathit{CF}-\mathrm{j}},{ℂ}_{\mathit{CF}-\mathrm{i}}\right)$;
• $\sup \left({ℂ}_{\mathit{CF}-\mathrm{i}},{ℂ}_{\mathit{CF}-\mathrm{j}}\right)\in \left[0,1\right];$
• $\sup \left({ℂ}_{\mathit{CF}-\mathrm{i}},{ℂ}_{\mathit{CF}-\mathrm{j}}\right)\ge \sup \left({ℂ}_{\mathit{CF}-{𝓂}_{\mathit{NE}}},{ℂ}_{\mathit{CF}-{𝓃}_{\mathit{NE}}}\right)$, if $\left|{ℂ}_{\mathit{CF}-\mathrm{i}}-{ℂ}_{\mathit{CF}-\mathrm{j}}\right|\le \left|{ℂ}_{\mathit{CF}-{𝓂}_{\mathit{NE}}}-{ℂ}_{\mathit{CF}-{𝓃}_{\mathit{NE}}}\right|$.

Definition 5 ([40]).

For any $\alpha ,\beta \in \left[0,1\right]$, then the Einstein T-norm and T-conorm are initiated by:

$$\alpha \oplus \beta =\frac{\alpha +\beta }{1+\alpha \times \beta },\alpha ,\beta \in \left[0,1\right]$$

(18)

$$\alpha \otimes \beta =\frac{\alpha \times \beta }{1+\left(1-\alpha \right)\times \left(1-\beta \right)},\alpha ,\beta \in \left[0,1\right]$$

(19)

3. Complex Linear Diophantine Uncertain Linguistic Sets

As shown above, we briefly revised some prevailing ideas are to elaborate the novel CLDULS are their useful laws. Some results based on elaborated approaches are also discussed to demonstration the rationality and consistency of the discovered ideas. By using the elaborated ideas, the idea of Einstein operational laws is also elaborated.

Definition 6 ([40]).

A CLDULS${ℂ}_{CLU}$ is initiated by:

$${ℂ}_{CLU}=\left\{\left({\mathbb{𝕩}}_{EL},\left[{\Xi }_{\alpha \left({\mathbb{𝕩}}_{EL}\right)},{\Xi }_{\beta \left({\mathbb{𝕩}}_{EL}\right)}\right],\left({\mathcal{T}}_{{ℂ}_{CLU}}\left({\mathbb{𝕩}}_{EL}\right),{\mathcal{F}}_{{ℂ}_{CLU}}\left({\mathbb{𝕩}}_{EL}\right)\right),\left({\mathfrak{U}}_{{ℂ}_{CLU}}\left({\mathbb{𝕩}}_{EL}\right),{\mathfrak{B}}_{{ℂ}_{CLU}}\left({\mathbb{𝕩}}_{EL}\right)\right)\right):{\mathbb{𝕩}}_{EL}\in {\mathbb{X}}^{UNI}\right\}$$

(20)

where $$\begin{gathered} {\mathcal{T}}_{{ℂ}_{CLU}}\left({\mathbb{𝕩}}_{EL}\right)={\mathcal{T}}_{{ℂ}_{RP}}\left({\mathbb{𝕩}}_{EL}\right)e^{i2\pi \left({\mathcal{T}}_{{ℂ}_{IP}}\left({\mathbb{𝕩}}_{EL}\right)\right)},{\mathcal{F}}_{{ℂ}_{CLU}}\left({\mathbb{𝕩}}_{EL}\right)= \\ {\mathcal{F}}_{{ℂ}_{RP}}\left({\mathbb{𝕩}}_{EL}\right)e^{i2\pi \left({\mathcal{F}}_{{ℂ}_{IP}}\left({\mathbb{𝕩}}_{EL}\right)\right)},{\mathfrak{U}}_{{ℂ}_{CLU}}\left({\mathbb{𝕩}}_{EL}\right)={\mathfrak{U}}_{{ℂ}_{RP}}\left({\mathbb{𝕩}}_{EL}\right)e^{i2\pi \left({\mathfrak{U}}_{{ℂ}_{IP}}\left({\mathbb{𝕩}}_{EL}\right)\right)},{\mathfrak{B}}_{{ℂ}_{CLU}}\left({\mathbb{𝕩}}_{EL}\right)= \\ {\mathfrak{B}}_{{ℂ}_{RP}}\left({\mathbb{𝕩}}_{EL}\right)e^{i2\pi \left({\mathfrak{B}}_{{ℂ}_{IP}}\left({\mathbb{𝕩}}_{EL}\right)\right)} \end{gathered}$$ 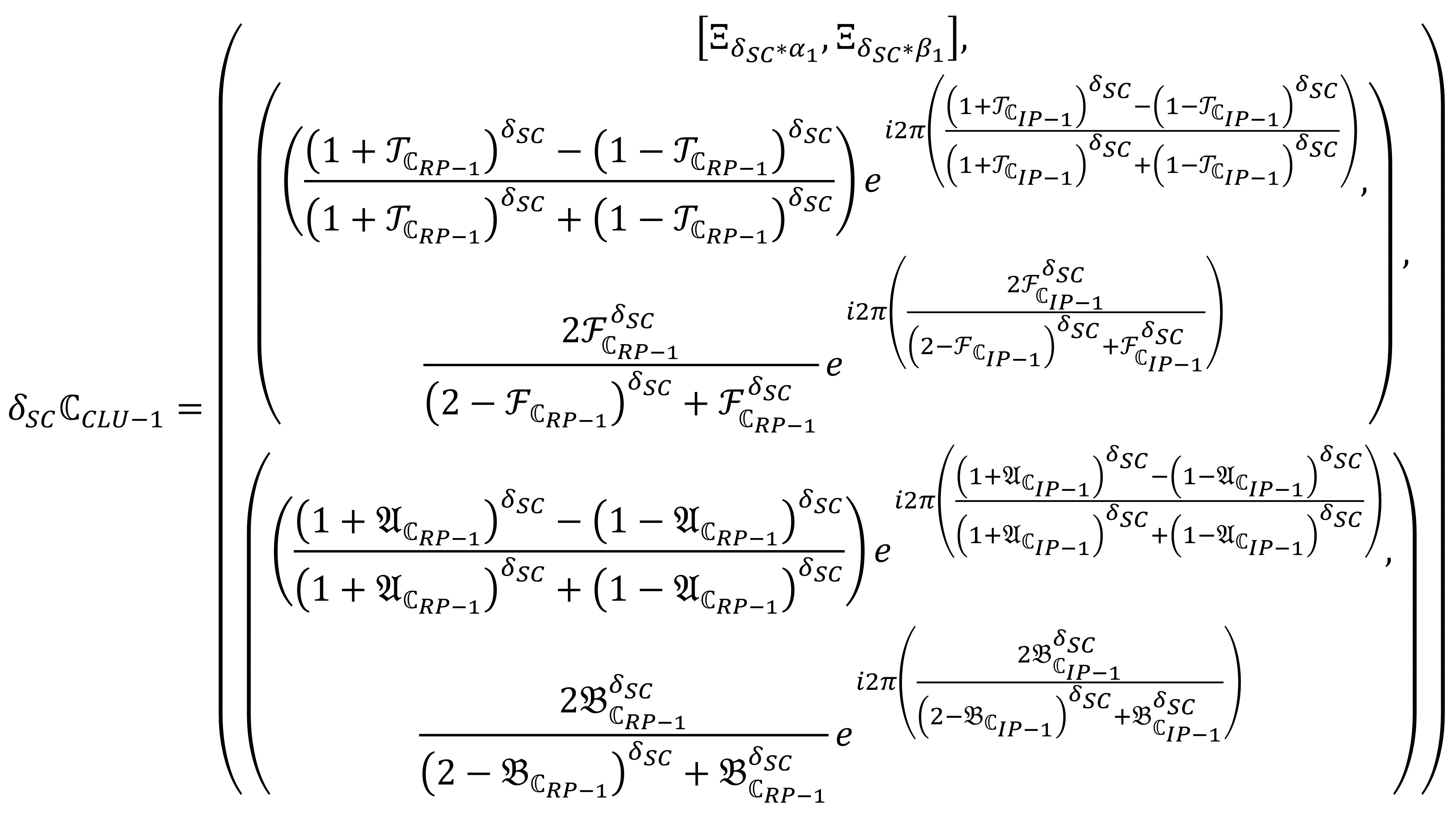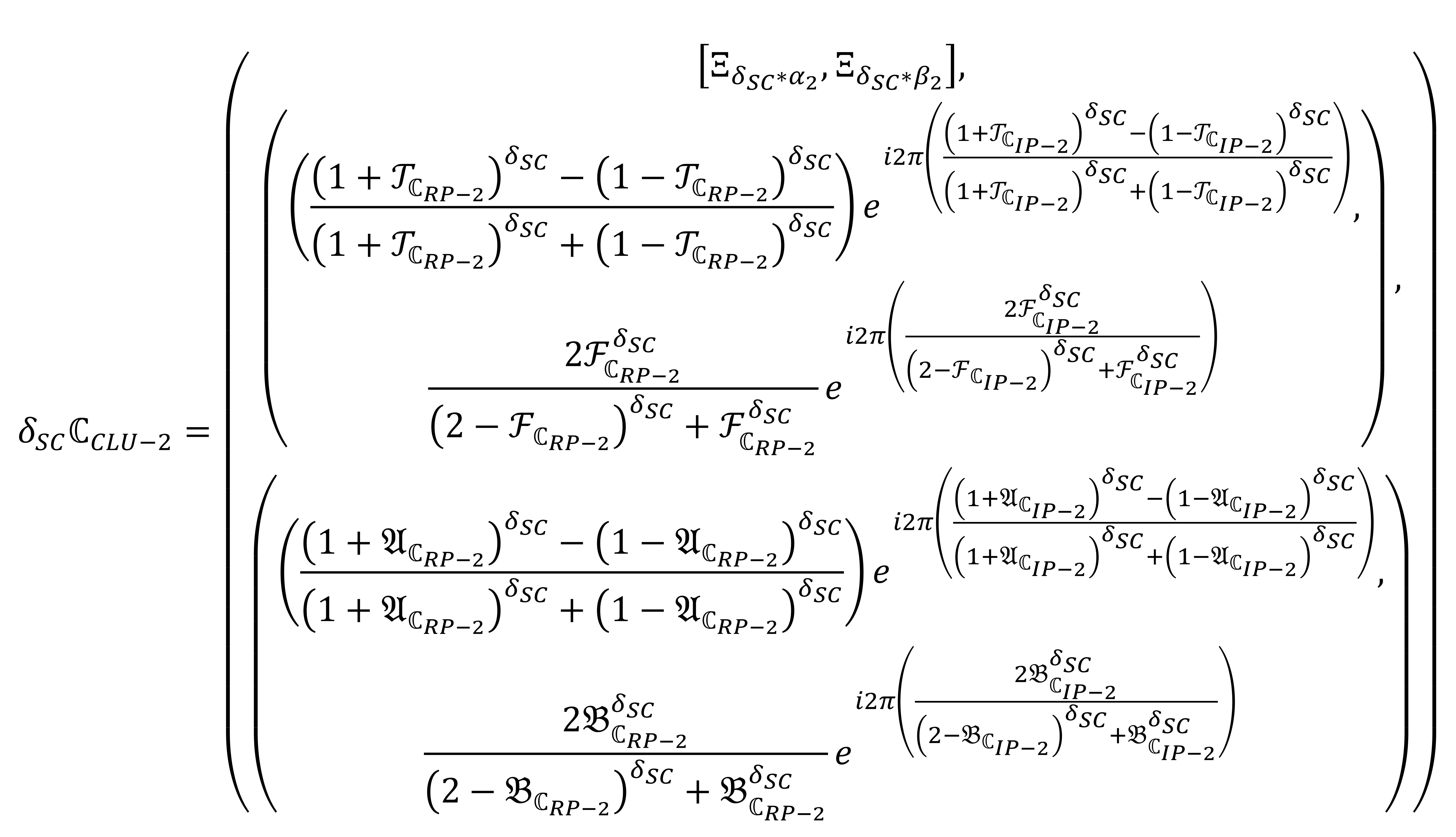are expressed the grade of truth, falsity, and reference parameters with some rules that are $0\le {\mathcal{T}}_{{ℂ}_{RP}}\left({\mathbb{𝕩}}_{EL}\right){\mathfrak{U}}_{{ℂ}_{RP}}\left({\mathbb{𝕩}}_{EL}\right)+{\mathcal{F}}_{{ℂ}_{RP}}\left({\mathbb{𝕩}}_{EL}\right){\mathfrak{B}}_{{ℂ}_{RP}}\left({\mathbb{𝕩}}_{EL}\right)\le 1,0\le {\mathcal{T}}_{{ℂ}_{RP}}\left({\mathbb{𝕩}}_{EL}\right){\mathfrak{U}}_{{ℂ}_{IP}}\left({\mathbb{𝕩}}_{EL}\right)+{\mathcal{F}}_{{ℂ}_{RP}}\left({\mathbb{𝕩}}_{EL}\right){\mathfrak{B}}_{{ℂ}_{IP}}\left({\mathbb{𝕩}}_{EL}\right)\le 1,0\le {\mathcal{T}}_{{ℂ}_{IP}}\left({\mathbb{𝕩}}_{EL}\right){\mathfrak{U}}_{{ℂ}_{RP}}\left({\mathbb{𝕩}}_{EL}\right)+{\mathcal{F}}_{{ℂ}_{IP}}\left({\mathbb{𝕩}}_{EL}\right){\mathfrak{B}}_{{ℂ}_{RP}}\left({\mathbb{𝕩}}_{EL}\right)\le 1$ and $0\le {\mathcal{T}}_{{ℂ}_{IP}}\left({\mathbb{𝕩}}_{EL}\right){\mathfrak{U}}_{{ℂ}_{IP}}\left({\mathbb{𝕩}}_{EL}\right)+{\mathcal{F}}_{{ℂ}_{IP}}\left({\mathbb{𝕩}}_{EL}\right){\mathfrak{B}}_{{ℂ}_{IP}}\left({\mathbb{𝕩}}_{EL}\right)\le 1$, where $0\le {\mathfrak{U}}_{{ℂ}_{RP}}\left({\mathbb{𝕩}}_{EL}\right)+{\mathfrak{B}}_{{ℂ}_{RP}}\left({\mathbb{𝕩}}_{EL}\right)\le 1$ and $0\le {\mathfrak{U}}_{{ℂ}_{IP}}\left({\mathbb{𝕩}}_{EL}\right)+{\mathfrak{B}}_{{ℂ}_{IP}}\left({\mathbb{𝕩}}_{EL}\right)\le 1$ and $\left[{\Xi }_{\mathsf{\alpha }\left({\mathbb{𝕩}}_{EL}\right)},{\Xi }_{\mathsf{\beta }\left({\mathbb{𝕩}}_{EL}\right)}\right],{\Xi }_{\mathsf{\alpha }},{\Xi }_{\mathsf{\beta }}\in \stackrel{=}{\Xi }$. The complex linear Diophantine uncertain linguistic numbers (CLDULNs) are dented by ${ℂ}_{\mathrm{CLU}-\mathrm{i}}=\left(\begin{array}{c}\left[{\Xi }_{{\mathsf{\alpha }}_{\mathrm{i}}},{\Xi }_{{\mathsf{\beta }}_{\mathrm{i}}}\right],\left({\mathcal{T}}_{{ℂ}_{RP-\mathrm{i}}}{\mathrm{e}}^{\mathrm{i}2\mathsf{\pi }\left({\mathcal{T}}_{{ℂ}_{IP-\mathrm{i}}}\right)},{\mathcal{F}}_{{ℂ}_{RP-\mathrm{i}}}{\mathrm{e}}^{\mathrm{i}2\mathsf{\pi }\left({\mathcal{F}}_{{ℂ}_{IP-\mathrm{i}}}\right)}\right),\\ \left({\mathfrak{U}}_{{ℂ}_{RP-\mathrm{i}}}{\mathrm{e}}^{\mathrm{i}2\mathsf{\pi }\left({\mathfrak{U}}_{{ℂ}_{IP-\mathrm{i}}}\right)},{\mathfrak{B}}_{{ℂ}_{RP-\mathrm{i}}}{\mathrm{e}}^{\mathrm{i}2\mathsf{\pi }\left({\mathfrak{B}}_{{ℂ}_{IP-\mathrm{i}}}\right)}\right)\end{array}\right),\mathrm{i}=1,2,\dots ,{𝓃}_{\mathit{NE}}$. By using any two CLDULNs ${ℂ}_{\mathrm{CLU}-1}=\left(\begin{array}{c}\left[{\Xi }_{{\mathsf{\alpha }}_1},{\Xi }_{{\mathsf{\beta }}_1}\right],\left({\mathcal{T}}_{{ℂ}_{RP-1}}{\mathrm{e}}^{\mathrm{i}2\mathsf{\pi }\left({\mathcal{T}}_{{ℂ}_{IP-1}}\right)},{\mathcal{F}}_{{ℂ}_{RP-1}}{\mathrm{e}}^{\mathrm{i}2\mathsf{\pi }\left({\mathcal{F}}_{{ℂ}_{IP-1}}\right)}\right),\\ \left({\mathfrak{U}}_{{ℂ}_{RP-1}}{\mathrm{e}}^{\mathrm{i}2\mathsf{\pi }\left({\mathfrak{U}}_{{ℂ}_{IP-1}}\right)},{\mathfrak{B}}_{{ℂ}_{RP-1}}{\mathrm{e}}^{\mathrm{i}2\mathsf{\pi }\left({\mathfrak{B}}_{{ℂ}_{IP-1}}\right)}\right)\end{array}\right)$ and ${ℂ}_{\mathrm{CLU}-2}=\left(\begin{array}{c}\left[{\Xi }_{{\mathsf{\alpha }}_2},{\Xi }_{{\mathsf{\beta }}_2}\right],\left({\mathcal{T}}_{{ℂ}_{RP-2}}{\mathrm{e}}^{\mathrm{i}2\mathsf{\pi }\left({\mathcal{T}}_{{ℂ}_{IP-2}}\right)},{\mathcal{F}}_{{ℂ}_{RP-2}}{\mathrm{e}}^{\mathrm{i}2\mathsf{\pi }\left({\mathcal{F}}_{{ℂ}_{IP-2}}\right)}\right),\\ \left({\mathfrak{U}}_{{ℂ}_{RP-2}}{\mathrm{e}}^{\mathrm{i}2\mathsf{\pi }\left({\mathfrak{U}}_{{ℂ}_{IP-2}}\right)},{\mathfrak{B}}_{{ℂ}_{RP-2}}{\mathrm{e}}^{\mathrm{i}2\mathsf{\pi }\left({\mathfrak{B}}_{{ℂ}_{IP-2}}\right)}\right)\end{array}\right)$, with constant ${\mathsf{\delta }}_{\mathit{SC}}$, then

$${ℂ}_{\mathrm{CLU}-1}\oplus {ℂ}_{\mathrm{CLU}-2}=\left(\begin{array}{c}\left[{\Xi }_{{\alpha }_1+{\alpha }_2},{\Xi }_{{\beta }_1+{\beta }_2}\right],\\ \left(\begin{array}{c}\left({\mathcal{T}}_{{ℂ}_{RP-1}}+{\mathcal{T}}_{{ℂ}_{RP-2}}-{\mathcal{T}}_{{ℂ}_{RP-1}}{\mathcal{T}}_{{ℂ}_{RP-2}}\right)e^{i2\pi \left({\mathcal{T}}_{{ℂ}_{IP-1}}+{\mathcal{T}}_{{ℂ}_{IP-2}}-{\mathcal{T}}_{{ℂ}_{IP-1}}{\mathcal{T}}_{{ℂ}_{IP-2}}\right)},\\ {\mathcal{F}}_{{ℂ}_{RP-1}}{\mathcal{F}}_{{ℂ}_{RP-2}}{e}^{i2\pi \left({\mathcal{F}}_{{ℂ}_{IP-1}}{\mathcal{F}}_{{ℂ}_{IP-2}}\right)}\end{array}\right),\\ \left(\begin{array}{c}\left({\mathfrak{U}}_{{ℂ}_{RP-1}}+{\mathfrak{U}}_{{ℂ}_{RP-2}}-{\mathfrak{U}}_{{ℂ}_{RP-1}}{\mathfrak{U}}_{{ℂ}_{RP-2}}\right)e^{i2\pi \left({\mathfrak{U}}_{{ℂ}_{IP-1}}+{\mathfrak{U}}_{{ℂ}_{IP-2}}-{\mathfrak{U}}_{{ℂ}_{IP-1}}{\mathfrak{U}}_{{ℂ}_{IP-2}}\right)},\\ {\mathfrak{B}}_{{ℂ}_{RP-1}}{\mathfrak{B}}_{{ℂ}_{RP-2}}{e}^{i2\pi \left({\mathfrak{B}}_{{ℂ}_{IP-1}}{\mathfrak{B}}_{{ℂ}_{IP-2}}\right)},\end{array}\right)\end{array}\right)$$

(21)

$${ℂ}_{\mathrm{CLU}-1}\otimes {ℂ}_{\mathrm{CLU}-2}=\left(\begin{array}{c}\left[{\Xi }_{{\alpha }_1\ast {\alpha }_2},{\Xi }_{{\beta }_1\ast {\beta }_2}\right],\\ \left(\begin{array}{c}{\mathcal{T}}_{{ℂ}_{RP-1}}{\mathcal{T}}_{{ℂ}_{RP-2}}{e}^{i2\pi \left({\mathcal{T}}_{{ℂ}_{IP-1}}{\mathcal{T}}_{{ℂ}_{IP-2}}\right)}\\ \left({\mathcal{F}}_{{ℂ}_{RP-1}}+{\mathcal{F}}_{{ℂ}_{RP-2}}-{\mathcal{F}}_{{ℂ}_{RP-1}}{\mathcal{F}}_{{ℂ}_{RP-2}}\right)e^{i2\pi \left({\mathcal{F}}_{{ℂ}_{IP-1}}+{\mathcal{F}}_{{ℂ}_{IP-2}}-{\mathcal{F}}_{{ℂ}_{IP-1}}{\mathcal{F}}_{{ℂ}_{IP-2}}\right)}\end{array}\right),\\ \left(\begin{array}{c}{\mathfrak{U}}_{{ℂ}_{RP-1}}{\mathfrak{U}}_{{ℂ}_{RP-2}}{e}^{i2\pi \left({\mathfrak{U}}_{{ℂ}_{IP-1}}{\mathfrak{U}}_{{ℂ}_{IP-2}}\right)},\\ \left({\mathfrak{B}}_{{ℂ}_{RP-1}}+{\mathfrak{B}}_{{ℂ}_{RP-2}}-{\mathfrak{B}}_{{ℂ}_{RP-1}}{\mathfrak{B}}_{{ℂ}_{RP-2}}\right)e^{i2\pi \left({\mathfrak{B}}_{{ℂ}_{IP-1}}+{\mathfrak{B}}_{{ℂ}_{IP-2}}-{\mathfrak{B}}_{{ℂ}_{IP-1}}{\mathfrak{B}}_{{ℂ}_{IP-2}}\right)}\end{array}\right)\end{array}\right)$$

(22)

$${\delta }_{\mathit{SC}}{ℂ}_{\mathrm{CLU}-1}=\left(\begin{array}{c}\left[{\Xi }_{{\delta }_{\mathit{SC}}\ast \alpha 1},{\Xi }_{{\delta }_{\mathit{SC}}\ast \beta 1}\right],\left(\left(1-{\left(1-{\mathcal{T}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{\mathit{SC}}}\right)e^{i2\pi \left(1-{\left(1-{\mathcal{T}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{\mathit{SC}}}\right)},{\mathcal{F}}_{{ℂ}_{RP-1}}^{{\delta }_{SC}}{e}^{i2\pi \left({\mathcal{F}}_{{ℂ}_{IP-1}}^{{\delta }_{SC}}\right)}\right),\\ \left(\left(1-{\left(1-{\mathfrak{U}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{\mathit{SC}}}\right)e^{i2\pi \left(1-{\left(1-{\mathfrak{U}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{\mathit{SC}}}\right)},{\mathfrak{B}}_{{ℂ}_{RP-1}}^{{\delta }_{SC}}{e}^{i2\pi \left({\mathfrak{B}}_{{ℂ}_{IP-1}}^{{\delta }_{SC}}\right)}\right)\end{array}\right)$$

(23)

$${ℂ}_{\mathit{CLU}-1}^{{\delta }_{\mathit{SC}}}=\left(\begin{array}{c}\left[{\Xi }_{{{\alpha }_1}^{{\delta }_{\mathit{SC}}}},{\Xi }_{{{\beta }_1}^{{\delta }_{\mathit{SC}}}}\right],\left({\mathcal{T}}_{{\delta }_{SC}}^{{ℂ}_{RP-1}}{e}^{i2\pi \left({\mathcal{T}}_{{\delta }_{SC}}^{{ℂ}_{RP-1}}\right)},\left(1-{\left(1-{\mathcal{F}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{\mathit{SC}}}\right)e^{i2\pi \left(1-{\left(1-{\mathcal{F}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{\mathit{SC}}}\right)}\right),\\ \left({\mathfrak{U}}_{{\delta }_{SC}}^{{ℂ}_{RP-1}}{e}^{i2\pi \left({\mathfrak{U}}_{{\delta }_{SC}}^{{ℂ}_{RP-1}}\right)},\left(1-{\left(1-{\mathfrak{B}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{\mathit{SC}}}\right)e^{i2\pi \left(1-{\left(1-{\mathfrak{B}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{\mathit{SC}}}\right)}\right)\end{array}\right)$$

(24)

By using any CLDULN ${ℂ}_{\mathrm{CLU}-1}=\left(\begin{array}{c}\left[{\Xi }_{{\mathsf{\alpha }}_1},{\Xi }_{{\mathsf{\beta }}_1}\right],\left({\mathcal{T}}_{{ℂ}_{RP-1}}{\mathrm{e}}^{\mathrm{i}2\mathsf{\pi }\left({\mathcal{T}}_{{ℂ}_{IP-1}}\right)},{\mathcal{F}}_{{ℂ}_{RP-1}}{\mathrm{e}}^{\mathrm{i}2\mathsf{\pi }\left({\mathcal{F}}_{{ℂ}_{IP-1}}\right)}\right),\\ \left({\mathfrak{U}}_{{ℂ}_{RP-1}}{\mathrm{e}}^{\mathrm{i}2\mathsf{\pi }\left({\mathfrak{U}}_{{ℂ}_{IP-1}}\right)},{\mathfrak{B}}_{{ℂ}_{RP-1}}{\mathrm{e}}^{\mathrm{i}2\mathsf{\pi }\left({\mathfrak{B}}_{{ℂ}_{IP-1}}\right)}\right)\end{array}\right)$, we have

$${\mathbb{S}}_{\mathrm{SV}}\left({ℂ}_{\mathrm{CLU}-1}\right)=\left({\mathsf{\alpha }}_1+{\mathsf{\beta }}_1\right)\ast \frac{1}{4}\left(\left({\mathcal{T}}_{{ℂ}_{RP-1}}+{\mathcal{T}}_{{ℂ}_{IP-1}}-{\mathcal{F}}_{{ℂ}_{RP-1}}-{\mathcal{F}}_{{ℂ}_{IP-1}}\right)+\left({\mathfrak{U}}_{{ℂ}_{RP-1}}+{\mathfrak{U}}_{{ℂ}_{IP-1}}-{\mathfrak{B}}_{{ℂ}_{RP-1}}-{\mathfrak{B}}_{{ℂ}_{IP-1}}\right)\right)$$

(25)

$${ℍ}_{\mathrm{AV}}\left({ℂ}_{\mathrm{CLU}-1}\right)=\left({\mathsf{\alpha }}_1+{\mathsf{\beta }}_1\right)\ast \frac{1}{4}\left(\left({\mathcal{T}}_{{ℂ}_{RP-1}}+{\mathcal{T}}_{{ℂ}_{IP-1}}+{\mathcal{F}}_{{ℂ}_{RP-1}}+{\mathcal{F}}_{{ℂ}_{IP-1}}\right)+\left({\mathfrak{U}}_{{ℂ}_{RP-1}}+{\mathfrak{U}}_{{ℂ}_{IP-1}}+{\mathfrak{B}}_{{ℂ}_{RP-1}}+{\mathfrak{B}}_{{ℂ}_{IP-1}}\right)\right)$$

(26)

For Equations (25) and (26), we obtained some rules, such that

•  When ${\mathbb{S}}_{\mathrm{SV}}\left({ℂ}_{\mathrm{CLU}-1}\right)>{\mathbb{S}}_{\mathrm{SV}}\left({ℂ}_{\mathrm{CLU}-2}\right)\Rightarrow {ℂ}_{\mathrm{CLU}-1}>{ℂ}_{\mathrm{CLU}-2}$;
• When ${\mathbb{S}}_{\mathrm{SV}}\left({ℂ}_{\mathrm{CLU}-1}\right)<{\mathbb{S}}_{\mathrm{SV}}\left({ℂ}_{\mathrm{CLU}-2}\right)\Rightarrow {ℂ}_{\mathrm{CLU}-1}<{ℂ}_{\mathrm{CLU}-2}$;
• When ${\mathbb{S}}_{\mathrm{SV}}\left({ℂ}_{\mathrm{CLU}-1}\right)={\mathbb{S}}_{\mathrm{SV}}\left({ℂ}_{\mathrm{CLU}-2}\right)\Rightarrow$
  •  When ${ℍ}_{\mathrm{AV}}\left({ℂ}_{\mathrm{CLU}-1}\right)>{ℍ}_{\mathrm{AV}}\left({ℂ}_{\mathrm{CLU}-2}\right)\Rightarrow {ℂ}_{\mathrm{CLU}-1}>{ℂ}_{\mathrm{CLU}-2}$;
  •  When ${ℍ}_{\mathrm{AV}}\left({ℂ}_{\mathrm{CLU}-1}\right)<{ℍ}_{\mathrm{AV}}\left({ℂ}_{\mathrm{CLU}-2}\right)\Rightarrow {ℂ}_{\mathrm{CLU}-1}<{ℂ}_{\mathrm{CLU}-2}$;
  •  When ${ℍ}_{AV}\left({ℂ}_{CLU-1}\right)={ℍ}_{AV}\left({ℂ}_{CLU-2}\right)\Rightarrow {ℂ}_{CLU-1}={ℂ}_{CLU-2}$.

Similarly, by using the Definition 5, we elaborated some operational laws are called Einstein operational laws which are discussed below. By using any two CLDULNs ${ℂ}_{CLU-1}=\left(\begin{array}{c}\left[{\Xi }_{{\alpha }_1},{\Xi }_{{\beta }_1}\right],\left({\mathcal{T}}_{{ℂ}_{RP-1}}{e}^{i2\pi \left({\mathcal{T}}_{{ℂ}_{IP-1}}\right)},{\mathcal{F}}_{{ℂ}_{RP-1}}{e}^{i2\pi \left({\mathcal{F}}_{{ℂ}_{IP-1}}\right)}\right),\\ \left({\mathfrak{U}}_{{ℂ}_{RP-1}}{e}^{i2\pi \left({\mathfrak{U}}_{{ℂ}_{IP-1}}\right)},{\mathfrak{B}}_{{ℂ}_{RP-1}}{e}^{i2\pi \left({\mathfrak{B}}_{{ℂ}_{IP-1}}\right)}\right)\end{array}\right)$ and ${ℂ}_{CLU-2}=\left(\begin{array}{c}\left[{\Xi }_{{\alpha }_2},{\Xi }_{{\beta }_2}\right],\left({\mathcal{T}}_{{ℂ}_{RP-2}}{e}^{i2\pi \left({\mathcal{T}}_{{ℂ}_{IP-2}}\right)},{\mathcal{F}}_{{ℂ}_{RP-2}}{e}^{i2\pi \left({\mathcal{F}}_{{ℂ}_{IP-2}}\right)}\right),\\ \left({\mathfrak{U}}_{{ℂ}_{RP-2}}{e}^{i2\pi \left({\mathfrak{U}}_{{ℂ}_{IP-2}}\right)},{\mathfrak{B}}_{{ℂ}_{RP-2}}{e}^{i2\pi \left({\mathfrak{B}}_{{ℂ}_{IP-2}}\right)}\right)\end{array}\right)$, with constant ${\delta }_{SC}$, then

$${ℂ}_{\mathrm{CLU}-1}\oplus {ℂ}_{\mathrm{CLU}-2}=\left(\begin{array}{c}\left[{\Xi }_{{\alpha }_1+{\alpha }_2},{\Xi }_{{\beta }_1+{\beta }_2}\right],\\ \left(\begin{array}{c}\left(\frac{{\mathcal{T}}_{{ℂ}_{RP-1}}+{\mathcal{T}}_{{ℂ}_{RP-2}}}{1+{\mathcal{T}}_{{ℂ}_{RP-1}}{\mathcal{T}}_{{ℂ}_{RP-2}}}\right)e^{i2\pi \left(\frac{{\mathcal{T}}_{{ℂ}_{IP-1}}+{\mathcal{T}}_{{ℂ}_{IP-2}}}{1+{\mathcal{T}}_{{ℂ}_{IP-1}}{\mathcal{T}}_{{ℂ}_{IP-2}}}\right)},\\ \frac{{\mathcal{F}}_{{ℂ}_{RP-1}}{\mathcal{F}}_{{ℂ}_{RP-2}}}{1+\left(1-{\mathcal{F}}_{{ℂ}_{RP-1}}\right)\left(1-{\mathcal{F}}_{{ℂ}_{RP-2}}\right)}{e}^{i2\pi \left(\frac{{\mathcal{F}}_{{ℂ}_{IP-1}}{\mathcal{F}}_{{ℂ}_{IP-2}}}{1+\left(1-{\mathcal{F}}_{{ℂ}_{IP-1}}\right)\left(1-{\mathcal{F}}_{{ℂ}_{IP-2}}\right)}\right)}\end{array}\right)\\ \left(\begin{array}{c}\left(\frac{{\mathfrak{U}}_{{ℂ}_{RP-1}}+{\mathfrak{U}}_{{ℂ}_{RP-2}}}{1+{\mathfrak{U}}_{{ℂ}_{RP-1}}{\mathfrak{U}}_{{ℂ}_{RP-2}}}\right)e^{i2\pi \left(\frac{{\mathfrak{U}}_{{ℂ}_{IP-1}}+{\mathfrak{U}}_{{ℂ}_{IP-2}}}{1+{\mathfrak{U}}_{{ℂ}_{IP-1}}{\mathfrak{U}}_{{ℂ}_{IP-2}}}\right)},\\ \frac{{\mathfrak{B}}_{{ℂ}_{RP-1}}{\mathfrak{B}}_{{ℂ}_{RP-2}}}{1+\left(1-{\mathfrak{B}}_{{ℂ}_{RP-1}}\right)\left(1-{\mathfrak{B}}_{{ℂ}_{RP-2}}\right)}{e}^{i2\pi \left(\frac{{\mathfrak{B}}_{{ℂ}_{IP-1}}{\mathfrak{B}}_{{ℂ}_{IP-2}}}{1+\left(1-{\mathfrak{B}}_{{ℂ}_{IP-1}}\right)\left(1-{\mathfrak{B}}_{{ℂ}_{IP-2}}\right)}\right)}\end{array}\right)\end{array}\right)$$

(27)

$${ℂ}_{\mathrm{CLU}-1}\otimes {ℂ}_{\mathrm{CLU}-2}=\left(\begin{array}{c}\left[{\Xi }_{{\alpha }_1\ast {\alpha }_2},{\Xi }_{{\beta }_1\ast {\beta }_2}\right],\\ \left(\begin{array}{c}\frac{{\mathcal{T}}_{{ℂ}_{RP-1}}{\mathcal{T}}_{{ℂ}_{RP-2}}}{1+\left(1-{\mathcal{T}}_{{ℂ}_{RP-1}}\right)\left(1-{\mathcal{T}}_{{ℂ}_{RP-2}}\right)}{e}^{i2\pi \left(\frac{{\mathcal{T}}_{{ℂ}_{IP-1}}{\mathcal{T}}_{{ℂ}_{IP-2}}}{1+\left(1-{\mathcal{T}}_{{ℂ}_{IP-1}}\right)\left(1-{\mathcal{T}}_{{ℂ}_{IP-2}}\right)}\right)},\\ \frac{{\mathcal{F}}_{{ℂ}_{RP-1}}+{\mathcal{F}}_{{ℂ}_{RP-2}}}{1+{\mathcal{F}}_{{ℂ}_{RP-1}}{\mathcal{F}}_{{ℂ}_{RP-2}}}{e}^{i2\pi \left(\frac{{\mathcal{F}}_{{ℂ}_{IP-1}}+{\mathcal{F}}_{{ℂ}_{IP-2}}}{1+{\mathcal{F}}_{{ℂ}_{IP-1}}{\mathcal{F}}_{{ℂ}_{IP-2}}}\right)}\end{array}\right),\\ \left(\begin{array}{c}\frac{{\mathfrak{U}}_{{ℂ}_{RP-1}}{\mathfrak{U}}_{{ℂ}_{RP-2}}}{1+\left(1-{\mathfrak{U}}_{{ℂ}_{RP-1}}\right)\left(1-{\mathfrak{U}}_{{ℂ}_{RP-2}}\right)}{e}^{i2\pi \left(\frac{{\mathfrak{U}}_{{ℂ}_{IP-1}}{\mathfrak{U}}_{{ℂ}_{IP-2}}}{1+\left(1-{\mathfrak{U}}_{{ℂ}_{IP-1}}\right)\left(1-{\mathfrak{U}}_{{ℂ}_{IP-2}}\right)}\right)},\\ \left(\frac{{\mathfrak{B}}_{{ℂ}_{RP-1}}+{\mathfrak{B}}_{{ℂ}_{RP-2}}}{1+{\mathfrak{B}}_{{ℂ}_{RP-1}}{\mathfrak{B}}_{{ℂ}_{RP-2}}}\right)e^{i2\pi \left(\frac{{\mathfrak{B}}_{{ℂ}_{IP-1}}+{\mathfrak{B}}_{{ℂ}_{IP-2}}}{1+{\mathfrak{B}}_{{ℂ}_{IP-1}}{\mathfrak{B}}_{{ℂ}_{IP-2}}}\right)}\end{array}\right)\end{array}\right)$$

(28)

$${\delta }_{SC}{ℂ}_{CLU-1}=\left(\begin{array}{c}\left[{\Xi }_{{\alpha }_1\ast {\alpha }_2},{\Xi }_{{\beta }_1\ast {\beta }_2}\right],\left(\begin{array}{c}\left(\frac{{\left(1+{\mathcal{T}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC}}-{\left(1-{\mathcal{T}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC}}}{{\left(1+{\mathcal{T}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC}}+{\left(1-{\mathcal{T}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC}}}\right)e^{i2\pi \left(\frac{{\left(1+{\mathcal{T}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC}}-{\left(1-{\mathcal{T}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC}}}{{\left(1+{\mathcal{T}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC}}+{\left(1-{\mathcal{T}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC}}}\right)},\\ \frac{2{\mathcal{F}}_{{ℂ}_{RP-1}}^{{\delta }_{SC}}}{{\left(2-{\mathcal{F}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC}}+{\mathcal{F}}_{{ℂ}_{RP-1}}^{{\delta }_{SC}}}{e}^{i2\pi \left(\frac{2{\mathcal{F}}_{{ℂ}_{IP-1}}^{{\delta }_{SC}}}{{\left(2-{\mathcal{F}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC}}+{\mathcal{F}}_{{ℂ}_{IP-1}}^{{\delta }_{SC}}}\right)}\end{array}\right)\\ \left(\begin{array}{c}\left(\frac{{\left(1+{\mathfrak{U}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC}}-{\left(1-{\mathfrak{U}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC}}}{{\left(1+{\mathfrak{U}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC}}+{\left(1-{\mathfrak{U}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC}}}\right)e^{i2\pi \left(\frac{{\left(1+{\mathfrak{U}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC}}-{\left(1-{\mathfrak{U}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC}}}{{\left(1+{\mathfrak{U}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC}}+{\left(1-{\mathfrak{U}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC}}}\right)},\\ \frac{2{\mathfrak{B}}_{{ℂ}_{RP-1}}^{{\delta }_{SC}}}{{\left(2-{\mathfrak{B}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC}}+{\mathfrak{B}}_{{ℂ}_{RP-1}}^{{\delta }_{SC}}}{e}^{i2\pi \left(\frac{2{\mathfrak{B}}_{{ℂ}_{IP-1}}^{{\delta }_{SC}}}{{\left(2-{\mathfrak{B}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC}}+{\mathfrak{B}}_{{ℂ}_{IP-1}}^{{\delta }_{SC}}}\right)}\end{array}\right)\end{array}\right)$$

(29)

$${\delta }_{\mathit{SC}}{ℂ}_{\mathit{CLU}-1}^{{\delta }_{\mathit{SC}}}=\left(\begin{array}{c}\left[{\Xi }_{{{\alpha }_1}^{{\delta }_{\mathit{SC}}}},{\Xi }_{{{\beta }_1}^{{\delta }_{\mathit{SC}}}}\right],\left(\begin{array}{c}\frac{2{\mathcal{T}}_{{ℂ}_{RP-1}}^{{\delta }_{SC}}}{{\left(2-{\mathcal{T}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC}}+{\mathcal{T}}_{{ℂ}_{RP-1}}^{{\delta }_{SC}}}{e}^{i2\pi \left(\frac{2{\mathcal{T}}_{{ℂ}_{IP-1}}^{{\delta }_{SC}}}{{\left(2-{\mathcal{T}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC}}+{\mathcal{T}}_{{ℂ}_{IP-1}}^{{\delta }_{SC}}}\right)},\\ \left(\frac{{\left(1+{\mathcal{F}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC}}-{\left(1-{\mathcal{F}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC}}}{{\left(1+{\mathcal{F}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC}}+{\left(1-{\mathcal{F}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC}}}\right)e^{i2\pi \left(\frac{{\left(1+{\mathcal{F}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC}}-{\left(1-{\mathcal{F}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC}}}{{\left(1+{\mathcal{F}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC}}+{\left(1-{\mathcal{F}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC}}}\right)}\end{array}\right),\\ \left(\begin{array}{c}\frac{2{\mathfrak{U}}_{{ℂ}_{RP-1}}^{{\delta }_{SC}}}{{\left(2-{\mathfrak{U}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC}}+{\mathfrak{U}}_{{ℂ}_{RP-1}}^{{\delta }_{SC}}}{e}^{i2\pi \left(\frac{2{\mathfrak{U}}_{{ℂ}_{IP-1}}^{{\delta }_{SC}}}{{\left(2-{\mathfrak{U}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC}}+{\mathfrak{U}}_{{ℂ}_{IP-1}}^{{\delta }_{SC}}}\right)},\\ \left(\frac{{\left(1+{\mathcal{B}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC}}-{\left(1-{\mathcal{B}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC}}}{{\left(1+{\mathcal{B}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC}}+{\left(1-{\mathcal{B}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC}}}\right)e^{i2\pi \left(\frac{{\left(1+{\mathcal{B}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC}}-{\left(1-{\mathcal{B}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC}}}{{\left(1+{\mathcal{B}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC}}+{\left(1-{\mathcal{B}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC}}}\right)}\end{array}\right)\end{array}\right)$$

(30)

By using the principles in Equations (27)–(30), we will get the following results.

Theorem 1.

By using any two CLDULNs${ℂ}_{CLU-1}=\left(\begin{array}{c}\left[{\Xi }_{{\alpha }_1},{\Xi }_{{\beta }_1}\right],\left({\mathcal{T}}_{{ℂ}_{RP-1}}{e}^{i2\pi \left({\mathcal{T}}_{{ℂ}_{IP-1}}\right)},{\mathcal{F}}_{{ℂ}_{RP-1}}{e}^{i2\pi \left({\mathcal{F}}_{{ℂ}_{IP-1}}\right)}\right),\\ \left({\mathfrak{U}}_{{ℂ}_{RP-1}}{e}^{i2\pi \left({\mathfrak{U}}_{{ℂ}_{IP-1}}\right)},{\mathfrak{B}}_{{ℂ}_{RP-1}}{e}^{i2\pi \left({\mathfrak{B}}_{{ℂ}_{IP-1}}\right)}\right)\end{array}\right)$and${ℂ}_{CLU-2}=\left(\begin{array}{c}\left[{\Xi }_{{\alpha }_2},{\Xi }_{{\beta }_2}\right],\left({\mathcal{T}}_{{ℂ}_{RP-2}}{e}^{i2\pi \left({\mathcal{T}}_{{ℂ}_{IP-2}}\right)},{\mathcal{F}}_{{ℂ}_{RP-2}}{e}^{i2\pi \left({\mathcal{F}}_{{ℂ}_{IP-2}}\right)}\right),\\ \left({\mathfrak{U}}_{{ℂ}_{RP-2}}{e}^{i2\pi \left({\mathfrak{U}}_{{ℂ}_{IP-2}}\right)},{\mathfrak{B}}_{{ℂ}_{RP-2}}{e}^{i2\pi \left({\mathfrak{B}}_{{ℂ}_{IP-2}}\right)}\right)\end{array}\right)$, with constants${\delta }_{SC-1},{\delta }_{SC-2},{\delta }_{SC}\ge 1$, then

•  ${ℂ}_{CLU-1}\oplus {ℂ}_{CLU-2}={ℂ}_{CLU-2}\oplus {ℂ}_{CLU-1}$ ;
•  ${ℂ}_{CLU-1}\otimes {ℂ}_{CLU-2}={ℂ}_{CLU-2}\otimes {ℂ}_{CLU-1}$ ;
•  ${\delta }_{SC}\left({ℂ}_{CLU-1}\oplus {ℂ}_{CLU-2}\right)={\delta }_{SC}{ℂ}_{CLU-1}\oplus {\delta }_{SC}{ℂ}_{CLU-2}$ ;
•  ${\delta }_{SC-1}{ℂ}_{CLU-1}\oplus {\delta }_{SC-2}{ℂ}_{CLU-1}=\left({\delta }_{SC-1}+{\delta }_{SC-2}\right){ℂ}_{CLU-1}$ ;
•  ${ℂ}_{CLU-1}^{{\delta }_{SC-1}}\otimes {ℂ}_{CLU-1}^{{\delta }_{SC-2}}={ℂ}_{CLU-1}^{\left({\delta }_{SC-1}+{\delta }_{SC-2}\right)}$ ;
•  ${ℂ}_{CLU-1}^{{\delta }_{SC}}\otimes {ℂ}_{CLU-2}^{{\delta }_{SC}}={\left({ℂ}_{CLU-1}\otimes {ℂ}_{CLU-2}\right)}^{{\delta }_{SC}}$.

Proof of Theorem 1.

From hypothesis, we know that the first two parts are trivial. Additionally, we will prove that the part 3, such that

$${ℂ}_{\mathrm{CLU}-1}\oplus {ℂ}_{\mathrm{CLU}-2}=\left(\begin{array}{c}\left[{\Xi }_{{\alpha }_1+{\alpha }_2},{\Xi }_{{\beta }_1+{\beta }_2}\right],\\ \left(\begin{array}{c}\left(\frac{{\mathcal{T}}_{{ℂ}_{RP-1}}+{\mathcal{T}}_{{ℂ}_{RP-2}}}{1+{\mathcal{T}}_{{ℂ}_{RP-1}}{\mathcal{T}}_{{ℂ}_{RP-2}}}\right)e^{i2\pi \left(\frac{{\mathcal{T}}_{{ℂ}_{IP-1}}+{\mathcal{T}}_{{ℂ}_{IP-2}}}{1+{\mathcal{T}}_{{ℂ}_{IP-1}}{\mathcal{T}}_{{ℂ}_{IP-2}}}\right)},\\ \frac{{\mathcal{F}}_{{ℂ}_{RP-1}}{\mathcal{F}}_{{ℂ}_{RP-2}}}{1+\left(1-{\mathcal{F}}_{{ℂ}_{RP-1}}\right)\left(1-{\mathcal{F}}_{{ℂ}_{RP-2}}\right)}{e}^{i2\pi \left(\frac{{\mathcal{F}}_{{ℂ}_{IP-1}}{\mathcal{F}}_{{ℂ}_{IP-2}}}{1+\left(1-{\mathcal{F}}_{{ℂ}_{IP-1}}\right)\left(1-{\mathcal{F}}_{{ℂ}_{IP-2}}\right)}\right)}\end{array}\right),\\ \left(\begin{array}{c}\left(\frac{{\mathfrak{U}}_{{ℂ}_{RP-1}}+{\mathfrak{U}}_{{ℂ}_{RP-2}}}{1+{\mathfrak{U}}_{{ℂ}_{RP-1}}{\mathfrak{U}}_{{ℂ}_{RP-2}}}\right)e^{i2\pi \left(\frac{{\mathfrak{U}}_{{ℂ}_{IP-1}}+{\mathfrak{U}}_{{ℂ}_{IP-2}}}{1+{\mathfrak{U}}_{{ℂ}_{IP-1}}{\mathfrak{U}}_{{ℂ}_{IP-2}}}\right)},\\ \frac{{\mathfrak{B}}_{{ℂ}_{RP-1}}{\mathfrak{B}}_{{ℂ}_{RP-2}}}{1+\left(1-{\mathfrak{B}}_{{ℂ}_{RP-1}}\right)\left(1-{\mathfrak{B}}_{{ℂ}_{RP-2}}\right)}{e}^{i2\pi \left(\frac{{\mathfrak{B}}_{{ℂ}_{IP-1}}{\mathfrak{B}}_{{ℂ}_{IP-2}}}{1+\left(1-{\mathfrak{B}}_{{ℂ}_{IP-1}}\right)\left(1-{\mathfrak{B}}_{{ℂ}_{IP-2}}\right)}\right)}\end{array}\right)\end{array}\right)$$

Similarly, we obtained for right hand side such that

and

Then, by using the above two results, we get

Hence, ${\delta }_{\mathit{SC}}\left({ℂ}_{CLU-1},\oplus ,{ℂ}_{CLU-2}\right)={\delta }_{\mathit{SC}}{ℂ}_{CLU-1}\oplus {ℂ}_{CLU-2}$. The proof of the part 4 is also trivial. Further, we prove that the part 5, such that

$${ℂ}_{CLU-1}^{{\delta }_{SC-1}}=(\begin{array}{c}\begin{array}{c}\left[{\mathsf{\Xi }}_{{\alpha }_1^{{\delta }_{SC-1}}},{\mathsf{\Xi }}_{{\beta }_1^{{\delta }_{SC-1}}}\right],\\ \left(\begin{array}{c}\frac{2{\mathcal{T}}_{{ℂ}_{RP-1}}^{{\delta }_{SC-1}}}{{\left(2-{\mathcal{T}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC-1}}+{\mathcal{T}}_{{ℂ}_{RP-1}}^{{\delta }_{SC-1}}}{e}^{i2\pi \left(\frac{2{\mathcal{T}}_{{ℂ}_{IP-1}}^{{\delta }_{SC-1}}}{{\left(2-{\mathcal{T}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC-1}}+{\mathcal{T}}_{{ℂ}_{IP-1}}^{{\delta }_{SC-1}}}\right)},\\ \left(\frac{{\left(1+{ℱ}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC-1}}-{\left(1-{ℱ}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC-1}}}{{\left(1+{ℱ}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC-1}}+{\left(1-{ℱ}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC-1}}}{e}^{i2\pi \left(\frac{{\left(1+{ℱ}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC-1}}-{\left(1-{ℱ}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC-1}}}{{\left(1+{ℱ}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC-1}}+{\left(1-{ℱ}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC-1}}}\right)}\right)\end{array}\right)\\ (\begin{array}{c}\frac{2{\mathfrak{A}}_{{ℂ}_{RP-1}}^{{\delta }_{SC-1}}}{{\left(2-{\mathfrak{A}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC-1}}+{\mathfrak{A}}_{{ℂ}_{RP-1}}^{{\delta }_{SC-1}}}{e}^{i2\pi \left(\frac{2{\mathfrak{A}}_{{ℂ}_{IP-1}}^{{\delta }_{SC-1}}}{{\left(2-{\mathfrak{A}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC-1}}+{\mathfrak{A}}_{{ℂ}_{IP-1}}^{{\delta }_{SC-1}}}\right)},\\ \left(\frac{{\left(1+{\mathfrak{B}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC-1}}-{\left(1-{\mathfrak{B}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC-1}}}{{\left(1+{\mathfrak{B}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC-1}}+{\left(1-{\mathfrak{B}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC-1}}}\right)e^{i2\pi \left(\frac{{\left(1+{\mathfrak{B}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC-1}}-{\left(1-{\mathfrak{B}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC-1}}}{{\left(1+{\mathfrak{B}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC-1}}+{\left(1-{\mathfrak{B}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC-1}}}\right)}\end{array}\end{array})\end{array}$$

$${ℂ}_{CLU-1}^{{\delta }_{SC-2}}=(\begin{array}{c}\begin{array}{c}\left[{\mathsf{\Xi }}_{{\alpha }_1^{{\delta }_{SC-2}}},{\mathsf{\Xi }}_{{\beta }_1^{{\delta }_{SC-2}}}\right],\\ \left(\begin{array}{c}\frac{2{\mathcal{T}}_{{ℂ}_{RP-1}}^{{\delta }_{SC-2}}}{{\left(2-{\mathcal{T}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC-2}}+{\mathcal{T}}_{{ℂ}_{RP-1}}^{{\delta }_{SC-2}}}{e}^{i2\pi \left(\frac{2{\mathcal{T}}_{{ℂ}_{IP-1}}^{{\delta }_{SC-2}}}{{\left(2-{\mathcal{T}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC-2}}+{\mathcal{T}}_{{ℂ}_{IP-1}}^{{\delta }_{SC-2}}}\right)},\\ \left(\frac{{\left(1+{ℱ}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC-2}}-{\left(1-{ℱ}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC-2}}}{{\left(1+{ℱ}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC-2}}+{\left(1-{ℱ}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC-2}}}{e}^{i2\pi \left(\frac{{\left(1+{ℱ}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC-2}}-{\left(1-{ℱ}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC-2}}}{{\left(1+{ℱ}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC-2}}+{\left(1-{ℱ}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC-2}}}\right)}\right)\end{array}\right)\\ (\begin{array}{c}\frac{2{\mathfrak{A}}_{{ℂ}_{RP-1}}^{{\delta }_{SC-1}}}{{\left(2-{\mathfrak{A}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC-1}}+{\mathfrak{A}}_{{ℂ}_{RP-1}}^{{\delta }_{SC-1}}}{e}^{i2\pi \left(\frac{2{\mathfrak{A}}_{{ℂ}_{IP-1}}^{{\delta }_{SC-1}}}{{\left(2-{\mathfrak{A}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC-1}}+{\mathfrak{A}}_{{ℂ}_{IP-1}}^{{\delta }_{SC-1}}}\right)},\\ \left(\frac{{\left(1+{\mathfrak{B}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC-1}}-{\left(1-{\mathfrak{B}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC-1}}}{{\left(1+{\mathfrak{B}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC-1}}+{\left(1-{\mathfrak{B}}_{{ℂ}_{RP-1}}\right)}^{{\delta }_{SC-1}}}\right)e^{i2\pi \left(\frac{{\left(1+{\mathfrak{B}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC-1}}-{\left(1-{\mathfrak{B}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC-1}}}{{\left(1+{\mathfrak{B}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC-1}}+{\left(1-{\mathfrak{B}}_{{ℂ}_{IP-1}}\right)}^{{\delta }_{SC-1}}}\right)}\end{array}\end{array})\end{array}$$

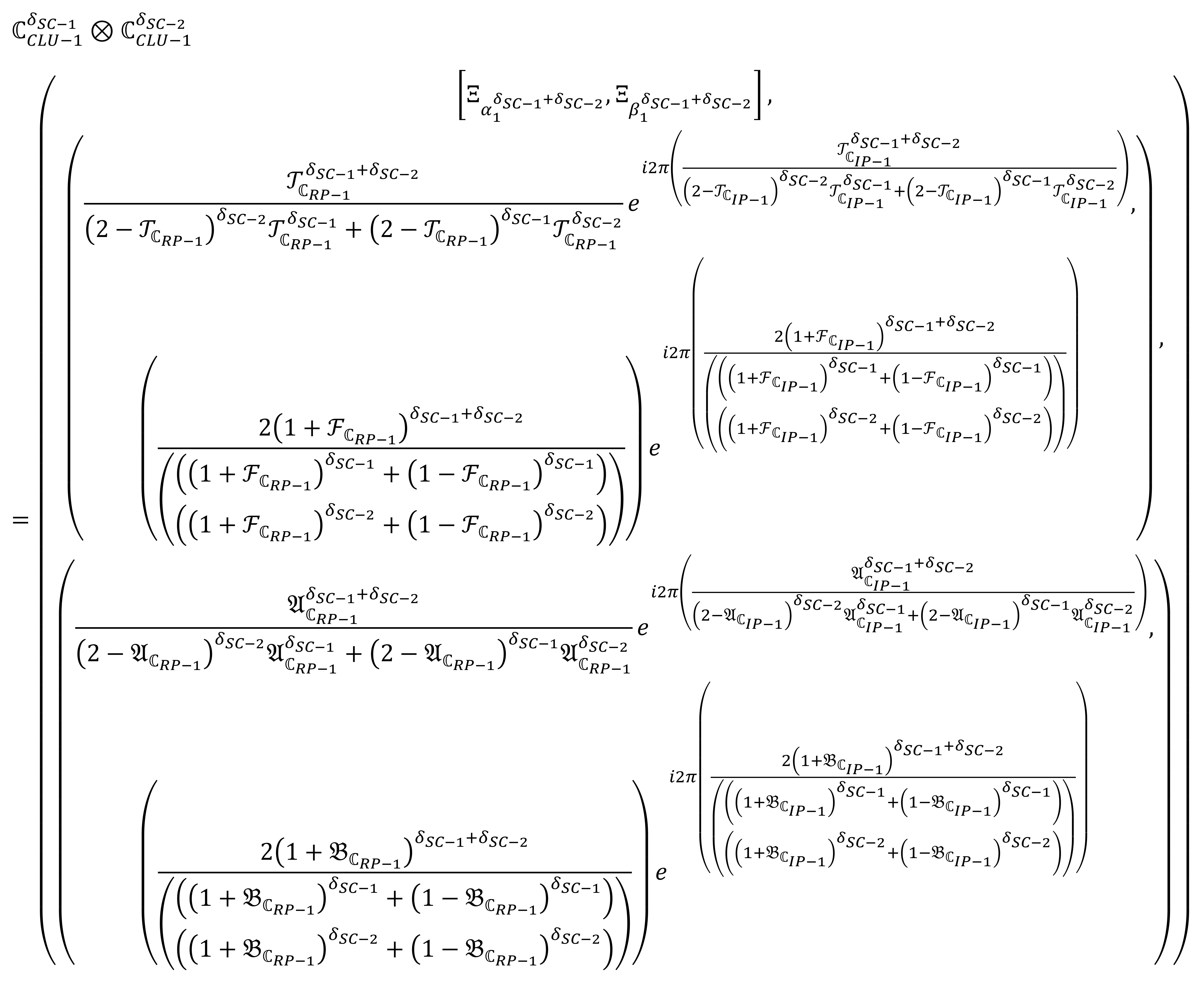
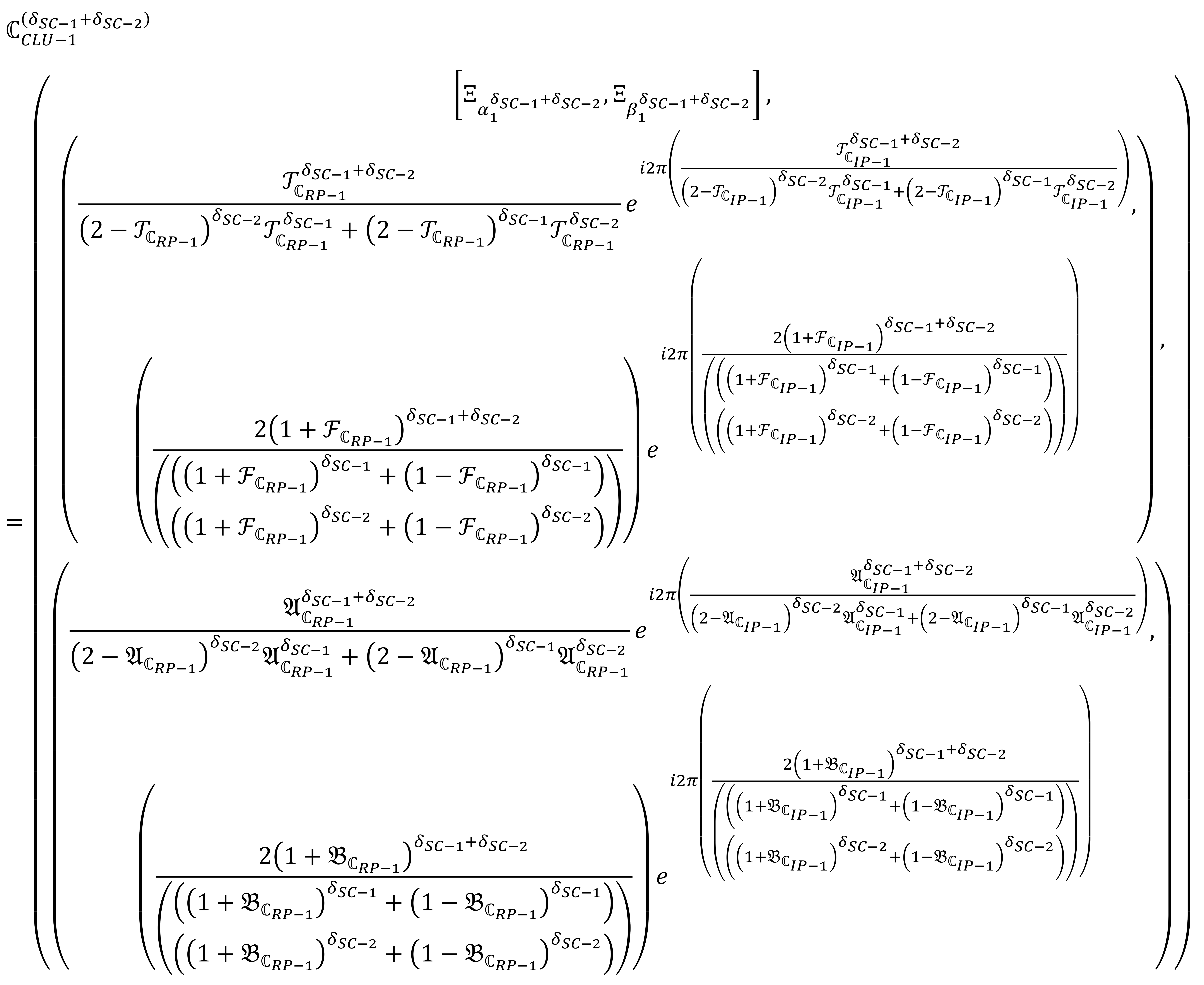
As shown above, we get the results ${ℂ}_{CLU-1}^{{\delta }_{SC-1}}\otimes {ℂ}_{CLU-1}^{{\delta }_{SC-2}}={ℂ}_{CLU-1}^{\left({\delta }_{SC-1}+{\delta }_{SC-2}\right)}$. The proof of the part 6 is trivial. □

4. Complex Linear Diophantine Uncertain Linguistic Power Einstein Aggregation Operators

To determine the relation among the family of attributes, the power Einstein (PE) aggregation operators (PEAOs) are very useful to manage unreliable troubles in numerous issues. Then by using the PEAOs based on CLDULS is to elaborate the CLDULPEA, CLDULPEWA, CLDULPEG, CLDULPEWG operators, and their useful results are also elaborated with the help of some remarkable cases.

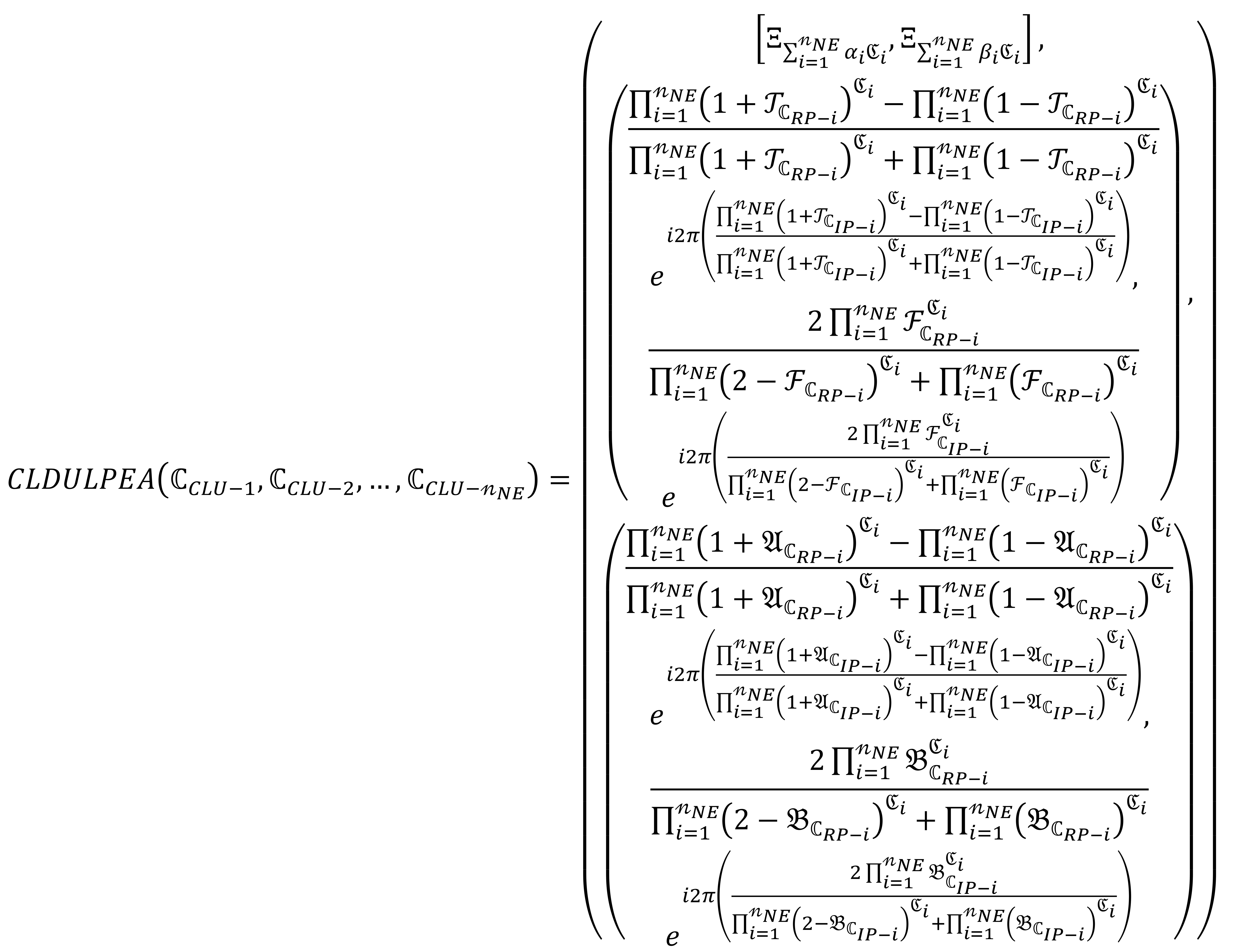
Definition 7.

By using any family of CLDULNs ${ℂ}_{CLU-i}=\left(\begin{array}{c}\left[{\Xi }_{{\alpha }_i},{\Xi }_{{\beta }_i}\right],\left({\mathcal{T}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathcal{T}}_{{ℂ}_{IP-i}}\right)},{\mathcal{F}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathcal{F}}_{{ℂ}_{IP-i}}\right)}\right),\\ \left({\mathfrak{U}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathfrak{U}}_{{ℂ}_{IP-i}}\right)},{\mathfrak{B}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathfrak{B}}_{{ℂ}_{IP-i}}\right)}\right)\end{array}\right),i=1,2,\dots ,{𝓃}_{NE}$, the CLDULPEA operator is initiated by:

$$\begin{gathered} LDULPEA\left({ℂ}_{CLU-1},{ℂ}_{CLU-2},\dots ,{ℂ}_{CLU-{𝓃}_{NE}}\right)=\frac{{\oplus }_{i=1}^{{𝓃}_{NE}}\left(\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right){ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)} \\ ={\oplus }_{i=1}^{{𝓃}_{NE}}\left(\frac{\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right){ℂ}_{CLU-i}}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}\right) \end{gathered}$$

(31)

where ${\mathbb{T}}^{LD}\left({ℂ}_{CF-i}\right)={\displaystyle \sum }_{j=1,i\ne j}^{{𝓃}_{NE}}\sup \left({ℂ}_{CLU-i},{ℂ}_{CLU-j}\right)$, where $\sup \left({ℂ}_{CLU-i},{ℂ}_{CLU-j}\right)$ is expressed the support for ${ℂ}_{CLU-i}$ and ${ℂ}_{CLU-j}$.

Theorem 2.

By using any family of CLDULNs${ℂ}_{CLU-i}=\left(\begin{array}{c}\left[{\Xi }_{{\alpha }_i},{\Xi }_{{\beta }_i}\right],\left({\mathcal{T}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathcal{T}}_{{ℂ}_{IP-i}}\right)},{\mathcal{F}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathcal{F}}_{{ℂ}_{IP-i}}\right)}\right),\\ \left({\mathfrak{U}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathfrak{U}}_{{ℂ}_{IP-i}}\right)},{\mathfrak{B}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathfrak{B}}_{{ℂ}_{IP-i}}\right)}\right)\end{array}\right),i=1,2,\dots ,{𝓃}_{NE}$, then by using the Equation (33), we get

(32)

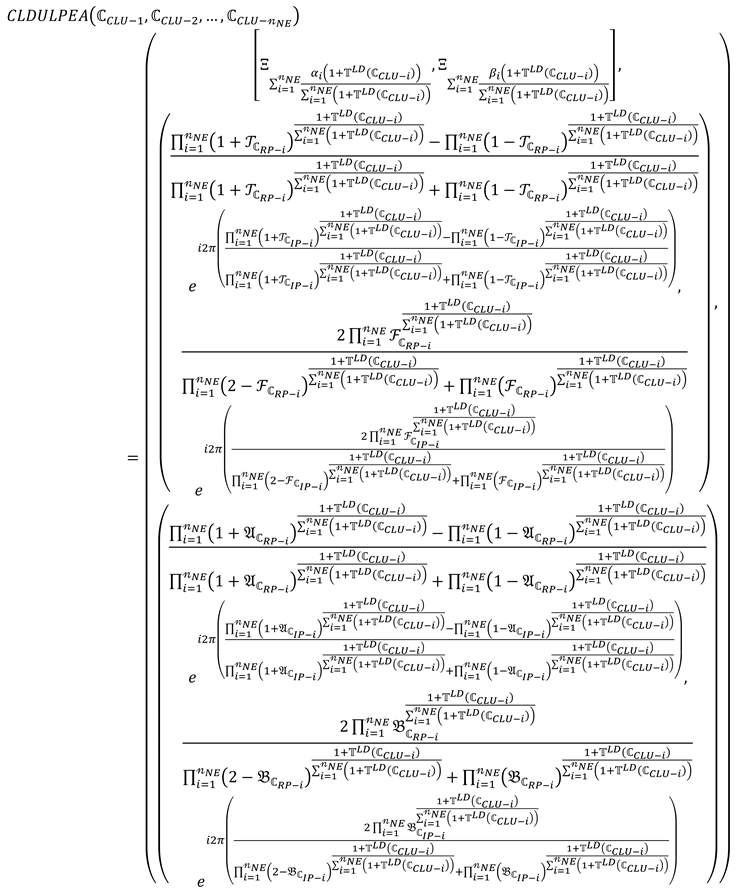where${\mathbb{T}}^{\mathrm{LD}}\left({ℂ}_{\mathrm{CF}-\mathrm{i}}\right)={\displaystyle \sum }_{\mathrm{j}=1,\mathrm{i}\ne \mathrm{j}}^{{𝓃}_{\mathit{NE}}}\sup \left({ℂ}_{\mathrm{CLU}-\mathrm{i}},{ℂ}_{\mathrm{CLU}-\mathrm{j}}\right)$, where$\sup \left({ℂ}_{\mathrm{CLU}-\mathrm{i}},{ℂ}_{\mathrm{CLU}-\mathrm{j}}\right)$is expressed the support for ${ℂ}_{\mathrm{CLU}-\mathrm{i}}$and${ℂ}_{\mathrm{CLU}-\mathrm{j}}$.

Proof of Theorem 2.

To prove the Equation (32), we fix that $\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}={ℭ}_i$, then the Equation (32) is initiated by:

(33)

By using mathematical induction, we will prove that the Equation (33). For ${𝓃}_{NE}$ = 1, the Equation (33) is trivial. Further, we choose the value of ${𝓃}_{NE}$ = k, then we get

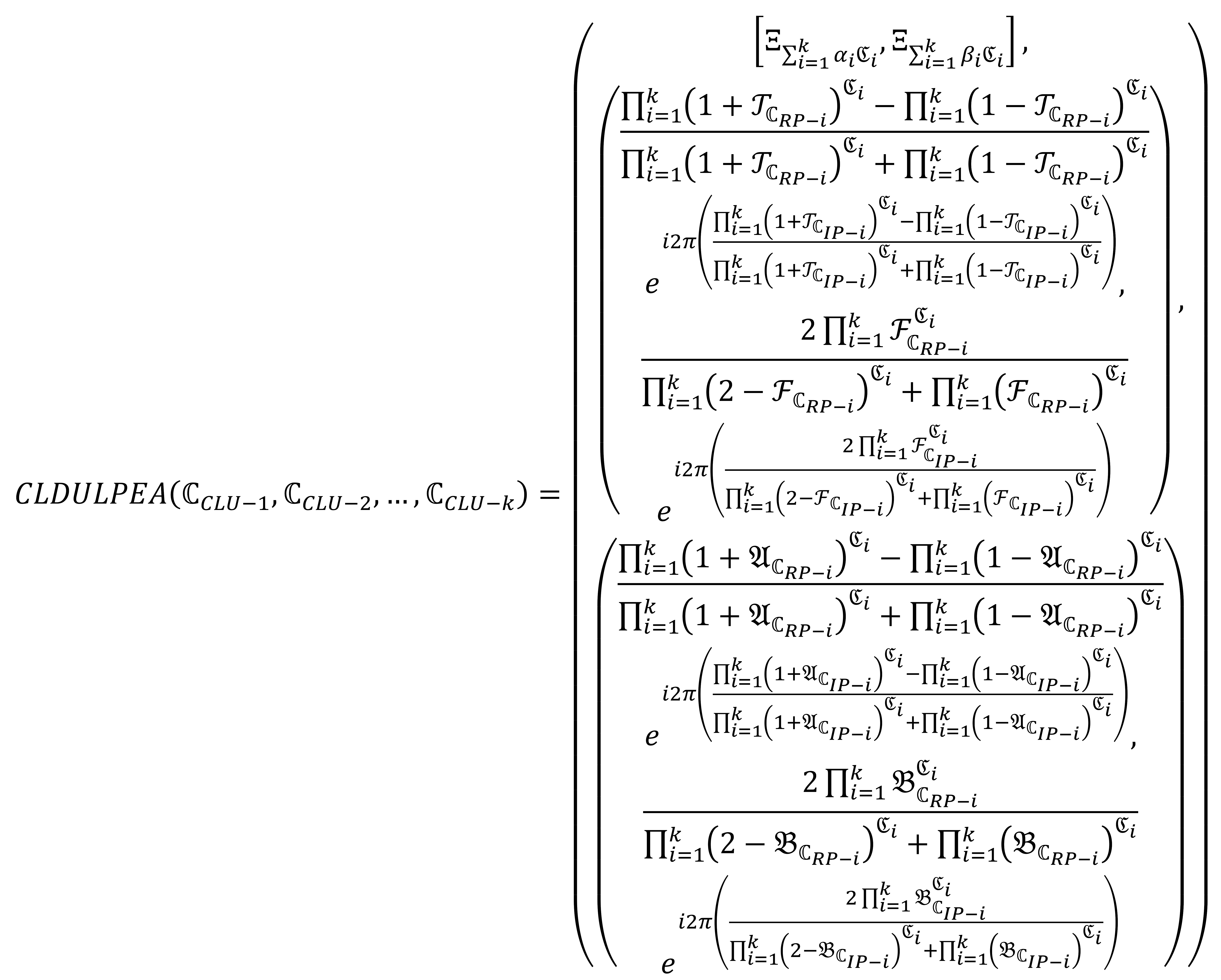
Then, by using the value of ${𝓃}_{NE}$ = k + 1, we prove that the Equation (33), such that $CLDULPEA\left({ℂ}_{CLU-1},{ℂ}_{CLU-2},\dots ,{ℂ}_{CLU-k+1}\right)=CLDULPEA\left({ℂ}_{CLU-1},{ℂ}_{CLU-2},\dots ,{ℂ}_{CLU-k+1}\right)\oplus {\mathfrak{C}}_{k+1}{\mathbb{C}}_{\mathit{CLU}-k+1}$

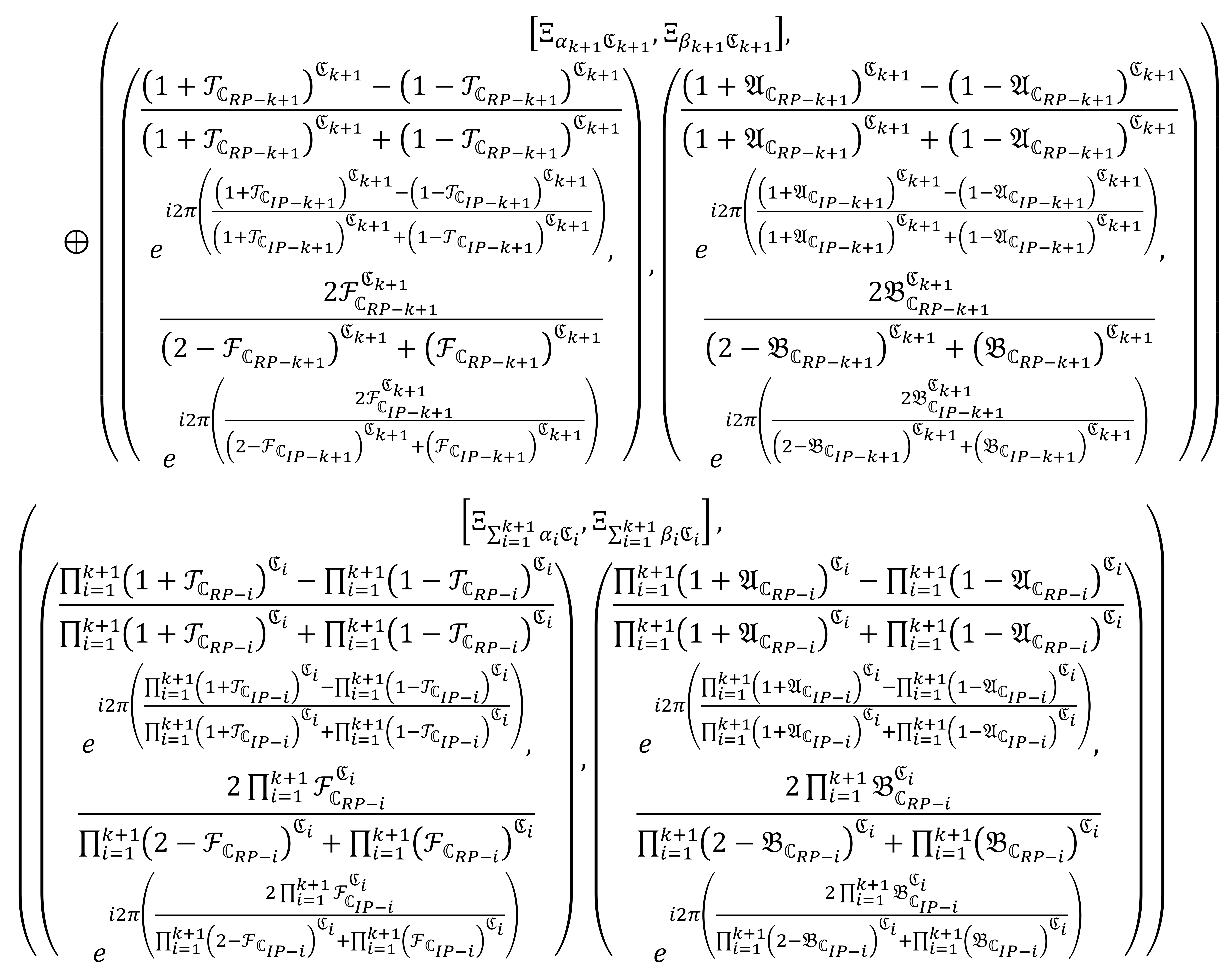
Hence, the Equation (33) is holds for all possible values of ${𝓃}_{NE}$.

Moreover, by using Equation (33), we discussed the following properties such as idempotency, boundedness, and monotonicity. □

Theorem 3.

By using any family of CLDULNs${ℂ}_{CLU-i}=\left(\begin{array}{c}\left[{\Xi }_{{\alpha }_i},{\Xi }_{{\beta }_i}\right],\left({\mathcal{T}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathcal{T}}_{{ℂ}_{IP-i}}\right)},{\mathcal{F}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathcal{F}}_{{ℂ}_{IP-i}}\right)}\right),\\ \left({\mathfrak{U}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathfrak{U}}_{{ℂ}_{IP-i}}\right)},{\mathfrak{B}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathfrak{B}}_{{ℂ}_{IP-i}}\right)}\right)\end{array}\right),i=1,2,\dots ,{𝓃}_{NE}$, if${ℂ}_{CLU-i}={ℂ}_{CLU}$, then

$$CLDULPEA\left({ℂ}_{CLU-1},{ℂ}_{CLU-2},\dots ,{ℂ}_{CLU-{𝓃}_{NE}}\right)={ℂ}_{CLU}$$

(34)

Proof of Theorem 3.

As shown above, we know that ${ℂ}_{CLU-i}={ℂ}_{CLU}$, that is ${\Xi }_{{\alpha }_i}={\Xi }_{\alpha },{\Xi }_{{\beta }_i}={\Xi }_{\beta },{\mathcal{T}}_{{ℂ}_{RP-i}}={\mathcal{T}}_{{ℂ}_{RP}},{\mathcal{T}}_{{ℂ}_{IP-i}}={\mathcal{T}}_{{ℂ}_{IP}},{\mathcal{F}}_{{ℂ}_{RP-i}}={\mathcal{F}}_{{ℂ}_{RP}},{\mathcal{F}}_{{ℂ}_{IP-i}}={\mathcal{F}}_{{ℂ}_{IP}}$ and ${\mathfrak{U}}_{{ℂ}_{RP-i}}={\mathfrak{U}}_{{ℂ}_{RP}},{\mathfrak{U}}_{{ℂ}_{IP-i}}={\mathfrak{U}}_{{ℂ}_{IP}},{\mathfrak{B}}_{{ℂ}_{RP-i}}={\mathfrak{B}}_{{ℂ}_{RP}},{\mathfrak{B}}_{{ℂ}_{IP-i}}={\mathfrak{B}}_{{ℂ}_{IP}}$, then

Theorem 4.

By using any family of CLDULNs${ℂ}_{CLU-i}=\left(\begin{array}{c}\left[{\Xi }_{{\alpha }_i},{\Xi }_{{\beta }_i}\right],\left({\mathcal{T}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathcal{T}}_{{ℂ}_{IP-i}}\right)},{\mathcal{F}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathcal{F}}_{{ℂ}_{IP-i}}\right)}\right),\\ \left({\mathfrak{U}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathfrak{U}}_{{ℂ}_{IP-i}}\right)},{\mathfrak{B}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathfrak{B}}_{{ℂ}_{IP-i}}\right)}\right)\end{array}\right),i=1,2,\dots ,{𝓃}_{NE}$, if${ℂ}_{CLU-max}=max\left({ℂ}_{CLU-1},{ℂ}_{CLU-2},\dots ,{ℂ}_{CLU-{𝓃}_{NE}}\right)$and${ℂ}_{CLU-min}=min\left({ℂ}_{CLU-1},{ℂ}_{CLU-2},\dots ,{ℂ}_{CLU-{𝓃}_{NE}}\right)$, then

$${ℂ}_{CLU-min}\le CLDULPEA\left({ℂ}_{CLU-1},{ℂ}_{CLU-2},\dots ,{ℂ}_{CLU-{𝓃}_{NE}}\right)\le {ℂ}_{CLU-max}$$

(35)

Proof of Theorem 4.

As shown above, we know that

Therefore,

$$\Rightarrow {\mathcal{T}}_{{ℂ}_{RP-max}}\ge \frac{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1+{\mathcal{T}}_{{ℂ}_{RP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}-{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1-{\mathcal{T}}_{{ℂ}_{RP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1+{\mathcal{T}}_{{ℂ}_{RP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}+{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1-{\mathcal{T}}_{{ℂ}_{RP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}\ge {\mathcal{T}}_{{ℂ}_{RP-min}}$$

Similarly, for unreal parts of the truth and real and unreal parts of the falsity grades such that

$$\Rightarrow {\mathcal{T}}_{{ℂ}_{IP-max}}\ge \frac{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1+{\mathcal{T}}_{{ℂ}_{IP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}-{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1-{\mathcal{T}}_{{ℂ}_{IP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1+{\mathcal{T}}_{{ℂ}_{IP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}+{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1-{\mathcal{T}}_{{ℂ}_{IP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}\ge {\mathcal{T}}_{{ℂ}_{IP-min}}$$

$$\Rightarrow {ℱ}_{{ℂ}_{RP-min}}\ge \frac{2{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{ℱ}_{{ℂ}_{RP-i}}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(2-{ℱ}_{{ℂ}_{RP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}+{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left({ℱ}_{{ℂ}_{RP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}\ge {ℱ}_{{ℂ}_{RP-max}}$$

$$\Rightarrow {ℱ}_{{ℂ}_{IP-min}}\ge \frac{2{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{ℱ}_{{ℂ}_{IP-i}}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(2-{ℱ}_{{ℂ}_{IP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}+{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left({ℱ}_{{ℂ}_{IP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}\ge {ℱ}_{{ℂ}_{IP-max}}$$

Similarly, we will find for the real and unreal parts of the reference’s parameters such that

$$\Rightarrow {\mathfrak{A}}_{{ℂ}_{RP-max}}\ge \frac{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1+{\mathfrak{A}}_{{ℂ}_{RP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}-{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1-{\mathfrak{A}}_{{ℂ}_{RP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}{\frac{}{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1+{\mathfrak{A}}_{{ℂ}_{RP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}+{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1-{\mathfrak{A}}_{{ℂ}_{RP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}}\ge {\mathfrak{A}}_{{ℂ}_{RP-min}}$$

$$\Rightarrow {\mathfrak{A}}_{{ℂ}_{IP-max}}\ge \frac{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1+{\mathfrak{A}}_{{ℂ}_{IP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}-{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1-{\mathfrak{A}}_{{ℂ}_{IP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}{\frac{}{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1+{\mathfrak{A}}_{{ℂ}_{IP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}+{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1-{\mathfrak{A}}_{{ℂ}_{IP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}}\ge {\mathfrak{A}}_{{ℂ}_{IP-min}}$$

$$\Rightarrow {\mathfrak{B}}_{{ℂ}_{RP-min}}\ge \frac{2{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\mathfrak{B}}_{{ℂ}_{RP-i}}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(2-{\mathfrak{B}}_{{ℂ}_{RP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}+{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left({\mathfrak{B}}_{{ℂ}_{RP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}\ge {\mathfrak{B}}_{{ℂ}_{RP-max}}$$

$$\Rightarrow {\mathfrak{B}}_{{ℂ}_{IP-min}}\ge \frac{2{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\mathfrak{B}}_{{ℂ}_{IP-i}}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(2-{\mathfrak{B}}_{{ℂ}_{IP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}+{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left({\mathfrak{B}}_{{ℂ}_{IP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}\ge {\mathfrak{B}}_{{ℂ}_{IP-max}}$$

Similarly, we determine the uncertain linguistic terms, such that

$$\Rightarrow {\Xi }_{{\alpha }_{min}}\le {\Xi }_{{\displaystyle \sum }_{i=1}^{{𝓃}_{NE}}\frac{{\alpha }_i\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}\le {\Xi }_{{\alpha }_{max}},\Rightarrow {\Xi }_{{\beta }_{min}}\le {\Xi }_{{\displaystyle \sum }_{i=1}^{{𝓃}_{NE}}\frac{{\beta }_i\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}\le {\Xi }_{{\beta }_{max}}$$

As shown above, we get the results, such that

$${ℂ}_{CLU-min}\le CLDULPEA\left({ℂ}_{CLU-1},{ℂ}_{CLU-2},\dots ,{ℂ}_{CLU-{𝓃}_{NE}}\right)\le {ℂ}_{CLU-max} \square$$

Theorem 5.

By using any two families of CLDULNs${ℂ}_{CLU-i}=\left(\begin{array}{c}\left[{\Xi }_{{\alpha }_i},{\Xi }_{{\beta }_i}\right],\left({\mathcal{T}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathcal{T}}_{{ℂ}_{IP-i}}\right)},{\mathcal{F}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathcal{F}}_{{ℂ}_{IP-i}}\right)}\right),\\ \left({\mathfrak{U}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathfrak{U}}_{{ℂ}_{IP-i}}\right)},{\mathfrak{B}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathfrak{B}}_{{ℂ}_{IP-i}}\right)}\right)\end{array}\right),i=1,2,\dots ,{𝓃}_{NE}$, and${ℂ}_{CLU-i}^{\ast }=\left(\begin{array}{c}\left[{\Xi }_{{\alpha }_i^{\ast }},{\Xi }_{{\beta }_i^{\ast }}\right],\left({\mathcal{T}}_{{ℂ}_{RP-i}}^{\ast }{e}^{i2\pi \left({\mathcal{T}}_{{ℂ}_{IP-i}}^{\ast }\right)},{\mathcal{F}}_{{ℂ}_{RP-i}}^{\ast }{e}^{i2\pi \left({\mathcal{F}}_{{ℂ}_{IP-i}}^{\ast }\right)}\right),\\ \left({\mathfrak{U}}_{{ℂ}_{RP-i}}^{\ast }{e}^{i2\pi \left({\mathfrak{U}}_{{ℂ}_{IP-i}}^{\ast }\right)},{\mathfrak{B}}_{{ℂ}_{RP-i}}^{\ast }{e}^{i2\pi \left({\mathfrak{B}}_{{ℂ}_{IP-i}}^{\ast }\right)}\right)\end{array}\right)$, if${ℂ}_{CLU-i}\le {ℂ}_{CLU-i}^{\ast }$, then

$$CLDULPEA\left({ℂ}_{CLU-1},{ℂ}_{CLU-2},\dots ,{ℂ}_{CLU-{𝓃}_{NE}}\right)\le CLDULPEA\left({ℂ}_{CLU-1}^{\ast },{ℂ}_{CLU-2}^{\ast },\dots ,{ℂ}_{CLU-{𝓃}_{NE}}^{\ast }\right)$$

(36)

Proof of Theorem 5.

As shown above, we know that ${ℂ}_{CLU-i}\le {ℂ}_{CLU-i}^{\ast }$ that is ${\Xi }_{{\alpha }_i}\le {\Xi }_{{\alpha }_i^{\ast }},{\Xi }_{{\beta }_i}\le {\Xi }_{{\beta }_i^{\ast }},{\mathcal{T}}_{{ℂ}_{RP-i}}\le {\mathcal{T}}_{{ℂ}_{RP}},{\mathcal{T}}_{{ℂ}_{IP-i}}\le {\mathcal{T}}_{{ℂ}_{IP}},{\mathcal{F}}_{{ℂ}_{RP-i}}\ge {\mathcal{F}}_{{ℂ}_{RP}},{\mathcal{F}}_{{ℂ}_{IP-i}}\ge {\mathcal{F}}_{{ℂ}_{IP}}$ and ${\mathfrak{U}}_{{ℂ}_{RP-i}}\le {\mathfrak{U}}_{{ℂ}_{RP}},{\mathfrak{U}}_{{ℂ}_{IP-i}}\le {\mathfrak{U}}_{{ℂ}_{IP}},{\mathfrak{B}}_{{ℂ}_{RP-i}}\ge {\mathfrak{B}}_{{ℂ}_{RP}},{\mathfrak{B}}_{{ℂ}_{IP-i}}\ge {\mathfrak{B}}_{{ℂ}_{IP}}$, then

$${\text{Ξ}}_{{\displaystyle \sum }_{i=1}^{{𝓃}_{NE}}\frac{{\alpha }_i\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}\le {\text{Ξ}}_{{\displaystyle \sum }_{i=1}^{{𝓃}_{NE}}\frac{{\alpha }_i^{*}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}},{\text{Ξ}}_{{\displaystyle \sum }_{i=1}^{{𝓃}_{NE}}\frac{{\beta }_i\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}\le {\text{Ξ}}_{{\displaystyle \sum }_{i=1}^{{𝓃}_{NE}}\frac{{\beta }_i^{*}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}$$

And similarly, for the real and unreal parts of truth and falsity grades, we have

$$\begin{array}{c}\frac{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1+{\mathcal{T}}_{{ℂ}_{RP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}-{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1-{\mathcal{T}}_{{ℂ}_{RP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1+{\mathcal{T}}_{{ℂ}_{RP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}+{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1-{\mathcal{T}}_{{ℂ}_{RP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}\\ \le \frac{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1+{\mathcal{T}}_{{ℂ}_{RP-i}}^{\ast }\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}-{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1-{\mathcal{T}}_{{ℂ}_{RP-i}}^{\ast }\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1+{\mathcal{T}}_{{ℂ}_{RP-i}}^{\ast }\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}+{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1-{\mathcal{T}}_{{ℂ}_{RP-i}}^{\ast }\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}\end{array}$$

and

$$\begin{array}{c}\frac{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1+{\mathcal{T}}_{{ℂ}_{IP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}-{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1-{\mathcal{T}}_{{ℂ}_{IP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1+{\mathcal{T}}_{{ℂ}_{IP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}+{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1-{\mathcal{T}}_{{ℂ}_{IP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}\\ \le \frac{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1+{\mathcal{T}}_{{ℂ}_{IP-i}}^{\ast }\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}-{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1-{\mathcal{T}}_{{ℂ}_{IP-i}}^{\ast }\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1+{\mathcal{T}}_{{ℂ}_{IP-i}}^{\ast }\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}+{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1-{\mathcal{T}}_{{ℂ}_{IP-i}}^{\ast }\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}\end{array}$$

$$\begin{array}{c}\frac{2{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\mathcal{F}}_{{ℂ}_{RP-i}}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(2-{\mathcal{F}}_{{ℂ}_{RP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}+{\displaystyle \prod }_{i=1}^{{𝓃}_{NE}}{\left({\mathcal{F}}_{{ℂ}_{RP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}\\ \ge \frac{2{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{{\mathcal{F}}^{\ast }}_{{ℂ}_{RP-i}}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(2-{\mathcal{F}}_{{ℂ}_{RP-i}}^{\ast }\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}+{\displaystyle \prod }_{i=1}^{{𝓃}_{NE}}{\left({\mathcal{F}}_{{ℂ}_{RP-i}}^{\ast }\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}\end{array}$$

and

$$\begin{array}{c}\frac{2{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\mathcal{F}}_{{ℂ}_{IP-i}}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(2-{\mathcal{F}}_{{ℂ}_{IP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}+{\displaystyle \prod }_{i=1}^{{𝓃}_{NE}}{\left({\mathcal{F}}_{{ℂ}_{IP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}\\ \ge \frac{2{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{{\mathcal{F}}^{\ast }}_{{ℂ}_{IP-i}}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(2-{\mathcal{F}}_{{ℂ}_{IP-i}}^{\ast }\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}+{\displaystyle \prod }_{i=1}^{{𝓃}_{NE}}{\left({\mathcal{F}}_{{ℂ}_{IP-i}}^{\ast }\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}\end{array}$$

With reference parameters

$$\begin{gathered} \frac{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1+{\mathfrak{A}}_{{ℂ}_{RP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}-{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1-{\mathfrak{A}}_{{ℂ}_{RP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1+{\mathfrak{A}}_{{ℂ}_{RP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}+{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1-{\mathfrak{A}}_{{ℂ}_{RP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}} \\ \le \frac{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1+{\mathfrak{A}}_{{ℂ}_{RP-i}}^{*}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}-{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1-{\mathfrak{A}}_{{ℂ}_{RP-i}}^{\ast }\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1+{\mathfrak{A}}_{{ℂ}_{RP-i}}^{\ast }\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}+{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1-{\mathfrak{A}}_{{ℂ}_{RP-i}}^{\ast }\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}} \end{gathered}$$

and

$$\begin{gathered} \frac{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1+{\mathfrak{A}}_{{ℂ}_{IP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}-{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1-{\mathfrak{A}}_{{ℂ}_{IP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1+{\mathfrak{A}}_{{ℂ}_{IP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}+{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1-{\mathfrak{A}}_{{ℂ}_{IP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}} \\ \le \frac{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1+{\mathfrak{A}}_{{ℂ}_{IP-i}}^{\ast }\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}-{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1-{\mathfrak{A}}_{{ℂ}_{IP-i}}^{\ast }\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1+{\mathfrak{A}}_{{ℂ}_{IP-i}}^{\ast }\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}+{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(1-{\mathfrak{A}}_{{ℂ}_{IP-i}}^{\ast }\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}} \end{gathered}$$

$$\begin{gathered} \frac{2{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\mathfrak{B}}_{{ℂ}_{RP-i}}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(2-{\mathfrak{B}}_{{ℂ}_{RP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}+{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left({\mathfrak{B}}_{{ℂ}_{RP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}} \\ \ge \frac{2{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\mathfrak{B}}^{\ast }{}_{{ℂ}_{RP-i}}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(2-{\mathfrak{B}}_{{ℂ}_{RP-i}}^{\ast }\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}+{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left({\mathfrak{B}}_{{ℂ}_{RP-i}}^{\ast }\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}} \end{gathered}$$

and

$$\begin{gathered} \frac{2{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\mathfrak{B}}_{{ℂ}_{IP-i}}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(2-{\mathfrak{B}}_{{ℂ}_{IP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}+{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left({\mathfrak{B}}_{{ℂ}_{IP-i}}\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}} \\ \ge \frac{2{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\mathfrak{B}}^{\ast }{}_{{ℂ}_{IP-i}}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}}{{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left(2-{\mathfrak{B}}_{{ℂ}_{IP-i}}^{\ast }\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}+{{\displaystyle \prod }}_{i=1}^{{𝓃}_{NE}}{\left({\mathfrak{B}}_{{ℂ}_{IP-i}}^{\ast }\right)}^{\frac{1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}}} \end{gathered}$$

From the above analysis, we get the results, such that

$$CLDULPEA\left({ℂ}_{CLU-1},{ℂ}_{CLU-2},\dots ,{ℂ}_{CLU-{𝓃}_{NE}}\right)\le CLDULPEA\left({ℂ}_{CLU-1}^{\ast },{ℂ}_{CLU-2}^{\ast },\dots ,{ℂ}_{CLU-{𝓃}_{NE}}^{\ast }\right) \square$$

Definition 8.

By using any family of CLDULNs ${ℂ}_{CLU-i}=\left(\begin{array}{c}\left[{\Xi }_{{\alpha }_i},{\Xi }_{{\beta }_i}\right],\left({\mathcal{T}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathcal{T}}_{{ℂ}_{IP-i}}\right)},{\mathcal{F}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathcal{F}}_{{ℂ}_{IP-i}}\right)}\right),\\ \left({\mathfrak{U}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathfrak{U}}_{{ℂ}_{IP-i}}\right)},{\mathfrak{B}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathfrak{B}}_{{ℂ}_{IP-i}}\right)}\right)\end{array}\right),i=1,2,\dots ,{𝓃}_{NE}$, the CLDULPEWA operator is initiated by:

$$\begin{gathered} CLDULPEWA\left({ℂ}_{CLU-1},{ℂ}_{CLU-2},\dots ,{ℂ}_{CLU-{𝓃}_{NE}}\right)=\frac{{\oplus }_{i=1}^{{𝓃}_{NE}}{w}_i\left(\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right){ℂ}_{CLU-i}\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}{w}_i\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)} \\ ={\oplus }_{i=1}^{{𝓃}_{NE}}\left(\frac{w_i\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right){ℂ}_{CLU-i}}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}{w}_i\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}\right) \end{gathered}$$

(37)

where ${\mathbb{T}}^{\mathrm{LD}}\left({ℂ}_{\mathrm{CF}-\mathrm{i}}\right)={\displaystyle \sum }_{\mathrm{j}=1,\mathrm{i}\ne \mathrm{j}}^{{𝓃}_{\mathit{NE}}}\sup \left({ℂ}_{\mathrm{CLU}-\mathrm{i}},{ℂ}_{\mathrm{CLU}-\mathrm{j}}\right)$, where $\sup \left({ℂ}_{\mathrm{CLU}-\mathrm{i}},{ℂ}_{\mathrm{CLU}-\mathrm{j}}\right)$ is expressed the support for ${ℂ}_{\mathrm{CLU}-\mathrm{i}}$ and ${ℂ}_{\mathrm{CLU}-\mathrm{j}}$ with weight vectors ${\mathfrak{w}}_{\mathrm{i}}$ such that $\mathfrak{w}=\left({\mathfrak{w}}_1,{\mathfrak{w}}_2,\dots ,{\mathfrak{w}}_{{\mathfrak{w}}_{\mathit{NE}}}\right)$ with a rule that is ${\displaystyle \sum }_{\mathrm{i}=1}^{{\mathfrak{w}}_{\mathit{NE}}}{\mathfrak{w}}_{\mathrm{i}}=1$.

Theorem 6.

By using any family of CLDULNs${ℂ}_{CLU-i}=\left(\begin{array}{c}\left[{\Xi }_{{\alpha }_i},{\Xi }_{{\beta }_i}\right],\left({\mathcal{T}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathcal{T}}_{{ℂ}_{IP-i}}\right)},{\mathcal{F}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathcal{F}}_{{ℂ}_{IP-i}}\right)}\right),\\ \left({\mathfrak{U}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathfrak{U}}_{{ℂ}_{IP-i}}\right)},{\mathfrak{B}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathfrak{B}}_{{ℂ}_{IP-i}}\right)}\right)\end{array}\right),i=1,2,\dots ,{𝓃}_{NE}$, then by using the Equation (37), we get

(38)

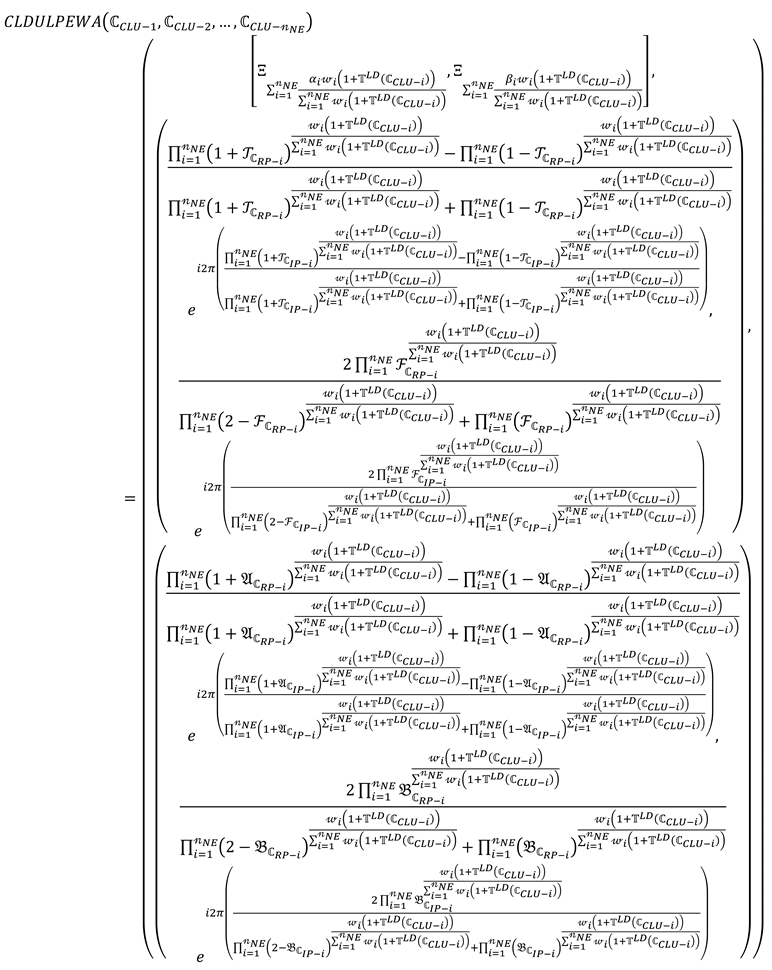where${\mathbb{T}}^{\mathrm{LD}}\left({ℂ}_{\mathrm{CF}-\mathrm{i}}\right)={\displaystyle \sum }_{\mathrm{j}=1,\mathrm{i}\ne \mathrm{j}}^{{𝓃}_{\mathit{NE}}}\sup \left({ℂ}_{\mathrm{CLU}-\mathrm{i}},{ℂ}_{\mathrm{CLU}-\mathrm{j}}\right)$, where$\sup \left({ℂ}_{\mathrm{CLU}-\mathrm{i}},{ℂ}_{\mathrm{CLU}-\mathrm{j}}\right)$is expressed the support for${ℂ}_{\mathrm{CLU}-\mathrm{i}}$and${ℂ}_{\mathrm{CLU}-\mathrm{j}}$with weight vectors$w_{\mathrm{i}}$such that$w=\left(w_1,w_2,\dots ,w_{{𝓃}_{\mathit{NE}}}\right)$with a rule that is${\displaystyle \sum }_{\mathrm{i}=1}^{{𝓃}_{\mathit{NE}}}{w}_{\mathrm{i}}=1$.

Proof of Theorem 6.

Trivial. □

Definition 9.

By using any family of CLDULNs ${ℂ}_{CLU-i}=\left(\begin{array}{c}\left[{\Xi }_{{\alpha }_i},{\Xi }_{{\beta }_i}\right],\left({\mathcal{T}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathcal{T}}_{{ℂ}_{IP-i}}\right)},{\mathcal{F}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathcal{F}}_{{ℂ}_{IP-i}}\right)}\right),\\ \left({\mathfrak{U}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathfrak{U}}_{{ℂ}_{IP-i}}\right)},{\mathfrak{B}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathfrak{B}}_{{ℂ}_{IP-i}}\right)}\right)\end{array}\right),i=1,2,\dots ,{𝓃}_{NE}$, the CLDULPEG operator is initiated by:

$$LDULPEG\left({ℂ}_{CLU-1},{ℂ}_{CLU-2},\dots ,{ℂ}_{CLU-{𝓃}_{NE}}\right)={\otimes }_{i=1}^{{𝓃}_{NE}}{ℂ}_{CLU-i}^{\left(\frac{\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}\right)}$$

(39)

where ${\mathbb{T}}^{\mathit{LD}}\left({ℂ}_{\mathit{CF}-\mathrm{i}}\right)={\displaystyle \sum }_{\mathrm{j}=1,\mathrm{i}\ne \mathrm{j}}^{{𝓃}_{\mathit{NE}}}\sup \left({ℂ}_{\mathit{CLU}-\mathrm{i}},{ℂ}_{\mathit{CLU}-\mathrm{j}}\right)$, where $\sup \left({ℂ}_{\mathit{CLU}-\mathrm{i}},{ℂ}_{\mathit{CLU}-\mathrm{j}}\right)$ is expressed the support for ${ℂ}_{\mathit{CLU}-\mathrm{i}}$ and ${ℂ}_{\mathit{CLU}-\mathrm{j}}$.

Theorem 7.

By using any family of CLDULNs${ℂ}_{CLU-i}=\left(\begin{array}{c}\left[{\Xi }_{{\alpha }_i},{\Xi }_{{\beta }_i}\right],\left({\mathcal{T}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathcal{T}}_{{ℂ}_{IP-i}}\right)},{\mathcal{F}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathcal{F}}_{{ℂ}_{IP-i}}\right)}\right),\\ \left({\mathfrak{U}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathfrak{U}}_{{ℂ}_{IP-i}}\right)},{\mathfrak{B}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathfrak{B}}_{{ℂ}_{IP-i}}\right)}\right)\end{array}\right),i=1,2,\dots ,{𝓃}_{NE}$, then by using the Equation (39), we get

(40)

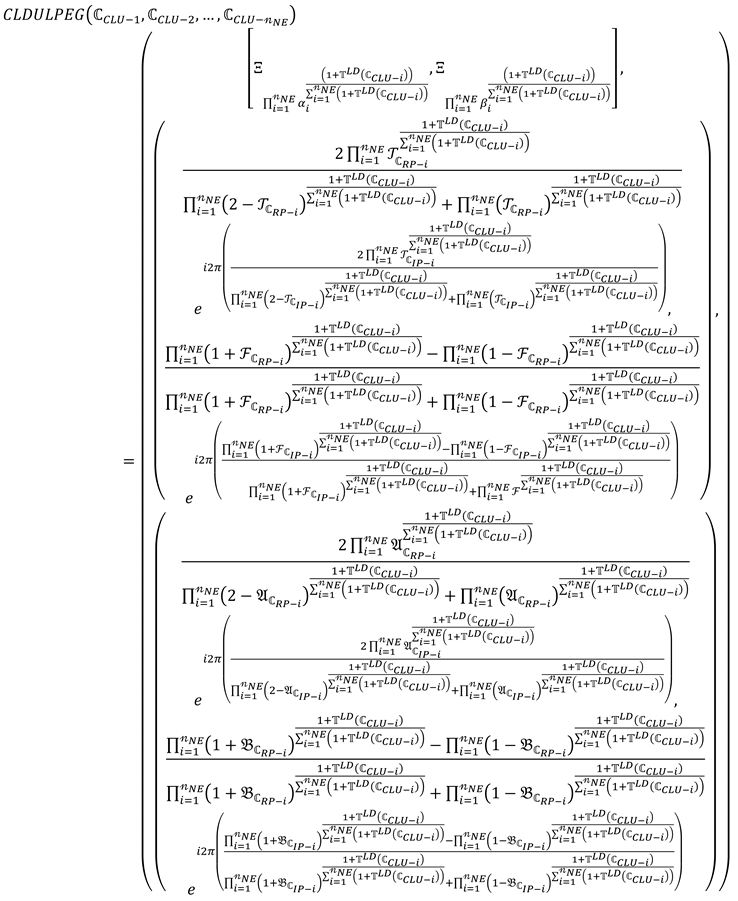where${\mathbb{T}}^{\mathit{LD}}\left({ℂ}_{\mathit{CF}-\mathrm{i}}\right)={\displaystyle \sum }_{\mathrm{j}=1,\mathrm{i}\ne \mathrm{j}}^{{𝓃}_{\mathit{NE}}}\sup \left({ℂ}_{\mathit{CLU}-\mathrm{i}},{ℂ}_{\mathit{CLU}-\mathrm{j}}\right)$, where$\sup \left({ℂ}_{\mathit{CLU}-\mathrm{i}},{ℂ}_{\mathit{CLU}-\mathrm{j}}\right)$ is expressed the support for${ℂ}_{\mathit{CLU}-\mathrm{i}}$and${ℂ}_{\mathit{CLU}-\mathrm{j}}$.

Proof of Theorem 7.

Trivial. □

Definition 10.

By using any family of CLDULNs ${ℂ}_{CLU-i}=\left(\begin{array}{c}\left[{\Xi }_{{\alpha }_i},{\Xi }_{{\beta }_i}\right],\left({\mathcal{T}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathcal{T}}_{{ℂ}_{IP-i}}\right)},{\mathcal{F}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathcal{F}}_{{ℂ}_{IP-i}}\right)}\right),\\ \left({\mathfrak{U}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathfrak{U}}_{{ℂ}_{IP-i}}\right)},{\mathfrak{B}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathfrak{B}}_{{ℂ}_{IP-i}}\right)}\right)\end{array}\right),i=1,2,\dots ,{𝓃}_{NE}$, the CLDULPEWG operator is initiated by:

$$CLDULPEWG\left({ℂ}_{CLU-1},{ℂ}_{CLU-2},\dots ,{ℂ}_{CLU-{𝓃}_{NE}}\right){\otimes }_{i=1}^{{𝓃}_{NE}}{ℂ}_{CLU-i}^{\left(\frac{w_i\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}{{{\displaystyle \sum }}_{i=1}^{{𝓃}_{NE}}{w}_i\left(1+{\mathbb{T}}^{LD}\left({ℂ}_{CLU-i}\right)\right)}\right)}$$

(41)

where ${\mathbb{T}}^{\mathrm{LD}}\left({ℂ}_{\mathrm{CF}-\mathrm{i}}\right)={\displaystyle \sum }_{\mathrm{j}=1,\mathrm{i}\ne \mathrm{j}}^{{𝓃}_{\mathrm{NE}}}\sup \left({ℂ}_{\mathrm{CLU}-\mathrm{i}},{ℂ}_{\mathrm{CLU}-\mathrm{j}}\right)$, where $\sup \left({ℂ}_{\mathrm{CLU}-\mathrm{i}},{ℂ}_{\mathrm{CLU}-\mathrm{j}}\right)$ is expressed the support for ${ℂ}_{\mathrm{CLU}-\mathrm{i}}$ and ${ℂ}_{\mathrm{CLU}-\mathrm{j}}$ with weight vectors $w_{\mathrm{i}}$ such that $w=\left(w_1,w_2,\dots ,w_{{𝓃}_{\mathit{NE}}}\right)$ with a rule that is ${\displaystyle \sum }_{\mathrm{i}=1}^{{𝓃}_{\mathrm{NE}}}{w}_{\mathrm{i}}=1$.

Theorem 8.

By using any family of CLDULNs${ℂ}_{CLU-i}=\left(\begin{array}{c}\left[{\Xi }_{{\alpha }_i},{\Xi }_{{\beta }_i}\right],\left({\mathcal{T}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathcal{T}}_{{ℂ}_{IP-i}}\right)},{\mathcal{F}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathcal{F}}_{{ℂ}_{IP-i}}\right)}\right),\\ \left({\mathfrak{U}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathfrak{U}}_{{ℂ}_{IP-i}}\right)},{\mathfrak{B}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathfrak{B}}_{{ℂ}_{IP-i}}\right)}\right)\end{array}\right),i=1,2,\dots ,{𝓃}_{NE}$, then by using the Equation (41), we get

(42)

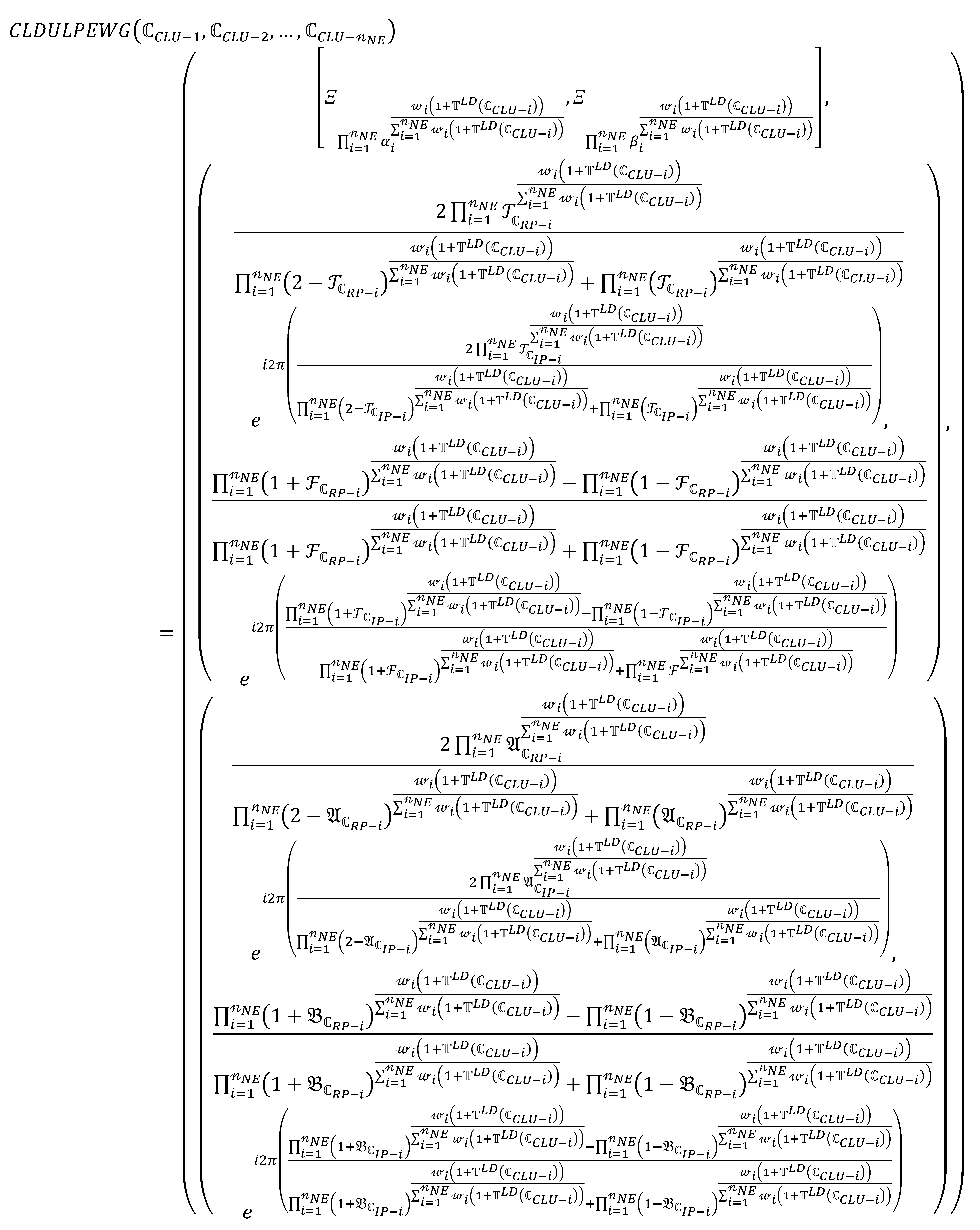where${\mathbb{T}}^{\mathit{LD}}\left({ℂ}_{\mathit{CF}-\mathrm{i}}\right)={\displaystyle \sum }_{\mathrm{j}=1,\mathrm{i}\ne \mathrm{j}}^{{𝓃}_{\mathit{NE}}}\sup \left({ℂ}_{\mathit{CLU}-\mathrm{i}},{ℂ}_{\mathit{CLU}-\mathrm{j}}\right)$, where$\sup \left({ℂ}_{\mathit{CLU}-\mathrm{i}},{ℂ}_{\mathit{CLU}-\mathrm{j}}\right)$is expressed the support for${ℂ}_{\mathit{CLU}-\mathrm{i}}$and${ℂ}_{\mathit{CLU}-\mathrm{j}}$with weight vectors$w_{\mathrm{i}}$such that$w=\left(w_1,w_2,\dots ,w_{{𝓃}_{\mathit{NE}}}\right)$with a rule that is${\displaystyle \sum }_{\mathrm{i}=1}^{{𝓃}_{\mathit{NE}}}{w}_{\mathrm{i}}=1$.

Proof of Theorem 8.

Trivial. □

Moreover, by using Equation (42), we discussed the following properties such as idempotency, boundedness, and monotonicity.

Theorem 9.

By using any family of CLDULNs${ℂ}_{CLU-i}=\left(\begin{array}{c}\left[{\Xi }_{{\alpha }_i},{\Xi }_{{\beta }_i}\right],\left({\mathcal{T}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathcal{T}}_{{ℂ}_{IP-i}}\right)},{\mathcal{F}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathcal{F}}_{{ℂ}_{IP-i}}\right)}\right),\\ \left({\mathfrak{U}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathfrak{U}}_{{ℂ}_{IP-i}}\right)},{\mathfrak{B}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathfrak{B}}_{{ℂ}_{IP-i}}\right)}\right)\end{array}\right),i=1,2,\dots ,{𝓃}_{NE}$, if${ℂ}_{CLU-i}={ℂ}_{CLU}$, then

$$CLDULPEWG\left({ℂ}_{CLU-1},{ℂ}_{CLU-2},\dots ,{ℂ}_{CLU-{𝓃}_{NE}}\right)={ℂ}_{CLU}$$

(43)

Proof of Theorem 9.

Trivial. □

Theorem 10.

By using any family of CLDULNs${ℂ}_{CLU-i}=\left(\begin{array}{c}\left[{\Xi }_{{\alpha }_i},{\Xi }_{{\beta }_i}\right],\left({\mathcal{T}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathcal{T}}_{{ℂ}_{IP-i}}\right)},{\mathcal{F}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathcal{F}}_{{ℂ}_{IP-i}}\right)}\right),\\ \left({\mathfrak{U}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathfrak{U}}_{{ℂ}_{IP-i}}\right)},{\mathfrak{B}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathfrak{B}}_{{ℂ}_{IP-i}}\right)}\right)\end{array}\right),i=1,2,\dots ,{𝓃}_{NE}$, if${ℂ}_{CLU-max}=\mathit{max}\left({ℂ}_{CLU-1},{ℂ}_{CLU-2},\dots ,{ℂ}_{CLU-{𝓃}_{NE}}\right)$and${ℂ}_{CLU-min}=\mathit{min}\left({ℂ}_{CLU-1},{ℂ}_{CLU-2},\dots ,{ℂ}_{CLU-{𝓃}_{NE}}\right)$, then

$${ℂ}_{CLU-min}\le CLDULPEWG\left({ℂ}_{CLU-1},{ℂ}_{CLU-2},\dots ,{ℂ}_{CLU-{𝓃}_{NE}}\right)\le {ℂ}_{CLU-max}$$

(44)

Proof of Theorem 10.

Trivial. □

Theorem 11.

By using any two families of CLDULNs${ℂ}_{CLU-i}=\left(\begin{array}{c}\left[{\Xi }_{{\alpha }_i},{\Xi }_{{\beta }_i}\right],\left({\mathcal{T}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathcal{T}}_{{ℂ}_{IP-i}}\right)},{\mathcal{F}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathcal{F}}_{{ℂ}_{IP-i}}\right)}\right),\\ \left({\mathfrak{U}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathfrak{U}}_{{ℂ}_{IP-i}}\right)},{\mathfrak{B}}_{{ℂ}_{RP-i}}{e}^{i2\pi \left({\mathfrak{B}}_{{ℂ}_{IP-i}}\right)}\right)\end{array}\right),i=1,2,\dots ,{𝓃}_{NE}$, and${ℂ}_{CLU-i}^{\ast }=\left(\begin{array}{c}\left[{\Xi }_{{\alpha }_i^{\ast }},{\Xi }_{{\beta }_i^{\ast }}\right],\left({\mathcal{T}}_{{ℂ}_{RP-i}}^{\ast }{e}^{i2\pi \left({\mathcal{T}}_{{ℂ}_{IP-i}}^{\ast }\right)},{\mathcal{F}}_{{ℂ}_{RP-i}}^{\ast }{e}^{i2\pi \left({\mathcal{F}}_{{ℂ}_{IP-i}}^{\ast }\right)}\right),\\ \left({\mathfrak{U}}_{{ℂ}_{RP-i}}^{\ast }{e}^{i2\pi \left({\mathfrak{U}}_{{ℂ}_{IP-i}}^{\ast }\right)},{\mathfrak{B}}_{{ℂ}_{RP-i}}^{\ast }{e}^{i2\pi \left({\mathfrak{B}}_{{ℂ}_{IP-i}}^{\ast }\right)}\right)\end{array}\right)$, if${ℂ}_{CLU-i}\le {ℂ}_{CLU-i}^{\ast }$, then

$$CLDULPEWG\left({ℂ}_{CLU-1},{ℂ}_{CLU-2},\dots ,{ℂ}_{CLU-{𝓃}_{NE}}\right)\le CLDULPEWG\left({ℂ}_{CLU-1}^{\ast },{ℂ}_{CLU-2}^{\ast },\dots ,{ℂ}_{CLU-{𝓃}_{NE}}^{\ast }\right)$$

(45)

Proof of Theorem 11.

Trivial. □

5. MADM Technique Based on Elaborated Operators

MADM procedure is one of the most important technique for finding the best optimal from the group of alternatives. Certain scholars have utilized it in the environment of different fields. Keeping the advantages of the decision-making procedure and by using complex linear Diophantine uncertain linguistic (CLDUL) information’s, a MADM procedure is developed based on PEAOs. For this, we choose the family of alternatives such that ${ℭ}_{CQ}=\left\{{ℭ}_{CQ-1},{ℭ}_{CQ-2},\dots ,{ℭ}_{CQ-\tilde{m}}\right\}$ and their attributes ${𝒞}_{CQ}=\left\{{𝒞}_{CQ-1},{𝒞}_{CQ-2},\dots ,{𝒞}_{CQ-\tilde{n}}\right\}$. For this we choose the weight vector whose expressions are follow as $w=\left\{w_1,w_2,\dots ,w_{{𝓃}_{NE}}\right\}$ with a rule that is the sum of all weight vector is equal to one i.e., ${\displaystyle \sum }_{i=1}^{{𝓃}_{NE}}{w}_i=1$. To cope with such type of case, the CLDULNs ${ℭ}_{CQ-ij}=\left(\begin{array}{c}\left[{\Xi }_{{\alpha }_{ij}},{\Xi }_{{\beta }_{ij}}\right],\left({\mathcal{T}}_{{ℂ}_{RP-ij}}{e}^{i2\pi \left({\mathcal{T}}_{{ℂ}_{IP-ij}}\right)},{\mathcal{F}}_{{ℂ}_{RP-ij}}{e}^{i2\pi \left({\mathcal{F}}_{{ℂ}_{IP-ij}}\right)}\right),\\ \left({\mathfrak{U}}_{{ℂ}_{RP-ij}}{e}^{i2\pi \left({\mathfrak{U}}_{{ℂ}_{IP-ij}}\right)},{\mathfrak{B}}_{{ℂ}_{RP-ij}}{e}^{i2\pi \left({\mathfrak{B}}_{{ℂ}_{IP-ij}}\right)}\right)\end{array}\right)$ are considered. For coping with such kind of issues, the steps of the algorithm are summarized in the following ways:

• Step 1: By using the complex linear Diophantine uncertain linguistic information, we develop the decision matrix, such that

  $$D=\left[\begin{array}{ccccc}{ℭ}_{CQ-11}& {ℭ}_{CQ-12}& {ℭ}_{CQ-13}& \dots & {ℭ}_{CQ-1n}\\ {ℭ}_{CQ-21}& {ℭ}_{CQ-22}& {ℭ}_{CQ-23}& \dots & {ℭ}_{CQ-2n}\\ {ℭ}_{CQ-31}& {ℭ}_{CQ-32}& {ℭ}_{CQ-33}& \dots & {ℭ}_{CQ-3n}\\ \dots & \dots & \dots & \dots & \dots \\ {ℭ}_{CQ-m1}& {ℭ}_{CQ-m2}& {ℭ}_{CQ-m3}& \dots & {ℭ}_{CQ-mn}\end{array}\right]$$
• Step 2: To aggregate the developed decision matrix, we use the CLDULPEA, CLDULPEWA, CLDULPEG and CLDULPEWG operators.
• Step 3: To determine the score values of the aggregated values, we use the score function.
• Step 4: By using the score values, we rank to all alternatives is to examine the best optimal from the group of alternatives.

Example 1.

Consider a decision-making issue taking from Garg [28] about the decision of the best creation system. In it, expect that an association needs to make another thing and they are exploring the best unbiased to procure the most raised benefits. For this, in the wake of analyzing the market, they have pondered the four likely strategies after their starter screening and are described as follows:

•  ${ℭ}_{CQ-1}$: Produce a development adjusted to the incredible organizations.
•  ${ℭ}_{\mathrm{CQ}-2}$: Produce a development adjusted to the mid-level organizations.
•  ${ℭ}_{\mathrm{CQ}-3}$: Produce a development adjusted to the Low-level organizations.
•  ${ℭ}_{\mathrm{CQ}-4}$: Produce a development adjusted to all organizations.

To survey these, the association consider the down to earth factor the key for the next year. In light of these, they need to evaluate each system under the going with five general characteristics:

• ${𝒞}_{\mathrm{CQ}-1}$: Beneficial in the Influential circumstances.
• ${𝒞}_{\mathrm{CQ}-2}$: Beneficial in the mid circumstances.
• ${𝒞}_{\mathrm{CQ}-3}$: Beneficial in the long circumstances.
• ${𝒞}_{\mathrm{CQ}-4}$: Cost of the production plan.

From the above problems, we choose the decision-making algorithm whose steps are discussed below.

Step 1: First, we develop the decision matrix which contains the complex linear Diophantine uncertain linguistic information’s are discussed in the form of

Table 2. Original decision matrix, which contains the CLDULNs.

	${𝒞}_{CQ-1}$	${𝒞}_{CQ-2}$	${𝒞}_{CQ-3}$	${𝒞}_{CQ-4}$
${ℭ}_{CQ-1}$	$\left(\begin{array}{c}\left[{\Xi }_1,{\Xi }_2\right],\\ \left(\begin{array}{c}0.9e^{i2\pi \left(0.8\right)},\\ 0.8e^{i2\pi \left(0.7\right)}\end{array}\right),\\ \left(\begin{array}{c}0.5e^{i2\pi \left(0.4\right)},\\ 0.4e^{i2\pi \left(0.3\right)}\end{array}\right)\end{array}\right)$	$\left(\begin{array}{c}\left[{\Xi }_2,{\Xi }_3\right],\\ \left(\begin{array}{c}0.91e^{i2\pi \left(0.81\right)},\\ 0.81e^{i2\pi \left(0.71\right)}\end{array}\right),\\ \left(\begin{array}{c}0.51e^{i2\pi \left(0.41\right)},\\ 0.41e^{i2\pi \left(0.31\right)}\end{array}\right)\end{array}\right)$	$\left(\begin{array}{c}\left[{\Xi }_0,{\Xi }_1\right],\\ \left(\begin{array}{c}0.92e^{i2\pi \left(0.82\right)},\\ 0.82e^{i2\pi \left(0.72\right)}\end{array}\right),\\ \left(\begin{array}{c}0.52e^{i2\pi \left(0.42\right)},\\ 0.42e^{i2\pi \left(0.32\right)}\end{array}\right)\end{array}\right)$	$\left(\begin{array}{c}\left[{\Xi }_1,{\Xi }_4\right],\\ \left(\begin{array}{c}0.93e^{i2\pi \left(0.83\right)},\\ 0.83e^{i2\pi \left(0.73\right)}\end{array}\right),\\ \left(\begin{array}{c}0.53e^{i2\pi \left(0.43\right)},\\ 0.43e^{i2\pi \left(0.33\right)}\end{array}\right)\end{array}\right)$
${ℭ}_{CQ-2}$	$\left(\begin{array}{c}\left[{\Xi }_2,{\Xi }_3\right],\\ \left(\begin{array}{c}0.8e^{i2\pi \left(0.7\right)},\\ 0.7e^{i2\pi \left(0.6\right)}\end{array}\right),\\ \left(\begin{array}{c}0.3e^{i2\pi \left(0.3\right)},\\ 0.2e^{i2\pi \left(0.1\right)}\end{array}\right)\end{array}\right)$	$\left(\begin{array}{c}\left[{\Xi }_2,{\Xi }_4\right],\\ \left(\begin{array}{c}0.81e^{i2\pi \left(0.71\right)},\\ 0.71e^{i2\pi \left(0.61\right)}\end{array}\right),\\ \left(\begin{array}{c}0.31e^{i2\pi \left(0.31\right)},\\ 0.21e^{i2\pi \left(0.11\right)}\end{array}\right)\end{array}\right)$	$\left(\begin{array}{c}\left[{\Xi }_1,{\Xi }_3\right],\\ \left(\begin{array}{c}0.82e^{i2\pi \left(0.72\right)},\\ 0.72e^{i2\pi \left(0.62\right)}\end{array}\right),\\ \left(\begin{array}{c}0.32e^{i2\pi \left(0.32\right)},\\ 0.22e^{i2\pi \left(0.12\right)}\end{array}\right)\end{array}\right)$	$\left(\begin{array}{c}\left[{\Xi }_2,{\Xi }_2\right],\\ \left(\begin{array}{c}0.83e^{i2\pi \left(0.73\right)},\\ 0.73e^{i2\pi \left(0.63\right)}\end{array}\right),\\ \left(\begin{array}{c}0.33e^{i2\pi \left(0.33\right)},\\ 0.23e^{i2\pi \left(0.13\right)}\end{array}\right)\end{array}\right)$
${ℭ}_{CQ-3}$	$\left(\begin{array}{c}\left[{\Xi }_2,{\Xi }_4\right],\\ \left(\begin{array}{c}0.7e^{i2\pi \left(0.6\right)},\\ 0.5e^{i2\pi \left(0.4\right)}\end{array}\right),\\ \left(\begin{array}{c}0.4e^{i2\pi \left(0.3\right)},\\ 0.3e^{i2\pi \left(0.2\right)}\end{array}\right)\end{array}\right)$	$\left(\begin{array}{c}\left[{\Xi }_1,{\Xi }_4\right],\\ \left(\begin{array}{c}0.71e^{i2\pi \left(0.61\right)},\\ 0.51e^{i2\pi \left(0.41\right)}\end{array}\right),\\ \left(\begin{array}{c}0.41e^{i2\pi \left(0.31\right)},\\ 0.31e^{i2\pi \left(0.21\right)}\end{array}\right)\end{array}\right)$	$\left(\begin{array}{c}\left[{\Xi }_2,{\Xi }_3\right],\\ \left(\begin{array}{c}0.72e^{i2\pi \left(0.62\right)},\\ 0.52e^{i2\pi \left(0.42\right)}\end{array}\right),\\ \left(\begin{array}{c}0.42e^{i2\pi \left(0.32\right)},\\ 0.32e^{i2\pi \left(0.22\right)}\end{array}\right)\end{array}\right)$	$\left(\begin{array}{c}\left[{\Xi }_0,{\Xi }_4\right],\\ \left(\begin{array}{c}0.73e^{i2\pi \left(0.63\right)},\\ 0.53e^{i2\pi \left(0.43\right)}\end{array}\right),\\ \left(\begin{array}{c}0.43e^{i2\pi \left(0.33\right)},\\ 0.33e^{i2\pi \left(0.23\right)}\end{array}\right)\end{array}\right)$
${ℭ}_{CQ-4}$	$\left(\begin{array}{c}\left[{\Xi }_3,{\Xi }_4\right],\\ \left(\begin{array}{c}0.6e^{i2\pi \left(0.3\right)},\\ 0.2e^{i2\pi \left(0.1\right)}\end{array}\right),\\ \left(\begin{array}{c}0.2e^{i2\pi \left(0.2\right)},\\ 0.1e^{i2\pi \left(0.1\right)}\end{array}\right)\end{array}\right)$	$\left(\begin{array}{c}\left[{\Xi }_2,{\Xi }_4\right],\\ \left(\begin{array}{c}0.61e^{i2\pi \left(0.31\right)},\\ 0.21e^{i2\pi \left(0.11\right)}\end{array}\right),\\ \left(\begin{array}{c}0.21e^{i2\pi \left(0.21\right)},\\ 0.11e^{i2\pi \left(0.11\right)}\end{array}\right)\end{array}\right)$	$\left(\begin{array}{c}\left[{\Xi }_2,{\Xi }_3\right],\\ \left(\begin{array}{c}0.62e^{i2\pi \left(0.32\right)},\\ 0.22e^{i2\pi \left(0.12\right)}\end{array}\right),\\ \left(\begin{array}{c}0.22e^{i2\pi \left(0.22\right)},\\ 0.12e^{i2\pi \left(0.12\right)}\end{array}\right)\end{array}\right)$	$\left(\begin{array}{c}\left[{\Xi }_0,{\Xi }_4\right],\\ \left(\begin{array}{c}0.63e^{i2\pi \left(0.33\right)},\\ 0.23e^{i2\pi \left(0.13\right)}\end{array}\right),\\ \left(\begin{array}{c}0.23e^{i2\pi \left(0.23\right)},\\ 0.13e^{i2\pi \left(0.13\right)}\end{array}\right)\end{array}\right)$

, such that

Step 2: Based on the proposed CLDULPEWA operator, we aggregate the decision matrix by using the weight vector $\left(0.3,0.3,0.3,0.1\right)$, then the final aggregated values are discussed in the form of

Table 3. Aggregated values by using PE aggregation operators.

	$CLDULPEWA Operator$
${ℭ}_{CQ-1}$	$\left(\begin{array}{c}\left[{\Xi }_{2.2324},{\Xi }_{3.2324}\right],\\ \left(\begin{array}{c}0.9124e^{i2\pi \left(0.8124\right)},\\ 0.8125e^{i2\pi \left(0.7125\right)}\end{array}\right),\\ \left(\begin{array}{c}0.5125e^{i2\pi \left(0.4125\right)},\\ 0.4125e^{i2\pi \left(0.3125\right)}\end{array}\right)\end{array}\right)$
${ℭ}_{CQ-2}$	$\left(\begin{array}{c}\left[{\Xi }_{2.2324},{\Xi }_{4.2324}\right],\\ \left(\begin{array}{c}0.8124e^{i2\pi \left(0.7124\right)},\\ 0.7123e^{i2\pi \left(0.6124\right)}\end{array}\right),\\ \left(\begin{array}{c}0.3124e^{i2\pi \left(0.3124\right)},\\ 0.2124e^{i2\pi \left(0.1125\right)}\end{array}\right)\end{array}\right)$
${ℭ}_{CQ-3}$	$\left(\begin{array}{c}\left[{\Xi }_{1.2635},{\Xi }_{4.3534}\right],\\ \left(\begin{array}{c}0.7135e^{i2\pi \left(0.6134\right)},\\ 0.5134e^{i2\pi \left(0.4142\right)}\end{array}\right),\\ \left(\begin{array}{c}0.4123e^{i2\pi \left(0.3144\right)},\\ 0.3134e^{i2\pi \left(0.2145\right)}\end{array}\right)\end{array}\right)$
${ℭ}_{CQ-4}$	$\left(\begin{array}{c}\left[{\Xi }_{2.464},{\Xi }_{4.4645}\right],\\ \left(\begin{array}{c}0.6123e^{i2\pi \left(0.3142\right)},\\ 0.2123e^{i2\pi \left(0.1156\right)}\end{array}\right),\\ \left(\begin{array}{c}0.2134e^{i2\pi \left(0.2155\right)},\\ 0.1156e^{i2\pi \left(0.1167\right)}\end{array}\right)\end{array}\right)$

, such that

Step 3: For finding the ranking values, we use the score function is to determine the score value of the aggregated values, which are discussed below.

$$\mathit{\text{CLDULPEWA}}\mathit{:} {\mathbb{S}}_{SV}\left({ℭ}_{CQ-1}\right)=0.5462,{\mathbb{S}}_{SV}\left({ℭ}_{CQ-2}\right)=0.8081,{\mathbb{S}}_{SV}\left({ℭ}_{CQ-3}\right)=0.8399,{\mathbb{S}}_{SV}\left({ℭ}_{CQ-4}\right)=1.1869$$

Step 4: By using the score values of the aggregated values, we discussed the ranking values of all alternatives is to examine the best one from the group of alternatives, such that

$${ℭ}_{CQ-4}\ge {ℭ}_{CQ-3}\ge {ℭ}_{CQ-2}\ge {ℭ}_{CQ-1}$$

As shown above, we get the best option is ${ℭ}_{CQ-4}.$ By using the information of CLDULSs, then the shortcoming theories are not able to survive with it, but if we choose the shortcoming sorts of theories such as FSs, CFSs, IFSs, CIFSs, PFSs, CPFSs, QROFSs, CQROFSs, and LDFSs, then the elaborated sorts of information are able to cope with it. Additionally, to express the validity of the elaborated operators, we choose the CLDULSs sorts of information resolve it by using the investigated operators in the form of Example 2.

Example 2 ([20]).

The information in this example is taken from Ref. [20], which contains four alternatives and three attributes in the form of supervisors. For this, the weighted vector is also discussed in Ref. [20]. By using the information of Tables 13–15 from Ref. [20], we determine the score values of the aggregated values of the information in Tables 13–15 are discussed below, under the elaborated CLDULPEWA operators, we have

$$\mathit{\text{CLDULPEWA}}\mathbf{:} {\mathbb{S}}_{SV}\left({ℭ}_{CQ-1}\right)=0.1474,{\mathbb{S}}_{SV}\left({ℭ}_{CQ-2}\right)=0.3542,{\mathbb{S}}_{SV}\left({ℭ}_{CQ-3}\right)=0.1546,{\mathbb{S}}_{SV}\left({ℭ}_{CQ-4}\right)=0.2970$$

By using the score values of the aggregated values, we discussed the ranking values of all alternatives is to examine the best one from the group of alternatives, such that

$${ℭ}_{CQ-2}\ge {ℭ}_{CQ-4}\ge {ℭ}_{CQ-3}\ge {ℭ}_{CQ-1}$$

As shown above, we get the best option is ${ℭ}_{CQ-2}.$

Comparative Analysis

The goal of this study, we analyze the legality of intended procedure, its tractability of aggregation to cope with distinct responses and productions, the impact of score values, compassion analysis, dominance and ultimately the assessment of suggested methodology with some prevailing procedures.

Validity and simplicity of the method: By using any sorts of information the elaborated operators based on CLDULNs are extensive valid and suitable to determine the consistency and validity of the elaborated operators. The elaborated operators are extensive suitable to manage with inconsistent and unreliable information in guanine life troubles. It is superior then the prevailing idea such as FSs, CFSs, IFSs, CIFSs, PFSs, CPFSs, QROFSs, and LDFSs with two extra grades are called reference parameters. To provides more range for TG and FG by altering the natural logic of these parameters are very useful to manage with awkward and complicated information’s we can utilize our version efficiently in various circumstances. Basically, the principle of CLDULSs is extensive powerful and more consistent to cope with such sorts of information which cannot resolve by prevailing theories. In certain MADM challenges, we are understanding dissimilar sorts of principles and response information corresponding to the offered circumstances. The planned CLDULS is straightforward and simple to recognize and can be utilized effortlessly on various sort of choices and characteristics.

To determine the reliability and dominance of the elaborated operators by using investigated and prevailing ideas with the help of comparative analysis. For this, we choose certain sorts of prevailing operators whose related information are discussed as follows: Riaz and Hashmi [20] elaborated the LDFS and their laws, Ali and Mahmood [36] elaborated the maclurin symmetric mean operators by using CQROFSs. The comparative analysis of the elaborated and prevailing operators is discussed in the form of

Table 4. Comparative analysis of the elaborated and prevailing operators by using Example 1.

Methods	Score Values	Ranking Values
Riaz and Hashmi [20]	Cannot be Calculated	Cannot be Calculated
Ali and Mahmood [36]	Cannot be Calculated	Cannot be Calculated
CLDULPEA operator	${\mathbb{S}}_{SV}\left({ℭ}_{CQ-1}\right)=0.5462,{\mathbb{S}}_{SV}\left({ℭ}_{CQ-2}\right)=0.8081,$ ${\mathbb{S}}_{SV}\left({ℭ}_{CQ-3}\right)=0.8399,{\mathbb{S}}_{SV}\left({ℭ}_{CQ-4}\right)=1.1869$	${ℭ}_{CQ-4}\ge {ℭ}_{CQ-3}\ge$ ${ℭ}_{CQ-2}\ge {ℭ}_{CQ-1}$
CLDULPEWA operator	${\mathbb{S}}_{SV}\left({ℭ}_{CQ-1}\right)=0.6573,{\mathbb{S}}_{SV}\left({ℭ}_{CQ-2}\right)=0.9192,$ ${\mathbb{S}}_{SV}\left({ℭ}_{CQ-3}\right)=0.9410,{\mathbb{S}}_{SV}\left({ℭ}_{CQ-4}\right)=1.2979$	${ℭ}_{CQ-4}\ge {ℭ}_{CQ-3}\ge$ ${ℭ}_{CQ-2}\ge {ℭ}_{CQ-1}$
CLDULPEG operator	${\mathbb{S}}_{SV}\left({ℭ}_{CQ-1}\right)=0.4351,{\mathbb{S}}_{SV}\left({ℭ}_{CQ-2}\right)=0.7071,$ ${\mathbb{S}}_{SV}\left({ℭ}_{CQ-3}\right)=0.7288,{\mathbb{S}}_{SV}\left({ℭ}_{CQ-4}\right)=1.0758$	${ℭ}_{CQ-4}\ge {ℭ}_{CQ-3}\ge$ ${ℭ}_{CQ-2}\ge {ℭ}_{CQ-1}$
CLDULPEWG operator	${\mathbb{S}}_{SV}\left({ℭ}_{CQ-1}\right)=0.3240,{\mathbb{S}}_{SV}\left({ℭ}_{CQ-2}\right)=0.6060,$ ${\mathbb{S}}_{SV}\left({ℭ}_{CQ-3}\right)=0.6177,{\mathbb{S}}_{SV}\left({ℭ}_{CQ-4}\right)=1.0647$	${ℭ}_{CQ-4}\ge {ℭ}_{CQ-3}\ge$ ${ℭ}_{CQ-2}\ge {ℭ}_{CQ-1}$

by using the information of Example 1.

Table 5. Comparative analysis of the elaborated and prevailing operators by using Example 2.

Methods	Score Values	Ranking Values
Riaz and Hashmi [20]	${\mathbb{S}}_{SV}\left({ℭ}_{CQ-1}\right)=0.1474,{\mathbb{S}}_{SV}\left({ℭ}_{CQ-2}\right)=0.3542,$ ${\mathbb{S}}_{SV}\left({ℭ}_{CQ-3}\right)=0.1546,{\mathbb{S}}_{SV}\left({ℭ}_{CQ-4}\right)=0.2970$	${ℭ}_{CQ-2}\ge {ℭ}_{CQ-4}\ge$ ${ℭ}_{CQ-3}\ge {ℭ}_{CQ-1}$
Ali and Mahmood [36]	Cannot be Calculated	Cannot be Calculated
CLDULPEA operator	${\mathbb{S}}_{SV}\left({ℭ}_{CQ-1}\right)=0.1474,{\mathbb{S}}_{SV}\left({ℭ}_{CQ-2}\right)=0.3542,$ ${\mathbb{S}}_{SV}\left({ℭ}_{CQ-3}\right)=0.1546,{\mathbb{S}}_{SV}\left({ℭ}_{CQ-4}\right)=0.2970$	${ℭ}_{CQ-2}\ge {ℭ}_{CQ-4}\ge$ ${ℭ}_{CQ-3}\ge {ℭ}_{CQ-1}$
CLDULPEWA operator	${\mathbb{S}}_{SV}\left({ℭ}_{CQ-1}\right)=0.2585,{\mathbb{S}}_{SV}\left({ℭ}_{CQ-2}\right)=0.4653,$ ${\mathbb{S}}_{SV}\left({ℭ}_{CQ-3}\right)=0.2657,{\mathbb{S}}_{SV}\left({ℭ}_{CQ-4}\right)=0.3981$	${ℭ}_{CQ-2}\ge {ℭ}_{CQ-4}\ge$ ${ℭ}_{CQ-3}\ge {ℭ}_{CQ-1}$
CLDULPEG operator	${\mathbb{S}}_{SV}\left({ℭ}_{CQ-1}\right)=0.0363,{\mathbb{S}}_{SV}\left({ℭ}_{CQ-2}\right)=0.2431,$ ${\mathbb{S}}_{SV}\left({ℭ}_{CQ-3}\right)=0.0435,{\mathbb{S}}_{SV}\left({ℭ}_{CQ-4}\right)=0.1860$	${ℭ}_{CQ-2}\ge {ℭ}_{CQ-4}\ge$ ${ℭ}_{CQ-3}\ge {ℭ}_{CQ-1}$
CLDULPEWG operator	${\mathbb{S}}_{SV}\left({ℭ}_{CQ-1}\right)=0.0252,{\mathbb{S}}_{SV}\left({ℭ}_{CQ-2}\right)=0.1320,$ ${\mathbb{S}}_{SV}\left({ℭ}_{CQ-3}\right)=0.0324,{\mathbb{S}}_{SV}\left({ℭ}_{CQ-4}\right)=0.0750$	${ℭ}_{CQ-2}\ge {ℭ}_{CQ-4}\ge$ ${ℭ}_{CQ-3}\ge {ℭ}_{CQ-1}$

shown the sensitive analysis of the elaborated and prevailing works for the data of Example 2.

As shown above, we known that the elaborated operators based on CLDULSs are extensive powerful and more useful than the prevailing ideas Refs. [20,36].

6. Conclusions

In this manuscript, we join the guideline of LDFS, ULS, and CFS is to expand the rule of CLDULS. CLDULS covers the grade of truth, deception, reference boundaries, and their unsure linguistic terms to achieve with off-kilter and complicated information in real life issues. Some functional laws by utilizing the explained CLDULSs are likewise settled. Moreover, by utilizing the PE collection administrators dependent on CLDULS is to expound the CLDULPEA, CLDULPEWA, CLDULPEG, CLDULPEWG administrators, and their valuable outcomes are additionally explained with the assistance of some noteworthy cases. Moreover, by utilizing the explained administrators dependent on CLDULS, a MADM problem. To decide the sanity and reliability of the explained administrators, some mathematical models are outlined. At last, the matchless quality and similar investigation of the expounded approaches with the assistance of graphical articulations are additionally evolved.

In the future, we will extend the idea of complex spherical fuzzy sets [52], T-spherical fuzzy sets [53], bipolar soft sets [37], Pythagorean m-polar fuzzy sets [54,55,56,57,58,59], and spherical fuzzy sets [60,61,62,63] are to improve the quality of the research works. By using these ideas, we will be also utilizing in the environment of pattern recognition, medical diagnosis, decision-making, Multiattribute decision-making, computer security threats, analysis of carcinoma/cancer, analysis of best crystalline solid based on melting and boiling points, and economics. The proposed CLDULS deal only with that information which covers the two grades truth and falsity like IFS, CIFS, PFS, CPFS, QROFS, CQROFSs, but when a decision provides information in the shape of picture fuzzy sets which covers the truth, abstinence, and falsity grades, then the picture fuzzy set is unable to cope with it. for coping with such types of issues, we will be proposed the theory of linear picture Diophantine fuzzy set, complex linear picture Diophantine fuzzy set, linear spherical Diophantine fuzzy set, complex linear spherical Diophantine fuzzy set, linear T-spherical Diophantine fuzzy set, complex spherical uncertain linguistic sets [63], and complex linear T-spherical Diophantine fuzzy set.