1. Introduction
Topology and decision-making have a long joint tradition since the modern statement of the classical Weierstrass Extreme Value Theorem. This result combines two topological notions, namely, the continuity of a real-valued function and the compactness of the domain (both with respect to a given topology). The success of this technique was amplified by its adoption in fields like mathematical economics. A most celebrated version for the maximization of binary relations is the Bergstrom–Walker theorem [
1,
2], stating that continuous acyclic relations defined on compact topological spaces possess maximal elements. These sufficient conditions are in fact necessary [
3].
Beyond the crisp setting, which is concerned with precise information, fuzzy set theory and other models of uncertain knowledge have given rise to new approaches to decision making since Zadeh’s pioneering work. Particularly, topological concepts have been merged with fuzzy set theory since Chang [
4] introduced fuzzy topology in 1968. This concept has been subsequently reformulated in renowned works like Goguen [
5] and Lowen [
6]. Topology has been combined with other models of vague knowledge too. Likewise, in 2011 Shabir and Naz [
7] launched soft topology, which amounts to its hybridization with soft set theory [
8]. Since then, many contributions have clarified the properties of soft topologies, whose performance has often been contrasted with the inspirational ideas from topology. For example, Das and Samanta [
9], Nazmul and Samanta [
10], and Zorlutuna et al. [
11] soon produced the notion of soft point which is helpful in the analysis of the properties of soft interior points and soft neighborhood systems. As separation axioms are classical elements for the investigation of topologies, their structures have been exported to soft topology since the seminal [
7]. Thus for example, El-Shafei et al. [
12], Al-shami and El-Shafei [
13], El-Shafei and Al-shami [
14], Hussain and Ahmad [
15], Min [
16], Terepeta [
17] and Al-shami et al. [
18] have investigated separation axioms in soft topology. Al-shami [
19] disclosed some relationships among different types of soft separation axioms and amended some alleged results given in previous studies. Soft connectedness is the subject of Hussain [
20]. Aygünoğlu and Aygün [
21] and Zorlutuna et al. [
11] promoted the study of soft compactness, and Al-shami et al. [
22] have recently defined novel classes of soft compact and Lindelöf spaces. Soft compactness and decision making are related by the properties of softarisons, in a result that reproduces the Weierstrass extreme value theorem in the framework of soft set theory [
23]. Kočinac et al. [
24] investigated Menger spaces in the context of soft sets. Separability axioms are another family of classical properties for topological research. It comes as no surprise that they are also becoming one of the important elements in the development of soft topology. They are being used to design well-behaved soft topologies in various forms [
25].
Some interesting relations of soft topology with set-theoretical topological structures have been put forward recently [
26]. In addition, other structures related to the combination of topology with the spirit of soft set theory have been proposed. Öztürk [
27] designed bipolar soft topological spaces with the inspiration of bipolar soft sets [
28]. Fuzzy soft topology has been studied since its introduction by Tanay and Kandemir [
29] (v., Roy and Samanta [
30] and Simsekler and Yuksel [
31] among other references). Riaz and Tehrim [
32] have put forward bipolar fuzzy soft topologies, Riaz et al. [
33] have introduced hesitant fuzzy soft topology, and Riaz et al. [
34] proposed
N-soft topology which builds on
N-soft sets (Fatimah et al. [
35]). Both papers have presented some applications to decision-making. Surely other hybridizations are yet to come, for example, topology with bipolar
N-soft set theory (Kamacı and Petchimuthu [
36]) or spherical fuzzy sets (Mahmood et al. [
37]).
Topological separability is not a universal concept. In the investigation of topological spaces that fail to satisfy this specific property, one can still check whether more general properties suffice to produce the required behavior. And the same argument applies to the notions of soft separability. With this motivation, this paper proposes some concepts that extend soft separability from very different perspectives, and then it studies their fundamental properties which make them valuable and worthy of further investigation. These new concepts are inspired by the notions of caliber of a topology, and the countable chain condition. We prove that they start a fruitful field of research with plenty of interactions among themselves and with respect to other soft topological properties.
This research paper consists of five sections.
Section 2 contains preliminary concepts from topology, soft set theory and soft topology.
Section 3 puts forward two novel soft topological concepts, namely, calibers and chain conditions. Examples defined by explicit constructions ensure that these notions are meaningful.
Section 4 proves our main results which concern the fundamental properties of the new axioms, inclusive of the fact that they are topological properties. We also investigate their relationships with other topological axioms. The goal of
Section 5 is to conclude our paper with a precise graphical summary of our main findings.
2.1. Elements of (Crisp) Topology
A topology
on the nonempty set
X is a collection of subsets of
X, called the open sets of
or the
-open sets, such that (1)
contains both
⌀ and
X, (2) the union of members of
(or open sets) belongs to
(or is an open set), and (3) the intersection of a finite number of members of
(or open sets) belongs to
(or is an open set). In this section we recall some fundamental topological concepts. For other notions in this field, we recommend Munkres [
38] and Willard [
39].
Let us fix a topology
on
X. Then a base for
is a collection of open sets such that each
is a union of members of the collection (cf., Willard ([
39], Definition 5.1)).
Topologies with countable bases are called second countable. Second countable topologies must be separable, that is, they must contain a countable and dense subset ([
39], Problem 5F). The next axioms are designed to weaken topological separability (hence second countability) in various forms. We shall be inspired by these properties and their performance in order to introduce novel axioms for soft topological spaces in
Section 3.
1. We say that
satisfies the countable chain condition, or CCC for short, if every disjoint family of
-open sets is countable. This family of pairwise disjoint open sets is also called a cellular open family [
40]. The countable chain condition is often called Suslin’s condition;
2. The topological space has caliber ℵ, a cardinal number, if whenever is a family of -open sets with cardinality ℵ, a subfamily with cardinality ℵ exists, such that .
Separability implies caliber
, which in turn implies CCC (cf., Willard ([
39], Problem 16C)). Therefore separability implies CCC; but the converse is not true (cf., Steen and Seebach ([
41], p. 22)).
2.2. Elements of Soft Set Theory and Soft Topology
Soft sets on the set
X consist of a pair
, where
E is composed of all the attributes that are needed to characterize the elements of
X, and
F is a mapping
Thus according to [
8], a soft set over
X is a parameterized family of subsets of
X. In mathematical terms, a soft set on
X is a multi-function (also called correspondence, point-to-set mapping, or multi-valued mapping)
F from the set of characteristics
E to
X. In this context, the set of all soft sets on
X will be expressed as
; when the set of attributes
E is common knowledge, we write
instead.
When , the set is a subset of X that is sometimes denoted as for higher accuracy.
Suppose that
is a soft set on
X such that
is finite (resp., countable) for each
. Then we say that
is a finite (resp., a countable) soft set on
X [
9,
10].
A soft set is frequently expressed as .
Two extreme examples are the null and the absolute or full soft sets on
X. The null soft set
satisfies
for all
. The absolute soft set
satisfies
for each
. Another special example of soft sets are soft points [
9,
11], which are soft sets
such that there are
and
with the property
and
when
. Such soft point shall be denoted as
. The reader should be aware that in the related literature, the term soft point is different: in [
17], it refers to
such that there is
with the property
for each
.
Many set-theoretic operations have been exported to soft set theory. For example, union, intersection, and inclusion are defined for
as follows [
42]: for any
,
- (1)
is the soft set such that for each .
This can also be written as when .
- (2)
is the soft set such that for each .
This can also be written as when .
- (3)
represents the property when .
Finally, each has a complement, which is the soft set such that for each .
Remark 1. The respective extensions of the concepts of union and intersection of two soft sets to arbitrary collections of soft sets are direct.
A concept of soft equality derives from soft inclusions. Thus means and . In other words, for all .
We say that are disjoint when . Clearly, disjoint non-empty soft sets are different (i.e., they are not soft equal).
The reader should be aware that different types of unions, intersections, and inclusions have been defined in the literature [
43,
44].
We are in a position to define soft topology on X (when the set of relevant characteristics is E). It consists of a family that satisfies the properties in the following definition:
Definition 1. [7,45] A soft topology τ on X is collection of soft sets on X, , that satisfies: - (1)
;
- (2)
The union of soft sets from τ is a member of τ;
- (3)
The intersection of a finite number of soft sets from τ is a member of τ.
Every member of τ is a soft open set, or τ-soft open set for better clarity.
When is a soft topology on X and E is the set of relevant characteristics, we sometimes write , and we call this triple a soft topological space.
Example 1. Some soft topologies on X have been defined by various scholars:
The indiscrete soft topology is , and the discrete soft topology is [7]. The cofinite soft topology was defined in [10] as
In addition to specific examples of soft topologies, two general procedures exist that generate soft topologies from crisp topologies. The first one is quite direct:
Definition 2. [17,25] Let be a collection of crisp topologies on X indexed by the set of attributes E. Then, defines a soft topology on X that is called the soft topology on X generated by Σ.
We can also write if for each .
Alcantud [
25] applies the construction above to prove that
, that is, the cofinite soft topology can be obtained from the cofinite crisp topology on
X, by the process in Definition 2.
The second procedure that generates soft topologies from crisp topologies relies on the behavior of soft open bases. Let us summarize some preliminary facts.
Remark 2. The soft topology given in Definition 2 was studied by Al-shami and Kočinac [46] under the name of extended soft topology. There is an equivalence between extended and enriched soft topologies ([46], Theorem 2): the soft topology τ is enriched if it contains all soft sets such that for each . An interchangeability property of the interior and closure operators between soft set and its components ([46], Theorem 3) is another important feature of these types of soft topologies. It has been used to study many properties in soft topological spaces using their counterparts in classical topological spaces and vice versa. Quite naturally, soft bases are defined as collections of soft sets that generate soft topologies by the proccess of selecting the set composed of the arbitrary soft unions of their elements. So
is a soft base for the soft topology
if we can express each
as a union of members of
[
45]. Roy and Samanta produced the more operative notion of a soft open base. Any soft open base can be used to generate a soft topology ([
47], Theorem 13) in such way that the soft open base is a soft base of the topology that it generates by this process ([
47], Theorem 16).
Alcantud ([
25], Proposition 1) proves that every base for a standard topology produces a soft open base by an explicit definition. Now a soft topology ensues from this soft open base ([
47], Theorem 13). Thus any base for a crisp topology defines an associated soft topology.
Notice that the two constructions of soft topologies defined above are closely related. Suppose that we fix a base for a crisp topology. We can produce both a crisp topology and a soft open base from it. Then we can apply Definition 2 to this crisp topology, and we can also produce a soft topology from the soft open base. The conclusion is that the respective soft topologies that we obtain are the same ([
25], Theorem 3).
Theoretical consequences follow from these constructions. For example, a soft topology is soft second-countable, or S2C for short, if a base for it exists that has a countable number of elements ([
9], Definition 4.32). Then, [
25],
Section 4 proves that Definition 2 produces a S2C soft topology, provided that each
is second-countable and
E is at most countable. Actually, a converse to this result holds true as well ([
25], Corollary 2).
It is also possible to combine soft topologies in order to produce new soft topological spaces, for example, as a sum of soft topological spaces [
48].
We now recall two related concepts defined in [
25]. Both concern adapted forms of topological separability for soft topological spaces.
Definition 3. [25] The soft topology τ on X is soft-points countably-dense, or SPCD for short, when a countable set of soft points exists that is soft τ-dense in X, and is soft τ-dense in X when for each , there is such that . Definition 4. [25] The soft topology τ on X is countably soft-set-dense, or CSD for short, when a countable soft set exists that is τ-soft dense in X. is τ-soft dense in X when for every , it must be the case that . There are arguments that avail of the fact that both SPCD and CS
D are good candidates for capturing separability-like axioms in the framework of soft topologies [
25]. In addition, S2C implies SPCD ([
25], Proposition 1), and SPCD implies CS
D ([
25], Lemma 2).
Any soft topology on a countable universe of discourse X is trivially SPCD therefore CSD.
In order to define properties that are preserved by suitable transformations, we need some previous definitions.
Definition 5. Ref. [49] Let us fix two mappings and . Then the pair defines a soft mapping as follows: when , is such that for each . Observe that, when is bijective, the expression defining reduces to for each and each .
Definition 6. Ref. [49] Let be a soft mapping associated with the pair . Then the pre-image of is such that for each . Definition 7. Ref. [11] A soft map is surjective (resp., injective, bijective) when both h and φ are surjective (resp., injective, bijective). Definition 8. Ref. [11] Suppose that τ and are soft topologies on X and Y, respectively. Then the soft map is: soft continuous, when implies ;
soft open when if ;
a soft homeomorphism when it is both soft continuous, soft open and bijective.
When a property is preserved by soft homeomorphisms, we say that it is a topological property.
3.1. Axioms in Soft Topology
The next definitions are directly inspired by the analogous concepts under the same name in crisp topology. We keep the terminology because the context suffices to distinguish between the crisp axioms (defined in
Section 2.1) and the soft axioms (that we introduce in this section). Anyhow some authors may prefer to add the adjective ‘soft’ to the terms in the new Definitions 9 to 11.
Definition 9. The soft topology τ on X has caliber ℵ, a cardinal number, if for each family formed by ℵ soft open sets, there is formed by ℵ soft open sets such that .
The next definition reformulates the concept of caliber of a soft topology:
Definition 10. The soft topology τ on X has caliber ℵ if for each family of pairwise different soft open sets and , there is with such that the subfamily satisfies .
To see why they are equivalent properties of a soft topology, observe first that the formulation of Definition 9 clearly implies Definition 10. Conversely, if satisfies Definition 10 then the Axiom of Choice allows us to ensure that it also satisfies Definition 9. Let us fix a family of soft open sets with ℵ members (which may be repeated). In order to avoid repetitions we apply the Axiom of Choice to select ℵ different members from the family, therefore without loss of generality we can assume and for each different . Now Definition 10 ensures the consequent in Definition 9.
The next section will show how the caliber of certain soft topological spaces can be found, provided that some properties are satisfied. Soft topological separability will be especially useful for that purpose.
We now define two properties in the same spirit. The next section will also prove that they are related to soft topological spaces with known calibers.
Definition 11. The soft topology τ on X satisfies:
1. The finite chain condition, FCC, if every family of disjoint soft open sets (i.e., such that holds when are members of the family) is finite;
2. The countable chain condition, CCC, if every family of disjoint soft open sets is countable.
There are trivial examples of soft topologies with the properties above. The indiscrete topology, and more generally, all soft hyperconnected topologies [
50] satisfy FCC because their only disjoint soft open sets are the null and absolute soft sets.
Section 4.1 proves to what extent the cardinalities of
X and
E ensure either FCC or at least CCC of any soft topology on
X.
3.2. Axioms in Soft Topology Derived from Topological Conditions
Definition 2 produces the soft topology generated by a family of crisp topologies (one for each attribute). It is often possible to prove that properties of the crisp topologies can be ‘transmitted’ to conveniently similar properties of the soft topology that they generate. In
Section 2.2 we have recalled some examples of this advantage of the construction given by Definition 2.
This section proves that results in this vein hold true also in the cases of calibers and chain conditions. We shall deduce that if the soft topology that a family of crisp topologies generates has any of the properties introduced in
Section 3.1, then these crisp topologies have the analogous behavior; and the converse is true when the cardinality of the set of attributes is not too high.
First we focus on calibers. A very neat statement explains what types of topologies can generate soft topologies with a given caliber:
Proposition 1. Let be a family of crisp topologies on X.
If the soft topology has caliber ℵ then has caliber ℵ, for each .
Proof. Let us fix . Suppose that is a family of -open sets whose cardinality is ℵ. By the Axiom of Choice, we can assume (informally: we delete all repeated elements in the family).
Let
be the family of pairwise different soft open sets in
defined as follows:
Then,
and we can appeal to Definition 10. Therefore there exists
with
such that the subfamily
satisfies
. Due to the construction of
, this fact warrants
, and the thesis follows. □
We proceed to investigate to what extent a converse of Proposition 1 can be stated. The sufficient conditions that we prove necessitate the finiteness of the set of attributes. Under this condition, our next result produces non-trivial examples of soft topological spaces that have caliber , and then Proposition 3 does the same with caliber :
Proposition 2. Suppose that E is finite. Suppose further that is a family of crisp topologies on X, each having caliber . Then the soft topology has caliber .
Proof. We appeal to Definition 10. Let be a family of pairwise different soft open sets in , with .
By construction, for each , is a family of -open sets. It must be the case that, for at least one , the corresponding family is countably infinite (i.e., it has countably many different members). Otherwise, the fact that E is finite would imply the contradiction that is finite too: notice that because the elements in are pairwise different.
We apply the assumption that has caliber in order to ensure the existence of such that and .
Now the thesis follows easily because . □
The proof of Proposition 2 can be replicated so as to prove the next variation, which allows us to design non-trivial soft topological spaces with caliber :
Proposition 3. Suppose that E is finite. Suppose further that is a family of crisp topologies on X, each having caliber . Then the soft topology has caliber .
Remark 3. Notice that we cannot extend the conclusion of Proposition 3 to infinite sets of attributes, because the countably infinite product of countable sets may not be countable. Thus, in the argument above, we cannot assure that one of the families has members when E is infinite.
Now we turn our attention to the countable chain condition. We can prove the following result with two targets. It ensures that the fact that the soft topology generated by a family of crisp topologies is CCC necessarily entails that each of these topologies is CCC. Furthermore, it provides an explicit construction of non-trivial soft topological spaces that satisfy CCC.
Proposition 4. Suppose that is a family of crisp topologies on X. The following properties hold true:
1. If is CCC, then is CCC for each ;
2. The soft topology satisfies CCC, provided that is CCC for each and E is countable.
Proof. We prove the first claim by contradiction. Suppose that, for some
, the topology
is not CCC. Then there is an uncountable family
of
-open sets that are pairwise disjoint. We can define the following uncountable family
of
-soft open sets that are pairwise disjoint:
This contradiction proves the claim.
In order to prove the second claim, let be a family of disjoint soft open sets in . We proceed to prove that must be countable. If we remove it from .
For each , the collection must be countable: notice that for each , the sets in the collection are disjoint because so is , and is CCC. Hence there is which is countable, such that if and only if .
Define the set
. Then
J is the union of countably many countable sets, since
E is countable and for each fixed
, the set
has the same cardinality as
. Therefore
J is countable (cf., Willard ([
39], 1.14 b))).
We appeal to the Axiom of Choice in order to select, for each , an with . By construction, .
Clearly, is injective because means that , therefore and .
Now the thesis
follows easily:
because
is injective (cf., ([
39], 1.12)), and
because
J is countable. □
4. Main Results
Our target in this Section is to investigate the properties of soft topologies introduced in
Section 3. To begin with, we focus on cardinality and its impact on FCC and CCC in the next subsection. Afterwards, we shall investigate more sophisticated sufficient conditions for the new properties to hold true. We also prove new relationships among soft topological properties. Finally, we formalize the fact that calibers (of a fixed cardinality), FCC and CCC are topological properties. These results will arise from a more general analysis of which types of mappings preserve these properties.
4.1. The Role of Cardinality in FCC and CCC
We proceed to argue that very simple cardinality conditions ensure the properties in Definition 11. The next Proposition 5 proves that if X and E are finite, resp. countable, then any soft topology on X satisfies FCC, resp. CCC. Examples 2 and 3 below assure that the assumptions in these two claims are tight, that is, we cannot dispense with any of them in the statement of Proposition 5. Afterwards we shall prove by examples that neither of these sufficient conditions are not necessary (cf., Example 4 below).
Proposition 5. If X and E are finite, resp. countable, then any soft topology on X satisfies FCC, resp. CCC.
Proof. The finite case is trivial, since is finite therefore is also finite.
Now suppose that X and E are countable. We proceed to prove that every family of disjoint soft sets on X is also countable, which in particular proves the claim that any soft topology on X satisfies CCC.
Let
be a family of disjoint soft sets on
X with attributes
E. We do not lose generality if we assume
: if
for some (and only one)
, we remove it from
. For each
, let us fix a pair
such that
. This can be done by the Axiom of Choice, because
. Consider the mapping
Then, we claim that is injective. To this purpose, observe that means that therefore by construction. However, and are disjoint when , therefore or equivalently, as desired.
Now the thesis follows easily because
is countable, being the product of two countable sets (cf., Willard ([
39], 1.14 c))). The reason is that because
is injective,
(cf., ([
39], 1.12)). □
Example 2. Neither of the two assumptions in the statement “when X and E are finite, FCC holds true” is redundant. Observe that:
1. does not satisfy FCC when X is finite but E is infinite.
Suppose and . The infinite family of -soft open sets withis formed by disjoint -soft open sets; 2. does not satisfy FCC when E is finite but X is infinite.
Suppose and . The infinite family of -soft open sets defined by for each is formed by disjoint -soft open sets.
Example 3. Neither of the two assumptions in the statement “when X and E are countable, CCC holds true” is redundant. Observe that:
1. does not satisfy CCC when X is countable but E is uncountable.
Suppose and . The uncountable family of -soft open sets withis formed by disjoint -soft open sets; 2. does not satisfy CCC when E is finite but X is uncountable.
Suppose and . The uncountable family of -soft open sets defined by for each is formed by disjoint -soft open sets.
Section 4.2 sets forth some relationships among known properties of soft topological spaces and the structures developed above. We also identify classes of spaces that satisfy the new properties stated in this section. As a consequence, we shall deduce that the set of conditions that Proposition 7 provides for FCC, resp. CCC, are not necessary.
Armed with these tools, in
Section 4.3 we shall produce new non-trivial examples of soft topological spaces that satisfy CCC.
4.2. Some Relationships among Properties
The proof of the next result is as simple as the crisp analogous:
Proposition 6. Suppose that the soft topology τ on X has caliber (resp., caliber ). Then τ satisfies FCC (resp., CCC).
Proof. We argue for the first statement, the second being a routine modification of it.
Suppose by contradiction that there exists an infinite family of pairwise disjoint soft open sets. By the Axiom of Choice, we select a countably infinite subfamily of non-empty, pairwise disjoint soft sets. Thus . Because has caliber , and disjoint non-empty soft sets are different, there is a subfamily with , , that satisfies in agreement with Definition 10. This is a contradiction because the soft sets are pairwise disjoint.
Consider now the second claim, which states that if has caliber then satisfies CCC. Suppose by contradiction that there exists an uncountably infinite family of pairwise disjoint soft open sets. By the Axiom of Choice, we can select an infinite subfamily of non-empty, pairwise disjoint soft sets whose cardinality is the first uncountable cardinal. Thus . Because has caliber , and disjoint non-empty soft sets are different, there is a subfamily with , , that satisfies in agreement with Definition 10. This is a contradiction because the soft sets are pairwise disjoint. □
Remark 4. Under the Continuum Hypothesis—which is independent from the Zermelo-Fraenkel axioms together with the axiom of choice— coincides with , which is the cardinality of the continuum (i.e., of ). Nevertheless, the argument that proves Proposition 6 is independent of whether we assume the Continuum Hypothesis or not. In other words, whether or is irrelevant to our purposes.
We now prove two propositions that show how properties related to the idea of “soft separability” permit us to identify the caliber of certain soft topological spaces.
Proposition 7. Suppose that E is finite. Suppose further that for the soft topology τ on X, there exists a finite that is τ-soft dense. Then τ has caliber .
Proof. The argument relies on cardinalities.
Let us fix a family of pairwise different soft open sets with . Without loss of generality we can also assume that is not one of the members of the family (if it is, we remove and we still have a family of pairwise different soft open sets with members).
Since is -soft dense, for each there is such that because .
Consider the mapping such that for each . Because , and E is finite, by cardinality we can assure the existence of such that . Let us define , then .
Because is finite and for each by construction, a similar cardinality argument guarantees that, for at least one , it must be the case that satisfies .
Notice that we have assured , thus proving . □
The gist of the argument in the proof of Proposition 7 is that a finite union of finite sets is finite. It is also true that the countable union of countable sets is a countable set. Therefore a routine modification of the proof of Proposition 7 produces the next statement:
Proposition 8. Suppose that E is countable. Suppose further that the soft topology τ on X is CSD. Then τ has caliber .
The next two Corollaries follow easily from the statements above in this section. Propositions 6 and 7 produce Corollary 1, whereas Propositions 6 and 8 produce Corollary 2:
Corollary 1. Suppose that E is finite. Suppose further that for the soft topology τ on X, there exists a finite that is τ-soft dense. Then τ satisfies FCC.
Corollary 2. Suppose that E is countable. Suppose further that for the soft topology τ on X is CSD. Then τ satisfies CCC.
It is now obvious that SPCD implies CCC when E is countable.
We take advantage of the relationships stated above to prove that although Proposition 7 gives a set of conditions that are sufficient for FCC, resp. CCC, they are by no means necessary: soft topological spaces that satisfy FCC (hence CCC) can be designed with arbitrarily large sets of options and attributes.
Example 4. Let us fix sets non-empty X and E, and an arbitrary element . Let be the particular point topology on X, that is, the open sets of are ⌀ and any subset of X that contains x.
Then, we claim that , the soft topology on X generated by according to Definition 2, satisfies the FCC thus the CCC, irrespective of the size of X or E.
We just need to observe that the finite soft set defined by for each is -soft dense (cf., Definition 4). Indeed, when and , there exists with the property ; therefore, . Now Corollary 1 applies.
4.3. A Construction of Soft Topologies That Satisfy CCC
So far, we have ensured that certain properties of soft topologies, or related to cardinalities, guarantee some performance in terms of calibers or chain conditions. Now we shall be more specific because we are fully aware that precise examples nourish the development of both topology and soft topology.
Our next result shows that the behavior of the soft topology defined in Definition 2 allows us to provide a concrete process that generates soft topologies that satisfy CCC:
Corollary 3. Suppose that E is countable. Suppose further that is a family of crisp topologies on X, and is separable for some . Then satisfies CCC.
Proof. The argument uses ([
25], Proposition 2), which ensures that
satisfies SPCD, therefore CS
D. The conclusion now follows from Corollary 2. □
Example 4 proves that FCC and CCC are not mere conditions of cardinality. Arbitrarily large universes of discourses and sets and attributes may be endowed with soft topologies that satisfy even FCC. We proceed to specialize the statement in Corollary 3 in order to design further examples of CCC soft topological spaces with an uncountably infinite universe of discourse X:
Example 5. Assume that E is countable. Let be the set all functions from to itself, whose cardinality is and is the cardinality of (hence ). This uncountable set endowed with the product topology of the Euclidean topologies is separable, being a product of a continuum of Hausdorff separable spaces (cf., Willard ([39], Theorem 16.4c))). Then satisfies CCC by Corollary 3.
4.4. Preservation of Properties by Mappings
To conclude this Section, we put forward some results on the preservation of properties when we transform a soft topological space by certain types of mappings. The next two propositions in particular prove that possessing a given caliber, FCC, and CCC are topological properties.
Proposition 9. The property of having a caliber number is preserved under bijective soft continuous mappings. In particular, having caliber ℵ is a topological property for each ℵ.
Proof. Suppose that is bijective soft continuous, and also that has caliber ℵ. In order to prove that has caliber ℵ, let be a family of pairwise different soft open sets in and . Since is soft continuous, then is a family of soft open sets in . It is easy to prove that they are pairwise different because is bijective. As has caliber ℵ, there is with such that the subfamily satisfies . Now, it is straightforward to check because is bijective. Therefore, we have proven that is a family of pairwise different soft open sets in as desired. □
Proposition 10. The finite (resp., countable) chain condition is preserved under bijective soft continuous mappings. In particular, they are topological properties.
Proof. Suppose that satisfy . It is easy to prove that, for any bijective soft mapping , the family has the same cardinality as . The fact that holds true too, as mentioned in the proof of Proposition 9.
Thus, when is a bijective soft continuous mapping and is a family of disjoint soft open sets, the family must be finite (resp. countable) when satisfies the finite (resp., countable) chain condition. This proves the claim because has the same cardinality as . □
5. Conclusions
This paper introduces the finite and countable chain conditions for soft topological spaces. We abbreviate them with FCC and CCC, respectively. They are designed to generalize the idea of soft separability while keeping a good theoretical performance. In passing, our results insist on the view that CSD and SPCD are important concepts in the investigation of separability issues in soft topology.
Considerations about cardinalities are quite relevant, although they do not exhaust the analysis of FCC and CCC. The reason is that soft topological spaces exist that satisfy FCC hence CCC, without restrictions to the sets of options and attributes (cf., Example 4).
Whenever cardinalities fail to ensure the required properties, calibers are a more advanced tool for the investigation of FCC and CCC. Calibers are a novel concept in the realm of soft topology. This paper proves that soft topological spaces with calibers or smaller satisfy CCC; if the caliber is then FCC holds true.
Explicit examples of the new concepts are presented in order to nurture their analysis and applications.
Let us summarize our main findings. Consider a soft topology .
- 1.
If on X has caliber (resp., caliber ) then satisfies FCC (resp., CCC): cf., Proposition 6;
- 2.
Suppose that E is finite.
(2.1) Then when X is finite, FCC holds true trivially.
(2.2) If this is not the case, but still there is a finite -soft dense set, then the caliber of is and in particular, FCC holds true as well.
(2.3) Observe that statement (2.1) is a particular case of (2.2), since a finite X ensures that the absolute soft set is a finite -soft dense set;
- 3.
Suppose instead that E is countable.
(3.1) Then when X is countable, CCC holds true: cf., Proposition 5.
(3.2) If this is not the case, but still there is a countable -soft dense set (i.e., is CSD), then the caliber of is (cf., Proposition 8) and in particular, CCC holds true as well.
(3.3) Again, statement (3.1) is a particular case of (3.2): notice that a countable X ensures that the collection of all soft points is soft -dense in X and of course it is countable, therefore satisfies SPCD and CSD.
Now consider the important example of , a soft topology that has been generated by , a family of crisp topologies. This fact is expressed as ;
- 4.
If has caliber ℵ then has caliber ℵ, for each : cf., Proposition 1;
- 5.
Suppose that E is finite. Then, when each has caliber , has caliber (v., Proposition 2) and, when each has caliber , has caliber (v., Proposition 3);
- 6.
If satisfies CCC then satisfies CCC, for each (v., part 1 of Proposition 4);
- 7.
Suppose that E is countable. Then when each satisfies CCC, satisfies CCC (v., part 2 of Proposition 4).
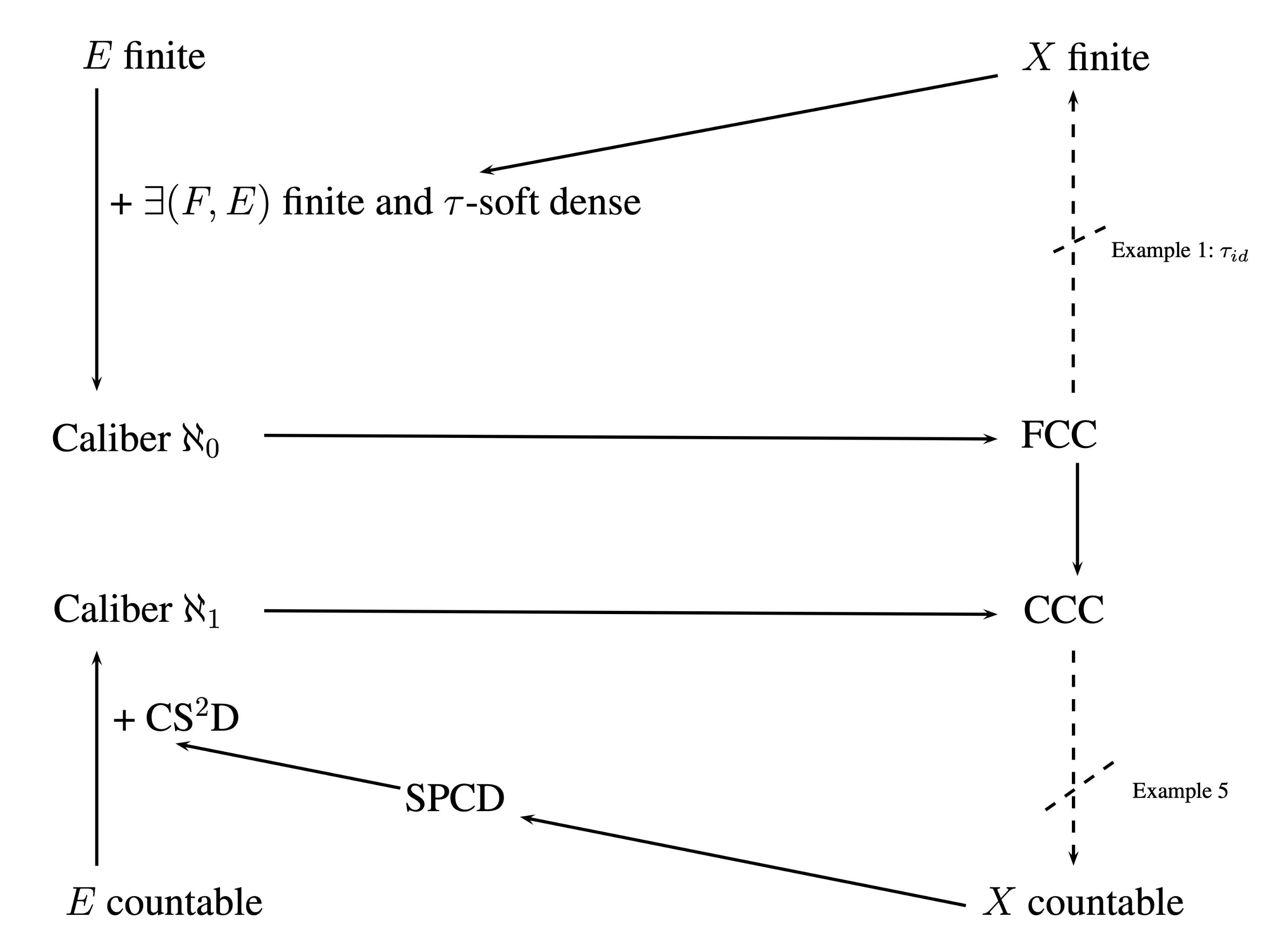
Figure 1 summarizes the results described above.