INF-GAN: Generative Adversarial Network for Illumination Normalization of Finger-Vein Images

Abstract

When images are acquired for finger-vein recognition, images with nonuniformity of illumination are often acquired due to varying thickness of fingers or nonuniformity of illumination intensity elements. Accordingly, the recognition performance is significantly reduced as the features being recognized are deformed. To address this issue, previous studies have used image preprocessing methods, such as grayscale normalization or score-level fusion methods for multiple recognition models, which may improve performance in images with a low degree of nonuniformity of illumination. However, the performance cannot be improved drastically when certain parts of images are saturated due to a severe degree of nonuniformity of illumination. To overcome these drawbacks, this study newly proposes a generative adversarial network for the illumination normalization of finger-vein images (INF-GAN). In the INF-GAN, a one-channel image containing texture information is generated through a residual image generation block, and finger-vein texture information deformed by the severe nonuniformity of illumination is restored, thus improving the recognition performance. The proposed method using the INF-GAN exhibited a better performance compared with state-of-the-art methods when the experiment was conducted using two open databases, the Hong Kong Polytechnic University finger-image database version 1, and the Shandong University homologous multimodal traits finger-vein database.

1. Introduction

Biometrics are replacing traditional authentication methods in several fields requiring security. Biometric identifiers include fingerprint, iris, face, and finger-vein. Biometrics using finger-vein have the following advantages [1]. (1) As veins are hidden inside the body, there is little risk of forgery or theft, and the surface conditions of the hands have no effect on authentication. (2) The use of infrared light allows for noninvasive, contactless imaging that ensures both convenience and cleanliness for the user experience. (3) Vein patterns are stable and clearly defined, allowing the use of low-resolution cameras to capture vein images for small-size, simple data image processing. As finger-vein images are captured using near-infrared (NIR) light when deoxygenated hemoglobin inside the vein absorbs NIR illumination [2], a blur may occur or low-quality images with poor illumination may be acquired due to the difference in thicknesses of fingers, the nonuniformity of illumination intensity, and light scattering as light passes through the skin layer [3,4]. Low-quality images due to blur or poor illumination, significantly affect the recognition performance; thus, with the advancements in deep-learning technology, extensive research is being conducted on finger-vein recognition using a convolutional neural network (CNN) [5,6]. For solving the problem of low-quality image recognition due to blur or nonuniform illumination in finger-vein images, various methods in which a blur is removed by restoring images or a vein pattern is restored using a generative adversarial network (GAN) have been studied [7,8]. Further, methods to ensure robust training through CNN recognition using a GAN in data augmentation have been studied [9]. However, the restoration of only optical blur was considered in the previous study [7]; the restoration method of focusing on a vein shape was difficult to apply to a severe case of nonuniformity of illumination where images were entirely or partially bright or dark due to nonuniform illumination in the previous study [8]. As in the previous study [9], performing data augmentation by adding random noise to input data is inappropriate for solving the problem of nonuniform illumination. Therefore, a method for restoring the severe nonuniformity of illumination based on a GAN for the illumination normalization of finger-vein images (INF-GAN) and for improving the performance of finger-vein recognition is proposed in this paper. The main contributions of our paper are as follows:

-

This study is the first to restore finger-vein images with nonuniform illumination using a GAN.

-

The INF-GAN is newly proposed for the restoration of a finger-vein image with nonuniform illumination.

-

The INF-GAN is based on the conventional Pix2Pix-HD, but uses a ResNet generator and only one PatchGAN discriminator, unlike the Pix2Pix-HD. A residual image-generation block (RIGB) is newly proposed for highlighting the vein texture of images distorted by the severe nonuniformity of illumination. In the INF-GAN, a one-channel residual image containing the finger-vein texture information is generated to be concatenated onto the input, thus improving the restoration performance. Furthermore, a feature encoder network was not used, unlike in Pix2Pix-HD.

-

For a fair performance assessment by other researchers, the nonuniform finger-vein images, INF-GAN, and algorithm proposed in this study are disclosed through [10].

The remainder of this paper is organized as follows. In Section 2, the previous studies are described, and the proposed method is described in Section 3. In Section 4, comparative experiments and experimental results with analysis are described. Finally, in Section 5, the conclusions of this study are provided.

2. Related Work

Finger-vein recognition can be largely divided into preprocessing, feature extraction, and recognition. During preprocessing, a region-of-interest (ROI) is extracted in addition to the enhancement, resizing, and alignment of finger-vein images for improving the performance of feature extraction and recognition to be performed subsequently. Feature extraction involves extracting a vein pattern or texture for recognition, and recognition involves determining the recognition decision based on the extracted features. Among the three processes, preprocessing can enhance image quality through image restoration or improve recognition performance by inducing the robust training of a recognition model through data augmentation. By focusing on the illumination quality of images, previous studies on finger-vein recognition were examined by dividing them into the cases of performing recognition without restoration or illumination compensation through robust training methods and the cases of performing recognition with restoration or after illumination compensation through robust training methods.

2.1. Finger-Vein Recognition without Illumination Compensation

Lee et al. [11] proposed a finger-vein recognition method based on the Hamming distance after performing feature extraction through minutia-based alignment and a local binary pattern (LBP). In the study, a finger region was localized for extracting the ROI in the image obtained through preprocessing, and the localized region was stretched for subsampling. Then, for aligning the subsampled image, affine transformation was applied to the minutia point of the subsampled image, and the LBP was used for extracting features. Song et al. [12] proposed a method in which a vein region is extracted through the mean curvature, and the finger-vein is recognized through a matched pixel ratio (MPR). In their study, the Laplacian kernel was used to detect the outline of a finger, and the features inside the vein region within the outline were extracted using the mean curvature to extract the ROI. For compensation of the misalignment due to in-plane rotation, which may occur during finger-vein image acquisition when recognizing the extracted features through the MPR, the input image was applied with an in-plane rotation of −10° to 10° in steps of 2° for matching for recognition. In previous studies [11,12], misalignment was corrected to a certain extent through in-plane rotation during minutia-based alignment and finger-vein matching, but there was no compensation for illumination.

Moreover, a similar level of performance cannot be expected when the same method is applied to the dataset acquired from a different environment, as the fitting method for the dataset used in the experiment is applied as a non-training-based method. Wu et al. [13] proposed a method for performing finger-vein recognition using a support vector machine (SVM) and adaptive neuro-fuzzy inference system (ANFIS) to overcome the drawbacks of non-training-based methods. In their study, images were cut and resized during preprocessing, and then features were extracted by reducing the dimension through principal component analysis (PCA) and linear discriminant analysis. The method proposed by Wu et al. can achieve more robust recognition compared with non-training-based methods. However, it still has a limitation in performance improvement, as feature extraction is a non-training-based method. Accordingly, studies are being conducted on deep-learning-based methods where both feature extraction and recognition are performed in a training-based manner to overcome such disadvantages. Hong et al. [5] suggested a training-based method for performing feature extraction and recognition using a CNN-based method. After extracting the ROI, the authors used the difference between the enrolled and target images as input to finetune the visual geometry group (VGG) Net-16 [14]. Thus, they performed feature extraction and recognition using training-based methods, which allowed more robust recognition against environmental factors compared with previous studies. However, the performance was substantially affected by image quality, as illumination was not compensated.

2.2. Finger-Vein Recognition with Illumination Compensation

When acquiring images for finger-vein recognition, the illumination quality of the images can change severely or weakly due to the difference in thicknesses of fingers, the nonuniformity of illumination intensity, or light scattering as light passes through the skin layer. The recognition performance can be improved through simple pixel normalization or by using a recognition model that is robust against illumination for weak changes in illumination intensity. Meanwhile, the recognition performance is difficult to improve without illumination restoration in the case of severe changes in illumination intensity. Therefore, previous studies were divided into the following two categories to be reviewed in this study.

2.2.1. Finger-Vein Recognition with Images Including Weak Nonuniformity of Illumination

Peng et al. [15] proposed a robust finger-vein recognition method in which the Gabor filter was used in eight directions to extract a vein pattern, and the features were extracted through fusion using the logical AND operator for the outputs where features were adequately extracted among the eight outputs. Then, the features were matched through the scale-invariant feature transform (SIFT). The Gaussian filter was used to remove noise, the Sobel filter was used to detect the edge region, and the ROI was extracted by resizing the respective region. Uneven illumination was compensated by normalizing pixel values through grayscale normalization. Van et al. [16] proposed a method in which features were extracted through the modified finite Radon transform (MFRAT) and GridPCA, and then the finger-vein was recognized using the Euclidean-distance-based k-nearest classifier. In this study, the edge region was detected using the Canny edge detector, and then the ROI was extracted by resizing the detected region. An orientation matrix was generated by applying the MFRAT to the extracted ROI, and a discriminant feature was created by encoding the matrix. The discriminant feature was generated in a feature with a reduced dimension through GridPCA, and the finger-vein was recognized using the k-nearest classifier. The advantage of the method proposed by Van et al. is that features that are robust against illumination and in-plane rotation can be obtained, as local invariant orientation features can be acquired through the MFRAT.

Qin et al. [17] suggested a recognition method for the fusion of finger-vein shape feature and orientation feature. The shape feature was extracted through the curvature of pixel difference, and the orientation feature was extracted through the difference curvature in two directions. Then, the shape feature and orientation feature were matched using the feature extracted through the SIFT. Then, the shape, orientation, and SIFT feature matching scores were combined through the weighted sum rule; recognition was then performed using the combined score as the input of an SVM. The recognition method proposed by Qin et al. is robust against noise, affine distortion, and illumination, as shape and orientation features are applied with fusion. Noh et al. [6] proposed a recognition method involving the score level fusion of the texture and shape of finger-veins using a CNN-based method. After detecting the finger region using the Sobel edge detection, the background was removed, and in-plane rotation compensation was applied to extract the ROI. The image was normalized through contrast-limited adaptive histogram equalization to detect only the shape region from the extracted ROI, and then only the shape region was extracted through repeated line tracking. The shape image was then created by applying dilation and erosion to the detected image. Using a model with two densely connected convolutional networks, DenseNet-161 [18], pretrained with the ImageNet database [19], texture and shape were finetuned using the three-channel composite image, where the enrolled and target images were mixed as input. After finetuning, the score from each model was applied with weighted-sum-rule-based fusion for recognition. Feature extraction and recognition were performed using the training-based method proposed by Noh et al., and the scores of shape feature and texture feature were applied with fusion for the recognition to be robust against image quality. The methods proposed in [6,15,16,17] are all illumination compensation methods. However, pixel normalization, robust feature extraction, and robust recognition through feature fusion have limitations in images that are distorted to be bright or dark due to the severe nonuniformity of illumination, where patterns are difficult to detect even after preprocessing.

2.2.2. Finger-Vein Recognition with Images Including Severe Nonuniformity of Illumination

In finger-vein images containing severe nonuniformity of illumination, the pattern of finger-vein shape or texture is difficult to detect even when pixels are normalized or contrast is adjusted during preprocessing, as the image is partially or entirely distorted to be bright or dark. The recognition performance is also poor, as a pattern is difficult to detect through robust feature extraction or recognition. To solve this problem, Lee et al. [4] proposed a method for enhancing image quality through hardware-based adaptive illumination when acquiring finger-vein images. The authors acquired finger-vein images with a default intensity and obtained an optimal image by adjusting the hardware-based illumination until an optimal value was obtained in the image evaluation using 2D entropy. However, this method requires additional hardware devices and cannot be used in a general finger-vein image acquisition device. Hence, this study newly proposes a method for restoring the severe nonuniformity of illumination based on the INF-GAN to improve the performance of finger-vein recognition, thus overcoming the drawbacks of previously mentioned methods. Table 1 presents the summaries of the proposed and previous studies on finger-vein recognition with or without illumination compensation.

Table 1. Summaries of the proposed and previous studies on finger-vein recognition with or without illumination compensation.

Category			Method	Advantage	Disadvantage
Without illumination compensation	Non-training-based		Minutia-based alignment and LBP [11]	Misalignment compensation through minutia-based alignment	Performance is affected by illumination quality, because there is no illumination compensation
			Mean curvature and MPR [12]	Misalignment compensation through in-plane rotation during finger-vein matching
	Training-based		ANFIS and SVM [13]	More robust recognition than non-training-based methods
			CNN with difference image [5]
With illumination compensation	Including weak nonuniformity of illumination	Non-training-based	Gabor filter and SIFT [15]	Illumination compensation through grayscale normalization	Recognition performance is difficult to improve in the case of severe nonuniformity of illumination
		Training-based	MFRAT, GridPCA, and k-nearest classifier [16]	Robust feature extraction through MFRAT
			Shape feature and orientation feature fusion [17]	Robust recognition through score-level feature fusion
			CNN with shape feature and texture feature using composite image and score level fusion [6]
	Including severe nonuniformity of illumination	Hardware-based	Hardware-based adaptive illumination [4]	Solves the problem of severe nonuniformity of illumination	Requires additional hardware devices and cannot be used in general finger-vein image acquisition devices
		Software-based (training-based)	INF-GAN-based illumination compensation (Proposed method)	Does not require additional hardware devices and can be used in general finger-vein image acquisition devices	Requires additional procedure of training of INF-GAN, including RIGB

3. Proposed Methods

3.1. Overview of the Proposed Method

Figure 1 shows the overall procedure of the proposed method. After obtaining finger-vein images, the finger ROI is detected through preprocessing. Using the INF-GAN proposed in this study, nonuniform illumination is restored. Then, a composite image is generated to be used as input for the CNN, and the final matching score is obtained through shift matching to perform finger-vein recognition.

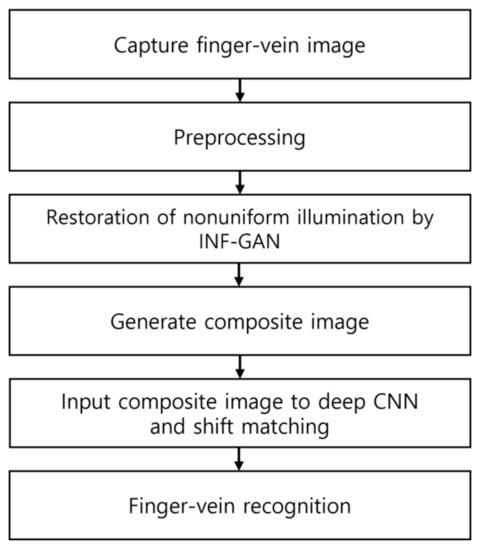
Figure 1. Overall procedure of the proposed method.

3.2. Preprocessing

The preprocessing shown in Figure 2 was performed to extract the finger ROI in a finger-vein image. For the input image shown in Figure 2a, image binarization using fixed threshold of 127 was performed to obtain the image shown in Figure 2b. That is, for the input image, a pixel value higher than (or the same as) 127 becomes 255 (white) and those lower than 127 becomes 0 (black). As shown in Figure 2c, an edge-map image is obtained by applying the Sobel edge detector to the original input image of Figure 2a. Then, a difference image is obtained as shown in Figure 2d, by subtracting the resulting edge-map image of Figure 2c from the binarized image of Figure 2b. In this case, 0 (black) is assigned to the pixel value of difference image if the subtracted value is less than 0. Then, with the difference image of Figure 2d, local binarization based on 25 × 25 window (binarization threshold is set as the Gaussian average value of pixels of difference image within 25 × 25 window) is performed as area thresholding, which produces the resulting image of Figure 2e. With Figure 2e, contour extraction is performed as shown in Figure 2f. As shown in Figure 2f, finger area is separated from background, and only the finger region is extracted as shown in Figure 2g by component labeling, size filtering based on the selection of largest isolated area, hole filling, and morphological erosion.

Figure 2. Examples of preprocessing: (a) Input image, (b) binarized image, (c) edge-map image, (d) difference image between the binarized and edge-map images, (e) resulting image by area thresholding with (d), (f) resulting image by contour extraction with (e), (g) mask image after component labeling, size filtering, hole filling, and morphological erosion with (f), (h) mask image after rotational alignment with (g), (i) mask image of the ROI with (h), and (j) finger-vein ROI image.

After obtaining the mask image, an in-plane rotation compensation method [20] was used for the rotational alignment of the finger image. Equation (1) was then used to determine the normalized second-order moments using the mask image.

$${\beta }_{11}=\frac{{{\displaystyle \sum }}_{\left(x,y\right)\in R}{\left(y-g_y\right)}^{2}I\left(x,y\right)}{{{\displaystyle \sum }}_{\left(x,y\right)\in R}I\left(x,y\right)}, {\beta }_{12}=\frac{{{\displaystyle \sum }}_{\left(x,y\right)\in R}\left(y-g_y\right)\left(x-g_x\right)I\left(x,y\right)}{{{\displaystyle \sum }}_{\left(x,y\right)\in R}I\left(x,y\right)}, {\beta }_{22}=\frac{{{\displaystyle \sum }}_{\left(x,y\right)\in R}{\left(x-g_x\right)}^{2}I\left(x,y\right)}{{{\displaystyle \sum }}_{\left(x,y\right)\in R}I\left(x,y\right)}$$

(1)

Here, $I(x,y$) and ($g_x,g_y)$ refer to the pixel value and the position of the center of the mask image, respectively. Using the value obtained from Equation (1), the angle value was calculated in Equation (2). Subsequently, the image in Figure 2h, to which rotational alignment was applied, was obtained.

$$\theta =\left\{\begin{array}{c}{\tan }^{-1}\left\{\frac{{\beta }_{11}-{\beta }_{22}+\sqrt{{\left({\beta }_{11}-{\beta }_{22}\right)}^2+4{\beta }_{12}^2}}{-2{\beta }_{12}}\right\} if {\beta }_{11}>{\beta }_{22}\\ {\tan }^{-1}\left\{\frac{-2{\beta }_{12}}{{\beta }_{22}-{\beta }_{11}+\sqrt{{({\beta }_{22}-{\beta }_{11})}^2+4{\beta }_{12}^2}}\right\} if {\beta }_{11}\le {\beta }_{22}\end{array}\right.$$

(2)

The ROI was extracted after performing rotational alignment using the mask image. As shown in Figure 2a, the vein pattern cannot be easily observed in the left and right sides of the image due to the fingernail or the thickness of the finger. Therefore, both sides of the image were cut. After cutting the image, a 4 × 20 filter was used to correct the excessively cut part of the image to create the final ROI. Figure 2i shows the mask image of the ROI, and Figure 2j shows the finger-vein image of the ROI.

3.3. Restoration of Nonuniform Illumination by INF-GAN

The performance of a recognition model is significantly reduced if the finger-vein image is transformed to be bright or dark due to severe nonuniform illumination. Features are difficult to find after image transformation due to illumination; thus, the performance cannot be improved through simple preprocessing, such as grayscale normalization or the robust training of a recognition model. Therefore, this study aims to improve the performance against severe nonuniform illumination through image restoration using the newly proposed INF-GAN. The Pix2Pix-HD model [21] was used as a baseline model of the INF-GAN. Pix2Pix-HD is used for obtaining high-resolution images, but it uses a ResNet generator, unlike the conventional image-to-image translation model. Features are extracted from multiple layers of a discriminator, thus generating more photorealistic images using a feature matching loss. In Pix2Pix-HD, two generators and multiple discriminators are used to obtain high-resolution images. However, this study aims to obtain nonuniform illumination restoration instead of obtaining high-resolution images. Thus, one ResNet generator and one discriminator are used in the proposed method. The Pix2Pix-HD model concatenates the instance map containing the image boundary information onto the input image, and generates an output image where the object boundary does not collapse by distinguishing the boundary between objects during training. This study newly proposes an RIGB and applies the concatenation of a residual image containing image texture information onto the input image, thus correcting the texture information that has weakened owing to the transformation of the image to be bright or dark.

3.3.1. Generator of INF-GAN

A ResNet generator is the generator using a residual block in the study by He et al. [22], which can easily train a very deep network where an image can be concentrated on major features to be transformed, thus exhibiting an excellent performance in an image-to-image translation network. However, for severe nonuniform illumination, illumination restoration is difficult, as the skin region and vein region of the finger-vein image become difficult to discern as the image becomes distorted. Using the RIGB proposed in this study, a residual image that evidently shows the vein texture of the input image was used. In this study, a ResNet generator consisting of one RIGB, two 2D convolutional layer blocks, four downsampling blocks, nine residual blocks, and four upsampling blocks was used. In the ResNet generator, a 2D convolutional layer, instance normalization [23], and rectified linear unit (ReLU) activation [24] were used. Table 2 presents the detailed architecture of the ResNet generator used in this study. The detailed architecture of the RIGB in Table 2 is presented in Table 3.

Table 2. Structure of the generator.

Layer	Filter (Number of Filters, Size, Stride) (Number of Blocks)	Padding	Input	Output
Input layer			224 × 224 × 3	224 × 224 × 3
RIGB	64, 3 × 3 × 3, 1 (1) 64, 1 × 1 × 64, 1 (2) 64, 3 × 3 × 64, 1 (3) 1, 1 × 1 × 64, 1 (1)		224 × 224 × 3	224 × 224 × 4 (Channel-wise concatenation)
Conv block 1	64, 7 × 7 × 4,1	3 × 3	224 × 224 × 4	224 × 224 × 64
Downsampling 1	128, 3 × 3 × 64, 2	1 × 1	224 × 224 × 64	112 × 112 × 128
Downsampling 2	256, 3 × 3 × 128, 2	1 × 1	112 × 112 × 128	56 × 56 × 256
Downsampling 3	512, 3 × 3 × 256, 2	1 × 1	56 × 56 × 256	28 × 28 × 512
Downsampling 4	1024, 3 × 3 × 512, 2	1 × 1	28 × 28 × 512	14 × 14 × 1024
Residual blocks (9)	1024, 3 × 3 × 1024, 1	1 × 1	14 × 14 × 1024	14 × 14 × 1024
Upsampling 1	512, 3 × 3 × 1024, 2	1 × 1	14 × 14 × 1024	28 × 28 × 512
Upsampling 2	256, 3 × 3 × 512, 2	1 × 1	28 × 28 × 512	56 × 56 × 256
Upsampling 3	128, 3 × 3 × 256, 2	1 × 1	56 × 56 × 256	112 × 112 × 128
Upsampling 4	64, 3 × 3 × 128, 2	1 × 1	112 × 112 × 128	224 × 224 × 64
Conv block 2	3, 7 × 7 × 64, 1	3 × 3	224 × 224 × 64	224 × 224 × 3

Conv block consists of 2D convolutional layer-instance normalization ReLU. Downsampling is configured identically as Conv block, whereas upsampling consists of a 2D transposed convolutional layer. A residual block is configured as 2D convolutional layer-instance normalization-ReLU-2D convolutional layer-instance normalization-residual connection.

Table 3. Structure of the RIGB.

Layer	Filter (Number of Filters, Size, Stride)	Padding	Input	Output
Input layer			224 × 224 × 3	224 × 224 × 3
Conv block 1	64, 3 × 3 × 3, 1	1 × 1	224 × 224 × 3	224 × 224 × 64
Conv block 2	64, 1 × 1 × 64, 1	1 × 1	224 × 224 × 64	224 × 224 × 64
Residual block 1	64, 3 × 3 × 64, 1	1 × 1	224 × 224 × 64	224 × 224 × 64
Conv block 3	64, 3 × 3 × 64, 1	1 × 1	224 × 224 × 64	224 × 224 × 64
Conv block 4	64, 1 × 1 × 64, 1	1 × 1	224 × 224 × 64	224 × 224 × 64
Residual block 2	64, 3 × 3 × 64, 1	1 × 1	224 × 224 × 64	224 × 224 × 64
Conv 1	1, 1 × 1 × 64, 1	1 × 1	224 × 224 × 64	224 × 224 × 1

Conv block consists of 2D convolutional-layer instance-normalization leaky ReLU (negative slope = 0.3), whereas the residual block is configured as 2D convolutional layer-instance normalization-ReLU-2D convolutional layer-instance normalization-residual connection. Conv indicates one 2D convolutional layer.

To restore distorted vein texture in this study, a one-channel residual image containing vein texture characteristics was generated from the input image, with a reduced quality due to severe nonuniform illumination, using the RIGB consisting of a 2D Conv block and residual block, as shown in Table 3. This residual image was then concatenated onto the input of the ResNet generator, as shown in Figure 3a. Two residual blocks were used in the RIGB to create a residual image. The vein texture of an image becomes more evident as a greater number of residual blocks are connected. However, only two residual blocks were used in this study, as the edge sharpness of the vein was weakened.

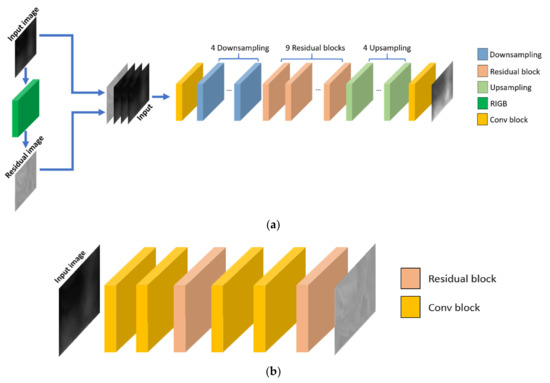
Figure 3. Network architecture of the INF-GAN. (a) ResNet generator and (b) RIGB.

3.3.2. Discriminator of INF-GAN

The PatchGAN discriminator [25] classifies whether an N × N patch is real or fake. PatchGAN computes at the unit of an image patch. Thus, it is fast and exhibits an excellent performance in the image-to-image translation network by training features in a local region by discriminating parts of an image, instead of an entire image. In this study, a 70 × 70 PatchGAN consisting of five convolutional layers, as shown in Figure 4, was used. A seven-channel input was used for the discriminator, as the number of input image channels of the generator is four, whereas the number of target (or restoration image) channels is three. Table 4 presents the detailed architecture of the PatchGAN discriminator used in this study.

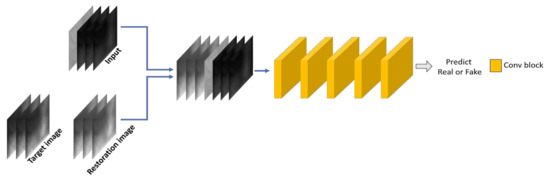
Figure 4. Network architecture of the discriminator.

Table 4. Structure of the discriminator.

Layer	Filter (Number of Filters, Size, Stride)	Padding	Input	Output
Input layer			224 × 224 × 4 224 × 224 × 3 (channel-wise concatenation)	224 × 224 × 7
Conv block 1 *	64, 4 × 4 × 7, 2	2 × 2	224 × 224 × 7	113 × 113 × 64
Conv block 2 **	128, 4 × 4 × 64, 2	2 × 2	113 × 113 × 64	57 × 57 × 128
Conv block 3 **	256, 4 × 4 × 128, 2	2 × 2	57 × 57 × 128	29 × 29 × 256
Conv block 4 **	512, 4 × 4 × 256, 1	2 × 2	29 × 29 × 256	30 × 30 × 512
Conv block 5 ***	1, 4 × 4 × 512, 1	2 × 2	30 × 30 × 512	31 × 31 × 1

* consists of 2D convolutional-layer leaky ReLU (negative slope = 0.2), whereas ** consists of 2D convolutional-layer instance-normalization leaky ReLU (negative slope = 0.2). *** consists of 2D convolutional-layer 2D average pooling.

3.3.3. Loss Function of INF-GAN

In this study, adversarial loss was used for training the INF-GAN in addition to feature matching loss [26] and perceptual loss [27]. The goal of the generator when using a GAN is to generate an image that is difficult to discriminate using the discriminator. Conversely, the goal of the discriminator is to distinguish the output of the generator from the actual target image. The goal of training a GAN is to induce the generator and discriminator to achieve Nash equilibrium by having them compete against each other using the adversarial loss [28]. However, both the generator and discriminator attempt to reduce their own loss, which thus cannot lead to an ideal convergence, and overtraining may occur as the discriminator tends to be trained relatively faster. In detail, as shown in Figure 3a, a generator usually tries to produce the whole image which is similar to the ground-truth (target) image, whereas a discriminator usually tries to only classify real (target) and fake (produced) images during the training procedure, as shown in Figure 4. Therefore, the task of the discriminator is relatively simpler compared with that of the generator, which causes the discriminator to be trained faster than the generator. Therefore, although the training of the discriminator is accomplished (low-value of training loss), further training proceeds because the training of generator is not accomplished (high-value of training loss). This procedure of further training causes the overtraining of discriminator.

To prevent the overtraining by the discriminator, the feature matching loss is used in our discriminator, which is calculated from the extracted feature sets through the discriminator from the produced output (fake) and target (real) image, and the difference between the extracted feature sets is reflected as the loss. In this study, the feature matching loss was calculated using the feature sets extracted from four layers: Conv blocks one–four, in Table 4. By using this feature matching loss, we can make the training convergence of the discriminator more difficult, which causes the reduction of training speed of the discriminator compared to that of the generator, and consequently prevents the overtraining of the discriminator. Equations (3) and (4) express the adversarial loss and feature matching loss used in this study, respectively.

$$\underset{G}{\min } \underset{D}{\max }{L}_{GAN}\left(G,D\right)={\mathbb{E}}_{\left(x,y\right)}\left[\log D\left(x,y\right)\right]+{\mathbb{E}}_x[\log \left(1-D\left(x,G\left(x\right)\right)\right]$$

(3)

$$L_{FM}\left(G,D\right)={\mathbb{E}}_{\left(x,y\right)}{\displaystyle \sum }_{l=1}^T{\mathbb{E}}_{\left(x,y\right)}{\displaystyle \sum }_{l=1}^T\frac{1}{N^l}\left[{\left|\left|D{F}^l\left(x,y\right)-D{F}^l\left(x,G\left(x\right)\right)\right|\right|}_1\right]$$

(4)

Here, G and D in Equations (3) and (4) represent the generator and discriminator, respectively; x is the four-channel input image where the residual image has been concatenated in a channel-wise manner, and y is the target image. In Equation (4), T is the total number of layers from which feature sets are extracted, $N^l$ is the feature-set size obtained from the lth layer of the discriminator, and $D{F}^l$ is the feature set obtained from the lth layer of the discriminator.

Perceptual loss is similar to feature matching loss, but it extracts feature sets from a specific layer using the pretrained CNN model, unlike feature matching loss. As a method for calculating the feature loss extracted from the generator’s output and target image, the perceptual loss was used for style transfer or for image-to-image translation [21,27]. The VGG Net-19 model pretrained with the ImageNet database was used as the pretrained model for perceptual loss. Equation (5) expresses the perceptual loss used in this study.

$$L_P\left(V,G\right)={\mathbb{E}}_{\left(x,y\right)}{\displaystyle \sum }_{l=1}^T\frac{1}{M^l}[|\left|V^l\left(y\right)-V^l\left(G\left(x\right)\right)\right|{|}_1]$$

(5)

Here, $V^l$ is the feature set obtained from the lth layer of the VGG Net-19 pretrained with the ImageNet database, whereas G denotes the generator. Moreover, x and y in this equation are identical to the x and y used in Equations (3) and (4); in VGG Net-19, feature sets are extracted from T number of layers, as in Equation (4). Furthermore, $M^l$ is the feature-set size obtained from the lth layer. The final loss equation can be expressed as follows by combining Equations (3)–(5).

$$\underset{G}{\min }(\underset{D}{\max }{L}_{GAN}\left(G,D\right)+{\lambda }_1{L}_{FM}\left(G,D\right)+{\lambda }_2{L}_p\left(V,G\right))$$

(6)

3.4. Differences between the Proposed INF-GAN and Pix2Pix-HD

The difference between the Pix2Pix-HD model and the proposed INF-GAN can be summarized as follows:

-

The generator of the Pix2Pix-HD was configured with a global generator, which is a ResNet generator, and a multiresolution pipeline as an additional local generator to transform low-resolution images into high-resolution images. The INF-GAN proposed in this study only used the ResNet generator, as it is a translation of nonuniform illumination to the uniform illumination of the images with an identical resolution.

-

Pix2Pix-HD used three multiscale discriminators to use three PatchGAN discriminators with different receptive field sizes, whereas the INF-GAN used one PatchGAN discriminator.

-

Pix2Pix-HD used a one-channel instance map containing the boundary region information of an object to ensure objects are distinguished for translation. In contrast, the newly proposed RIGB was used in the INF-GAN to highlight the vein texture of images distorted by severe nonuniformity of illumination. In the INF-GAN, a one-channel residual image containing the vein texture information was generated to be concatenated onto the input, thus improving the restoration performance.

-

Pix2Pix-HD used a feature encoder network to generate images of various styles to obtain output diversity. In contrast, the INF-GAN did not use a feature encoder network, as it focused on an accurate restoration of nonuniform illumination rather than output diversity.

3.5. Generation of Composite Image and Recognition by DenseNet-161 with Shift Matching

A composite image is created through the composition of enrolled and input images. When authentic and imposter matching is performed using a composite image, training is more robust against noise [6] compared with a difference image matching method [7]. A composite image consists of a 224 × 224 enrolled image in the first channel, a 224 × 224 input image in the second channel, and a 224 × 224 image created by vertically concatenating the enrolled and input images that have been vertically squeezed into a size of 224 × 112, where three images are applied with channel-wise concatenation. Figure 5 shows the example of a three-channel composite image.

Figure 5. Example of a three-channel composite image.

DenseNet-161 [6,7,18] was used in this study to recognize finger-vein images. The growth rate of the DenseNet-161 model was set to 32, and the weights pretrained with the ImageNet database were used. While 1000 vectors are output in the last output layer of the original DenseNet-161, DenseNet-161 in this study was trained by revising the output nodes of the fully connected layer to output two vectors, as it had been determined whether the enrolled and input images were same-class images (genuine matching) or different-class images (imposter matching). The Conv block, dense block, and transition block of DenseNet-161 are all orderly configured with batch normalization [29], ReLU, and a convolutional layer. The detailed structure of DenseNet-161 is shown in Table 5.

Table 5. Structure of DenseNet-161.

Layer	Filter (Number of Filters, Size, Stride)	Padding	Input	Output
Input layer			224 × 224 × 3	224 × 224 × 3
Conv block	96, 7 × 7 × 3, 2	3 × 3	224 × 224 × 3	112 × 112 × 96
Max Pooling	96, 3 × 3 × 96, 2	1 × 1	112 × 112 × 96	56 × 56 × 96
Dense Block 1	6 × 192, 1 × 1 × 96, 1		56 × 56 × 96	56 × 56 × 384
	6 × 48, 3 × 3 × 192, 1	1 × 1
Transition Block 1	192, 1 × 1 × 384, 1 192, 2 × 2 × 192, 2		56 × 56 × 384	28 × 28 × 192
Dense Block 2	12 × 192, 1 × 1 × 192, 1		28 × 28 × 192	28 × 28 × 768
	12 × 48, 3 × 3 × 48, 1	1 × 1
Transition Block 2	384, 1 × 1 × 768, 1 384, 2 × 2 × 384, 2		28 × 28 × 768	14 × 14 × 384
Dense Block 3	36 × 192, 1 × 1 × 384, 1		14 × 14 × 384	14 × 14 × 2112
	36 × 48, 3 × 3 × 192, 1	1 × 1
Transition Block 3	1056, 1 × 1 × 2112, 1 1056, 2 × 2 × 1056, 2		14 × 14 × 2112	7 × 7 × 1056
Dense Block 4	24 × 192, 1 × 1 × 1056, 1		7 × 7 × 1056	7 × 7 × 2208
	24 × 48, 3 × 3 × 192, 1	1 × 1
Global average pooling	2208, 7 × 7 × 2208, 1		7 × 7 × 2208	1 × 1 × 2208
Fully connected layer			1 × 1 × 2208	1 × 1 × 2

The dense block has two different 2D convolutional filters. The transition block has a convolutional filter and average pooling filter.

DenseNet exhibits an excellent performance in finger-vein recognition tasks, as low-level features are efficiently delivered using the dense block even when the network is deep [6,7]. During final recognition, shift matching was used based on eight-way translation (up, down, left, right, diagonal to left-up, diagonal to left-down, diagonal to right-up, and diagonal right-down) by five pixels (left-right) and three pixels (up-down) [6]. Shift matching shifts the input image to match with the enrolled image, thus preventing a reduction in the recognition performance due to misalignment between the input and enrolled images. When recognition is performed using a composite image, the spatial difference between the enrolled and input images included in each channel is used for recognition. If there is misalignment between the input and enrolled images, the recognition performance is degraded due to increased spatial difference. Hence, shifting matching was applied in this study.

The output class of DenseNet-161 was set to two classes: genuine matching and imposter matching. Genuine matching refers to the case where enrolled and recognized finger-vein images are of the same class data, whereas imposter matching refers to the case where enrolled and recognized finger-vein images are of different class data. Genuine matching or imposter matching is determined based on the output score obtained from the last layer of DenseNet-161. It is determined as genuine matching when the CNN output score of the testing data is less than the threshold determined based on the genuine matching distribution of the output score obtained from the training data and the equal error rate (EER) of the imposter matching distribution. Otherwise, it is determined as imposter matching if the CNN output score of the testing data is greater than the threshold. EER is the error rate at the point when the false acceptance rate (FAR), which is the error rate of incorrectly accepting imposter data as genuine data, becomes identical to the false rejection rate (FRR), which is the error rate of incorrectly rejecting genuine data as imposter data.

4. Experimental Results and Analysis

4.1. Dataset and Experimental Environments

In this study, experiments were conducted using the session one images of the Hong Kong Polytechnic University finger image database version one (HKPU-DB) [20] and the Shandong University homologous multimodal traits finger-vein database (SDUMLA-HMT-DB) [30], which are open databases. For convenience, the SDUMLA-HMT-DB is referred to as SDU-DB in this paper. There are other open databases such as MMCBNU_6000 [31] and THU-FVFDT1 [32]. However, because the nonuniformity of illumination of finger-vein images in MMCBNU_6000 is not severe, it is not appropriate for our experiments of finger-vein recognition considering severe nonuniformity of illumination. Although THU-FVFDT1 includes the images of nonuniform illumination, the HKPU-DB and SDUMLA-HMT-DB used in our experiments have been most widely adopted for experiments in previous research on finger-vein recognition [5,6,7,9,16,20]. Therefore, we used these two open databases for experiments.

As shown in Table 6, six images of index and middle fingers each were obtained from 156 individuals for session one for a total of 1,872 images (156 people × two fingers × six images) for the HKPU-DB. Furthermore, for the SDU-DB, six images of index, middle, and ring fingers each were obtained from 106 individuals for a total of 3816 images (106 people × two hands × three fingers × six images).

Table 6. Summary of the experimental databases.

Database	People	Hands	Fingers	Classes	Images	Augmented Images
						INF-GAN Training	DenseNet-161 Training
HKPU-DB	156	1	2	312	1872	2600	9360
SDU-DB	106	2	3	636	3816	4580	19,080

In this study, the classes of the HKPU-DB and SDU-DB were divided into half to perform training and testing for twofold cross-validation. It was ensured that the same class data were not used for training and testing (open-world setting). For example, 156 classes of data were used for training in the first fold validation for the HKPU-DB, whereas the remaining 156 classes of data were used for testing. In the second fold validation, the training and testing data used during the first fold validation were switched for the experiment; the average value of the two testing accuracies was determined as the final testing accuracy. A similar operation was performed with the SDU-DB.

Furthermore, to facilitate model training and prevent overfitting due to insufficient training data, data augmentation was applied for the training data of the two open databases, as shown in Table 6. Specifically, images that are five times the size of the original images were generated by applying five-pixel and three-pixel translation and cropping in the vertical and horizontal directions. The original images that were not augmented were used as the testing data.

The computing environment of this study is a desktop computer equipped with Intel(R) Core(TM) i7-7700 CPU @ 3.60 GHz with 16 GB RAM and NVIDIA GeForce GTX 1070 (1920 compute unified device architecture (CUDA) cores) graphic processing unit (GPU) card with a graphics memory of 8 GB [33]. Compute unified device architecture (CUDA) (version 10.2) and CUDA deep neural network library (cuDNN) (version 7.6.5) environments were used; the algorithms and models were implemented using OpenCV (version 4.4.0), PyCharm, and PyTorch (version 1.7.0) [34].

4.2. Generation of the Nonuniform Illumination Dataset

The quality of the finger-vein images may vary depending on the intensity of NIR illumination. Due to the intensity of NIR illumination and finger thickness, the finger region may be saturated quite brightly or a nonuniformly illuminated image that is too dark may be obtained, as shown in Figure 6, which reduces the recognition accuracy. The following method was used in this study to generate images containing nonuniform illumination from the images of the HKPU-DB and SDU-DB. First, based on Equation (7) [35,36,37], extremely dark and bright images were generated by nonlinearly transforming the intensity signal of light through a nonlinear transfer function using gamma correction. A Gaussian blur was also applied, as the vein pattern may become blurry when the images are transformed to be bright or dark. Unlike the case in Figure 6, the overall brightness of an image is changed when gamma correction is simply applied; thus, image contrast was adjusted using Equation (8).

$$Y^0=B_G\left(C·{\left(I\right)}^{\gamma }\right)+N_G+N_P$$

(7)

$$Y^1=2Y^M-Y^0$$

(8)

Figure 6. Examples of original images with nonuniform illumination from (a) HKPU-DB and (b) SDU-DB.

In Equations (7) and (8),$I$ is the two-dimensional finger-vein image pixel value in grayscale, whereas $C$ and $\gamma$ are gamma correction parameters. $B_G$ is the Gaussian blur function for which a 3 × 3 kernel was used in this study, and the standard deviation value was 0.8. Further, N_G is the Gaussian noise, and N_P is the Poisson noise. The contrast was adjusted from $Y^0$ in Equation (7), and the nonuniform illumination image $Y^1$ was finally generated, as shown in Figure 7. Here, $Y^M$ is the average pixel value of $Y^0$, and $\gamma$ and $C$ values were applied differently to the HKPU-DB and SDU-DB for brightly adjusted and darkly adjusted cases, respectively. To generate a bright image for the HKPU-DB, $\gamma =2.5$ and $C=1$ were applied; to generate a dark image, $\gamma =2$ and $C=0.3$ were applied. Moreover, $\gamma =2.5$ and $C=1$ were applied for generating a bright image for the SDU-DB, whereas $\gamma =2.5$ and $C=0.2$ were applied to generate a dark image.

Figure 7. Examples of original images with normal illumination (left) and generated images with nonuniform illumination (middle and right) from (a) HKPU-DB and (b) SDU-DB.

Equations (7) and (8) were applied to the HKPU-DB and SDU-DB divided twofold to examine how the performance is affected by the changes in illumination. These equations were randomly applied to 936 images out of 1872 images in the HKPU-DB and 1908 images out of 3816 images in the SDU-DB for conducting an experiment to compare the performance with that of the original image during testing and to measure the restoration performance.

4.3. Training of INF-GAN

The training data used for training the INF-GAN were selected by comparing the average pixel distribution of the original image and the average pixel distribution of the illumination-adjusted image. As shown in Table 6, 1040 images were randomly selected in the HKPU-DB among the images with the average pixel value of less than 50 or greater than 160, and half of 5200 images generated based on the data augmentation method described in Section 4.1, or 2600 images, were used in the training set. For the SDU-DB, 1832 images were randomly selected among the images with the average pixel distribution of less than 50 or greater than 120, and half of the 9160 images generated based on the data augmentation method described in Section 4.1, or 4580 images, were used in the training set. All the experiments were conducted as twofold cross-validation.

The hyperparameters had a learning rate of 0.0002, a batch size of 1, and 90 epochs during the INF-GAN training. An adaptive moment estimation (ADAM) optimizer [38] was used, where the first and second moment estimates were set to be 0.9 and 0.99, respectively, for the training. Using the training data, the optimal hyperparameters were determined as the values when the best accuracies of finger-vein recognition were obtained. Figure 8 shows the training loss graphs of the generator and discriminator with the HKPU-DB and SDU-DB. As shown in Figure 8, the INF-GAN was sufficiently trained with the training data.

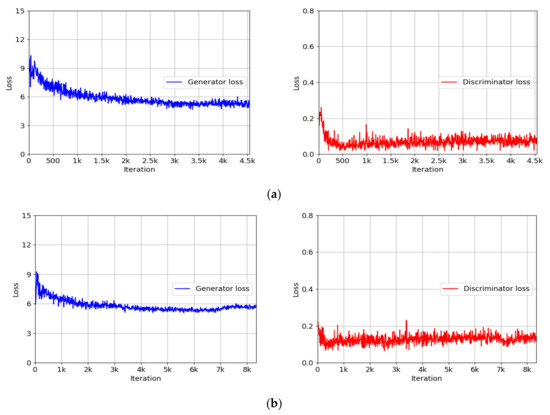
Figure 8. Training loss graphs of the INF-GAN. Training loss curves of the generator and discriminator with the (a) HKPU-DB and (b) SDU-DB.

4.4. Training of the CNN Model for Finger-Vein Recognition

The DenseNet-161 was trained for finger-vein recognition in two classes: authentic matching and imposter matching. With respect to the number of augmented images in Table 6, the number of authentic matching cases in HKPU-DB was 140,400, whereas that of imposter matching cases was 21,762,000, creating a substantial imbalance between the two classes. Therefore, imposter cases were trained through undersampling to correspond to authentic cases for both the databases. Additionally, 90% of the data was used as training data and the remaining 10% was used as validation data. The hyperparameters had a learning rate of 0.0001, a batch size of four, and four epochs during the training of the DenseNet-161. The Adam optimizer [38] was used, where the first and second moment estimates were set to be 0.9 and 0.99, respectively, for the training. Using the training data, the optimal hyperparameters were determined as the values when the best accuracies of finger-vein recognition were obtained. Figure 9 and Figure 10, respectively show the training loss and accuracy graphs and the validation loss and accuracy graphs of DenseNet-161 with the HKPU-DB and SDU-DB. As shown in Figure 9 and Figure 10, DenseNet-161 was sufficiently trained with the training data.

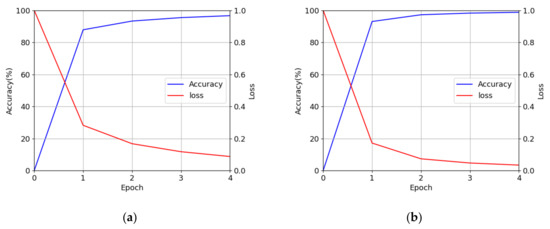
Figure 9. Training loss and accuracy graphs of the DenseNet-161 with (a) HKPU-DB and (b) SDU-DB.

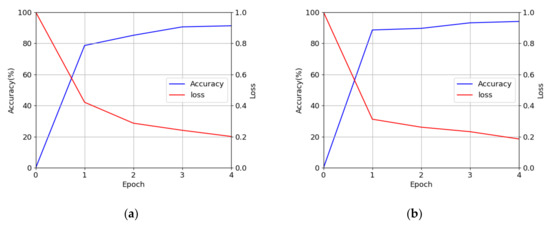
Figure 10. Validation loss and accuracy graphs of DenseNet-161 with (a) HKPU-DB and (b) SDU-DB.

4.5. Testing of the Proposed Method

4.5.1. Ablation Study

As the first ablation study, the performance was compared with respect to the number of residual blocks in the RIGB in Table 3. Figure 11 shows the result images; when two residual blocks were used, as shown in Figure 11c, more fine textures of the vein pattern were observed than when one residual block was used, as shown in Figure 11b.

Figure 11. Examples of residual images generated by the RIGB. (a) Input finger-vein image and generated residual images by using (b) one residual block in the RIGB and (c) two residual blocks in the RIGB.

Table 7 shows the comparison of the finger-vein recognition accuracies according to the number of residual blocks in the RIGB. Here, the EER of finger-vein recognition described in Section 3.5 was used as the performance evaluation metric. As shown in Table 7, using two residual blocks resulted in more accurate finger-vein recognition than using other numbers of residual blocks for the HKPU-DB. In contrast, using one residual block resulted in more accurate finger-vein recognition than using other numbers of residual blocks for the SDU-DB. As the image quality of the SDU-DB is poorer than that of the HKPU-DB, the high-frequency information of features before passing through the convolutional layer is preserved more when two residual blocks are used, while also generating more noise, thus reducing the accuracy of finger-vein recognition.

Table 7. Comparisons of finger-vein recognition accuracies according to the number of residual blocks in the RIGB (unit: %).

Number of Residual Blocks	EER
	HKPU-DB	SDU-DB
1	4.78	2.95
2	1.65	3.17
3	3.09	5.55
4	3.82	5.61

Table 8 shows the comparison of the finger-vein recognition accuracies when the RIGB was used and when the RIGB was not used. As shown in Table 8, the finger-vein recognition accuracy was higher when the RIGB was used compared with when the RIGB was not used.

Table 8. Comparisons of finger-vein recognition accuracies with or without the RIGB (unit: %).

Method	EER
	HKPU-DB	SDU-DB
Without RIGB	4.87	5.83
With RIGB	1.65	3.17

4.5.2. Comparison of Distribution of Generated Images by INF-GAN and Original Images

In this section, various methods (proposed INF-GAN, Pix2Pix [39], CycleGAN [40], Pix2Pix-HD [21], attention-guided image-to-image translation GAN [41], and EnlightenGAN [42]) were used to compare the distributions of the average pixel value of the restored images and the distributions of the average pixel value of the original images, as shown in Figure 12. The experiment results showed that the distributions of the average pixel value by the INF-GAN (Figure 12c), Pix2Pix (Figure 12d), and Pix2Pix-HD (Figure 12f) were similar to the average pixel distribution (Figure 12a) of the original image.

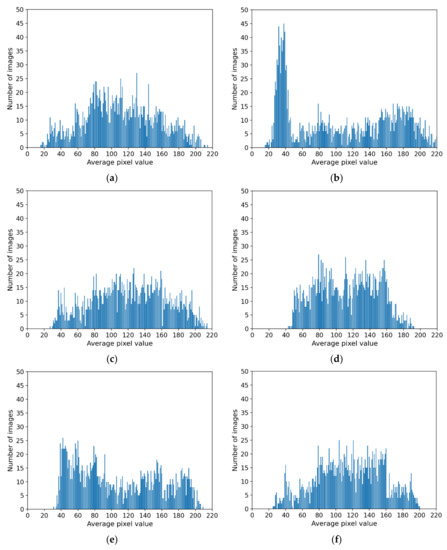
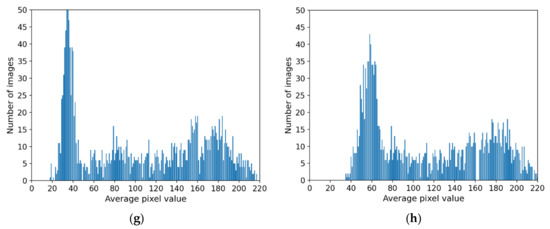
Figure 12. Distribution of the average pixel value of the (a) original image, (b) nonuniformly illuminated image, and images restored by the (c) INF-GAN, (d) Pix2Pix, (e) CycleGAN, (f) Pix2Pix-HD, (g) attention-guided image-to-image translation GAN, and (h) EnlightenGAN.

For the next experiment, the similarity between the distributions of the average pixel value of the original image and the distributions of the average pixel value of the images restored by various methods in Figure 12 was quantitatively compared using d-prime (d′) [43], Wasserstein distance [44], and Fréchet inception distance (FID) [45], as shown in Table 9.

$$d^{\prime }=\frac{\left|{\mu }_s-{\mu }_n\right|}{\sqrt{\frac{1}{2}\left({\sigma }_s^2+{\sigma }_n^2\right)}}$$

(9)

$$W{D}_p\left(P,Q\right)={\left(\underset{\mathsf{\pi }\in \mathsf{\Gamma }\left(\mathrm{P},\mathrm{Q}\right)}{inf}{{\displaystyle \int }}_{{ℝ}^d\times {ℝ}^d}{\left|X-Y\right|}^{p}d\pi \right)}^{1/p}$$

(10)

$$\mathrm{FID}={\left|{\mu }_x-{\mu }_y\right|}^2+Tr\left({\sum }_x+{\sum }_y-2 {\sum }_x{\sum }_y\right)$$

(11)

d′ was calculated through mean ${\mu }_s, {\mu }_n$ and standard deviation ${\sigma }_s, {\sigma }_n$ calculated from two distributions as in Equation (9). Equation (10) is Wasserstein distance and is calculated through combined probability distribution Γ(P, Q) for the two probability distributions P and Q, marginal probability distribution ${ℝ}^d\times {ℝ}^d$, Random variables X and Y in each probability distribution, and dπ which is the joint probability for random variables X and Y. The inf in Equation (10) is infimum, meaning the greatest lower bound, and through this, the value estimated with the smallest expected value for the distance between random variables X and Y among all joint probability distributions Γ(P, Q) is divided into two distributions. Equation (11) is Fréchet inception distance and is calculated through mean ${\mu }_x, {\mu }_y$ and covariance matrix ${\sum }_x, {\sum }_y$ and Tr which is the diagonal sum function, by using 2048 size feature x, y extracted through Inception-v3 which is pretrained using the ImageNet database. Unlike the results in Figure 12, the similarity between the original image and the images generated with the INF-GAN was relatively lower than that of the other methods. In the case of d′, simple mean and standard deviation are used for computation under the assumption that the distribution follows a Gaussian distribution [43]. The Wasserstein distance, which is the earth mover’s distance for calculating the cost required for ensuring two distributions to be identical by moving the distribution, also cannot accurately reflect the similarity between two distributions because from the point of view of cumulative distribution, the frequency of individual variables cannot be reflected [44]. The FID is a feature-based distance extracted from the image that is input into Inception-v3 [46], pretrained with the ImageNet database, thus showing a difference from the average pixel distribution of the image [45].

Table 9. Comparisons of the d′ value, Wasserstein distance, and FID between the original and nonuniformly illuminated images in addition to those between the original and restored images by various methods.

Database	Metric	Nonuniform Illumination	Pix2Pix [39]	CycleGAN [40]	Pix2Pix-HD [21]	Attention-Guided Image-to-Image Translation GAN [41]	EnlightenGAN [42]	INF-GAN
HKPU-DB	d′	0.0689	0.0624	0.0489	0.1455	0.0841	0.0775	0.2482
	Wasserstein distance	21.154	6.8135	10.705	6.63	20.03	16.734	10.728
	FID	7.93	8.44	28.8	2.89	5.92	4.72	4.82
SDU-DB	d′	0.191	0.502	0.031	0.215	0.030	0.490	0.171
	Wasserstein distance	24.314	10.774	2.83	4.25	11.77	19.53	3.545
	FID	4.61	6.48	4.18	2.03	9.33	3.81	3.37

As shown in Table 9, the INF-GAN produced slightly poorer results compared with the other methods from the perspective of the similarity between the original image and the generated image, but in Figure 13, the similarity of the generated image compared to the original image was high. This is because of the characteristics described above for d′, Wasserstein distance, and FID used in Table 9. In the case of d′, the average pixel value distribution does not follows a Gaussian distribution, and in the case of Wasserstein distance, the metric does not reflect the difference in frequency of individual variables from the point of view of cumulative distribution. In addition, in the case of FID, it can differ from average pixel value distribution because it is a distribution comparison method through feature. However, this study focused on improving the finger-vein recognition accuracy, rather than the quality of the generated image. Therefore, the results were compared from the perspective of finger-vein recognition accuracy in the following subsection. Figure 13 shows the examples of the original image, nonuniformly illuminated image, and images generated using various methods.

Figure 13. Examples of the (a) original image, (b) nonuniformly illuminated image, and images restored by the (c) INF-GAN, (d) Pix2Pix, © CycleGAN, (f) Pix2Pix-HD, (g) attention-guided image-to-image translation GAN, and (h) EnlightenGAN.

4.5.3. Comparisons of Finger-Vein Recognition Accuracies by the Proposed Method

Figure 14 shows the original images, nonuniformly illuminated images, residual images generated by the RIGB, and images restored by the INF-GAN. As shown in Figure 14, the INF-GAN restored even a low-quality image with nonuniform illumination so that it is closer to the original image.

Figure 14. Examples of (a) original images, (b) nonuniformly illuminated images, (c) residual images generated by the RIGB, and (d) images restored by the INF-GAN. The first row is an example of restoration of a relatively brightened images and the second row is an example of restoration of a relatively darkened images due to nonuniform illumination.

In Table 10, the EERs of finger-vein recognition were computed when the original images and nonuniformly illuminated images were used for the baseline performance. The EERs of finger-vein recognition were also computed for the cases where the images restored by the INF-GAN were used. Figure 15 shows the receiver-operating characteristic (ROC) curves of each case. The x-axis of the ROC curve is the FAR, whereas the y-axis is the genuine acceptance rate (GAR) (100−FRR (%)) where the graph is placed more toward the top left as the accuracy is higher. As shown in Table 10 and Figure 15, the finger-vein recognition accuracies were lower when the images restored by the INF-GAN were used compared with when the original images were used. However, the finger-vein recognition accuracies were considerably improved compared with when the nonuniformly illuminated images were used.

Table 10. Comparisons of EER of finger-vein recognition with the original images, nonuniformly illuminated images, and images restored by the INF-GAN (unit: %).

Database	Original Image	Nonuniformly Illuminated Image	Restored Image by INF-GAN
HKPU-DB	0.37	16.23	1.65
SDU-DB	1.65	19.3	3.17

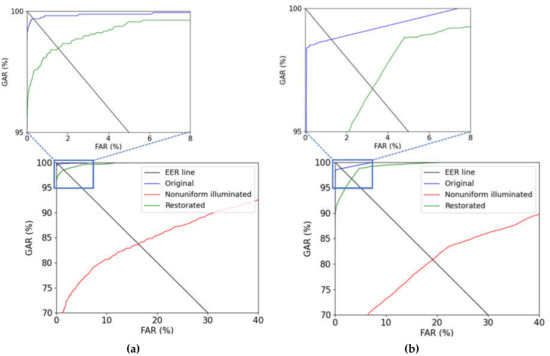
Figure 15. ROC curves of finger-vein recognition with the original images (blue lines), nonuniformly illuminated images (red lines), and images restored by the INF-GAN (green lines) on the (a) HKPU-DB and (b) SDU-DB.

4.5.4. Comparisons of the Proposed Method and State-of-the-Art Methods

In this subsection, we compared our method with the state-of-the-art methods in terms of finger-vein recognition accuracies. For fair comparisons, the DenseNet-161-based finger-vein recognition methods described in Section 3.5 were applied to all the methods. As shown in Table 11, the proposed INF-GAN (with the RIGB) had a higher finger-vein recognition accuracy for all the cases compared with state-of-the-art methods.

Table 11. Comparisons of EER for the proposed method with those of state-of-the-art methods.

Database	Pix2Pix [39]	CycleGAN [40]	Pix2Pix-HD [21]	Attention-Guided Image-to-Image Translation GAN [41]	EnlightenGAN [42]	INF-GAN (without RIGB)	INF-GAN (with RIGB)
HKPU-DB	4.24	8.31	2.84	15.48	8.72	4.87	1.65
SDU-DB	8.81	4.28	3.66	10.39	12.52	5.83	3.17

Figure 16 shows the ROC curves of each case. As shown in Figure 16, the proposed INF-GAN (with RIGB) had a higher finger-vein recognition accuracy for all the cases compared with the state-of-the-art methods.

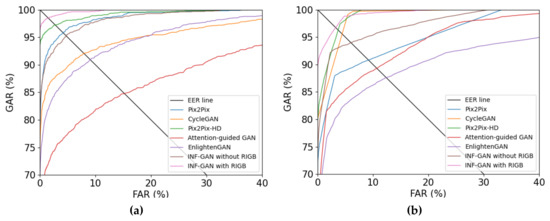
Figure 16. ROC curves of finger-vein recognition by proposed method and the state-of-the-art methods on (a) HKPU-DB and (b) SDU-DB.

Figure 17a,c shows the cases of authentic and imposter matching, respectively, before restoration, which are examples of incorrect matching, as the vein pattern and texture information have been transformed due to nonuniform illumination. For incorrect matching, authentic matching was classified as imposter matching through false rejection, whereas imposter matching was classified as authentic matching through false acceptance, thus degrading the recognition performance. From the left, the images correspond to enrolled, recognized, and concatenated images of Figure 5, respectively. Figure 17b,d shows the cases where the incorrect matching in (a) and (c) was determined to be correct matching by restoring with the INF-GAN proposed in this study. Authentic matching was correctly classified into correct acceptance, whereas imposter matching was correctly classified into correct rejection.

Figure 17. Example of recognition result with or without image restoration by INF-GAN. (a) Incorrect authentic matching before restoration (middle image), (b) correct authentic matching after restoration (middle image), (c) incorrect imposter matching before restoration (middle image), and (d) correct imposter matching after restoration (middle image). Images in (a–d) show the enrolled, recognized, and concatenated images of Figure 5, respectively, from the left.

Figure 18 shows the examples of false rejection and false acceptance even when the images were restored by the INF-GAN. The cause of these errors is that the visibility of the finger-vein pattern in the enrolled and recognized images has weakened.

Figure 18. Examples of recognition depending on the application of image restoration by the INF-GAN. (a) Incorrect authentic matching before restoration (middle image), (b) incorrect authentic matching after restoration (middle image), (c) incorrect imposter matching before restoration (middle image), and (d) incorrect imposter matching after restoration (middle image). Images in (a–d) show the enrolled, recognized, and concatenated images of Figure 5, respectively, from left to right.

4.5.5. Testing on the Unseen Dataset

We performed additional experiments on the unseen dataset. For this purpose, INF-GAN is trained with HKPU-DB, and tested with SDUMLA-HMT-DB in the first trial. Then, INF-GAN is trained with SDUMLA-HMT-DB and tested with HKPU-DB in the second trial. As shown in Figure 19, our INF-GAN can produce the images where the nonuniformity of illumination can be removed and which are similar to original target images. From that, we confirm that our INF-GAN can be operated well on the unseen dataset, also.

Figure 19. Testing examples on the unseen dataset. In (a) INF-GAN is trained with HKPU-DB, and tested with SDUMLA-HMT-DB, and (b) INF-GAN is trained with SDUMLA-HMT-DB, and tested with HKPU-DB. In (a,b), original image of uniform illumination (target image), image of severely nonuniform illumination, and restored image by INF-GAN are shown from left to right, respectively. In (a,b), each row represents the different examples of testing results.

4.5.6. Analysis of Feature Maps by Grad-CAM

In this subsection, we analyzed the feature maps from DenseNet-161 using a class activation map (CAM). A CAM expresses which parts were concentrated on by a classifier, such as a CNN, for distinguishing specific classes [47]. The feature maps extracted from dense blocks one, two and three in Table 5 were compared through a Grad-CAM [48]. Accordingly, the cases of matching using the original image, nonuniformly illuminated image, and images restored by the INF-GAN were compared by separating into authentic matching and imposter matching, as shown in Figure 17. For the composite image, the restored image and the original image showed similarities; for authentic matching in Figure 20a, the similarity in activation maps between the original image and the restored image was higher than between the original image and the nonuniformly illuminated image for dense blocks one, two and three. For imposter matching in Figure 20b, despite the similarity between the nonuniformly illuminated image and the enrolled image, the similarity in activation maps was higher between the original image and the restored image than between the original image and the nonuniformly illuminated image for both dense blocks three. The features extracted from the images restored by the INF-GAN were more similar to the features extracted from the original image than the features extracted from the nonuniformly illuminated image. Thus, it was confirmed that the features extracted from the images restored by the INF-GAN are helpful in improving the accuracy of finger-vein recognition.

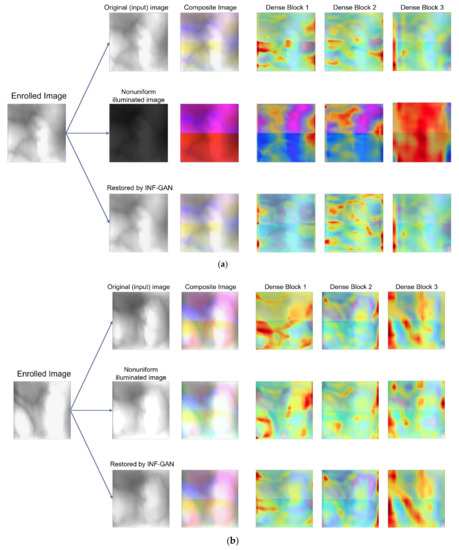
Figure 20. Grad-CAM by different layers from DenseNet-161 in the case of (a) authentic matching and (b) imposter matching.

4.5.7. Processing Time of the Proposed Method

In this subsection, the processing time of the proposed restoration model with the INF-GAN and DenseNet-161 was measured. The processing time was measured using the desktop computer described in Section 4.1 and the Jetson TX2 embedded system in Figure 21 [49]. Because finger-vein recognition is often used with an embedded system as it is adopted in an environment where access is restricted due to security reasons, the processing time was also measured using a Jetson TX2 board in this study. The Jetson TX2 board is an embedded system with an NVIDIA Pascal^TM GPU architecture with 256 NVIDIA CUDA cores, 8 GB 128-bit LPDDR4 memory, and Dual-Core NVIDIA Denver 2 64-Bit CPU. The Jetson TX2 board execution environment was implemented in Ubuntu 18.04, CUDA (version 10.2), and cuDNN (version 8.0.0). As presented in Table 12, restoration through the INF-GAN required 15.62 ms and 33.77 ms on the desktop computer and Jetson TX2 board, respectively, whereas finger-vein recognition through DenseNet-161 required 13.12 ms and 227.45 ms, respectively, on these systems. Accordingly, it was confirmed that the proposed method is applicable in an embedded environment where resources and computing power are limited.

Figure 21. Jetson TX2 embedded system.

Table 12. Comparisons of processing speed by the proposed method on the desktop computer and embedded system (unit: ms).

	INF-GAN	DenseNet-161	Total
Desktop computer	15.62	13.12	28.74
Jetson TX2	33.77	227.45	261.22

5. Conclusions

This paper proposed an image restoration method through the INF-GAN to prevent performance degradation in finger-vein recognition due to severe nonuniformity of illumination. An RIGB was used to supplement the distinction between vein textures in the image weakened due to nonuniform illumination. The finger-vein recognition performance through a deep CNN was improved when the restoration was performed by concatenating a one-channel residual image, which is generated by the RIGB and includes vein texture information, onto the input image. Through the experiment conducted using two open databases, HKPU-DB and SDU-DB, the quality of the image generated through the INF-GAN was compared using the state-of-the-art methods, d′, Wasserstein distance, and FID; the accuracy of finger-vein recognition was also compared using EER and ROC curves. The experiment results showed that the image quality of the INF-GAN was slightly poorer than that of the state-of-the-art-methods, but the accuracy of finger-vein recognition of the INF-GAN was better. Furthermore, the activation maps extracted from the DenseNet-161 were compared using a Grad-CAM, and the applicability of the proposed method on a desktop computer and embedded system was verified.

In future work, we would evaluate our method with more databases such as the MMCBNU_6000, THU-FVFDT1, etc. In addition, the quality of images generated by the proposed INF-GAN would be improved to examine the applicability for nonuniform illumination restoration in general scene images, instead of the finger-vein recognition examined in this study. Moreover, the possibility of using the INF-GAN-based nonuniform illumination restoration proposed in this study in various other biometric modalities of face-, iris-, and body-based recognition will be examined.