Abstract
This study proposed different techniques to estimate the isotope composition (δ18O), salinity and temperature/potential temperature in the Mediterranean Sea using five different variables: (i–ii) geographic coordinates (Longitude, Latitude), (iii) year, (iv) month and (v) depth. Three kinds of models based on artificial neural network (ANN), random forest (RF) and support vector machine (SVM) were developed. According to the results, the random forest models presents the best prediction accuracy for the querying phase and can be used to predict the isotope composition (mean absolute percentage error (MAPE) around 4.98%), salinity (MAPE below 0.20%) and temperature (MAPE around 2.44%). These models could be useful for research works that require the use of past data for these variables.
1. Introduction
The semi-enclosed Mediterranean Sea [1,2,3] is characterised by dry and warm summers and temperate and wet winters [3]. The Mediterranean Sea is considered a continentally influenced ocean basin [4] and occupies an area around 2.5 million km2 between Africa and Europe [5]. The Mediterranean Sea is divided into two basins, western and eastern basins, and the Straits of Sicily is considered the point of the division [5,6].
The Mediterranean Sea has different gradients or distributions of oxygen isotope composition [7], temperature [1,3,8] and salinity [1,3,8], and it is considered an oligotrophic sea that presents moderate levels of primary production and low nutrient concentrations [9,10]. In the Mediterranean Sea, the precipitation is less than mean evaporation, which has important implications on their biogeochemistry and circulation [8]. The thermohaline circulation introduces warm and fresh surface waters through the Strait of Gibraltar, and the Mediterranean Sea returns cooler and saltier deep waters into the North Atlantic [3]. The thermohaline circulation is guided by the seasonal variations on surface water temperature and salinity [7]. The thermohaline circulation through the Strait of Gibraltar maintains oxygenated the depths of the Mediterranean Sea [3] and causes a decrease of salinity in the western, in contrast to the water of the eastern Mediterranean Sea [8]. Different studies consider that the time to renewal for eastern Mediterranean deep water is longer than western Mediterranean deep waters [8,11,12].
The Mediterranean Sea represents a complex marine environment; due to the fact of this, a large number of researchers have developed different studies on modern biogeochemical and physical processes (including their interactions) [3]. In this sense, the stable isotope composition, with temperature and salinity data, provided information about the mixing and origin pattern of water masses [13]. The isotopic mass balance can be used as a recorder of past climate variations [6]. Moreover, stable isotopes ratios can be employed to obtain information of organic matter origin and transformations [14]. 18O-salinity allows identifying different input components: sea ice meltwater, marine standard water and continental freshwater [15]. Sea surface temperature data are important to comprehend the interaction between the ocean and the Earth’s atmosphere [16]. Ocean temperature prediction has importance in different fields related to the ocean [17]; in fact, the sea surface temperature (SST) prediction is a very important parameter to marine production and protection, and to the climate prediction [18]. Nevertheless, the ocean internal temperature prediction is larger important for practical applications [17].
Therefore, the stable isotope composition, salinity and temperature can be used to determine the Mediterranean Sea evolution and obtain important information on other parameters of interest. Due to this, four different kinds of models (two artificial neural networks (ANNs)—ANN1 and ANN2, based on multilayer perceptron (MLP), a random forest (RF) and a support vector machine (SVM) model) were used in this research to predict isotope composition (δ18O), salinity and temperature:
- Artificial neural networks are a computational method inspired on the cell of the nervous system (known as neuron) [19] to try to analyse and reproduce the learning mechanism that owned by the more highly evolved animal species [20]. These models can find the relationships between inputs and outputs variables [21]. When the relationships are complex and highly non-linear, this kind of model needs a relatively huge training data group [22]. The ANNs are used as an option to statistical methods for different purposes such as estimation, classification, among others [23]. ANN approaches are popular due to their flexibility to fit random data and their reasonably uncomplicated development [23,24]. As previously stated, ANN models developed in this research are based on an MLP neural network, a popular ANN architecture [25]. ANNs are applied in different fields such as chemistry [26], medicine [27], food authenticity [28], among others [29,30]. This type of model can be part of more complex systems such as a smart healthcare monitoring system to predict heart disease that used ensemble deep learning [31] or to classify skin disease through deep learning neural networks stand on MobileNet V2 and long short-term memory [32].
Within the research field of this article, it can be said that the capacity of artificial neural networks to sense out the trends and patterns in sea surface temperature is validated by the oceanographic community [23], the fact that is demonstrated with the use of this kind of approach by different researchers who used it to predict the SST at different spatial and temporal scales around the world [23]. An example of the use of this type of model can be found in the work carried out by Aparna et al. (2018) to determine the sea surface temperature (SST) and delineate SST fronts. Secondly, Patil and Deo (2017) developed wavelet neural networks to predict daily SST values at different locations in the Indian Ocean [24]. Neural networks can also be used to determine the sea surface salinity (SSS), in addition to temperature. In this case, Buongiorno Nardelli (2020) developed an innovative deep learning algorithm based on a stacked long short-term memory neural network and was applied over the North Atlantic Ocean data [33]. ANNs (back-propagation and radial basis function) can also be used applied to predict the salinity variations in a tidal estuary, which were compared with an Eulerian–Lagrangian Circulation model (ELCRIC) [34]. According to the authors, the prediction from the artificial neural network models was better than the prediction determined by the physically based hydrodynamic model. Finally, this kind of approach can also be used to predict the isotope composition of oxygen (δ18O) in shallow groundwater, which can be used to study the water cycle [35]. In this case, Cerar et al. (2018) compared different models such as ordinary kriging, and others, and based on three variables (average annual precipitation, elevation and distance from the sea) concluded that, based on validation data sets, the ANN model was the most suitable approach to predict δ18O in the groundwater [35].
- The second kind of model used is a random forest model. RF is a computational method for regression and/or classification [36] proposed by Breiman (2001) [36,37]. A random forest model is formed by decision trees where each tree utilizes a sample subset of available data [38], and the random forest’s prediction value is the average of all predicted values [38,39]. Random forest is one of the most capable machine learning approaches for forecasting [40] and can be used in different fields such as environmental science [38] and chemistry [41], among others [42,43].
Within the research field of this article, RFs can be used to estimate the ocean’s interior salinity using surface remote sensing data [44]. In this sense, Su et al. (2019) used two different methods (one of them, random forest) to predict the subsurface salinity anomaly in the upper 2000 m which can help to understand the response of subsurface and deeper ocean environment to the global warming [44]. Another example of the use of models based on random forest was developed by Lui et al. (2015) to predict sea surface salinity in the Hong Kong Sea [45]. The random forest model was compared with three models (back-propagation ANN, classification and regression trees and multiple linear regression) and showed lower estimation error and good correlation coefficient so that, this model demonstrated its capability to estimate sea surface salinity in coastal waters [45]. RF is also used to estimate the errors dispersion and the central tendency in satellite-derived SST retrievals [46].
- Finally, the last model developed is a support vector machine. An SVM model is a method enunciated by Boser et al. in 1992 [47,48]. Originally, the SVM models were developed for pattern recognition, nevertheless, nowadays they can be used to solve nonlinear regression problems or time series prediction [49,50] and due to its mathematical simplicity it has received much attention lately [51]. An SVM model creates a hyperplane, or hyperplanes, in a high- or infinite- dimensional space [52]. The hyperplane separates the dataset into a number of classes consistently with the training examples [53]. The principal advantage of SVM (compared to other classification techniques such as partial least square discriminant analysis) is its flexibility to model non-linear classification problems [54]. SVM models can be used in different areas such as: Engineering [55,56], Medicine [57,58], among others [59,60]. Related to this research field, SVM models can be used to estimate the SST in the tropical Atlantic [61] or to forecast the tropical Pacific SST anomalies [62]. In this case, Aguilar-Martinez used support vector regression and was compared with Bayesian neural network and linear regression models.
Finally, these three types of models (ANN, RF and SVM) can also be compared to each other. An example of this is the article developed by Sunder, et al. (2020) to estimate the daily cloud-free sea surface temperature from a single sensor (MODIS Aqua) [53].
Taking into account the above information, it can be said that all these studies used different machine learning models to predict one, or more, variables of interest (isotope composition (δ18O), salinity and temperature) time ahead. Given the good results offered in these investigations, it has been thought that it is possible to use these models to determine these variables in a determined past time. These models could be used to complete databases and study the Mediterranean Sea evolution.
In this study, the use of artificial neural networks, random forest and support vector machine models to determine these variables in the past, were analysed. For this purpose, five input variables were used (geographic coordinates—Longitude, Latitude—, year, month and depth), and an attempt was made to relate to the isotope composition (δ18O), salinity, and temperature/potential temperature.
2. Materials and Methods
2.1. Database Used
In this study, a large database collected by Schmidt et al. (1999) [63]—partially collected in previous publications of Schmidt (1999) and Bigg and Rohling (2000) [64,65]—were used. The data were downloaded between Longitude (° E) −4.73° and 36.00° and Latitude (° N) 31.30° and 46.00°. Nevertheless, this database presents missing values for many variables (the isotope composition, salinity or temperature/potential temperature —the temperature determinations can be in-situ or potential temperature [63]—); for this reason, cases with missing values and a case with anomalous temperature, were deleted and as a result, the database is reduced to 470 experimental cases. According to this, the database used in this research come from different original research [7,13,66,67]). The data used are distributed as follows: from (i) Pierre et al. (1986) a total of 92 samples (collected in 1986) were used, (ii) from Pierre (1999) were used 267 samples collected between 1988 and 1990, (iii) from Gat et al. (1996) 109 samples (between 1988 and 1989) were collected, and (iv) from the original research of Stahl and Rinow (1973) 2 samples were used (collected in 1971). All these data bring a total of 470 experimental cases (Table 1).

Table 1.
Statistics for data used in this research.
2.2. Experimental Design
Five input variables: (i–ii) geographic coordinates —Longitude (° E), Latitude (° N)—, (iii) year, (iv) month and (v) depth (m) were used to model three independent variables: (a) the isotope composition (δ18O, ‰), (b) the salinity (‰) and (c) the temperature (°C) measured in situ or potential temperature in the Mediterranean Sea.
In this case, 470 experimental cases were collected from the original database of Schmidt et al. (1999) [63] and were used to establish three different groups; (i) one group (training group, formed by the training cases —60% of the total cases—) to develop the different models, (ii) a second group (validation group, formed by validation cases —20% of the total cases—) to validate the different models developed and (iii) a third group (querying group, —the last 20%—) to check the chosen prediction model. The data distribution on the different sets was random.
2.3. Methodologies
It is possible to find in the literature different models applied in fields related to the different purposes of this paper, for example, Cerar et al. applied artificial neural networks to predict the oxygen-18 isotope composition in Slovenia’s groundwater [35] or even to palaeoceanographic data analysis [68]. Neurological networks models were introduced for the first time in 1943 when McCulloh and Pitts [69] reported the ability of simple neural networks to calculate just about any logic or arithmetic function [70,71]. A neural network is formed by interconnected neurons that work as independent computational units [23]. Normally, neurons are grouped in layers (input, intermediate/s and output layer) and signals moves from the input layer to the output layer, going through the different hidden layers located between them [23]. An MLP is formed by different layers of neurons (input, intermediate/s and output layer) where each layer is connected to the next layer [72].
In this research, two different ANN models were developed: (i) a neural model (ANN1) with the sigmoidal function implemented in the hidden neurons and the linear function implemented in the output neuron and (ii) a second artificial neural model (ANN2) with the sigmoidal function implemented in all the hidden and the output neurons. As is known, to obtain good neural network models it is required to develop models with different topologies (models with different neurons in hidden layers), models with different training cycles, and so on. This procedure is called trial and error method and was used to find the best model based on the statistics of the validation phase.
A disadvantage of ANN models is that it is time consuming, due to the fact of this disadvantage, and taking into account the bibliography previously seen in the introduction and the experience of the research group, other two techniques, random forest and support vector machine models, have been developed in this research.
The random forest regression model is a computational learning method formed by simple decision trees where the prediction value is the average of individual prediction values [38,39]. In the same way as the ANN models, these models were made based on the trial error method to find the best model for the validation phase. In this case, the parameters analysed were the number of trees, the maximal depth and the use of prepruning.
Finally, the support vector machine is a strong technique for classification and regression [52] that in this research was used in regression mode using epsilon-SVR and nu-SVR SVM types. To develop the different SVM models, the LIBSVM learner by Chang and Lin [52,73,74] was used. The SVM models were developed using the RBF kernel and the gamma and C parameters were studied according to the updated guide provide by Hsu et al. [75]. The support vector machine models were made with the normalized input variables and without normalizing; however, in this research, only the models developed with the non-normalized variables are shown, because, in general, these were the models with the best adjustments.
2.4. Fitting of Data and Modelling
As stated above, the database was split randomly into three groups: (i) training group —60% cases—, (ii) validation group —20% cases— and (iii) querying group —20% cases—. To determine the good prediction power of the different developed models, different statistical parameters were used. For this purpose, squared correlation coefficient (r2) to evaluate the correlation between predicted and real values, root mean square error (RMSE) —Equation (1)— and mean absolute percentage error (MAPE) —Equation (2)— were calculated. Best models were selected using the RMSE for the validation phase and then were checked with querying cases.
2.5. Computational Resources
The research group has several servers to carry out these tasks, in this case, a computer equipped with a processor AMD Ryzen 7 1800X (Advanced Micro Devices, Inc., Sunnyvale, CA, USA) and 16 GB of random access memory were used. The models ANN1, RF and SVM developed in this research were made using different versions of RapidMiner Studio (RapidMiner, Inc., Boston, MA, USA). The ANN2 models were developed with EasyNN plus v14.0d (Neural Planner Software Ltd., Cheshire, UK). Excel 2013 (Microsoft Office Professional Plus 2013, Microsoft, Redmond, WA, USA) were used to fit the data, and Sigmaplot 13 (Systat Software Inc., San Jose, CA, USA) were used to plot figures.
3. Results and Discussion
To find the best prediction model (artificial neural networks, random forest or support vector machine) it was necessary to develop a large number of models using trial and error method. The best models (Table 2) were chosen by the results obtained for the validation phase. In the following paragraphs, the best models for each variable are analysed.

Table 2.
Models developed with Longitude, Latitude, Year, Month and Depth. The model corresponds with the best implemented model: artificial neural networks type I (ANN1), artificial neural networks type II (ANN2), random forest (RF) and support vector machine (SVM). r2 is the squared correlation coefficient, RMSE is the root mean square error (in ‰ for δ18O and salinity, and °C for temperature/potential temperature) and MAPE is the mean absolute percentage error (%), for the real and the predicted data. Subscript T identifies the training phase, V the validation phase and Q the querying phase. (Bold shows the best model for each block.)
3.1. δ18 O Model
Stable isotope composition can provide, along with other variables, information about the origin and mixing pattern of water masses [13]. Table 2 shows the squared correlation coefficient for training, validation and querying phases for the best ANN1, ANN2, RF and SVM models selected. Taking into account Figure 1, it can be said that the ANN1, ANN2 and SVM models present a huge dispersion for the training phase. This fact is especially clear in the SVM model that presents the worst adjust with a root mean square error for the training phase (0.167‰) and the lowest squared correlation coefficient (0.554); this fact may be due to the flat area that is located on the right side of the figure. According to this, the results for the validation phase shows a low squared correlation coefficient (0.520) and a high root mean square error value (0.132‰); once again, it can be seen as a flat area on the right. The other models, ANN1 and ANN2, show slightly better results for the validation phase with squared correlation coefficients of 0.614 and 0.641, respectively—in these cases without a flat area to the right. The best model, according to the results showed in Table 2, is the random forest model. This model is characterized by the absence, both in the training and validation phase, of the flat prediction zone. This fact can be observed attending to the statistics r2 showing a 0.889 for the training phase and a 0.682 for the validation phase. In the same way, the other statistics, RMSE and MAPE, present the minimum value for each phase (due to the low dispersion of the model).
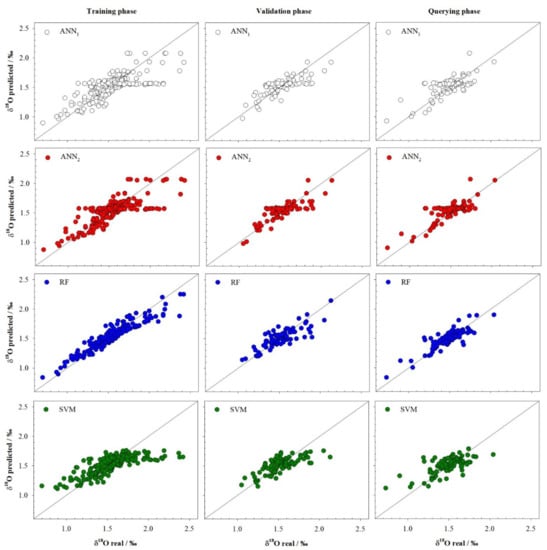
Figure 1.
Real values vs. predicted values for δ18O (‰) by artificial neural models ANN1 and ANN2, random forest model (RF) and support vector machine model (SVM) developed. The black lines correspond to the line with slope one.
As stated above, the models are chosen based on the statistics of the validation phase. These adjustments are used as estimators of the use of the model in the real world. To ensure its good performance, the best model will be applied to the query phase data group (Table 2 and Figure 1). In this phase, similar behaviour to the observed in the training and validation phase can be seen. Once again, the worst model is the SVM model that shows the worst adjustments for the querying phase in terms of r2 and root mean square error (0.454 and 0.142‰, respectively) and a mean absolute percentage error of 7.38%. The adjustments provided by the SVM model are similar to those obtained for the training and validation phase. For the two models based on artificial neural networks, a similar behaviour to the reported values for the training and validation phases can be observed, that is, better squared correlations and lower prediction errors than the SVM model. Finally, it can be seen how the model based on random forest shows the best results with an r2Q of 0.739 and an MAPEQ of 4.98%.
According to the observed flat zone in the training phase, it is unusual that the flat prediction zone occurs only at high values of the δ18O. With low values of the δ18O, this flat zone is only slightly detected in the case of the model based on a support vector machine. This fact may lead us to think that the models based on neural networks and support vector machines do not work as well as they should when the δ18O exceeds values around 1.7‰. This behaviour was clearly reduced in the validation phase, probably due to the small number of cases with values higher than the limits described above. Flat prediction area is not observed in any of the three phases of the RF model, in fact, this model is the one that presents the best adjustments in all phases in terms of r2 and also in the terms related to the measurement of dispersion (the root mean square error and the mean absolute percentage error), that is, data fit well to the line with slope one (black line).
Given the results obtained by the RF model, it can be concluded that the model is useful for predicting the δ18O in the Mediterranean Sea.
3.2. Salinity Model
The other interesting variable predicted using the proposed models is salinity. Table 2 shows the adjustments for the best models developed. The models show, in general, better adjustments for all phases compared to the previous models (δ18O models). This fact is clearly visible in the training phase where the adjustments are higher in terms of squared correlation (between 0.891 and 0.978) than the models presented in the previous section (between 0.554 and 0.889). In terms of mean absolute percentage error, the improvement is notorious for this same phase (training), going from range 3.84–7.13% (δ18O models) to the range 0.12–0.27% (salinity models). This improvement can be seen in Figure 2, where only a few points are away from the line with slope one; this occurs for ANN1, ANN2 and SVM models. If we analyse the worst model in the training phase, the ANN1 model, we can see a point with an important error (prediction value 39.01‰ vs. real value 37.90‰ (Figure 2)), presenting an individual percentage error (IPE) of 2.94% (overestimated the real value). Taking into account the low IPE value it can be concluded that all points outside the line with slope one, are not really outliers due to their low relative error.
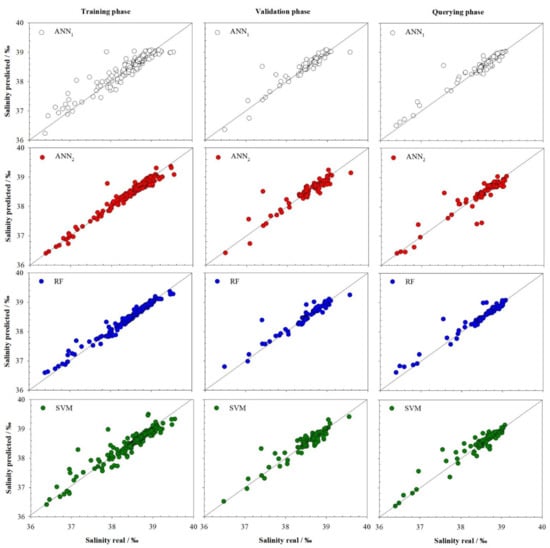
Figure 2.
Real values vs. predicted values for salinity (‰) by artificial neural models ANN1 and ANN2, random forest model (RF) and support vector machine model (SVM) developed. The black lines correspond to the line with slope one.
For the validation phase, the adjustments present good values of r2V between 0.870 and 0.914 for the ANN2 and RF model, respectively (Table 2). The root mean square errors present a small increment in their values although they are still low (under 0.30%). In the same way, as in the training phase, there are some points away from the line with slope one. All models presented some of these points, even the RF model that presented a case with an IPE of 2.66 (37.40‰ vs. 38.39‰, overestimated the real value) (see Figure 2). Once again, taking into account the low IPE value it can be concluded that this point cannot be considered an outlier
Once the correct prediction power of the models has been verified, the chosen models were applied to querying cases. The models still worked with accuracy; that is, the models could predict the experimental values of salinity with small errors, RMSEV under 0.210‰ that corresponded with small mean absolute percentage errors values (MAPEV) of approximately 0.29%. The models in this phase presented squared correlation coefficients between 0.864 and 0.942. The ANN2 model presented three points away from the line with slope one. One case with an IPE of −2.65% (38.47‰ vs. 37.45‰) and two cases with the same value, but a different sign, −2.45% (38.35‰ vs. 37.41‰) and 2.45% (37.55‰ vs. 38.47‰), that is, two cases were underestimated and one overestimated -see Figure 2-. Once again, the low value of the IPE determines that these two points are not outliers.
Given the results obtained by the RF model, it can be concluded that the random forest model can predict with accuracy the salinity in the Mediterranean Sea.
3.3. Temperature/Potential Temperature Model
Finally, a new group of models to predict, in this case, the Mediterranean’s seawater temperature/potential temperature were developed. Table 2 shows the results obtained for the best prediction models selected. The ANN1 model is the worst model for presenting the worst result in the validation phase.
The ANN1 model presents a well squared correlation coefficient for the training phase (0.937) with an RMSET value of 0.745 °C that corresponded with a MAPET value of 3.95%. ANN models present a similar behaviour between them, that is, ANN1 and ANN2 present good adjustments for the training phase with r2 values of 0.937 and 0.934 and similar root mean square errors (0.745 °C and 0.717 °C with MAPET values of 3.95% and 3.07%), respectively. The SVM model presents similar adjustments to those reported by the ANN models (although with a slight improvement in the RMSE and MAPE values). Once again, the RF model presented the best adjustment for the training phase with an r2T of 0.972 and an RMSE T of 0.467 °C that corresponded with a MAPE T of 1.99%. In Figure 3, it can be seen that the ANN2 model and SVM model presented, for the training phase, two points away from the line with slope one (top right of the figure). For the ANN2 model, these two points (28.09 °C and 27.91 °C) present predicted values of 24.79 °C and 24.99 °C, respectively (IPE values of −11.76% and −10.47%), that is, the model underestimated the real values. For the SVM model, in the training phase, the same two points present bad predictions with IPE values of −20.03% and −18.93% (both cases underestimated.) In the ANN1 model, one of these two points were also far from the line with slope one (28.09 °C vs. the predicted value of 24.59 °C).
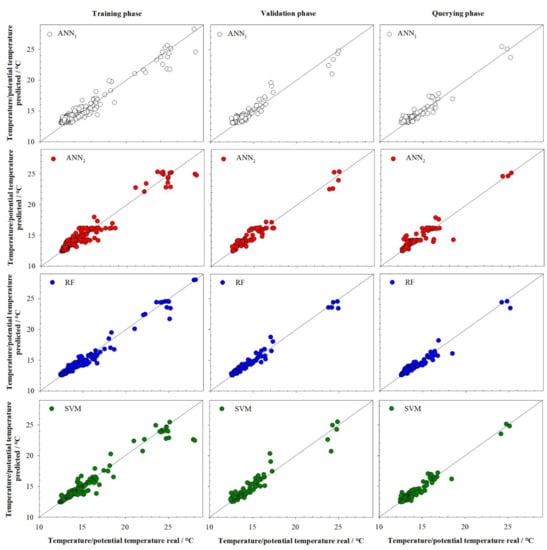
Figure 3.
Real values vs. predicted values for temperature/potential temperature (°C) by artificial neural models ANN1 and ANN2, random forest model (RF) and support vector machine model (SVM) developed. The black line corresponds to the line with slope one.
In the validation phase, all models present good results according to the squared correlation coefficient that includes values between 0.926 and 0.972 with RMSEV values in the range 0.452–0.757 °C (Table 2). It can be said that an error under one degree may be acceptable. In the SVM model (Figure 3) can be seen the presence of three points away from the line with slope one that present IPE values of −14.13%, 11.31% and 19.60%. The same three points can also be seen away from the line with slope one in the ANN1 model (IPE values between −12.94% and 15.13%).
For the querying phase, the ANN models present the worse results. This can be clearly seen for the ANN2 model where the RMSE increased to 0.777 °C that corresponds to a MAPE of 3.34%. The prediction is slightly improved by the ANN1 model (0.699 °C). Once again, the random forest model presents the best adjustments for the querying phase (with similar values for the SVM model). The RF model showed the best squared correlation coefficient (0.953), the lowest root mean square error (0.513 °C) and a MAPE value of 2.44%. Due to the fact of these results, the RF model can be used to predict the temperature in the Mediterranean Sea.
All the models developed in this research to determine δ18O, salinity, and temperature/potential temperature worked quite well, showing acceptable errors below 8.00%. The low percentage of error and the good square correlation coefficient values shown by the models to predict salinity and temperature/potential temperature seemed to indicate that there was a high correlation between the input variables and the variables to be predicted. This fact did not seem so marked in the case of the models to predict δ18O, where, despite the low percentage errors, a low square correlation coefficient of the different models is observed in all phases, except in the training phase of the RF model where a value of 0.889 is reached. This low correlation, not only in the random forest models but also in the rest of the models to predict δ18O, might suggest that the variables selected to determine this parameter should be complemented with other input variables to improve the squared correlation coefficients and the percentage of error (made by decreasing the RMSE).
The models developed in this research can be used to determine with relative safety the levels of δ18O, salinity and temperature/potential temperature of the waters of the Mediterranean Sea, taking into account the geographical coordinates, year, month and depth.
These models have the disadvantage of requiring a longer processing time and computational cost than other types of more traditional models, such as models based on simple multiple linear regressions (models that are practically instantaneous compared to machine learning models such as those presented in this research). However, this inconvenience is overcome by the great capacity of these models (ANN, RF and SVM) to find the necessary relationships between the independent and dependent variables and achieve a good result.
Our models could be useful for all those research works that require, or need, the use of past data for these variables. These models work well between the dates analysed in this research. Outside of these dates, the model could lose predictive power due to the possible temporal evolution of the Mediterranean Sea caused by different factors that could influence it such as climate change, pollution phenomena, among others.
These models are far from being perfect models because they present points distant from the line with slope one and points, that although they are close to it, can present high values of IPE (points located in the lower areas of the line with slope one). These models should be optimized by including more sampling data, different locations and depths, as well as different measurement dates, studying different combinations of model parameters (increasing their study ranger or analysing more parameters), among others. Another possible way to improve the models is to establish independent databases for each variable under study (avoiding the elimination of cases that have only one missing value). In addition to taking into account these possible improvements, it is necessary to carry out a more exhaustive treatment of the data to discriminate and better choose the input variables avoiding possible noise such as due to the joint inclusion of values of temperature and potential temperature.
4. Conclusions
In this study, different models were developed to predict the isotope composition (δ18O), salinity and temperature/potential temperature in the Mediterranean Sea using five variables: (i–ii) geographic coordinates (Longitude, Latitude), (iii) year, (iv) month and (v) depth. δ18O models present a regular power prediction (MAPEQ between 7.38% and 4.98%). Salinity models can predict the salinity value with accuracy (under a MAPEQ value of 0.30%). Models to predict water temperature/potential temperature presented good power prediction with MAPEQ values between 3.99% and 2.44%.
Taking into account the different models implemented in this research and the results obtained, authors can say that random forest models proved a valid prediction tool to determine with accuracy the oxygen-18 isotope composition, the salinity and the temperature/potential temperature of the Mediterranean Sea.
The authors suggest that new models trained with a larger number of samplings, and a more detailed study of the data, could improve the accuracy of the developed models in this research.
Author Contributions
Conceptualisation, G.A.; methodology, G.A.; formal analysis, G.A.; data curation, G.A.; writing—original draft preparation, G.A.; writing—review and editing, B.S., E.B., J.F.G. and J.C.M.; visualisation, G.A.; supervision, J.C.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used in this research to develop the different models were collected by Schmidt et al. (1999) [63] from different sources and are available at https://data.giss.nasa.gov/o18data/. Please see “2.1. Database Used” for more information.
Acknowledgments
Gonzalo Astray thanks the Universidade de Vigo for his last financial support from the “Programa de retención de talento investigador da Universidade de Vigo para o 2018” budget application 0000 131H TAL 641. Authors thanks to Xunta de Galicia for the Research Units Consolidation and Structuring Grant: Competitive Reference Groups 2018 (ED431C 2018/42). Gonzalo Astray thanks Xunta de Galicia (Consellería de Cultura, Educación e Ordenación Universitaria) for the computer equipment financed in 2017 from his postdoctoral grant B, POS-B/2016/001, K645P.P.0000421S140.08 The authors thank RapidMiner Inc. for the different versions of RapidMiner Studio software used to develop this academic research. The funders had no role in study conceptualisation, data collection/analysis or the manuscript preparation.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Theodor, M.; Schmiedl, G.; Mackensen, A. Stable Isotope Composition of Deep-Sea Benthic Foraminifera Under Contrasting Trophic Conditions in the Western Mediterranean Sea. Mar. Micropaleontol. 2016, 124, 16–28. [Google Scholar] [CrossRef]
- Gonzalez-Mora, B.; Sierro, F.J.; Schönfeld, J. Temperature and Stable Isotope Variations in Different Water Masses from the Alboran Sea (Western Mediterranean) between 250 and 150 Ka. Geochem. Geophys. Geosyst. 2008, 9, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Rohling, E.J.; Marino, G.; Grant, K.M. Mediterranean Climate and Oceanography, and the Periodic Development of Anoxic Events (Sapropels). Earth Sci. Rev. 2015, 143, 62–97. [Google Scholar] [CrossRef]
- Herbert, T.D.; Ng, G.; Cleaveland Peterson, L. Evolution of Mediterranean Sea Surface Temperatures 3.5-1.5 Ma: Regional and Hemispheric Influences. Earth Plan. Sci. Lett. 2015, 409, 307–318. [Google Scholar] [CrossRef]
- Schroeder, K.; Garcìa-Lafuente, J.; Josey, S.A.; Artale, V.; Nardelli, B.B.; Carrillo, A.; Gacic, M.; Gasparini, G.P.; Herrmann, M.; Lionello, P.; et al. Circulation of the mediterranean sea and its variability. In The Climate of the Mediterranean Region; Lionello, P., Ed.; Elsevier: London, UK, 2012; pp. 187–256. [Google Scholar]
- Roberts, C.N.; Zanchetta, G.; Jones, M.D. Oxygen Isotopes as Tracers of Mediterranean Climate Variability: An Introduction. Glob. Planet. Chang. 2010, 71, 135–140. [Google Scholar] [CrossRef]
- Pierre, C. The Oxygen and Carbon Isotope Distribution in the Mediterranean Water Masses. Mar. Geol. 1999, 153, 41–55. [Google Scholar] [CrossRef]
- Tanhua, T.; Hainbucher, D.; Schroeder, K.; Cardin, V.; Álvarez, M.; Civitarese, G. The Mediterranean Sea System: A Review and an Introduction to the Special Issue. Ocean Sci. 2013, 9, 789–803. [Google Scholar] [CrossRef] [Green Version]
- Banaru, D.; Carlotti, F.; Barani, A.; Grégori, G.; Neffati, N.; Harmelin-Vivien, M. Seasonal Variation of Stable Isotope Ratios of Size-Fractionated Zooplankton in the Bay of Marseille (NW Mediterranean Sea). J. Plankton Res. 2014, 36, 145–156. [Google Scholar] [CrossRef] [Green Version]
- Estrada, M. Primary Production in the Northwestern Mediterranean. Sci. Mar. 1996, 60, 55–64. [Google Scholar]
- Stratford, K.; Williams, R.G. A Tracer Study of the Formation, Dispersal, and Renewal of Levantine Intermediate Water. J. Geophys. Res. Ocean. 1997, 102, 12539–12549. [Google Scholar] [CrossRef]
- Stratford, K.; Williams, R.G.; Drakopoulos, P.G. Estimating Climatological Age from a Model-Derived Oxygen–age Relationship in the Mediterranean. J. Mar. Syst. 1998, 18, 215–226. [Google Scholar] [CrossRef]
- Gat, J.R.; Shemesh, A.; Tziperman, E.; Hecht, A.; Georgopoulos, D.; Basturk, O. The Stable Isotope Composition of Waters of the Eastern Mediterranean Sea. J. Geophys. Res. C Ocean. 1996, 101, 6441–6451. [Google Scholar] [CrossRef]
- Fry, F.; Sherr, E. d13C Measurements as Indicators of Carbon Flow in Marine and Freshwater Ecosystems. Contrib. Mar. Sci. 1984, 27, 13–47. [Google Scholar]
- Bédard, P.; Hillaire-marcel, C.; Pagé, P. 18O Modelling of Freshwater Inputs in Baffin Bay and Canadian Arctic Coastal Waters. Nature 1981, 293, 287–289. [Google Scholar] [CrossRef]
- Sarkar, P.P.; Janardhan, P.; Roy, P. Prediction of Sea Surface Temperatures using Deep Learning Neural Networks. SN Appl. Sci. 2020, 2, 1458. [Google Scholar] [CrossRef]
- Zuo, X.; Zhou, X.; Guo, D.; Li, S.; Liu, S.; Xu, C. Ocean Temperature Prediction Based on Stereo Spatial and Temporal 4-D Convolution Model. IEEE Geosci. Remote Sens. Lett. 2021, 1–5. [Google Scholar] [CrossRef]
- Zhang, Z.; Pan, X.; Jiang, T.; Sui, B.; Liu, C.; Sun, W. Monthly and Quarterly Sea Surface Temperature Prediction Based on Gated Recurrent Unit Neural Network. J. Mar. Sci. Eng. 2020, 8, 249. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez-Fernandez, I.; Iglesias-Otero, M.; Esteki, M.; Moldes, O.A.; Mejuto, J.C.; Simal-Gandara, J. A Critical Review on the use of Artificial Neural Networks in Olive Oil Production, Characterization and Authentication. Crit. Rev. Food Sci. Nutr. 2019, 59, 1913–1926. [Google Scholar]
- Sánchez-Mesa, J.A.; Galan, C.; Martínez-Heras, J.A.; Hervás-Martínez, C. The use of a Neural Network to Forecast Daily Grass Pollen Concentration in a Mediterranean Region: The Southern Part of the Iberian Peninsula. Clin. Exp. Allergy 2002, 32, 1606–1612. [Google Scholar] [CrossRef]
- Falah, F.; Rahmati, O.; Rostami, M.; Ahmadisharaf, E.; Daliakopoulos, I.N.; Pourghasemi, H.R. Artificial Neural Networks for Flood Susceptibility Mapping in Data-Scarce Urban Areas. In Spatial Modeling in GIS and R for Earth and Environmental Sciences; Hamid Reza Pourghasemi, C., Gokceoglu, A., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 323–336. [Google Scholar]
- Hijazi, A.; Al-Dahidi, S.; Altarazi, S. A Novel Assisted Artificial Neural Network Modeling Approach for Improved Accuracy using Small Datasets: Application in Residual Strength Evaluation of Panels with Multiple Site Damage Cracks. Appl. Sci. 2020, 10, 8255. [Google Scholar] [CrossRef]
- Aparna, S.G.; D’Souza, S.; Arjun, N.B. Prediction of Daily Sea Surface Temperature using Artificial Neural Networks. Int. J. Remote Sens. 2018, 39, 4214–4231. [Google Scholar] [CrossRef]
- Patil, K.; Deo, M.C. Prediction of Daily Sea Surface Temperature using Efficient Neural Networks. Ocean Dyn. 2017, 67, 357–368. [Google Scholar] [CrossRef]
- Dawson, C.W.; Wilby, R.L. Hydrological Modelling using Artificial Neural Networks. Prog. Phys. Geogr. 2001, 25, 80–108. [Google Scholar] [CrossRef]
- Cid, A.; Astray, G.; Manso, J.A.; Mejuto, J.C.; Moldes, O.A. Artificial Intelligence for Electrical Percolation of Aot-Based Microemulsions Prediction. Tenside Surfactants Deterg. 2011, 48, 477–483. [Google Scholar] [CrossRef]
- Papadopoulos, A.; Fotiadis, D.I.; Likas, A. Characterization of Clustered Microcalcifications in Digitized Mammograms using Neural Networks and Support Vector Machines. Artif. Intell. Med. 2005, 34, 141–150. [Google Scholar] [CrossRef]
- Astray, G.; Mejuto, J.C.; Martínez-Martínez, V.; Nevares, I.; Alamo-Sanza, M.; Simal-Gandara, J. Prediction Models to Control Aging Time in Red Wine. Molecules 2019, 24, 826. [Google Scholar] [CrossRef] [Green Version]
- Makarynskyy, O. Improving Wave Predictions with Artificial Neural Networks. Ocean Eng. 2004, 31, 709–724. [Google Scholar] [CrossRef]
- Iglesias-Otero, M.A.; Fernández-González, M.; Rodríguez-Caride, D.; Astray, G.; Mejuto, J.C.; Rodríguez-Rajo, F.J. A Model to Forecast the Risk Periods of Plantago Pollen Allergy by using the ANN Methodology. Aerobiologia 2015, 31, 201–211. [Google Scholar] [CrossRef]
- Ali, F.; El-Sappagh, S.; Islam, S.M.R.; Kwak, D.; Ali, A.; Imran, M.; Kwak, K. A Smart Healthcare Monitoring System for Heart Disease Prediction Based on Ensemble Deep Learning and Feature Fusion. Inf. Fusion 2020, 63, 208–222. [Google Scholar] [CrossRef]
- Srinivasu, P.N.; SivaSai, J.G.; Ijaz, M.F.; Bhoi, A.K.; Kim, W.; Kang, J.J. Classification of Skin Disease using Deep Learning Neural Networks with MobileNet V2 and LSTM. Sensors 2021, 21, 2852. [Google Scholar] [CrossRef]
- Buongiorno Nardelli, B. A Deep Learning Network to Retrieve Ocean Hydrographic Profiles from Combined Satellite and in Situ Measurements. Remote Sens. 2020, 12, 3151. [Google Scholar] [CrossRef]
- Chen, W.; Liu, W.; Huang, W.; Liu, H. Prediction of Salinity Variations in a Tidal Estuary using Artificial Neural Network and Three-Dimensional Hydrodynamic Models. Comput. Water Energy Environ. Eng. 2017, 6, 107–128. [Google Scholar] [CrossRef] [Green Version]
- Cerar, S.; Mezga, K.; Žibret, G.; Urbanc, J.; Komac, M. Comparison of Prediction Methods for Oxygen-18 Isotope Composition in Shallow Groundwater. Sci. Total Environ. 2018, 631–632, 358–368. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Yan, C.; Zhang, T.; Tang, H.; Li, H.; Yu, J.; Bernard, J.; Chen, L.; Martin, S.; Delepine-Gilon, N.; et al. Classification of Wines According to their Production Regions with the Contained Trace Elements using Laser-Induced Breakdown Spectroscopy. Spectrochim. Acta Part B At. Spectrosc. 2017, 135, 91–101. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Kamińska, J.A. A Random Forest Partition Model for Predicting NO2 Concentrations from Traffic Flow and Meteorological Conditions. Sci. Total Environ. 2019, 651, 475–483. [Google Scholar] [CrossRef]
- Vigneau, E.; Courcoux, P.; Symoneaux, R.; Guérin, L.; Villière, A. Random Forests: A Machine Learning Methodology to Highlight the Volatile Organic Compounds Involved in Olfactory Perception. Food Qual. Preference 2018, 68, 135–145. [Google Scholar] [CrossRef]
- Benali, L.; Notton, G.; Fouilloy, A.; Voyant, C.; Dizene, R. Solar Radiation Forecasting using Artificial Neural Network and Random Forest Methods: Application to Normal Beam, Horizontal Diffuse and Global Components. Renew. Energy 2019, 132, 871–884. [Google Scholar] [CrossRef]
- Partopour, B.; Paffenroth, R.C.; Dixon, A.G. Random Forests for Mapping and Analysis of Microkinetics Models. Comput. Chem. Eng. 2018, 115, 286–294. [Google Scholar] [CrossRef]
- Jog, A.; Carass, A.; Roy, S.; Pham, D.L.; Prince, J.L. Random Forest Regression for Magnetic Resonance Image Synthesis. Med. Image Anal. 2017, 35, 475–488. [Google Scholar] [CrossRef] [Green Version]
- Quiroz, J.C.; Mariun, N.; Mehrjou, M.R.; Izadi, M.; Misron, N.; Mohd Radzi, M.A. Fault Detection of Broken Rotor Bar in LS-PMSM using Random Forests. Measurement 2018, 116, 273–280. [Google Scholar] [CrossRef]
- Su, H.; Yang, X.; Yan, X. Estimating Ocean Subsurface Salinity from Remote Sensing Data by Machine Learning. In Proceedings of the IGARSS 2019 — 2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July – 2 August 2019; pp. 8139–8142. [Google Scholar]
- Liu, M.; Liu, X.; Liu, D.; Ding, C.; Jiang, J. Multivariable Integration Method for Estimating Sea Surface Salinity in Coastal Waters from in Situ Data and Remotely Sensed Data using Random Forest Algorithm. Comput. Geosci. 2015, 75, 44–56. [Google Scholar] [CrossRef]
- Kumar, C.; Podestá, G.; Kilpatrick, K.; Minnett, P. A Machine Learning Approach to Estimating the Error in Satellite Sea Surface Temperature Retrievals. Remote Sens. Environ. 2021, 255, 112227. [Google Scholar] [CrossRef]
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A Training Algorithm for Optimal Margin Classifiers. In Proceedings of the 5th Annual Workshop on Computational Learning Theory (COLT’92), Pittsburgh, PA, USA, 27–29 July 1992; pp. 144–152. [Google Scholar]
- Moguerza, J.M.; Muñoz, A. Support Vector Machines with Applications. Stat. Sci. 2006, 21, 322–336. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Du, H.; Liu, H.; Yao, X.; Hu, Z.; Fan, B. Prediction of Surface Tension for Common Compounds Based on Novel Methods using Heuristic Method and Support Vector Machine. Talanta 2007, 73, 147–156. [Google Scholar] [CrossRef]
- Liu, H.X.; Hu, R.J.; Zhang, R.S.; Yao, X.J.; Liu, M.C.; Hu, Z.D.; Fan, B.T. The Prediction of Human Oral Absorption for Diffusion Rate-Limited Drugs Based on Heuristic Method and Support Vector Machine. J. Comp. Aided Mol. Des. 2005, 19, 33–46. [Google Scholar] [CrossRef]
- Li, Z.; Tian, Y.; Li, K.; Zhou, F.; Yang, W. Reject Inference in Credit Scoring using Semi-Supervised Support Vector Machines. Expert Syst. Appl. 2017, 74, 105–114. [Google Scholar] [CrossRef]
- RapidMiner GmbH. RapidMiner Documentation Support Vector Machine (LibSVM). 2021. Available online: https://docs.rapidminer.com/latest/studio/operators/modeling/predictive/support_vector_machines/support_vector_machine_libsvm.html (accessed on 21 September 2021).
- Sunder, S.; Ramsankaran, R.; Ramakrishnan, B. Machine Learning Techniques for Regional Scale Estimation of High-Resolution Cloud-Free Daily Sea Surface Temperatures from MODIS Data. ISPRS J. Photogramm. Remote Sens. 2020, 166, 228–240. [Google Scholar] [CrossRef]
- Ríos-Reina, R.; Elcoroaristizabal, S.; Ocaña-González, J.A.; García-González, D.L.; Amigo, J.M.; Callejón, R.M. Characterization and Authentication of Spanish PDO Wine Vinegars using Multidimensional Fluorescence and Chemometrics. Food Chem. 2017, 230, 108–116. [Google Scholar] [CrossRef] [Green Version]
- Karimi, F.; Sultana, S.; Shirzadi Babakan, A.; Suthaharan, S. An Enhanced Support Vector Machine Model for Urban Expansion Prediction. Comput. Environ. Urban Syst. 2019, 75, 61–75. [Google Scholar] [CrossRef]
- Jing, G.; Cai, W.; Chen, H.; Zhai, D.; Cui, C.; Yin, X. An Air Balancing Method using Support Vector Machine for a Ventilation System. Build. Environ. 2018, 143, 487–495. [Google Scholar] [CrossRef]
- Nirala, N.; Periyasamy, R.; Singh, B.K.; Kumar, A. Detection of Type-2 Diabetes using Characteristics of Toe Photoplethysmogram by Applying Support Vector Machine. Biocybern. Biomed. Eng. 2019, 39, 38–51. [Google Scholar] [CrossRef]
- Zhong, M.; Xuan, S.; Wang, L.; Hou, X.; Wang, M.; Yan, A.; Dai, B. Prediction of Bioactivity of ACAT2 Inhibitors by Multilinear Regression Analysis and Support Vector Machine. Bioorg. Med. Chem. Lett. 2013, 23, 3788–3792. [Google Scholar] [CrossRef]
- Samghani, K.; HosseinFatemi, M. Developing a Support Vector Machine Based QSPR Model for Prediction of Half-Life of some Herbicides. Ecotoxicol. Environ. Saf. 2016, 129, 10–15. [Google Scholar] [CrossRef]
- Ahn, J.J.; Oh, K.J.; Kim, T.Y.; Kim, D.H. Usefulness of Support Vector Machine to Develop an Early Warning System for Financial Crisis. Expert Syst. Appl. 2011, 38, 2966–2973. [Google Scholar] [CrossRef]
- Lins, I.D.; Araujo, M.; Moura, M.d.C.; Silva, M.A.; Droguett, E.L. Prediction of Sea Surface Temperature in the Tropical Atlantic by Support Vector Machines. Comput. Stat. Data Anal. 2013, 61, 187–198. [Google Scholar] [CrossRef]
- Aguilar-Martinez, S.; Hsieh, W.W. Forecasts of Tropical Pacific Sea Surface Temperatures by Neural Networks and Support Vector Regression. Int. J. Oceanogr. 2009, 2009, 167239. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, G.A.; Bigg, G.R.; Rohling, E.J. Global Seawater Oxygen-18 Database—v1.22. 1999. Available online: https://data.giss.nasa.gov/o18data/ (accessed on 21 July 2021).
- Schmidt, G.A. Forward Modeling of Carbonate Proxy Data from Planktonic Foraminifera using Oxygen Isotope Tracers in a Global Ocean Model. Paleoceanography 1999, 14, 482–497. [Google Scholar] [CrossRef]
- Bigg, G.R.; Rohling, E.J. An Oxygen Isotope Data Set for Marine Waters. J. Geophys. Res. Ocean. 2000, 105, 8527–8535. [Google Scholar] [CrossRef]
- Pierre, C.; Vergnaud-Grazzini, C.; Thouron, D.; Saliège, J.F. Compositions Isotopiques De L’Oxygène Et Du Carbone des Masses D’Eau En Méditerranée. Mem. Soc. Geol. It. 1986, 36, 165–174. [Google Scholar]
- Stahl, W.; Rinow, U. Sauerstoffisotopenanalysen an Mittelmeerwaessern; Ein Beitrag Zur Problematik von Palaeotemperaturbestimmungen, Meteor-Forschungsergebnisse. Reihe C Geol. Geophys. 1973, 14, 55–59. [Google Scholar]
- Pozzi, M.; Malmgren, B.A.; Monechi, S. Sea Surface-Water Temperature and Isotopic Reconstructions from Nannoplankton Data using Artificial Neural Networks. Palaeontol. Electron. 2000, 3, 14. [Google Scholar]
- McCulloch, W.S.; Pitts, W. A Logical Calculus of the Ideas Immanent in Nervous Activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Kriesel, D. A Brief Introduction to Neural Networks. 2007. Available online: http://www.dkriesel.com (accessed on 21 September 2021).
- Basheer, I.A.; Hajmeer, M. Artificial Neural Networks: Fundamentals, Computing, Design, and Application. J. Microbiol. Methods 2000, 43, 3–31. [Google Scholar] [CrossRef]
- RapidMiner GmbH. RapidMiner Documentation. Neural Net. 2021. Available online: https://docs.rapidminer.com/latest/studio/operators/modeling/predictive/neural_nets/neural_net.html (accessed on 21 September 2021).
- Chang, C.C.; Lin, C.J. LIBSVM: A Library for Support Vector Machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 27. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, C.J. LIBSVM: A Library for Support Vector Machines. Available online: https://www.csie.ntu.edu.tw/~cjlin/libsvm/ (accessed on 24 September 2021).
- Hsu, C.W.; Chang, C.C.; Lin, C.J. A Practical Guide to Support Vector Classification. 2003, pp. 1–16. Available online: https://www.csie.ntu.edu.tw/~cjlin/papers/guide/guide.pdf (accessed on 24 September 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).