Abstract
Much applied research uses expert judgment as a primary or additional data source, thus the problem solved in this publication is relevant. Despite the expert’s experience and competence, the evaluation is subjective and has uncertainty in it. There are various reasons for this uncertainty, including the expert’s incomplete competence, the expert’s character and personal qualities, the expert’s attachment to the opinion of other experts, and the field of the task to be solved. This paper presents a new way to use the Bayesian method to reduce the uncertainty of an expert judgment by correcting the expert’s evaluation by the a posteriori mean function. The Bayesian method corrects the expert’s evaluation, taking into account the expert’s competence and accumulated long-term experience. Since the paper uses a continuous case of the Bayesian formula, perceived as a continuous approximation of experts’ evaluations, this is not only the novelty of this work, but also a new result in the theory of the Bayesian method and its application. The paper investigates various combinations of the probability density functions of a priori information and expert error. The results are illustrated by the example of the evaluation of distance learning courses.
1. Introduction
In any field of activity, a person faces choices. Different decisions are made in different ways; sometimes people think them over too long, structuring the rationalization process, or, vice versa, they reach conclusions quickly and intuitively, without a clear logic or justification and without wondering about the consequences [1]. According to Hartley and French, a judgment should be a well thought-out opinion that considers the degree of scientific or other knowledge about previous experiences [2]. In decision-making, particular attention is given to the uncertainty of the initial data. The uncertainty of the data can be estimated in different ways, depending on its source [3]. Methods have been developed for this purpose on the basis of specific mathematical theories such as fuzzy set theory and mathematical statistics [4].
In solving decision-making tasks, we meet with problems of incomplete information [5]. In situations in which the object under study cannot be measured with a device and the empirical data are unavailable, incomplete, uninformative, or contradictory [6], the data can be supplemented with an evaluation by a qualified specialist, an expert in the relevant field who has knowledge and skills. An expert evaluation is a moment indicator that can change over time and under the influence of acquired knowledge. Experts are selected based on their professional competence, taking into account characteristics such as work experience, academic degree, experience in the research activity, and ability to solve specific tasks in the relevant field.
Unfortunately, the selection of a competent expert does not solve the problem of uncertain data because of human factors and incomplete knowledge of the true meaning of the object being evaluated. The existence of human errors does not imply or assume that people are incompetent in terms of perception or cognition [7]. An expert’s experience in one particular field does not necessarily mean that the expert is also good at assessing uncertainty in another or a related field [2]. Similarly, attachment to the opinion of other experts, a wish to influence the final result, excessive self-confidence or an unwillingness to agree with the opinion of others, the framing effect, disregard for the a priori probability [8], a lack of concentration, and a lack of interest can lead to an inaccurate evaluation. The data obtained based on expert judgments therefore have a stochastic nature. Changing the composition of the experts, reducing or increasing the number of experts, and repeating the evaluations will lead to ambivalent results [9]. If it is to be studied quantitatively, uncertainty must be represented by a mathematical concept such as probability [10].
The main difference between expert judgment and empirical data is that expert opinion is personal and has a so-called ‘subjective probability’ [2]. There is one opinion that it is impossible to get accurate results on the basis of subjective probability. Brownstein and others refute this view by arguing that science itself has a subjective component, aspects of which can be reported probabilistically and must be interpreted according to the theory of subjective probability [11,12]. Although judgments are subjective, expert evaluation results from a synthesis of relevant prior knowledge and experience based on observable evidence and careful reasoning [11]. In the Bayesian theory, subjective probabilities are based on a well-known accurate and comprehensible system of axioms, and in this way, there is no doubt from a mathematical point of view [13]. Cooke and Goossens believe that, within the subjective interpretation of probability, uncertainty is the degree of a person’s conviction, and can be measured by observing the person’s behaviour during the choice [10].
When considering expert opinions, special attention is paid to the psychology of experts, taking into account their competence to the same extent as the quantitative information, or the evaluation, that they provide [8]. One view is that if observers are allowed to influence each other, the sample size will decrease, and, because of this, the accuracy of the group evaluation will decrease. If useful information is to be obtained from multiple sources, then one should ensure that those sources are independent of each other [14]. However, if we combine all the individual judgments, the result will be unexpectedly good [8].
Experts express their judgments in different ways. In particular, the information owned by the expert is extracted, and a probabilistic representation of this knowledge is constructed [15], using pairwise comparisons, linguistic variables, and fuzzy and natural numbers [3,9].
The trial roulette method is used to elicit the distribution [16], or experts are asked questions about probabilities or quantiles that the analyst converts into parameters of probability distributions [17]. According to Hartley and French, it can be difficult in practice for experts to think in terms of distributions. Therefore, it is often wise to simplify the problem without directly identifying the distribution of the associated parameters [2]. In this paper, experts evaluate quality on the usual 10-point scale. The next section presents a review of the scientific literature on the Bayesian approach and expert judgment in the Web of Science database was performed since this study is carried out within the Bayesian method in decision-making.
2. Literature Review
The Bayesian approach is widely used in the theory and practice of various fields of science. According to Arimone et al., almost all probabilistic approaches are derived from Bayes’ theorem [18]. In Bayesian statistics, the preliminary distribution containing the probable values for each model parameter is updated with data, resulting in an a posteriori distribution. Bayesian methods based on models of the objective statistical function are optimal from the point of view of the average. Regardless of the stochasticity of the data, the average value remains constant [13,19]. The updated result can increase trust in the initial opinions of the experts or adapt these views. As a rule, reliable information is given in a narrow distribution received from an expert [2].
Podofillini et al. employed a Bayesian model to aggregate expert judgments to identify human failures in the field of radiation therapy. A qualitative scale was used for the expert judgments; the judgments were then interpreted as information about the order of magnitude of the error probability, and were aggregated according to the Bayesian scheme [20]. Bigün presented a study on the analysis of the risks of major aviation accidents in Europe using expert evaluation and a Bayesian approach. Models combining expert judgments to predict future risks were investigated [21]. In the work of Leden et al., expert judgments were taken into account using the Bayesian error model in a study of the evaluation of the effect on safety of a new bicycle crossing design [22]. Zavadskas et al. applied a Bayesian approach to modelling the uncertainty associated with the probability of failure, showing that the uncertainty can be reduced when new data are obtained. The method of technological risk management proposed by these authors applies to many industrial and non-industrial facilities that are subject to accidents [23].
A future direction in psychological research is the inclusion of the preliminary knowledge of experts in the statistical analysis [15]. Ramli and colleagues developed a new fuzzy Bayesian Network framework for modelling the psychological reaction and human behaviour in a fire. Experts used fuzzy linguistic terms to determine a priori and conditional probabilities in the Bayesian Network [24]. Zhou et al. offered a method using the Bayesian Network auxiliary model to study the parameters of this network. Together with the data set, expert judgments are used, and result in a more accurate machine learning result with a more minor data set [25]. Sigurdsson et al. presented an overview of Bayesian belief nets for managing expert judgments, and described their use in modelling system reliability [26]. Varis et al. presented a probabilistic Bayesian matrix approach for obtaining expert judgments using belief networks from artificial intelligence. The authors studied the impact of surface water on climate change [27]. Rosqvist also followed the Bayesian approach for the aggregation of expert evaluations and the use of expert judgment for new or regularly modified systems [28].
Wisse et al. used moment methods to combine expert judgments, showing how expert evaluations of moments can be combined in a non-Bayesian way to build an a priori estimate [29]. Smets compared the transferable belief model and the Bayesian approach in her study of expert judgment and the reliability problem. The author claimed that it is impossible to prove which solution is correct since each approach matches different regulatory requirements [30]. Hartley proposed the Bayesian Framework for Structural Expert Judgment (SEJ) alternative to traditional non-Bayesian methods. Posterior distributions are created using the clustering, calibration, and aggregation stages [2].
Mockus argued that, when comparing heuristic algorithms that reflect real-life conditions, the Bayesian approach improves efficiency. Researchers often work hard to determine the best parameters for a proposed heuristic. In Mockus’s work, the Bayesian approach is used to adjust heuristic parameters automatically to find optimal combinations of heuristics [31]. Capa Santos et al. used a Bayesian approach to model operational risk, including macroeconomic effects and expert evaluations [32]. Mazzuchi and van Dorp provided a Bayesian model of expert evaluation to determine lifetime distributions for optimizing maintenance [33]. Jiang et al. proposed a method based on Bayesian theory to identify the relationship between product reliability indicators and quality characteristics in production [34].
Koh et al. applied the Bayesian framework to research into the intensity of exposure to lead in the air in industry. The lead measurement data were logarithmically converted to log-transformed geometric means (LGM) and log-transformed geometric standard deviations (LGSD) values. The experts’ prior distributions were updated with the corresponding LGMS and LGSD values using the Bayesian approach [35]. Åström et al. used the Bayesian approach to include expert judgments in regional evaluations of the sensitivity and specificity of the analysis of the source of drinking water [36] and Parent and Bernier used for studying the risks of extreme hydrological events [37]. Washington and Oh applied Bayes’ theory in a study of the safety of railway crossings in Korea [38], and Ramachandran et al. did the same in the field of occupational health [39]. These authors claimed that expert judgment improved their knowledge about dangers in the workplace, and suggested combining expert assessments with sparse data [39]. Ramachandran et al. also noticed a very high degree of agreement among the experts, although the experts represented different areas of interest. They concluded that there is presumably a vast amount of specialized knowledge that experts use to make similar judgments [39]. Vinogradova et al., to clarify the values of the weights of multi-criteria methods, used the idea of a revaluation of the Bayes hypotheses, combining various evaluations of the weights obtained by various methods into an aggregate, integral judgment [9].
One of the critical points in the decision-making process is the identification of uncertainties, such as the consistency between parameters and the combination of judgments. Werner et al. paid great attention to the dependence between variables [40]. Wilson investigated the dependence of several expert evaluations, both within and between experts [17]. Werner et al. and French et al. discussed mathematical methods for the aggregation of evaluations, such as the pool of opinions, Cooke’s Classical Model, and Bayesian aggregation [6,40].
Considerable attention has been paid to verifying the stability of the methods themselves. Vinogradova has also researched the stability of decision-making methods, including Analytic Hierarchy Process (AHP), Fuzzy Analytic Hierarchy Process (FAHP) [3], Simple Additive Weighting (SAW), Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS), Multi-objective Optimization (MOORA), and Preference ranking organization method for enrichment evaluation (PROMETHEE) [41,42], and the influence of data uncertainty on the final results. Ziemba uses stochastic analysis to study the uncertainty of the parameters of alternatives in the PROSA-C (PROMETHEE for Sustainability Assessment—Criteria) method [43]. Lam et al. proposed an entropy–fuzzy VIKOR (VIseKriterijumska Optimizacija I Kompromisno Resenje) model in which objective weights are used, avoiding subjectivity in determining the weights of criteria [44].
A new concept is used to model uncertainty in decision-making problems—linear Diophantine fuzzy information. Diophantine equations have, as a rule, many solutions, therefore, are called indefinite. The problems of linear Diophantine fuzzy information were dealt with by Riaz et al., proposing new aggregation operators for modeling uncertainty that remove the strict restrictions of existing operators [45]. Particular attention should be paid to the works of Narayanamoorthy et al. [46,47,48,49,50] on decision making, using the methodology of MCDM in hesitant fuzzy. Narayanamoorthy uses Normal Wiggly Hesitant Pythagorean Fuzzy Set with DEMATEL (Decision Making Trial and Evaluation Laboratory Model) and COPRAS methods [46], the scenarios of hesitant fuzzy number with MOORA, TOPSIS, VIKOR [47], and SWARA (Step-wise Weight Assessment Ratio Analysis) [48] methods, proposed normal wiggly hesitant fuzzy set (NWHFS), as an extension of hesitant fuzzy set [49], also the new methodology HF-CRITIC (Hesitant Fuzzy Criteria Importance Through Inter-criteria Correlation) and HF-MAUT (Hesitant Fuzzy Multi Attribute Utility Theory) to get hesitant fuzzy information in order to select the best alternative [50]. Zavadskas et al. presented a new multi-criteria decision-making approach that reduces errors and instabilities caused by novice evaluators using the heuristic evaluation methodology HEBIN (Heuristic Evaluation Based on Interval Numbers) under MULTIMOORA-IVNS (Multi-Objective Optimization by Ratio Analysis under Interval-Valued Neutrosophic Sets [51]. When optimizing under uncertainty, two different approaches are widely used: Min-Max and Bayesian [31].
Literary analysis confirms the relevance of the task solved in this publication. Scientists have proposed many methods, methodologies, and theories working with data, trying to reduce their uncertainties, depending on the different source of their occurrence. There is no single correct solution or best method, which explains the emergence of new solution alternatives. This research proposes a new view of data uncertainty, using the accumulated experience of expert evaluations and the expert’s competence, based on the optimality of the Bayesian method in terms of the mean. The a posteriori mean function corrects the expert’s estimate. A continuous set of possible values of some finite interval of the evaluation scale is used, describing the accumulated experience and competence of the expert by some distributions—such a Bayesian approach has not been proposed in the literature, which gives grounds for conducting this research. This research is possible using mathematical packages that approximate each value of the estimation interval on a straight line. The optimality of the proposed approach is interpreted as the averaged value of the a posteriori function, depending on the a priori information and the expert’s competence.
The publication consists of seven sections. Section 1 is an introduction to the issues of the paper and Section 2 is a literary analysis. Section 3 describes the proposed theory of applying the Bayesian method in expert judgment, while Section 4 is devoted to the study and testing of the proposed theory. In Section 5, cases of using different density functions to describe the accumulated experience of expert estimates and expert error are considered. The cases are tested by changing the parameters used. In Section 5, the problem of the evaluation of the quality of distance courses is solved, in which the proposed theory is applied. In Section 6, the results are discussed, while Section 7 presents the conclusions.
3. Application of the Bayesian Approach
In this paper, the Bayesian method is used to adjust the expert’s evaluation using the value of the a posteriori probability mean function , which depends on the experience of the a priori estimation that has been collected and the qualification of the expert making the decision. The expert evaluates the grade of the quality as . The a posteriori probability mean function (from now on, the mean function) adjusts the expert’s evaluation:
where [a, b] is the interval of expert evaluations. In this research, a = 1, b = 10.
In this case, the function is the adjusted evaluation of the expert, and represents the best approximation to the expert’s judgment when is the expert’s grade. The adjustment (correction) of the expert’s evaluation is the difference between the adjusted value and the grade X.
The Bayesian method uses all the accumulated experience (i.e., all the past information about the evaluation and qualifications of a particular expert) to determine the a posteriori probability density function. This publication uses the continuous case of the Bayesian formula, which can be written in the following way [5]:
where the density function is the a posteriori probability distribution of the parameter using empirical information about the random variable The parameter is the true quality, otherwise known as the state of nature.
The conditional density function in the Bayesian formula is the conditional probability distribution of the new evaluation when the true state of nature is . This function defines the error that is made by the expert when accepting the grade instead of the true quality . The conditional density function of the expert error depends on the qualification of the expert.
The a posteriori probability density function updates the a priori information about according to the sample data . The a priori information accesses the a posteriori probability density function through the a priori probability density function , with all the sample information entered via the function .
The a priori probability density function is the accumulated evaluation experience, where is the true quality. The primary quality information is based on a subjective expert judgment or derived from previous observations and evaluations. The accumulation of expert judgment provides valuable knowledge for decision-makers [52]. Washington and Oh thought that, in most cases, the inclusion of a priori information in the evaluation process increases the reliability of the result [38].
The a priori probability distribution is adjusted according to the empirical information; it is not necessary to specify , and sometimes, it is enough to identify the a priori distribution type, which includes . More broadly, a priori information can be information based either on science or on accumulated objective data or self-assessment, research, or another type of subjective information. The use of a priori information depends on the purpose of the analysis. A comparison of a priori and a posteriori information identifies how the sample information changed the initial assumptions.
The function is a density function of the judgments for all possible values of the parameter , estimating their subjective probabilities [5]:
For a better understanding, the proposed Bayesian approach is illustrated in Figure 1.

Figure 1.
The flowchart presenting the procedure of the proposed Bayesian approach.
The following section details the prior and expert error density functions used in the further research. The research analyses the possibility of using various combinations of probability density functions to evaluate the quality of distance learning courses.
3.1. A Priori Probability Density Functions
In this research, the a priori information is given by a uniform, triangular or Gaussian probability density function. If experience has not been accumulated or is unknown, then a uniform distribution is used as the a priori probability function. In other cases in this paper, when experience has been collected, the a priori information is set by the triangle or Gaussian distributions that are most suitable for describing expert judgments.
The a priori triangular distribution is used so that, in further research, the results obtained can be approximated and compared with other works in the field of expert judgments that use fuzzy numbers. Triangular fuzzy numbers specify the range of possible judgments, indicating the minimum and maximum values and the most likely evaluation that belongs to the specified interval. One of the most commonly used Gaussian distributions is characterized by random variables that sum up a set of independent factors. The Gaussian distribution is limiting for many other distributions.
3.1.1. The Uniform Distribution for Defining the a Priori Information
When the density of all random variables in the range is constant, it is given by a continuous uniform distribution. The uniform distribution probability density function is used when there is no collected experience. Alternatively, it may be supposed that the scores of the quality of the evaluated objects are uniformly distributed over the whole range; this means that it is assumed that is equally distributed over the possible evaluation scale. The probability density function of a uniform distribution is determined by the following formula:
The quality is evaluated on a ten-point scale, i.e., a = 1, b = 10.
3.1.2. The Triangular Distribution for Defining the a Priori Information
A triangular distribution is used when the most probable mean value in a given range is known. The probability density function plot consists of two segments, one of which increases when changes from the minimum to the mean, and the other of which decreases from the mean to the maximum value .
When the collected information is known in the case of expert evaluations, it is not difficult to write down three values: the minimum, the maximum, and the most likely () values. In this paper, we calculated the value of the mean of all the accumulated evaluations, but one can also use the mode.
Since a priori experience may not be enough, the usual interval from the evaluation scale [a, b] is used to determine the minimum and maximum values of the triangle:
3.1.3. The Gaussian Distribution for Defining the a Priori Information
The probability density function of the normal or the Gaussian distribution is symmetric relative to the mean value, and gives a good characterization of many measurement results; it is therefore one of the most frequently used continuous distributions. The parameters when the a priori probability density function has a Gaussian distribution, i.e., an average value µ and standard deviation σ, are set based on the information collected by the institution for the previous years:
The standard deviation describes the change in a set of values about the mean and is calculated using the formula:
where is the sample element, the sample mean, and n the sample size.
3.2. The Conditional Density Function
The conditional density function describing the expert’s error depends on the expert’s competence, and shows how much the expert’s evaluation deviates from the true score.
The function is defined by the parameters , where is the expert’s evaluation when the true quality is θ. The expert’s error , given by the distribution , depends on the expert’s competence and is the deviation of the expert’s score of from the true quality θ. The error of an experienced expert is set at no more than 1, and is used in this paper. The more competent the expert, the smaller the error will be; the error of the most experienced expert is . Correspondingly, the error of the least experienced expert is .
3.2.1. The Triangular Distribution for Defining the Expert’s Error
The density function of the expert error is given by a triangular distribution, which is symmetric relative to the state of nature θ. The error is determined as the deviation of the evaluation from the true goodness
The conditional probability density function given by the triangular distribution describing the expert’s error is written as follows:
3.2.2. Gaussian Distribution Used for Defining the Expert’s Error
The conditional probability density function given by the Gaussian distribution for the expert’s error is defined as:
The function is symmetric relative to the state of nature .
The probability density functions described above are used in the following sections to analyse the possibility of combining them in the expert judgment. The influence of changes in the parameters of the functions describing the a priori information and the expert error on the clarification of the evaluation , depending on the expert’s competence, is analysed.
The complexity of the problem solved in this article is that and are considered to be continuous random variables, while experts usually use integers in the range from 1 to 10 in their evaluations. For a continuous approximation to be acceptable, it is necessary to make a correct selection of the ranges of changes in the and values.
4. Case Study Using the Bayesian Approach for Expert Judgment
When the Bayesian approach is used in expert judgment, the expert evaluates the quality of the object in the usual way on a 10-point scale, giving a score of . The conditional density function of the expert error, depends on the competence of the evaluating expert. The complete evaluation of the estimated object is generalized by the a posteriori mean function, which is calculated using Formula (1).
This paper discusses the use of five different cases of combinations of the a priori and conditional density functions described in Section 2. During the analysis, the parameters describing the a priori information function and the expert error function change, and this tends to change the values of the mean functions. In the first and second cases, combinations of the a priori probability uniform distribution with the conditional triangular and Gaussian distributions are studied. In the third case, a triangular distribution is used for the a priori information and the expert error functions. An a priori probability Gaussian distribution is considered in the fourth and fifth options, with triangular and Gaussian distributions.
4.1. Case 1: Uniform Distribution with a Triangular Distribution
Since the true quality is unknown, may lie at any point in the range [a, b], thus the expert’s error triangle slides across the range of the a priori distribution. One of the separate cases is shown in Figure 2 when is found at Point 7.
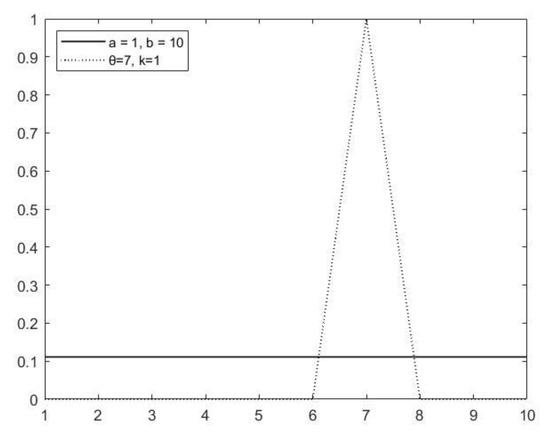
Figure 2.
The probability density functions of uniform (a priori information) and triangle (expert error) distributions.
Since is an integral of the product of two functions, the density of the function when , and Formula (3) is rewritten as follows:
The function of the estimates for all possible values of for the a priori uniform and conditional triangle distributions is as follows:
The a posteriori probability function equals:
The mean function of (12) is calculated according to Formula (1):
When the a priori probability density function is described by a uniform distribution and by a triangular distribution, the mean function equals , regardless of the expert’s error . In this case, the correction of the expert’s evaluation is equal to 0. Therefore, it is convenient to compare the evaluation results based on the accumulated a priori information with a linear function, which implies the absence of initial information.
4.2. Case 2: Uniform Distribution with a Gaussian Distribution
The conditional density function of the Gaussian distribution shifts over the entire a priori uniform distribution interval. The function of the estimate for all possible values of the parameter is as follows:
In this case, the a posteriori function is:
According to Formula (1), the mean function of the a posteriori function (15) is calculated as follows:
Combining a uniform and a Gaussian distribution gives an analogous result . It is convenient to compare the corrected values of the expert’s evaluation with the graphic showing the zero correction of the expert’s evaluation.
Thus, for a priori probability having a uniform distribution with conditional density functions of the triangular or Gaussian distributions, the mean functions are , regardless of the parameter of the conditional density function. In the absence of accumulated experience in the evaluation, the expert scores are not adjusted and remain the same.
4.3. Case 3: Triangle Distribution That Determines a Priori Information and Expert’s Error
The a priori information is described by the triangle distribution given in Formula (5). The expert’s error is described by the conditional density function of the triangle (Formula (8)) with the mean at the point . The triangle is moving within the a priori function.
Formula (10) calculates the function of the evaluations for all possible values of the parameter
Using the Bayesian Formula (2), the a posteriori function is calculated as follows:
Table 1 and Table 2 provide the corrected expert evaluations for different scores of by changing the parameter of the mean of the a priori probability triangle function (Table 1) and the expert error variable (Table 2). When studying the influence of on the function , the expert error parameter remains unchanged and is equal to .

Table 1.
Dependence of the function value on the parameter and the grade in case 3.

Table 2.
Dependence of the value of the function on the expert error and the grade in case 3, when .
Analysing the results of Table 1, we notice a trend in the way in which the mean value of the a priori probability density function affects the refinement of the evaluation of by the function . When , the value of the evaluation of is adjusted upwards, and, accordingly, when , the evaluation of decreases. In the case of , the change in the value of is the most insignificant.
The closer the value of is to the value of , the smaller the correction, and vice versa. Note that for and , the results of refining the evaluations are inaccurate and illogical. Figure 3 shows the graphic for = 9.5, on the segment 𝝐 [0;10]. At the end of the interval, the graphic is bent, which can be explained by the use of a triangular distribution for the a priori density function; since , when , when integrating, the conditional triangular distribution goes beyond the interval by a distance .
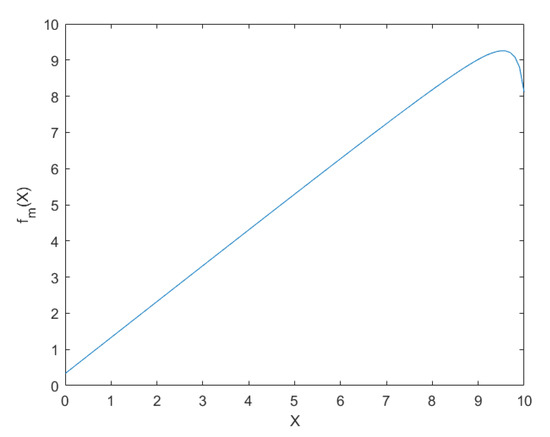
Figure 3.
Function for case 3, when , .
This is especially evident when the value of is high. Therefore, for a high value of the mean of the function this option is not recommended because of inaccuracies at the ends of the function .
When studying the dependence of the parameter on the function , at , this pattern is observed (Table 2). The smaller the value of , the more minor the correction of the evaluation of . If the expert making the decision is of high competence, then his judgment is more trustworthy, and the a priori evaluation has less influence on the correction of his score.
Despite the size of the change in the evaluation depending on the value of , the tendency to correct the score remains the same. The evaluation decreases if the mean value of the function is less than the evaluation and increases in the opposite case.
4.4. Case 4: Gaussian Distribution with a Triangle Distribution
The a priori information is defined by a Gaussian distribution, and the expert error by a conditional triangle distribution. For this case, the function is as follows:
Accordingly, the a posteriori function is:
We will examine the dependence of the mean function on the parameters of the mean , the standard deviation , and the expert error of the Gaussian distribution function .
Let us study the case for different when and (Table 3). Analysing the results of Table 3, we can notice the same trend as we saw in case 3. When , the value of the evaluation of is adjusted up, and, in the same way, when , the evaluation of decreases. Unlike the previous case, if then the values of remain unchanged and are not adjusted.

Table 3.
Dependence of the function value on the mean of and the grade in case 4.
The problem of correcting the evaluation appears at when the mean value of the function is high (). A single case of the graph of , when and the parameters are , is shown in Figure 4.
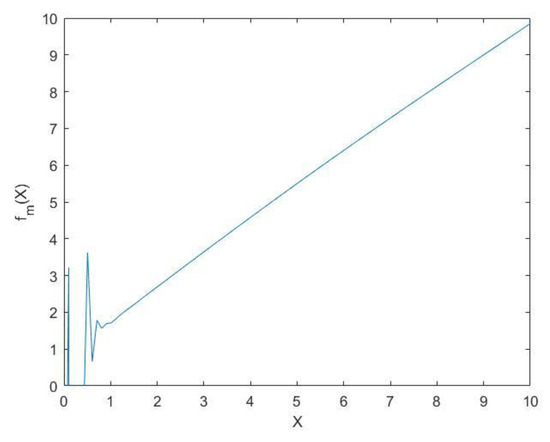
Figure 4.
The function for case 4, when .
The explanation for this is the thin Gaussian tail of the a priori distribution and the conditional triangular distribution that goes beyond the interval by a distance . Despite this problem, this option can be used, since the evaluation of is unlikely when evaluating quality, and it is possible to narrow the evaluation scale to .
When , this problem does not arise, with the same parameter of the a priori function of (Table 4). Changing the parameter , which reflects the expert’s competence, the correction of the evaluation increases with the value of . In the case of , the evaluation correction is zero for any value of .

Table 4.
Dependence of the value of the function on the expert error and the grade in case 4, when .
To study the influence of the parameter on the function , the remaining parameters and are left unchanged (Table 5). For a higher value of , the a priori function has a flatter form, and the correction of the evaluation of is insignificant. When the parameter decreases, the correction of the function increases. In the case of , the evaluation correction is zero for any value of the parameter .

Table 5.
Dependence of the value of the function on the standard deviation parameter, and the grade in case 4, when , .
In all the cases of changes to the parameters studied here, the tendency to correct the evaluation remains the same. The evaluation of is corrected according to the regression principle: it decreases if and increases if . When , the evaluation of does not change.
4.5. Case 5: Gaussian Distribution That Determines a Priori Information and Expert’s Error
The a priori information is distributed according to a Gaussian distribution (Formula (6)). The conditional density function of the Gaussian distribution is given in Formula (9). The probability function of the observations for all possible values of the parameter is as follows:
Accordingly, the a posteriori function is:
For the case when the probability density functions and are Gaussian distributions, we analyse the effect of the parameter of the a priori function on the function for different values of (Table 6). The parameter of the function is set to and the expert error . The values of the function increase as the parameter increases. The function has no breaks at the beginning or the end, unlike the previous cases 3 and 4.

Table 6.
Dependence of the function value on the mean of and the grade in case 5.
If the value of the expert’s evaluation is , then the value of is corrected upwards; if , then the value of ; if , then the value of is less than the value of due to the low mean evaluation of the accumulated experience given by the probability distribution.
A study of the influence of the expert error on the function (, ) shows that with a smaller value of , the value of is smaller, and increasing the value of means that the value of increases (Table 7).

Table 7.
Dependence of the function value on the expert error and the grade in case 5, when , .
By changing the parameter for the a priori function , for , (Table 8) and , k = 1 (Table 9), the results are comparable to the fourth case, which also uses the a priori Gaussian function (Table 5). For a smaller value of , the correction of the evaluation of is more significant; correspondingly, for a larger value of , the values of are lower.

Table 8.
Dependence of the value of the function on the standard deviation parameter of the function and the grade in case 5, when , .

Table 9.
Dependence of the value of the function on the standard deviation parameter of the function and the grade X in case 5, when , .
The parameters , 0.5 of the a priori function show that the scores were high for a long period of the evaluation and differed little from the mean value (Table 8). With a small spread of a priori scores, has a more significant impact on the correction of the evaluations. If the mean value of the a priori function is high, then at 0.5 the correction of the evaluation of is more significant than at 1.5.
Comparing the results of Table 8 and Table 9, the values of the function are higher with a larger value of .
When the spread of the accumulated estimates is higher, the influence on the result of the mean value of the function is less. Regardless of the size of the parameter , for , the function . In this case, when (Table 9). It can be seen from Figure 5 that the trend of the correction of the score X for different values of is the same.
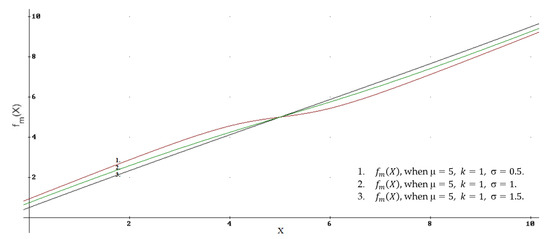
Figure 5.
Dependence of the function in case 5 on different , when .
Comparing the different combinations of a priori and conditional functions, case 5 appears to be the best for use in a quality evaluation. In cases 3 and 4, there are inaccuracies at the ends of the function .
5. Experimental Application of the Bayesian Approach for Evaluation of Distance Learning Courses
In this section, the above theory is applied to the evaluation of the quality of distance learning courses in one of the higher educational institutions of Lithuania. Distance learning courses are evaluated at least every semester, i.e., twice a year. For several years, the experience was collected. The courses are evaluated by a group of experts, with each expert making a decision independently, and only then the average mark for each course is calculated.
In this example, a group of six experts with different experiences and skills in distance learning education participate in evaluating the quality of the distance learning courses. The first two experts have been working in distance learning for over 12 years; therefore, for these more experienced specialists, the expert error is k = 0.8. The next three specialists have sufficient experience in teaching or writing curriculums, but they are not specialized in distance learning education, thus the error of these experts is k = 1. Moreover, a beginner specialist, specializing in the video recording of lectures and other videos and the animation design of the course, participates in evaluating the distance learning courses, with k = 1.2.
After determining the competence and the value of the expert error k for each commission member, the parameters of the a priori function are calculated. In practice, a specific statistical distribution is selected after confirming the statistical hypothesis about the type of distribution over a significantly large number of measurements. In this analytical work, the variants mentioned above of the combinations of distributions are used. For the a priori probability triangular function, the mean value of the evaluations is calculated. For the a priori Gaussian function, two parameters are calculated: the mean value and the standard deviation of the evaluations.
For an example of the application of the theory, three courses of different quality were selected. The first course, from the field of computer science and applied mathematics was ‘Machine learning and neural networks’, while the others, from the field of construction, were ‘Structural engineering’ and ‘Building management’.
To determine the parameters for the functions, we use the experience of the previous two years. In the subject area of mathematics and computer science, 39 courses were evaluated in these two years, with a mean value of 8.638 and a standard deviation of 1.463. In the construction field, 36 courses were evaluated, with a mean value of 8.864, and a standard deviation of 0.995.
Table 10 presents the experts’ evaluations X and their corrected values according to their competence.

Table 10.
Machine learning and neural networks’ course evaluations; , .
The previously described combinations of distributions show how they can be used in expert evaluation. The corrections in cases 4 and 5 are similar to each other, and both options use the a priori Gaussian function. When using the triangular function , the corrected evaluations are lower than in the other two cases, with a high average value of . In case 3, the value is not taken into account. The value indicates a large spread of a priori estimates relative to the mean value.
For subsequent courses, the parameters of the functions are the same, since both courses are from the field of construction (Table 11 and Table 12). The mean value of the function is high (), and the variation of the evaluations relative to the mean value is not large. Therefore, the influence of accumulated experience on the evaluations of the experts is more significant.

Table 11.
‘Structural engineering’ course evaluations; ,

Table 12.
True and upgraded ‘Building management’ course grades; ,
The ‘Structural engineering’ course was evaluated ambiguously by the experts. The most highly qualified specialists gave a low rating to the course (scores of 4 and 5). Since , these evaluations are adjusted upwards. Since the expert error is not large, , the evaluation corrections are less significant than for the other expert groups. The least experienced expert, working in the multimedia field, rated the course . Despite this expert’s error being , his evaluation is corrected only slightly because of the high mean value of the function . In cases 4 and 5, the mean of the corrected evaluations is rounded up to a score of 7, but the mean of the X evaluations is rounded up to a score of 6.
By contrast, the ‘Building management’ course was judged highly. Most of the X scores exceeded the mean value , thus the evaluations were adjusted downwards. In case 5, the same value of X = 10 was corrected for k = 1.2 to 9.6292, for k = 1 to 9.7230, and for k = 0.8 to 9.8111. Since the mean value of the function is high, it did not significantly affect the overall result. The mean value of the evaluations X and the corrected values for all the options considered is equal to the score of 9 (Table 12).
The graphs of all the functions described in this paper, clarifying the evaluations of the courses from the construction field for k = 1, are shown in Figure 6.
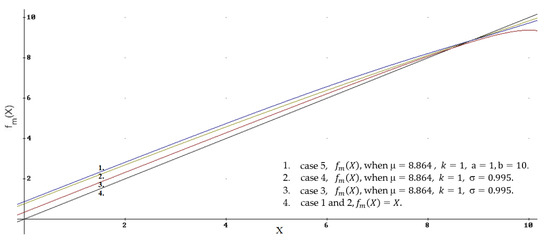
Figure 6.
functions for different cases; .
It is convenient to start considering the graphs from the bottom, from the line numbered 4 (black). These are cases 1 and 2, where the function is given by a uniform distribution, which means the absence of accumulated, a priori, information. This function is ; i.e., the estimate is not adjusted. It is convenient to compare the other cases with the line numbered 4 by fixing the influence of a priori information on changes in the function . Deviations from this line illustrate the influence of the a priori information on decision-making.
The next line of the function, number 3 (red), is for case 3, when the a priori information is described by a triangular function, and a triangle also gives the conditional function. This function corrects the evaluation of X least of all for and most of all for . Since is big enough, the line for the function bends; this is the weak point of this combination.
The following lines, numbers 2 and 1, differ little from each other. Both cases use the a priori Gaussian function . The line for function number 2 uses a triangular conditional function (case 4), and that numbered 1 uses a Gaussian function (case 5). Nonetheless, the most significant correction of the evaluated X for is in case 5 (line number 1).
6. Discussion
The Bayesian approach proposed in the paper has shown its capabilities for evaluating data uncertainty, particularly for distance learning courses. In this paper, the analytical part is also applicable to similar problems of quality evaluation, such as a re-evaluation of an exam score taking into account the student’s work during the entire semester.
This research demonstrates the possibility of using different combinations of distributions (their density functions) in the most suitable way for describing a priori information and expert error. In practice, the a priori probability distribution can be selected after confirming the statistical hypothesis about the type of distribution, according to a significant number of accumulated evaluations. The research presented in this paper is analytical, thus more general variants of distributions, such as Gauss and triangle distributions, are chosen.
It is proved that, using a uniform distribution ( density function) with conditional triangle and Gaussian distributions, the mean function . This result is interpreted as a lack of accumulated a priori experience, thus the evaluation of is not corrected. The function is convenient to use for comparison with other options, to give a better determination of the influence of a priori experience on the final result of correcting the experts’ evaluation.
The research results for case 3 (a priori triangle with a conditional triangle distribution), case 4 (a priori Gaussian with a conditional triangle distribution), and case 5 (a priori Gaussian with a conditional Gaussian distribution) are similar, and show that the function of the averages logically changes depending on the accumulated a priori experience. When , the values of the function increase, and, correspondingly, when , they decrease.
The opinion of a highly qualified expert (expert error ) corresponds to greater trust, thus the correction of the evaluation is minor. With an increase in the error (expert error ), the size of the correction of the evaluation also increases.
When the a priori information is given by a Gaussian function, the result is also affected by the spread of the evaluations. A small spread of a priori evaluations has a more significant impact on the corrections of the X scores. Thus, if the mean value of the function is high, then at 0.5 the correction of the evaluation X is greater than it is at 1.5. If is large, then the result of the correction does not differ much from the expert evaluation X itself.
After studying the third case of the combination of the triangular function with a triangular conditional distribution, it becomes clear that with a high mean value of the function and the expert error k = 1, the values of function are not logical at the end of the interval. Inaccuracies at the end of the function appear because the function of the expert error at the ends of the range goes beyond the a priori distribution of the triangle. Therefore, when the mean value of the function is high or low (close to the ends of the interval), this option is not recommended because of inaccuracies at the ends of the function. The correction of the X scores, in this case, is the most minor, compared to the other combinations.
Combining the Gaussian function with a triangular conditional distribution (case 4) in the case of a high a priori mean value is not suitable for correcting low evaluations, since the graph of the function is not homogeneous at the very beginning of the interval. When the mean value of the a priori Gaussian function is very large (or very small), and the expert error is given by a narrow triangle (), illogical results arise at the beginning (respectively, at the end) of the function related to the continuous approximation of random integers.
The fifth case, when both functions are Gaussian functions, appears to be the most stable. Even if the a priori function mean value is very high (or very low), the function results are logical in the entire interval. This combination shows the most relevant result of all the studied cases and it is recommended that this is applied in practice.
There is a plan for future work to compare the results of this paper with the application of the theory of fuzzy sets. This is possible and it will be interesting to use other combinations of probability distributions.
Even though the adjustment of the values of the expert evaluations is minor and varies within the range of ±1 point, this score can have a significant impact on decisions. In the work of Washington and Oh, applying a Bayesian approach to improving the safety of railway crossings, the authors concluded that the use of a priori information slightly changed the result, and argued that it is good when the expert’s evaluation and the a priori information do not contrast strongly with each other [38]. In this example of evaluating the quality of distance learning courses, a score of 9–10 increases the teacher’s salary at the above-mentioned higher education institution. Another example, the re-evaluation of an exam score based on a priori experience, can be decisive in obtaining a positive exam mark.
7. Conclusions
To reduce the uncertainty of an expert evaluation, the refinement of the experts’ scores is proposed through the use of an a posteriori mean function, taking into account all the collected a priori information and the experts’ competence. This paper illustrates a new way of using the well-known Bayes formula. The continuous case of the Bayesian formula is perceived as a continuous approximation of expert evaluations. The complexity of the task lies in the fact that the parameters of the a priori and conditional density functions for θ (state of nature, true goodness) and X (expert score) are considered as continuous random variables, but experts use integers X in making a decision. In this paper, a 10-point evaluation system is used for expert judgments. The difficulty in obtaining the results of this research lies in the correct choice of the intervals of change for the parameters θ and X for continuous approximation.
It is shown that, when using an a priori probability density function of a continuous uniform distribution, which means the absence of accumulated information, and conditional density functions of triangular and Gaussian distributions, the experts’ evaluation is not corrected. It can be seen that an a priori probability density function of a triangular distribution with a conditional density function also given by a triangle does not give entirely accurate or logical results for the function at the ends of the argument interval. When using a combination of the a priori density function of a Gaussian distribution with a narrow conditional density function of a triangular distribution, illogical results for the function values arise at the ends of the evaluation interval X when the mean value of the Gaussian distribution is very large or very small. When both functions are set by a Gaussian distribution, the result is the most stable and suitable for use in expert judgments.
The results of the research for different combinations are similar and show the following trend. The a posteriori mean function corrects the expert’s evaluation depending on the mean value of the a priori distribution, reducing the evaluation if the mean value is less than the expert’s evaluation, and otherwise increasing it. With a small spread of a priori evaluations, the mean value of the a priori density function has a weightier impact on the correction of the expert’s scores. Trust in the opinion of a highly qualified expert is significant and, accordingly, the correction of such an expert’s evaluation is small. By increasing the expert’s error parameter k, which means the expert is not sufficiently competent, the correction of the expert’s evaluation also increases.
The proposed method of correcting expert evaluations was used to assess the quality of distance learning courses. Even though the correction of the expert assessments appeared to be minor, this adjustment can have an impact on the final result in making a decision.
The goal of this study is to illustrate the approach of Bayesian approach in experts’ judgments for reducing uncertainty in data. This is the first part of a general study devoted to comparing probability and degrees of truth. There is a plan for future work to compare the results of this paper with the application of the theory of fuzzy sets. Therefore, the paper considers in detail different combinations of distributions and the influence of changes in their parameters on the result.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
This publication is dedicated to the bright memory of my supervisor, Jonas Mockus. You became for us an example to be followed. This research was implemented inspired by the discussions and your advices.
Conflicts of Interest
The author declares no conflict of interest.
References
- Tredger, E.; Lo, J.; Haria, S.; Lau, H.; Bonello, N.; Hlavka, B.; Scullion, C. Bias, guess and expert judgement in actuarial work. Br. Actuar. J. 2016, 21, 545–578. [Google Scholar] [CrossRef]
- Hartley, D.; French, S. A Bayesian method for calibration and aggregation of expert judgement. Int. J. Approx. Reason. 2020, 130, 192–225. [Google Scholar] [CrossRef]
- Vinogradova-Zinkevič, I.; Podvezko, V.; Zavadskas, E.K. Comparative assessment of the stability of AHP and FAHP methods. Symmetry 2021, 13, 479. [Google Scholar] [CrossRef]
- Klir, G.J. Uncertainty and Information. Foundations of Generalized Information Theory; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Mockus, J. Experimental Investigation of Distance Graduate Studies of the Open-source Environment by Models of Optimal Sequential Decisions and the Bayesian Approach. In Optimization and Its Applications; Springer: New York, NY, USA, 2007. [Google Scholar] [CrossRef]
- French, S.; Hanea, A.M.; Bedford, T.; Nane, G.F. Introduction and Overview of Structured Expert Judgement. In Expert Judgement in Risk and Decision Analysis; Stanford University: Stanford, CA, USA, 2021; pp. 1–16. [Google Scholar]
- Tversky, A.; Kahneman, D. Extensional Versus Intuitive Reasoning: The Conjunction Fallacy in Probability Judgment. In Heuristics and Biases: The Psychology of Intuitive Judgment; Gilovich, T., Griffin, D., Kahneman, D., Eds.; Cambridge University Press: New York, NY, USA, 2002; pp. 19–49. [Google Scholar]
- Kahneman, D. Thinking Fast and Slow; Farrar, Straus and Giroux: New York, NY, USA, 2011. [Google Scholar]
- Vinogradova, I.; Podvezko, V.; Zavadskas, E.K. The recalculation of the weights of criteria in MCDM methods using the Bayes approach. Symmetry 2018, 10, 205. [Google Scholar] [CrossRef] [Green Version]
- Cooke, R.; Goossens, L.H.J. Procedures guide for structural expert judgement in accident consequence modelling. Radiat. Prot. Dosim. 2000, 90, 303–309. [Google Scholar] [CrossRef]
- Brownstein, N.C.; Louis, T.A.; O’Hagan, A.; Pendergast, J. The role of expert judgment in statistical inference and evidence-based decision-making. Am. Stat. 2019, 73, 56–68. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anscombe, F.J.; Aumann, R.J. A definition of subjective probability. Ann. Math. Statist. 1963, 34, 199–205. [Google Scholar] [CrossRef]
- Mockus, J.; Vinogradova, I. Bayesian approach to evaluation of distance courses. Liet. Matem. Rink. LMD Darb. B. 2014, 55, 90–95. [Google Scholar] [CrossRef]
- Surowiecki, J. The Wisdom of Crowds; Anchor Books: New York, NY, USA, 2005. [Google Scholar]
- Veen, D.; Stoel, D.; Zondervan-Zwijnenburg, M.; van de Schoot, R. Proposal for a five-step method to elicit expert judgment. Front. Psychol. 2017, 8, 2011. [Google Scholar] [CrossRef] [Green Version]
- Zondervan-Zwijnenburg, M.; van de Schoot-Hubeek, W.; Lek, K.; Hoijtink, H.; van de Schoot, R. Application and evaluation of an expert judgment elicitation procedure for correlations. Front. Psychol. 2017, 8, 90. [Google Scholar] [CrossRef] [Green Version]
- Wilson, K.J. An investigation of dependence in expert judgement studies with multiple experts. Int. J. Forecast. 2017, 33, 325–336. [Google Scholar] [CrossRef] [Green Version]
- Arimone, Y.; Begaud, B.; Miremont, G.; Fourrier-Réglat, A.; Molimard, M.; Moore, N.; Haramburu, F. A new method for assessing drug causation provided agreement with experts’ judgment. J. Clin. Epidemiol. 2006, 59, 308–314. [Google Scholar] [CrossRef]
- Vinogradova, I. Distance Course Selection Optimization. Ph.D. Thesis, Vilnius University, Vilnius, Lithuania, 2015. Available online: https://talpykla.elaba.lt/elaba-fedora/objects/elaba:8264594/datastreams/MAIN/content (accessed on 17 May 2021).
- Podofillini, L.; Pandya, D.; Emert, F.; Lomax, A.J.; Dang, V.N.; Sansavini, G. Bayesian aggregation of expert judgment data for quantification of human failure probabilities for radiotherapy. In Safety and Reliability—Safe Societies in a Changing World; CRC Press: Boca Raton, FL, USA, 2018; pp. 501–508. [Google Scholar]
- Bigün, E.S. Risk analysis of catastrophes using experts’ judgements: An empirical study on risk analysis of major civil aircraft accidents in Europe. Eur. J. Oper. Res. 1995, 87, 599–612. [Google Scholar] [CrossRef]
- Leden, L.; Gårder, P.; Pulkkinen, U. An expert judgment model applied to estimating the safety effect of a bicycle facility. Accid. Anal. Prev. 2000, 32, 589–599. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Vaidogas, E.R. Bayesian reasoning in managerial decisions on the choice of equipment for the prevention of industrial accidents. Eng. Econ. 2008, 5, 32–40. [Google Scholar] [CrossRef]
- Ramli, N.; Ghani, N.A.; Ahmad, N.; Hashim, I.H.M. Psychological response in fire: A fuzzy Bayesian network approach using expert judgment. Fire Technol. 2021, 57, 2305–2338. [Google Scholar] [CrossRef]
- Zhou, Y.; Fenton, N.; Neil, M. Bayesian network approach to multinomial parameter learning using data and expert judgments. Int. J. Approx. Reason. 2014, 55, 1252–1268. [Google Scholar] [CrossRef]
- Sigurdsson, J.; Walls, L.; Quigley, J. Bayesian belief nets for managing expert judgment and modeling reliability. Qual. Reliab. Eng. Int. 2001, 17, 181–190. [Google Scholar] [CrossRef]
- Varis, O.; Kuikka, S. Bene-Eia: A Bayesian approach to expert judgment elicitation with case studies on climate change impacts on surface waters. Clim. Chang. 1997, 37, 539–563. [Google Scholar] [CrossRef]
- Rosqvist, T. Bayesian aggregation of experts’ judgements on failure intensity. Reliab. Eng. Syst. Saf. 2000, 70, 283–289. [Google Scholar] [CrossRef]
- Wisse, B.; Bedford, T.; Quigley, J. Expert judgement combination using moment methods. Reliab. Eng. Syst. Saf. 2008, 93, 675–686. [Google Scholar] [CrossRef]
- Smets, P. The transferable belief model for expert judgements and reliability problems. Reliab. Eng. Syst. Saf. 1992, 38, 59–66. [Google Scholar] [CrossRef]
- Mockus, J. Investigation of examples of e-education environment for scientific collaboration and distance graduate studies, Part 1. Informatica 2006, 17, 259–278. [Google Scholar] [CrossRef]
- Capa Santos, H.; Kratz, M.; Mosquera Munoz, F. Modelling macroeconomic effects and expert judgements in operational risk: A Bayesian approach. J. Oper. Risk 2012, 7, 3–23. [Google Scholar] [CrossRef]
- Mazzuchi, T.A.; van Dorp, J.R. A Bayesian expert judgement model to determine lifetime distributions for maintenance optimisation. Struct. Infrastruct. Eng. 2012, 8, 307–315. [Google Scholar] [CrossRef]
- Jiang, P.; Guo, B.; Lim, J.-H.; Zuo, M. Group judgment of relationship between product reliability and quality characteristics based on Bayesian theory and expert’s experience. Expert. Syst. Appl. 2010, 37, 6844–6849. [Google Scholar] [CrossRef]
- Koh, D.H.; Park, J.H.; Lee, S.G.; Kim, H.C.; Choi, S.; Jung, H.; Park, D.U. Combining lead exposure measurements and experts’ judgment through a Bayesian framework. Ann. Work. Expo. Health 2017, 61, 1054–1075. [Google Scholar] [CrossRef] [PubMed]
- Åström, J.; Pettersson, T.; Reischer, G.; Norberg, T.; Hermansson, M. Incorporating expert judgments in utility evaluation of bacteroidales qPCR assays for microbial source tracking in a drinking water source. Environ. Sci. Technol. 2014, 49, 1311–1318. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Parent, E.; Bernier, J. Encoding prior experts judgments to improve risk analysis of extreme hydrological events via POT modeling. J. Hydrol. 2003, 283, 1–18. [Google Scholar] [CrossRef]
- Washington, S.; Oh, J. Bayesian methodology incorporating expert judgment for ranking countermeasure effectiveness under uncertainty: Example applied to at grade railroad crossings in Korea. Accid. Anal. Prev. 2006, 38, 234–247. [Google Scholar] [CrossRef] [PubMed]
- Ramachandran, G.; Banerjee, S.; Vincent, J.H. Expert judgment and occupational hygiene: Application to aerosol speciation in the nickel primary production industry. Ann. Occup. Hyg. 2003, 47, 461–475. [Google Scholar] [CrossRef] [Green Version]
- Werner, C.; Bedford, T.; Cooke, R.M.; Hanea, A.M.; Morales-Nápoles, O. Expert judgement for dependence in probabilistic modelling: A systematic literature review and future research directions. Eur. J. Oper. Res. 2017, 258, 801–819. [Google Scholar] [CrossRef] [Green Version]
- Vinogradova, I. Multi-attribute decision-making methods as a part of mathematical optimization. Mathematic 2019, 7, 915. [Google Scholar] [CrossRef] [Green Version]
- Vinogradova, I.; Kliukas, R. Methodology for evaluating the quality of distance learning courses in consecutive stages. Proc. Soc. Behav. Sci. 2015, 191, 1583–1589. [Google Scholar] [CrossRef] [Green Version]
- Ziemba, P. Multi-Criteria Stochastic Selection of Electric Vehicles for the Sustainable Development of Local Government and State Administration Units in Poland. Energies 2020, 13, 6299. [Google Scholar] [CrossRef]
- Lam, W.S.; Lam, W.H.; Jaaman, S.H.; Liew, K.F. Performance Evaluation of Construction Companies Using Integrated Entropy–Fuzzy VIKOR Model. Entropy 2021, 23, 320. [Google Scholar] [CrossRef]
- Riaz, M.; Farid, H.M.A.; Aslam, M.; Pamucar, D.; Bozanić, D. Novel Approach for Third-Party Reverse Logistic Provider Selection Process under Linear Diophantine Fuzzy Prioritized Aggregation Operators. Symmetry 2021, 13, 1152. [Google Scholar] [CrossRef]
- Narayanamoorthy, S.; Ramya, L.; Kalaiselvan, S.; Kureethara, J.V.; Kang, D. Use of DEMATEL and COPRAS method to select best alternative fuel for control of impact of greenhouse gas emissions. Socio-Econ. Plan. Sci. 2021, 76, 100996. [Google Scholar] [CrossRef]
- Narayanamoorthy, S.; Annapoorani, V.; Kalaiselvan, S.; Kang, D. Hybrid Hesitant Fuzzy Multi-Criteria Decision Making Method: A Symmetric Analysis of the Selection of the Best Water Distribution System. Symmetry 2020, 12, 2096. [Google Scholar] [CrossRef]
- Geetha, S.; Narayanamoorthy, S.; Kang, D. Extended hesitant fuzzy SWARA Techniques to Examine the Criteria Weights and VIKOR Method for Ranking Alternatives. Available online: https://aip.scitation.org/doi/abs/10.1063/5.0017049?journalCode=apc (accessed on 17 May 2021).
- Narayanamoorthy, S.; Ramya, L.; Kang, D. Normal wiggly hesitant fuzzy set with multi-criteria decision-making problem. In Proceedings of the AIP Conference Proceedings; Institute of Physics: London, UK, 2020; Volume 2261, p. 030023. [Google Scholar] [CrossRef]
- Narayanamoorthy, S.; Annapoorani, V.; Kang, D.; Ramya, L. Sustainable Assessment for Selecting the Best Alternative of Reclaimed Water Use Under Hesitant Fuzzy Multi-Criteria Decision Making. IEEE Access 2019, 7, 137217–137231. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Bausys, R.; Lescauskiene, I.; Usovaite, A. MULTIMOORA under Interval-Valued Neutrosophic Sets as the Basis for the Quantitative Heuristic Evaluation Methodology HEBIN. Mathematics 2021, 9, 66. [Google Scholar] [CrossRef]
- Roest, I. Expert Opinion. Use in Practice; Vrije Universiteit: Amsterdam, The Netherlands, 2002. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).