Norms That Regulate the Theorem Construction Process in an Inquiry Classroom of 3D Geometry: Teacher’s Management to Promote Them

Abstract

This paper aims to illustrate how a teacher instilled norms that regulate the theorem construction process in a three-dimensional geometry course. The course was part of a preservice mathematics teacher program, and it was characterized by promoting inquiry and argumentation. We analyze class excerpts in which students address tasks that require formulating conjectures, that emerge as a solution to a problem and proving such conjectures, and the teacher leads whole-class activities where students’ productions are exposed. For this, we used elements of the didactical analysis proposed by the onto-semiotic approach and Toulmin’s model for argumentation. The teacher’s professional actions that promoted reiterative actions in students’ mathematical practices were identified; we illustrate how these professional actions impelled students’ actions to become norms concerning issues about the legitimacy of different types of arguments (e.g., analogical and abductive) in the theorem construction process.

1. Introduction

In an inquiry classroom, an atmosphere of intellectual challenge is generated in which students are expected to: (i) propose and defend mathematical ideas and conjectures and (ii) respond thoughtfully to the mathematical arguments of their peers. In our study, mathematical inquiry begins when a task is proposed that requires solving an open-ended problem using a Dynamic Geometry Software (DGS), formulating a conjecture that encapsulates the solution of the problem, and proving the conjecture.

The mathematical practice of a classroom with these characteristics requires focusing on students’ production and teacher and students collectively building norms (social and socio-mathematical) that regulate and support these practices [1]. Examples of social norms are: (i) active listening, intellectual risk-taking (sharing incomplete ideas), and building on the ideas of others [2]; and (ii) assuming the responsibility of solving the given task [3]. Examples of socio-mathematical norms are: research in mathematics involves creatively solving problems; valid arguments should be based on properties of mathematical objects [1,4,5]; open-ended problems require exploration, formulation of conjecture, and argumentation of conjecture [3].

The cited authors have illustrated how classroom norms that tend to promote argumentation in the classroom are generated. In this research line, the complexity of the negotiation norms process has been illustrated, particularly when the production of convincing arguments by students is elicited. Additionally, teachers’ professional actions regarding the promotion of norms aimed at that goal have been proposed. Conner et al. [6] suggest professional actions such as: asking for justifications, conjectures, or explanations; summarizing, explaining, or capitalizing on other students’ ideas. Makar et al. [2,7] indicate general teacher strategies such as: using posters displaying expectations, remembering the standards frequently, highlighting exemplary student actions, and modeling expectations with their actions. Assis et al. [3] allude to posing open-ended problems and asking students to share their ideas with the whole class, acknowledging the authorship of the discovery; these actions encourage students and promote inquiry and discussion. Yackel and her colleagues point out that the teacher can guide or redirect conversations among students with the objective of promoting arguments and making the elements of an argument that are implicit or omitted explicit [1,8].

These studies imply that teachers who are likely to support student participation in argumentation do not emphasize the different types of arguments that arise in the process of constructing a theorem and, consequently, do not refer to issues that may legitimize them during that process. Emphasizing these aspects contributes to students distinguishing between an acceptable or unacceptable argument and, therefore, acting with more autonomy when they perform mathematics.

The analysis carried out under the onto-semiotic approach (OSA) [9] allowed us to see in detail the complexity of the mathematical activity behind the teacher’s strategies and, with it, the preponderant role of each type of argument during the theorem construction process. The fact that the setting of the study was a 3D geometry course made us recognize the role of analogical arguments in that process.

Our study aims to complement studies on teacher management to promote argumentation. Specifically, the purpose of this paper is to expose professional teacher actions that encourage the constitution of norms that promote the legitimacy of different types of arguments in the theorem construction process, in particular the role of analogical and abductive arguments in the process. We distinguish between valid argument and legitimate argument; the former is an argument that satisfies all the requirements that the expert community has determined to be considered valid from a mathematical point of view; an argument is legitimate when a specific community (e.g., classroom) accepts its use in a given practice (e.g., solving a problem, formulating conjectures, proving conjectures).

The study illustrates the important role of the teacher in inquiry classrooms, where the purpose is for students to construct theorems more autonomously. Thus, we focus on the following research question: how did the teacher instill norms that promote the legitimacy of different types of arguments in the process of constructing a theorem in a 3D geometry course?

In attempting to answer this question, we focus on some specificities or concretizations of teachers’ professional actions described in the literature (as mentioned above), and we illustrate how, in the course, the students’ and teacher’s actions feed upon each other (e.g., use of analogical arguments by students is highlighted by the teacher; she explicitly states it to the whole class, cataloging it as an exemplary action that constitutes part of a norm that regulates the practices of the theorem construction process). In this way, we specify more detailed teacher actions that seek to instill norms on aspects relating to the acceptability of an argument in the theorem construction process, which we understand as the explicitness of criteria to legitimize different types of arguments (abductive, analogical) in practices relative to this process (e.g., an analogical or abductive argument is legitimate when it leads to the solution of a problem, provides the antecedent of the conjecture that encapsulates the solution of the problem, or provides theoretical elements needed or ways to construct the proof).

2. Conceptual Framework

The onto-semiotic approach (OSA) is a comprehensive general theoretical framework that provides specific conceptual tools for the didactical analysis of different aspects involved in the teaching and learning of mathematics [9,10].

Mathematical activity plays a central role in OSA. It is modeled in terms of practices, primary objects, and processes. In this theory, mathematical practice is conceived as a set of actions, regulated by institutionally established norms, oriented towards a goal (e.g., solving a problem, formulating conjectures, proving conjectures). In the OSA ontology, the term object is used in a broad sense to refer to any entity which, in some way, is involved in mathematical practice and can be identified as a unit. Problems, languages, definitions, propositions, procedures, and arguments are considered as objects, specifically as the six mathematical primary objects. A set or system of objects that are related to each other is called a configuration of objects. Any configuration of objects can be seen both from a personal and from an institutional perspective, which leads to the distinction of cognitive (personal) and epistemic (institutional) configurations of primary objects.

In addition to practices and configurations of primary objects, the OSA also considers processes, understood as a sequence of practices involving configurations of primary objects. In our study, we are interested in a very specific process: theorem construction. The theorem construction process is considered as a sequence of several practices in which different types of primary objects are involved.

For better clarity of the conceptual references of the study, we present a more detailed description of the key primary object and central process of the study, argument, and theorem construction, respectively; likewise, we present a conceptualization of the other main constructs of the study, norm, and teachers’ professional actions.

2.1. Argument and Argumentation

If a primary object emerges in practice, this object can be considered as the result of a process involving primary practices and objects; so, a representation (language in OSA) can be considered as the result of a representation process, a procedure relates to the process of automation, an argument is the result of a process of argumentation, etc. In this sense, we consider argumentation as a process carried out by an individual or a group to convince others of a position taken regarding a given claim or action (Stylianides et al., 2016). The primary object argument is the product of this process [11,12].

We use Toulmin’s basic model [13] to make this conceptualization operative. Based on this model, an argument includes three main elements: the speaker’s claim (C), data (D) supporting the claim C, and warrant (W) or the inference rule, which relates the data with the claim by means of the proposition if D then C. The model is quite useful for specifying different types of arguments (informal or not) according to how the three elements are related [14].

Deduction is an inference allowing the construction of a C starting from some D and a W, usually by using the inference rule Modus Ponens. Abduction is an inference of a likely D from an observed fact C and the evocation or discovery of W; in this case, an invalid inference rule “C$\to$D and D, therefore C” is used. Induction is the inference of a likely C from some cases of D in which a pattern of regularity W is observed; W also has a probable character and can be considered as an inference. Given the analogy p’ is to q’ as p is to q where p’ is to q’ is in a domain O and p is to q is in a domain S, by means of an analogical argument a likely C: p’ is to q’ is inferred from using the analogy W and the proposition D: p is to q [15]. Figure 1 shows the diagrams for each type of argument using Toulmin’s Model. The rectangles with a thicker line indicate what is inferred in each type of argument; those with dotted lines (or discontinued lines) indicate that the inference of each type of argument is likely. For example, in an inductive argument, both C and W are inferred and probable; therefore, the lines of the respective rectangles are thick and dotted.

We consider proof as a type of argument composed of one or several deductive arguments logically connected and whose warrants are objects of a theoretical system [16]. The theoretical system of the 3D geometry course should be understood as the subset of elements (postulates, definitions, and theorems) of Euclidean Geometry that had been studied in the previous geometry courses and that have been introduced in the current course.

2.2. Theorem Construction Process

For our case, the theorem construction process consists of three specific practices: solving an open-ended problem, formulating a conjecture, and proving the conjecture. The development of these practices leads to the conjecture, formulated as the solution of the problem, becoming a theorem. An open-ended problem is a problem that has several correct answers and several ways to obtain the correct answer(s) [17]; a conjecture expresses relationships of dependence between elements or properties of the entities involved in the situation [18]; a theorem is a set of three elements: statement, proof of the statement, and theoretical system that supports the proof [19].

Each of these practices involves different actions (acting to achieve an aim) or procedures (enunciation of a set of actions that conform to a step-by-step process to be followed). To exemplify this,

Table 1. Norms and practices of the course related to the theorem-construction process.

Practices: Solving Open-Ended Problems and Formulating Conjectures
Meta-norm (epistemic)	To solve an open-ended problem, it is necessary to:
Procedure	Identify the conditions and questions given in the task statement. Use a DGS to construct the objects given in the statement. Use the DGS to carry out explorations that allow answering the question. Formulate a conjecture (conditional proposition) that solves the problem based on the explorations.
Practice: Proving A Conjecture
Norm (epistemic)	To elaborate a proof of a conditional proposition, it is necessary to:
Procedure	Determine the data and the thesis of the conditional to be proved. Determine which elements of the corresponding theoretical system can be used as a warrant for each argumentative step. Configure a deductive chain of arguments that responds to a specific way of proceeding (direct proof; indirect proof by contradiction, case study, or use of contrapositive; and mathematical induction). Determine the validity of the proof (that is, determine if it is based on all the data, reasoning schemes are valid, and only elements of the course’s theoretical system are used).

shows two procedures related to arguments, which we identified in the course that was the setting for the research. The first one is a relatively consensual procedure related to the practice of proving a conjecture; the second one is a very particular procedure of this classroom related to the practice of solving an open-ended problem. These procedures involve different types of arguments (abductive, analogical, and deductive), as we will show based on the results of the analysis.

It should be noted that we recognize a close link between procedure and actions. Sometimes, when a procedure is known, the execution of each of its steps leads to action. At other times, a set of actions are executed and, once recognized, are stated as steps of a procedure.

2.3. Norm

We use the normative dimension based on OSA [20]. This approach assumes that notions such as didactic contract [21] and social and socio-mathematical norms [1] are used to refer to patterns that regulate practice. Additionally, they are expressions of teacher expectations or students’ responsibilities. These patterns provide opportunities for students to articulate and reflect on their own and others’ mathematical practices [1,22] and provide explanations, justifications, and assessments of situations that occurred in class [20]. We use this approach because it allows us to have a broader view of the types of norms proposed by Yackel and her colleague. In this paper, we concentrate on two types of norms: epistemic or socio-mathematical norms, which regulate mathematical practices and contents in correspondence with the mathematical discourse that can be developed in an institution (e.g., definitions, propositions, and procedures, because of their role in mathematical practice, are epistemic norms, and so are the norms that specify when a type of argument is valid or legitimate in a mathematical practice); and mediational norms, which regulate resources used in practices (e.g., a norm that specifies when and for what purpose a DGS is used in a mathematical practice). The OSA refers to other types of norms, such as: interactional norms or social ones, which regulate the modes of interaction among people involved in the mathematical practice or instructional process; ecological norms, which are external aspects –curricular guidelines, educational policies– that regulate classroom practices.

Given the way some procedures are used in the practices of a specific community, these become a norm (or rule) that must be followed. To illustrate this, we again take the procedures in Table 1, highlighting two aspects: on the one hand, each of the steps of each procedure can be considered as a norm and, of course, be typified (e.g., steps 2 and 3 of the procedure concerning the practices of solving open-ended problems and formulating conjectures are mediational norms). Likewise, if a set of norms determines a procedure for something, it can be considered as a norm (the procedures in Table 1 are norms that regulate the corresponding practices). On the other hand, it is worth saying that there are procedures (norms) that regulate mathematical practices and that are agreed upon by the mathematical community (e.g., the procedure for proving a conditional or each step of this procedure); however, there are other norms that rather regulate how to perform mathematics and that are not necessarily agreed upon by the whole community. Clearly, these latter norms are situated at a meta-level that is not a matter of consensus for the whole community but a requirement for a particular community (e.g., the course that is the setting for the research). These norms are called meta-norms by the OSA and can also be typified; for example, a procedure for solving a problem can be an epistemic meta-norm.

2.4. Teacher’s Professional Actions

In this paper, we aim to specify detailed teacher actions that seek to instill norms on aspects related to the legitimacy of various types of arguments in the process of theorem construction. The OSA proposes as the core of professional practice the actions the teacher uses to induce his or her students to perform the intended mathematical practices [23]; in this case, the practices of solving open-ended problems, formulating conjectures, and proving them.

To illustrate, we present an example from the data. A general professional action is to ask students to argue their results. A professional action that concretizes such a general action is to ask questions during the elaboration of a proof that leads to possible already validated propositions that can be used (stating sufficient data or warrants of an argumentative step). This concrete action favors the emergence of abductive arguments and, depending on the usefulness of their inference, they could be legitimate. If abductive arguments are used repeatedly for the purpose described, this becomes a norm for the course.

3. Methodology

3.1. Context and Participants

The case study data come from a project on argumentation in a 3D geometry course of a preservice mathematics teacher program in Bogotá, Colombia. The aim of this study was to improve our understanding of how argumentation can be promoted in classrooms. We wanted to target a course like this one because we suspected that the teacher promoted different norms due to students’ actions in relation to the study of the geometric content of 3D objects. In other words, we suspected that solving problems involving 3D objects, formulating conjectures that encapsulate the solution, and proving them implied alluding to new norms in comparison to those of the 2D geometry course of the same preservice program.

The classroom used as the research setting consisted of the teacher (Mrs. López) and 31 students. Mrs. López is an experienced teacher who has taught inquiry classrooms for more than 15 years and has been a researcher in several projects about geometry education. She is particularly interested in promoting argumentation in an inquiry classroom; also, she has managed geometry courses using open-ended problems and the use of DGS to address them. Given her involvement in research projects, she has knowledge of norms that can be established in such a classroom and of the different types of arguments that can be formulated. Mrs. López’s knowledge and experience and the course features made this setting different from typical university classrooms (at least in Colombia). On the other hand, the 31 students (17–24 years old) had completed a 2D geometry course but had not taken one that deals with 3D geometry objects; hence, they had not used 3D DGS. About half of the students took the 2D geometry course with Mrs. López, so they had close knowledge about the “style of class” she managed.

3.2. Data Collection

In correspondence with studies relative to norms [1,2,4], the collected information occurred in 26 sequenced sessions (120 min in length) in which the class addressed open-ended problems. All sessions were videotaped. Additionally, occasionally, students and the teacher were interviewed after the lessons to complete the information.

The data chosen for this document comes from the following supplies: transcripts of four episodes belonging to four class sessions (3, 4, 6, and 15), which are representative of what happened in class; and transcripts of the interviews of the students involved in the fragments and of the teacher. Four written documents were constructed, one for each selected fragment, made up of the respective transcripts and responses to the interviews. These four documents are the study data.

The four episodes were chosen for the following reasons. Episode A of session 3 is important because a group of students executed new actions that specify steps of an incorporated procedure (regarding norms relative to the practice solving open-ended problems); we glimpse the germ of a new procedure (at least the precision of steps of the procedure for an existing practice). Episodes B and C of sessions 4 and 6 were chosen because the teacher executed professional actions to promote those steps during a dialog with students. In addition, the practice proving a conjecture (and associated norms) took place in these episodes. Episode D of session 15 was chosen because there was evidence of new actions being used again, demonstrating that the teacher’s actions were effective, and of norms established. The following is a brief description of what we have determined to be the research data.

Episode A. Class session 3: Mrs. López posed an open-ended problem concerning congruent triangles that can be addressed both in 2D and 3D geometry. Students’ production illustrates certain norms, stable at that time, and the execution of actions that specify steps of an incorporated procedure. The problem statement is as follows:

Problem 1.

Given $\overline{AB}$ and $\overline{CD}$ congruent segments, is it possible to determine a point E so that ∆ABE and ∆CDE are congruent?

When asked about her expectations for the students’ performance on the problem, Mrs. López said: “The students should solve the problem in 2D and 3D geometry domains, considering three scenarios: $\overline{AB}$, $\overline{CD}$, and E are coplanar; $\overline{AB}$ and $\overline{CD}$ are coplanar, but E is non-coplanar with respect to them; $\overline{AB}$ and $\overline{CD}$ are non-coplanar”. In these contexts, she expected at least two exploration practices: an empirical one and a theoretical one. The first one, in which in a DGS, a point E is drawn and moved around the screen randomly to discover a position that insinuates a solution—i.e., wandering dragging [24] is carried out—then, the geometric characteristic of that point must be determined by carrying out a movement while ensuring that the desired property is maintained (e.g., E equidistant from A and C and E equidistant from B and D), i.e., maintaining dragging [18] is completed.

The theoretical exploration practice is one in which, through an abductive process, data and warrants to establish congruent triangles are determined, and then, among these, the most convenient option is chosen. The teacher expected that the explorations would lead to construction procedures in which E is the intersection of the perpendicular bisector lines of $\overline{AC}$ and of $\overline{BD}$, or E is a point of m, m the intersection line of the perpendicular bisecting planes of each segment; with this last possible solution (which arises when $\overline{AB}$ and $\overline{CD}$ are not coplanar), the teacher intended to make the need to introduce the perpendicular bisecting plane explicit, an object not yet studied in the course. If $\overline{AB}$ and $\overline{CD}$ are parallel and configure a quadrilateral ABCD, the intersection of $\overline{AC}$ and $\overline{BD}$ would generate the point E. As is evident, this problem is open-ended because there are several ways to establish its solution.

Episode B. Class session 4: Adriana and Armando shared their ideas about the problem solutions. Empirical evidence illustrates actions that could become reiterative actions (and associated procedure or epistemic meta-norm) that emerged from the students’ activity and negotiations oriented by Mrs. López. We recognize professional teacher actions to promote those actions (e.g., Mrs. López legitimated actions that involve analogical and abductive arguments).

Episode C. Class session 6: Proofs of the conjectures were elaborated by the whole class. Empiric evidence illustrates actions that could be steps of a procedure that emerged from the proving conjecture practice. We recognize professional teacher actions to promote those actions (e.g., Mrs. López legitimated potential procedures or meta-norms which involve abductive and analogical arguments).

Episode D. Class session 15: Mrs. López posed a problem as follows:

Problem 2.

Given four non-coplanar points, is it possible to determine an E point so that it is equidistant from the given points?

When asked about her expectations for students’ performance to solve the problem, she expressed that students would approach the problem by performing actions like those in classes 4 and 6. When a student acted in an unexpected way (that induced the violation of a norm), several students pointed it out and suggested ways to act according to the actions executed in those sessions. There is evidence that the teacher’s actions are effective, and norms are being set.

3.3. Analysis

Once the data was chosen, the analysis of the episodes was based on the didactic analysis proposed by the OSA [23,25], which has been suggested to describe and explain the instructional process because it helps to understand and answer the question “what happened here and why”. It is composed of five elements: identification of mathematical practices, identification of mathematical objects and processes, description of interactions, identification of norms, and assessment of the suitability of the instructional process. For this paper, we use the first four elements simultaneously.

Table 2. Didactical analysis elements.

Elements	Tools
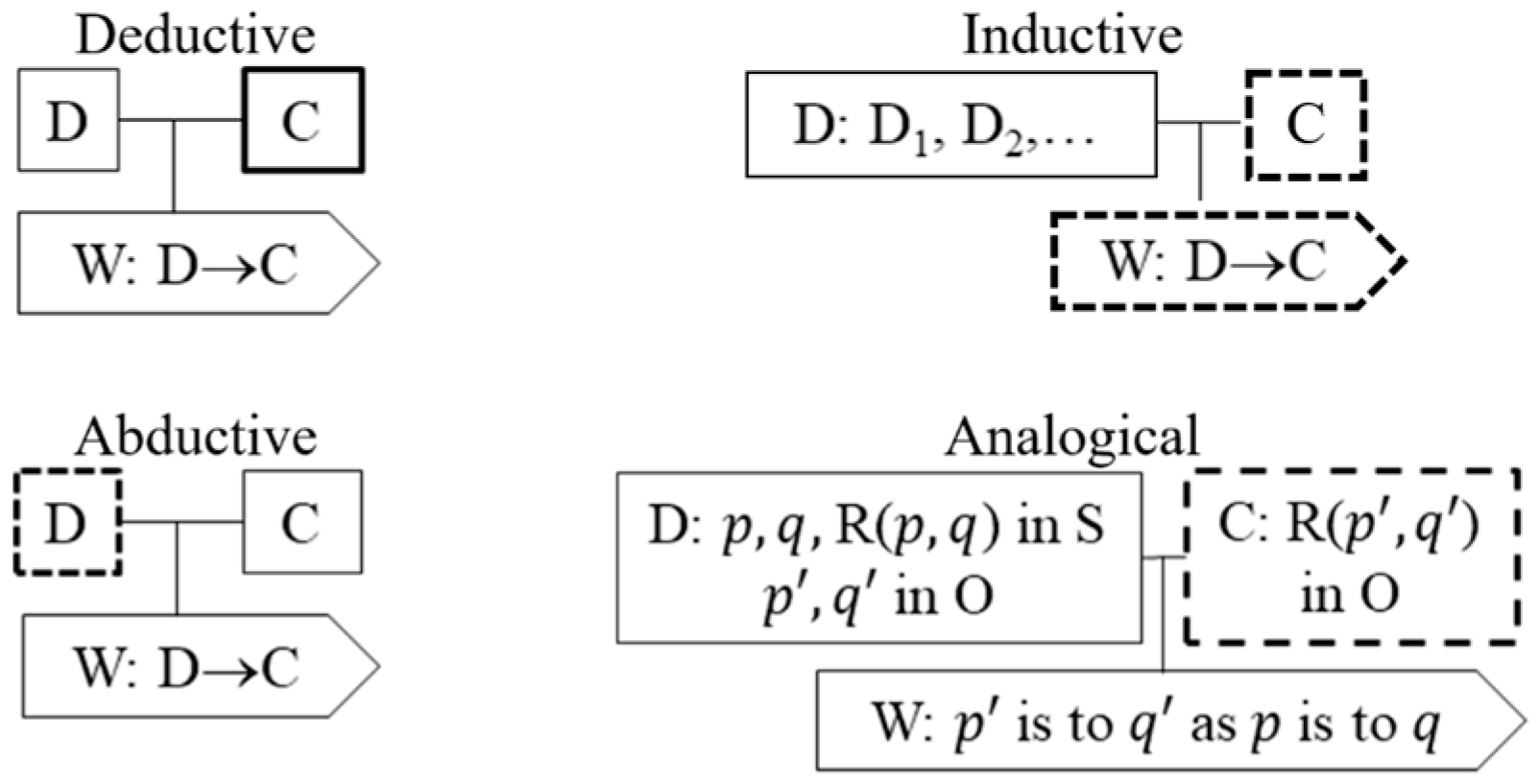
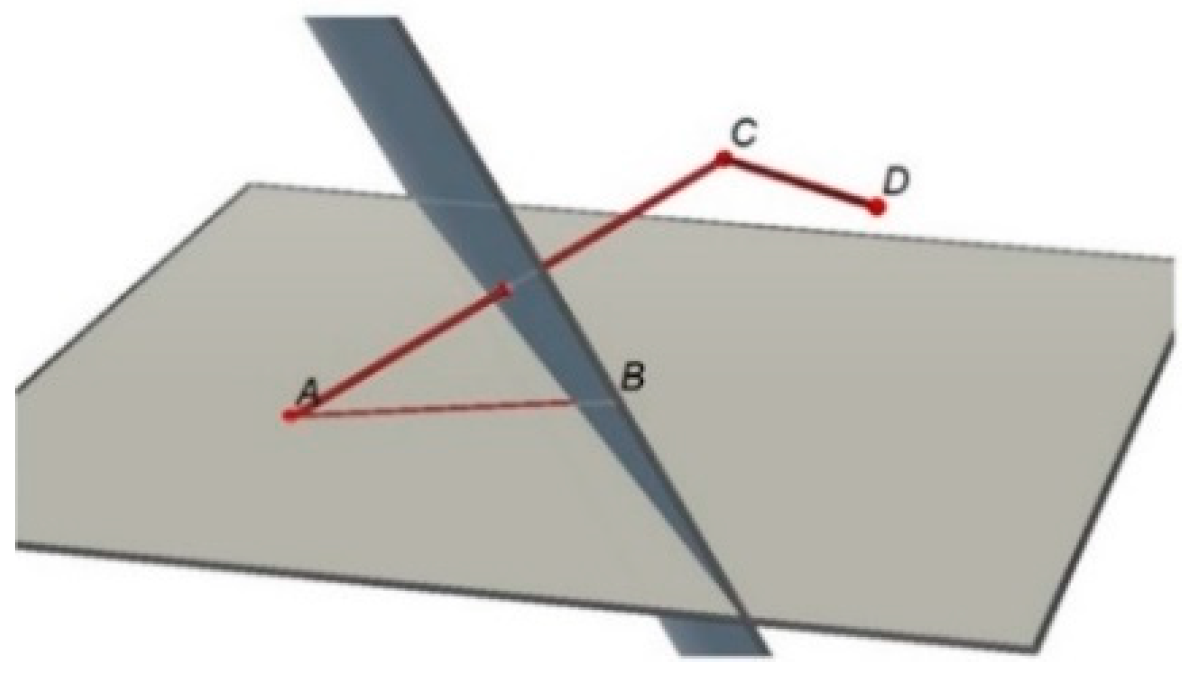
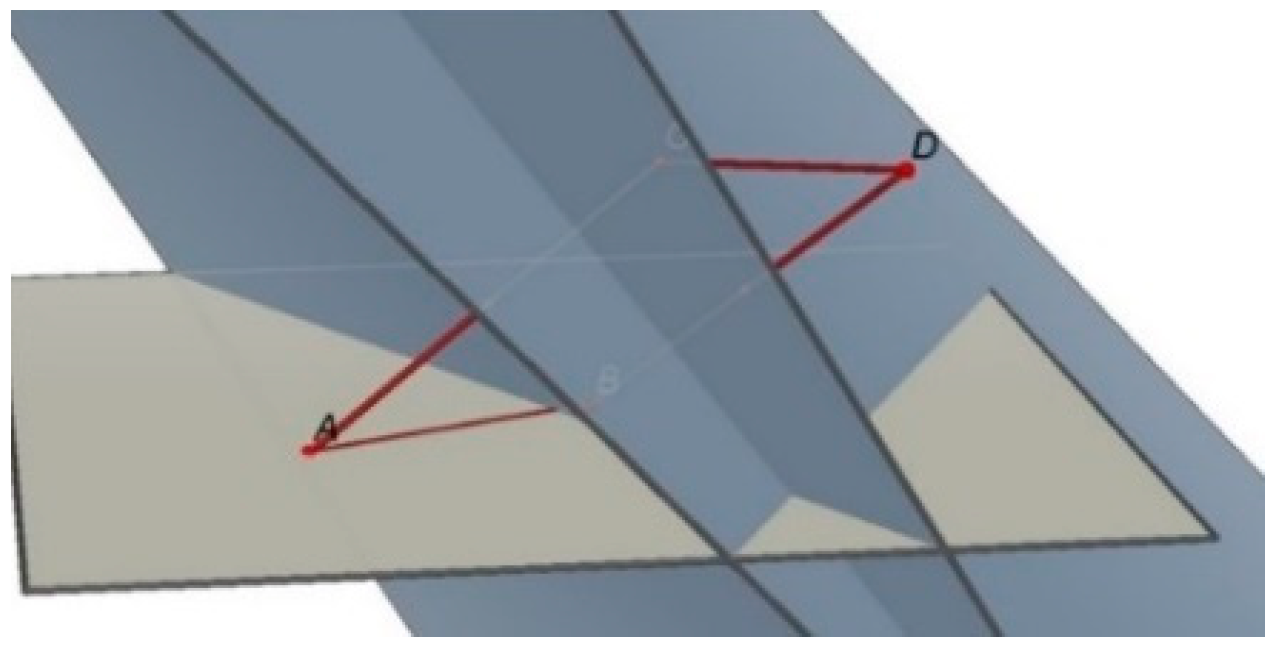
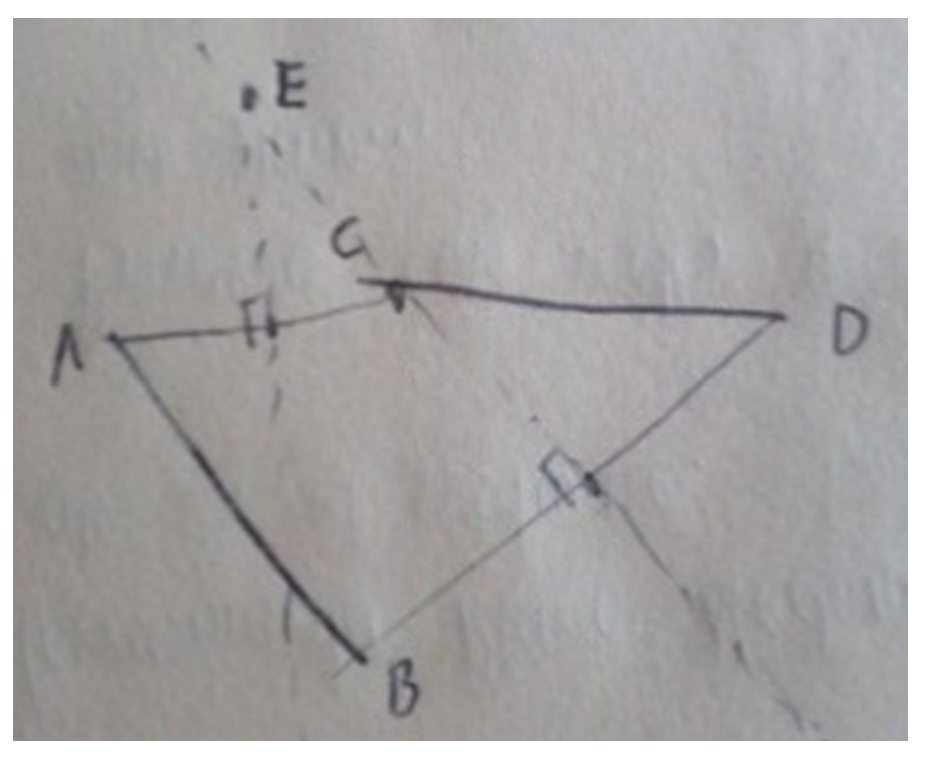
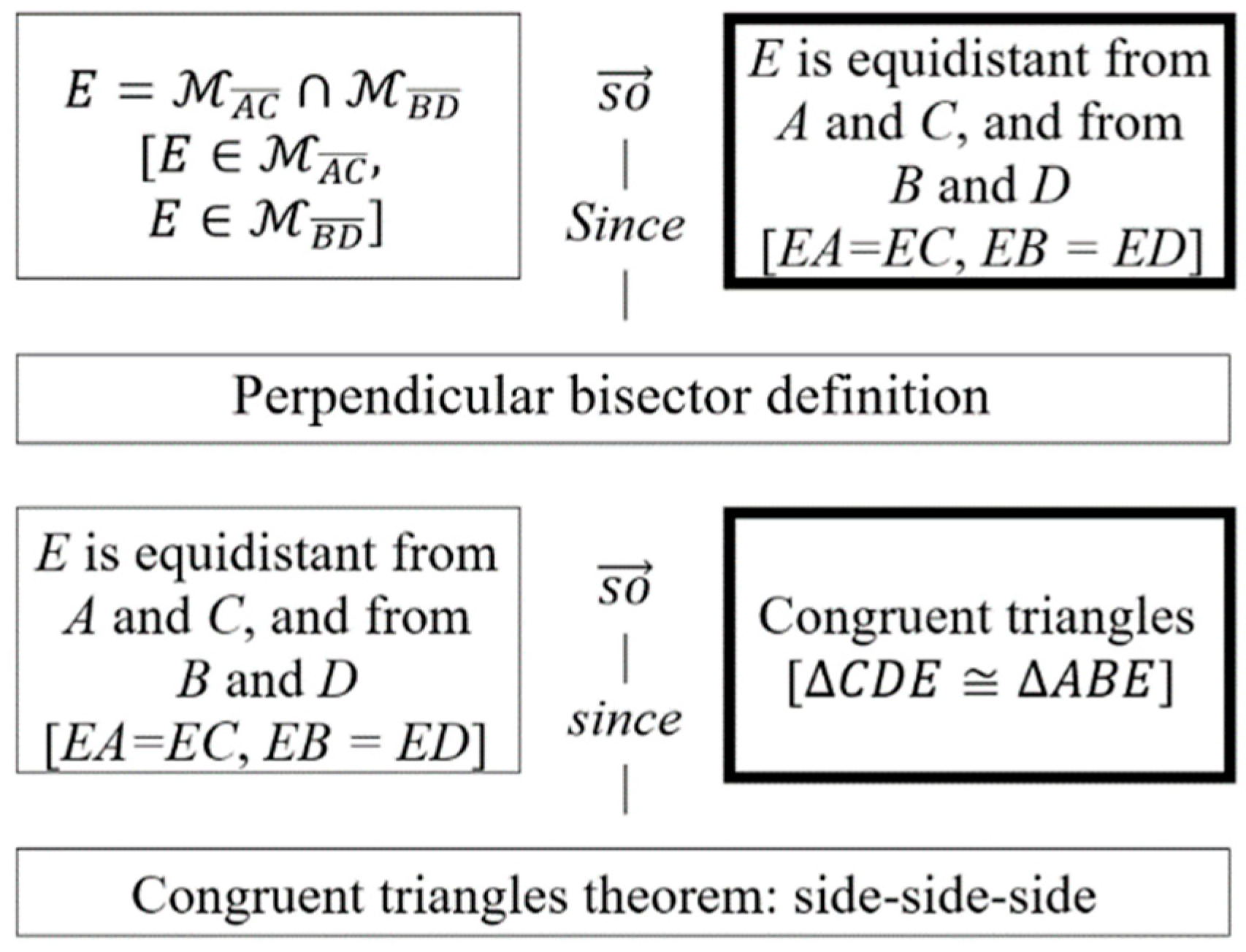
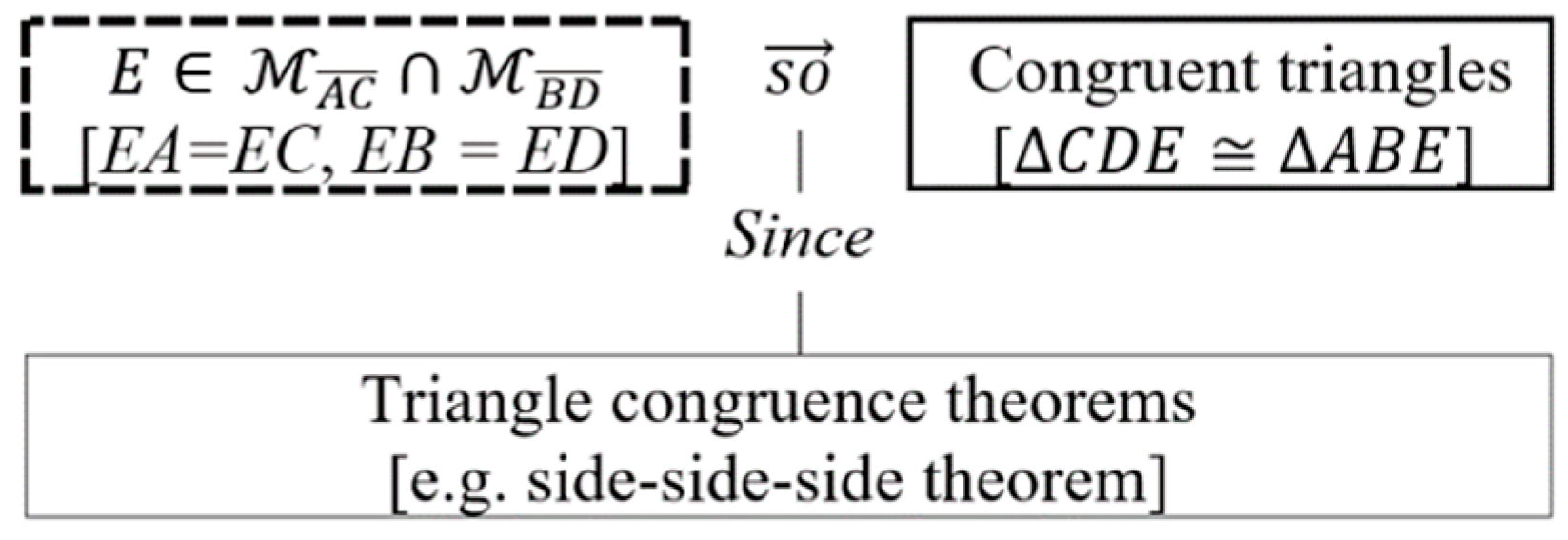
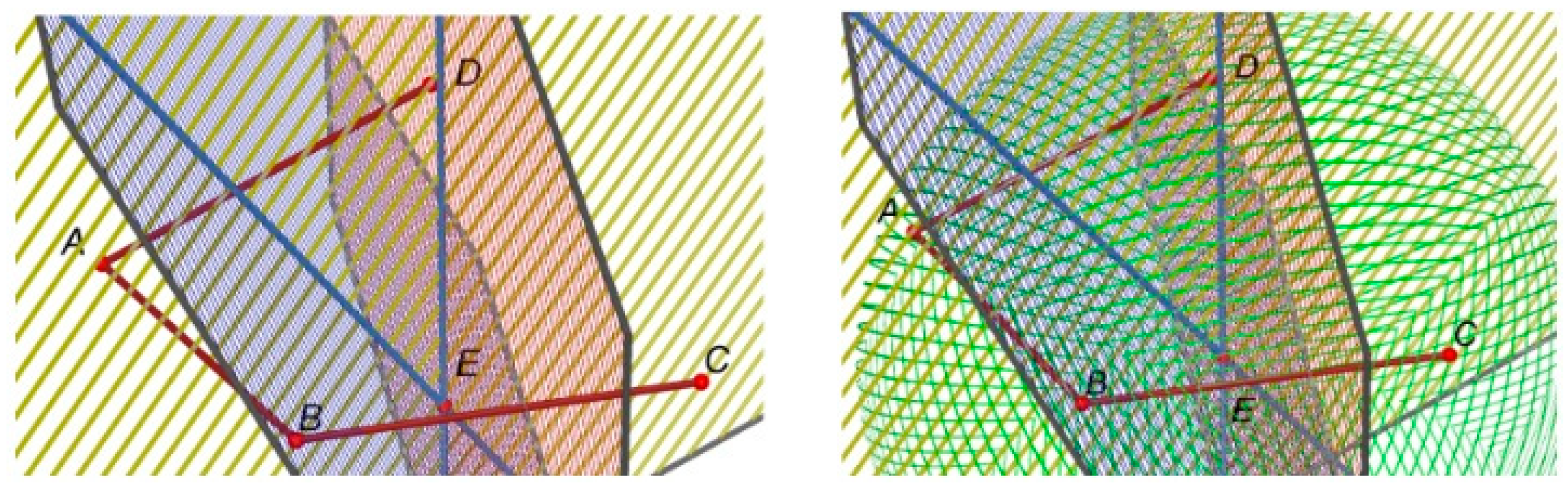
Identification of practices and norms: the analysis of practices was focused on the identification and description of mathematical practices such as solving open-ended problems, formulating conjectures, and proving them. Taking these practices as a reference, we focus on determining norms that involve issues about the legitimacy of arguments.	We used the OSA proposal about normative dimension [20] to enunciate and typify the norms identified. In the section “Results”, we use codes to indicate actions that could be reiterative and potentially become norms. For actions referring to solving open-ended problems, formulating a conjecture, and proving the conjecture practices, we use, respectively, the codes Solve, Formulate, and Prove followed by a number to indicate a specific norm. At the end of the analysis of each episode, we present tables describing the possible norms identified (i.e., coded actions suggesting norms), indicating the type of the possible norm. To illustrate the codification of actions, we present the following examples. (1) The action “Armando told Juan which objects he should build. Juan had already built the congruent non-coplanar segments” was typified as Solve 1. This is because it alludes to the norm “Use the DGS to construct the objects given in the statement” of the solving open-ended problems practice. (2) The action “the conjectures that emerged after using abductive and analogical arguments, once legitimized, were as follows. In both cases, what is inferred from the argument is the antecedent of the conjecture; the given property is the consequent” was typified as Formulate 1. This is because it alludes to the norm “The data inferred from the abductive argument are placed as the antecedent of the conjecture; the given property is set as the consequent” of the formulating a conjecture practice. (3) The action “determining the data ($\overline{AB}$$,\overline{CD}$ are coplanar) and the thesis of the conditional to be proved (∆CDE ≅ ∆ABE)” was typified as Prove 1. This is due to the fact that it alludes to the norm “Determine the data and the thesis of the conditional to be proved” of the proving a conjecture practice.
Identification of primary objects: this analysis focuses on specifying the primary objects that emerge from a specific practice. For this case, we focus on the arguments that emerge from the indicated practices.	We used Toulmin’s basic model to typified arguments as deductive, inductive, analogical, or abductive.
Description of interactions: this analysis focuses on specifying the teacher’s professional actions to promote student learning; in this case, we concentrate on determining professional actions that encouraged the establishment of norms.	Although we had in mind the actions proposed by Makar et al. [2], Assis et al. [3], Yackel and Cobb [1], Yackel [8], and Conner et al. [6], our intention was to identify more detailed actions that specify actions as the following ones: remembering the norms frequently, highlighting exemplary student actions, modeling expectations with their actions, posing open-ended problems, asking students to share their ideas with the whole class, and asking students opinions about others’ ideas (conjectures, arguments). To present the results, we used the code TA and a number to indicate a specific professional action (e.g., TA1 indicates the first specific professional action identified).

presents a description of the elements and the analytical tool used.

The analysis had two phases. In the first one, each researcher conducted an analysis separately. The purpose was to identify norms on matters related to the legitimacy of arguments and professional actions that promoted it; the norms were identified, either by the recognition of repeated actions of the students [1] or by the students’ affirmation of a statement about wrongful actions [4]. Given the interest of the study, we concentrated on students’ actions or affirmations relative to arguments that emerged from practices involved in the theorem construction process.

In the second phase, discussions among members of the research team took place to compare their analyses and negotiate potential interpretations; where doubts arose, transcripts were shown to Mrs. López or the specific students, who assisted in clarifying the actions. Finally, the analyses were shown to Mrs. López to gain confidence that the intentions of her actions were well interpreted.

4. Results

We present the results obtained from the analysis of the data, following the ideas presented in the previous section.

4.1. Episode A. Actions of Armando–Juan–Valentín Group to Solve the Problem

In session 3, Mrs. López posed Problem 1. Armando read it and wrote some notes on a sheet of paper for about 5 min. Then, he told Juan what objects he should build. Juan had already built the congruent non-coplanar segments ($\overline{AB}$ and $\overline{CD}$) (Solve1). Armando asked him to build the perpendicular plane through the midpoints of $\overline{AC}$ and of $\overline{DB}$, respectively. Juan made the construction using the Perpendicular tool (Figure 2 and Figure 3). Finally, Armando said: “I think… the intersection… a point in the intersection line between these planes is equidistant from the endpoints of the segments. I think so, but I do not know”. Valentín wrote the report of the construction procedure proposed by Armando (Figure 4).

In the episode, the students carried out procedures relative to solving open-ended problem practice and proving a statement practice. The first practice occurred when Armando proposed a construction procedure to solve the problem when the segments were non-coplanar. Juan followed the procedure in the DGS (Solve 2), and Valentín reported it in written form (Solve 3). The procedure was based on the perpendicular bisecting plane (in accordance with the teacher’s expectation for the problem’s solution), an object that was not yet part of the theoretical system of the course.

While Mrs. López collected the written reports and the other groups of students left the room, Armando and Valentín discussed their procedure. When Valentín asked Armando how he came up with that procedure, Armando mentioned that he first solved the problem in the plane; so, he produced a construction procedure considering that the given segments were coplanar. He drew the perpendicular bisector lines of $\overline{AC}$ and of $\overline{BD}$ and set E as the intersection point of such lines (Figure 5). The procedure is not reported in written form because it was proposed when the class session was over. Therefore, Mrs. López did not know what they had achieved. The students did not formulate a conjecture that encapsulates the solution to the problem.

Proving a statement practice occurred when the students produced two deductive arguments to validate that, for point E, ∆CDE ≅ ∆ABE. Armando said: “We have that the segments AB and AC are coplanar; E is equidistant (from A and C, and B and D) by the perpendicular bisector definition (the perpendicular bisector of a segment is the line whose points are equidistant from the segment endpoints)”. Valentin said: “Additionally, then, we have the (triangle congruence) by (congruence triangle theorem) side-side-side”.

Based on this performance, we recognize the following students’ actions: determining the data ($\overline{AB}$, $\overline{CD}$ are coplanar) and the thesis of the conditional to be proved (∆CDE ≅ ∆ABE) (Prove 1); determining warrants used in each argument (perpendicular bisector definition, side-side-side theorem) (Prove 2); configure a deductive chain of arguments (Prove3). Figure 6 shows the diagram of these deductive arguments using Toulmin’s model.

After the arguments were produced, the first author of this paper took part in the dialog to complete the data. He asked Armando two questions: how he came up with such a procedure and which is the solution in the 3D domain. Regarding the first one, Armando said: “Because I was taking the Multivariable Calculus course and there the teacher told us that a plane is to space as a line is to the plane, and from there the generalization came to me. Then, the idea of using the Perpendicular Plane tool came to me (he refers to the Perpendicular Plane tool of DGS). Additionally, well, instead of using perpendicular bisector line, we made these planes.”

Regarding the second question, he said that he thought the solution was a point belonging to the intersection line of the planes. Considering Armando’s answer, we identify he used the analogy: a plane is to space as a line is to a plane to solve the problem in the 3D domain. Based on this analogy, he assumed that the perpendicular plane to a segment through the midpoint (perpendicular bisecting plane) solves the problem in the 3D domain as the perpendicular bisector line to segment (analog line) solves the problem in the 2D domain. Thus, he produces an analogical argument (Figure 7).

From this answer, an argument is produced to explain the emergence of the procedure that solves the problem in the 3D domain (Solve 4). A striking issue is that the key argument suggested by Armando is not deductive (formal) but analogical (informal) (something Mrs. López did not expect). His actions (using an analogical argument that links objects in 2D and 3D geometry to infer the usefulness of a 3D object in a situation in space, knowing that its 2D analogical object is useful for a similar situation in plane geometry Solve 4) suggested a step that could be part of the procedure to solve open-ended problems in a 3D geometry domain.

To summarise,

Table 3. Students’ actions that could be norms.

Practices	Students’ Action	Type of Possible Norm
Solving open-ended problems	Solve 1. Identify the conditions and questions given in the task statement. Solve 2. Use the DGS to construct the objects given in the statement. Solve 4. Consider an analogy that relates 2D and 3D domains and infer a solution in the 3D domain by means of an analogical argument. Of course, a solution in the 2D domain is known and validated. Solve 3. Write a report of the productions; in this case, of the construction procedure.	Epistemic meta-norm: this set of actions could be a meta-norm that alludes to how to perform mathematics; in this case, to how to approach the solution of a problem with a DGS (meta-level aspect). In particular, Solve 2 could be a mediational norm that encourages the use of a DGS to construct objects involved in a problem.
Proving a statement/conjecture	Prove 1. Determine the data (antecedent) and the thesis (consequent) of the conditional to be proved. Prove 2. Determine the elements of the corresponding theoretical system that are used as a warrant for each argumentative step. Prove 3. Configure a deductive chain of arguments that responds to a specific way of proceeding (direct proof in this case).	Epistemic norm: this set of actions regulates the proving a conjecture practice.

shows the actions involved in this episode that could be monitored to determine whether they are reiterated (i.e., become norms) and whether there are professional actions by the teacher that encourage them.

It is important to say that Mrs. López informed us that one purpose of the previous course was to instill the procedure (or epistemic norm) related to the proving a conjecture practice. The fact that students performed in accordance with it may be a sign that this purpose was achieved (i.e., such a norm was a part of the class).

4.2. Episode B. Professional Actions by Teacher

In Session 4, Mrs. López directed the presentation of students’ productions for the problem, which she was able to read before the class session. After the proposals of various groups (all based on coplanar segments) were heard and discussed, she asked Adriana to present her group’s production. Adriana used the computer employed to project the images to the whole class. The solution proposed by her group corresponded to the procedure carried out by Armando when the segments were coplanar. Then, Mrs. López asked a member of the Armando–Juan–Valentín group to present their solution; Armando used the same computer and manipulated the software while describing their solution. He said, “the solution was similar to that of the previous group (refers to the proposal of Adriana’s group) but in space”. Armando executed the procedure outlined above for the 3D domain and emphasized that they used an object that was not part of the theoretical system available in class: the perpendicular plane through the midpoint of a segment $(\overline{AC}$ and $\overline{DB}$ in this case). He chose E as a point of the intersection line of the planes and found the following measurements: AE, EC, EB, and ED; he verified that EA = EC and EB = ED. Immediately, Mrs. López said:

Intervention a: Thank you very much. What surprised me about you (refers to the whole class) is that I did not see on your sheets (refers to the sheets where the students reported their solution) (that) the problem is asking that two triangles be congruent. So, the first thing that comes to mind is, well, what makes me think that two triangles are congruent? So, one says, well, I have some criteria: either I construct the angles, for example, I construct an angle congruent to the other, or I try to look for congruent segments. They (Adriana’s group) chose that. In other words, point $E$ must generate congruent segments. If I look for congruent segments if I want (segments) $BE$ and $DE$ to be congruent, then $E$ should be in the perpendicular bisector line of (segment) $BD$; if I want (segments) $AE$ and $CE$ to be congruent, then $E$ should be in the perpendicular bisector line of segment AC. So, that is a solution in the plane. We have insisted on the strategy of going backwards. I am surprised you do not all use it.

Intervention b: Now, this (points to Armando’s solution) is exactly what they did (points to Adriana’s Group) but in space; that is, the line becomes a plane, in the solution he (Armando) proposes. So, instead of constructing a perpendicular line to that segment (marks $\overline{AC}$) through the midpoint, he constructs a perpendicular plane to the segment through its midpoint, and he did the same with the other segment (marks $\overline{BD}$), yes? He did the same. So, notice that their plan (Adriana’s group) in the plane can be passed to the space where, instead of a perpendicular bisector line, a plane is used. So, this is a solution for any pair of congruent non-coplanar segments; the measurements are the same on the (DGS) screen.

In the episode, the practice carried out by the class corresponds to solving an open-ended problem. Two issues related to norms stand out; the former is more general than the last one. On the one hand, there was an interest in considering the ideas of others to build knowledge (emergent social norm: listening and building on others’ ideas), which is evidenced by Armando’s and Mrs. López’s actions. In both cases, Adriana’s group production (problem solution in the 2D domain) was alluded to in order to describe Armando’s group production (problem solution in the 3D domain).

On the other hand, the teacher’s professional actions to encourage the emergence of norms were manifested in three ways: asking students to share their ideas with the whole class, enhanced by her intention to acknowledge the authorship of correct solutions to problems; illustrating or modeling expectations with her actions (emerged from intervention a) (TA1); and using student actions as exemplary (emerged from intervention b) (TA2).

Regarding TA2, through intervention b, Mrs. López accepted the actions carried out by Armando. She tacitly alluded to the analogy used by him and explained the analogical argument used in his solution. For us, this is a way in which Action Solve 4 was legitimated by the teacher. Her management highlighted the student’s action as exemplary to the point of legitimizing it; in this case, her professional action led to the legitimization of the analogical argument because it provided an adequate solution based on the perpendicular bisecting plane of a segment, an object analogous to the perpendicular bisector line of the segment.

Regarding TA1, Mrs. López, through intervention a, aimed to illustrate an action (on which she has insisted throughout the course) that can be followed by the students in similar situations: the strategy of going backward. We interpreted the strategy as the use of an abductive argument in search of a solution (Solve 5). She remarked that if the problem asked for congruent triangles (claim), one should think about triangle congruence theorems (warrant) and thus determine the necessary objects to be constructed or found (data). For example, if using the side-side-side theorem is desired (warrant), constructing an object involving congruent segments is necessary; the perpendicular bisector line fulfills this goal (data) Figure 8. In this case, the teacher’s professional action allows the legitimization of an abductive argument, provided that the useful data or warrant inferred allows the implication of the fact that is wanted.

Finally, the conjectures that emerged after using the abductive and analogical arguments, once legitimized, were as follows. In both cases, what is inferred from the argument is set as the antecedent of the conjecture; the given property is placed as the consequent (Formulate 1 when the argument is abductive; Formulate 2 when the argument is analogical):

Conjecture 1.

Given $\overline{AB},\overline{CD}\subset \alpha$, $\alpha$ a plane, $\overline{AB}\cong \overline{CD}$ and $E\in {ℳ}_{\overline{AC}}\cap {ℳ}_{\overline{BD}}$, then $\mathsf{\Delta }CDE\cong \mathsf{\Delta }ABE$ (Adriana’s group).

Conjecture 2.

Given $\overline{AB},\overline{CD}$ non-coplanar, $\overline{AB}\cong \overline{CD}$, ${\beta }_{\overline{AC}}\cap {\beta }_{\overline{BD}}=m$, and $E\in m$, then $\mathsf{\Delta }CDE\cong \mathsf{\Delta }ABE$ (Armando’s group).

We consider the teacher’s actions to specify professional actions proposed in the literature in the sense that they involve the use of abductive and analogical arguments. We understand this as the teacher’s deliberate intention to make these aspects reiterative (become the norm) because of their usefulness in solving open-ended problems and formulating conjectures practices; an interesting point is that it also hints at a criterion for establishing when such arguments may be legitimate in those practices (Solve 6).

Table 4. Professional actions and actions which could be norms in Episode B.

General Professional Actions	Specify Professional Actions	Actions Which Could Be Norms	Practice
Highlighting exemplary student actions	TA1. Assess the students’ actions as exemplary by explaining the usefulness of an analogical argument and when it is legitimate.	Solve 4—for problems that ask for enough conditions to be able to conclude a given property, considering an analogy that relates 2D and 3D domains and inferring a solution in the 3D domain by means of an analogical argument. Of course, a solution in the 2D domain is known and validated. If the inference effectively solves the problem, the analogical argument is legitimized.	Solving open-ended problems
		Formulate 1. The data inferred from the abductive argument are set as the antecedent of the conjecture; the given property is placed as the consequent.	Formulating a conjecture
Modeling expectations with their actions	TA2. Model expectations with her actions, showing the usefulness of an abductive argument, and highlighting when it is legitimate.	Solve 5—for problems that ask for enough conditions to be able to conclude a given property, considering an abductive argument whose warrant is a proposition belonging to the theoretical system available, the assertion is the property given in the statement, and the inference (data) could be the conditions to solve the problem. If the data effectively solve the problem, the abductive argument is legitimized.	Solving open-ended problem
		Formulate 2. The relation inferred from the analogical argument is placed as the antecedent of the conjecture; the given property is set as the consequent.	Formulating a conjecture

details what has just been said: it sets out the general professional actions involved, their specifications according to Mrs. Lopez’s performance, and the aspects that could be normatively promoted by the teacher’s actions; the norms, by their connotation (regulate how to formulate conjectures or solve a problem) allude to an epistemic meta-norm.

4.3. Episode C. Proof of Conjectures

After what happened in Episode B, the class activity focused on the elaboration of the proofs of the conjectures. Adriana insisted on the need for the perpendicular bisecting plane to be part of the theoretical system to validate Armando’s solution. Her request points to the realization of an action that could be the norm (i.e., the antecedent of the conjecture must be valid in the theoretical system available for the course (Prove 4)). Thus, she insisted on the need to define this object and to prove its existence. Her insistence was effective, and the practices relative to formulating definition and proving a conditional were carried out, both based on the analogy referenced above (comparison with the perpendicular bisector line object). In other words, when Mrs. Lopez asked for the definition of the object and the construction of the proof, Adriana said: “I think we can base it on the perpendicular bisector (line); the definition of perpendicular bisecting plane would be the same as that of perpendicular bisector line but using points of the space that are equidistant from the segment endpoints. The existence proof would be the same as the one we did before (to prove the existence of the perpendicular bisector line) but using the existence theorem of the perpendicular plane through the midpoint and the fact that the points of that plane are equidistant from those endpoints. The latter we did for homework”.

On the other hand, to elaborate the proof of Conjecture 1, Mrs. López suggested using the abductive argument presented in Figure 8 (TA2) but in a “different direction”. She said: “Now take the perpendicular bisector line as given, use the definition, and then the side-side-side criterion to deduce the congruence that is asked for, right (Prove 5)? It is as doing what we did to solve the problem in the plane, but in a different direction” (Prove 6). To elaborate the proof of Conjecture 2, Juan proposed a similar proof to Conjecture 1 using the analogy cited (Prove 7); he said: “It can be made in an analogous way, but replacing the perpendicular bisector line for this plane (perpendicular bisecting plane)”.

Based on proposals of Adriana and Juan to achieve, respectively, the existence proof and the proof for Conjecture 2, Mrs. Lopez said: “this procedure using the analogy is an excellent way to prove in cases as these” (TA1). The proofs of the conjectures that were elaborated in class are presented in Figure 9. With this, the conjectures became theorems.

Based on this episode, we identified that the teacher’s professional actions were (i) related to the proof for Conjecture 1, suggesting the use of the abductive argument but in a different direction with which she models expectations through her actions (TA2), and (ii) related to the proof for Conjecture 2, legitimizing the use of analogy with which she uses the students’ actions as exemplary (TA1).

Table 5. Professional actions and actions which could be norms in Episode C.

General Professional Actions	Specify Professional Actions	Actions Which Could Be Norms
All Practices
Posing open-ended problems	TA3. Posing open-ended problems to provoke the need to introduce new objects into the theoretical system.	Prove 4. Defining an object and proving its existence is necessary to be able to use it legitimately in mathematical practices.
Proving a Conjecture Practice
Highlighting exemplary student actions	TA1. Assess the students’ actions as exemplary by explaining the usefulness of an analogical argument and when it is legitimate.	Prove 7. Regarding 3D geometry: if an analogical argument was used in the solution of a problem and in proofs relative to the 2D domain, then analogous objects can be used in the proof in a 3D domain in a similar deductive chain.
Modeling expectations with their actions	TA2. Modeling expectations with her actions, showing the usefulness of an abductive argument and highlighting when it is legitimate.	Prove 5. The warrants of abductive arguments arising in the solution of a problem can be used to determine the warrants of deductive arguments in a proof.

shows general professional actions involved, their specifications according to Mrs. Lopez’s performance, and the aspects that could be normative. Again, she highlights criteria for legitimizing analogical and abductive arguments, now for the proving a conjecture practice. Another interesting issue in this episode is that the teacher’s objective with this problem becomes evident: to introduce the perpendicular bisecting plane as an object of the theoretical system (TA3). This professional action, together with the solution proposed by Armando, led to actions (proposed by Adriana) that could become a norm: defining the object and providing the proof of its existence to be able to use it.

Regarding Table 5, we present two comments on normative issues. On the one hand, if the actions that could become norms finally become norms, they would be typified as follows: Prove 4 would be an epistemic norm because it refers to an indispensable aspect to legitimize an object in a theoretical system; the other norms would be epistemic meta-norms because they allude to a way of constructing a proof of a conjecture whenever an analogical or abductive argument has been used to elaborate the conjecture. On the other hand, the procedure to construct a proof shown in Table 4 was implicitly used by Adriana and Juan when presenting their proof proposals; this confirms that they have conceived this procedure as a norm.

4.4. Episode D. Actions Became Norms

In session 15, Mrs. López directed the presentation of student’s productions regarding Problem 2. She had read and organized them. Mrs. López said several groups performed similarly; so, she asked Viviana to present the production of her group, which “represents the production of several groups” (as Mrs. López said). Viviana used the computer employed to project images to the whole class and exposed her production in a 3D domain (Figure 10). She said: “We took the non-coplanar points (A, B, C, D). Then, we traced these segments (indicates $\overline{AB}$, $\overline{BC}$, $\overline{AD}$); then, we traced their perpendicular bisecting planes. The intersection point of those planes is the center (of a sphere) … equidistant from the points (A, B, C, D)”. When Mrs. López asked Viviana why her group had made that proposal, she said: “we used the construction (procedure) to find the circumference center given three points (this had been studied in session 10) but in space; in that case, we used perpendicular bisector line of three segments (whose endpoints are the given points) in the plane. Thus, in this case (3D domain), the perpendicular bisecting plane must work”. The conjecture formulated as the problem solution is:

Conjecture 3.

Given A, B, C, and D non-coplanar points and ${\beta }_{\overline{AD}}\cap {\beta }_{\overline{AB}}\cap {\beta }_{\overline{BC}}=\left\{E\right\}$, then B, C, and D belong to the sphere of center E and radius AE.

When Mrs. López asked for a plan to prove it, Lola said that properties of a sphere would be needed. In response to Lola’s comment, Viviana replied saying: “this is not possible because doing a proof implies using known elements and, of the sphere, we only know the definition”. Thus, it was necessary to prove the existence of a sphere. Subsequently, about four students proposed: “doing it analogously”. One of them (Andy) wrote the proof on the board (Figure 11). When he wrote step 3, he said: “instead of a perpendicular bisector line, we use a perpendicular bisecting plane”; in addition, when he wrote step 4, he said: “we used the definition of a sphere and not the (definition of) circumference”.

In this episode, the teacher’s action was focused on posing a problem with similar features to the first one (ask for sufficient conditions to conclude a property given in the statement). Her expectation was that students would tackle the problem by executing actions like those of the class before this session. Indeed, that occurred: Solve 1, Solve 2, Solve 3, and Solve 4 were again executed to address Problem 2. In addition, Formulate 2 and Prove 7 were executed to formulate and prove Conjecture 3, respectively. The mention of terms such as “analogously”, “instead”, and “used... and not...” is evidence of that. Prove 4 was recognized from Adriana’s reply to Lola, which warned about action not legitimate for the course (using elements whose existence had not been proven); in this case, the normative aspect was identified as a result of its violation and the notification of that violation.

5. Discussion and Final Remarks

Our study aims to complement studies on teacher class management to promote argumentation. Existing proposals provide very important lenses for analyzing teacher management by identifying professional actions such as [2,3,6,8]: posing open-ended problems; asking for arguments (or elements of these), conjectures, or explanations; encouraging the study of peer proposals (conjectures or arguments); summarizing, explaining, or acting out their expectations; and capitalizing on or highlighting other students’ ideas to be taken as exemplars. Using these lenses, we consider that our analysis brings to light three professional actions that specify some of those already mentioned and that make the creation and consolidation of very concrete norms, referring to the legitimization of abductive and analogical arguments, possible. Moreover, we follow Nathan and Knuth’s [26] invitation by specifying professional actions that involve the consolidation of norms concerning the legitimacy of different types of arguments, not only deductive ones. Specifically, our study reveals the following professional actions:

(i) The teacher posed open-ended problems with two specific purposes: on the one hand, favoring the production of abductive or analogical arguments; on the other hand, involving objects that did not yet belong to the theoretical system of the course, but that were close to the students’ development zone (TA3). Regarding the latter, the teacher intended to make the students see the need to introduce objects in the theoretical system and, with this, she encouraged the following norm: defining an object and proving its existence is necessary to be able to use it in mathematical practices legitimately (Prove 4). Regarding the former, abductive or analogical arguments were encouraged since the problems either asked for sufficient conditions to conclude a given property or encouraged a solution in 3D geometry by taking as reference analogous objects from 2D geometry. The norms relating to this issue will be outlined in what follows.

(ii) The teacher illustrated her expectations with her actions or questions; specifically, she showed how an abductive argument is used when trying to solve a problem and prove the corresponding conjecture (TA2). In fact, with her actions, she intended to promote the following norms: producing an abductive argument can generate a plan for solving problems that require conditions to conclude a given property; considering this type of argument as legitimate when: it allows to solve the problem (Solve 4), provides the antecedent of the corresponding conjecture (Formulate 1), and provides a way or useful theoretical elements to construct the proof (Prove 6, Prove 5).

(iii) The teacher allowed students to present their productions (construction procedures, conjectures, and arguments); this allowed her to obtain information from which she could find exemplary student performances. Specifically, she highlighted the usefulness of the analogical argument produced by a student when trying to solve a problem and prove the corresponding conjecture (TA1). In fact, with this action, she intended to promote the following norms: producing an analogical argument linking objects from 2D geometry to some in 3D geometry can generate a plan for solving the problem in the latter domain; considering this type of argument as legitimate when: it allows to solve (Solve 4), provides elements to formulate the corresponding conjecture (Formulate 2), and provides theoretical elements to elaborate the proof of the conjecture (Prove 7).

If, for each practice of the theorem construction process, a set of norms promoted by the teacher is formed, it is possible to generate a procedure that constitutes a great norm or meta-norm related to the respective practice. This happened in the classroom that was the setting for the research; Mrs. López, in Session 16, took a moment to present the norms (or actions that she intended to make reiterative for the students) as steps of a “normative” procedure for that course (

Table 6. Normative procedures of the course.

Solving Open-Ended Problems Practice
Epistemic Meta-Norm 1: To solve an open problem, it is necessary to: Solve 1. Identify the conditions and questions given in the task statement. Solve 2. Use the DGS to construct the objects given in the statement. Solve 4. For problems that ask for conditions to conclude a given property, (i) consider an analogy that relates 2D and 3D domains and infer a solution in the 3D domain by means of an analogical argument. Of course, a solution in the 2D domain must be known and validated. If the inference effectively solves the problem, the analogical argument is legitimized. (ii) Make a construction in a DGS that involves the objects that solve the problem to verify their effectiveness. Or Solve 5. For problems that ask for conditions to conclude a given property, (i) consider an abductive argument whose warrant is a proposition belonging to the theoretical system available, the assertion is the property given in the statement, and the inference (data) are the sufficient conditions needed to solve the problem. If the data effectively solves the problem, the abductive argument is legitimized. (ii) Make a construction in DGS that involves the objects that solve the problem to verify their effectiveness. Solve 3. Present a written report of their productions, in this case, of the construction procedure.
Formulating A Conjecture Practice
Epistemic Meta-Norm 2: To formulate a conjecture, it is necessary to: Formulate 1. The data inferred from the abductive argument must be set as the antecedent of the conjecture, and the given property must be placed as the consequent. This fact legitimizes the abductive argument. Or Formulate 2. The relation inferred from the analogical argument must be placed as the antecedent of the conjecture and the given property set as the consequent. These facts legitimize the analogical argument.
Proving A Conjecture Practice
Epistemic Norm 3: To elaborate a proof of a conditional proposition, it is necessary to: Prove 1. Determine the data and the thesis of the conditional to be proved. Prove 2. Determine the elements of the corresponding theoretical system that can be used as a warrant for each argumentative step. Prove 3. Configure a deductive chain of arguments that responds to a specific way of proceeding (direct in this case). Prove 4. Define an object and prove its existence to be able to use it legitimately in mathematical practices.
Epistemic Meta-Norm 4: If an abductive argument was used in the solution of a conjecture problem, then this abductive argument can be used to: Prove 5. Provide the warrants of the deductive arguments in a proof. Prove 6. Elaborate a deductive chain of a proof, but in a “different direction” (i.e., the deductive chain starts with the inference (data) of the abductive argument, while assertion and warrants remain the same). These facts legitimize the abductive argument. Regarding 3D geometry: Prove 7. If an analogical argument was used in the solution of a problem and in proofs relative to 2D domain, then analogous objects can be used in the proof in a 3D domain in a similar deductive chain. This fact legitimizes the analogical argument.

). With this professional action, her intention was that her students register the information about the norms so as to favor their autonomous performance during the theorem construction process [1,22], as happened with some students in Session 15.

As can be seen from Table 6, the teacher was interested in instilling meta-level norms. This is an interesting topic because it denotes her interest in regulating ways in which students can solve problems with a DGS, formulate conjectures, and prove them using types of arguments such as abductive and analogical ones. She wanted the students to recognize the importance of this type of argument in mathematical practices and, with this, to bring to light ways in which mathematics is performed based on them, not only using deductive arguments. Undoubtedly, this is evidence that verifies our assumption regarding the appearance of norms in the 3D geometry course that are not present in a 2D geometry course. Specifically, norms that allude to the use of analogical arguments comparing elements of these domains was an interesting finding, which concretizes functions of this type of arguments which, in turn, complement studies on these, e.g., [27,28]. At this point, it is convenient to clarify that we do not want to give the message that the analogical or abductive arguments are valid from a mathematical point of view, in other words, that their inference mechanisms are schemas, valid from logic, to elaborate a proof; rather, we want to highlight their usefulness to not only solve open problems but also to construct deductive arguments that make up the proof of a statement. Prove 5, Prove 6, and Prove 7 norms are evidence of the usefulness of the latter, and therefore, of their legitimacy in the proving a statement practice.

Finally, we present two comments. On the one hand, with this study, we have evidence to highlight that our study is interesting from a theoretical point of view. It extends and articulates the objects argument and theorem construction through the application of OSA tools and their link with Toulmin’s model of arguments. The result is a powerful analytical tool, the use of which allowed not only to determine norms that deal with the legitimacy of abductive and analogical arguments in the theorem construction process but was also useful to reveal that the promotion of argumentation in this process, within a didactic model of inquiry classrooms, is very complex, given the variety of onto-semiotic aspects involved in the corresponding practices. The development of analogical, abductive, and deductive arguments involves the implementation of sequences of mathematical practices subject to epistemic norms or meta-norms that must be known and applied systematically. These norms must be promoted by the teacher, whose role cannot be merely that of a manager of classroom interactions, but must include the responsibility of ensuring that the norms are understood and shared meaningfully, not just by a few students but by the class as a whole.

On the other hand, we agree with Yackel [8], Stylianides et al. [29], and Sala et al. [30] in that the management of inquiry classrooms implies having deep knowledge about mathematics and argumentation. However, the study allowed us to see this idea can be complemented, specifying pieces of didactic–mathematical knowledge and competences that a teacher must develop relative to norms [5,24]. For the reported case, the teacher’s competences did not come from the natural improvisation with which she sometimes acts; rather, they were the product of her knowledge of aspects of mathematics education. Mrs. López had knowledge about (i) norms that should be considered to generate an inquiry classroom, (ii) types of arguments and their role in mathematical activity, and (iii) the role that a DGS and the types of problems can have in exploration processes. This setting allowed her to have an adequate interpretation of student actions and to execute specific professional actions, even actions that she had not contemplated (e.g., legitimizing the use of analogical arguments).