Abstract
This paper reports sophistication levels in third grade children’s understanding of polygon concept and polygon classes. We consider how children endow mathematical meaning to parts of figures and reason to identify relationships between polygons. We describe four levels of sophistication in children’s thinking as they consider a figure as an example of a polygon class through spatial structuring (the mental operation of building an organization for a set of figures). These levels are: (i) partial structuring of polygon concept; (ii) global structuring of polygon concept; (iii) partial structuring of polygon classes; and (iv) global structuring of polygon classes. These levels detail how cognitive apprehensions, dimensional deconstruction, and the use of mathematical language intervene in the mental process of spatial structuring in the understanding of the classes of polygons.
1. Introduction
Understanding relationships between polygons implies recognizing relevant attributes and identifying similarities and differences between polygons [1,2]. Developing this understanding is a gradual process that begins with considering figures as a whole to reasoning about their attributes for identifying perceptually different figures as examples of the same class of polygons. Battista [1] indicated that students initially give informal descriptions and then move on to reason about the figure’s properties, using a combination of formal and informal terms. This development is based on a progressive cognitive structuring of the information generated from geometric figures: it involves recognizing parts of figures and endow those mathematical meaning using increasingly precise geometry terms. This progressive cognitive structuring of information implies making the geometric properties compatible with the figures’ perceptual characteristics, bringing together the double nature—figural and conceptual—of geometric figures [3,4], which is a key aspect in the development of geometrical thinking in primary education.
The process by which students eventually master the perceptual characteristics by endowing them mathematical meaning is a form of abstraction that allows students to identify some aspects of the figures and to relate them. Battista et al. [5] called this mental process—in which students select and organize information of parts of geometric figures in order to understand them—spatial structuring. In this process, the transition from the ability to consider a figure’s attributes to that of generating a certain structure between these attributes is linked to the ability to identify similarities and differences between polygons. This transition is an example of how students structure their knowledge of geometric figures, provide them mathematical meaning and allowing them to establish relationships between perceptually different figures. That is, spatial structuring allows associating a mathematical meaning to a set of representations of that meaning [6]. For example, students recognize the symmetry in a figure, and they are able to identify symmetry in a set of perceptually different figures.
This process of assigning the same mathematical meaning to a group of figures that are perceptually different underlies the ability to understand classes of figures and their classification [7]. This would be the case when students identify a common attribute in two perceptually different figures and differentiate these two figures from a third figure. For example, having an interior angle above 180° is a criterion that allows grouping perceptually different polygons and differentiating them from other figures. However, this process of structuring the polygons’ information, which leads to the emergence of the idea of a class of polygons, is still not well understood in primary education.
Van Hiele [8] characterized sequential and hierarchical levels of geometrical thinking to describe how students move from identifying shapes (Level 1) to attend to their properties (Level 2) and classifying and define shapes (Level 3). Some researchers have reformulated some of these levels [1,9,10]. These authors suggested the need to consider some intermediate levels: Pre-recognition level [9] in which students attend only to visual characteristics of a shape and cannot identify common shapes or distinguish between shapes of the same kind; Syncretic level, characterized by a synthesis of verbal declarative and imaginary knowledge [10] (p. 206); and Descriptive/Analytic level in which students recognize and can characterize shapes by their properties; they reason with the set of properties they associate with shapes, but they do not make inclusive classifications; and Abstract/Relational level where students can form abstract definitions, distinguishing between a set of necessary and sufficient conditions for a concept, and understand, and in some cases provide logical arguments. Also, students can make inclusive classifications. This last level indicates that students can justify that a figure belongs to a class of polygons identifying the attribute that defines the class. Identifying the attribute that defines a class of polygons is a process that provides evidence of how students endow mathematical meaning to parts of figures.
Recent studies about the development of the students’ understanding of shapes have allowed us to learn about the processes through which students endow mathematical meaning to parts of figures at various ages: in preschool students [11,12,13], in primary education [14,15], and in secondary education [7,16,17,18], but less is known in primary education [19,20]. Specifically, research on the geometric thinking of primary school students suggests that conceptual development in geometry involves multiple skills and mental constructs that build upon one another [21], and that primary school students have a limited ability to recognize figures through analysis [22]. However, if students are shown a wide range of examples and non-examples of geometric figures, they were able to recognize and establish relationships between the parts of geometric shapes [23] and shifting from informal to more formal descriptions of attributes [14]. Nevertheless, a more detailed description of the information structuring process that enables primary school students to understand the polygon concept and polygon classes is needed. Hence, this study aims to comprehend how primary students understand the polygon concept and the polygon classes.
2. Theoretical Framework
The transition from seeing figures as a whole to reason about their attributes is based on the process by which students assign a mathematical meaning to parts of figures and reason about this meaning using increasingly specific geometrical terms. The process of endowing mathematical meaning to geometric objects has been a focus of notable interest in research on the development of geometric thinking allowing refining general levels of development [1,5]. On the other hand, Duval’s approach attends to the interplay between the verbal and the visual forms of communications and offers some potentially productive avenues for the design of learning sequences [19]. Whereas the van Hiele model targets the role of the visual in its first two levels, Duval’s takes the perception of the figures and the language to stating and deducing properties as a fundamental component of geometrical thinking. Duval [24,25] indicates that this process is supported by the dimensional deconstruction of the figure and the coordination of different forms of apprehensions.
Dimensional deconstruction allows us to focus on parts of figures to endow them with mathematical meaning. For example, this process leads us to identify common attributes in figures that are perceptually different and is present in any process in which we define and reason about geometric figures [25]. This process is known as categorization [26] and allows the concept formation (e.g., [27,28]) when from different experiences with some objects we abstract certain invariant properties [29] (p. 10). For example, when, faced with an isosceles right triangle and a scalene right triangle, which are perceptually different, students can identify the fact of having a right angle as a common attribute. To support the dimensional deconstruction, Duval [30] proposes construction as a recommended point of entry in geometrical teaching. The construction process enables discursive procedures in geometry (e.g., statement of properties or definitions) because, during the construction of a geometrical figure, the properties of the concept to be constructed are affirmed and, besides making possible the discursive procedures as a way of providing information about the interplay between the verbal and spatial elements of geometric thinking [19].
On the other hand, cognitive apprehensions allow to associate parts of figures with mathematical statements or properties, for example, justifying why a triangle is an isosceles triangle (discursive apprehension); modify a figure such as modifying a non-example of a polygon to transform it into a polygon (operative apprehension); and to construct or draw a figure that fulfils a condition, as drawing a concave quadrilateral (sequential apprehension) [24].
Dimensional deconstruction and cognitive apprehensions lie at the heart of how students identify a common attribute in two perceptually different figures indicating that another figure does not possess this attribute. For example, identify six sides as a common attribute shared by two polygons to differentiate them from another polygon that does not have six sides.
Furthermore, endowing mathematical meaning to parts of a shape is linked to the development of mathematical language [31,32,33,34]. Language development starts from what Gee [31] called primary discourse, mathematical language informally used in the family and social contexts whereas the language linked to a secondary discourse is used in formal practices in institutions such as schools. In the case of polygon concept and polygon classes, a primary discourse uses non-standardized terms such as: lines instead of sides, peaks instead of vertices, and inward peaks, instead of concavities, while a secondary discourse makes use of standardized geometric terms such as parallelism, axes of symmetry or having six sides. In this sense, secondary discourse favors reasoning about the parts of figures through the coordination of cognitive apprehensions, which makes it possible to construct the polygon concept and polygons classes.
Objective of the Present Study
The objective of this research was to characterize sophistication levels in third grade children’s understanding of polygon concept and polygon classes. For this, we assumed that the ability to endow mathematical meaning to figure parts—which allows identifying the attribute that defines a class of polygons and recognizing a polygon as an example of that class—reveals itself during the dimensional deconstruction process through the coordination of apprehensions and forms of discourse. Based on Clements and Sarama [35], we define levels of sophistication as benchmarks of complex growth that represent distinct ways of thinking. Sophistication levels can be informed by both the shifts observed in students’ thinking during a specific intervention and a type of thinking that may be regarded as more sophisticated from a disciplinary perspective [36,37,38].
3. Materials and Methods
3.1. Participants and Curricular Context
The study reported here is part of a larger project in which we explore primary students’ geometrical thinking [39]. Here, we focused on the nine students selected from the 59 pupils (total sample) of the third year of primary education (aged 9–10 years) in a Spanish state school. The teaching conducted in previous courses with these students had been based on the textbook. The third-grade curriculum includes the concept of polygon and the recognition of attributes of the polygon classes such as concavity/convexity, symmetry and number of sides, while classes of triangles and quadrilaterals are introduced in fourth grade. We considered the concept of polygon as a plane closed figure with straight and non-crossed sides.
We chose to conduct a teaching experiment as this type of research is directly addressed to solve student learning problems and how this learning can be supported by teaching, addressing key issues in the current practice of mathematics in the classroom [40]. We designed a teaching experiment to favour the progressive understanding of the polygon concept and polygons class through the recognition and use of the attributes of geometric figures, a difficulty that we have indicated in previous research (e.g., [10,20]).
In this study, we asked the school and parents for permission to carry out the teaching experiment and conduct the interviews and informed them that the data from this research would only be used for research or teacher training at the university, maintaining the anonymity of the participants [41]. During all the interviews, the well-being of the participants was considered. To do this, we started with a short conversation with the student to find out how they felt about the teaching experiment and to see what their attitude towards it was.
3.2. Teaching Experiment
The teaching experiment consisted of a sequence of 10 teaching sessions, in conjunction with three individual interviews in different moments, and a questionnaire before and after the teaching sequence (Table 1) [42]. From the questionnaires, we characterized the changes in the children’s reasoning (pre-post) through an implicative analysis with the software CHIC (see more in [39]). Furthermore, to provide additional formation about how 8–9 years-old children built polygon concept and polygon classes, we conduct interviews with nine students. We selected the nine students taking into account their answers to the initial questionnaire regarding how they recognized the attributes of shapes and reasoned with them. We chose:

Table 1.
Teaching experiment: interviews, questionnaires, and sessions.
- three students who initially had difficulty recognizing figures as polygons;
- three students who recognized polygons but had difficulty identifying classes of polygons; and
- three students who recognized polygons, drew polygons that fulfilled some conditions and identified some classes of polygons.
We interviewed to these nine students three times during the teaching experiment to identify how they reasoned with polygons attributes. These interviews provided additional information about the children’s reasoning processes in three different times. We conducted 27 interviews that were approximately one hour each.
The first author of this study conducted the teaching sessions, acquiring the role of teacher. During the teaching sessions, students shared their task solutions and compared their answers with those of their peers. The teacher asked questions such as why or how they completed the exercise. Next, the students individually solved additional tasks. The teacher introduced the use of standardized geometrical terms as well as inclusive definitions of classes of polygons. For example, an isosceles triangle is a triangle with two congruent sides, so an equilateral triangle is an example of an isosceles triangle because it has at least two congruent sides. The tasks in the teaching sessions showed a variety of examples and non-examples of geometric figures to encourage students to analyze and reason about the attributes. In this teaching experiment, we emphasized the importance of non-examples in abstracting common attributes in perceptually different figures [12]. Using the Drawing Machine [43], we tried to help students enlarge the number of examples liked to a polygon class and support with this approach the hierarchical definitions (linked to inclusive classifications) favoring learning effectiveness of class inclusion. Furthermore, didactic resources as meccano or geoplane were used during the sessions and interviews to construct different geometrical figures as an assertion of properties of figures.
3.3. Interviews
The interviews were relied on task-based interviews [44] and inserted in the teaching experiment. The tasks in the interviews were linked to the activities performed during the teaching. We adapted the Drawing Machine metaphor [43] in the tasks aimed at identifying a common attribute in a set of polygons (Table 1). The Drawing Machine can do figures that have certain attributes (examples of a class) and cannot do figures that do not have those attributes (non-examples of a class) (Figure 1). Furthermore, the students’ justification could be verbal and/or non-verbal (drawings, constructions), allowing to make inferences about children’s understanding of polygon concepts and polygons class. The interviews were aimed at generating information on what students knew and how they reasoned with the attributes (dimensional deconstruction) through the coordination of cognitive apprehensions, using standardized geometric terms.

Figure 1.
Example of a task in the questionnaire and initial interview: identify the attribute that defines a class (having 6 sides) and represent examples and non-examples of the class.
In the initial interview (II), we used answers to the Initial Questionnaire and 4 additional tasks were carried out focused on recognizing and justifying when a figure was a polygon and on identifying classes of polygons (concave/convex, classes of triangles, and quadrilaterals with two pairs of parallel sides, with one pair of parallel sides and without parallel sides). For example, Figure 2 illustrates the task in which students were asked to turn a non-polygon into a polygon and to justify the transformation. In this task, students had to recognize which attributes in the polygon’s definition were not present in the figure. Solving this task requires dimensional deconstruction of the figure and related the parts with the definition to justify what must be modified through discursive apprehension. Furthermore, modifying part of the figure to transform it into a polygon call on operative and sequential apprehensions.

Figure 2.
Example of task in the initial interview: transform a non-polygon into a polygon.
In the middle interview (MI), the tasks focused on recognizing attributes of polygons and recognizing different polygon classes (concavity/convexity, number of sides, symmetry, the measurement of the internal angles, and polygons with two axes of symmetry). Figure 3 shows the task in which students had to recognize different attributes in a polygon using standardized geometrical terms. This task presented a concave pentagon and pupils had to justify if this polygon was a convex quadrilateral. As they were primary school students, we wanted them reason with the attributes of polygons, so in this type of task we considered as correct whether they refused at least one of the two conditions.

Figure 3.
Task in the middle interview: recognize figure attributes.
The Drawing Machine metaphor [42] was used in the tasks in the middle interview aimed at identifying a common attribute in a group of polygons. For example, Figure 4 shows the task of identifying two axes of symmetry as a common attribute in a set of shapes. The children had to identify the attribute that defines the class and draw examples and non-examples of that class (by sequential apprehensions). In an additional task, the pupils had to recognize whether a figure fulfilled this attribute (for example, a regular hexagon as an example of a polygon with two axes of symmetry). These tasks provided information on dimensional deconstruction and different apprehensions and helped to verify the extent to which students used standardized terms and how a figure was considered an example of a polygons class through discursive apprehensions.

Figure 4.
Example of a task in the middle interview: identify the attribute that defines a class (having two axes of symmetry), represent examples and non-examples of the class and identify examples of figures of the identified class.
In the final interview (FI), the tasks focused on recognizing figure attributes and identifying the common attribute in a set of polygons (classes of triangles according to their sides or angles and classes of quadrilaterals according to their parallel sides or their diagonals) and identifying examples and non-examples of figures. For example, they were asked whether the representation of a scalene triangle could be an example of an equilateral triangle and whether the representation of an obtuse scalene triangle could be an example of an acute isosceles triangle. These tasks made it possible to determine how children reasoned with the attributes of polygon classes and to what extent dimensional deconstruction allowed students to focus their attention on certain parts of the figure, and to observe how the mathematical meaning linked to the use of standardized geometric terms supported discursive apprehensions.
The tasks of drawing and transforming polygons made it possible to show the link between the sequential, operative, and discursive apprehensions through the dimensional deconstruction. For example, one task asked pupils to construct and draw an obtuse isosceles triangle (Figure 5), and quadrilaterals fulfilling various conditions; an obtuse equilateral triangle (which is not possible); a parallelogram with diagonals of the same length; and a parallelogram with right angles and perpendicular diagonals.
Figure 5.
Example of a task in the final interview: draw polygons with certain attributes using an isometric geoplane and explain why.
In the tasks of identifying the attribute, that defines the class, the Drawing Machine and the attributes of quadrilaterals with congruent sides were used. Pupils had to identify the class and draw examples and non-examples of that class. These tasks allowed for obtaining evidence of how dimensional deconstruction was articulated (to identify the attribute that defines the class), as well as sequential apprehension to draw examples and non-examples of polygons with this attribute. The fact that students were given the possibility to justify their drawings allowed us to observe to what extent discursive apprehensions linked mathematical meanings to figure parts using standardized geometric terms.
3.4. Analysis
Our analysis aimed at identifying different levels of sophistication in students’ understanding of the polygon concept and polygon classes through a qualitative analysis. These levels of sophistication allowed characterizing the mental spatial structuring processes supported by the dimensional deconstruction of figures through discursive, sequential and operative apprehensions while students resolved the tasks of the interviews.
The qualitative analysis was based on the Grounded Theory approach developed by Corbin and Strauss [45]. Our levels of sophistication do not generally characterize the understanding of the polygon concept and polygon classes but are a local approximation of this understanding that is conditioned by the teaching experiment, the context, and the participants of our study, but providing information about children’s structuring processes. The data corresponds to the transcripts of the twenty-seven interviews conducted throughout the experiment, the pupils’ written task solutions, and photographs of the constructions, in cases in which they had to draw or construct a polygon (purposing sampling).
For the data analysis, we took indications from previous studies into account regarding how students assign mathematical meaning to figure parts (the research background). Besides, constant theoretical sampling was carried out during the analysis, which consisted of following clues in the data and looking at different students’ answers to verify what the initial data under analysis seemed to indicate (the pre-analytical comments and the first ideas that seemed to emerge). To carry out the initial coding, we compared the answers to each task and of each student to identify initial patterns and similarities. We drew up a detailed description of the data and inferred how students reasoned based on the attributes (memos). We considered:
- how students used polygon attributes when they solved tasks in which they had to recognize polygons and transform non-polygon figures into polygons; and how they identified common attributes in a group of polygons (which defined a class) to draw or identify examples and non-examples of the class and
- how they used standardized or non-standardized geometric terms to describe their reasoning.
Figure 6 shows the memo of the answer of student G2S18 (student 18 of group 2) during the initial interview to the task of recognizing whether a square (in a non-prototypical position) could be an example of a quadrilateral with one pair of parallel sides. Figure 7 shows the memo of the student’s answer to the task of identifying the attribute that defines a class (the concave polygon class) and drawing an example and a non-example of the class in the initial interview.

Figure 6.
Memo of the solution of student G2S18 when performing the task of recognize polygon attributes (initial interview).

Figure 7.
Memo of the solution of student G2S18 when performing the task of identifying the attribute that defines a class and represent an example and a non-example of the class (initial interview).
Comparing the different memos of the different tasks and students, we inferred the characteristics of children’s structuring processes of the understanding of polygon concept and polygon classes. Specifically, we identified differences in student answers based on the attribute that defines the class of polygons. Thus, for example, in the middle interview, the previous student (G2S18) had difficulties when the attribute that defined the class was polygons with two axes of symmetry (Figure 8) but had no difficulties in the initial interview when the class was defined by the attribute be concave (Figure 7).

Figure 8.
Memo of the answer of student G2S18 when performing the task of identifying the attribute that defines a class and representing an example and a non-example of the class (middle interview).
By means of a constant comparative analysis between the generated memos, we refined the characteristics of benchmarks until no evidence of new characteristics emerged. The focus of attention in the constant comparative analysis was on how the classes of polygons were identified and examples and non-examples of the identified class were drawn, as well as how standardized geometric terms were used to designate the attributes and justify their answers. The coding of students’ ways of knowing and structuring processes constituted an intermediate coding, helping to transform the initial data into characteristics that defined the levels of sophistication in the understanding of polygon concept and polygon classes (categories). The constant comparative analysis allowed refining the categories (advanced coding) to generate an explanation of the levels of understanding of the polygon concept and polygon classes, considering how the students assigned mathematical meaning to figure parts by way of dimensional deconstruction and discursive, sequential and operative apprehensions.
The three researchers compared the memos based on the data and the inferences made from the differences between students and between tasks. The aspects on which we disagreed were discussed, looking for additional evidence to support or refute the inferences made to validate them. The objective of this part of the analysis was to search for evidence that confirmed or not the characteristics of children’s structuring processes when we compared answers of different students. Following this examination, we determined four levels of sophistication in students’ understanding of the polygon concept and polygon classes. These four levels are described in the next section.
4. Results
The results reported here show four levels of sophistication in the understanding of the polygon concept and polygon classes in third-grade student. These levels were characterized based on the analysis of the responses to the contextualized interviews in the teaching experiment. This characterization is thus linked to the instructional sequence followed in the study. The analysis allowed us to infer characteristics linked to the recognition of polygons, how attributes were used to reason, and how classes of polygons were identified and about the use of standardized geometric terms. The characterization of the levels considers the mental process through which students select, organize, and coordinate the information of parts of geometric figures to understand them or to establish relationships between them based on the discursive, sequential and operative apprehensions that are mobilized during dimensional deconstruction. From this perspective, the levels describe both students’ behaviors in specific tasks and our inferences about the mental mechanisms that could explain these behaviors.
4.1. Level 1. Partial Structuring of Polygon Concept
Students at this level recognized some relevant attributes in the polygon’s definition, but not all (one or two of the three relevant attributes). For example, they can recognize in a figure the cross sides and is open as non-relevant attributes of polygon concept but not the curved side. That is, if students have to transform a non-polygon into a polygon, they can recognize and transform the crossed sides into non-crossed sides and close the figure if it is open; but if the figure has a curved side, they still keep the curved side. Thus, although they can consider two attributes together, they have difficulty in considering the three attributes that together determine a polygon. At this level, students do not recognize attributes of polygon classes since they are not able to identify the common attribute in a set of perceptually different polygons. Students at this level are starting to look at parts of the figures, but they do not have a structural approach that allows them to consider the three attributes that determine together that a figure is a polygon. This way of proceeding can be considered as evidence that the perceptual and the analytical dimensions are starting to be related, though without being able to globally organize the three conditions that a figure must meet to be a polygon. At this level, students typically used non-standardized geometric terms to justify their actions.
An example of this type of thinking is the answers of student G1S1 (student 1 in group 1). On the one hand, to the task of transforming a non-polygon into a polygon in the initial interview (Figure 9), this student explained that the cross had to be removed, referring to the crossed sides (using non-standardized geometric terms), but did not consider the curved side.

Figure 9.
The answer given by G1S1 when performing the task of transforming a non-polygon into a polygon.
By other hand, this student had difficulties to recognize the polygon classes (for example, consider two different labels to the same figure). So, student G1S1 could not recognize if a square (polygon represented) fulfilled the attributes of having four sides and two parallel sides. In task 6, this student wrote: Yes, because it is a figure that cannot be made (Figure 10).

Figure 10.
The answer given by G1S1 to the task of recognizing if a figure is an example of a polygon class (it can have two different labels).
4.2. Level 2. Global Structuring of Polygon Concept
Students at this level recognized all examples and non-examples of polygons, justifying when a figure had the attributes given in the polygon’s definition. Additionally, they were able to recognize only some additional attributes. For example, students can recognize being concave or the number of sides, but not other attributes such as symmetry or attributes that characterize classes of triangles and quadrilaterals (attributes of the polygon classes considered in this research). At this level, a global structure of the polygon concept is generated (that is, considering the three attributes together to be polygon: a closed figure with straight sides that do not cross each other), and a partial structuring of other attributes starts to appear. When students recognize additional attributes, they can draw examples of that class, thus demonstrating the assignment of mathematical meaning to figure parts by means of dimensional deconstruction and sequential apprehension (drawing a figure that fulfils certain conditions). At this level, they begin to use standardized geometric terms along with non-standardized terms: this provides evidence that they are assigning mathematical meaning to figure parts through discursive apprehension.
For example, when performing the task of transforming non-polygons into polygons (section b in Figure 11), student G2S7 indicated that for the figure to be a polygon, it should be closed, have straight sides, and non-crossed sides. In addition, the student recognized that the figure is opened and has a curved side, explaining that for being a polygon would be closed and have straight sides (section c in Figure 11).

Figure 11.
The answer given by student G2S7 when performing the task of transforming non-polygons into polygons.
In addition, this student had difficulties to represent (draw and construct) polygons with conditions, specifically, when he had to consider three attributes at the same time. For example, to construct and draw a polygon with six sides, concave, and with at least one axis of symmetry. In this case, this student was able to consider some of the additional conditions, to be concave and have at least one axis of symmetry, but not to have six sides (Figure 12).
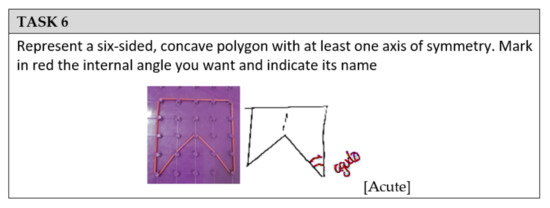
Figure 12.
The answer given by student G2S7 when performing the task of constructing and drawing a polygon with conditions.
Furthermore, at this level, students could identify an additional attribute in some cases but not in other cases. For example, students could identify to be more open as the common attribute in a set of concave polygons and drew an example of that class although using non-standardized terms (Figure 13).
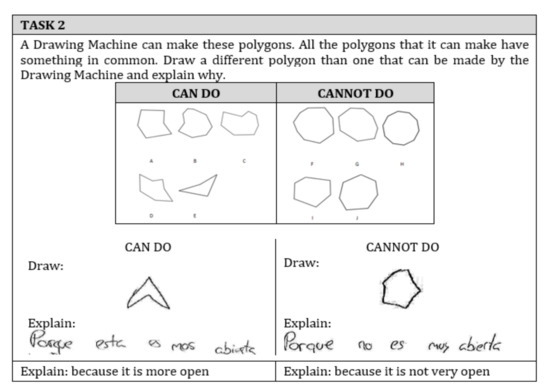
Figure 13.
The answer given by student G2S7 when performing the task of transforming non-polygons into polygons.
However, in other cases, students have difficulties identifying the additional attributes of polygons. For example, triangles with two equal sides to differentiate them from a triangle without equal sides (scalene triangles) (Figure 14).

Figure 14.
The answer given by student G2S7 when performing the task of recognizing the equilateral triangle as an example of an isosceles triangle (identified class).
4.3. Level 3. Partial Structuring of Polygon Classes
At this level, students use mainly standardized geometric terms to refer to the attributes of polygons, but they also use sometimes non-standardized geometric terms. For example, student G2S27 (Figure 15) in the task of recognizing whether a scalene triangle could be an example of an acute isosceles triangle, indicated that the representation of the obtuse scalene triangle was not an example of an acute isosceles triangle because it has the different sides and an obtuse angle. To reason about the attributes and to justify whether or not the given representation of a triangle fulfilled the mathematical meanings of acute isosceles triangle, this student used the standard terms (obtuse).

Figure 15.
The answer given by student G2S27 when performing the task of recognizing and reasoning about the triangle’s attributes.
One characteristic of how pupils manage additional attributes at this level is given when the student tries to build and draw a polygon that fulfils certain conditions (as the drawing of the G2S27: an obtuse isosceles triangle) (Figure 16). This way of proceeding demonstrates the role of sequential apprehension when they try to draw a polygon that fulfils certain conditions and discursive apprehension when having to specify them.
Figure 16.
The answer given by student G2S27 when performing the task of drawing a polygon that fulfils certain conditions (obtuse isosceles triangle).
However, at this level, students have difficulties in identifying some polygons classes depending on the attribute defining the class. At this level, students can identify some classes, but they could have difficulties in identifying other attributes that define a class. For example, they identify symmetry or concavity as a common attribute in a set of polygons, but not having two axes of symmetry in other cases. This is a different process from the processes of recognizing whether a polygon has certain attributes or drawing a polygon that fulfils certain conditions (as it happened in level 2). Concerning the difficulties to identify attributes that define a class. For example, the student G2S27 did not identify having two axes of symmetry as the criterion that defined a class and did not draw examples of the class. However, this student used to be a symmetrical figure as the attribute that defines the class, without taking into account that there were symmetrical polygons in the set of non-examples (polygon 10 and 14 in the Cannot do section) (Figure 17).
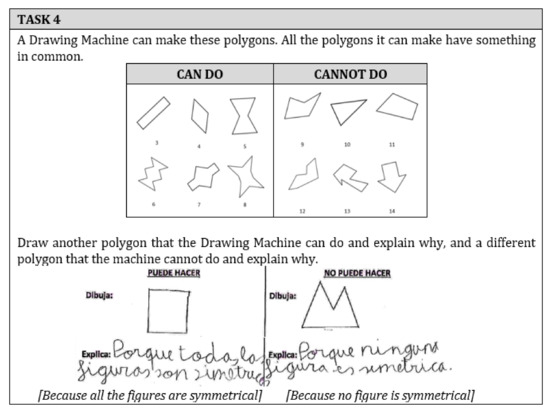
Figure 17.
The answer given by student G2S27 when performing the task of identifying the common attribute into a set of polygons (having two axes of symmetry).
4.4. Level 4. Global Structuring of Polygon Classes
Students at this level generally identified the attribute that defines the polygons class, drew examples of polygons belonging to the class, and recognized examples of the class in the cases used in the teaching experiment. At this level, students began to use different attributes of quadrilaterals, such as the notion of symmetry to characterize some classes of quadrilaterals, instead of focus on properties of sides, angles and so forth. Furthermore, students at this level reasoned mostly using standardized geometry terms, which provided evidence of the bi-directionality of discursive apprehension, giving mathematical meaning to the parts of the figures (from discourse to figure and from figure to discourse).
For example, student G1S18 used symmetry as the attribute to determine that the kit is a nonexample of the set of figures since exists a diagonal that is not symmetry axe using standardized geometry terms (Figure 18). This student indicated that the Drawing Machine can do figures whose diagonals are axes of symmetry and form perpendicular straight lines, and then explained that the kite is a non-example of this class because a line does not “mark” an axis of symmetry, referring to the diagonal as a line.
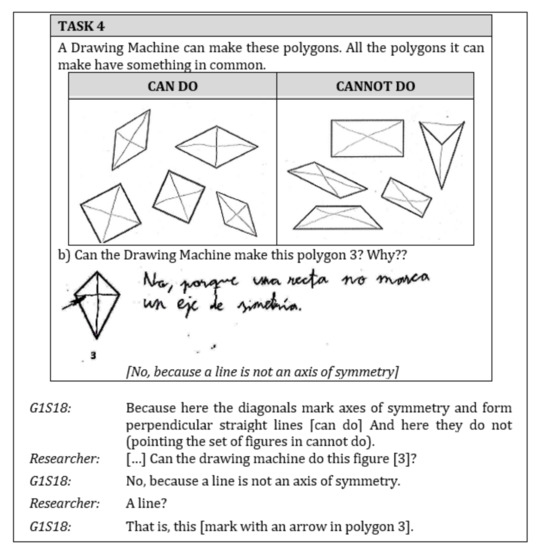
Figure 18.
The answer given by student G1S18 in the middle interview when performing the task of identifying the common attribute in a set of polygons (having diagonals marking axes of symmetry).
5. Discussion
The objective of this study was to characterize levels of sophistication in third-grade pupils’ understanding of polygon concept and polygon classes. We used Duval’s dimensional deconstruction and coordination of cognitive apprehensions to draw our attention to students’ spatial structuring. The analysis of the answers to the initial, middle and final interviews during a teaching experiment allowed us to identify four levels of sophistication in the way students endow mathematical meaning to parts of figures and how they organize the information about polygons and polygons class.
The level featured by a partial structuring of polygon (Level 1) can be assimilated to pre-cognition and syncretic levels [10,29], in which students attend to visual characteristics of a shape evidencing a synthesis of verbal declarative and imaginary knowledge, but cannot identify common shapes or distinguish between shapes of the same kind. At this level, by the dimensional deconstruction and discursive, sequential and operative apprehensions (modifying and drawing figures that meet certain conditions), students recognize figures perceptually using non-standardized terms. While global structuring of polygon concept and partial structuring of polygon class levels (levels 2 and 3) provide a finer detail of analytic level in which students reason with the set of properties of figures although they still do not manage inclusive relationships [8]. So, at level 2, students can transform non-polygons into polygons through sequential and operational apprehension, evidencing a global structuring of the polygon concept. Furthermore, students can identify different attributes using standardized and non-standardized geometric terms, but they have difficulties in reasoning with them. Meanwhile, at level 3, students use standardized geometric terms to endow mathematical meaning to parts of polygons and draw polygons coordinating discursive and sequential apprehensions, although they are not always able to identify the common attribute of a set of polygons. Finally, at level 4 (global structuring of polygons classes), students can identify the attribute defining a polygons class considered in this teaching experiment. Students reason using mostly standardized geometric terms. The characteristics of this level confirm the beginning of the relational level (Table 2).

Table 2.
Levels of sophistication of polygon concept and polygons classes.
The sophistication levels were characterized considering how students reasoned using the figural and conceptual information of the figures [3] based on the dimensional deconstruction and the coordination of discursive, sequential and operative apprehensions. The coordination allowed transforming a figure that is not a polygon into a polygon or drawing a polygon that fulfilled certain conditions. For example, when students recognize concavity or identify being concave as the attribute in a set of figures, being able to draw or recognize examples of the class. This process evidenced a way of knowing that goes beyond being perceptually aware of a difference or similarity between the polygons.
5.1. Relationships between the Levels of Sophistication
The levels of sophistication show students’ ways of knowing as they assign mathematical meaning to figure parts using discursive apprehension related to dimensional deconstruction and regarding how students use the geometrical terms. Considering a list of a figure’s attributes or a certain structure in this information are processes of thinking different and they are initially linked to the constitution of the polygon concept. Specifically, this is the case when students accept that a figure is a polygon when recognizing three attributes in the figure (a closed figure, with straight sides that do not cross each other). Next, they reason about a list of polygon attributes recognizing, for example, that a certain triangle is an obtuse triangle because it has an angle greater than 90 degrees or recognizing that a polygon has an axis of symmetry or is a concave polygon. These processes are linked to giving mathematical meaning to parts of a figure evidenced when they draw polygons that fulfil certain conditions or give reasons explaining why a figure does not fulfil certain conditions. However, reasoning based on elements of a list of attributes does not imply that students have built a global structure allowing them to identify a common attribute that defines a class in a set of perceptually different figures and to decide when a figure is or is not an example of that class.
From this perspective, our results indicate that identifying a common attribute in perceptually different figures represents cognitive progress since it implies abstraction concerning the information of some of the figures. This change consists of a shift from local to global structuring but depending on the attributes used. In the characterization generated in our study—linked to the tasks performed in the teaching experiment— the global structuring began with attributes such as being concave (having an angle greater than 180 degrees) and was more difficult in symmetrical figures [39]. What is relevant in the results of this study is the identification of the students’ mental processes as they reason about the attributes evidencing changes from local to global structuring.
Our results also indicate that the use of standardized geometry terms and non-standardized terms characterizes the mental processes described. Introducing standardized geometry words during the instruction helped the students’ speech to evolve from primary speech to secondary speech [31]. In this way, we can consider that the use of standardized geometry terminology is linked to the development of forms of reasoning about figure attributes [32,33,34].
The results of this study are a step forward in the research on the links between how the figures are perceived and how they are analyzed [22,23], describing this relationship in more detail. Specifically, we refer to the sophistication levels 2 and 3, which show the change from reasoning with a list of attributes to making mathematical sense of this list through spatial structuring as a form of abstraction [5].
5.2. Cognitive Apprehensions and Dimensional Deconstruction in the Characterization of Spatial Structuring
The coordination of discursive, sequential, and operative apprehensions through dimensional deconstruction is a characteristic of student learning [24,25]. The processes of recognizing whether a figure is an example of a polygon, or drawing polygons that fulfil certain conditions, differ from that of identifying the attribute that defines a class and drawing an example of that class. Building an organization of information based on the analysis of a group of figures implies identifying the attribute that defines the class and is based on the result of the dimensional deconstruction applied to the different figures. Identifying the attribute that defines the class is a form of abstraction that allows students to create an organization for a set of figures. This process of generating information beyond individual cases is what Battista et al. [5] called spatial structuring. In this sense, discursive apprehension and the use of standardized geometric terms allow assigning a mathematical meaning to the attribute that defines the class (what has been abstracted) and sequential and operative apprehensions allow to draw examples of figures with this attribute or transform a figure to fulfil the attributes of the class (by abstracting the concept). These are ways of seeing that are transformational engaging the dimensional deconstruction [19].
6. Conclusions
Our results indicate that identifying a common attribute in a group of perceptually different figures to define a class is a mental process that should be generated to progress in the understanding of polygons. The tasks in the teaching experiment seem to have encouraged the development of this mental process in some students by allowing them to compare examples of perceptually different polygons but sharing some common attribute. In addition, the introduction of standardized geometric terms allowed the use of common terms for the mathematical meanings that defined the class of polygons.
The description of different levels of sophistication of students’ understanding of the polygon concept and polygon classes expands our understanding of the development of geometric thinking in primary school students. These levels could be used in teacher training programs to help to pre-service primary school teachers learn about the sophistication levels of understanding of the polygon concept and polygon classes. However, further research is needed, to characterize learning trajectories in other levels and with other geometric objects. The characterization of different learning trajectories linked to specific task sequences would allow us to complement our understanding of the structuring processes regarding the relationship between figures or shapes, supported by the processes of dimensional deconstruction, cognitive apprehensions, and the use of standardized geometric terms.
Author Contributions
Conceptualization, M.B., S.L. and M.M.; methodology, M.B., S.L. and M.M.; software, M.B., S.L. and M.M.; validation, M.B., S.L. and M.M.; formal analysis, M.B., S.L. and M.M.; investigation, M.B., S.L. and M.M.; resources, M.B., S.L. and M.M.; data curation, M.B., S.L. and M.M.; writing—original draft preparation, M.B., S.L. and M.M.; writing—review and editing, M.B., S.L. and M.M.; visualization, M.B., S.L. and M.M.; supervision, M.B., S.L. and M.M.; project administration, M.B., S.L. and M.M.; funding acquisition, M.B., S.L. and M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported in part by the project PROMETEO/2017/135 of the Generalitat Valenciana (Spain) and by the University of Alicante (FPU2017-014).
Institutional Review Board Statement
All subjects and the center involved gave their informed consent for inclusion before they participated in the study.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Battista, M. Cognition-based assessment & teaching of geometric shapes: Building on students’ reasoning. In Second Handbook of Research on Mathematics Teaching and Learning; Lester, F., Ed.; NCTM-IAP: Reston, VA, USA, 2007; pp. 843–908. [Google Scholar]
- Levenson, S.; Tirosh, D.; Tsamir, P. Preschool Geometry. Theory, Research and Practical Perspectives; Sense Publishers: Rotterdam, The Netherlands, 2011. [Google Scholar]
- Fischbein, E. The theory of figural concepts. Educ. Stud. Math. 1993, 24, 139–162. [Google Scholar] [CrossRef]
- Hershkowitz, R. Visualization in geometry—Two sides of the coin. Focus Learn. Probl. Math. 1989, 11, 61–76. [Google Scholar]
- Battista, M.; Clements, D.; Arnoff, J.; Battista, K.; Borrow, C. Students’ spatial structuring of 2D arrays of squares. J. Res. Math. Educ. 1998, 29, 503–532. [Google Scholar] [CrossRef]
- Parzysz, B. “Knowing” vs. “seeing”, problems of the plane representations of space geometry figures. Educ. Stud. Math. 1988, 19, 79–92. [Google Scholar] [CrossRef]
- Fujita, T. Learners’ level of understanding of the inclusion relations of quadrilaterals and prototype phenomenon. J. Math. Behav. 2012, 31, 60–72. [Google Scholar] [CrossRef]
- Van Hiele, P. Structure and Insight: A Theory of Mathematics Education; Academic Press: New York, NY, USA, 1986. [Google Scholar]
- Clements, D.; Battista, M.T. Geometry and spatial reasoning. In Handbook of Research on Mathematics Teaching and Learning; Grouws, D.A., Ed.; Macmillan: New York, NY, USA, 1992; pp. 420–464. [Google Scholar]
- Clements, D.; Swaminathan, S.; Hannibal, M.; Sarama, J. Young children’s concepts of shape. J. Res. Math. Educ. 1999, 30, 192–212. [Google Scholar] [CrossRef] [Green Version]
- Elia, I.; Gagatsis, A. Young children’s understanding of geometric shapes: The role of geometric models. Eur. Early Child. Educ. Res. J. 2003, 11, 43–61. [Google Scholar] [CrossRef]
- Tsamir, P.; Tirosh, D.; Levenson, E. Intuitive nonexamples: The case of triangles. Educ. Stud. Math. 2008, 69, 81–95. [Google Scholar] [CrossRef]
- Verdine, B.; Lucca, K.; Golinkoff, R.; Hirsh-Pasek, K.; Newcombe, N. The shape of things: The origin of young children’s knowledge of the names and properties of geometric forms. J. Cogn. Dev. 2016, 17, 142–161. [Google Scholar] [CrossRef] [Green Version]
- Kaur, H. Two aspects of young children’s thinking about different types of dynamic triangles: Prototypicality and inclusion. ZDM Math. Educ. 2015, 47, 407–420. [Google Scholar] [CrossRef]
- Satlow, E.; Newcombe, N. When is a triangle not a triangle? Young children’s developing concepts of geometric shape. Cogn Dev. 1998, 13, 547–559. [Google Scholar] [CrossRef]
- Gal, H.; Linshevski, L. To see or not to see: Analysing difficulties in geometry from the perspective of visual perception. Educ. Stud. Math. 2010, 74, 163–183. [Google Scholar] [CrossRef]
- Gogou, V.; Gagatsis, A.; Gridos, P.; Elia, I.; Deliyianni, E. The double nature of the geometrical figure: Insights from empirical data. Medite. J. Rese. Math. Educ. 2020, 17, 7–23. [Google Scholar]
- Seah, R.; Horne, M. The construction and validation of a geometric reasoning test item to support the development of learning progression. Math. Educ. Res. J. 2020, 32, 607–628. [Google Scholar] [CrossRef]
- Sinclair, N.; Cirillo, M.; de Villiers, M. The learning and teaching of geometry. In Compendium for Research in Mathematics Education; Cai, J., Ed.; National Council of Teachers of Mathematics: Reston, VA, USA, 2017; pp. 457–489. [Google Scholar]
- Sinclaire, N.; Bruce, C. New opportunities in geometry education at the primary school. ZDM Math. Educ. 2015, 47, 319–329. [Google Scholar] [CrossRef]
- Walcott, C.; Mohr, D.; Kastberg, S.E. Making sense of shape: An analysis of children’s written responses. J. Math. Behav. 2009, 28, 30–40. [Google Scholar] [CrossRef]
- Loc, N.P.; Tong, D.H.; Hai, N.T.B. The investigation of primary school students’ ability to identify quadrilaterals: A case of rectangle and square. Int. J. Eng. Sci. 2017, 6, 93–99. [Google Scholar] [CrossRef]
- Ambrose, R.; Kenehan, G. Children’s evolving understanding of polyhedra in the classroom. Math. Think. Learn. 2009, 11, 158–176. [Google Scholar] [CrossRef]
- Duval, R. Geometrical pictures: Kinds of representation and specific processings. In Exploiting Mental Imagery with Computers in Mathematics Education; Sutherland, R., Mason, J., Eds.; Springer: Berlin/Heidelberg, Germany, 1995; pp. 142–157. [Google Scholar]
- Duval, R. Understanding the Mathematical Way of Thinking—The Registers of Semiotic Representations; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Rosch, E. Principles of categorization. In Cognition and Categorization; Rosch, E., Loyd, B.B., Eds.; Lawrence Elbaum Associates: Hillsdale, NJ, USA, 1978; pp. 28–71. [Google Scholar]
- Hershkowitz, R. Psychological aspects of learning geometry. In Mathematics and Cognition; Nesher, P., Kilpatrick, J., Eds.; Cambridge University Press: Cambridge, UK, 1990; pp. 70–95. [Google Scholar]
- Vinner, S. Concept definition, concept image and the notion of function. Int. J. Math. Educ. Scienc. Techn. 1983, 14, 293–305. [Google Scholar] [CrossRef]
- Skemp, R. The Psychology of Learning Mathematics, Expanded American ed.; Transferred to Digital Print; Routledge: Abingdon, NY, USA, 2009. [Google Scholar]
- Duval, R. Les conditions cognitives de l’apparentissage de la géométrie: Développement de la visualisation, differenciation des raisonnement et coordination de leurs fonctionnements. Ann. Didact. Sci. Cogn. 2005, 10, 5–53. [Google Scholar]
- Gee, J. What is literacy. In Rewriting Literacy: Culture and the Discourse of the Other; Mitchell, C., Weiler, K., Eds.; Bergin & Gavin: Westport, CT, USA, 1991; pp. 3–11. [Google Scholar]
- Lobato, J.; Walters, C. A taxonomy of approaches to learning trajectories and progressions. In Compendium for Research in Mathematics Education; Cai, J., Ed.; NCTM: Reston, VA, USA, 2017; pp. 74–101. [Google Scholar]
- Riccomini, P.; Smith, G.; Hughes, E.; Fries, K. The language of mathematics: The importance of teaching and learning mathematical vocabulary. Read. Writ. Q. 2015, 31, 235–252. [Google Scholar] [CrossRef]
- Vukovic, R.; Lesaux, N. The language of mathematics: Investigating the ways language counts for children’s mathematical development. J. Exp. Child Psychol. 2013, 115, 227–244. [Google Scholar] [CrossRef] [PubMed]
- Clements, D.; Sarama, J. Early childhood mathematics learning. In Second Handbook of Research on Mathematics Teaching and Learning; Lester, J.F.K., Ed.; Information Age Publishing: New York, NY, USA, 2007; Volume 1, pp. 461–555. [Google Scholar]
- Battista, M. Applying cognition-based assessment to elementary school students’ development of understanding of area and volume measurement. Math. Think. Learn. 2004, 6, 185–204. [Google Scholar] [CrossRef]
- Blanton, M.; Brizuela, B.; Gardiner, A.M.; Sawrey, K.; Newman-Owens, A. A learning trajectory in 6-year-olds’ thinking about generalizing functional relationships. J. Res. Math. Educ. 2015, 46, 511–558. [Google Scholar] [CrossRef] [Green Version]
- Stephens, A.; Fonger, N.; Strachota, S.; Isler, I.; Blanton, M.; Knuth, E.; Murphy-Gardiner, A. A learning progression for elementary students’ functional thinking. Math. Think. Learn. 2017, 19, 143–166. [Google Scholar] [CrossRef]
- Bernabeu, M.; Moreno, M.; Llinares, S. Primary school students’ understanding of polygons and the relationships between polygons. Educ. Stud. Math. 2021, 106, 251–270. [Google Scholar] [CrossRef]
- Stylianides, A.J.; Stylianides, G.J. Seeking research-grounded solutions to problems of practice: Classroom-based interventions in mathematics education. ZDM Math. Educ. 2017, 45, 333–341. [Google Scholar] [CrossRef]
- British Educational Research Association [BERA]. Ethical Guidelines for Educational Research, 4th ed.; BERA: London, UK, 2018; Available online: https://www.bera.ac.uk/researchers-resources/publications/ethicalguidelines-for-educational-research-2018 (accessed on 2 August 2021).
- Bernabeu, M.; Moreno, M.; Llinares, S. Experimento de enseñanza como una aproximación metodológica a la investigación en Educación Matemática. Uni-Pluriversidad 2019, 19, 103–123. [Google Scholar] [CrossRef] [Green Version]
- Battista, M. Cognition-Based Assessment & Teaching of Geometric Shapes: Building on Students’ Reasoning; Heinemann: Portsmouth, VA, USA, 2012. [Google Scholar]
- Goldin, G. A scientific perspective on structured, task-based interviews in mathematics education research. In Handbook of Research Design in Mathematics and Science Education; Kelly, A., Lesh, R., Eds.; LEA Publishers: Mahwah, NJ, USA, 2000; pp. 517–545. [Google Scholar]
- Corbin, J.; Strauss, A. Grounded theory research: Procedures, canons, and evaluative criteria. Qual. Sociol. 1990, 13, 3–21. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).