Abstract
The use of dynamic, three-dimensional software with virtual reality offers new possibilities for the teaching and learning of geometry. We explore the effects of introducing the immersive virtual reality software NeoTrie VR in real classes. Within a Design Research framework, we present qualitative observational data to report how the collaboration among a software development company, university researchers, and schools produces improvements in the design and updating of the software; the geometrical content, representations, and mathematical activity that students have access to as well as the way teachers conceive and manage the teaching of geometry.
1. Introduction
The explosion of digital technology in society and the field of education has led to changes in how we understand and use it, offering tools that extend beyond the prosthetic devices underlying past pedagogical styles and curricular standards, and considered now as tools for transforming the way in which we think and reason [1]. Digital technology is not considered neutral, in epistemological terms, and the type of knowledge resulting from its use differs from that resulting from the use of pencil and paper [1,2,3,4,5]. Therefore, these technologies are considered mediation tools in the creation, structuring, and development of cognitive processes. They constitute an additional participant in these processes [6] and offer new opportunities for learning [7].
For over 30 years, the so-called ‘dynamic geometry systems (DGS)’ have been studied and implemented in mathematics classrooms, as demonstrated by the works of [8,9,10,11]. Over the years, the virtues of DGS in two-dimensional geometry have been evident, especially in terms of student improvement with respect to visualization, representation, and testing and argumentation processes. Today, it continues to be a topic of interest in the research of mathematics education [12,13,14], especially for the teaching and learning processes of three-dimensional geometry, although research continues to be insufficient on the specific effects of working with DGS-3D.
Designed as an ‘extension’ of the flat world, the use of DGS-3D is opening up new areas in educational exploration, particularly in the fields of modeling, spatial sense, and geometry [15]. It is well-known that the development of the three-dimensional geometric sense, based on two-dimensional geometry, is not necessarily easy or natural [16], and the new developments of DGS-3D attempt to solve this problem. Numerous authors have noted the need to learn more about the possibilities of DGS-3D with regard to the role of spatial reasoning on 3D drawing; on the degree of influence of virtual representations on the geometry involved in DGS-3D; on the creation of geometric meanings, and on the role of the influence of new forms of interacting and visualizing on the perception and understanding of the key characteristics of 3D figures [13,17,18,19].
On the other hand, the outburst of Virtual Reality (VR) on the social, business, and educational scenarios has opened up a new range of possibilities. Although there are diverse names and uses of the term Immersive Virtual Reality (IVR), in this work, we refer to the definition of [20] (p. 8): “Virtual reality is a scientific and technical domain that uses computer science and behavioral interfaces to simulate in a virtual world the behavior of 3D entities, which interact in real time with each other and with one or more users in pseudo-natural immersion via sensorimotor channels”.
According to this definition, it is natural that IVR is developing in terms of visualization and interaction with a clear increase in the number of studies examining its potential in teaching-learning processes, both standardized-curricular as well as specialized or professional [21,22,23,24,25,26]. IVR software generates new methods of learning in which, through dynamic interaction, the touch (motor), visual and auditory senses intervene. It is possible to think that we are at the start of a new revolution in the educational field, the so-called “Kinesthetic Revolution”.
The initial results related to the use of DGS-3D IVR suggest that students improve their reasoning skills, spatial sense, and ability to identify and recognize the main characteristics of 3D geometric shapes “… improving pupils’ performance after intervention proves that students have been able to understand the geometric solids fully, as well as to perceive the difference between the objects of the three-dimensional space and those of the two-dimensional area” [27] (p. 397).
In addition, students are able to create more coherent discourse (arguments and reasoning) when using tactile IVR devices for dynamic exploration [28]. Similarly, improvements have been documented with respect to attitudes and motivation towards mathematics [27,28,29,30,31,32,33,34,35,36]: “… Importantly, according to the observations, the students were highly motivated by the interesting, fresh, new 3D manipulative software. Such an effect may have caused students to put more effort than usual into using the tools to explore geometry problems” [30] (p. 238).
Among the explanations offered for the detected improvements, the role of kinesthetic cognitive abilities in students has gained increasing popularity since in the current DGS-3D IVR it has been suggested that “… from points in space, users can construct uni-, two-, and three-dimensional mathematical objects through iterations of gesture-based operators” [37] (p. 323). The possibility of sensory-motor manipulations provides “a space where learners at all levels could use their hands to act directly on mathematical objects, without the need to mediate intuitions through equations, symbol systems, keyboards, or mouse clicks” [37] (p. 325).
Furthermore, the DGS-3D IVR permits: (a) new characteristics of visualization and exploration of shapes that allow students “to enter” them, move them and modify them dynamically through “grabbed dragging” [38], as well as to visualize changing the point of view through the flight [24]; (b) the creation of classes of shapes through the dynamic extrusion of points to be transformed into segments, from segments into flat shapes, or from flat shapes into three-dimensional shapes; (c) to make dynamic deformations of shapes using grabbed dragging of vertices or edges; or (d) to obtain shapes and visual verifications, impossible to carry out using desktop 3D technologies.
Although initial studies have provided information on the possibilities of the stable DGS-3D IVR, currently, there is a lack of empirical studies on the design and development of DGS-3D IVR software to expand our understanding of the educational implications of their use [27] (Our literature review has allowed us to detect the following DGS-3D IVR in distinct levels of development: Construct3D [32]; HandWaver [37]; VRMath2 [39]; Geometry Explorer [40]; NeoTrie VR [41]; Geogebra MR [42], and CalcFlow [43]. The main common characteristics of all of these is the possibility of carrying out dynamic actions with the three-dimensional figures through gestures-hands or controllers. The level of development of the software is variable). The following is one of the key elements of the current and short-term agenda:
“Evaluations of educational VR applications need to be conducted both in terms of technical feasibility (i.e., from a software engineering standpoint) and of the learning outcomes (i.e., from a pedagogical standpoint). We also suggest that future evaluations assess whether developed applications reflect the users’ needs, from the perspective of both teachers and students”.[44] (p. 22)
Therefore, within the framework of “design science”, it is necessary to develop knowledge related to the design and the scientific methods, which will better reflect on the fact that, although engineers are concerned with the device, the development of software should include experimental studies. Such studies constitute a significant part of both the design and the construction of knowledge, especially in designs related to social sciences, such as education [45].
In the field of education, the company–university–school collaboration turns out to be essential, and Design-Based Research (DBR) offers the ideal framework to explore a variety of designs, including those related to teaching and learning and the use of technology [46,47,48,49]. The general purpose, from an educational and technology usage perspective, according to DBR methodology, is to transfer the research from the laboratories to the classrooms, in order to obtain additional insight regarding how, when, and why innovations function in practice [50,51,52,53,54].
From a software engineering perspective, the cyclical structure of DBR is considered to be one of the operational steps in the design, development, and evaluation of the lifecycles needed to create and maintain an educational product or software [48,55], with the systematic evaluation of usage conditions of products under development being fundamental [56].
In this article, we present a work in progress for the design and development of a DGS-3D IVR known as “NeoTrie VR”, abbreviated as Neotrie in what follows, from an educational perspective. The work is currently being conducted by university researchers, in collaboration with the spin-off “Virtual Dor” of the Universidad de Almería, and with primary and secondary teachers. Our purpose is to show how the company–university–school collaboration has a positive impact on:
- the software improvements and updating, in a continuous feedback process with its implementations in classroom settings;
- the new geometric skills and knowledge that students develop through its use; and
- the way teachers design geometry teaching and how they manage it.
Next, we will briefly describe the DGS-3D IVR Neotrie and report some of the results related to the previous points, obtained from four teaching experiments (as characterized in [57]) in which the Neotrie software was used in real classrooms.
2. Neotrie: A Software for the Teaching and Learning of Three-Dimensional Geometry
Neotrie is a dynamic 3D geometry software of immersive virtual reality designed in the Unity 3D (Unity 3D is downloadable from http://unity.com, accessed on 26 September 2021) game engine by Virtual Dor, a spin-off of the Universidad de Almería (For more information visit http://www.virtualdor.com, accessed on 26 September 2021). From an educational perspective, Neotrie permits the creation, visualization, handling, and dynamic interaction with 3D geometric objects and models, similar to how this occurs in DGS-2D, but in a fully immersive, three-dimensional environment. For teachers, the software is a new working tool to be used in the classroom to help students in the acquisition of stereometry, the improvement of 3D visualization, the understanding of geometrical and topological properties, and the transition from 2D to 3D (and vice versa) [34,58,59], among other content.
As previously mentioned, the current design of Neotrie was carried out in a collaborative workspace among the company, the university, and the schools, in a continuous experimentation and feedback process conducted by all of the relevant participants. The version of Neotrie published on the STEAM (For more information visit https://store.steampowered.com/app/878620/Neotrie_VR/, accessed on 26 September 2021) video game platform has the following characteristics:
2.1. Technical Requirements, Interface, and Basic Actions
The use of Neotrie requires Virtual Reality equipment (consisting of a VR visor and controllers) and a standard videogame computer, with (at least) a GTX-970 graphics card with 8 Gb of RAM and an i5-4600 processor.
The pre-defined scenario for Neotrie is the interior of a neoclassical Greek temple, surrounded by a forest, mountains, and a lake. Students can move around in the scenario by walking, flying, or teleporting themselves. The software also includes a voice recognition system based on Microsoft’s Cortana assistant, allowing users to invoke shapes by naming them out loud (graphs, polyhedra, and round bodies). These shapes are preloaded in the software.
The basic actions of Neotrie are performed by pressing a button in a physical controller. Upon doing so, a menu of actions appears, which are activated when the user passes over the virtual hands (Figure 1a). These actions include: creating vertices (points), edges, faces, modification of their position in space, erasing elements of the figures, making 3D annotations, translating shapes as a whole without rotations, or visualizing the basic information of each constructed shape as well as the number of vertices, edges, faces, lengths, areas, volumes, etc.

Figure 1.
(a) Virtual hands action menu. (b) Basic actions and tools.
In addition to the basic actions, Neotrie contains a diversity of tools, some of which are common to all DGS, but have been adapted to 3D, and others that are specifically developed based on the systematic evaluation of the software offered by teachers and researchers. The goal is for the tools to be intuitive, easy, and coherent, both in terms of their mathematical meaning and the user experience.
2.2. Common Tools of the 2D and 3D DGS
The Neotrie interface includes a table from which the user may select classic drawing tools, such as a paintbrush and pallet of colors, a stamp to copy and paste, an eraser to eliminate whole shapes, a tool for rotation, reflection, middle points, an angle transporter, a ruler, and parallel lines (Figure 1b). Given the three-dimensional environment, some of the tools have different characteristics than those normally found in a DGS-2D, for example, the perpendicular tool shows a line that is perpendicular to another line or plane, and the intersection tool shows the intersection point of two straight lines when they meet or the two closest points if they cross, the intersection point of a plane and a straight line, or the intersection line of two planes, etc.
As mentioned above, the research and development team pays special attention to the usability of the tools, such that:
- Each tool has a drop-down menu with instructions for use.
- All of the tools and shapes created may be held by the virtual hands to move them to wherever the user wishes.
- All of the shapes and their elements can be colored.
- Some tools are color-coded, making their use more intuitive. Red parts indicate the need to make an entry to use them; green parts indicate the outgoing elements that will be obtained, and a blue point in each tool acts as a three-dimensional mouse cursor.
- The tools are optimized based on natural gestures made with the hands. For example, simultaneous dragging with both hands produces a homothetic transformation of the shape that is being dragged, and the option of a union allows the user to make more complex shapes based on others by simply bringing together any two vertices of the same.
- Some shapes depend on the parameters that are visualized and may be modified virtually by touching the menu of buttons for these tools, as is the case with the tools for rotation (Figure 2), slider, or interpolator between two points (Figure 3).
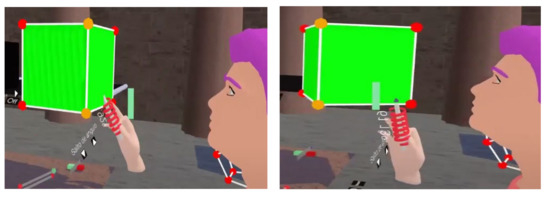 Figure 2. Using the rotation tool.
Figure 2. Using the rotation tool.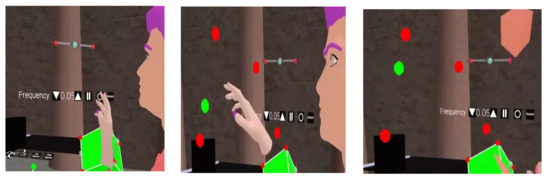 Figure 3. Using the slider tool between points.
Figure 3. Using the slider tool between points.
One of the main characteristics of the DGS is that it offers tools for tracing and automatic movement, especially useful for observing geometric loci. In this case, Neotrie offers both tools, permitting the user to see the tracing of the objects when they are dragged or when movement is incorporated. These tracings are curves in the space (for the vertices) or ruled surfaces (for the edges). On the other hand, there is also a labeling tool that adds information on the elements of the shapes, such as: (a) vertices: name, coordinates (x, y, z) in decimeters; (b) edges: length or weight (for graph theory activities); (c) faces: the general equation ax + by + cz = d, and the area in dm2; and (d) all of the data are updated dynamically when the student modifies the position of these elements; to do so, the coordinates and the equations are based on a Cartesian moveable coordinate system (Figure 4).

Figure 4.
The labeling tool and the 3D axis system.
2.3. Specific Tools and Resources for DGS-3D
DGS-3D IVR Neotrie has certain specific tools to carry out activities in a three-dimensional space. For example, the “magnet” tool makes movements followed by a rotation to place the shape in the correct position in the joining actions (For some examples showing how to use the magnet tool visit https://youtu.be/mTVKv1W4shw, accessed on 26 September 2021). This is very useful when making mosaics, 3D tessellations, or fractals; the views offer the floor, profile, and elevation of the shapes; and the “scanner” tool shows the projection of a shape in any direction, as well as the section of the same with the plane (This resource was developed in collaboration with the “Palais de la Découverte”, Paris, to simulate X-rays of crystals). The scanner also allows for shapes to be hidden in order to perform “mysterious shape” exercises (Figure 5).

Figure 5.
Scanner tools and a multi-view plane.
2.4. STEAM in Neotrie
Neotrie also allows for STEAM activities to be carried out. In addition to the regular 3D geometry shapes, it is also possible to insert 3D objects in STL or OBJ formats, imported from 3D design software. For example, it is possible to study the modeling of a chair (Figure 6a) and to insert sounds, recordings, or musical notes in WAV format, assigning them to any object in the scene. Or, manipulable images and videos may be added, for example, personalizing scenarios with 360° images. In Figure 6b, a 360° photo of the Courtyard of the Lions of Spain’s famous Alhambra complex (Granada) has been inserted. Students can construct geometric tiling and take photos using the Alhambra as the background. Specific tools are also available, such as the “gravity” tool, to assign weight to 3D objects, or the “ball launcher” tool, to visualize and measure trajectories.

Figure 6.
(a) Modeling a chair. (b) Personalized scene of the Courtyard of the Lions of the Alhambra.
3. Methods
This study, conducted under the Design-Based-Research (DBR) paradigm, consists of two interconnected components. On the one hand is the development and design of the software, using the DBR methodology from the Software Engineering perspective [48]. On the other hand is the experimentation and assessment of the findings obtained in diverse teaching experiments carried out in real classrooms [54,57,60]. Thus, through a systematic, flexible and collaborative research process carried out in design-development-implementation-analysis cycles, a greater understanding of the phenomenon is achieved during both the experimental execution and product development.
The work team is multi-disciplinary and consists of the “Virtual Dor” spin-off and its software engineers, a mathematician specializing in geometry and topology, and two researchers in Mathematics Education. The users are four teachers and their students from Primary and Secondary Education classrooms in Spain and Poland. All subjects gave their informed consent for inclusion before they participated in the study.
Below, we offer a brief description of how the software has been developed in a dynamic, continuous feedback process from the demands and results of the teaching experiments. Then, the four teaching experiments are presented, together with some of their results, which serve to illustrate the mediation of Neotrie in: the mathematical content available to students; the representations that they could use; and the kind of mathematical activity they could perform. Next, some of the effects of this software on the teachers participating in the experiments are shown.
4. Influence of the Use of Neotrie in Software Design
In this section, we briefly describe how the development of the product is influenced by the distinct usage experiences in real-life learning environments. It is based on the 2017 launch of version 1.0 of Neotrie, in which the Virtual Dor team of developers focused their efforts on creating a stable software of dynamic 3D geometry with basic functions.
According to the Software Engineering perspective, the DBR methodology not only corrects lag and other code errors through real experiences with the software but also obtains and designs activity proposals and significant information from the opinions of teachers, students, and education researchers. Therefore, the activity proposals are enriched by this set of information, permitting the design, development, and testing of new tools and functions that are necessary to carry them out. To achieve this inter-relationship between developers, teachers, researchers, and users, it is necessary to maintain and promote ongoing communication, both during the educational experiment execution and research and in subsequent retrospective analyses of the experiences.
To reflect on how this communication has specifically influenced developers, in Figure 7, we show some of the milestones achieved when using the methodological cycles schema.
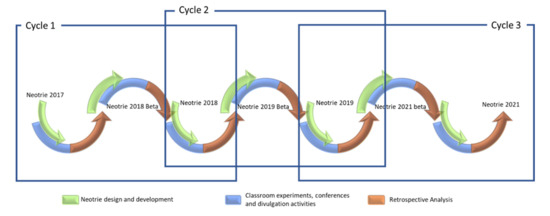
Figure 7.
Development cycles.
Cycle 1 (2017–2018): Following the launch of version 1.0, the need to attract more student attention was detected. Therefore, various basic tools were improved (paintbrush and pallet, parallel lines, intersections, etc.), based on an experience with polygons, prisms, and pyramids. Similarly, the VR Greek temple scene was designed and decorative elements were added, both inside and outside of it. Another aspect that was improved was the fluidity of the movements in the 3D Neotrie environment.
For this, a tele-transport and flight mode was implemented, allowing the user/student to move across the VR scene with greater freedom. Furthermore, it was necessary to review the students’ actions for their subsequent analysis, and so that students can review their constructions; for this, video and photo cameras were included, allowing the recording of scenes and activities. Some of the referred aspects are included in the works of [58,61], and in the materials published on the Scientix web (For more information visit http://www.scientix.eu/projects/project-detail?articleId=689498, accessed on 26 September 2021). The Neotrie 2018 (2.0) version was published on the Steam platform.
Cycle 2 (2018–2019): During this second cycle, diverse educational experiences and studies [24,34,62,63,64] promoted the design of new functions and tools, such as a system of multi-view planes to dynamically study the views of the shapes, sliders, and tracer brushes to create and study revolving bodies based on their generatrix (cones, cylinders), the tracing of conics, quadrics, etc.
Similarly, the file saving and loading system was also improved, as requested by most of the teachers. The importing and exporting of 3D objects was included in the STL formats of 3D and OBJ printing to enable STEAM experiences. Panoramic 360° photos of monuments were inserted as well as sounds for shapes and musical balls. The design of these elements also resulted from the need for a Neotrie project adapted to individuals with intellectual disabilities (This project was funded by the Plan UALTransfiere of the University of Almería, ref.: TRFE-SI-2018/009).
Although the team of developers tests the activities that are designed by teachers and researchers prior to their implementation in the classroom, the experiences created in this cycle have revealed that it is only once they have been effectively applied in real environments that new and unexpected approaches arise, as well as the creation of more complex shapes or the distinct use of the designed elements. In these situations, contact with the team of developers allows for a greater creation of potential solutions. This is the case of the experience to bring the world of fractals to the school, in which a flaw was detected in the attachment of fractal iterations that would have prevented advances in the development of the experience. However, the continuous contact and exchange of information with the developers permitted the correction of the error in only two days, developing the experience in the initially foreseen times [65].
Cycle 3 (2019–2020): Until this cycle, experiences and studies were carried out in pre-university educational phases. In this cycle, however, classroom experiences in the undergraduate mathematics degree and in the Master’s degree in secondary education teaching were included. The distinct perspective regarding the use of Neotrie that was contributed by these students, as well as their needs, served as decisive positive influences to help improve the tool of intersections of lines and planes, the design of a system of three axes of coordinates, the labeling tool for coordinates of vertices, and information on edges and planes, among others. Likewise, the use of Neotrie in university teaching has resulted in the completion of a final project in the Mathematics degree, related to the development and implementation of a 3D graphing calculator [66].
In parallel, experiences with primary and secondary school students have resulted in improvements in the system of axes, the incorporation of movement restrictions in the translations of 3D elements, and the detection and correction of flaws in the calculation of volume in certain cases of cube stacking [67].
Cycle 4 (2021–): In the academic school year of 2020–2021, the situation caused by the COVID-19 pandemic led to the adaptation of Neotrie to VR glasses for mobile devices, with the new possibility of emitting lessons live or recording stereoscopicvideos to synchronously or non-synchronously visualize them, while also designing diverse activities and manuals [68].
5. The Teaching Experiments
In this section, we reflect on how Neotrie has impacted the teaching and learning of geometry in the four classrooms that we considered for this study. First, we briefly describe the teaching experiments. Next, we show the influence of the software on the geometrical skills and knowledge developed by the students. In particular, we address the new geometric content to which they have access; the different types of representations they use; and the mathematical activities they performed [69,70]. At the end of the section, we discuss how the use of Neotrie has affected the teachers participating in the experiments, in terms of how they conceive their teaching, their students’ learning, and the management of the teaching–learning process mediated by this software.
5.1. Contextualization of the Teaching Experiments
The experiments were carried out in public schools (one in Poland and three in Spain), with students aged 10 to 15 years. Following the Design–Research methodology, cycles of design, implementation, observation, analysis, and redesign were implemented. Lengths and scopes differed, according to the different experiments. For each of them, a descriptive and qualitative study was conducted, following the guidelines of observational methodology [71,72,73].
In all of the teaching experiments, a virtual reality system was used (HTC Vive, Oculus Rift, or Windows Mixed Reality), as well as one computer per class. Normally, students were grouped together in teams of four or five members. The first sessions were dedicated to demonstrating the functioning of the basic actions of Neotrie. In some sessions, the software was used by the teacher to offer explanations and/or to conduct inquiry based explorations based on the inquiry, with the assistance of a “Sherpa student” [74], while the rest of the class followed the explanations given over a large monitor.
In most of the sessions, the software was used by one of the teams to complete the tasks, while the other groups worked on the same concepts using pencil and paper and/or manipulative materials. These roles were interchanged from task to task. Within this basic configuration, the distinct dynamics were orchestrated by the teachers and researchers, according to their didactic needs. All of the sessions were videotaped and observational field notes were taken for their subsequent analysis. Below, we briefly explain each of the teaching experiments.
Teaching experiment 1.
This was conducted in Poland with primary and secondary school students, aged 11 to 14 years. Over two academic years (2018–2019 and 2019–2020), three different classes worked on the official geometry curricular content, including the recognition of shapes and their main elements, angles, polygons, prisms, pyramids, etc. (These lessons may be consulted at the website: http://www2.ual.es/neotrie/comunidad/, accessed on 26 September 2021). The classroom dynamic, led by the teacher and researchers, fostered inter- and intra-group collaboration.
When a group of three to five students used Neotrie, the other mates participated actively, helping in the resolution of the Neotrie tasks, which were interconnected to the tasks that the other groups had to perform, supported by structured material, such as 3D Polyfelt. On other occasions, competitions were proposed, in order for the groups to develop distinct strategies to tackle the same task. In order to promote the initiative of the students, voluntary classes were programmed with Neotrie to tackle more complex problems.
Teaching experiment 2.
This was conducted in a Spanish primary school class with students aged 11 and 12 years, in the 2018–2019 school year. Using gamified dynamics, the goal was established to find the minimum surface volume for cuboids of a given volume. For this, students were grouped in teams of four or five members. They worked one group at a time, by sharing Neotrie controllers among the members of the group in turns. While one member of the team worked in the immersive virtual reality environment, the other members supported him or her by working with flat representations and manipulative materials (Centicubes, Magformers, etc.). Some additional lessons for the whole class were given in order to support this process by offering clarifications of theoretical elements as needed.
Teaching experiment 3.
This was conducted in a Spanish secondary school class with students aged 14 and 15 years. The participants worked on content associated with platonic solids and their symmetries (reflexive and rotational). Similarly to the previous experiments, the classroom dynamic involved working in a game-based environment [75], inter-mixing whole-group sessions with group work in teams of four students, while the other groups carried out parallel tasks to those of Neotrie, using materials such as Zome Geometry©.
Teaching experiment 4.
This was conducted in a Spanish secondary school classroom with students aged 12 to 13 years. They worked on extra-curricular content on 2 and 3-dimensional fractals, in a Project Based Learning (PBL) environment [63]. A work session was implemented for the large group, to present the fractal concept, followed by various work sessions with three groups of four students. Once again, the members of the groups took turns working with Neotrie while the rest of the team supported the student with the controllers in the construction of fractals by considering representations of these, both flat and using manipulative 3D materials for the case of 3D fractals. This experience was integrated within a PBL project called “The museum” and as a part of it, students learned to build fractals using virtual reality and taught the visitors of the museum how to construct them in Neotrie.
5.2. Influence on Mathematical Content
Digital technologies, such as Neotrie, place an emphasis on new aspects of familiar content and provide access to relevant mathematical content that do not form a part of the regular curriculum (technology as an amplifier and technology as a reorganizer, according to [76]). In our case, Neotrie can deal with:
- Mandatory curricular content that presents reported difficulties for students, such as the distinction between perimeter, surface area, or volume of solids, together with the induction and understanding of the associated formulas [77] (Teaching Experiments 1 and 2).
- Mandatory curricular content, such as geometric figures, which are usually treated in a superficial manner, using examples and prototypical properties. This may prevent a full and operational conceptualization of these shapes, especially the three-dimensional ones. In the case of geometric bodies, Neotrie also permitted the consideration of such aspects, such as the symmetry of these solids, which are difficult to access using physical materials [78,79] (Teaching Experiments 1 and 3).
- New content of great interest to current mathematics and other fields that are accessible to secondary education students through the use of current technologies, but that do not form a part of most geometry curricula, such as fractal geometry [13] (Teaching Experiment 4).
5.3. Influence on Mathematical Representations
As a DGS-3D, Neotrie influences two-dimensional representations; on the one hand, in terms similar to those documented for the DGS-2D and, on the other hand, with new approaches and ways of defining two-dimensional representations. The possibility afforded by the software to create flat shapes in the three-dimensional space and to convert these shapes into objects with which the student can interact (by dragging or placing them with respect to the other perspective) may help overcome difficulties related to non-prototypical examples of figures, as suggested by [80]. For example, when students consider the polygon concept, they tend to begin their construction in Neotrie by drawing various points in the scenario and joining them with lines. If no restrictions are placed on the movement, these points do not tend to be coplanar, resulting in a shape that is not flat (Figure 8).

Figure 8.
Non-planar quadrilateral.
Likewise, the representation in Neotrie draws attention to this fundamental property that defines polygons and that may go unnoticed if working exclusively in the plane. This may have repercussions on the conceptualization of polyhedra, since, if the faces of a geometric body are not planar, the figure is not a polyhedron (Figure 9).

Figure 9.
Geometric solid with non-planar faces.
As for the representations of three-dimensional shapes, the software offers access to representations differing from those offered in 2D and those previously created using materials. Neotrie permits teachers and students to easily create non-prototypical examples and counterexamples of these figures (At the website: http://www2.ual.es/neotrie/comunidad/sample (accessed on 26 September 2021) activities for work are presented (prototypical and non-prototypical) and counterexamples, such as “Classify the polyhedra”, “An exclusive club within the polyhedra”, “A prism or not a prism, that is the question” or “Identifying pyramids”).
This offers a major advantage since, in order for relevant learning to take place, it is necessary to access both the prototypical examples as well as examples showing irrelevant properties and counterexamples that do not comply with relevant properties of the geometric shapes [81]. The discussion based on the shapes created provides fundamental support for identifying the figures belonging to a specific family, based on their properties, as well as for inducing characterizations of polyhedron families (Figure 10).

Figure 10.
Polyhedron Classification from examples and counterexamples.
Furthermore, the possibility of projecting the figures created in the virtual reality onto a large screen allows teachers to orchestrate large group discussions, overcoming the difficulties associated with the size of the manipulative to be simultaneously visualized by all of the students in a class.
Neotrie also permits access to the dynamic facet of some definitions. For example, students can experiment with the definitions of segment, quadrilateral, or geometric body, obtained as the extrusion of a point, segment, or flat figure (face), respectively (Figure 11). This helps in their understanding of the differences between the different dimensions and allows for their interpretation of the upper dimensions as an extension of the lower ones, thereby establishing a connection between the two [82].
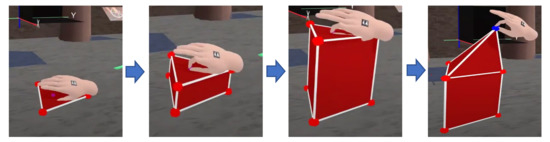
Figure 11.
Triangle extrusion to obtain a prism and point extrusion to obtain a pyramid on top.
This dynamic nature of the software has also permitted a flexible approach by students to the coordinate system in the space, in which the axes are considered from distinct positions. In this way, the bases of any object no longer have to always be those parts situated in the “lower position”, but rather, are those that are the most suitable at a given time for the dynamic observer, who moves around the objects and is situated in the space in the most efficient manner to perform actions such as identification of the type of shape, its elements of symmetry or the calculation of its dimensions.
Finally, we highlight that the immersive virtual space is a very different work area as compared to those typically used by students. For example, the sizes may be too large to be situated and oriented (as in the creation of fractals); it is necessary to maintain an ordered scene, interacting with the shapes in their “real-life” size; and it is difficult to coordinate what an individual inside this immersive environment sees with that seen by those having access to the work via a flat screen. The fact that only one person (student or teacher) has access to the immersive virtual reality environment, while the others have to interact with him/her to resolve tasks, having access to other types of representations (screen projections, physical models, and other planar representations), opens up a new environment of mathematical communication, as we will see in the following section.
5.4. Influence on Mathematics Activity
The access to new types of representations provided by the DGS-3D, and especially those facilitated by the IVR, is linked to new types of mathematics activity in the classroom. We highlight the influence of Neotrie on the activity performed in the promotion of the Joint Problem Space (JPS) [83], and on the types of reasoning that students made when interacting in this space: analytic, analogic, and structural.
In the teaching experiments, it has been found that Neotrie plays a critical and explicit role in the maintenance of the JPS [55,84], especially in the discussion, acceptance, refutation, and implementation of plans. Furthermore, the software has allowed students to not be exclusively dependent on the mathematics language to build and maintain their shared understanding of mathematics since, through the interactivity of the immersive virtual environment, a context is created that facilitates the production of actions and gestures accompanying the discourse.
This is necessary when students do not manage to communicate their ideas through language, especially if the subject handling Neotrie, interacting directly with the virtual 3D objects, does not capture the indications/suggestions of the students that are collaborating in the activity and they observe the actions on the computer, on the screen projection (2D), or in 3D physical models (Figure 12). Thus, it has been observed that the use of Neotrie offers new possibilities for students to maintain the JPS, from early ages.

Figure 12.
Example of students observing and producing gestures.
For this, it has been fundamental the orchestration of different dynamics by the teachers, in order to ensure all the students are involved in the same problem or activity, in either small or large groups [67]. For example, in Figure 12, corresponding to the calculation of a volume enclosed in a net, it is observed that the production of gestures (the girl signals to the computer screen to indicate where to begin counting), cognitive changes were created in the group, revealing changes of direction in the solving of the mathematical activity [85,86].
Within this JPS, the progressive control of the spaces and movements by students fosters them to go beyond their gestures. Assisted by the teacher’s mediation, the work with Neotrie has promoted the development of geometric vocabulary and analytic reasoning based on the properties of the geometric objects [87]. The possibility of painting the vertices, edges, and faces of the geometric bodies in different colors, of dragging the figures and showing them from distinct perspectives, of placing them in distinct positions, etc., has facilitated the deconstruction and analysis of geometric shapes and their classification. The interest of the students in the resource has supported individual analytic reasoning, which is strongly increased by the group discussions and the game-based dynamics designed by the teachers.
Furthermore, the above mentioned extrusion actions, along with the painting of the edges and faces, helped students to distinguish between the magnitudes of length, surface area, and volume. This, together with the activity of filling the cuboids with cubes contributed, in experiments 1 and 2, to the assimilation with the multiplicative principle for volume. The students applied this principle in different ways, multiplying the three dimensions in the order that was the most convenient at each given moment, noting that they could begin from any of the sides and multiply by the remaining dimension to obtain the cuboid volume (Figure 13).

Figure 13.
Student explaining the procedure through gestures and a scene of the proposed activity in Neotrie.
The students participating in experiments 1 and 3 also developed their analogic thinking skills when passing from the parallelism and perpendicularity between the lines to the parallelism and perpendicularity between the faces of the geometric solids. We have detected that the three-dimensional visualization of these relations allows them to surmount the difficulty arising from their assimilation through planar representations [16,88].
This same analogic reasoning within the three-dimensional space has facilitated the passage of symmetry axes and rotation centers in the flat figures to planes of symmetry and rotation axes in the regular polyhedra, something very difficult to achieve with other types of representations and that the students from experiment 3 were able to successfully achieve. Similarly, the possibility of visualizing the polyhedra from the inside allows students to naturally extrapolate the notion of flat angle to that of an angle in space, an element to consider when characterizing the properties of geometric solids [87] (Figure 14).

Figure 14.
Example of analogy in the comparison of the flat and three-dimensional symmetry.
Finally, students from experiment 2 developed structural awareness [89] when combining cubes in distinct possibilities to obtain cuboids of a minimum surface area for a given volume. This structural type of reasoning [90] was also highlighted by the students in experiment 4 upon constructing planar and spatial fractals. As the complexity of the fractals increased, as in the case of the Menger sponge, students developed structural awareness in order to determine not only the number of copies needed to construct the next iteration, but also the positions in which they had to be placed within the three-dimensional space. In this way, they showed a structural reasoning that made them aware of the recursive process in the fractal generation (Figure 15).

Figure 15.
Pasting iterations. Help with a physical model of the second iteration of the Menger sponge.
5.5. Influence on the Teachers
The close collaboration and exchange of information between the software developers, the researchers and the teachers has allowed us to detect the influence of Neotrie on how the latter conceive geometry teaching, the learning of their students, and the classroom management. Through the exchange of opinions and the analysis of classroom events, especially during the retrospective analysis phase of the teaching experiments, it was possible to observe how the teachers modified their initial lesson plans and tasks from a more traditional methodology, in which software accompanied the tasks, to a perspective in which the teaching took on a more inductive approach, based on spatial structuring and reasoning. Currently, the tasks are designed as a scaffolding to face challenges, and the questions have evolved from only requesting specific results to requesting inferences (Extracts 1 and 2).
Extract 1.
Geometry tends to be shoved away at the end of the topics that are taught every school year, being overlooked due to a lack of time and motivation at the end of the academic courses. Neotrie is a breath of fresh air, leaving behind the geometry that consists of formulas and lists, and creating learning that is based on memory and abstraction. This memory of what geometry can be, of the implicit fun and intuition with which its content is put into practice, is something that I will not forget. I will try to take it with me in every geometry lesson that I teach, including those in which I cannot use Neotrie.
Extract 2.
I think that my experience using Neotrie changed how I teach geometry. I am constantly looking for a way to teach difficult topics in spatial geometry in an easy and attractive way. Most students have trouble with spatial imagination, and often these topics are disliked by them.
I find that videos made with the program are a very good way to convey knowledge. Students can play them many times, they can hear their teacher’s voice and find the solution to the problem with his/her help.
As for the learning, the huge motivational potential generated by virtual reality in students has been taken advantage of by the teachers who propose more complex challenges and problems than those that students can solve using the traditional methods. Students have shown interest from the start, and thanks to a suitable scaffolding, they have attempted to solve the problems and complete the proposed challenges. This has allowed teachers to achieve the curricular objectives established (Extracts 3 and 4).
Extract 3.
I observed that during the lessons using Neotrie, the pupils were: focused, disciplined, mobilized to work, and satisfied with the tasks successfully performed.
Extract 4.
Supported by extremely recreational activities and the attractiveness of the software itself, it makes the lessons more easily understood, impulsed by an extra motivation which marks the difference as compared to more traditional teaching styles.
Another aspect that typically is of concern to teachers is that of “hooking” students who have a lower level of mathematics skills. The teachers have affirmed that Neotrie favorably influenced the interests of these students, and they also detected that with the collaboration and teamwork, the students’ skills reached more homogenous levels (Extracts 5 and 6).
Extract 5.
I noticed a greater interest in geometry with students who were struggling to learn math. These students were more willing to complete assignments and were active during lessons. They were also more willing to participate in additional activities.
Extract 6.
If the activities and lessons are designed from the work and cooperation, math skills, at distinct levels, may easily be matched. It is important to seek activities that can be reconverted to a “mentoring” by the students to favor this matching.
It is important to note that these achievements depend fully on the efficient management surrounding the work with the resource in the classroom. Because Neotrie currently does not offer the possibility of multiple players, teachers have been forced to abandon individual work (considered that in which the tasks are taken on individually), for collaborative work, both in small groups as well as large ones. The design of lesson plans and tasks, as well as the classroom management at every moment, has had to be adapted to this format.
To ensure the participation and implication of all students, teachers have created and implemented successfully diverse strategies, such as proposing game dynamics based on overcoming challenges; rotating students who handle the software; giving an active role to students who do not have the controllers to direct and help those who have them to achieve a common objective; offering physical or structured material to the group members that are not handling the software, such that they can provide relevant information; create the “Neotrie Coach” student figure, which passes information on the skills and knowledge acquired in one group to another group, etc. (Extracts 7 and 8).
Extract 7.
Manipulative materials are important. In my case, the use of centicubes, magnetic and construction pieces along with the classic chalkboard, permit work at distinct levels of attention and activities at the same time. All of this, while using, as the foundation of the work, the topic to be developed in each lesson with the software.
Extract 8.
To facilitate the attention of students that are not using the controllers, I organized the lessons such that the students had most or even all of the instructions. It was their responsibility to guide the other student having the controllers, so that they made the calculations or activities that were proposed in the lesson.
6. Conclusions
DGS-3D and DGS-3D IVR open up a new range of possibilities in the teaching and learning of geometry. The initial results related to their use suggest that they afford students to improve their spatial sense, reasoning skills, argumentation, interest, and motivation. Although initial studies have provided information on the possibilities of DGS-3D IVR, currently, there is a lack of empirical studies on the design and development of this software, which is necessary to expand our understanding of the educational implications of their use [27]. Our study addresses one of the key elements in the current research agenda, namely, the evaluation of VR applications conducted in terms of technical feasibility (i.e., from a software engineering standpoint) and of the learning outcomes (i.e., from a pedagogical standpoint, from the perspective of both teachers and students) [44].
A collaborative work among software developers, educational researchers, and teachers, following a Design Research Based methodology, has been a fruitful approach for this purpose. The continuous feedback between the successive versions of the DGS-3D IVR Neotrie and their use in classroom environments has permitted improvements and updates for this software, adapting it to real classrooms in terms of: (a) the current curricular needs and new possibilities; (b) the type of representations it can afford; (c) the geometrical activity that students can perform through it; and (d) the teachers’ needs and interests.
We demonstrated how Neotrie enhanced the learning of traditional topics, such as polygons and polyhedra of different types, by allowing the manipulation and editing of the figures and their elements, as well as to easily construct a rich variety of examples and counterexamples over which to reason and discuss, both in small groups and in a large group. The use of Neotrie also opened a new door to contents, such as the symmetries of solids, their surface area and volume, or 2D and 3D fractals. It provided students with dynamic representations of 2D and 3D figures in a 3D space, with the extrusion tool being useful to relate one-, two-, and three dimensions.
The flexible approach to the coordinate system in space (by changing perspectives, moving, and flying around) allowed students to establish analogies between concepts such as parallelism, perpendicularity, or axis and plane of symmetry in 2D and 3D. It also permitted them to understand the difference between surface area and volume of cuboids, as well as to develop flexible strategies to calculate their measurements and solve optimization problems. Students developed visual structural reasoning in order to do so, and in order to construct 3D fractals by making copies of iterations and placing them in the right positions.
The introduction of Neotrie also had a transformative effect on the teachers participating in the experiments. Their role has been fundamental as creative agents in the design and management of the lessons with Neotrie, which have evolved from the use of the software as a companion to traditional tasks to the design of gamified dynamics around Neotrie, using a more inductive approach to solve problems and challenging tasks involving spatial visualization.
They managed to capitalize their students’ initial enthusiasm and motivation into a genuine interest, focus, and extra effort to explore and solve geometry problems. It was a remarkable achievement from the teachers to be able to invent different collaborative strategies in order to involve all the students, whether in small or larger groups, in generating knowledge with a device in which only one person at a time has access to the immersive virtual reality. Even those students with a lower level of mathematical skills were interested and included in the classroom dynamics, which contributed to raising their geometrical competence.
A byproduct of this research is the lessons designed for Neotrie that may be used by other teachers or taken as examples to create new ones. The implementations of these lessons and the report on their effects may serve as feedback for readjusting the lessons, as well as for improving the software. This may lead to a larger sphere of influence of DGS-3D IVR, especially Neotrie, to more teachers and educational institutions.
Author Contributions
Conceptualization, I.R. and A.C.; methodology, J.L.R., I.R. and A.C.; software, J.L.R.; validation, A.C. and I.R.; formal analysis, J.L.R., I.R. and A.C.; investigation, J.L.R. and I.R.; resources, J.L.R. and I.R.; data curation, I.R. and A.C.; writing—original draft preparation, J.L.R., I.R. and A.C.; writing—review and editing, J.L.R., I.R. and A.C.; visualization, J.L.R., I.R. and A.C.; supervision, J.L.R., I.R. and A.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by AEI/FEDER grant MTM2016-76453-C2-2-P, FEDER-Junta de Andalucía grant UAL2020-SEJ-B2086, by the Ministry of Science and Innovation grant PID2020-117971GB-C22, and the Junta de Andalucía research group HUM886.
Institutional Review Board Statement
Ethical review and approval were waived for this study, due to its anonymized nature. The activities were revised and authorized by the respective teachers. The parents were informed before their children participated in the study.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Not applicable.
Acknowledgments
Diego Cangas for his implication in the development of Neotrie, and the teachers, students, and schools participating in the teaching experiments, especially Grazyna Morga, Pepe Roma, Silvia Moral, and Dante Y. Chavil for their pioneering work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hegedus, S.; Moreno, L. Intersecting Representation and Communication Infrastructures. ZDM Int. J. Math. Educ. 2009, 41, 399–412. [Google Scholar] [CrossRef]
- Hegedus, S. Young Children Investigating Advanced Mathematical Concepts With Haptic Technologies: Future Design Perspectives. Math. Enthus. 2013, 10, 87–108. Available online: https://scholarworks.umt.edu/tme/vol10/iss1/6 (accessed on 26 September 2021).
- Kieran, C.; Yerushalmy, M. Research on the Role of Technological Environments in Algebra Learning and Teaching. In The Future of the Teaching and Learning of Algebra: The 12th ICMI Study; Stacey, K., Chick, H., Kendal, M., Eds.; Springer: Dordrecht, The Netherlands, 2004; pp. 99–152. [Google Scholar] [CrossRef]
- Santos-Trigo, M.; Camacho-Machín, M. Mathematical Problem Solving and the Use of Digital Technology for Interactive Book Design. Educ. Siglo XXI 2018, 36, 21–40. [Google Scholar] [CrossRef]
- Santos-Trigo, M.; Barrera-Mora, F.; Camacho-Machín, M. Teachers’ Use of Technology Affordances to Contextualize and Dynamically Enrich and Extend Mathematical Problem-Solving Strategies. Mathematics 2021, 9, 793. [Google Scholar] [CrossRef]
- Gadanidis, G.; Geiger, V. A Social Perspective on Technology-Enhanced Mathematical Learning: From Collaboration to Performance. ZDM Int. J. Math. Educ. 2010, 42, 91–104. [Google Scholar] [CrossRef]
- Bakker, A.; Cai, J.; Zenger, L. Future Themes of Mathematics Education Research: An International Survey before and during the Pandemic. Educ. Stud. Math. 2021, 107, 2411–2502. [Google Scholar] [CrossRef]
- Balacheff, N.; Sutherland, R. Epistemological Domain of Validity of Microworlds: The Case of Logo and Cabri-Géomètre. In Lessons from Learning, IFIP TC3/WG3. 3 Conference; Lewis, R., Mendelsohn, P., Eds.; North Holland Publishing: Amsterdam, The Netherlands, 1994; pp. 137–150. [Google Scholar]
- Healy, L.; Hoelzl, R.; Hoyles, C.; Noss, R. Cabri Constructions. Micromath 1994, 2, 13–16. [Google Scholar]
- Holzl, R. How Does “dragging” Affect the Learning of Geometry. Int. J. Comput. Math. Learn. 1996, 1, 169–187. [Google Scholar] [CrossRef]
- Hoyles, C.; Noss, R. Dynamic Geometry Environments: What’s the Point? Math. Teach. 1994, 87, 716–717. [Google Scholar] [CrossRef]
- Inglis, M.; Foster, C. Five Decades of Mathematics Education Research. J. Res. Math. Educ. 2018, 49, 462–500. [Google Scholar] [CrossRef]
- Sinclair, N.; Bartolini, M.; De Villiers, M.; Jones, K.; Kortenkamp, U.; Leung, A.; Owens, K. Recent Research on Geometry Education: An ICME-13 Survey Team Report. ZDM Int. J. Math. Educ. 2016, 48, 691–719. [Google Scholar] [CrossRef]
- Wassie, Y.A.; Zergaw, G.A. Capabilities and Contributions of the Dynamic Math Software, GeoGebra—A Review. N. Am. GeoGebra J. 2018, 7, 68–86. [Google Scholar]
- Codina, A.; Rodríguez, J.L.; Morales, C.-S. NeoTrie VR, Realidad Virtual Inmersiva para el Aprendizaje de la Geometría 3D. In Investigaciones y Experiencias en Enseñanza de las Ciencias y la Matemática; Cuevas-Vallejo, C., Martínez-Reyes, M., Páez, R., Hernández, J., Eds.; UAEM: Toluca, México, 2021; in press. [Google Scholar]
- Gutiérrez, A. Las Representaciones Planas de Cuerpos 3-Dimensionales en la Enseñanza de la Geometría Espacial. Rev. EMA 1998, 3, 193–220. [Google Scholar]
- Confrey, J.; Hoyles, C.; Jones, D.; Kahn, K.; Maloney, A.; Nguyen, K.; Noss, R.; Pratt, D. Designing Software for Mathematical Engagement through Modeling. In Mathematics Education and Technology-Rethinking the Terrain. The 17th ICMI Study; Springer: London, UK, 2010; pp. 19–45. [Google Scholar] [CrossRef]
- Hoyles, C.; Lagrange, J.B.; Jones, K.; Mackrell, K.; Stevenson, I. Mathematics Education and Technology-Rethinking the Terrain. The 17th ICMI Study; Hoyles, C., Lagrange, J.B., Eds.; Springer: New York, NY, USA, 2010. [Google Scholar] [CrossRef]
- Sinclair, N.; Bruce, C. New Opportunities in Geometry Education at the Primary School. ZDM Int. J. Math. Educ. 2015. [Google Scholar] [CrossRef]
- Fuchs, P.; Moreau, G.; Guitton, P. Introduction to Virtual Reality. In Virtual Reality: Concepts and Technologies; Fuchs, P., Moreau, G., Guitton, P., Eds.; CRC Press: New York, NY, USA, 2011; pp. 3–10. [Google Scholar] [CrossRef]
- Barrett, T.J.; Stull, A.T.; Hsu, T.M.; Hegarty, M. Constrained Interactivity for Relating Multiple Representations in Science: When Virtual Is Better than Real. Comput. Educ. 2015, 81, 69–81. [Google Scholar] [CrossRef]
- Jang, S.; Vitale, J.M.; Jyung, R.W.; Black, J.B. Direct Manipulation Is Better than Passive Viewing for Learning Anatomy in a Three-Dimensional Virtual Reality Environment. Comput. Educ. 2017, 106, 150–165. [Google Scholar] [CrossRef]
- Kim, S.; Heo, R.; Chung, Y.; Kim, J.M.; Kwon, M.P.; Seo, S.C.; Park, G.H.; Kim, M.K. Virtual Reality Visualization Model (VRVM) of the Tricarboxylic Acid (TCA) Cycle of Carbohydrate Metabolism for Medical Biochemistry Education. J. Sci. Educ. Technol. 2019, 602–612. [Google Scholar] [CrossRef]
- Martín, A. Geometría a Través de Realidad Virtual. Master’s Thesis, University of Almería, Almería, Spain, 2019. Available online: http://hdl.handle.net/10835/9770 (accessed on 30 July 2021).
- Rau, P.L.P.; Zheng, J.; Guo, Z.; Li, J. Speed Reading on Virtual Reality and Augmented Reality. Comput. Educ. 2018, 125, 240–245. [Google Scholar] [CrossRef]
- Richards, D.; Taylor, M. A Comparison of Learning Gains When Using a 2D Simulation Tool versus a 3D Virtual World: An Experiment to Find the Right Representation Involving the Marginal Value Theorem. Comput. Educ. 2015, 86, 157–171. [Google Scholar] [CrossRef]
- Demitriadou, E.; Stavroulia, K.E.; Lanitis, A. Comparative Evaluation of Virtual and Augmented Reality for Teaching Mathematics in Primary Education. Educ. Inf. Technol. 2020, 25, 381–401. [Google Scholar] [CrossRef]
- Güven, B.; Kosa, T. The Effect of Dynamic Geometry Software on Students Mathematics Teacher’s Spatial Visualizations Skills. Turk. Online J. Educ. Technol. 2008, 7, 100–107. [Google Scholar]
- Hartatiana, H.; Darhim, D.; Nurlaelah, E. Improving Junior High School Students’ Spatial Reasoning Ability Through Model Eliciting Activities with Cabri 3D. Int. Educ. Stud. 2018, 11, 148–154. [Google Scholar] [CrossRef]
- Hwang, W.Y.; Su, J.H.; Huang, Y.M.; Dong, J.J. A Study of Multi-Representation of Geometry Problem Solving with Virtual Manipulatives and Whiteboard System. Educ. Technol. Soc. 2009, 12, 229–247. [Google Scholar]
- Sedig, K.; Parsons, P.; Dittmer, M.; Haworth, R. Human-Centered Interactivity of Visualization Tools: Micro-and Macro-Level Considerations. In Handbook of Human Centric Visualization; Huang, W., Ed.; Springer: New York, NY, USA, 2013; pp. 717–743. [Google Scholar] [CrossRef]
- Kaufmann, H.; Schmalstieg, D.; Wagner, M. Construct3D: A Virtual Reality Application for Mathematics and Geometry Education. Educ. Inf. Technol. 2000, 5, 263–276. [Google Scholar] [CrossRef]
- Kaufmann, H.; Schmalstieg, D. Designing Immersive Virtual Reality for Geometry Education. In Proceedings of the IEEE Virtual Reality Conference, Alexandria, VA, USA, 25–29 March 2006; pp. 51–58. Available online: https://conferences.computer.org/vr/2006/index.htm (accessed on 26 September 2021).
- Morales, C.S. La Metacognición En Un Ambiente de Realidad Virtual. Geometría Con NeoTrie VR. Master’s Thesis, University of Almería, Almería, Spain, 2019. Available online: http://hdl.handle.net/10835/8075 (accessed on 30 July 2021).
- Song, K.S.; Lee, W.Y. A Virtual Reality Application for Geometry Classes. J. Comput. Assist. Learn. 2002, 18, 149–156. [Google Scholar] [CrossRef]
- Stranger-Johannessen, E. Exploring Math Achievement Through Gamified Virtual Reality. In Proceedings of the 13th European Conference on Technology Enhanced Learning, Leeds, UK, 3–5 September 2018; Pammer-Schindler, V., Pérez-Sanagustín, M., Drachsler, H., Elferink, R., Scheffel, M., Eds.; Springer: Leeds, UK, 2018; pp. 613–616. [Google Scholar] [CrossRef]
- Dimmel, J.; Bock, C. HandWaver: A Gesture-Based Virtual Mathematical Making Environment. In Proceedings of the 13th International Conference on Technology in Mathematics Teaching, Lion, France, 3–6 July 2017; Aldon, G., Trgalova, J., Eds.; HAL Repositories: Lion, France, 2017; pp. 323–330. [Google Scholar]
- Möllers, M.; Zimmer, P.; Borchers, J. Direct Manipulation and the Third Dimension: Co-Planar Dragging on 3D Displays. In Proceedings of the 2012 ACM International Conference on Interactive Tabletops and Surfaces, Cambridge, MA, USA, 11–14 November 2012; Shaer, O., Shen, C., Ringel, M., Horn, M., Eds.; Association for Computing Machinery: New York, NY, USA, 2012; pp. 11–20. [Google Scholar]
- Yeh, A. Mathematics, Virtual Reality and Programming. In Electronic Proceedings of the 22nd Asian Technology Conference in Mathematics, Chungli, Taiwan, 15–19 December 2017; Yang, W.C., Meade, D., Chung, Y., Eds.; Mathematics and Technology, LLC: Chungli, Taiwan, 2017; pp. 1–9. [Google Scholar]
- Lai, C.; Mcmahan, R.P.; Kitagawa, M.; Connolly, I. Geometry Explorer: Facilitating Geometry Education with Virtual Reality. In Virtual, Augmented and Mixed Reality. VAMR 2016. Lecture Notes in Computer Science; Lackey, S., Shumaker, R., Eds.; Springer: Toronto, ON, Canada, 2016; pp. 702–713. [Google Scholar] [CrossRef]
- VirtualDor: NeoTrie VR; Universidad de Almería: Almería, Spain. 2017. Available online: http://www2.ual.es/neotrie/ (accessed on 4 May 2021).
- Geogebra.org: Geogebra MR. 2017. Available online: https://www.geogebra.org/ (accessed on 23 June 2021).
- Simon, A. CalcFlow. Nanome. 2017. Available online: https://store.steampowered.com/app/547280/Calcflow/ (accessed on 7 July 2021).
- Radianti, J.; Majchrzak, T.A.; Fromm, J.; Wohlgenannt, I. A Systematic Review of Immersive Virtual Reality Applications for Higher Education: Design Elements, Lessons Learned, and Research Agenda. Comput. Educ. 2020, 147, 103778. [Google Scholar] [CrossRef]
- Cash, P.; Stanković, T.; Štorga, M. Experimental Design Research: Approaches, Perspectives, Applications; Springer: Zurich, Switzerland, 2016. [Google Scholar] [CrossRef]
- Anderson, T.; Shattuck, J. Design-Based Research: A Decade of Progress in Education Research? Educ. Res. 2012, 41, 16–25. [Google Scholar] [CrossRef]
- Dede, C.; Nelson, B.; Ketelhut, D.; Clarke, J.; Bowman, C. Design-Based Research Strategies for Studying Situated Learning in a Multi-User Virtual Environment. In Proceedings of the 6th International Conference on Learning Sciences. International Society of the Learning Sciences, Santa Mónica, CA, USA, 23–26 June 2004; Kafi, Y.B., Sandoval, W., Enyedy, N., Eds.; International Society of the Learning Sciences: Santa Mónica, CA, USA, 2004. [Google Scholar]
- Özyurt, Ö.; Özyurt, H. Implementation of Design-Based Research in Software Engineering Education: A Case of Final Project Course. J. Comput. Educ. Res. 2019, 7, 213–227. [Google Scholar] [CrossRef]
- Özyurt, Ö.; Özyurt, H. Reflections of Design-Based Research Approach on Learning Experience of Visual Programming Course. J. Pedag. Res. 2020, 4, 12–21. [Google Scholar] [CrossRef]
- Barab, S. Design-Based Research: A Methodological Toolkit for the Learning Scientist. In The Cambridge Handbook of the Learning Sciences; Keith, R., Ed.; Cambridge University Press: Cambridge, UK, 2006; Volume 13, pp. 153–169. [Google Scholar] [CrossRef]
- Barab, S.; Squire, K. Design-Based Research: Putting a Stake in the Ground. J. Learn. Sci. 2004, 13, 1–14. [Google Scholar] [CrossRef]
- Confrey, J. The Evolution of Design Studies as Methodology. In The Cambridge Handbook of the Learning Sciences; Keith, R., Ed.; Cambridge University Press: New York, NY, USA, 2006; pp. 135–152. [Google Scholar]
- Dede, C. Commentary: The Growing Utilization of Design-Based Research. Contemp. Issues Technol. Teach. Educ. 2005, 5, 345–348. [Google Scholar]
- Prediger, S.; Gravemeijer, K.; Confrey, J. Design Research with a Focus on Learning Processes: An Overview on Achievements and Challenges. ZDM Math. Educ. 2015, 47, 877–891. [Google Scholar] [CrossRef]
- Codina, A. Interacción e Interactividad con Nuevas Tecnologías en la Resolución de Problemas Matemáticos. Ph.D. Thesis, Universidad de Granada, Granada, Spain, 2015. Available online: http://hdl.handle.net/10481/41755 (accessed on 25 May 2020).
- Dönmez, O.; Yaman, F.; Şahin, Y.L.; Yurdakul, I.K. Developing Mobile Applications for Hearing-Impaired: Wheel of Fortune. Educ. Technol. Theory Pract. 2016, 6, 22–41. Available online: https://dergipark.org.tr/en/download/article-file/271653 (accessed on 26 September 2021).
- Confrey, J.; Lachance, A. Transformative Teaching Experiments through Conjecture-Driven Research Design. In Handbook of Research Design in Mathematics and Science Education; Kelly, A., Lesh, R., Eds.; Lawrence Erlbaum: Mahwah, NJ, USA, 2000; pp. 17–34. [Google Scholar]
- Cangas, D.; Crespo, D.; Rodríguez, J.L.; Zarauz, A. NeoTrie VR: Nueva Geometría En Realidad Virtual. Pi-InnovaMath 2019, 1–8. [Google Scholar] [CrossRef]
- Rodríguez, J.L.; Morga, G.; Cangas, D. Geometry Teaching Experience in Virtual Reality with NeoTrie VR. Psychol. Soc. Educ. 2019, 11, 355–366. [Google Scholar] [CrossRef]
- Cobb, P.; Confrey, J.; diSessa, A.; Lehrer, R.; Schauble, L. Design Experiments in Educational Research. Educ. Res. 2003, 1, 9–13. [Google Scholar] [CrossRef]
- Morga, G. NeoTrie VR: New Geometry in Virtual Reality. Available online: http://blog.scientix.eu/2018/11/neotrie-vr-new-geometry-in-virtual-reality (accessed on 27 July 2021).
- Rodríguez, J.A.; Romero, I.M. Optimización de Superficies a Partir de Un Volumen Dado Mediante Realidad Virtual: Una Experiencia En 6o de Primaria. In Innovación y Tecnología en Contextos Educativos; Sánchez, E., Ruiz, J., Sánchez, E., Eds.; Universidad de Málaga: Málaga, Spain, 2019; pp. 591–601. [Google Scholar]
- Chavil, D.Y.; Rodríguez, J.L.; Romero, I.M. NeoTrie VR como Espacio de Trabajo para La Introducción de La Geometría Fractal. In Proceedings of the Actas del XXIV Simposio de la Sociedad Española de Investigación en Educación Matemática, Valencia, Spain, 8–10 September 2021; Diago, P., Ed.; SEIEM: Valencia, Spain, 2021. in press. [Google Scholar]
- Cangas Moldes, D.; Codina Sánchez, A.; Chavil, D.Y.; Fernández, J.M.; García, M.M.; Kamerling, J.; López, E.; Morga, G.; Rodríguez Blancas, J.L.; Romero Albaladejo, I.M. Using NeoTrie VR for STEM Education in Virtual Reality. In Proceedings of the 11th International Conference the Future of Education, Florence, Italy, 1–2 July 2021; Filodiritto Editore: Florence, Italy, 2021; pp. 511–517. [Google Scholar]
- Chavil, D.Y.; Romero, I.M.; Rodríguez, J.L. Introducción Al Concepto de Fractal En Enseñanza Secundaria Usando Realidad Virtual Inmersiva. Desde Sur Rev. Cienc. Hum. Soc. 2020, 12, 615–629. [Google Scholar] [CrossRef]
- Sánchez, C. Visualización y Tratamiento de Gráficas 3D en Neotrie VR. Master’s Thesis, Univeristy of Almería, Almería, Spain, 2020. [Google Scholar]
- Rodríguez, J.A.; Romero, I.M.; Rodríguez, J.L. Optimización de La Superficie de Ortoedros Con Realidad Virtual y Materiales Manipulativos. Enseñanza Cienc. 2021. under review. [Google Scholar]
- Rodríguez, J.L. Exploring Dynamic Geometry through Immersive Virtual Reality and Distance Teaching. In Mathematics Education in the Digital Era; Springer: Berlin, Germany, 2021; in press. [Google Scholar]
- Heid, M.K. Digital Tools in Lower Secondary School Mathematics Education: A Review of Qualitative Research on Mathematics Learning of Lower Secondary School Students. In Uses of Technology in Primary and Secondary Mathematics Education. ICME-13 Monographs; Ball, L., Drijvers, P., Ladel, S., Siller, H.S., Tabach, M., Vale, C., Eds.; Springer: Zurich, Switzerland, 2018; pp. 177–201. [Google Scholar] [CrossRef]
- Zbiek, R.M.; Heid, M.K.; Blume, G.W.; Dick, T.P. Research on Technology in Mathematics Education: A Perspective of Constructs. In Second Handbook of Research on Mathematics Teaching and Learning; Lester, F., Ed.; Information Age Publishing: Charlotte, NC, USA, 2007; pp. 1169–1207. [Google Scholar]
- Anguera, M.T. Posibilidades y Relevancia de la Observación Sistemática por el Profesional de la Psicología. Pap. Psicól. 2010, 31, 122–130. [Google Scholar]
- Anguera, M.T.; Izquierdo, C. Methodological Approaches in Human Communication. From Complexity of Situation to Data Analysis. In From Communication to Presence. Cognition, Emotions and Culture towards the Ultimate Communicative Experience; Riva, G., Anguera, M.T., Mantovani, F., Wiederhold, H., Eds.; IOS Press: Amsterdam, The Netherlands, 2006; Volume 9, pp. 203–222. [Google Scholar]
- Portell, M.; Sene-Mir, A.M.; Anguera, M.T.; Jonsson, G.K.; Losada, J.L. Support System for the Assessment and Intervention during the Manual Material Handling Training at the Workplace: Contributions from the Systematic Observation. Front. Psychol. 2019, 10, 11247. [Google Scholar] [CrossRef]
- Trouche, L. Managing the Complexity of Human/Machine Interactions in Computerized Learning Environments: Guiding Students’ Command Process through Instrumental Orchestrations. Int. J. Comput. Math. Learn. 2004, 281–307. [Google Scholar] [CrossRef]
- Holguin García, F.Y.; Holguin Rangel, E.G.; Garcia Mera, N.A. Gamificación En La Enseñanza de Las Matemáticas: Una Revisión Sistemática. Telos 2020, 22, 62–75. [Google Scholar] [CrossRef]
- Pea, R. Cognitive Technology for Mathematics Education. In Cognitive Science and Mathematics Education; Schoenfeld, A., Ed.; Lawrence Erlbaum: Hillsdale, NJ, USA, 1987; pp. 89–122. [Google Scholar]
- Sisman, G.T.; Aksu, M. A Study on Sixth Grade Students’ Misconceptions and Errors in Spatial Measurement: Length, Area, and Volume. Int. J. Sci. Math. Educ. 2016, 14, 1293–1319. [Google Scholar] [CrossRef]
- Bernabeu, M.; Llinares, S. Comprensión de Las Figuras Geométricas En Niños de 6-9 Años. Educ. Mat. 2017, 29, 9–35. [Google Scholar] [CrossRef][Green Version]
- Duval, R. Les Conditions Cognitives de l’apprentissage de La Géométrie: Développement de La Visualisation, Différenciation Des Raisonnement et Coordination de Leurs Fonctionnements. Ann. Didact. Sci. Cogn. 2005, 10, 5–53. Available online: http://docs.irem.univ-paris-diderot.fr/up/annales_de_didactique_et_de_sciences_cognitives/volume_10/Duval.pdf (accessed on 18 April 2020).
- Ng, O.-L.; Sinclair, N. Drawing in Space: Doing Mathematics with 3D Pens. In Uses of Technology in Primary and Secondary Mathematics Education; Tools, Topics and Trends. ICME-13 Monographs; Ball, L., Drijvers, P., Lade, S., Siller, H.S., Tabach, M., Vale, C., Eds.; Springer: Cham, Switzerland, 2018; pp. 301–313. [Google Scholar] [CrossRef]
- Vinner, S. Concept Definition, Concept Image and the Notion of Function. Int. J. Math. Educ. Sci. Technol. 1983, 14, 293–305. [Google Scholar] [CrossRef]
- Duval, R. A Cognitive Analysis of Problems of Comprehension in a Learning of Mathematics. Educ. Stud. Math. 2006, 61, 103–131. [Google Scholar] [CrossRef]
- Roschelle, J.; Teasley, S.D. The Construction of Shared Knowledge in Collaborative Problem Solving. In Computer-Supported Collaborative Learning; O’Malley, C.E., Ed.; Springer: Berlin, Germany, 1995; pp. 69–197. [Google Scholar] [CrossRef]
- Hennessy, S.; Murphy, P. The Potential for Collaborative Problem Solving in Design and Technology. Int. J. Technol. Des. Educ. 1999, 9, 1–36. [Google Scholar] [CrossRef]
- Arzarello, F.; Robutti, O. Approaching Functions through Motion Experiments. Educ. Stud. Math. 2004, 57, 305–308. [Google Scholar] [CrossRef]
- Reynolds, F.J.; Reeve, R.A. Gesture in Collaborative Mathematics Problem-Solving. J. Math. Behav. 2001, 4, 447–460. [Google Scholar] [CrossRef]
- Pittalis, M.; Christou, C. Types of Reasoning in 3D Geometry Thinking and Their Relation with Spatial Ability. Educ. Stud. Math. 2010, 75, 191–212. [Google Scholar] [CrossRef]
- Ma, H.L.; Wu, D.; Chen, J.W.; Hsieh, K.J. Mithelmore’s Development Stages of the Right Rectangular Prisms of Elementary School Students in Taiwan. In Proceedings of the 33rd Conference of the International Group for the Psychology of Mathematics Education, Thessaloniki, Greece, 19–24 July 2009; Tzekaki, M., Kaldrimidou, M., Sakonidis, H., Eds.; PME: Thessaloniki, Greece, 2009; Volume 4, pp. 57–64. [Google Scholar]
- Mulligan, J.; Mitchelmore, M. Awareness of Pattern and Structure in Early Mathematical Development. Math. Educ. Res. J. 2009, 21, 33–49. [Google Scholar] [CrossRef]
- Hawthorne, C.; Druken, B.K. Looking For and Using Structural Reasoning. Math. Teach. 2018, 112, 294–301. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).