1. Introduction
The Fundamental Review of the Trading Book (FRTB) is a market risk measurement and management regulation recently issued by the Basel Committee. This reform, often referred to as “Basel IV”, intends to strengthen the financial system. The new proposals were initially published in January 2016 and revised in January 2019, and are now titled “Explanatory note on the minimum capital requirements for market risk” (In our manuscript the regulation will be referred to as FRTB for simplification purposes). These proposals are supposed to be implemented in January 2022. The FRTB objective is to address the limitations of past regulations related to the existing Standardised Approach (SA) and Internal Models Approach (IMA) and, in particular, with respect to:
“Trading book” and “banking book” boundaries, in other words, i.e., assets intended for active trading versus assets expected to be held to maturity. It is noteworthy to mention that in the 2008 crisis, the largest losses were related to the trading book;
The use of expected shortfall (ES) to ensure that largest risks are properly captured. The VaR is being abandoned for risk measurement purposes in the latest regulation;
Market liquidity risk.
FRTB defines higher standards for financial institutions when it comes to using internal models for calculating capital as opposed to the SA. The SA is directly implementable, but carries more capital; the IMA should carry a lower capital charge, but the modelling is more complex, requiring the use of the ES, coupled with add-ons for “non-modellable risk factors” lacking sufficient data. Considering the difficulties associated with the implementation of internal models, to be authorised to use such an approach, a model implemented for a desk has to pass two tests: a profit-and-loss attribution test and a back-test.
“Under the revised framework, the model approval is granted at the level of banks’ trading desks. This is in contrast to the Basel 2.5 framework, which determined supervisory approval/removal of internal models at the bank-wide level. The revised framework’s granular, desk-level approach makes it easier for supervisors to disallow the use of internal models for particular trading desks for which risks are not adequately captured by a bank’s internal model, without causing a sudden change or cliff effect in overall capital requirements” [
1]. The use of ES requires the acquirement of sufficient information in the tails to ensure the robustness of the risk measure, as it has to be alimented by a sufficient quantity of relevant data (above the 97.5 percentile in the case of this regulation). Therefore, we will mainly focus on the IMA. After presenting ES theoretical aspects, we will address the lack of information in the tails of the underlying distributions used to compute the risk measure and deal with the matter holistically. In this paper, we will review the possibilities available to address such an issue with a range of methodologies permitting data augmentation, from statistical approaches to more advanced AI strategies. We will apply traditional statistical methodologies, such as distribution fittings, kernel density estimation, Gaussian mixtures, conditional fitting by Expectation-Maximisation and AI-related strategies, for instance, Synthetic Minority Oversampling Technique (SMOTE) regression and Generative adversarial networks (GANs). In particular, we shall show how AI allows to address this problem in a consistent way. Indeed, in the past few years, AI has been used in many environments, such as the education industry [
2], the transportation industry [
3], for industrial controls and risks prevention [
4], or in the pharmaceutical industry [
5] (among others), and we believe that some of the approaches used in other fields could be of interest for risk measurement purposes.
The paper aims at addressing all aspects related to market risk measurement under the FRTB, from both a theoretical and a practical point of view. As such, in the next section, we will present the mathematics behind the FRTB market risk measurement, when the application part of the paper focuses on ensuring the reliability of ES estimates, as theoretical weaknesses have to be bore in mind at all time for appropriate interpretation of the results. In the subsequent section, we will present the different methodologies enabling data augmentation to ensure the reliability of the risk measure. Finally, we will compare the results obtained from a risk-measurement point of view using these methodologies, and we will discuss these approaches with respect to their relevance considering the underlying situation when it comes to available data, allowing practitioners to select the most appropriate approach. The last section will conclude the study.
2. The Mathematics behind the FRTB—VaR vs. ES
According to the FRTB, market risk will be measured and reported using ES at a 97.5% level. The VaR which was measured at a 99% level has now been abandoned, though it is noteworthy to mention that for Gaussian distributions, the two risk measures are identical. If other distributions were to be used, as ES is supposed to capture fat tails in a better fashion (both in univariate and multivariate environments), the capital requirements associated are expected to be much higher.
2.1. VaR
Since 1996, the Basel regulation required the use of VaR to measure market risk. As of today, it is the only IMA allowed for the measurement of market risk in financial institutions. This measure, first developed by [
6], was popularised by RiskMetric (1995) and became the financial industry standard.
The definition of VaR implies a time horizon and a level of confidence. Typically, VaR is calculated at a level of confidence (
) with a defined time horizon
T (typically one day): if
X is a T-days loss distribution (loss being positive and profit negative, that is,
is a Profit and Loss (P&L) distribution) with cumulative distribution function
, the
is the amount such that:
In other words, the probability for a loss bigger than is . Previous Basel versions have been requiring a 99% VaR calculation. VaR is used to compute the market capital that is set aside to cover potential market risk losses. A 99th percentile VaR with a 10-day holding period has been the regulatory standard for market risk capital calculation. The 10-day VaR is generally obtained by scaling the one-day VaR using the “square root of time rule”. Then, this result is multiplied by a scaling factor to offset VaR intrinsic problems (Despite the fact that several justifications were investigated a posteriori, the value of the factor was never justified). The scaling factor may be higher than 3 if the regulator decides as such, especially, if the number of exceptions in the last 250 days is bigger than 5.
VaR characterises a market-to-market loss on a position or static portfolio over a specific time frame. In spite of the 10-day horizon, it does not really incorporate aspects such as liquidity risk, which may have enormous effects on realised losses. Nevertheless, VaR became very popular at the end of the previous century, very often in combination with the use of the Gaussian distributions for the modelling of the returns, which allowed the measurement of the VaR in terms of standard deviations and allocate risk to sub-portfolios based on the properties (subadditivity of the standard deviation) of the Gaussian distributions.
Gaussian Monte Carlo simulations became the complementary tool for VaR systems. Obviously, VaR meant a real improvement upon previous practices, but it was clear from the beginning that it presented serious inconvenience: observed fat tails in the markets were not compatible with Gaussian models, the assumption of the portfolio being static for 10 days was unrealistic and the inclusion of the dynamic effect of expected trading (stop-loss order) was not easy, not to mention the lack of subadditivity for observed distributions. A partial solution for the non-Gaussianity required the use of historical simulation.
An interesting property of VaR was its backtestability: a one-day VaR prediction comprises a 99% percentile; 250 days are sufficient in order to test how a bank estimates this percentile, and this has become one of the requirements of the market risk measurement based on the VaR approach. No less interesting is the fact that VaR, confirmed in the Basel II framework, is the only IMA proposed that allows backtesting. Even if they could be theoretically backtestable, credit VaR and operational risk VaR are not backtested due to the maturity horizon imposed (one year) and the very high level of confidence (99.9%); they imply looking for exceptions, which happen once in a thousand years. In practice, this interpretation of VaR is rather limited.
Weaknesses of VaR—A Step towards ES
Many criticisable aspects of VaR regulatory requirements appeared over time, some of them from the very beginning. Let us first highlight a question that is inherent not to the methodology but to the way it was applied. Until 2009, a regulatory arbitrage was possible, moving assets from the banking book to the trading book, something that has been discarded with the due adequacy of the norm.
One of the rules imposed by the Basel regulatory framework is that the capital charge pertaining to market risks is supposed to be calculated on a daily basis using VaR measurement and usually relying on an internal model. This rule needs to develop methods to estimate the loss probability distribution function every day, in order to compute VaR and ES using (at least) a one-year data period, assuming, in practice, the stationarity of the loss distribution over time.
This assumption has proved to be unrealistic, as financial assets properties and behaviours are generally not the same: for example, during stable periods and crisis, the results obtained during a turmoil using a model calibrated on data obtained during a stable period is unlikely to be useful. For example, during a long period, after the “dotcom” crisis until the Big Depression, markets experienced an expansion situation characterised by low volatility. As demonstrated by [
7], prior the financial crisis of 2008, banks were barely reporting exceptions. The subsequent years have shown how wrong that was. Indeed, to comply with the Basel committee requirements and, therefore, to be reliable, the parameters of banks’ models should have been integrating extreme market movements, so that, even under stress, no or few exceptions would have been reported (implying, however, a larger capital charge).
A last remark regarding the observed number of exceptions per time unit is as follows: VaR exceptions are a poor predictor of banks future failures. For example, Lehman Brothers had a model that was more reactive to changes in the volatility regime because it used an exponentially weighted moving average in order to give more weight to recent observations; it reported a few exceptions prior to its collapse. However, from the last quarter of 2006 to the moment of the collapse, its VaR increased by an average of 30% per quarter.
The non-stationarity of the loss distribution is clearly a problem for a satisfactory implementation of VaR. However, this is only part of the problem. Additionally, this approach is blind to the tail risk; it does not see the far-in-the-tail (beyond 99%) behaviour: two loss distributions
with the same 99% percentiles (let us say
x) but very different behaviours beyond this level (for example
) would suppose the same amount of regulatory capital, having very different market risk profiles. This weakness could lead to an inappropriate or sub-optimal portfolio selection [
8].
Last but not least, VaR presented another inconvenience: this measure was required to be calculated on a daily basis; nevertheless, banks were required to “update their data sets no less frequently than once every three months and should also reassess them whenever market prices are subject to material changes”. In practice, this implied the risk of critical biases on the estimator of the risk measure because of the datasets used for its calibration.
Because of all this, the VaR value could provide an inadequate representation of risk because, in addition to not being sub-additive and as such not coherent, it is not adapted for risk allocation (see [
9]). Coherence makes risk measures useful for risk management.
A coherent risk measure is a function
, with
being the set of all risks (following [
9]):
Monotonicity: If and then ;
Sub-additivity: If then ;
Positive homogeneity: If and then ;
Translation invariance: , .
Examples of coherent measures of risk are ES and
expectiles. The ES, also known as conditional VaR (see, for example, [
10]), is the average loss, knowing that the VaR has been exceeded: for
X, a loss distribution (
) whose probability function
F is continuous, we have:
Following [
11], given a random variable
X with finite mean and distribution function
F, for any
, we define the
-expectile functional of
F as the unique solution
to the equation:
Except for
, which is the mean of
X, expectiles lack an intuitive interpretation and have to be estimated, in general, numerically. In fact, academic interest for expectiles has more to do with (real or supposed) theoretical weaknesses in VaR and ES than with a huge interest across the industry and are related with the fact that expectiles are coherent measures of risk (see [
12,
13,
14]).
2.2. Expected Shortfall
From a risk management point of view, it makes more sense to use ES than to use VaR: the capital defined by the shortfall (if available) is not just covering till the threshold, it covers the average loss, once the threshold is exceeded. Adding this to the previously explained criticism of VaR, it seems understandable that the Basel Committee decided to replace a 99% VaR by a 97.5% ES.
2.2.1. Non-Normality
If the underlying distribution of a specific risk factor
X is normal, then neither the coherence issues reported by [
9] nor tail risk issues are appearing. Regarding the new percentile 97.5%, we obtain for a normally distributed
X with the parameters
As such, in a Gaussian environment, there is no upside using ES over VaR (for more details regarding risk measures please refer to [
15]).
Definitely, the choice of ES as the new measure for market risk implies the renunciation to the use of Gaussian (and more generally elliptic) distributions for the modelling of the loss distribution: for
,
being the quantile function, we have
and
N, respectively, being the pdf and cdf of the standard normal distribution. That is, the unexpected capital charge (ES minus expected value) is measured by the standard deviation
. For the normal distribution, the ES at level 97.5% is equivalent to the VaR at level 99%.
A similar result is true for t-Student distributions or for the margins of elliptic distributions, in general. As a consequence, stress scenarios should not be built using elliptic distributions.
2.2.2. Elicitability
The term elicitable appeared in the scientific literature only recently (see [
16]), but this concept had already been studied in Osband’s thesis [
17]. In order to explain its meaning, we introduce the following definitions [
18]:
A scoring function is a function
where
x and
y are the point forecasts and observations, respectively. Some of the most common scoring functions are as follows:
| absolute error |
| square error |
| absolute percentage error |
| relative error |
Given a certain class
of probability measures on
, let
be a functional on
:
In general, for any
,
is a subset of
. When it comes to risk measures as quantiles, expectiles or conditional value at risk,
is an element (a point) of
. A scoring function is said to be consistent for the functional
, relative to
if and only if, for all random variables
X with law
, and all
and
, we have:
If
s is consistent for the functional
and
we say
s is strictly consistent.
The functional
is said to be elicitable relative to
if and only if there is a scoring function
s which is strictly consistent for
relative to
. For example, the expectation defined by
is elicitable:
is strictly consistent for
. Quantiles are also elicitable. If we define,
, the following scoring function is strictly consistent relative to
:
For elicitable functionals, we have
An interesting feature of elicitable functionals is that the score allows to rank predictive models: given forecasts
and realisations
, we define the mean score:
The lower the mean score, the better the predictive model. A necessary condition for
being elicitable is the convexity of level sets [
11]:
Standard deviation and ES do not satisfy this property because they are not elicitable. Nevertheless, we have
However, as shown in [
16], the variance is jointly elicitable with the mean and the expected shortfall is jointly elicitable with the value at risk [
19].
2.2.3. Elicitability and Backtesting
When a functional
is elicitable, a statistics to perform backtesting is the average expected score
introduced in Equation (
12).
The discovery of the non-elicitability of ES led many authors to the conclusion that ES was not backtestable [
20]. The fact that ES was considered not backtestable made practitioners reluctant to its usage though the measure had been adopted by the Basel Committee. As a matter of fact, the Basel Committee in its consultation paper about FRTB [
1] replaced VaR by ES for capital requirement calculations, but VaR was kept for backtesting purposes, which might seem rather strange. Contrary to a certain “common” belief, elicitability has nothing to do with backtestability. The usual backtest of VaR (exceptions test) keeps no relation with any scoring function and does not rely on its elicitability. The first reason for this is that quantiles define a Bernoulli random variable which allows to backtest, simply, by counting exceptions.
The mean score function allows to compare different models (for VaR or ES), based on the same empirical data, in order to select the best one. It gives a relative ranking, not an absolute one. In this sense, elicitability is in fact connected with model selection. “It is not for model testing making it almost irrelevant for choosing a regulatory risk standard” [
19].
As outlined by [
21], “contrary to common belief, ES is not harder to backtest than VaR.” Furthermore, the power of the test they provide for ES (with the critical values for the limits of the Basel-like yellow and red zones) is considerably higher. In a study by [
19], three different approaches are analysed in detail for backtesting ES, as well as their power. In a study by [
22], a statistics called exceedance residuals is used as a score for backtesting ES. Refs. [
23,
24] proposed easily implementable backtest approaches for ES estimates.
2.2.4. Complementary Remarks
ES, even more once we know it is backtestable, is generally considered a better risk measure than VaR. Nevertheless, it requires, of course, a higher amount of data to ensure its reliability [
25] and will be anyway not as robust as VaR [
26]. Ironically, it is the VaR failure to capture the information contained in the tails of the distributions above and beyond a particular level of confidence that ensure its robustness.
This fact cannot be interpreted as a defence of VaR against ES. The impossibility for the VaR to cover tail risk associated with a curious way of backtesting it, meant a change was needed. Finally, Basel penalises only the quantity of violations when one may think that magnitudes either aggregated or individual could be more interesting.
3. Data Augmentation
As presented above, as VaR is a quantile, the sensitivity of the risk measure to the quantity of information contained in the distribution tail is not as important as what is required when using ES. Indeed, the larger the quantity of information in the tails of the underlying distributions the more reliable the ES, as the spectrum allowing to calculate the ES measure is located where the information is likely to be scarce (see Equation (
5)), i.e., above the 97.5 percentile. Consequently, to ensure the reliability of the risk measure, a data augmentation (in other words, the generation of synthetic data points) procedure must be undertaken.
In the following subsections, we present several methodologies that allow adding information in the tail of the distributions to address the robustness issue aforementioned. After presenting the methodologies theoretically, these will be applied to a real dataset in the last section, and the results will be discussed accordingly.
3.1. Traditional Parametric Approaches
The most common way of generating some information in the tails of an empirical distribution is to fit a parametric distribution to the data. In the following sections, we briefly introduce distributions that have interesting characteristics, namely, skewness and kurtosis. In the subsequent subsection, we present distribution mixtures.
3.1.1. Distribution Fittings
In this section, we briefly introduce parametric fittings; however, as this topic has been extensively discussed in other papers, we will mainly refer to [
27], who fit various distributions on a risk dataset, such as a lognormal distribution, a generalised hyperbolic distribution or an alpha-stable distribution (among others), and subsequently compute various VaRs and ESs in each case. They demonstrated that the debate between the two types of risk measure is more a debate related to the underlying distributions than of risk measures themselves. Indeed, as demonstrated, given two different underlying distributions fitted on the same dataset, the ES at 99% obtained on a first distribution can be lower than a VaR at 97.5% obtained on another.
The important point to remember considering the matter of interest is that the fitting of parametric distributions defined on infinite support mechanically generates some information beyond the last point of the empirical distribution. Some of the distributions mentioned above serve as a benchmark for other less traditional methodologies in
Section 4.
3.1.2. Distribution Mixtures
A possible approach for the modelling of events, in particular in the tails, consists in the fitting of a mixture of distributions [
28] on an historical dataset.
Let
be a finite set of probability density functions,
the related cumulative distribution functions,
a set of weights (
and
) and some set of parameters
(if parametric distributions were to be considered), the distribution mixture density,
f, and distribution function,
F, can be expressed as follows,
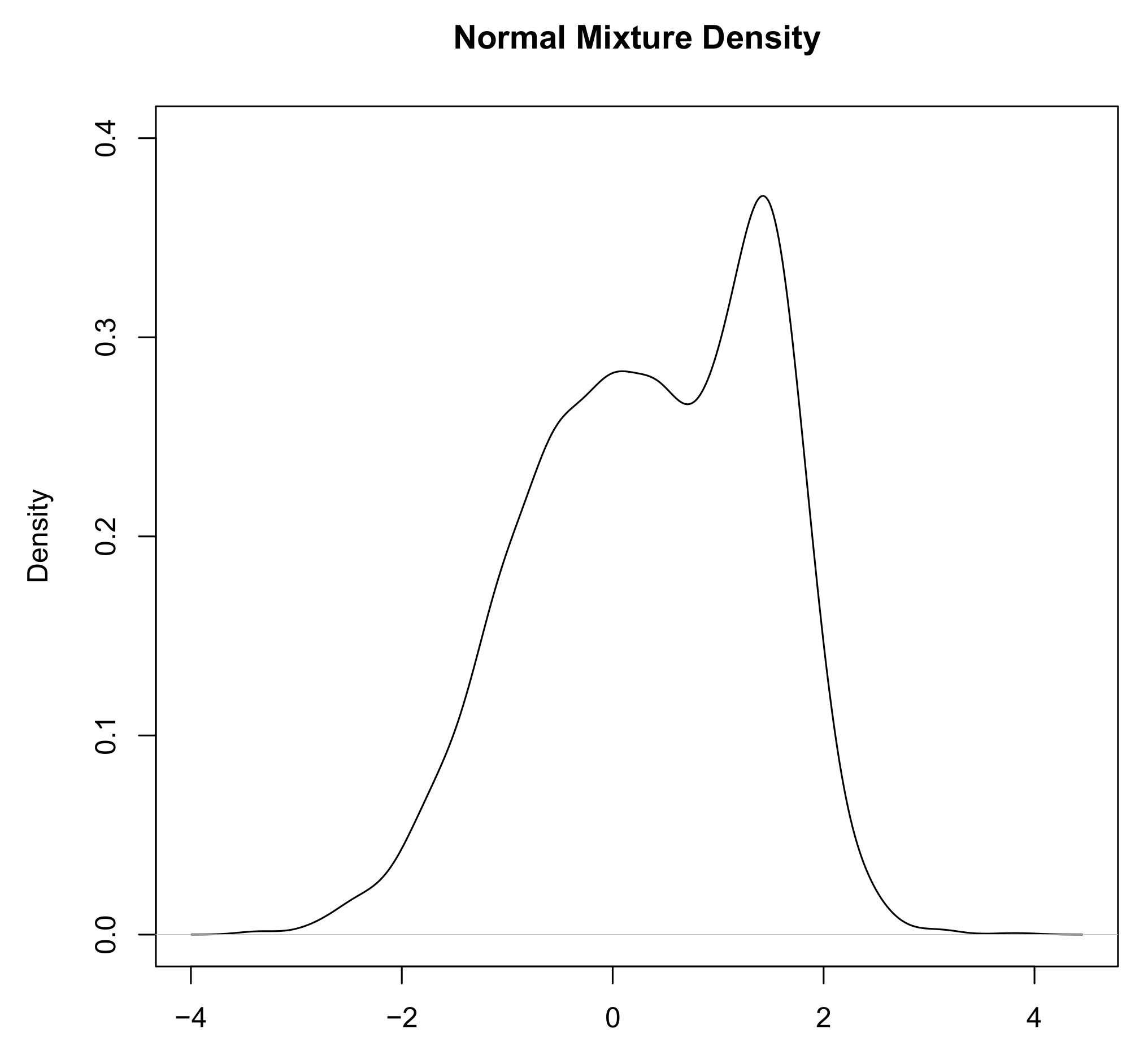
Figure 1 illustrates a mixture model considering Gaussian distributions.
3.2. Kernel Density Estimation
Kernel density estimation (KDE) is a non-parametric approach that allows estimating the probability density function of a random variable. KDE makes inferences about populations. These inferences are based on a finite data sample, making it indeed viable to address our problem. In our particular case, KDE has the major advantage that it allows for the transformation of a discrete empirical distribution into a continuous one.
In a univariate environment, considering
an independent and identically distributed data sample following some distribution of unknown density
f, the associated kernel density estimator is given by
where
K is a non-negative function, namely, the kernel, and
, usually referred to as the bandwidth, is a smoothing parameter. The scaled kernel is defined as
. Usually,
h is chosen as small as possible with respect to the data; however, the trade-off between the bias of the estimator and its variance remains. It is noteworthy to mention that the kernel bandwidth has a non-negligible impact on the resulting density estimate.
Various kernels can be used, the most frequent being uniform, triangular, biweight, triweight, Epanechnikov, normal, among others. The Epanechnikov kernel is theoretically optimal when it comes to its mean squared error; however, for other kernels, the loss of efficiency, with respect to the metric previously mentioned, is very little [
29].
The most commonly used optimisation criterion for selecting this parameter is the expected
risk function, also referred to as the mean integrated mean squared error or MISE
Under weak assumptions on
f (the unknown real density function) and
K,
where
o characterises the asymptotic behaviour of the function [
30]. The AMISE is the Asymptotic MISE which can be expressed as follows,
where
given a function
,
and
is the second derivative of
f. Considering the previous definition of the AMISE, the optimal smoothing bandwidth is given by
However, cannot be used in practice as it requires knowing f, but most techniques traditionally rely on an estimate of the AMISE or, of some component of the latter.
It is noteworthy to mention that the selection of the bandwidth when it comes to heavy-tailed underlying empirical distribution might be difficult, implying potentially inadequate risk measures as the bandwidth that was uniquely selected over the distribution as a whole can be inappropriate in the tails.
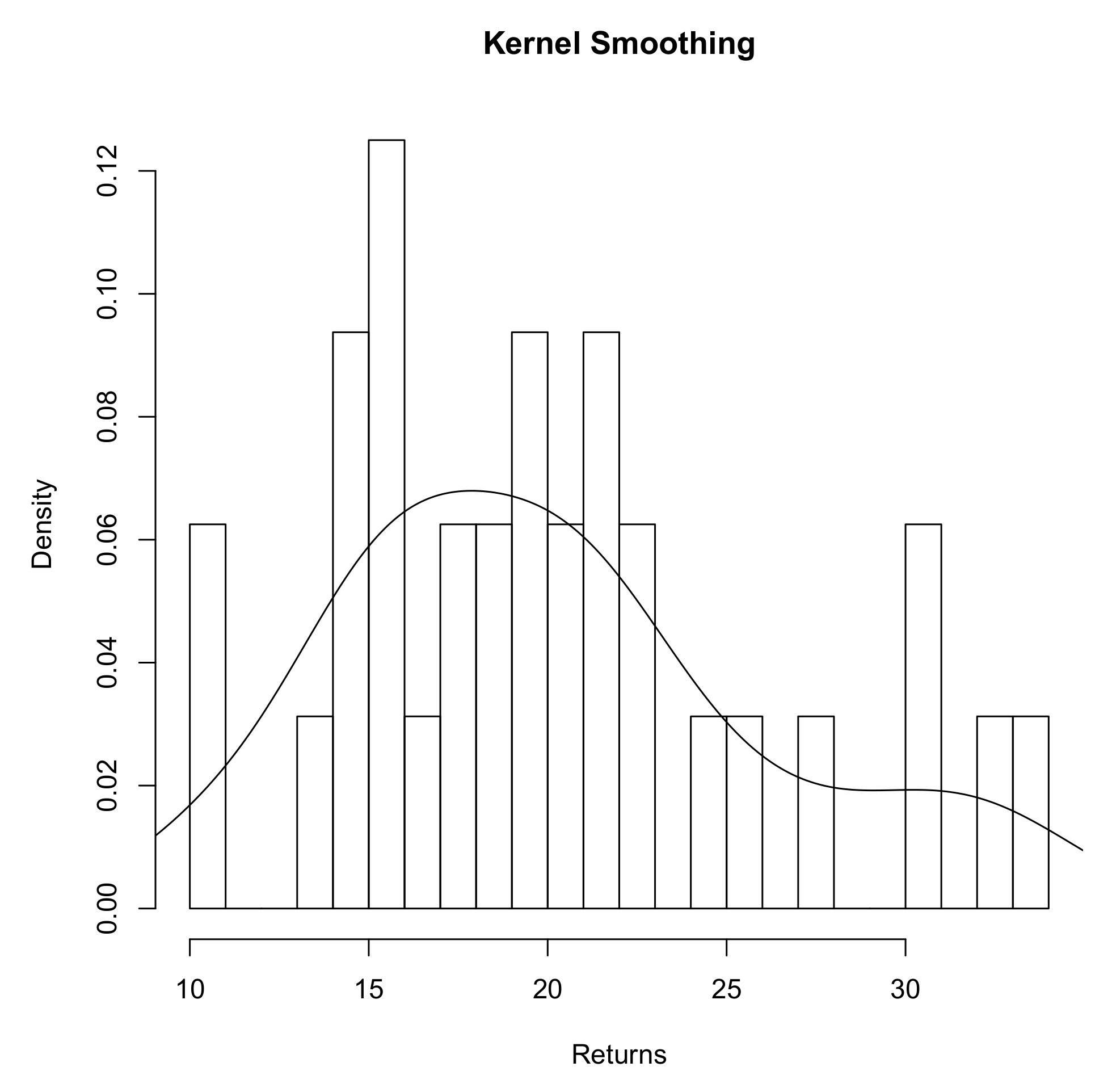
Figure 2 illustrates a kernel density estimation applied to a randomly generated dataset.
3.2.1. Expectation-Maximisation for Truncated Distributions
The Expectation-Maximisation (EM) algorithm allows finding maximum likelihood (MLE) parameters of a statistical model when underlying equations cannot be solved for them directly [
31]. It is noteworthy to mention that this maximum is likely to be local. Assuming the existence of further unobserved data points, the EM progressively generates new pieces of information using latent variables and known data.
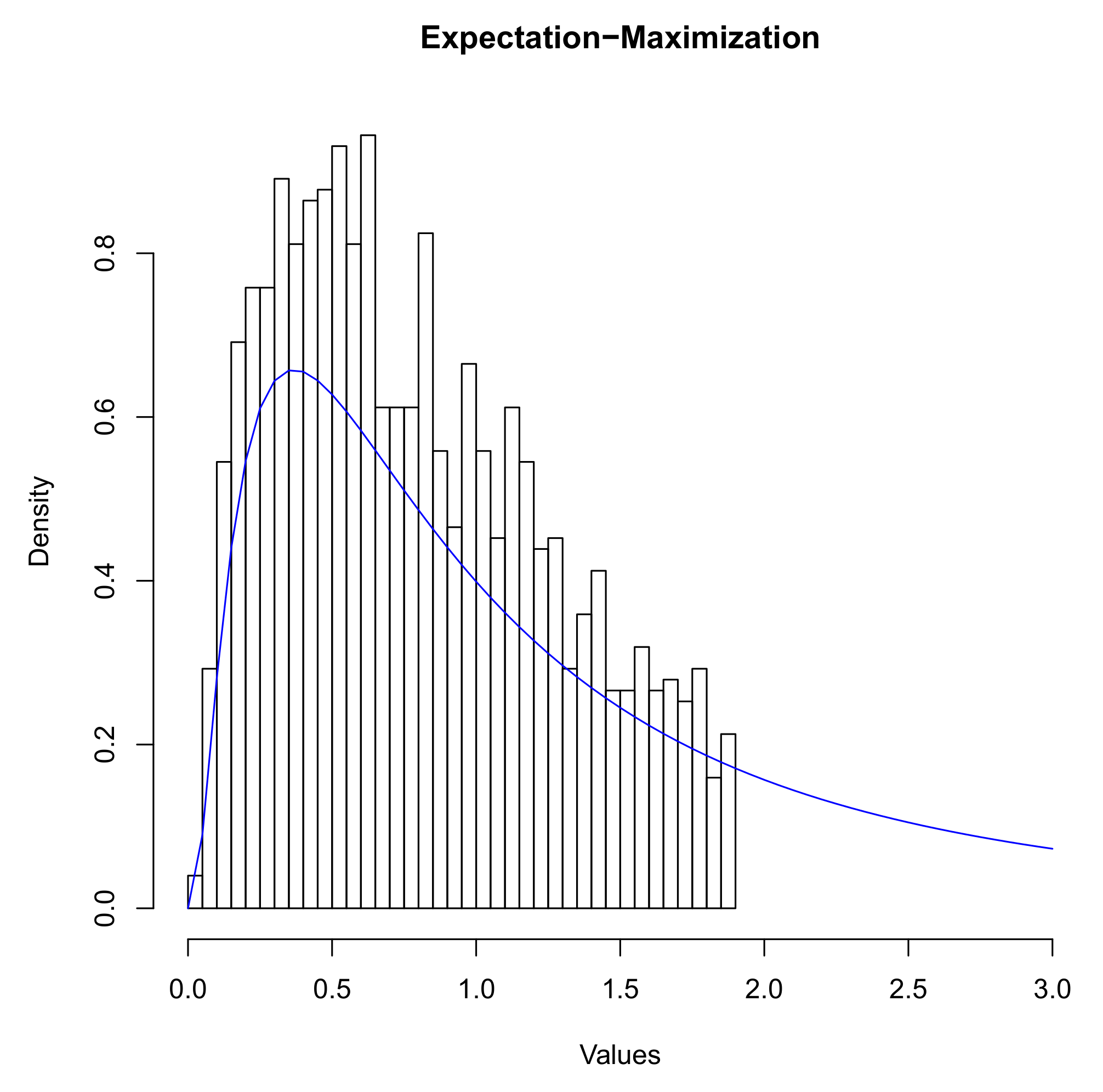
Figure 3 illustrates the added value of the EM considering a lognormal distribution.
The EM algorithm relies on an expectation evaluation step, where the expectation of the likelihood is calculated taking into account the last observed variables, and a maximisation step, in which the maximum likelihood of the parameters is estimated maximising the likelihood found in the previous step. Then, the parameters obtained in the maximisation step are used as a starting point for a new expectation evaluation phase, and the process is repeated until the resulting parameters are deemed acceptable (see Algorithm 1 for details).
Given
a set of observed data,
a set of missing values, and
a vector of unknown parameters, i.e., parameters yet to be found, along with a likelihood function
, the unknown parameters are obtained maximising the following function representing the marginal likelihood of observed data
The two iterative steps aforementioned can then be formalised as
Expectation step: Define
the expected value of the log likelihood function of
with respect to both relevant conditional distribution of
given
and estimates of the parameters
:
Maximisation step: Find the parameters maximising the following quantity:
| Algorithm 1: |
Initialisation Step: , the initial values of a set of parameters are chosen, and an estimation of the quantity of missing data, is provided. Expectation Step: Given , we compute:
- -
Estimation of : - -
values are drawn from the theoretical distribution of interest, with respect to the constraint - -
, where is the new set to be considered in the subsequent steps (in other words, the new partially synthesised dataset) - -
Loglikelihood function computation
Maximisation Step: is computed If convergence is reached, i.e., , the algorithm stops and is obtained. If the algorithm does not converge then step 2 and 3 are prepeated with in the Expectation Step until convergence.
|
3.2.2. The Generative Adversarial Nets
A generative adversarial network (GAN) ([
32,
33]) is a machine learning environment in which two neural nets, the generator and the discriminator, compete with each other in a zero-sum game. Given a training set, this approach learns to create new data “similar" to those contained in the training set. The generator synthesises candidates while the discriminator assesses them. In summary, the generator intends to fool the discriminator by making it believe that the data have not been artificially created.
There are 5 main components to carefully consider in the approach: the original and authentic dataset; the source of entropy, which takes the form of a random noise, fed into the generator; the generator itself, which intends to forge the behaviours of the original dataset; the discriminator which intends to distinguish the generator’s output from the initial dataset and the actual “training” loop where we teach the generator to trick the discriminator and the discriminator to beware of the generator.
In our case, we are starting with a simple original dataset randomly generated from a Gaussian distribution, and we use the GAN to try to replicate the dataset and eventually add more data points where some may lack, i.e., in the tails (mechanically) (The experimental setup is very similar to the one provided at the following URL
https://blog.evjang.com/2016/06/generative-adversarial-nets-in.html, accessed on 19 July 2021). The input fed to the generator is also random, and in our illustration, we used a uniform distribution rather than a normal one, therefore, our generator has to non-linearly remould the data (Note that in a production environment, if the shape of the final dataset is known, one may choose a more informative distribution to drive the generator).
The generator takes the form of a feedforward network. The network possesses two hidden layers and three linear mappings. A tangent hyperbolic is used as an activation function. The generator is going to take the uniformly distributed data samples as input intending to mimic the form of the initial data, i.e., a Gaussian distribution.
The discriminator is almost identical to the generator, the only difference being that the activation function considered is now a sigmoid. The discriminator is either going to take samples from the real data or the generator and will output a single scalar between 0 and 1, that can be translated as “fake” or “real”. The training loop alternates between initially training the discriminator on real data versus fake ones, with accurate labels, and then training the generator to fool the discriminator, with inaccurate labels. It is noteworthy to mention that GANs can be complicated to handle and that the generated data might not be usable. As such, it is usually necessary to rerun it multiple times or combine it with goodness-of-fit tests to ensure the reliability of the generated data.
In what follows, the process of training a neural network to sample from a simple Gaussian distribution with and is illustrated. The generator takes a single sample of a uniform(0,1) distribution as input. We want the generator to map points to , in such a way that resulting points cluster compactly where pdata(X) is dense. Thus, the generator takes in y and generates fake data x.
The backpropagation process is summarised in what follows. The discriminator returns
, a value allowing to assess the likelihood for
x to be a genuine data point. The objective is to maximise the likelihood to recognise authentic data points as being genuine and synthesised ones as forged. The objective function relies on the cross-entropy, formulated
. For real data points,
p (the true label) equals 1. For synthesised data, the label is reversed (i.e., one minus label). So, the objective function becomes:
The objective of the generator (through its associated objective function), is to create data points with the largest
possible in order to fool the discriminator.
As such, GANs are often represented as a min/max game in which
G intends to minimise
V while
D wants to maximise it.
Implementing a gradient descent approach, both networks are then trained alternatively until the generator produces data points of sufficient quality to fool the discriminator. However, it is possible to face a gradient diminishing problem with the generator making the selected optimisation strategy very slow. Indeed, the discriminator has a tendency to win early against the generator as the task of distinguishing generated data points from authentic ones is generally easier early in training. To overcome that issue, several solutions have been proposed, see for instance [
34,
35].
GANs are interesting for our ES calculation problem as by attempting to mimic authentic data, the algorithm creates scenario data points “consistent” with the data it has been trained with, even in part of the initial distribution where there were none or only a few, i.e., in the tails.
Figure 4 illustrates a data generation implementing a GAN, in which we can see that more data points have been created in the tails (green line), mechanically engendering a more conservative if not more reliable risk measure. This phenomenon will be analysed in the next section.
3.2.3. SMOTE Regression
Traditionally, imbalanced classification involves developing predictive models on classification datasets for which at least one class is underrepresented (imbalanced). The main issue having imbalanced datasets to work with is that machine learning algorithms have a tendency to ignore the minority class, and therefore perform poorly on this one, although, it is generally where it matters most. A solution to deal with imbalanced datasets is to “over-sample" the class which is underrepresented. A viable approach is to synthesise new data points from existing examples. This approach is called Synthetic Minority Oversampling Technique, or SMOTE for short. The authors of [
36] suggest creating artificially new data points implementing an interpolation approach. For each data point of the minority set, they propose to choose from the set one of its k-nearest neighbours at random. With the selected two data points, a new one is generated whose “attribute values are an interpolation of the values of the two original cases”, and as such belongs to the former minority class.
To be applied in a regression environment, three important elements of the SMOTE algorithm must be addressed in order to adapt it [
37]:
“How to define which are the relevant observations and the normal cases”;
“How to create new synthetic examples (i.e., over-sampling)”; and
“How to decide the target variable value of these new synthetic examples.”
With respect to the first issue, the original algorithm relies on the information provided by the user regarding the qualification of the minority class. In the regression case, “a potentially infinite number of values of the target variable could be encountered”. The “proposal mentioned in [
37] is based on the existence of a relevance function and on a user-specified threshold on the relevance values”, which leads to the rare set definition. The proposed algorithm over-samples data in the minority set and under-samples the remaining elements. This approach permits the creation of a new and more balanced training dataset. With respect to the second component aforementioned, the generation of synthetic examples, an approach similar to the original algorithm as been implemented only slightly modified to properly deal with both numeric and nominal features. Finally, concerning the third element related to the target variable value selection of the created data points, in their approach, the “cases that are to be over-sampled do not have the same target variable value, although they do have a high relevance score”, meaning “that when a pair of examples is used to generate a new synthetic case, they will not have the same target variable value.” Therefore, the proposal mentioned in [
37] relies on the use of the weighed average of the target variable values of the two initially selected data points. “The weights are calculated as an inverse function of the distance of the generated case to each of the two seed examples.”
This approach allows creating new data points in the distribution of interest, as it mechanically over-samples information in the tails of the distributions (the rarest elements). Therefore, this approach is promising for data augmentation purposes, in particular, in an ES computation environment. Besides, an interesting collateral lies in the fact that by over-sampling elements, the algorithms have to create the features associated to each data point generated, allowing to analyse the pertaining market conditions for risk management purposes.
4. Risk Measurement—Application
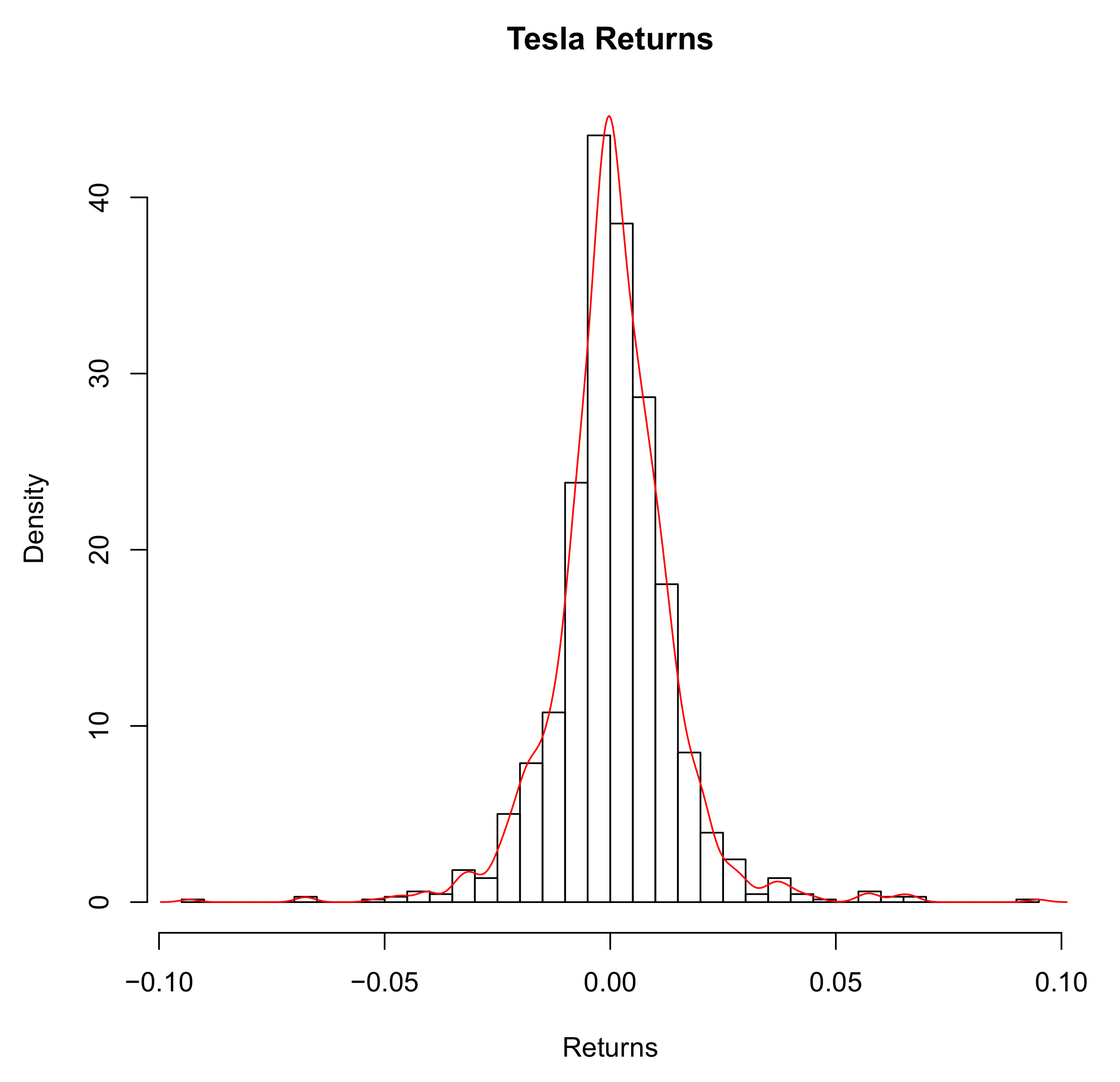
In this section, the results obtained with the various methodologies presented above are compared and discussed such that the pros and cons are clearly displayed. The methodologies have been applied to the Tesla returns. Tesla’s daily closing prices are presented in
Figure 5, and the equivalent daily returns are represented in
Figure 6. The dataset containing Tesla’s closing prices also contains information pertaining to the market conditions, such as the daily price variations, the volumes, the opening prices, etc. The reported prices are from 3 January 2012 to 30 April 2017 (The dataset can be downloaded following the url,
https://github.com/mrafayaleem/dive-in-ml/blob/master/tesla-random-forests, accessed on 19 July 2021).
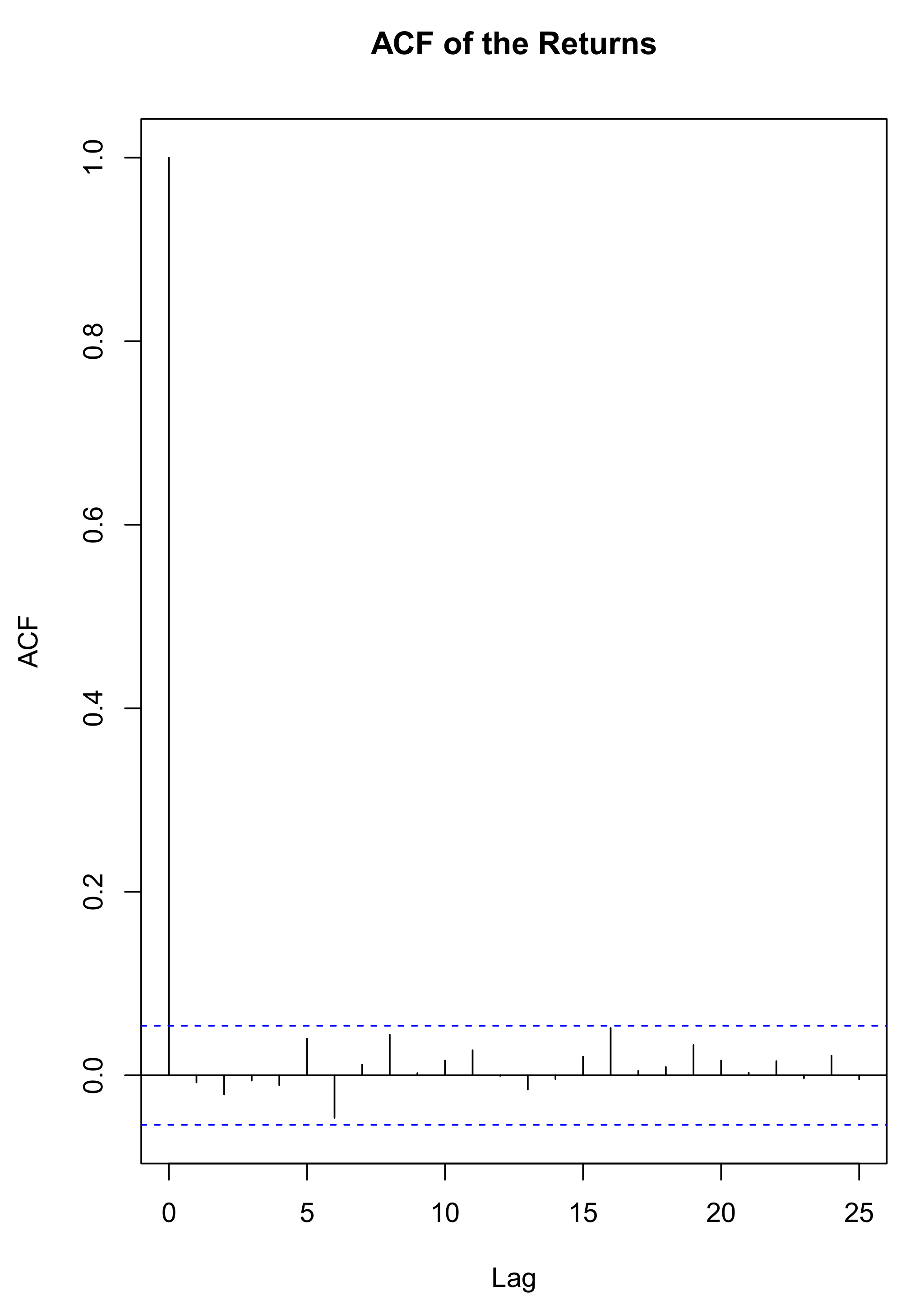
For the methodologies assuming independent and identically distributed distributions, the auto-correlation function plot obtained on the series does not show any serial correlation (
Figure 7), therefore, the assumption of independence cannot be rejected (However, it does not necessarily mean that the returns are independent). It is noteworthy to mention that despite an adapted version of the SMOTE regression is used, most methodologies presented in this paper would not be suitable if the underlying returns were not i.i.d., and therefore, the resulting risk measures likely to be inadequate. Alternatives relying on time series processes, GARCH models for instance, might be of interest in such a situation (see [
15,
38,
39] among others). For the methodologies requiring parameters to drive their behaviour, those obtained through the methodologies aforementioned are provided in
Table 1.
Starting from the beginning, we observe that depending on the type of distributions used, in particular, the theoretical foundations of the distribution with respect to the tails of these ones, the risk measures may vary quite a lot; for example, the ES of the Gaussian distribution fitted to the data is equal to 0.03077, while the one obtained using a stable distribution (The parametric distribution approaches have been implemented in R using the packages fitdistrplus, stabledist and fBasics) on the same data is equal to 0.0878. For the stable distribution, the Anderson–Darling test validates the fitting. We observe that the fatter tailed the distribution, the larger the risk measures. Consequently, some distributions might be overly conservative and may lead to inappropriate capital charges for market risks. It is noteworthy to mention that though goodness-of-fit tests might be of interest, they are limited by the information contained in the data used; for example, the goodness-of-fit tests are only valid if the sample of data used covers the full range of potential values, which is rarely the case, and even so, it tends to be biased by the behaviour of the (more numerous) data which represent the body of the distribution when in our case distribution tails matter the most. Consequently, their usefulness here might be relatively limited, however, we believe that without them our analysis would lack some rigour.
Table 2 allows comparing the risk measures obtained with each methodology. Anderson–Darling test p-values are provided for each approach.
Regarding the KDE, as the kernel is positioned on the underlying points, though the resulting distribution is continuous, the thickness of the tail is somehow proportional to the “quantity” of information contained in the tail of the empirical distribution; hence, the added value might be rather limited. However, in a situation in which there is sufficient information above and beyond the confidence level of the risk measure, the methodology is a viable option. Besides, the methodology, being non-parametric, does not force any specific form onto the data, allowing them to be closer to reality (The KDE approach has been developed in R using base packages). The ES obtained using KDE is equal to 0.0367.
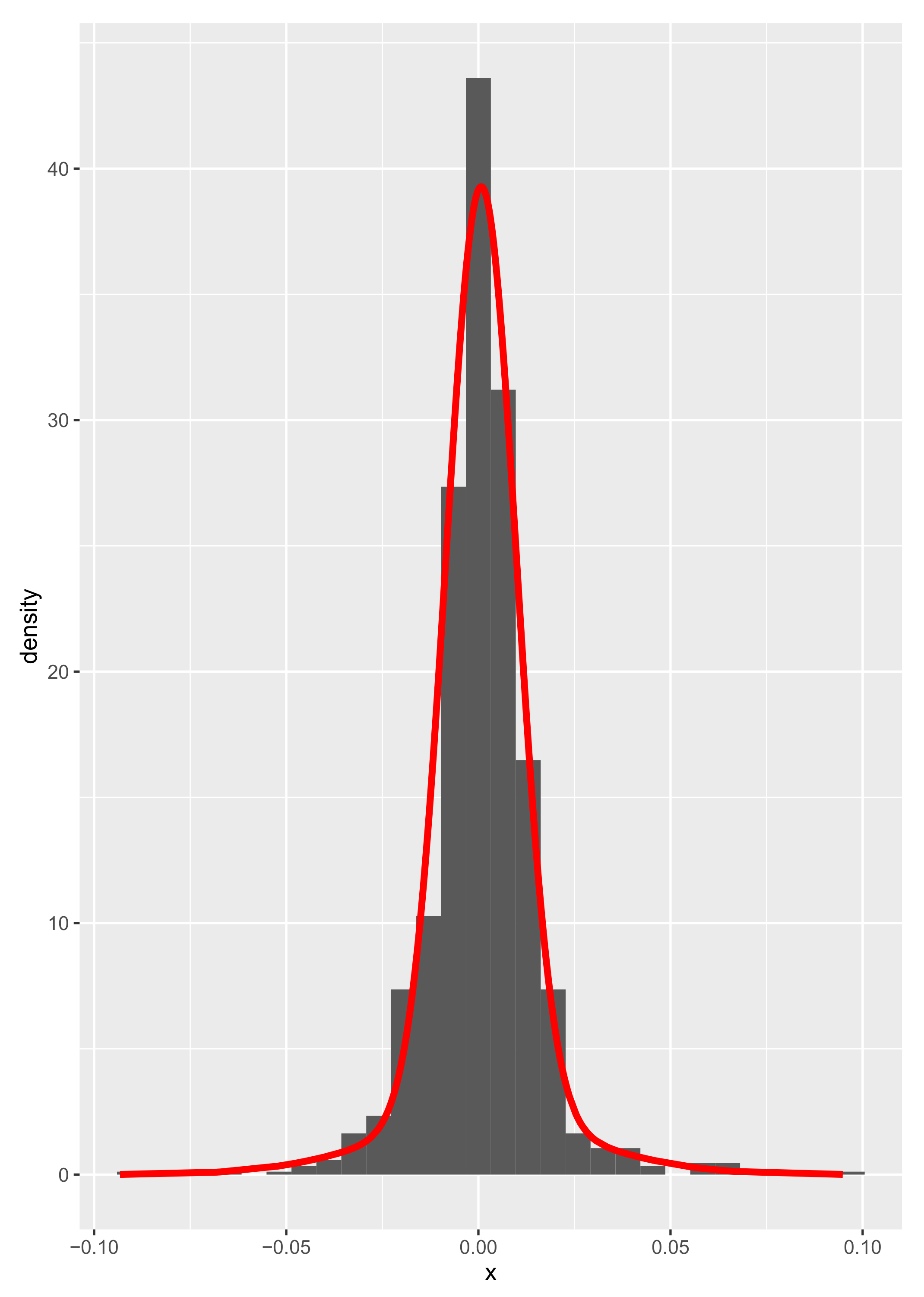
The mixture of Gaussian distributions is also a viable option, as with (at least) 5 parameters, it allows for the capture of multimodality, fat tails, skewness, etc. The approach is stable—more parameters have to be estimated—but the distribution allows fitting tails in a better fashion. While traditional problems of “mixture distributions” are related to deriving the properties of the overall population from those of the sub-populations, in our specific case, as there is no sub-population characteristic to be inferred, there is in fact no such problem. In the specific application of this approach, the slightly fatter tails allow for more conservative risk measures (i.e., the ES of the Gaussian Mixture is equal to 0.0404, which is slightly superior to the empirical ES of 0.038).
Figure 8 represents the Gaussian mixture obtained on the Tesla returns (The Gaussian mixture has been developed in R using the nvmix package. A code somehow similar to the one developed could be found at
http://sia.webpopix.org/mixtureModels.html, accessed on 19 July 2021 ).
The EM is used here, considering the lower and upper truncations at, respectively, the maximum and the minimum values contained in the dataset and assuming a Gaussian distribution. Here, with respect to the Gaussian distribution, we obtained risk measures inferior to the one obtained with the empirical distribution (i.e., we obtained 0.029 with the EM while we obtained 0.038 empirically). However, this approach would have provided different results assuming another type of parametric distribution (The EM algorithm has been developed in R. This is a proprietary version of the algorithm as such the code cannot be disclosed, however, the algorithm is detailed in
Section 3.2.1).
The GANs (The GAN approach has been developed in Python. The code used in this paper has been adapted from the following GIT:
https://github.com/ericjang/genadv_tutorial/blob/master/genadv1.ipynb, accessed on 19 July 2021) are really interesting, as the methodology allows synthesising data in the tails; however, the calibration of the methodology is fairly complicated and capricious, even though, it generates scenario points in the tail. In this paper, we set the number of iterations at 500,000 and the size of minibatch at 2000, and the performance of the network training was evaluated using the mean square error. It generally takes several runs before reaching algorithm stability; however, this method is the most conservative, as we obtained an ES of 0.09787413.
The SMOTE regression (The SMOTE regression has been developed in Python. The code used in this paper relies on the packaged smogn that can be found at:
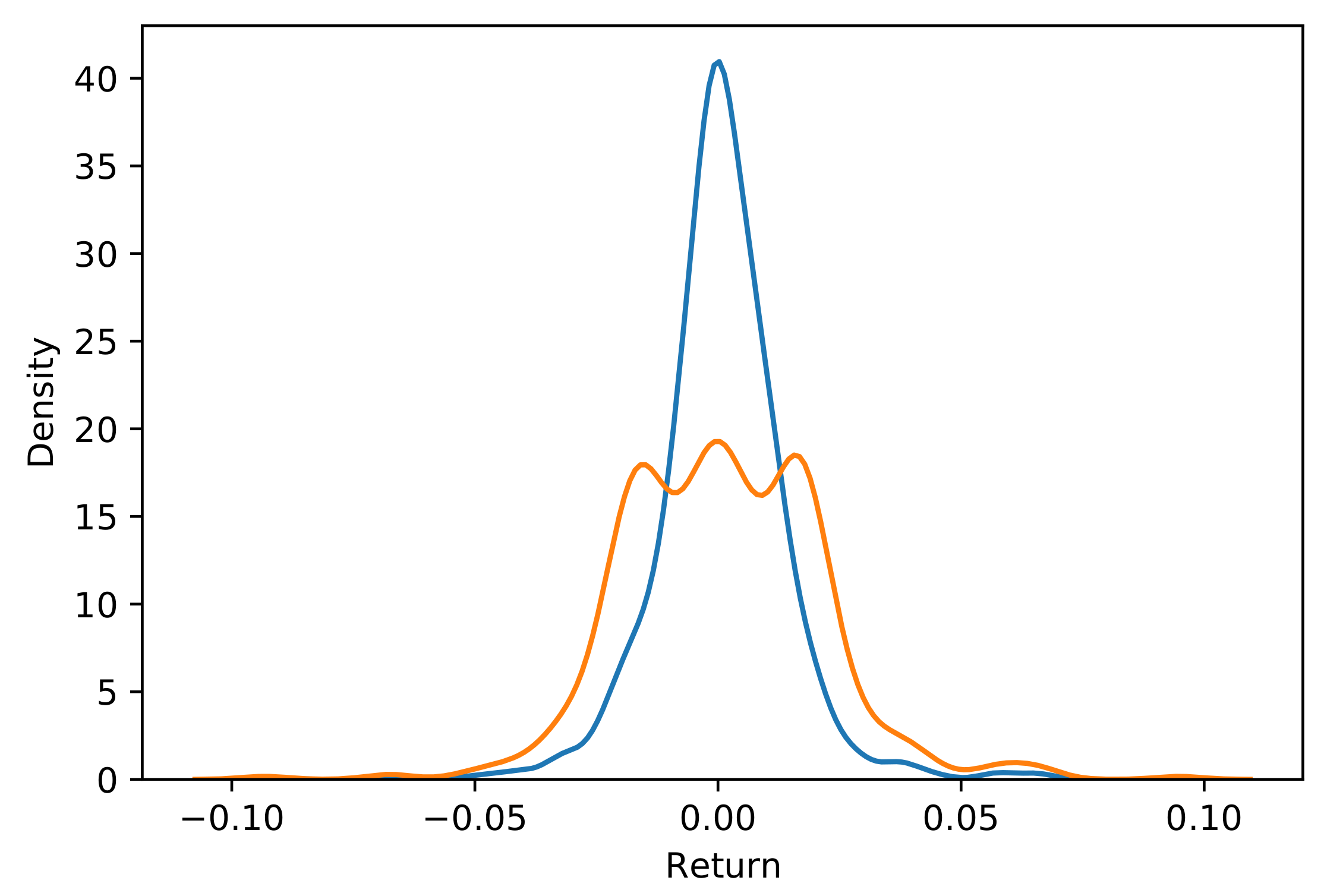
https://github.com/nickkunz/smogn, accessed on 19 July 2021) is in fact the most promising, as the methodology permits generating points by reverse engineering the level of the variables considered in the underlying regression such that it not only provides points in the tails but also the market conditions or scenarios for these values to appear. Thus, the values could be interpreted and validated with respect to the underlying state of nature. In our application, the ES obtained is in between the most conservative and the least, as it is equal to 0.0496, which might be considered as too conservative by banks but is likely to provide some stability to the risk measures over time.
Figure 9 provides an illustration of the return distribution obtained considering a SMOTE regression applied to the Tesla-related dataset.
5. Conclusions
In this paper, after clarifying the theoretical foundations of both VaR and ES (in the most extensive manner for the ES, as the measure is still a controversial matter), we presented several methodologies to ensure the reliability of the latter. Indeed, it requires as much information in the tails as possible. If there are no data points beyond the VaR set as a threshold (97.5% in the case of the newest market risk capital standards), the ES will not be robust, and in the most extreme case, can be equal to the VaR itself.
As a consequence, we tested the impact of several methodologies coming from the fields of statistics and AI. Though all seem somehow viable, it might be interesting to select one option over another, depending on the initial situation. If one considers that the data sample as being representative of the general population, then one may want to consider KDE, as its application here will ensure to be as close as possible to the dataset while allowing the creation of a continuous version of it. If your dataset presents similar characteristics to some parametric distributions, fitting one of these might be of interest. If the underlying distribution appears multimodal, a mixture of distributions might be more suited. If one considers that the datasets are censored, then a conditional fitting using an EM algorithm should be considered. The two AI approaches presented have, to our knowledge, not been used in such an environment before. The GANs could be of interest if the underlying data are considered unreliable and if a synthetic dataset has to be generated to reshape the underlying distribution as a whole. Finally, the use of the SMOTE regression is a powerful option to generate data points in the tails of the profit-and-loss distributions. Besides, this last methodology allows reverse engineering the market conditions, which facilitates the acquirement of the log return of interest in the tails. Furthermore, GANs, SMOTE regressions, Distribution Mixtures and KDE allow better capturing the asymmetry between the right and the left tails of the P&L distributions, while this is not the case when relying on Gaussian distributions.
As a conclusion, we presented several viable options that could be considered to ensure the robustness of the selected risk measure; however, the GAN approach has to be further investigated to stabilize the outcomes.