Modified Operators Interpolating at Endpoints
Abstract
:1. Introduction
2. Limit of Iterates
3. Modified Durrmeyer Operators
- (i)
- If , then the desired eigenvector k can be choosen asInstead of unknowns, we have only j unknowns .
- (ii)
- If , k has the formInstead of , we have only unknowns.
4. The Linking Operator and Voronovskaja-Type Results
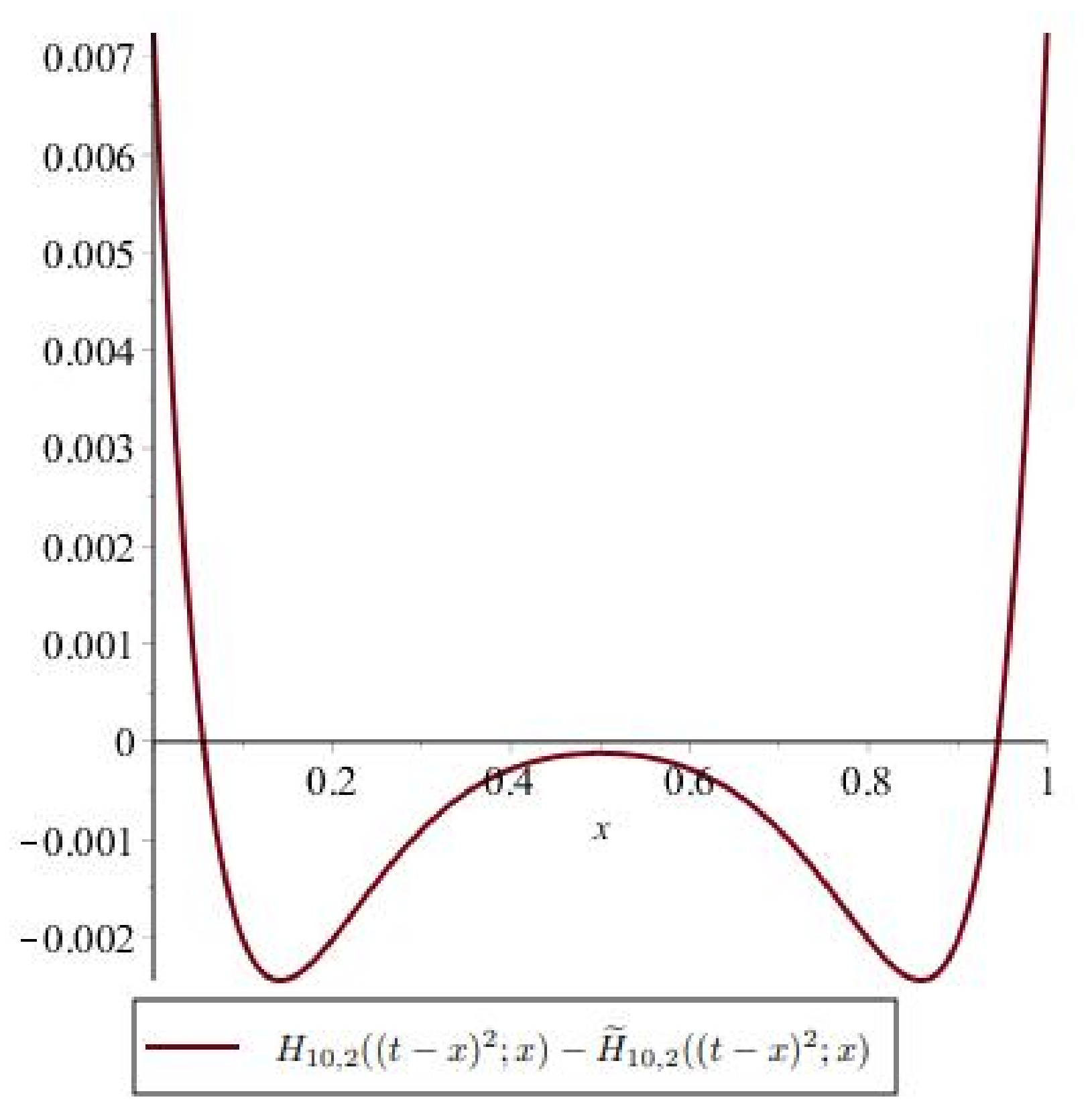
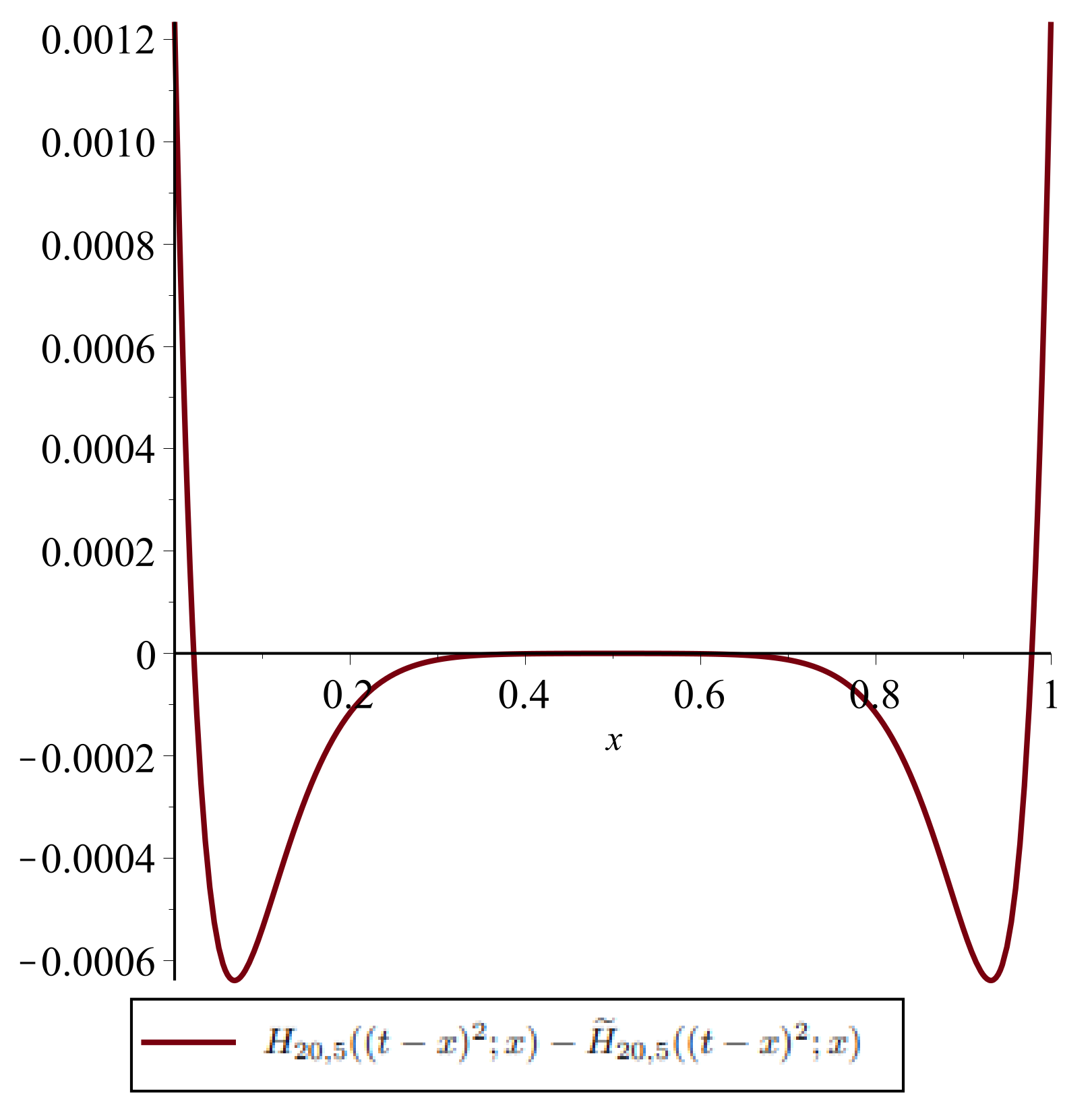
5. Differences in Positive Linear Operators
- (i)
- (ii)
- ,
- (i)
- (ii)
- ,
6. Conclusions and Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Acu, A.M.; Raşa, I. Iterates and invariant measures for Markov operators. 2021, submitted.
- Acu, A.M.; Bascanbaz-Tunca, G.; Raşa, I. Differences of Positive Linear Operators on Simplices. J. Funct. Spaces 2021, 2021, 5531577. [Google Scholar]
- Acu, A.M.; Raşa, I. Estimates for the differences of positive linear operators and their derivatives. Numer. Algorithms 2020, 85, 191–208. [Google Scholar] [CrossRef] [Green Version]
- Acu, A.M.; Hodis, S.; Raşa, I. Estimates for the Differences of Certain Positive Linear Operators. Mathematics 2020, 8, 798. [Google Scholar] [CrossRef]
- Acu, A.M.; Hodis, A.M.S.; Raşa, I. A survey on estimates for the differences of positive linear operators. Constr. Math. Anal. 2018, 1, 113–127. [Google Scholar] [CrossRef]
- Acu, A.M.; Raşa, I. New estimates for the differences of positive linear operators. Numer. Algorithms 2016, 73, 775–789. [Google Scholar] [CrossRef]
- Brémaud, P. Markov Chains; Springer: New York, NY, USA, 1999. [Google Scholar]
- Chung, K.L. Elementary Probability Theory with Stochastic Processes; Springer: Berlin, Germany, 1974. [Google Scholar]
- Kemeny, J.G.; Snell, J.L. Finite Markov Chains; Springer: Berlin, Germany, 1976. [Google Scholar]
- Păltănea, R. A class of Durrmeyer type operators preserving linear functions. Ann. Tiberiu Popoviciu Sem. Funct. Eq. Approx. Conv. (Cluj-Napoca) 2007, 5, 109–117. [Google Scholar]
- Heilmann, M.; Raşa, I. A Nice Representation for a Link between Bernstein-Durrmeyer and Kantorovich Operators. In Proceedings of the Mathematics and Computing, ICMC 2017, Communications in Computer and Information Science, Haldia, India, 17–21 January 2017; Giri, D., Mohapatra, R., Begehr, H., Obaidat, M., Eds.; Springer: Singapore, 2017; Volume 655. [Google Scholar]
- Heilmann, M.; Raşa, I. k-th order Kantorovich type modification of the operators Unρ. J. Appl. Funct. Anal. 2014, 9, 320–334. [Google Scholar]
- Dancs, M. Differences of classical and modified operators. Gen. Math. 2021, 29, 3–12. [Google Scholar]
- Gupta, V.; López-Pellicer, M.; Srivastava, H.M. Convergence estimates of a family of approximation operators of exponential type. Filomat 2020, 34, 4329–4341. [Google Scholar] [CrossRef]
- Gupta, V.; Acu, A.M.; Srivastava, H.M. Difference of some positive linear approximation operators for higher-order derivatives. Symmetry 2020, 12, 915. [Google Scholar] [CrossRef]
- Braha, N.L.; Mansour, T.; Srivastava, H.M. A parametric generalization of the Baskakov-Schurer-Szász-Stancu approximation operators. Symmetry 2021, 13, 980. [Google Scholar] [CrossRef]
- Gupta, V.; Srivastava, H.M. A general family of the Srivastava-Gupta operators preserving linear functions. Eur. J. Pure Appl. Math. 2018, 11, 575–579. [Google Scholar] [CrossRef]
- Usta, F. On approximation properties of a new construction of Baskakov operators. Adv. Differ. Equ. 2021, 2021, 269. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Acu, A.M.; Raşa, I.; Srivastava, R. Modified Operators Interpolating at Endpoints. Mathematics 2021, 9, 2051. https://doi.org/10.3390/math9172051
Acu AM, Raşa I, Srivastava R. Modified Operators Interpolating at Endpoints. Mathematics. 2021; 9(17):2051. https://doi.org/10.3390/math9172051
Chicago/Turabian StyleAcu, Ana Maria, Ioan Raşa, and Rekha Srivastava. 2021. "Modified Operators Interpolating at Endpoints" Mathematics 9, no. 17: 2051. https://doi.org/10.3390/math9172051
APA StyleAcu, A. M., Raşa, I., & Srivastava, R. (2021). Modified Operators Interpolating at Endpoints. Mathematics, 9(17), 2051. https://doi.org/10.3390/math9172051







