Abstract
Investors’ decisions on capital markets depend on their anticipation and preferences about risk, and volatility is one of the most common measures of risk. This paper proposes a method of estimating the market price of volatility risk by incorporating both conditional heteroscedasticity and nonlinear effects in market returns, while accounting for asymmetric shocks. We develop a model that allows dynamic risk premiums for the underlying asset and for the volatility of the asset under the physical measure. Specifically, a nonlinear in mean time series model combining the asymmetric autoregressive conditional heteroscedastic model with leverage (NGARCH) is adapted for modeling return dynamics. The local risk-neutral valuation relationship is used to model investors’ preferences of volatility risk. The transition probabilities governing the evolution of the price of the underlying asset are adjusted for investors’ attitude towards risk, presenting the asset returns as a function of the risk premium. Numerical studies on asset return data show the significance of market shocks and levels of asymmetry in pricing the volatility risk. Estimated premiums could be used in option pricing models, turning options markets into volatility trading markets, and in measuring reactions to market shocks.
1. Introduction
Financial derivatives and instruments for risk reduction provide a practical means to hedge and manage the risk from trading financial securities. In complete markets, risk deriving from financial derivatives and insurance instruments can be perfectly hedged and there is no volatility risk premium to estimate. The Black–Scholes–Merton option valuation model [1,2], as a fortress pricing model for financial instruments, specifies option prices independent of investors’ preferences, their expectations and risk aversion, and this independence is a direct consequence of constant volatility. On the other hand, prices of financial derivatives and hedging instruments observed on option markets contain rich information about the market’s expectation of the underlying asset’s future distribution, the risk premium for unhedgeable risk, or the compensation demanded by investors for bearing risk related to abrupt changes in volatility. Furthermore, option prices reflect investors’ willingness to pay in order to hedge against future increases in yields on the underlying instrument. This price is called the market price of volatility risk (i.e., estimated volatility risk premium), and it also represents the price of risk arising from holding a financial derivative or insurance instrument. Estimating the market price of volatility risk is important in understanding the preferences of market participants and allows for better modeling of investors’ behavior. This will then allow us to manage risk more easily and facilitate the evaluation and hedging of options, but also financial derivatives in general. By incorporating the market price of volatility risk into the option pricing model, option markets may also become volatility trading markets.
In this paper, we consider a stochastic volatility model framework with leverage effect, since this is consistent with a number of additional stylized facts that characterize asset returns, such as volatility clustering, semi-heavy-tailed non-normal return distributions with skewness and excess kurtosis and negative correlation of volatility with asset returns. Since the unhedgeable second source of randomness is present, the concept of market completeness is lost. Consequently, we no longer have straightforward risk-neutral pricing and the price of volatility risk will be non zero. Stochastic volatility models have been studied from various points of view in mathematical finance and related fields [3,4]. Unfortunately, it seems that statistical estimation of the model is the most difficult problem, and most of the work in that area is focused on computationally intensive methods. Therefore, in practice, it is proposed to use discrete models of stochastic volatility instead of the continuous ones. As an alternative to continuous stochastic volatility modeling, a non-linear heteroscedastic time series model with leverage effect (NGARCH, sometimes also denoted NAGARCH) is proposed, since it has the property of convergence towards a continuous process that satisfies a stochastic volatility model and it may accommodate both the leverage effect and the market price of volatility risk. As firstly put forth by [5], a low-volatility environment is likely to be accompanied by rising asset valuations since low volatility is associated with increased willingness to take on risk. Alternatively, a fall in equity prices would generally imply a rise in the debt-equity ratio, and in turn increase the riskiness of a given stock. Recent economic theory emphasizes the endogenous nature of volatility, labeled as a “financial instability paradox” or “volatility paradox” in [6], where a prolonged period of low volatility could paradoxically lead to a build-up in risk. Moreover, further compression of risk premia may be due to market participants’ expectations of the continuation of low volatility and genuine financial conditions that may encourage these participants to build up large positions in asset classes of higher risk [7]. We go one step further and consider this asymmetry in analyzing the news impact curve defined by [8] to measure the impact of news or unexpected shocks into volatility estimates.
The contributions of this paper are twofold. First, we price the volatility risk premium capturing both conditional heteroscedasticity and nonlinearities in asset returns and their stochastic volatility. Specifically, the asymmetric NGARCH (stochastic) volatility model [8] is used to model nonlinearities in the mean specification of asset returns and the leverage effect. The pricing of the volatility risk premium is done by following the locally risk-neutral valuation relationship (LRNVR) by [9], shown to hold under certain combinations of preference and distribution assumptions. We tackle stochastic volatility with a discrete NGARCH model from the general autoregressive conditional heteroscedasticity family and show that the discrete NGARCH process is an approximation of the stochastic volatility diffusion model. Second, we develop a model that allows a dynamic, time-varying risk premium for the underlying asset under the physical measure. We show that the risk-neutral version for a discrete NGARCH model with a time-dependent Sharpe ratio would also involve a time-varying market price of risk.
In some approaches, the volatility risk premium is determined using option prices and inferring about the differences between implied volatility derived from option prices and physical volatility, but we do not adopt this approach further. Instead, we would like to propose a novel approach that is capable of estimating the market price of volatility risk using just asset returns and physical volatility, while relying on the time-varying Sharpe ratio and the leverage effect. The leverage effect explains a possible relationship between volatility and possible changes in attitudes towards risk, and by incorporating it directly as a (significant) parameter in the model, we are able to eschew option pricing altogether. Our analysis suggests that one could first use the historic stock prices to estimate the process parameters needed for estimating the real volatility drift and the volatility risk premium. As a second step, the volatility risk premium information could be incorporated for pricing and hedging purposes, pricing VIX derivatives, including VIX futures and VIX options. Our findings enable future analysis of intensified speculative activity on volatility, since net short positions on VIX futures held by non-commercial traders have been empirically documented to change over time and to be driven by market’s stress episodes of different intensities.
The paper is organized as follows. Section 2 gives an overview of existing research and methods of estimating the volatility risk premium. Section 3 describes the discrete time stochastic volatility model with leverage (NGARCH), provides the link to its continuous version and presents the evolution of the asset in a locally risk-neutral setting, adjusted for investors’ attitude towards risk. Data and estimation results are discussed in Section 4 and Section 5 concludes, highlighting future research directions.
2. Literature Review
Several studies have been conducted on world markets aiming to determine the market price of volatility risk. The obtained results are varying, since different approaches were used to determine both its price and valuation. For example, ref. [10] uses an approach that does not depend on any particular model to fairly evaluate options. The authors observe the differences between the implicit volatility derived from option prices (VIX index) and the volatility observed in the market, and investigate the impact of macroeconomic factors. A similar approach is used in [11], where a no-arbitrage model was estimated to relate both variations in volatility and stock market volatility to the business cycle. The authors show that volatility risk premiums are strongly counter-cyclical, even more than stock volatility. Additionally, in out-of-sample experiments, it is shown that volatility risk premiums partially explain the large swings of the VIX index during the 2007–2009 subprime crisis. The author of [12] provides a theoretical investigation of the market price of volatility risk, where it is considered to be a function of two variables: the price of an underlying asset and its volatility. The author provides evidence that the correlation between the underlying price and its volatility has no impact on the price of volatility risk.
A completely different approach was adopted in [13]. In order to overcome empirically poor pricing and hedging performances of the GARCH option-pricing model with a locally risk-neutral valuation relationship (LRNVR) firstly introduced by [9], the authors develop a GARCH option model with a new pricing kernel allowing for a variance premium. An explicit relationship between the conditional variances under the physical and risk-neutral probability measures is presented, and the market price of volatility risk enters analytically into the equation. However, the persistence parameter remains unchanged in the two probability measures. On the other hand, a new risk-neutral valuation relationship (mLRNVR) in GARCH option-pricing models is presented in [14], where the conditional variances under the physical and risk-neutral measures are designed to be different. Nevertheless, the asset risk premium is considered to be constant in their analytical approach. In order to capture the variance risk premium, the authors choose the variance process to be more persistent in the risk-neutral measure. Moreover, they show that GARCH option-pricing models designed in that way are able to price the SPX one-month variance swap rate, i.e., the CBOE Volatility Index (VIX), more accurately. The authors emphasize that a source of poor pricing and hedging performances from previous empirical research may arise from the restriction required by the LRNVR, and consequently choose to capture the variance risk premium in the risk-neutral dynamics only. Their numerical results provide evidence that the GARCH (1,1) option pricing model under the mLRNVR is more suitable to price variance swap. However, empirical research documents time-varying conditional first and second moments of asset returns accompanied with a strong financial leverage effect, i.e., a non-zero correlation between the stock process and the volatility process. Consequently, this must be accounted for when valuating both the asset risk premium and the volatility risk premium. The authors of [14] realized that developing a new risk-neutral valuation relationship is an urgent task, but missed to incorporate a time-varying valuation of the volatility risk premium and did not consider the volatility risk premium to affect the conditional variance process globally. Moreover, the authors do not investigate further the potential power of the leverage effect or level of asymmetry in the news impact curve as a standard measure of how news is incorporated into volatility estimates. Namely, since asset’s volatility is a major factor in option pricing valuation, a significant difference in predicted volatilities after the arrival of some major news would theoretically lead to significant differences in option prices and produce different hedging strategies. This idea was firstly designed in [15], where the author attempts to explain the volatility smile by incorporating the leverage effect using the NGARCH process, firstly introduced by [8]. Furthermore, the risk-neutral version for a discrete NGARCH model considers that the market price of risk for the stock is not separable from the leverage parameter. Using both option prices and returns under the risk-neutral as well as the physical probability measure, the authors of [16] evaluated different GARCH models out-of-sample. Their analysis favors a relatively parsimonious model that, besides volatility clustering, only allows for a standard leverage effect. We benefit from this idea and design a discrete stochastic volatility model for pricing the volatility risk premium, accounting for the fact that level-depending volatility is an important feature observed in option markets as well as in the underlying prices.
3. Stochastic Volatility and the Market Price of Risk
3.1. Volatility Risk Premium
A continuous stochastic volatility (SV) model is given in its general form as
where denotes asset price at time t, is the expected rate of return on the asset, is the volatility of returns, and , are Brownian motions with . Correlation captures the empirically observed (negative) relationship between volatility and price.
Given that the value of interest is usually the log-return on asset, using Itô’s formula the SV model can be rewritten as
Note that we can write , so that and are now independent Brownian motions.
Following the Girsanov theorem, it can be shown (e.g., [17]) that under the risk-neutral measure the process (1) can be rewritten as
with
and
where denotes the asset risk premium and is the market price of volatility risk. Similarly, is an adapted process (under the risk-neutral measure) that denotes market price of risk associated with [18,19].
In the special case of , i.e., if the asset price and the volatility were driven by the same source of uncertainty, the volatility risk premium would be exactly equal to the asset risk premium. However, in all real cases, it is a combination of the asset risk premium and the price of the remaining risk that drives Equation (1).
3.2. NGARCH Stochastic Volatility Model
Duan [9] introduced the seminal model for the log-returns of an asset
where is a sequence of i.i.d. random variables with standard normal distribution (under the real-world probability measure ). With this notation, r is the (one-period) risk-free rate and can be interpreted as the unit risk premium.
We will modify this model to allow for a time-varying asset risk premium, still using the traditional Sharpe ratio. Assuming, for simplicity, that the mean asset return is constant, i.e., , we introduce
The log-returns model is then
As previously noted, if the variance is driven by a second source of randomness, a (global) risk-neutral measure cannot be found. Still, a generalized version of the conventional risk-neutral valuation relationship needs to be introduced to account for heteroscedasticity, which prompted the following definition [9].
Definition 1.
A pricing measure is said to satisfy the locally risk-neutral valuation relationship (LRNVR) if measure is absolutely continuous with respect to measure ,
- (i)
- is lognormally distributed (under ),
- (ii)
- , almost surely with respect to ,
where denotes all information available at time , i.e., .
Note that the last property of Definition 1 allows us to estimate the current conditional variance from historical data even under measure .
Traditionally, variance is modeled using GARCH(1,1), first introduced in [20]. In order to incorporate the asymmetry in the distribution of returns, Engle and Ng [8] suggested the nonlinear asymmetric GARCH model (NGARCH)
Parameter c is called the leverage parameter. A positive value of c implies that negative returns have a greater effect on future volatility than positive returns, which is also called the leverage effect. Note that Equation (5) also models the correlation between returns and variance.
It has been shown in [21] that the following theorem holds.
Theorem 1.
The LRNVR implies that under measure the log-return dynamics are
where are i.i.d. standard normal random variables with respect to measure .
This property will allow us to eschew the computational complexity of certain continuous SV models by estimating only the parameters of the approximating discrete model.
Theorem 2.
Under the locally risk-neutral measure , the discrete NGARCH process (6) is an approximation of the SV diffusion model
where , , and , are Brownian motions.
Proof.
Observe the interval and let denote the equidistant subdivision of the interval by . Then, Equation (6) can be approximated by [9,22]
where now . Note again that with , this is exactly the model in Equation (6), and are i.i.d. standard normal r.v.’s under the locally risk-neutral measure.
From Theorem 3 in [22], we have that the approximating NGARCH model (8) converges weakly to the unique strong solution of the following diffusion model
where and are independent Brownian motions under .
From Equation (3), it now follows that in the discrete NGARCH SV model adjusted for risk, the market price of volatility risk is given by
Remark 1.
Proof of Theorem 2 holds for i.i.d. with zero mean and unit variance (not necessarily normal). One might relax condition (i) from Definition 1 to require only that have the same distribution (not necessarily lognormal) under both measures, which would allow us to posit the same results for a more general set of residuals. With this in mind, in this work, we will consider time series with possibly non-normal sample residuals, if all other assumptions hold.
4. Model Estimation and Numerical Results
If we denote the residuals by , model (5) can be rewritten as
We will use the traditional maximum likelihood approach to estimate the vector of unknown parameters . The log-likelihood function for a set of n observations from the NGARCH model is
The vector of parameters that maximizes Equation (11) (conditioning on the first observation) needs to satisfy the following stationarity constraints from the NGARCH model:
where the last constraint is in fact the persistence of the model.
The NGARCH discrete stochastic volatility model will be fitted to daily log-returns of the Standard and Poor’s 500 (SPX) stock market index and the Bitcoin (BTC) digital currency. The SPX stock market index is from the New York Stock Exchange (NYSE), Nasdaq, Chicago Board Options Exchange (CBOE) and BZX Exchange whereas BTC is a decentralized digital currency on the peer-to-peer network without the need for intermediaries. The data span over roughly nine years starting in 18 July 2010 to 31 May 2018 for both assets. There were 1982 observations of daily closing prices for SPX data and 2875 observations for BTC data, given that bitcoin is traded on weekends as well. Their log-returns time series are shown in Figure 1 (left) and Figure 2 (left). This gives us a first visual impression about the data used and their characteristics in the period of interest, and the fluctuations and movements in volatility suggest that a heteroscedastic model is appropriate. Sample measures of skewness and kurtosis of the log-returns are −0.5419 and 8.0294, respectively, for SPX and 2.6482 and 76.9094 for BTC, implying that in the BTC case, for example, positive returns in the observed period are more frequent than negative returns in comparison to the SPX case.
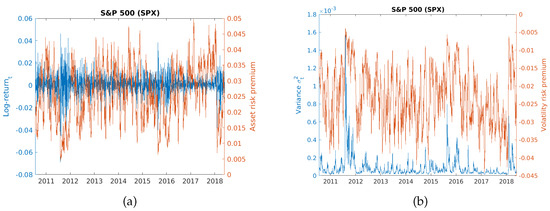
Figure 1.
(a): S&P 500 returns and the asset risk premium. (b): S&P 500 variance and the volatility risk premium.
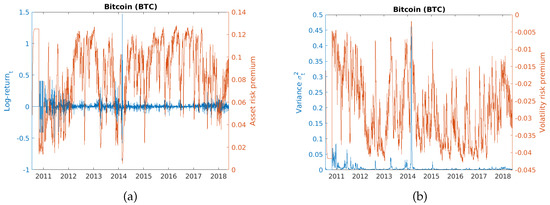
Figure 2.
(a): Bitcoin returns and the asset risk premium. (b): Bitcoin variance and the volatility risk premium.
We chose to analyze the US stock market index in order to represent a passive index investing strategy. On the other hand, bitcoin—a type of digital asset—is the world’s first decentralized cryptocurrency and, as argued in [23], considered to be a speculative investment for investors with very high risk tolerance. There is currently a debate on whether they are correlated, since both Bitcoin and the S&P 500 index have rocketed up at the same time. However, we assume the common financial narrative at the moment that bitcoin can not be seen as a short-term hedge against collapses in the equity markets. Therefore, we have selected them as representatives of two very distinctive investment strategies.
Nonlinear maximization of Equation (11) with nonlinear constraints was performed in Matlab [24] by customized functions using the fmincon function (Matlab code can be provided by the authors upon reasonable request). The iterative algorithm was tested for robustness from various initial values, and ultimately the initial values were adapted from [16,25] for SPX and BTC, respectively. The one-period risk-free interest rate r was calculated according to [25], using the US Treasury Bill Rate for 13 weeks bank discount on 31 May 2018, which was 1.89% for a 360-day year. Therefore, . Standard errors used for the (one-sided) test of parameter significance were calculated from an approximation of the Fisher information matrix (see Appendix A).
4.1. Parameter Estimates and Interpretation
Table 1 presents the estimated parameter values for the SPX stock market index and the BTC digital currency. All parameters are statistically significant at 1% level, except for for SPX, which is significant at the 10% level. In the SPX case, the parameters imply that daily log-returns have (unconditional) mean 0.014% (3.4% annually) and variance (0.0483 annually). The leverage parameter c is positive and statistically significant. In the BTC case, the parameters imply that daily log-returns have (unconditional) mean 0.077% (27.88% annually) and variance 0.0063 (2.2577 annually). The leverage parameter c is positive and statistically significant, but almost six times smaller in magnitude than in the SPX case. Using the estimated parameters, the time-varying market price of asset risk (4) and the market price of volatility risk (10) have been estimated, along with the volatility processes. These time series for the SPX stock index and the BTC currency are shown in Figure 1 and Figure 2, respectively.

Table 1.
Estimated parameters of the NGARCH SV model.
Descriptive statistics (min, max, median, mean, standard deviation, skewness, kurtosis) of the estimated volatility risk premium time series are given in Table 2. A negative volatility risk premium reflects investors’ preference to pay a risk premium to hedge the volatility risk. Consequently, a lower (more negative) value of the premium or, equivalently, a bigger value in absolute terms indicates investors’ willingness to pay even a higher price to provide insurance against unexpected and sharp price changes. Moreover, estimated values of the volatility risk premium enable us to quantify the degree of market’s “crash-o-phobia” in the observed period.

Table 2.
Descriptive statistics of the volatility risk premium time series for SPX and BTC data.
From the right part of Figure 1 and Figure 2, we clearly notice that when volatility spikes in stress episodes, the volatility risk premium usually follows, regardless of the magnitude of the volatility spike. Namely, if we consider the volatility risk premium as a proxy for investors’ attitude towards risk, we may argue that investors are less willing to hold positions in risky assets or to provide insurance against sharp asset price changes. More interestingly, estimates of the volatility risk premium in the SPX case, for example, have dropped quite substantially since mid-2012 and since the beginning of 2018. In the BTC case, estimates of the volatility risk premium have dropped substantially a few times in the observed period, and even more dramatically at the beginning of 2015 and 2018. Lastly, note from Figure 1 and Figure 2 and Table 2 that, although BTC returns have significantly larger variance than SPX returns, their market prices of volatility risk are still of similar magnitude, due to the leverage effect.
In order to summarize the effect of news on volatility implied by the discrete stochastic volatility NGARCH model, the news impact curves defined by [8] are shown in Figure 3 for both series. The news impact curve plots variance against preceding residuals, which are interpreted as the unexpected (log-)return i.e., shock or “news”. The curves in Figure 3 clearly illustrate the level of asymmetry and highlight differences in volatility levels caused by positive and negative returns shocks of the same size. As specified in [8], differences between the news impact curves of the models have important implications not only for portfolio selection and asset pricing, but also for option pricing. For example, the vertex of the BTC news impact curve () is further to the right than the vertex of the SPX news impact curve (). This implies that after a major unexpected price drop or negative shock, the predictable market volatility for the BTC currency is of higher magnitude, and this in turn may imply a higher risk premium for unhedgeable risk. Moreover, investors’ willingness to pay more in order to hedge risk related to abrupt changes in volatility may be reflected in higher option prices for this specific underlying instrument. Since asset volatility is a major factor in option pricing valuation, a significant difference in predicted volatilities after the arrival of some major news would theoretically lead to a significant difference in current option prices of the corresponding assets. Consequently, different volatilities that follow from major bad news (unexpected shocks of negative value) should produce different hedging strategies dependent on the choice of asset. In the context of risk management and portfolio selection, for example, differences of the two news impact curves reflected in two different vertices will imply very different market risk premiums and, hence, different risk premiums for individual assets under a conditional version of the capital asset-pricing model. As presented in [8], the quality of the model can be inspected additionally by testing whether the news impact curve of a model offers a good fit to the data. However, in this work, the model fit focuses on the analysis of the (standardized) residuals, and opening an alternative direction of model fit is beyond the scope of the present work.
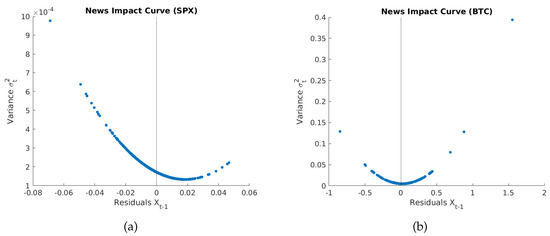
Figure 3.
News impact curve for (a) SPX and (b) BTC data.
4.2. Model Fit
From the estimated parameters , the residuals and volatility can be found as
with . Standardized residuals are calculated as .
Figure 4 indicates that the log-returns are heavy-tailed, which is consistent with the assumption of conditional normality. The estimated mean, standard deviation, skewness and kurtosis of the standardized residuals for both assets are summarized in Table 3. The Shapiro–Wilk test of normality was performed on standardized residuals of both the time series, and the null hypothesis was rejected in both instances (p-value close to zero). In other words, standardized residuals might behave like an i.i.d. sample with zero mean and unit variance but their distribution has heavier tails than the standard normal.
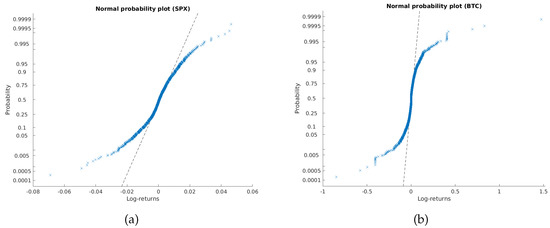
Figure 4.
Normal probability plot of the log-returns for (a) SPX and (b) BTC data.

Table 3.
Mean, standard dev., skewness and kurtosis of the SPX and BTC standardized residuals.
Figure 5 shows the sample autocorrelation functions of the squared log-returns and squared residuals, indicating no significant correlations for both the SPX and BTC standardized residuals. To further investigate the model fit, we performed a Ljung–Box test for squared standardized residuals for both datasets. The test statistic used 20 lags of the corresponding empirical autocorrelation function and the null hypothesis of no autocorrelation was not rejected, with a p-value of close to 1 in both cases.
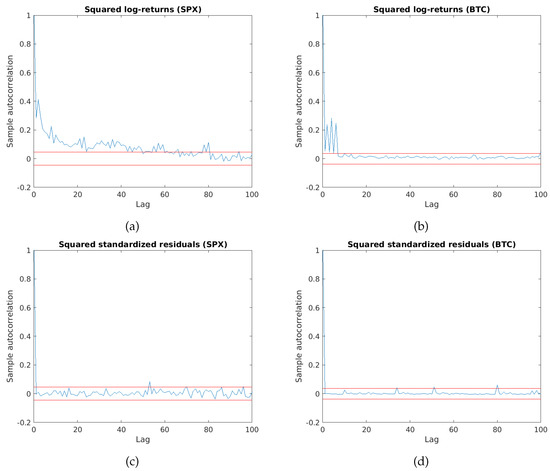
Figure 5.
Autocorrelation function for the squared returns for (a) SPX and (b) BTC data and squared standard residuals for (c) SPX and (d) BTC data.
These results are congruent with our model except for the assumption of normality which, as was stated in Remark 1, can be relaxed. Given that previous work [8,16] suggests that the NGARCH model is suitable and, in fact, recommended in most cases over other models from the GARCH family, we consider this a satisfactory model fit.
5. Conclusions
In this paper, we introduce a new variant of the discrete stochastic volatility NGARCH model, where both the asset risk premium and the variance risk premium are allowed to be time-varying. By modeling two state variables, the stock price and its volatility, we are able to estimate the market price of volatility risk. Following the option-pricing framework of [9], we consider the local risk-neutral valuation relationship, which shows that the volatility risk premium affects the conditional variance process globally, although the risk has been locally neutralized. This relationship also allows the use of historical data to estimate the volatility risk premium.
We consider a stochastic volatility model framework with a leverage effect, which is the limiting diffusion process of the NGARCH process under the local risk-neutral measure. In this framework, the volatility risk premium is determined by the volatility process, the leverage parameter and excess mean return.
The discrete stochastic volatility NGARCH model is fitted to daily Standard and Poor’s 500 (SPX) index returns and Bitcoin (BTC) digital currency from 2010 to 2018. For both time series, we find that negative shocks introduce more volatility than positive shocks of the same magnitude, with this effect being more pronounced for the BTC asset, which generates a negative market price of volatility risk. Additionally, the news impact curve is presented to show how news and shocks affect volatility estimates. According to the residual analysis and the distribution of returns, the model fit is in many aspects quite satisfactory, except for heavier tails than the normal distribution would predict. The analysis was performed for daily data, but the approach would apply to any sampling frequency since it is based on the continuous time diffusion stochastic volatility model. In particular, the approach could be applied directly to high frequency data.
Estimating the market price of volatility risk is important in understanding the preferences of market participants and allows for better modeling of investors’ behavior. This will then allow us to manage risk more easily and facilitate the evaluation and hedging of options, but also financial derivatives in general. By incorporating the market price of volatility risk into the option pricing model, options markets may also become volatility trading markets. Our findings enable future analysis of intensified speculative activity on volatility, since net short positions on VIX futures held by non-commercial traders have been empirically documented to change over time and to be driven by market’s stress episodes of different intensities. The model proposed in this paper emphasizes that the volatility does not change under the risk-neutral measure. Consequently, the estimated volatility from asset prices and the physical measure are the ones that could be used in the option pricing formula for those interested in using option prices and implied volatility measures. Future research might also expand on the approach presented here to include alternative parameter estimation (e.g., the quasi-maximum likelihood method) and additional diagnostic tests to assess whether the asymmetry in data is adequately modeled.
Author Contributions
Conceptualization, P.P.Š. and A.T.; methodology, P.P.Š. and A.T.; software, A.T.; validation, P.P.Š. and A.T.; formal analysis, P.P.Š. and A.T.; investigation, P.P.Š. and A.T.; resources, P.P.Š. and A.T.; data curation, P.P.Š. and A.T.; writing—original draft preparation, P.P.Š. and A.T.; writing—review and editing, P.P.Š. and A.T.; visualization, P.P.Š. and A.T.; supervision, P.P.Š.; project administration, P.P.Š. Both authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: https://www.investing.com/indices/us-spx-500-historical-data, https://www.investing.com/crypto/bitcoin/historical-data (accessed on 15 June 2021).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The variance of the maximum likelihood estimation is approximately equal to the inverse of the Information matrix I [26]
where I is the negative expected value of the Hessian matrix of the likelihood function. For estimated parameters , we have
where denotes the set of n observations. The standard errors of individual estimations are the diagonal elements of
Due to the computational complexity of the log-likelihood function, the expression on the right of Equation (A1) can be approximated by a simplified expression [26]
Recalling that
the partial derivatives are
for , where
and
References
- Black, F.; Scholes, M. The Pricing of Options and Corporate Liabilities. J. Political Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef] [Green Version]
- Merton, R.C. Theory of Rational Option Pricing. Bell J. Econ. Manag. Sci. 1973, 4, 141–183. [Google Scholar] [CrossRef] [Green Version]
- Barndorff-Nielsen, O.E.; Shephard, N. Non-Gaussian Ornstein-Uhlenbeck-Based Models and Some of Their Uses in Financial Economics. J. R. Stat. Soc. Ser. (Stat. Methodol.) 2001, 63, 167–241. [Google Scholar] [CrossRef]
- Hubalek, F.; Posedel, P. Joint analysis and estimation of stock prices and trading volume in Barndorff-Nielsen and Shephard stochastic volatility models. Quant. Financ. 2011, 11, 917–932. [Google Scholar] [CrossRef] [Green Version]
- Pindyck, R. Risk, Inflation, and the Stock Market. Am. Econ. Rev. 1984, 74, 335–351. [Google Scholar]
- Brunnermeier, M.K.; Sannikov, Y. A Macroeconomic Model with a Financial Sector. Am. Econ. Rev. 2014, 104, 379–421. [Google Scholar] [CrossRef] [Green Version]
- Miyajima, K.; Shim, I. Asset managers in emerging market economies. BIS Q. Rev. 2014, 19–34. Available online: https://www.bis.org/publ/qtrpdf/r_qt1409e.htm (accessed on 1 June 2021).
- Engle, R.F.; NG, V.K. Measuring and Testing the Impact of News on Volatility. J. Financ. 1993, 48, 1749–1778. [Google Scholar] [CrossRef]
- Duan, J.C. The GARCH option pricing model. Math. Financ. 1995, 5, 13–32. [Google Scholar] [CrossRef]
- Bollerslev, T.; Gibson, M.; Zhou, H. Dynamic estimation of volatility risk premia and investor risk aversion from option-implied and realized volatilities. J. Econom. 2011, 160, 235–245. [Google Scholar] [CrossRef] [Green Version]
- Corradi, V.; Distaso, W.; Mele, A. Macroeconomic determinants of stock volatility and volatility premiums. J. Monet. Econ. 2013, 60, 203–220. [Google Scholar] [CrossRef]
- Negrea, B. The Volatility Premium Risk: Valuation and Forecasting. J. Appl. Quant. Methods 2009, 4, 154–165. [Google Scholar]
- Christoffersen, P.; Heston, S.; Jacobs, K. Capturing option anomalies with a variance-dependent pricing kernel. Rev. Financ. Stud. 2013, 26, 1963–2006. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, J.E. GARCH Option Pricing Models and the Variance Risk Premium. J. Risk Financ. Manag. 2020, 13, 51. [Google Scholar] [CrossRef] [Green Version]
- Duan, J.C. Cracking the smile. Risk 1996, 9, 55–59. [Google Scholar]
- Christoffersen, P.; Jacobs, K. Which GARCH Model for Option Valuation? Manag. Sci. 2004, 50, 1204–1221. [Google Scholar] [CrossRef] [Green Version]
- Fouque, J.P.; Papanicolaou, G.; Sircar, K.R. Derivatives in Financial Markets with Stochastic Volatility; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Hobson, D.G. Stochastic Volatility; School of Mathematical Sciences, University of Bath: Bath, UK, 1996. [Google Scholar]
- Javaheri, A. Inside Volatility Arbitrage: The Secrets of Skewness; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 317. [Google Scholar]
- Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef] [Green Version]
- Posedel, P. Analysis of the exchange rate and pricing foreign currency options on the croatian market: The ngarch model as an alternative to the black-scholes model. Financ. Theory Pract. 2006, 30, 347–368. [Google Scholar]
- Duan, J.C. Augmented GARCH (p, q) process and its diffusion limit. J. Econom. 1997, 79, 97–127. [Google Scholar] [CrossRef]
- Peetz, D.; Mall, G. Why Bitcoin is Not a Currency But a Speculative Real Asset. 2017. Available online: https://ssrn.com/abstract=3098765 (accessed on 1 June 2021). [CrossRef]
- MATLAB; Version 2021a; The MathWorks Inc.: Natick, MA, USA, 2021.
- Siu, T.K.; Elliott, R.J. Bitcoin option pricing with a SETAR-GARCH model. Eur. J. Financ. 2020, 27, 564–595. [Google Scholar] [CrossRef]
- Greene, W.H. Econometric Analysis, 4th ed.; International, Ed.; Prentice Hall: Hoboken, NJ, USA, 2000; pp. 201–215. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).