Analysis of Elastic–Plastic Problems Using the Improved Interpolating Complex Variable Element Free Galerkin Method
Abstract
:1. Introduction
2. Implementation of the Elastic–Plastic Problem Based on the IICVEFG Method
2.1. Brief Descriptions of the Two-Dimensional Elastic–Plastic Problem
2.2. The IICVEFG Method for the Elastic–Plastic Problem
2.3. Incremental Tangent Stiffness Matrix Method
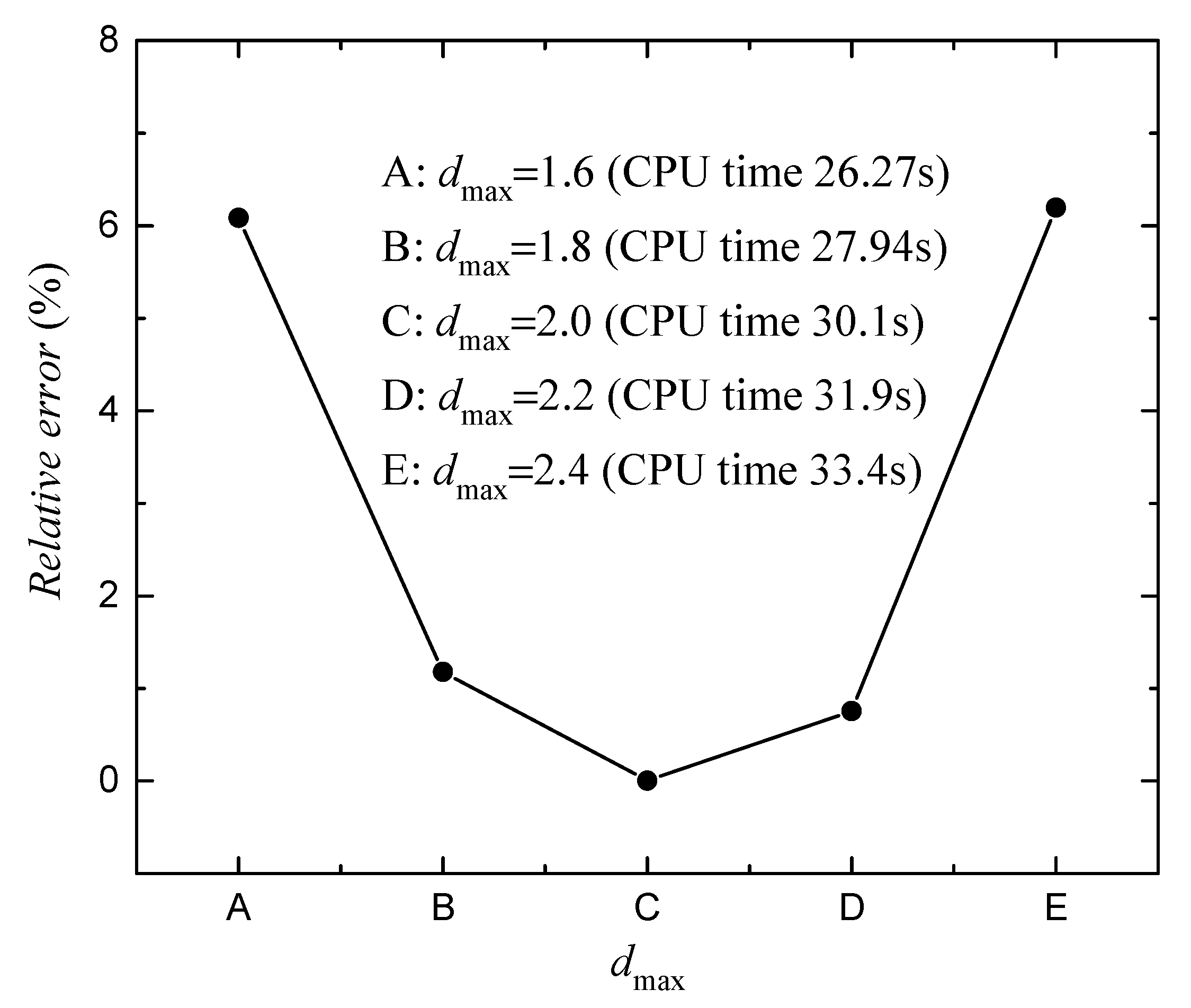
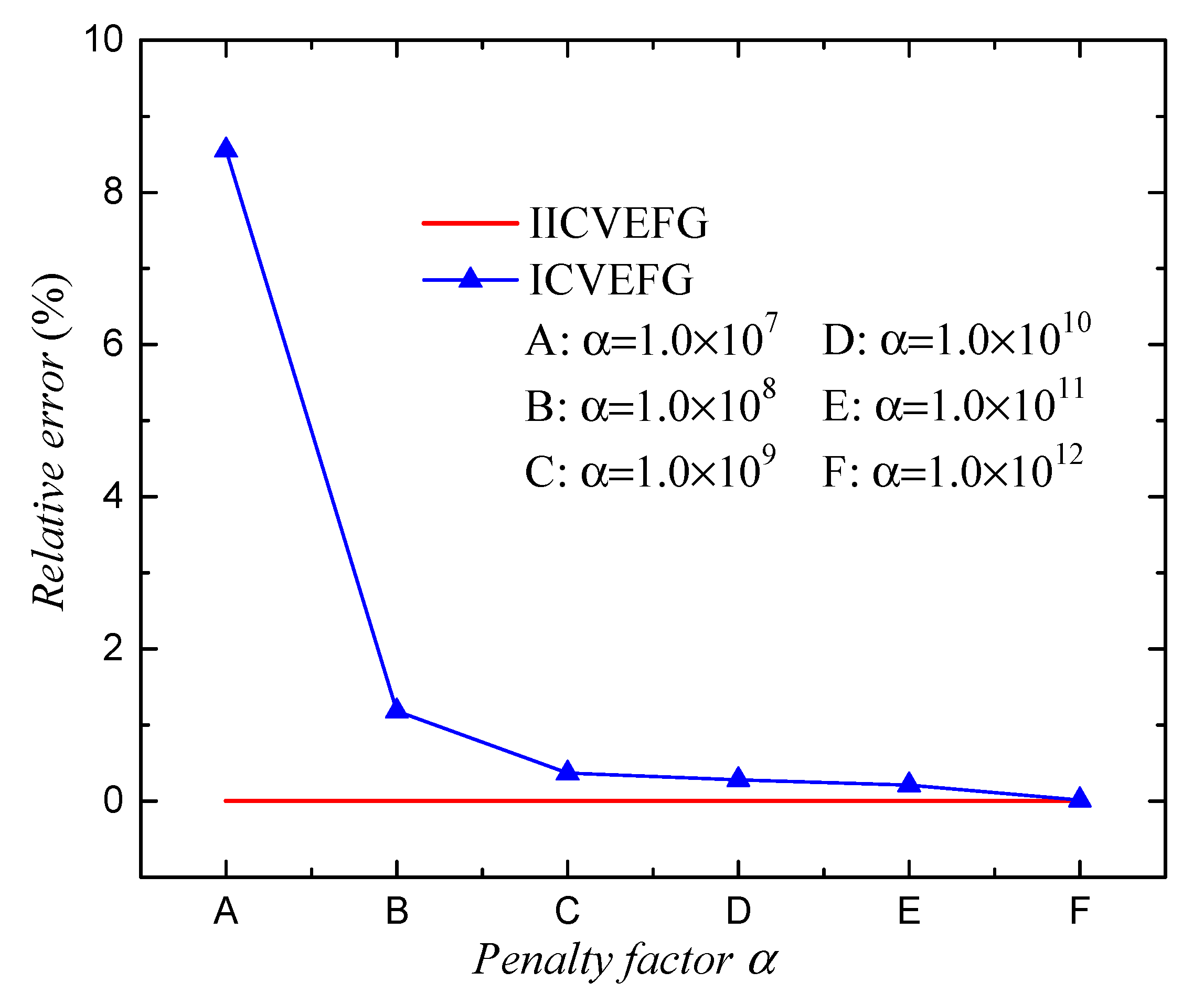
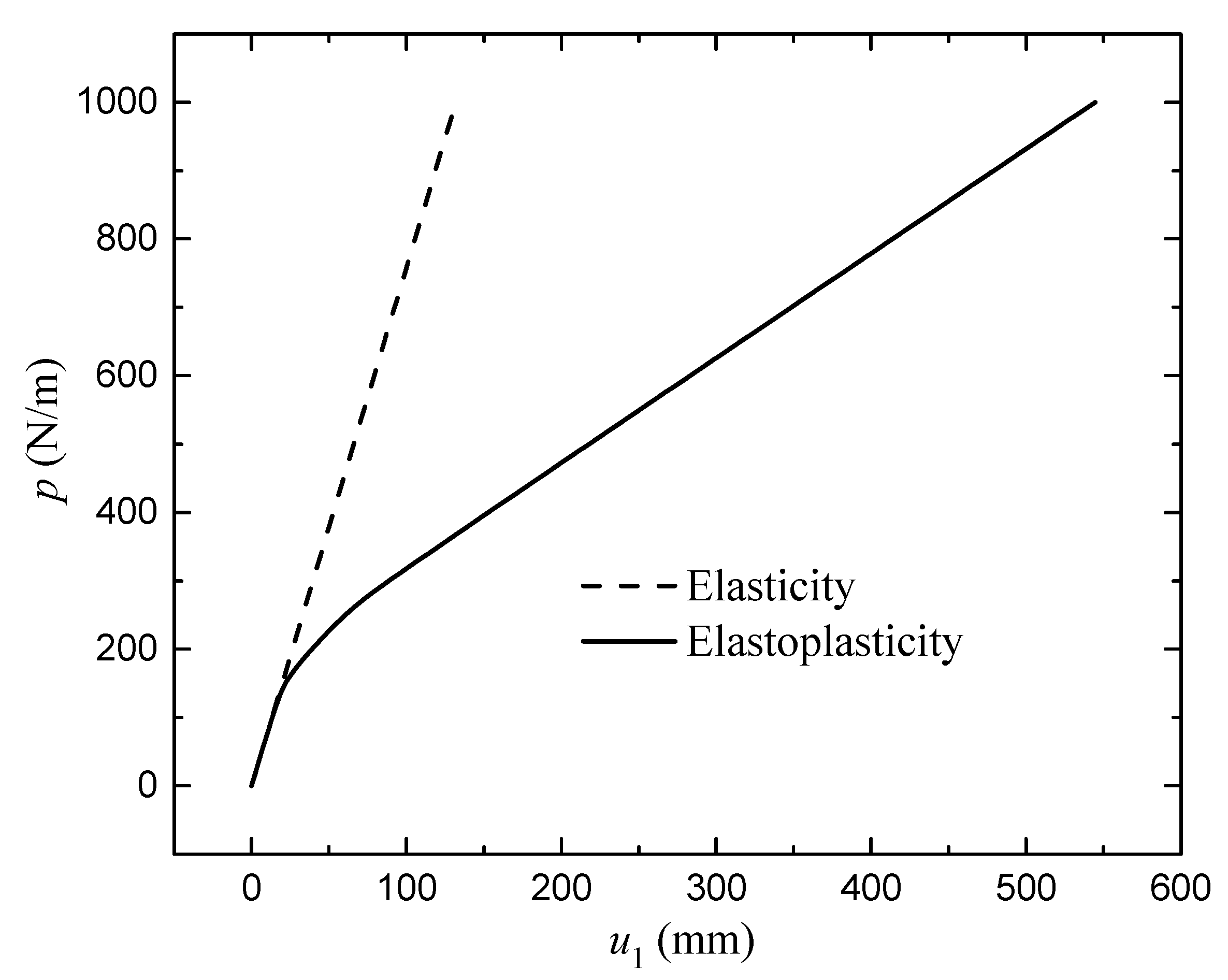
3. Numerical Examples
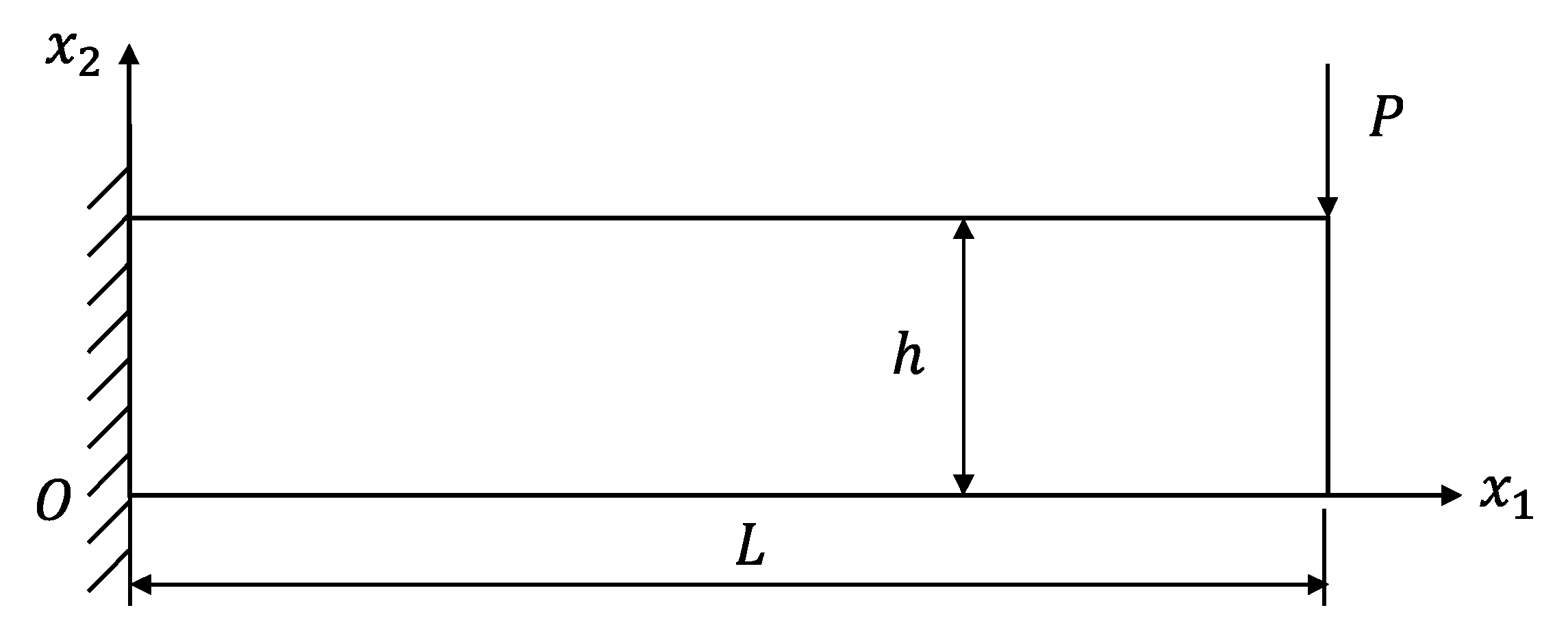
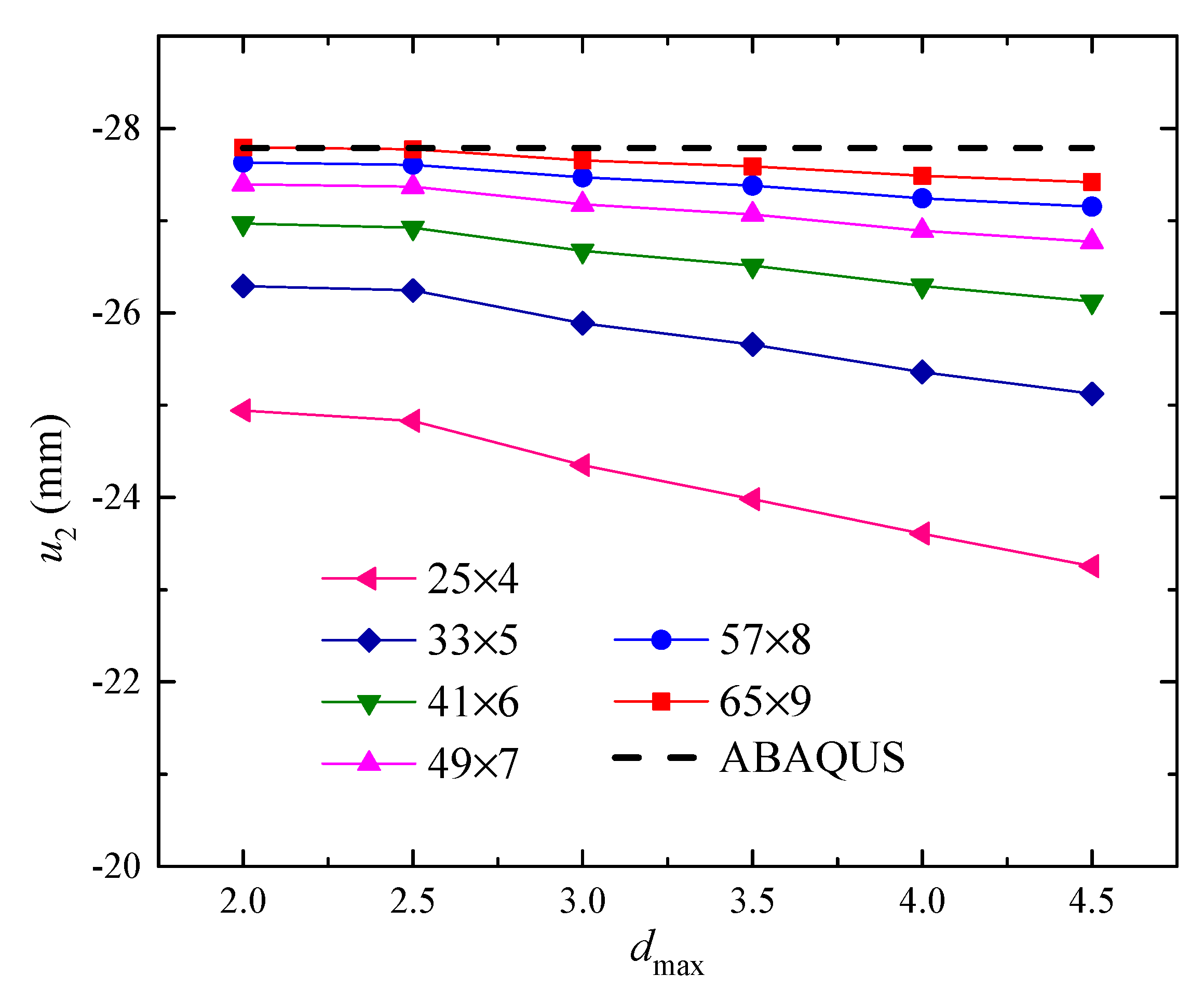
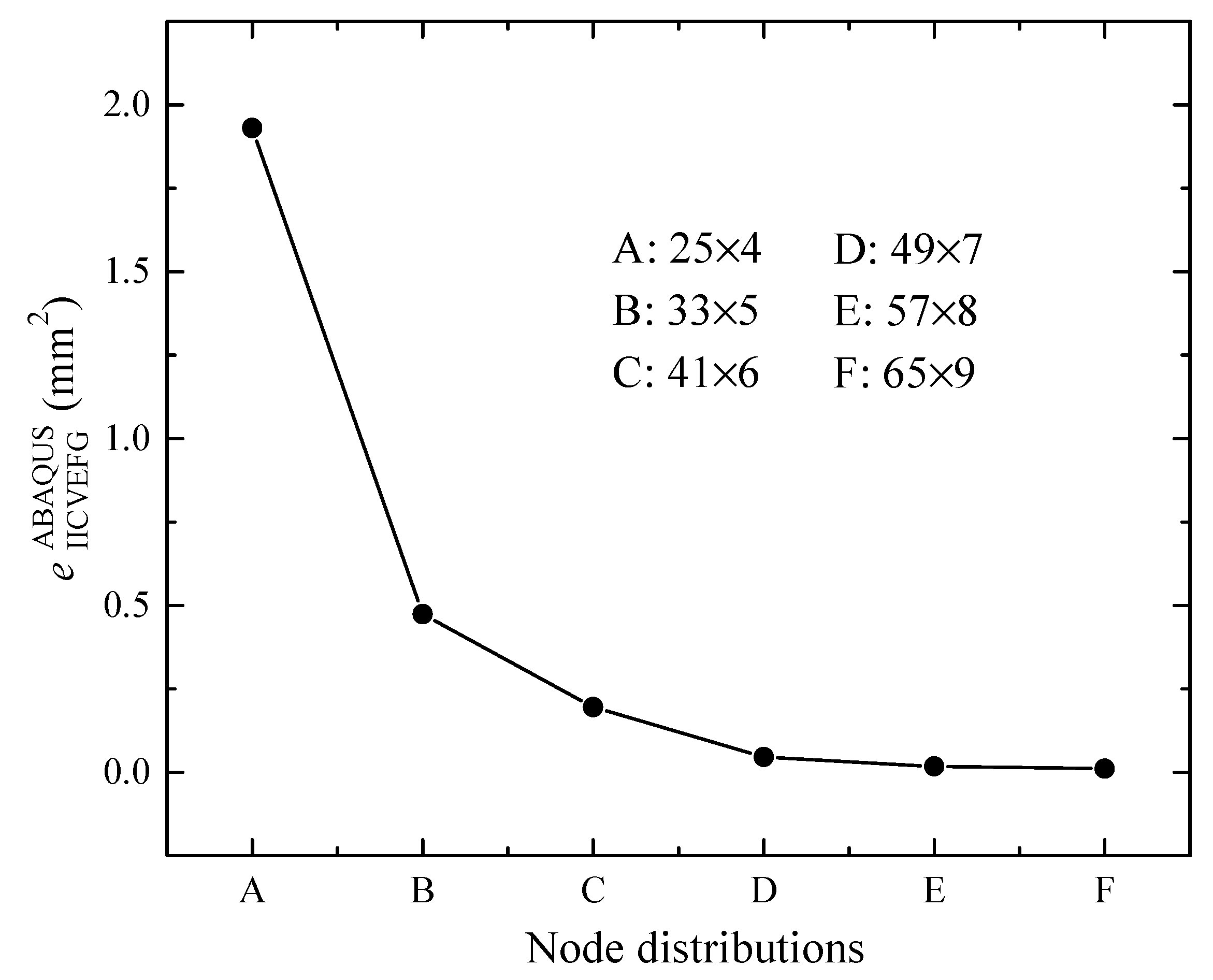
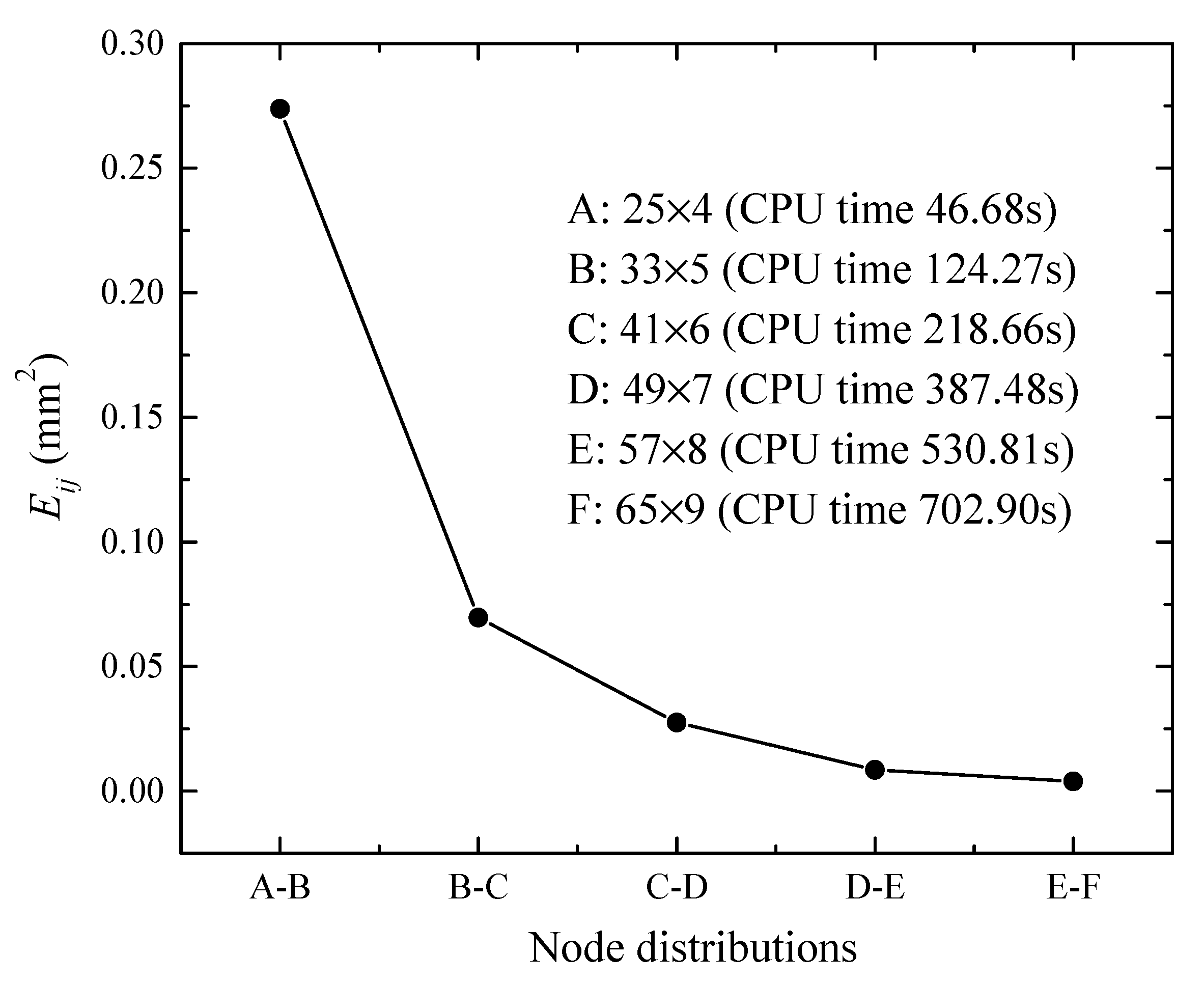
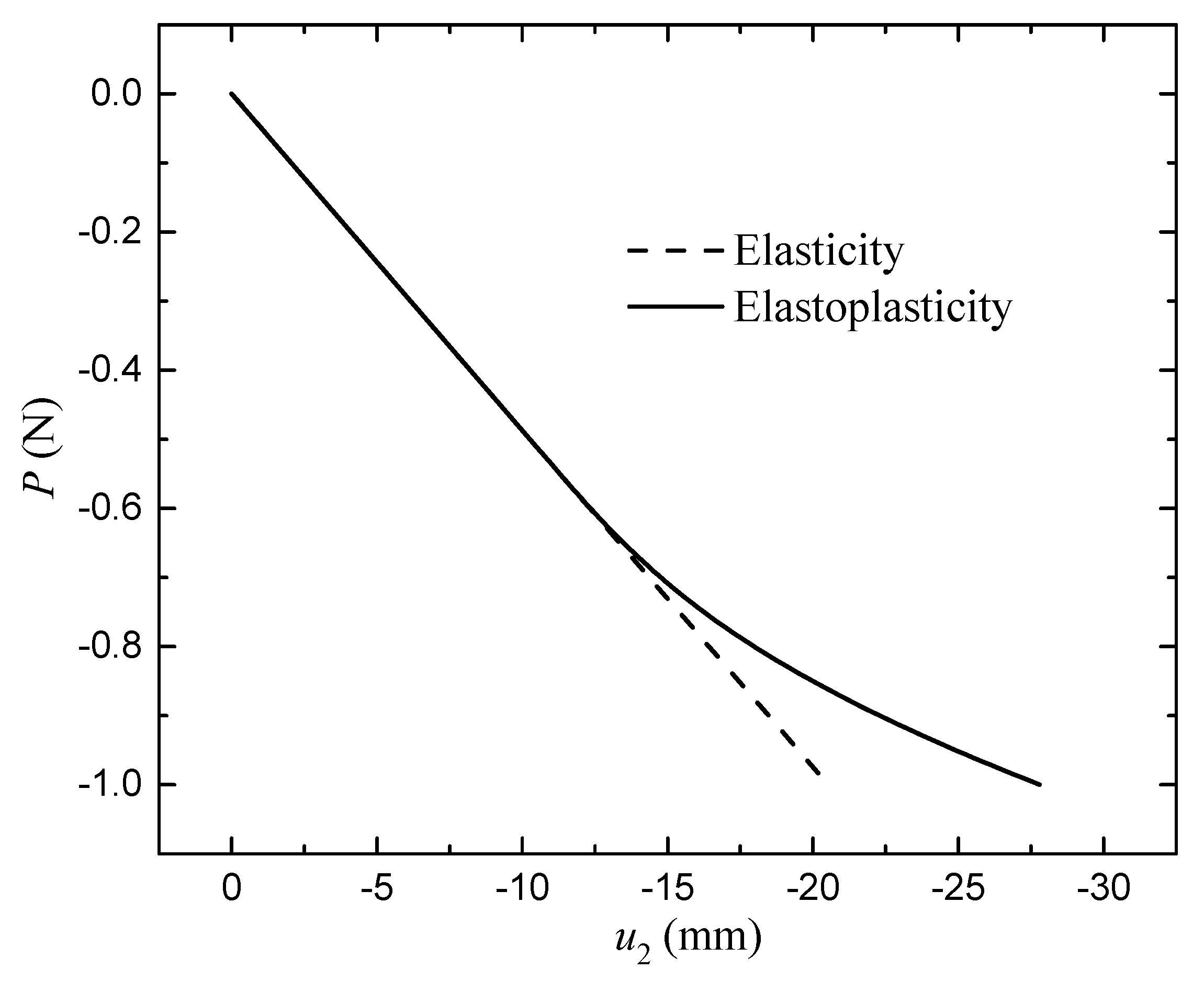
3.1. A cantilever Beam Constrained with a Concentrated Force
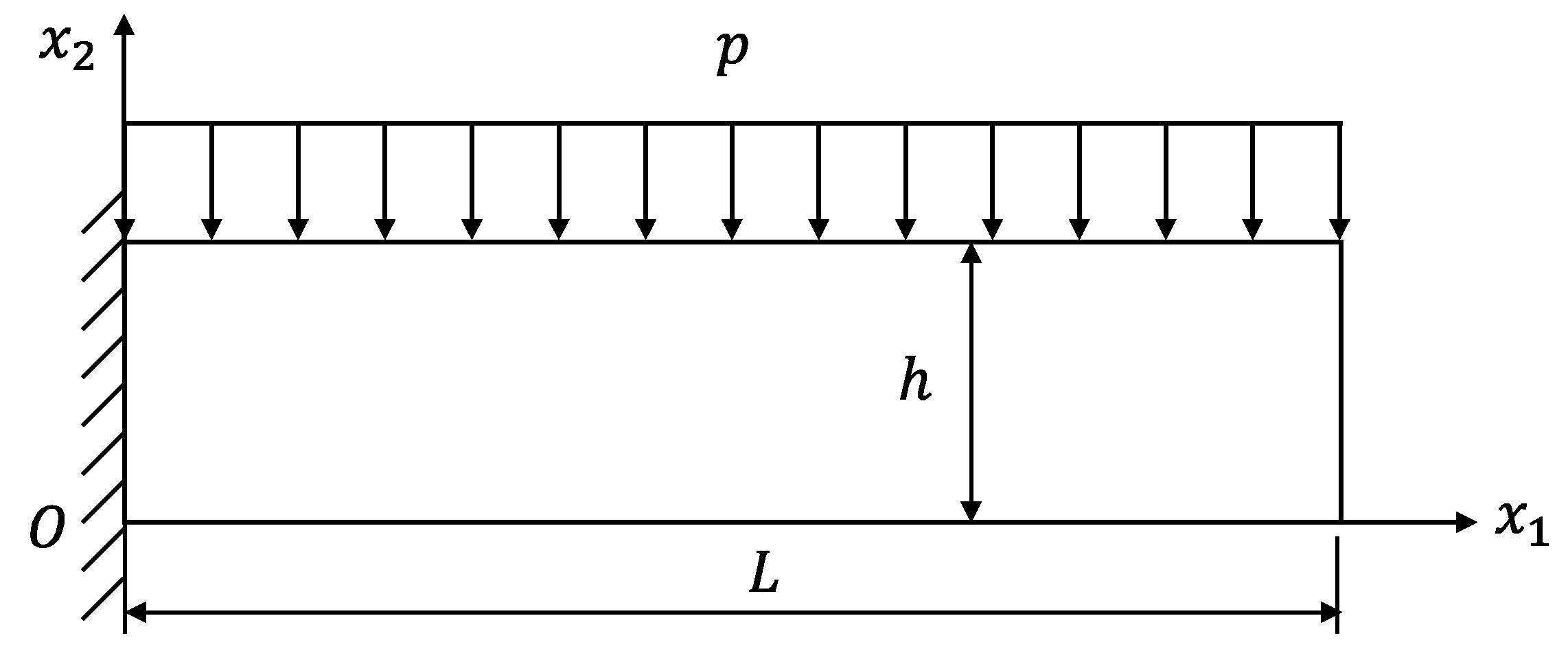
3.2. A Cantilever Beam Constrained with a Distributed Load
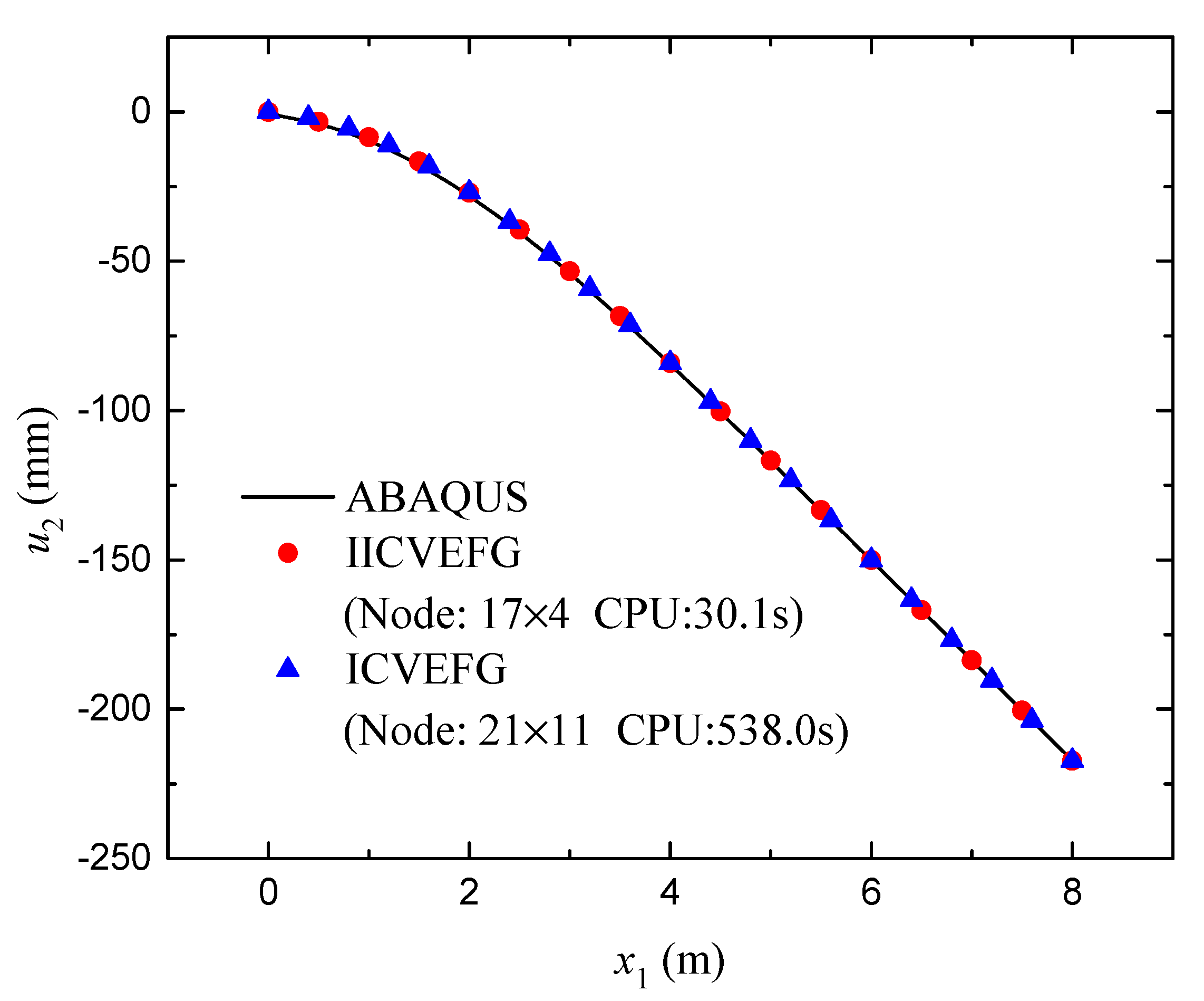
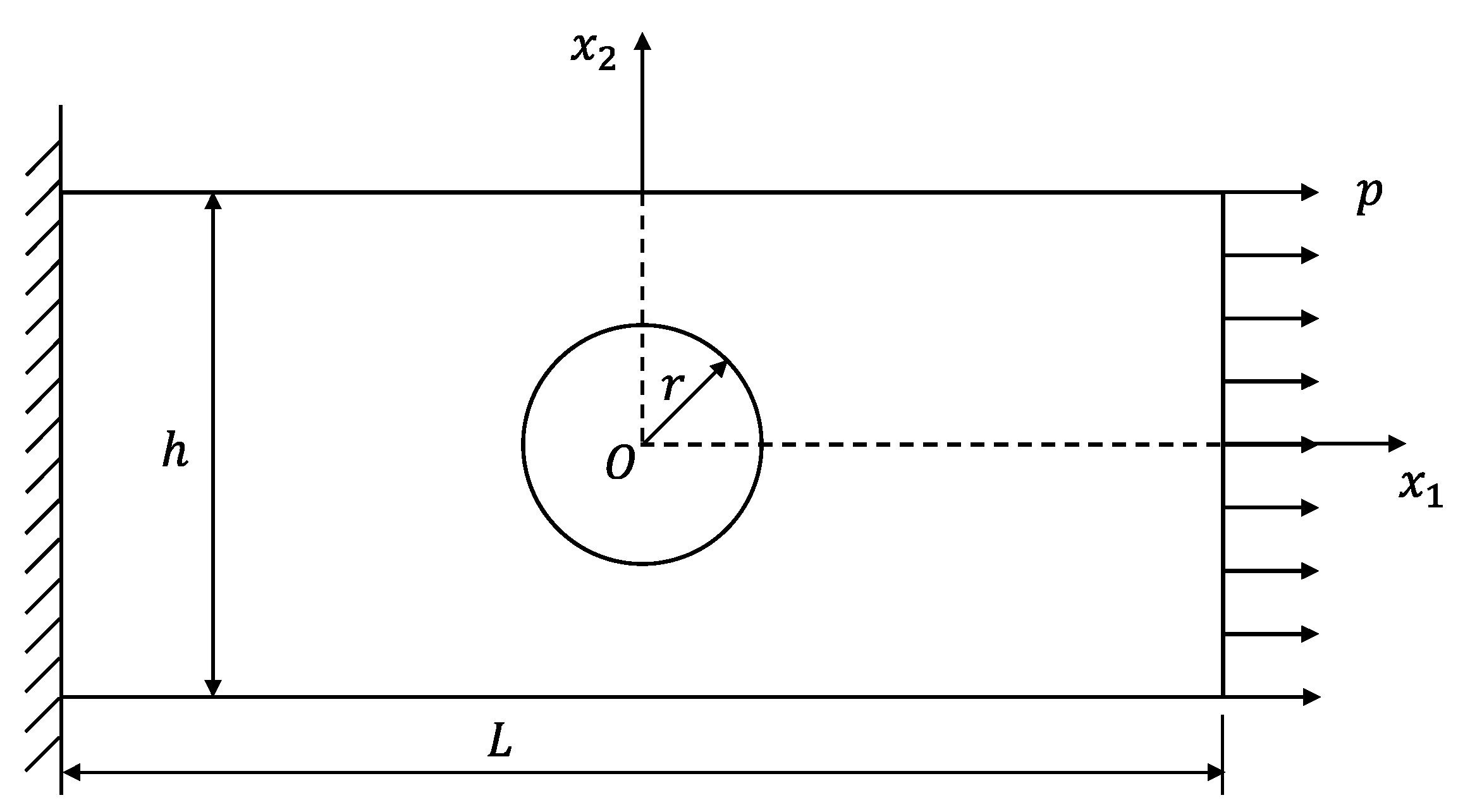
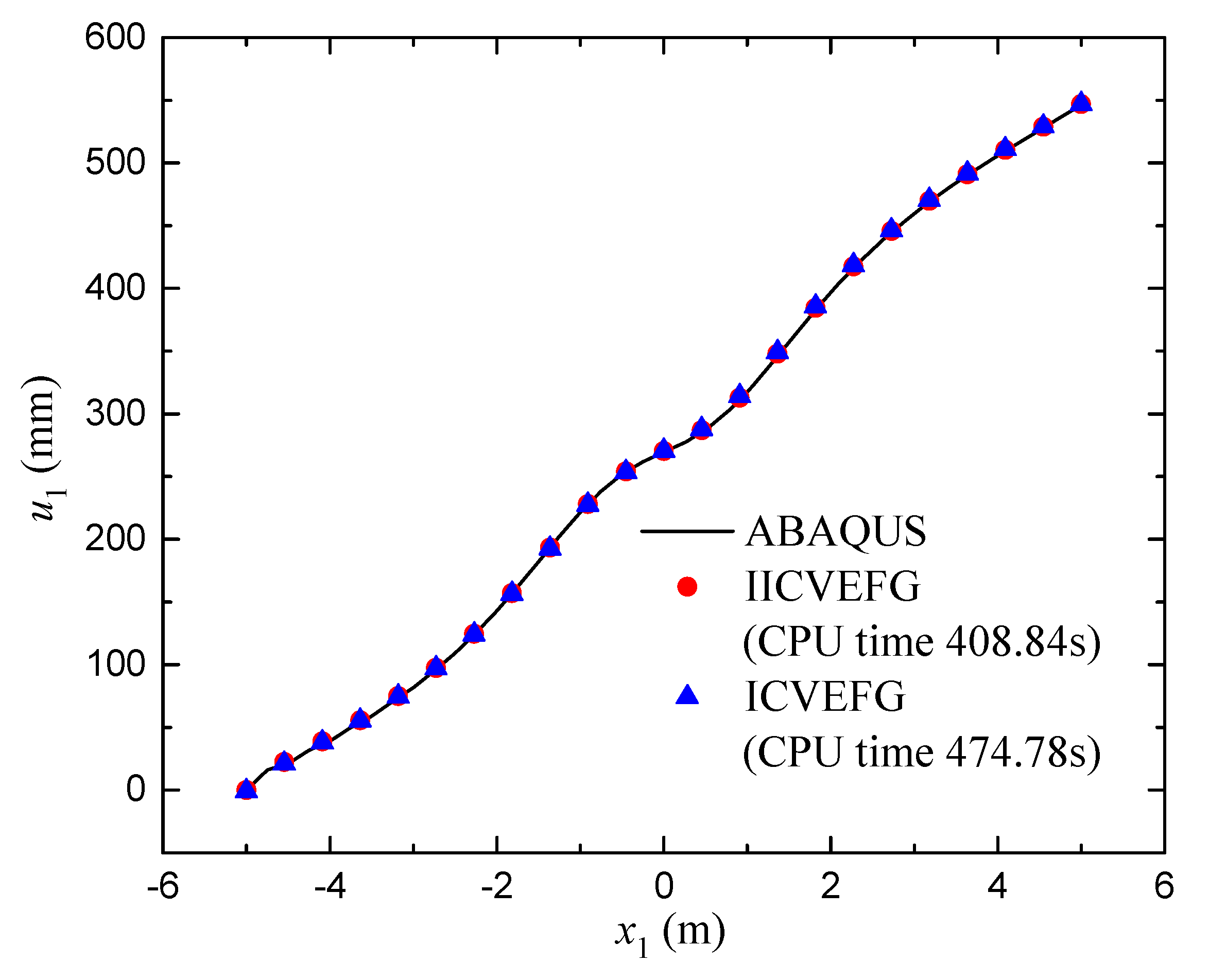
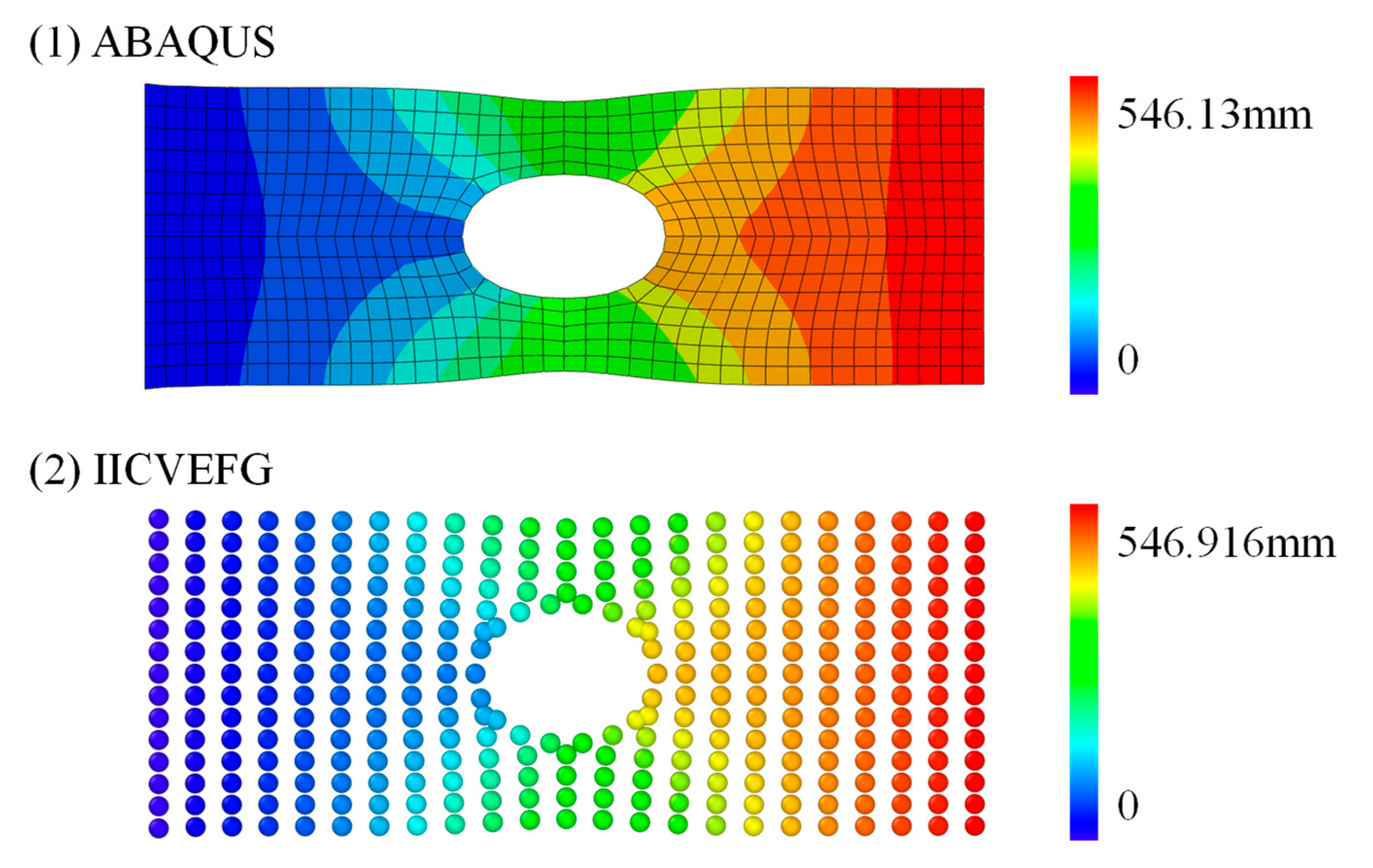
3.3. A Rectangular Plate with a Central Hole under a Distributed Traction
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mcmeeking, R.M.; Rice, J.R. Finite-element formulations for problems of large elastic-plastic deformation. Int. J. Solids Struct. 1975, 11, 601–616. [Google Scholar] [CrossRef] [Green Version]
- Barry, W.; Saigal, S. A three-dimensional element-free Galerkin elastic and elastoplastic formulation. Int. J. Numer. Meth. Eng. 1999, 46, 671–693. [Google Scholar] [CrossRef]
- Schreyer, H.L.; Kulak, R.F.; Kramer, J.M. Accurate Numerical Solutions for Elastic-Plastic Models. J. Press. Vess-T 1979, 101, 226–234. [Google Scholar] [CrossRef]
- Rong, B.; Rui, X.T.; Tao, T.; Wang, G.P. Theoretical modeling and numerical solution methods for flexible multibody system dynamics. Nonlinear Dyn. 2019, 98, 1519–1553. [Google Scholar] [CrossRef]
- Ostiguy, G.L.; Sassi, S. Effects of initial geometric imperfections on dynamic behavior of rectangular plates. Nonlinear Dyn. 1992, 3, 165–181. [Google Scholar] [CrossRef]
- Mahdiabadi, M.K.; Tiso, P.; Brandt, A.; Rixen, D.J. A non-intrusive model-order reduction of geometrically nonlinear structural dynamics using modal derivatives. Mech. Syst. Signal Process. 2021, 147, 107126. [Google Scholar] [CrossRef]
- Vaiana, N.; Losanno, D.; Ravichandran, N. A novel family of multiple springs models suitable for biaxial rate-independent hysteretic behavior. Comput. Struct. 2021, 244, 106403. [Google Scholar] [CrossRef]
- Vaiana, N.; Sessa, S.; Rosati, L. A generalized class of uniaxial rate-independent models for simulating asymmetric mechanical hysteresis phenomena. Mech. Syst. Signal Process. 2021, 146, 106984. [Google Scholar] [CrossRef]
- Vaiana, N.; Sessa, S.; Paradiso, M.; Rosati, L. Accurate and efficient modeling of the hysteretic behavior of sliding bearings. In Proceedings of the 7th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering Methods in Structural Dynamics and Earthquake Engineering, Crete, Greece, 24–26 June 2019. [Google Scholar]
- Belytschko, T.; Lu, Y.Y.; Gu, L. Element-free Galerkin methods. Int. J. Numer. Meth. Eng. 1994, 37, 229–256. [Google Scholar] [CrossRef]
- Belytschko, T.; Krongauz, Y.; Organ, D.; Fleming, M.; Krysl, P. Meshless methods: An overview and recent development. Comput. Methods Appl. Mech. Eng. 1996, 139, 3–47. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.S.; Pan, C.; Wu, C.T.; Liu, W.K. Reproducing kernel particle methods for large deformation analysis of non-linear structures. Comput. Methods Appl. Mech. 1996, 139, 195–227. [Google Scholar] [CrossRef]
- Cheng, Y.M.; Bai, F.N.; Liu, C.; Peng, M.J. Analyzing nonlinear large deformation with an improved element-free Galerkin method via the interpolating moving least-squares method. Int. J. Comput. Mater. Sci. Eng. 2016, 5, 1650023. [Google Scholar] [CrossRef]
- Fleming, M.; Chu, Y.A.; Moran, B.; Belytschko, T. Enriched element-free Galerkin methods for crack tip fields. Int. J. Numer. Meth. Eng. 1997, 40, 1483–1504. [Google Scholar] [CrossRef]
- Memari, A.; Mohebalizadeh, H. Quasi-static analysis of mixed-mode crack propagation using the meshless local Petrov-Galerkin method. Eng. Anal. Bound. Elem. 2019, 106, 397–411. [Google Scholar] [CrossRef]
- Jiang, F.; Oliveira, M.S.A.; Sousa, A.C.M. Mesoscale SPH modeling of fluid flow in isotropic porous media. Comput. Phys. Commun. 2007, 176, 471–480. [Google Scholar] [CrossRef]
- Moradi, D.R.; Radhi, A.; Behdinan, K. Damped dynamic behavior of an advanced piezoelectric sandwich plate. Compos. Struct. 2020, 243, 112243. [Google Scholar] [CrossRef]
- Liu, M.B.; Liu, G.R. Smoothed particle hydrodynamics (SPH): An overview and recent developments. Arch. Comput. Methods Eng. 2010, 17, 25–76. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.K.; Chen, Y.; Jun, S.; Chen, J.S.; Belytschko, T.; Pan, C.; Uras, R.A.; Cheng, C.T. Overview and applications of the reproducing kernel particle methods. Arch. Comput. Methods Eng. 1996, 3, 3–80. [Google Scholar] [CrossRef]
- Peng, M.J.; Li, D.M.; Cheng, Y.M. The complex variable element-free Galerkin (CVEFG) method for elasto-plasticity problems. Eng. Struct. 2011, 33, 127–135. [Google Scholar] [CrossRef]
- Liew, K.M.; Feng, C.; Cheng, Y.M.; Kitipornchai, S. Complex variable moving least-squares method: A meshless approximation technique. Int. J. Numer. Meth. Eng. 2007, 70, 46–70. [Google Scholar] [CrossRef]
- Cheng, Y.M.; Li, J.H. Complex variable meshless method for fracture problems. Sci. China Ser. G 2006, 49, 46–59. [Google Scholar] [CrossRef]
- Bai, F.N.; Li, D.M.; Wang, J.F.; Cheng, Y.M. An improved complex variable element-free Galerkin method for two-dimensional elasticity problems. Chin. Phys. B 2012, 21, 020204. [Google Scholar] [CrossRef]
- Li, D.M.; Liew, K.M.; Cheng, Y.M. An improved complex variable element-free Galerkin method for two-dimensional large deformation elastoplasticity problems. Comput. Methods Appl. Mech. 2014, 269, 72–86. [Google Scholar] [CrossRef]
- Zhang, L.W.; Deng, Y.J.; Liew, K.M. An improved element-free Galerkin method for numerical modeling of the biological population problems. Eng. Anal. Bound. Elem. 2014, 40, 181–188. [Google Scholar] [CrossRef]
- Wang, J.F.; Sun, F.X.; Cheng, Y.M. An improved interpolating element-free Galerkin method with nonsingular weight function for two-dimensional potential problems. Chin. Phys. B 2012, 21, 090204. [Google Scholar] [CrossRef]
- Sun, F.X.; Wang, J.F.; Cheng, Y.M.; Huang, A.X. Error estimates for the interpolating moving least-squares method in n-dimensional space. Appl. Numer. Math. 2015, 98, 79–105. [Google Scholar] [CrossRef]
- Ren, H.P.; Cheng, Y.M. The interpolating element-free Galerkin (IEFG) method for two-dimensional elasticity problems. Int. J. Appl. Mech. 2011, 3, 735–758. [Google Scholar] [CrossRef]
- Deng, Y.J.; Liu, C.; Peng, M.J.; Cheng, Y.M. The interpolating complex variable element-free Galerkin method for temperature field problems. Int. J. Appl. Mech. 2015, 7, 1550017. [Google Scholar] [CrossRef]
- Deng, Y.J.; He, X.Q. An improved interpolating complex variable meshless method for bending problem of Kirchhoff plates. Int. J. Appl. Mech. 2017, 9, 1750089. [Google Scholar] [CrossRef]
- Ren, H.P.; Cheng, J.; Huang, A.X. The complex variable interpolating moving least-squares method. Appl. Math. Comput. 2012, 219, 1724–1736. [Google Scholar] [CrossRef]
- Deng, Y.J.; He, X.Q.; Dai, Y. The improved interpolating complex variable element free Galerkin method for two-dimensional potential problems. Int. J. Appl. Mech. 2019, 11, 1950104. [Google Scholar] [CrossRef]
- Deng, Y.J.; He, X.Q.; Sun, L.G.; Yi, S.H.; Dai, Y. An improved interpolating complex variable element free Galerkin method for the pattern transformation of hydrogel. Eng. Anal. Bound. Elem. 2020, 113, 99–109. [Google Scholar] [CrossRef]
- Yu, S.Y.; Peng, M.J.; Cheng, H.; Cheng, Y.M. The improved element-free Galerkin method for three-dimensional elastoplasticity problems. Eng. Anal. Bound. Elem. 2019, 104, 215–224. [Google Scholar] [CrossRef]
- Cheng, Y.M. Meshless Methods; Science Press: Beijing, China, 2015. [Google Scholar]
- Cheng, Y.M.; Bai, F.N.; Peng, M.J. A novel interpolating element-free Galerkin (IEFG) method for two-dimensional elastoplasticity. Appl. Math. Model. 2014, 38, 5187–5197. [Google Scholar] [CrossRef]
- Sun, F.X.; Wang, J.F.; Cheng, Y.M. An improved interpolating element-free Galerkin method for elastoplasticity via nonsingular weight functions. Int. J. Appl. Mech. 2016, 8, 1650096. [Google Scholar] [CrossRef]
- Cheng, Y.M.; Wang, J.F.; Bai, F.N. A new complex variable element-free Galerkin method for two-dimensional potential problems. Chin. Phys. B. 2012, 21, 090203. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, Y.; Shen, X.; Tao, J.; Dai, Y. Analysis of Elastic–Plastic Problems Using the Improved Interpolating Complex Variable Element Free Galerkin Method. Mathematics 2021, 9, 1967. https://doi.org/10.3390/math9161967
Deng Y, Shen X, Tao J, Dai Y. Analysis of Elastic–Plastic Problems Using the Improved Interpolating Complex Variable Element Free Galerkin Method. Mathematics. 2021; 9(16):1967. https://doi.org/10.3390/math9161967
Chicago/Turabian StyleDeng, Yajie, Xingkeng Shen, Jixiao Tao, and Ying Dai. 2021. "Analysis of Elastic–Plastic Problems Using the Improved Interpolating Complex Variable Element Free Galerkin Method" Mathematics 9, no. 16: 1967. https://doi.org/10.3390/math9161967
APA StyleDeng, Y., Shen, X., Tao, J., & Dai, Y. (2021). Analysis of Elastic–Plastic Problems Using the Improved Interpolating Complex Variable Element Free Galerkin Method. Mathematics, 9(16), 1967. https://doi.org/10.3390/math9161967





