Abstract
This paper describes a particular use of the hybrid FEM-DBCI, for the computation of low-frequency electromagnetic fields in open-boundary domains. Once the unbounded free space enclosing the system has been truncated, the FEM is applied to the bounded domain thus obtained, assuming an unknown Dirichlet condition on the truncation boundary. An integral equation is used to express this boundary condition in which the integration surface is selected in the middle of the most external layer of finite elements, very close to the truncation boundary, so that the integral equation becomes quasi-singular. The method is described for the computation of electrostatic fields in 3D and of eddy currents in 2D, but it is also applicable to the solution of other kinds of electromagnetic problems. Comparisons are made with other methods, concluding that FEM-DBCI is competitive with the well-known FEM-BEM and coordinate transformations for what concerns accuracy and computing time.
1. Introduction
Computational electromagnetics (CEM) in industrial applications are continuously growing due to the increasing performances of electronic computers and to the development of several commercial codes based on the finite element method (FEM) [1,2], by means of which complex geometries and materials can be dealt with.
However, serious difficulties appear when the device to be analyzed exhibits electromagnetic fields extending to infinity. Unfortunately, these fields are highly common in several electromagnetic systems.
In order to apply FEM, the unlimited domain must be cut by means of a closed truncation boundary ΓT. Once the interior bounded domain has been discretized by finite elements, a boundary condition must be imposed on such a boundary, which should be very close to the true one, which is clearly not known. The simplest way to overcome this difficulty is to place ΓT far away from the system core and impose on it a homogeneous condition, very often of the Dirichlet type. This approach exhibits poor accuracy-computational effort ratios, especially in the optimized design of three-dimensional electromagnetic devices.
For this reason, several specific methods have been devised to make the FEM able to compute scalar and vector fields in unbounded domains in a more efficient way.
In almost all these methods, the unbounded domain is partitioned into two parts by means of a cutting closed surface ΓT, in such a way that the interior domain is sufficiently small and encloses the core of the system, whereas the unbounded exterior domain is homogeneously constituted of free space.
The interior domain is analyzed by means of the FEM, whereas for the exterior one several auxiliary methods have been devised in the literature, starting from the 1970s [3]. The research is still continuing, especially toward methods appropriate to the design optimization, which very often requires thousands of analyses and, therefore, short computing times to be effective.
In the CEM scenario, these auxiliary methods vary notably from low frequency (LF) to high frequency (HF) applications. For LF problems, we mention the coordinate transformations (CT) [4,5], infinite elements [6] and asymptotic boundary conditions (LF-ABC) [7], whereas for HF problems we mention the absorbing boundary conditions (HF-ABC) [8,9], and the perfectly matched layer (PML) [10].
All the methods mentioned above have the merit of leading to sparse algebraic systems, but they have the disadvantage of requiring a connected and convex truncation boundary. Then, these methods are not efficient when the system consists of several objects distributed in space, since a large free space must be meshed.
In these cases, hybrid methods are more suitable. The term hybrid comes from the fact that an integral equation (IE) is coupled with a partial differential equation (PDE) for the interior domain. The PDE is numerically treated by means of the FEM, whereas the IE is used to express the unknown boundary condition on the truncation surface ΓT, which now can be constituted by several closed surfaces in such a way to minimize the meshing of the free space (domain decomposition). These methods are collectively called FEM-IE.
By considering that the boundary conditions on ΓT can be of three types, namely Dirichlet, Neumann and Robin, and that the surface ΓIE, support of the integral equation, may coincide or may not with ΓT, theoretically we can have six hybrid methods. Table 1 reports some of these methods. Here again we observe two scenarios for LF and HF problems. For LF problems, we mention the FEM-DBCI (Dirichlet boundary condition iteration) [11,12,13,14,15,16], the FEM-SDBCI (singular DBCI) [17,18] and the well-known FEM-BEM [19,20], whereas for HF problems the FEM-MoM (Method of moments) [21], FEM-RBCI (Robin boundary condition iteration) [22,23], the FEM SRBCI (singular RBCI) [24] and the FEM-AABC (adaptive absorbing boundary condition) [25].

Table 1.
Various FEM-IE methods.
The use of Dirichlet or Neumann conditions on ΓT for HF problems may give rise to internal resonances [2], so that these boundary conditions are not recommended, even if in particular cases the relative methods may work correctly. On the contrary, the use of a suitable Robin boundary condition avoids completely the internal resonances, whatever the frequency [22].
The BCI acronym to designate some of the hybrid methods in Table 1 comes from a particular solving iterative procedure, devised by the authors and reported in Section 4 for readers’ convenience. Note that this procedure is fully applicable also to FEM-BEM algebraic systems.
In this paper, we are focused on the FEM-DBCI method for LF problems. The truncation boundary ΓT is selected by the user in such a way to enclose all the conductors and non-homogeneous objects and to truncate the unbounded free space around the system. On this boundary, a Dirichlet condition is assumed and initially guessed in order to obtain a first solution by means of standard FEM. An improvement of the Dirichlet condition on ΓT can be obtained starting from this solution, by means of an integral equation, whose support is another closed surface ΓIE, enclosing the system but strictly enclosed by ΓT. This procedure is repeated iteratively until convergence is reached. A geometrically simple ΓIE is obtained in 3D as a set of triangular or quadrangular faces of internal tetrahedra or bricks, respectively, or as set of segments which are sides of triangles or quadrangles in 2D.
This paper describes a particular use of the FEM-DBCI method in which the integration surface is selected as constituted by patches connecting the middle points of the edges leaving from the truncation boundary ΓT. In this way, the free space between ΓIE and ΓT reduces to half a layer of finite elements and, due to the proximity of ΓIE and ΓT, the integral equation becomes quasi-singular.
The paper is organized as follows: in Section 2 and Section 3, the FEM-DBCI formulations are described for an electrostatic problem in 3D and for a time-harmonic skin effect problem in 2D, respectively. In Section 4, various algorithms to solve the hybrid global algebraic system are outlined. In Section 5 and Section 6, analytical and numerical examples are given, respectively. The authors’ conclusions follow in Section 7.
2. The FEM-DBCI Method for Electrostatics
Consider an electrostatic system constituted by dielectric objects, charge distributions and voltaged conductors embedded in free space, as shown in Figure 1. The conductor potentials Vi, i = 1, .., NC, are relative to the zero potential at infinity.
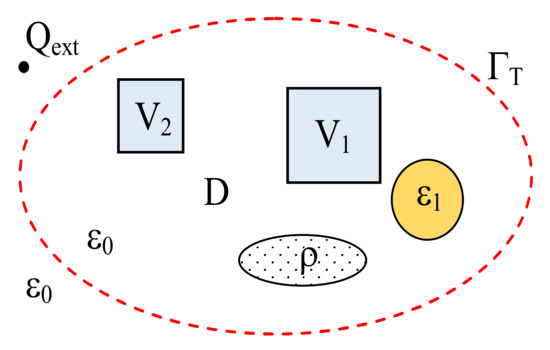
Figure 1.
Fictitious boundary enclosing an electrostatic system of voltaged conductors, non-homogeneous dielectric objects and distributed sources.
In order to apply the FEM, a fictitious truncation boundary ΓT is introduced in such a way to enclose all the conductors and non-homogeneous objects. Some lumped or distributed charges may be left out. In the bounded domain D, the Poisson equation holds [1]:
where ε0 is the vacuum electric permittivity, εr is the relative permittivity, v is the electric scalar potential and ρ is the charge density. An unknown Dirichlet condition is assumed on ΓT.
By meshing the domain D by means of nodal finite elements and applying the FEM, the following algebraic system is derived [11]:
where v and vT are the arrays of the nodal values of the potential v(x,y,z) at the internal nodes and at the nodes lying on ΓT, respectively, M and MT are sparse matrices of coefficients depending on geometry and materials and k0 is the known term array due to the conductor voltages and internal sources.
The Dirichlet condition on ΓT is expressed by means of the integral equation:
where vext is the potential due to the external sources, ΓIE is the closed surface which connect the middle points of the edges leaving the nodes of ΓT, as shown in Figure 2, n′ is the outward normal unit vector and G is the free-space Green’s function:
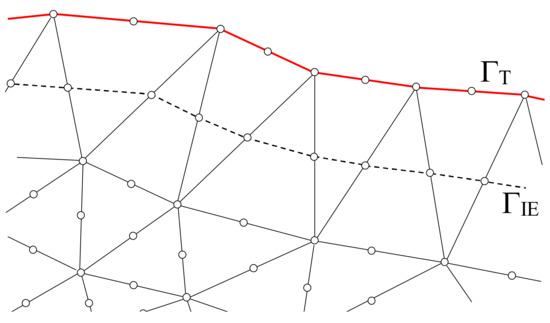
Figure 2.
Truncation boundary ΓT and integration curve ΓIE (dashed line) in a mesh of triangular finite elements of the second order.
Note that Equation (3) is valid if the space outside ΓIE consists of free-space only. In numerical form, Equation (3) reads
where:
where Sk is the k-th patch of ΓIE, αm is the shape function of the m-th node of the finite element in which the patch lies, ri is the coordinate vector of the i-th node on ΓT and vi is the potential value at this node. Note that the patches Sk, which constitute ΓIE, are triangles and quadrangles for a tetrahedral mesh and quadrangles for bricks [26].
Since the patch Sk is detached from ΓT, the integrals (6) and (7) are regular and can be computed by means of the Gauss quadrature with varying accuracy. When the centre of the integration patch Sk is far apart from the node ri on ΓT, one-point Gauss quadrature is enough. When the centre of Sk is very close to ri, a large number of Gauss points are needed. Denoting by L the length of the longest edge of Sk and by d the distance of its centre from node ri on ΓT, for first-order tetrahedra a good trade-off between accuracy and speed is the following: if L/d < 0.2 one-point Gauss is used; if 0.2 < L/d < 1.1, three or four Gauss points are used for triangular or quadrangular patches, respectively; otherwise, six or nine points are used. If ri is very near to Sk, analytical formulas may be also used [27].
In matrix form, Equation (5) read:
where matrices H and G are dense. H is square by construction.
Equations (2) and (8) constitute the hybrid global algebraic system to be solved.
3. The FEM-DBCI Method for Skin Effect
The system considered consists of a set of NC parallel straight conductors embedded in free space. We denote by Sk (k = 1, ..., NC) their cross sections and by Ik the phasors of the total currents, supposed to be time-harmonic of the same angular frequency ω. Each conductor is homogeneous, with reluctivity νk and conductivity σk. The current densities in these conductors are not known due to the skin and proximity effects.
Other conductors of small cross sections may exist carrying sinusoidal currents of the same angular frequency ω, represented by the phasors Ik, k = NC+1, …, Ntot (it is assumed that the sum of the currents of all the conductors be equal to zero). In these conductors the skin-effect is negligible, so that the current density is known and equal to Ik/Sk. From the point of view of the magnetic field, these conductors may or may not be homogeneous with the free space.
Now we truncate the unbounded free space by means of a fictitious boundary ΓT, which must include all the skin-effect conductors and also the inhomogeneous skin-effect free ones. The skin-effect free conductors may be left outside ΓT if magnetically homogeneous with free space. In the following, they are referred to as external sources.
The magnetic vector potential A is parallel to the conductor direction and in the k-th conductor satisfies the integro-differential equation [28]:
In the internal skin-effect free conductors, Equation (9) simplifies into the Poisson one, obtained by setting σk = 0 in it. In free space, the potential satisfies the Laplace equation.
Meshing the bounded domain by means of nodal finite elements and assuming a Dirichlet condition on ΓT, the following matrix equation is obtained [14]:
where a and aT are the arrays of the complex potential values of the magnetic vector potential at the internal and boundary nodes, respectively, M is a square symmetric matrix which depends on geometry and materials, k0 is the known term array due to the internal source currents, and MT is a matrix of coefficients similar to M.
Arrays a and aT can be further related by means of the integral equation:
where Aext is the potential due to the external source currents, if any, ΓIE is the closed broken line which connect the middle points of the element sides leaving the nodes of ΓT, and G is the two-dimensional free-space Green’s function:
In the numerical approximation, Equation (11) reads:
where H and G are dense matrices of geometrical coefficients and aext depends on the external sources. Matrix H is square. Equations (10) and (13) constitute the global algebraic system to be solved.
4. Solution of the Global Algebraic System
In the FEM-DBCI methods described previously, the global algebraic systems have the forms
where M and MT are sparse matrices, H and G are dense matrices, x and xT are unknown vectors relative to the FEM unknowns and to the truncation boundary condition unknowns, respectively, and k0 and kext are known arrays. M and H are square.
System (14) can be solved by iteration. Starting from a first guess for xT, the FEM equation is solved for x(0); then, the integral equation is used to improve this guess. These two steps are iterated. At the generic p-th iteration step:
By considering the symmetry and sparsity of matrix M, the algebraic system (15) is conveniently solved by means of the conjugate gradient (CG) solver [29]. System (16) may be solved by means of the LU factorization of matrix H, which, however, is performed only once at the 0-th step.
The convergence behavior of this iterative procedure can be studied as follows. When systems (15) and (16) are solved, we obtain:
where:
The step matrix P determines the convergence of the iterative procedure. In fact, if its spectral radius ρ is lower than 1, convergence is obtained to the true solution of the unbounded problem whatever the initial guess . In [30], it is shown that the condition ρ < 1 is satisfied if the mean distance of ΓT from the conductors is greater than the mean radius of the conductor system.
If relaxation is used, the step Equation (17) changes into:
With a suitable value of the relaxation parameter λ, the iterative procedure converges even when the non-relaxed procedure does not [31]. Unfortunately, only heuristic rules have been derived for setting λ, so that this approach is not satisfactory.
By looking at the iterative algorithm more deeply, it is simple to realize that Equations (17) and (20) can be seen as the iterative relations to solve the reduced algebraic systems:
respectively, by means of Richardson’s method [29], which is a weak and possibly non-converging solver.
In order to find a more efficient solver, we consider the reduced system:
where:
Obviously, due to the impossibility to obtain the inverse matrix M−1, matrix A and vector b are not available directly. However, it is still possible to obtain b in a simple way and to use matrix A to perform matrix-vector multiplications. In fact, vector b is obtained as follows:
- (1)
- Set a zero initial guess for the Dirichlet condition on ΓT;
- (2)
- Solve the FEM equation (by means of the CG) to find ;
- (3)
- Compute .
In a similar way, matrix A can be used to multiply it by an array :
- (a)
- Given the array ;
- (b)
- Solve the FEM equation with k0 = 0 (by means of the CG) to find ;
- (c)
- Compute .
Then, we can solve system (22) by means of a variety of non-stationary CG-like solvers for non-symmetric matrices [29]. Among these, GMRES [32] should be preferred, as it really minimizes the number of matrix-by-vector multiplications, which are highly expensive in this context. As it is well known, the greater drawbacks of GMRES are the CPU time and the memory amount required to build and store the orthonormal base. However, in this application of GMRES, these requirements are moderately low, since GMRES virtually acts on a small system, whose unknowns are the potential values at the nodes of the truncation boundary [33].
This virtual use of the GMRES is fully applicable also to the solution of FEM-BEM algebraic systems, as described in [34].
5. An Analytical Example
This example is a very simple one: a perfectly conducting sphere voltaged at V0, embedded in free space. The analytical solution is well known, but here numerical solutions will be considered, based on the FEM-DBCI method.
In order to do this, a spherical truncation boundary is introduced at a distance d from the conductor surface. By virtue of the radial symmetry, the analysis can be conveniently led in the one-dimensional domain D = [R, R + d], where R is the radius of the spherical conductor. In D, the Laplace equation holds:
with the relative boundary conditions.
The domain D is regularly meshed by means of N first-order segments of the same length d/N; the total number of nodes is N+1; their abscissas are ri = R + id/N, i = 0, ..., N. By virtue of the FEM-DBCI, the following system of algebraic equations is obtained:
subject to the Dirichlet boundary condition .
The coefficients ai are given by:
whereas the coefficient h depends on the choice of ΓIE. By selecting ΓIE as the spherical surface of radius
in the middle of the last segment, the coefficient h is given by:
By solving the FEM-DBCI system (26)–(27), we get the potential value on the fictitious boundary:
where:
In order to check the validity of the FEM-DBCI method, we define the error indicator:
where is the exact value of the potential on the fictitious boundary:
where δ is the normalized distance of the truncation boundary from the conductor surface:
By substituting (31) and (34) in (33), the error indicator reads:
where is a non-dimensional values given by:
Since it is possible to show that
we have also
and the numerical solution tends to the exact one. This validates the proposed method.
To compare the accuracy of the FEM-DBCI with that of other methods, consider the following FEM-BEM global algebraic system:
where is the unknown value of the outward normal derivative of the potential on ΓT. By solving the system (40)–(42) subject to the Dirichlet boundary condition , we obtain the numerical solution for :
so that the error indicator is:
where:
In Figure 3, the behaviours of and for a fixed number of finite elements N = 10 are plotted as a function of δ. Good accuracies are obtained with both the methods, but FEM-DBCI is a little bit more accurate than FEM-BEM. Analogous results are obtained by increasing the number of finite elements. For higher values of N, the two lines tends to coincide with the η = 0 line. Mathematically, this is exactly obtained for N→∞.
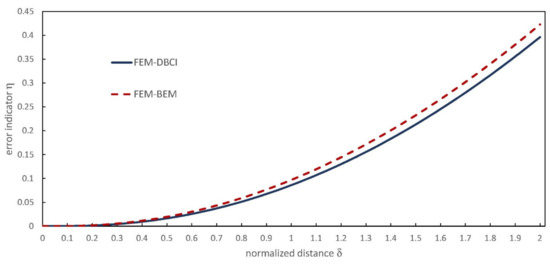
Figure 3.
Behaviour of the error indicators of the FEM-DBCI and FEM-BEM methods for the analytical example of the charged conducting sphere.
However, in general, FEM-DBCI is a little bit less accurate than FEM-BEM, but much more fast since it works with a lower number of unknowns [35], the nodal values of the normal derivative of the potential not being used in the first one. This characteristic will be illustrated in the next section by means of a set of numerical examples.
6. Numerical Examples
6.1. Capacitance of a Strip Line
Consider the transmission line shown in Figure 4, where a conductor strip (width w = 5 mm, negligible thickness) is separated from a ground plane by a dielectric sheet (height h = 1.5 mm, width s = 15 mm, permittivity ε1 = 4.7ε0). The line is embedded in the free-space of permittivity ε0. The strip conductor is voltaged at V0 = 1 V. Due to symmetry reasons, the two-dimensional analysis can be restricted to half the system, by imposing a homogeneous Neumann boundary condition on the y-axis. The truncation boundary is placed at a distance d = 0.05 mm from the conductor/dielectric, as shown in Figure 4. The mesh is formed with 1057 second-order triangles and 2240 nodes. Only one layer of 204 finite elements is in free-space; 206 nodes lie on ΓT. The FEM-DBCI converges in six GMRES iterations, with an end-iteration tolerance of 0.01 per cent. The contours of the potential are shown in Figure 5. The capacitance per unit length is conveniently evaluated by means of the cross-energy formula:
where w is an arbitrary function such that w = 1 on the strip and w = 0 on the ground plane and on ΓT. This computation gives: c = 130.7 pF/m.
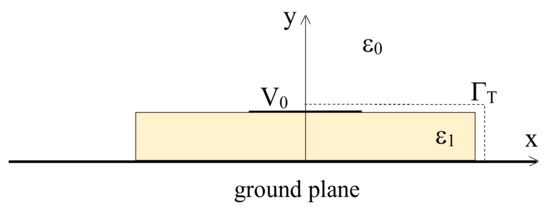
Figure 4.
Microstrip line over a ground plane.
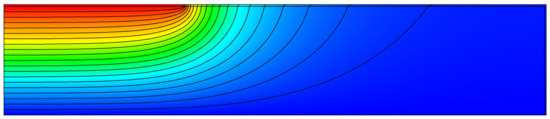
Figure 5.
Contours of the electrical potential.
6.2. Two-Wire Transmission Line
The line considered is constituted by two circular wires of radius R whose centers are separated by a distance of D = 2.4R. The wire potentials are V0/2 and −V0/2, so that the analytical solution is [36]:
where:
and the capacitance per unit length is given by:
For this line, Formula (49) gives c = 5.047850 ε0. The truncation boundary is selected as two circumferences of radius 1.14R, concentric with the two wires. The air gap between the conductors and the truncation boundary ΓT is d = 0.14R. Due to symmetry, the analysis can be conveniently limited to the first quadrant only, by imposing homogeneous Neumann and Dirichlet conditions on the x- and y-axis, respectively. Note that the y-axis is completely left outside the domain of analysis. The air gap is regularly meshed with four layers of second-order triangular elements, for a total 724 elements and 1637 nodes. To improve the accuracy of the numerical solution, curved elements are used at the conductor-air interface. The integration curve ΓIE is selected in three different ways: (a) triangle sides at a distance d/4 from the conductor; (b) segments internal to the 2nd layer of triangles at a mean distance of 3d/8 from the conductor; (c) segments internal to the 4th layer of triangles at a mean distance of 7d/8 from the conductor. Another analysis is performed by means of the non-standard FEM-BEM described in [20]. The various algebraic systems are solved with the GMRES schemes (restarting parameter m = 10). The following error indicator is employed to measure the accuracy of the numerical solutions:
where D1 is the analysis domain in the first quadrant. Table 2 summarizes the results obtained by reporting the number of steps performed (with an end-iteration tolerance of 10−3 per cent for the GMRES and for the CG), the normalized CPU time for the solution of the linear systems, the error indicators ζ and the normalized capacitances c/ε0, evaluated by means of the cross-energy formula. We can see that all the FEM-DBCI solutions are less accurate with respect to the FEM-BEM, but notably faster. Moreover, note the FEM-DBCI (c) solution is practically accurate as the (b) one, and this means that we can reduce the mesh to two layers only, by also reducing the relative CPU time.

Table 2.
Comparison between various FEM-DBCI and FEM-BEM for the 2nd example.
6.3. Capacitance of a Cube Conductor
The third example is relative to the computation of the capacitance C of a conductor cube of edge size s, voltaged at V0 and embedded in free space. For this classical three-dimensional electrostatic problem, a highly accurate estimate is known of the normalized capacitance c = C/4πε0s: c = 0.6606780 ± 2.7 × 10−7 [37]. The FEM-DBCI method is applied by introducing a cube fictitious boundary ΓT, placed homologously to the conductor surface at a distance d = s/8. This distance is justified by the need of spacing ΓT from the cube edges, where the electrical field theoretically diverges. Thanks to symmetry, the analysis domain is limited to the first octant only. The free-space gap between the two cubes is meshed with 56,220 first-order tetrahedra with 11,948 nodes. Two estimates of the capacitance c are obtained by means of the FEM-DBCI and FEM-BEM. The number of GMRES steps (with an end-iteration tolerance of 10−2 per cent for the GMRES and 10−4 per cent for the CG), the CPU times for the solution of the linear algebraic systems and the normalized capacitances c are reported in Table 3. As before, FEM-DBCI exhibits an accuracy comparable with that of the FEM-BEM, but FEM-DBCI requires much less computing time. The contours of the potential are shown in Figure 6.

Table 3.
Comparison between FEM-DBCI and FEM-BEM for the 3rd example.
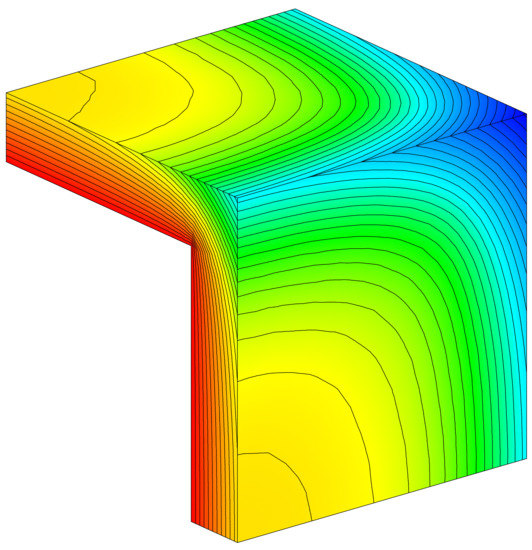
Figure 6.
Contours of the potential around the cube conductor.
6.4. Skin Effect in a Two Wire Transmission Line
The transmission line is constituted by two conductors having circular cross-sections of radius R = 5 mm. The distance between the two centers is D = 20 mm (see Figure 7). The line carries two opposite sinusoidal currents of magnitude I = 1 A at frequency f = 1 kHz. The two wires are made of copper with conductivity σ = 56 × 106 S/m. This example is given to compare FEM-DBCI with other methods: FEM truncation, FEM-CT (Coordinate Transformations) [4,5], and FEM-BEM.
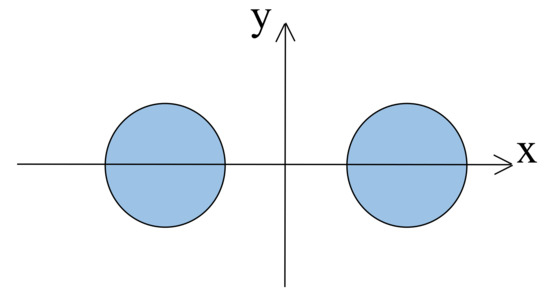
Figure 7.
Two-wire transmission line.
By selecting the Cartesian reference frame in Figure 7, the transmission line exhibits a double symmetry with respect to the two axes, so that the various analyses can be restricted to the first quadrant only, by imposing a homogeneous Neumann condition on the x-axis and a homogeneous Dirichlet one on the y-axis.
Since no analytical solution exists for this problem, in the following we assume that the best solution be obtained by means of the FEM-CT method by employing a great radius of the circular domain RCT = 6 R = 30 mm of the Kelvin transformation [4].
The interior domain is meshed with 370 triangular finite elements of the second order (see Figure 8). A total of 128 elements lay in the conductor; 242 elements lay in air (64 of which in the exterior air). The complex CG solver is used to solve the global algebraic system with a CPU time of TS = 0.26 s on a small PC.
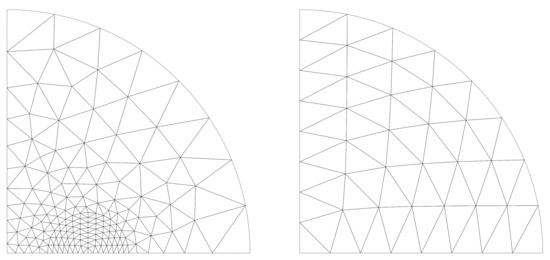
Figure 8.
Finite element mesh in the interior and exterior regions in the FEM-CT analysis.
The FEM truncation method is then applied by means of a circular truncation boundary Γ0 of radius R0, centered at the origin. On Γ0, a homogeneous Dirichlet condition is imposed. The radius of this circle is increased until a satisfactory accuracy is obtained with respect to the FEM-CT solution. To measure this accuracy, we use the following error indicator:
where A and A(T) are the FEM-CT and truncation solutions, respectively, and C denotes the conductor subdomain. Numerically, η is computed as:
where n and m are indices of nodes in the k-th finite element (belonging to the conductor), star denotes conjugation and tnm is an entry of the metric matrix of the k-th element [1]. We found that by setting R0 = 30 R, the error indicator η decreases to 0.15% and the CPU increases to 1.90 TS.
The system is also analyzed by means of FEM-BEM. The air-copper interface is used as the truncation boundary. In the conductor, the mesh is formed with 128 second-order triangular finite elements, exactly coinciding with those of the previous analyses. The FEM-BEM system is solved by means of the GMRES solver, as explained in [15]. Solution is achieved in four iterations, but the CPU time rises to 1.52 TS, while the error indicator η decreases to 0.08%.
Finally, the FEM-DBCI method is applied by employing a circular truncation boundary of radius RT = 6.0 mm. The air in between the conductor and the truncation boundary is meshed by means of one layer of 32 triangular finite elements; the conductor is meshed as in the previous analyses. The resulting global algebraic system is solved by means of the GMRES solver. The solution is reached in four iterations, with a CPU time of 1.14 TS; the error indicator is 0.11%. Figure 9 reports the contours of the current density magnitude inside the conductor.
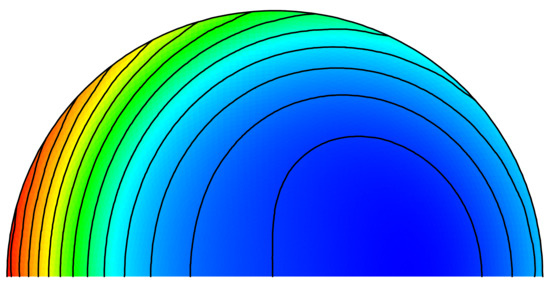
Figure 9.
Contours of the current density magnitude.
The results obtained show that FEM-DBCI is competitive with respect to the well-known FEM-BEM and FEM-CT methods, both from the accuracy and CPU time points of view. Moreover, note that the FEM-BEM and FEM-DBCI performances can increase with respect to those of FEM-CT if the system analyzed consists of several conductors, the distances between which are much greater than their diameters.
6.5. Skin Effect in a Non-Symmetric Transmission Line
The last example concerns a non-symmetric transmission line constituted by a couple of conductors having different sections, as depicted in Figure 10. The geometrical data are: left conductor Section 1 cm × 1 cm, right conductor Section 2 cm × 2 cm, distance between their centres 2.3 cm. The conductors are made of copper (σ = 56 × 106 S/m), whereas the surrounding medium is assumed to have zero conductivity and vacuum permeability. The conductors carry two opposite time-harmonic currents I and −I of magnitude 1 A at frequency f = 1 kHz.
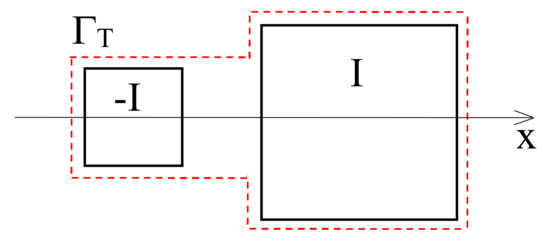
Figure 10.
Non-symmetric two-wire transmission line.
This example is selected to show that the FEM-DBCI method is fully applicable also using a non-convex truncation boundary ΓT (see dashed line in Figure 10), which is constituted by a single curve placed at a distance of 1 mm from the conductor surfaces. Due to symmetry reasons, the analysis is restricted to half the system, by imposing a homogeneous Neumann condition on the x-axis. The resulting bounded domain is regularly discretized. The mesh is constituted by 712 s-order triangles and 1483 nodes, of which 127 lie on ΓT. Having set an end-iteration tolerance of 10−4 per cent, convergence is obtained with 13 GMRES iterations. Figure 11 and Figure 12 show the contours of the real and imaginary parts of the magnetic vector potential.
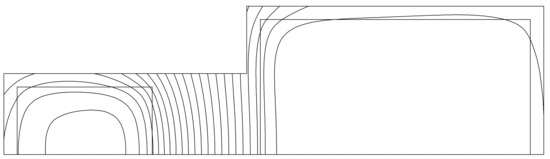
Figure 11.
Contours of the real part of the magnetic vector potential.
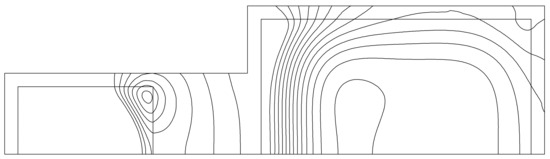
Figure 12.
Contours of the imaginary part of the magnetic vector potential.
The solution obtained has been compared with the FEM-BEM one: a mean relative error of about 1.14 per cent is pointed out in the conductors, but the CPU time increases of about 55 per cent.
7. Conclusions
In this paper, a particular use of the hybrid FEM-DBCI method has been described for the solution of a variety of open-boundary electromagnetic problems, such as electrostatic and time-harmonic skin effect ones. In the proposed method, the surface of the integral equation is selected in the middle of the more external layer of finite elements, very near to the truncation boundary. This method leads to accurate numerical results similar to those obtained with the FEM-BEM, but with lower computing times.
For this reason, we can conclude that FEM-DBCI appears to be more appropriate for FEM analyses requiring short computing times, such as in the stochastic optimization of electromagnetic devices. In these applications, generally, several thousands of FEM analyses must be performed to reach satisfactory results [38,39]. On the contrary, FEM-BEM appears more appropriate when high accuracies are required in a single computation.
However, all the hybrid methods suffer from the complexity of the integral equation, which naturally is quadratic. Then, for real industry applications in 3D, it is important to reduce this complexity at the price of adding further approximation to the basic integral equation. In such a perspective, in addition to the well-known fast multipole method (FMM) [40,41], recently the use of H- and H2-matrices seems to be highly promising [42].
The FEM-DBCI method and the non-standard FEM-BEM one used in this paper have been implemented in ELFIN, a large FEM code developed by the authors for scientific research [43].
Author Contributions
Conceptualization, G.A., S.A. and N.S.; methodology, S.A.; software, S.A., S.A.R. and N.S.; All authors have read and agreed to the published version of the manuscript.
Funding
This paper has been partially supported by the Italian Ministry for University and Research (MUR).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Silvester, P.P.; Ferrari, R.L. Finite Elements for Electrical Engineers; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Jin, J. The Finite Element Method in Electromagnetics; John Wiley & Sons: New York, NY, USA, 2002. [Google Scholar]
- Chen, Q.; Konrad, A. A review of finite element open boundary techniques for static and quasi-static electromagnetic field problems. IEEE Trans. Magn. 1997, 33, 663–676. [Google Scholar] [CrossRef]
- Lowther, D.A.; Freeman, E.M.; Forghani, B. A sparse matrix open boundary method for finite element analysis. IEEE Trans. Magn. 1989, 25, 2810–2812. [Google Scholar] [CrossRef]
- Imhoff, J.F.; Meunier, G.; Sabonnadiere, J.C. Finite element modeling of open boundary problems. IEEE Trans. Magn. 1990, 26, 588–591. [Google Scholar] [CrossRef]
- Bettess, P. Infinite element. Int. J. Numer. Methods Eng. 1977, 11, 53–64. [Google Scholar] [CrossRef]
- Chen, Q.; Konrad, A.; Biringer, P.P. Computation of three-dimensional unbounded eddy current problems using asymptotic boundary conditions. IEEE Trans. Magn. 1995, 31, 1348–1351. [Google Scholar] [CrossRef]
- Engquist, B.; Majda, A. Absorbing boundary conditions for the numerical simulation of waves. Math. Comput. 1977, 31, 629–651. [Google Scholar] [CrossRef]
- Bayliss, A.; Gunzburger, M.; Turkel, E. Boundary conditions for the numerical solution of elliptic equations in exterior regions. SIAM J. Appl. Math. 1982, 42, 430–451. [Google Scholar] [CrossRef]
- Berenger, J.-P. A perfectly matched layer for the absorption of electromagnetic waves. J. Comput. Phys. 1994, 114, 185–200. [Google Scholar] [CrossRef]
- Aiello, G.; Alfonzetti, S.; Coco, S. Charge iteration: A procedure for the finite element computation of unbounded electrical fields. Int. J. Numer. Methods Eng. 1994, 37, 4147–4166. [Google Scholar] [CrossRef]
- Aiello, G.; Alfonzetti, S.; Borzì, G. A generalized minimal residual acceleration of the charge iteration procedure. J. Phys. III 1997, 7, 1955–1966. [Google Scholar] [CrossRef]
- Aiello, G.; Alfonzetti, S.; Rizzo, S.A.; Salerno, N. FEM-DBCI solution of open-boundary electrostatic problems in the presence of floating potential conductors. IEEE Trans. Magn. 2015, 52, 1–4. [Google Scholar] [CrossRef]
- Aiello, G.; Alfonzetti, S.; Coco, S.; Salerno, N. Finite element iterative solution to skin effect problems in open boundaries. Int. J. Numer. Model. 1996, 9, 125–143. [Google Scholar] [CrossRef]
- Aiello, G.; Alfonzetti, S.; Borzì, G.; Salerno, N. An improved solution scheme for open-boundary skin effect problems. IEEE Trans. Magn. 2001, 37, 3474–3477. [Google Scholar] [CrossRef]
- Aiello, G.; Alfonzetti, S.; Dilettoso, E. Finite element solution of eddy current problems in unbounded domains by means of the hybrid FEM−DBCI method. IEEE Trans. Magn. 2003, 39, 1409–1412. [Google Scholar] [CrossRef]
- Aiello, G.; Alfonzetti, S.; Salerno, N. Solution of skin-effect problems by means of the hybrid SDBCI method. COMPEL 2014, 33, 1935–1949. [Google Scholar] [CrossRef][Green Version]
- Aiello, G.; Alfonzetti, S.; Rizzo, S.A.; Salerno, N. Eddy Current Computation by the FEM-SDBCI Method. IEEE Trans. Magn. 2015, 52, 1–4. [Google Scholar] [CrossRef]
- Brebbia, C.A.; Telles, J.C.F.; Wrobel, L. Boundary Element Technique; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Alfonzetti, S.; Salerno, N. A non-standard family of boundary elements for the hybrid FEM-BEM method. IEEE Trans. Magn. 2009, 45, 1312–1315. [Google Scholar] [CrossRef]
- Yuan, X.; Lynch, D.R.; Strohbehn, J.W. Coupling the finite element and moment methods for electromagnetic scattering from inhomogeneous objects. IEEE Trans. Antennas Propag. 1990, 38, 386–393. [Google Scholar] [CrossRef]
- Alfonzetti, S.; Borzì, G.; Salerno, N. Iteratively-improved Robin boundary conditions for the finite element solution of scattering problems in unbounded domains. Int. J. Numer. Methods Eng. 1998, 42, 601–629. [Google Scholar] [CrossRef]
- Alfonzetti, S.; Borzì, G. Finite element solution to electromagnetic scattering problems by means of the Robin boundary condition iteration method. IEEE Trans. Antennas Propag. 2002, 50, 132–140. [Google Scholar] [CrossRef]
- Alfonzetti, S.; Borzì, G.; Salerno, N. Electromagnetic scattering computation by means of the hybrid FEM-SRBCI method. IEEE Trans. Magn. 2015, 51, 7401504. [Google Scholar] [CrossRef]
- Liu, J.; Jin, J.M. A novel hybridization of higher order finite element and boundary integral methods for electromagnetic scattering. IEEE Trans. Antennas Propag. 2001, 50, 132–140. [Google Scholar]
- Aiello, G.; Alfonzetti, S.; Dilettoso, E.; Salerno, N. Improving the accuracy of the integral equation in the hybrid FEM-DBCI method for open boundary electrostatic problems. IEEE Trans. Magn. 2006, 42, 579–582. [Google Scholar] [CrossRef]
- Graglia, R.D. Static and dynamic potential integrals for linearly varying source distributions in two- and three-dimensional problems. IEEE Trans. Antennas Propag. 1987, 35, 662–669. [Google Scholar] [CrossRef]
- Konrad, A. Integrodifferential finite element formulation of two-dimensional steady-state skin effect problems. IEEE Trans. Magn. 1982, 18, 284–292. [Google Scholar] [CrossRef]
- Golub, G.H.; van Loan, C.F. Matrix Computations; Johns Hopkins University Press: Baltimore, MD, USA, 1996. [Google Scholar]
- Aiello, G.; Alfonzetti, S.; Coco, S.; Salerno, N. A theoretical study of charge iteration. COMPEL 1996, 15, 22–46. [Google Scholar] [CrossRef]
- Aiello, G.; Alfonzetti, S.; Coco, S.; Salerno, N. Overrelaxing the charge iteration procedure. IEEE Trans. Magn. 1996, 32, 694–697. [Google Scholar] [CrossRef]
- Saad, Y.; Schultz, M.H. GMRES: A generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Stat. Comput. 1986, 7, 856–869. [Google Scholar] [CrossRef]
- Aiello, G.; Alfonzetti, S.; Salerno, N. Solution of skin effect problems by means of the DBCI-GMRES method. COMPEL 2002, 21, 474–475. [Google Scholar]
- Aiello, G.; Alfonzetti, S.; Borzì, G.; Dilettoso, E.; Salerno, N. A GMRES iterative solution of FEM-BEM global systems in skin effect problems. COMPEL 2008, 27, 1286–1295. [Google Scholar] [CrossRef]
- Aiello, G.; Alfonzetti, S.; Borzì, G.; Rizzo, S.A.; Salerno, N. A comparison between hybrid methods: FEM-BEM versus FEM-DBCI. COMPEL 2013, 32, 1900–1920. [Google Scholar] [CrossRef]
- Durand, E. Electrostatique; Masson Editeur: Paris, France, 1968. [Google Scholar]
- Mascagni, M.; Simonov, N.A. The random walk on the boundary method for calculating capacitance. J. Comput. Phys. 2004, 195, 465–473. [Google Scholar] [CrossRef]
- Alfonzetti, S.; Dilettoso, E.; Salerno, N. Simulated annealing with restarts for the optimization of electromagnetic devices. IEEE Trans. Magn. 2006, 42, 1115–1118. [Google Scholar] [CrossRef]
- Aiello, G.; Rizzo, S.A.; Alfonzetti, S.; Salerno, N. Optimization of the shape of an induction heating device in the presence of skin effect in the coils. COMPEL 2019, 39, 525–531. [Google Scholar] [CrossRef]
- Rokhlin, V. Rapid solution of integral equations of classical potential theory. J. Comput. Phys. 1985, 60, 187–207. [Google Scholar] [CrossRef]
- Engheta, N.; Murphy, W.D.; Rokhlin, V.; Vassiliou, M. The fast multipole method for electromagnetic scattering computation. IEEE Trans. Antennas Propag. 1992, 40, 634–641. [Google Scholar] [CrossRef]
- Hackbusch, W. Hierarchical Matrices: Algorithms and Analysis; Springer Series in Computational Mathematics; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Aiello, G.; Alfonzetti, S.; Borzì, G.; Salerno, N. An overview of the ELFIN code for finite element research in electrical engineering. In Software for Electrical Engineering Analysis and Design; Konrad, A., Brebbia, C.A., Eds.; WIT Press: Southampton, UK, 1999. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).