On Machine-Learning Morphological Image Operators
Abstract
:1. Introduction
2. Morphological Representations
2.1. Binary Image Processing
2.1.1. Translation Invariance and Local Definition
2.1.2. Connection with Boolean Functions
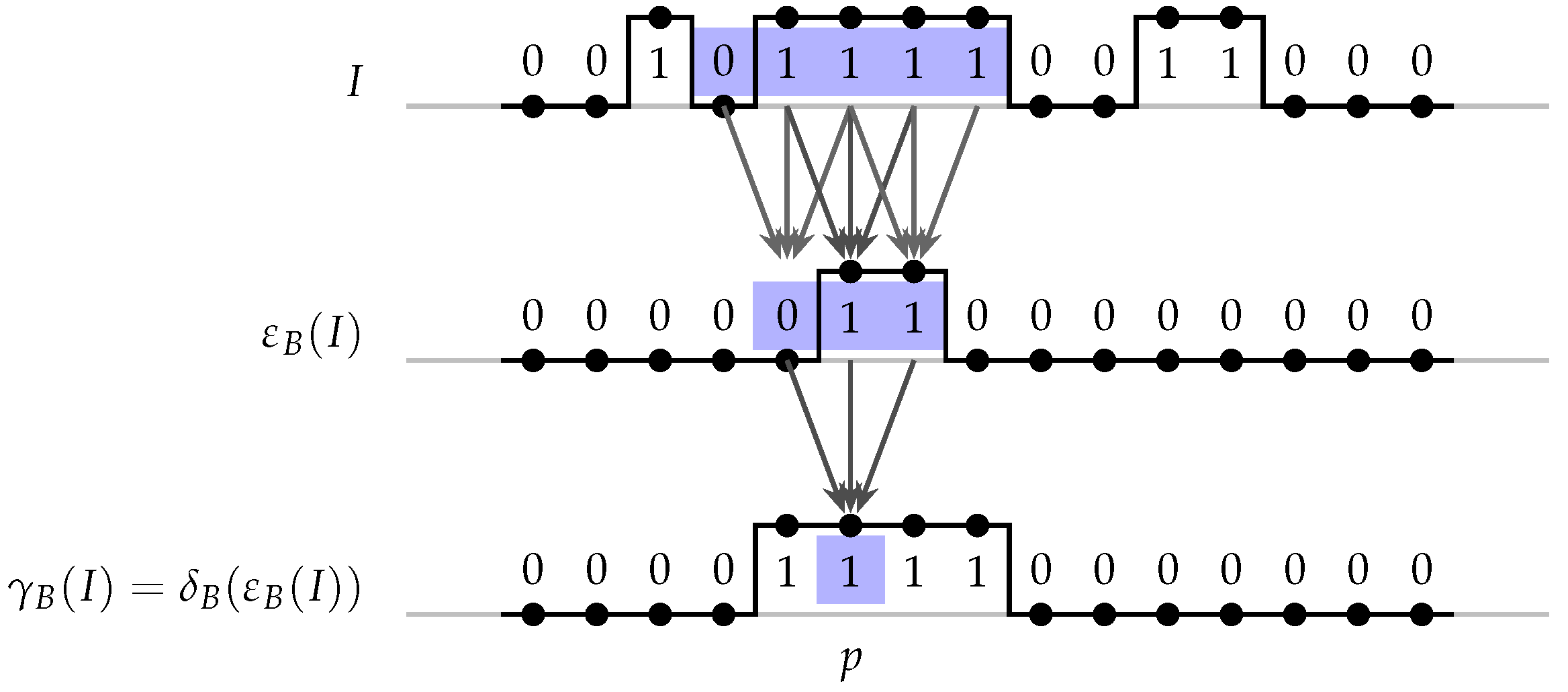
2.1.3. The Lattice of Translation-Invariant and Locally Defined Binary Image Operators
2.1.4. Representation Structures
2.2. Grayscale Image Processing
3. Machine-Learning Morphological Image Transformations
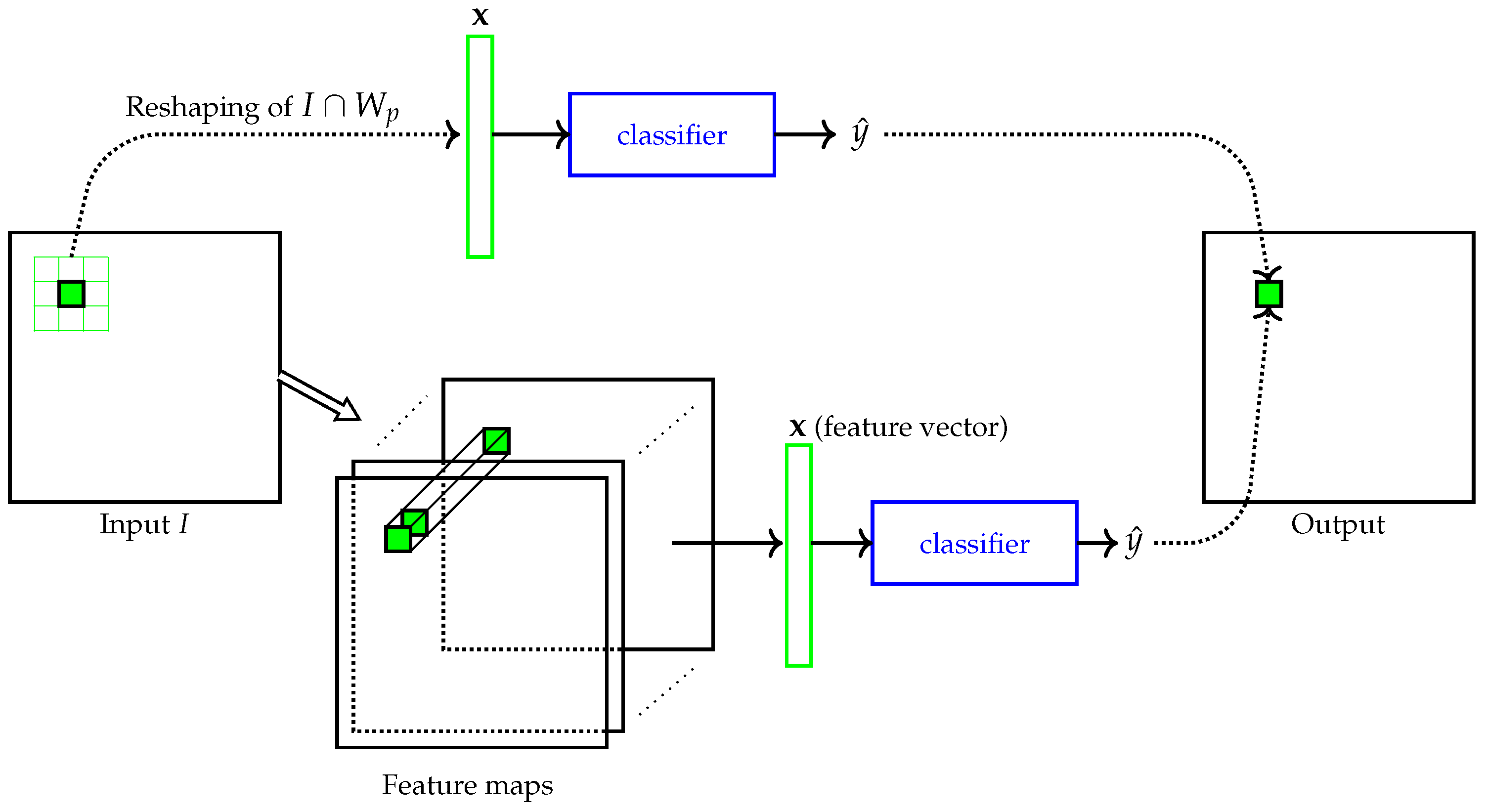
3.1. The Morphological Image Operator Learning Problem
3.2. Learning Methods That Preserve Morphological Representation
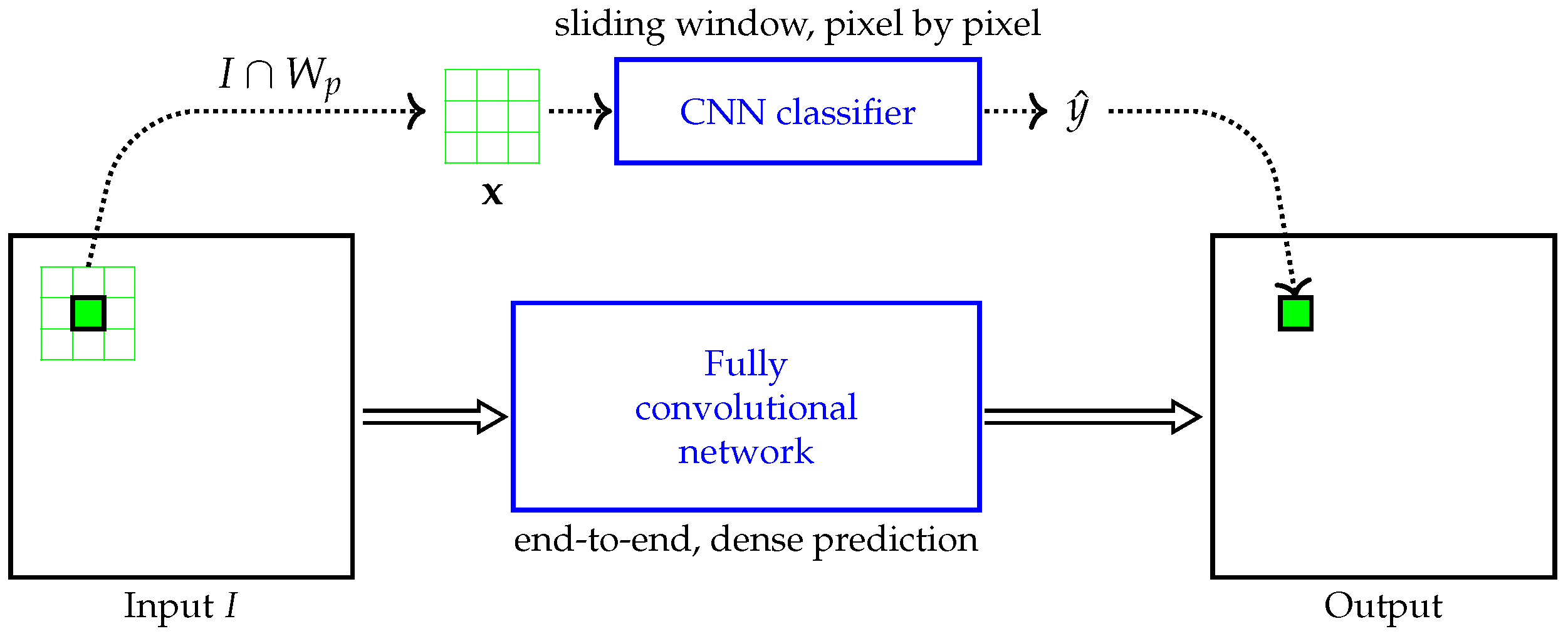
3.3. Links to Standard Machine Learning and Deep Learning
4. Morphological Networks
4.1. Morphological Neural Networks
4.2. Deep Morphological Networks
4.2.1. Morphological Neuron Modeling
4.2.2. Types of Tasks and Architectures
5. Discussion
- Neurons that implement other morphological operators: Erosions and dilations are largely regarded as the building blocks of Mathematical Morphology. However, as we have seen, interval (hit-or-miss) operator is also a fundamental building block. This and possibly other operators could be implemented as morphological neurons, especially aiming more compact and expressive networks.
- Development of standard architecture modules: Linear combination seems to be, so far, the most common way to compose the results regarding multiple input channels or multiple branches into a single result. Another possibility would be to perform composition using lattice operations such as supremum, infimum and negation. Such possibilities should be further investigated and developed. In particular, if we employ only morphological processing units and lattice operations, the whole network would correspond to a morphological expression, possibly improving its interpretability and further handling.
- Hybrid networks: An obvious way to build hybrid networks is to use both convolutional as well as morphological layers in a single network, as already done in some of the reported experiments. However, there might be an optimal way of composing them, possibly, as distinct branches or modules within the architecture. In principle, there is no reason to assume that purely convolutional or purely morphological networks are preferable against the hybrid ones for a given task.
- Systematic evaluation and comparison: Once some standard architectures become available, systematic evaluation and comparison should be performed among them as well as with convolution-based deep neural networks. This should include for instance networks of different sizes and multiple processing tasks.
- Prior knowledge and regularization: In machine learning, the ability to constrain the space of predictor functions to a smaller space, without ruling out good predictors, is an important issue to improve generalization. Subfamilies of morphological image operators can be characterized based on properties such as idempotence, increasingness, anti-extensivity, and others. They can be also characterized in terms of representation; for instance, by limiting the number of intervals in the decomposition or constraining the structuring element shape. Thus, a challenging issue is how to translate prior knowledge about the task to be solved into appropriate constraints and how to enforce these constraints in the definition of the network architecture, as well as during the training process.
- Iterative operators: Many useful morphological image operators such as thinning [20] are iterative applications of simpler operators, until convergence. Would recurrent network be the right approach to learn such operators?
- Feature extraction process: On the one hand, there is an expectation that morphological neurons will reveal the nature of its processing more clearly than convolutional networks. On the other hand, they may end up just being an efficient data transformation function, not necessarily producing visually meaningful features. In this sense, it would be interesting to compare features extracted by convolutional layers and those extracted by morphological layers.
- AutoML: Morphological pipelines designed heuristically to solve real image processing problems consist of a complex composition of multiple morphological operators. For learning such pipelines, rather than using a fixed network architecture, it may make more sense to experiment a variety of composition structures, much like the way genetic programming algorithms perform. In the deep-learning field, architecture search approaches are known as AutoML. For instance, approaches such as the one in [78] could be employed to build complex processing architectures, by combining morphological building block operators.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Baheti, R.; Gill, H. Cyber-physical systems. Impact Control Technol. 2011, 12, 161–166. [Google Scholar]
- Sharma, A.B.; Ivančić, F.; Niculescu-Mizil, A.; Chen, H.; Jiang, G. Modeling and Analytics for Cyber-Physical Systems in the Age of Big Data. Sigmetr. Perform. Eval. Rev. 2014, 41, 74–77. [Google Scholar] [CrossRef]
- Garcia Lopez, P.; Montresor, A.; Epema, D.; Datta, A.; Higashino, T.; Iamnitchi, A.; Barcellos, M.; Felber, P.; Riviere, E. Edge-Centric Computing: Vision and Challenges. Sigcomm Comput. Commun. Rev. 2015, 45, 37–42. [Google Scholar] [CrossRef]
- Merenda, M.; Porcaro, C.; Iero, D. Edge Machine Learning for AI-Enabled IoT Devices: A Review. Sensors 2020, 20, 2533. [Google Scholar] [CrossRef] [PubMed]
- Maragos, P. Chapter Two—Representations for Morphological Image Operators and Analogies with Linear Operators. In Advances in Imaging and Electron Physics; Elsevier: Amsterdam, The Netherlands, 2013; Volume 177, pp. 45–187. [Google Scholar]
- Serra, J. Image Analysis and Mathematical Morphology; Academic Press: Cambridge, MA, USA, 1982. [Google Scholar]
- Heijmans, H.J.A.M. Morphological Image Operators; Academic Press: Boston, MA, USA, 1994. [Google Scholar]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional networks for biomedical image segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Isola, P.; Zhu, J.; Zhou, T.; Efros, A.A. Image-to-Image Translation with Conditional Adversarial Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5967–5976. [Google Scholar]
- Wen, W.; Wu, C.; Wang, Y.; Chen, Y.; Li, H. Learning Structured Sparsity in Deep Neural Networks. In Proceedings of the 30th Annual Conference on Neural Information Processing Systems 2016, Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- Sze, V.; Chen, Y.; Yang, T.; Emer, J.S. Efficient Processing of Deep Neural Networks: A Tutorial and Survey. Proc. IEEE 2017, 105, 2295–2329. [Google Scholar] [CrossRef] [Green Version]
- Frankle, J.; Carbin, M. The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks. In Proceedings of the Seventh International Conference on Learning Representations (ICLR: 2019), New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- DRIVE: Digital Retinal Images for Vessel Extraction. Available online: https://drive.grand-challenge.org/ (accessed on 9 May 2021).
- Hedjam, R.; Cheriet, M. Historical document image restoration using multispectral imaging system. Pattern Recognit. 2013, 46, 2297–2312. [Google Scholar] [CrossRef]
- Hedjam, R.; Cheriet, M. Ground-Truth Estimation in Multispectral Representation Space: Application to Degraded Document Image Binarization. In Proceedings of the 12th International Conference on Document Analysis and Recognition, Washington, DC, USA, 25–28 August 2013; pp. 190–194. [Google Scholar]
- Aizawa, K.; Fujimoto, A.; Otsubo, A.; Ogawa, T.; Matsui, Y.; Tsubota, K.; Ikuta, H. Building a Manga Dataset “Manga109” with Annotations for Multimedia Applications. IEEE Multimed. 2020, 27, 8–18. [Google Scholar] [CrossRef]
- Matsui, Y.; Ito, K.; Aramaki, Y.; Fujimoto, A.; Ogawa, T.; Yamasaki, T.; Aizawa, K. Sketch-based Manga Retrieval using Manga109 Dataset. Multimed. Tools Appl. 2017, 76, 21811–21838. [Google Scholar] [CrossRef] [Green Version]
- Soille, P. Morphology Image Analysis, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Dougherty, E.R.; Lotufo, R.A. Hands-on Morphological Image Processing; SPIE Press: Bellingham, WA, USA, 2003. [Google Scholar]
- Barrera, J.; Dougherty, E.R.; Tomita, N.S. Automatic Programming of Binary Morphological Machines by Design of Statistically Optimal Operators in the Context of Computational Learning Theory. Electron. Imaging 1997, 6, 54–67. [Google Scholar]
- Hirata, N.S.T. Multilevel Training of Binary Morphological Operators. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 707–720. [Google Scholar] [CrossRef] [PubMed]
- Dellamonica, D., Jr.; Silva, P.J.S.; Humes, C., Jr.; Hirata, N.S.T.; Barrera, J. An Exact Algorithm for Optimal MAE Stack Filter Design. IEEE Trans. Image Process. 2007, 16, 453–462. [Google Scholar] [CrossRef]
- Montagner, I.S.; Hirata, N.S.T.; Hirata, R., Jr. Staff removal using image operator learning. Pattern Recognit. 2017, 63, 310–320. [Google Scholar] [CrossRef]
- Masci, J.; Angulo, J.; Schmidhuber, J. A Learning Framework for Morphological Operators Using Counter—Harmonic Mean. In Mathematical Morphology and Its Applications to Signal and Image Processing; Hendriks, C.L.L., Borgefors, G., Strand, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 329–340. [Google Scholar]
- Mellouli, D.; Hamdani, T.M.; Sanchez-Medina, J.J.; Ayed, M.B.; Alimi, A.M. Morphological Convolutional Neural Network Architecture for Digit Recognition. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 2876–2885. [Google Scholar] [CrossRef] [PubMed]
- Mondal, R.; Purkait, P.; Santra, S.; Chanda, B. Morphological Networks for Image De-raining. In Discrete Geometry for Computer Imagery; Couprie, M., Cousty, J., Kenmochi, Y., Mustafa, N., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; pp. 262–275. [Google Scholar]
- Franchi, G.; Fehri, A.; Yao, A. Deep morphological networks. Pattern Recognit. 2020, 102, 107246. [Google Scholar] [CrossRef]
- Matheron, G.; Serra, J. The birth of mathematical morphology. In Proceedings of the VIth International Symposium on Mathematical Morphology, Sydney, Australia, 3–5 April 2002; Talbot, H., Beare, R., Eds.; pp. 1–16. [Google Scholar]
- Serra, J. Image Analysis and Mathematical Morphology. Volume 2: Theoretical Advances; Academic Press: Cambridge, MA, USA, 1988. [Google Scholar]
- Maragos, P. A Representation Theory for Morphological Image and Signal Processing. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 586–599. [Google Scholar] [CrossRef]
- Maragos, P. Morphological Signal and Image Processing. In Digital Signal Processing Handbook; Madisetti, V., Williams, D., Eds.; CRC Press: Boca Raton, FL, USA, 1998; pp. 74:1–74:30. [Google Scholar]
- Banon, G.J.F.; Barrera, J. Minimal Representations for Translation-Invariant Set Mappings by Mathematical Morphology. SIAM J. Appl. Math. 1991, 51, 1782–1798. [Google Scholar] [CrossRef] [Green Version]
- Matheron, G. Random Sets and Integral Geometry; John Wiley: Hoboken, NJ, USA, 1975. [Google Scholar]
- Ross, K.A.; Wright, C.R.B. Discrete Mathematics, 3rd ed.; Prentice Hall: Hoboken, NJ, USA, 1992. [Google Scholar]
- Naegel, B.; Passat, N.; Ronse, C. Grey-Level Hit-or-Miss Transforms-Part I: Unified Theory. Pattern Recogn. 2007, 40, 635–647. [Google Scholar] [CrossRef] [Green Version]
- Ronse, C. A Lattice-Theoretical Morphological View on Template Extraction in Images. J. Vis. Commun. Image Represent. 1996, 7, 273–295. [Google Scholar] [CrossRef]
- Kaburlasos, V.G. Towards a Unified Modeling and Knowledge-Representation Based on Lattice Theory. In Computational Intelligence and Soft Computing Applications (Studies in Computational Intelligence); Springer: Berlin/Heidelberg, Germany, 2006; Volume 27. [Google Scholar]
- Kaburlasos, V.G. The Lattice Computing (LC) Paradigm. In Proceedings of the 15th International Conference on Concept Lattices and Their Applications (CLA), Tallinn, Estonia, 29 June–1 July 2020. [Google Scholar]
- Dougherty, E.R. Optimal Mean-Square N-Observation Digital Morphological Filters I. Optimal Binary Filters. CVGIP Image Underst. 1992, 55, 36–54. [Google Scholar] [CrossRef]
- Dougherty, E.R. Optimal Mean-Square N-Observation Digital Morphological Filters II. Optimal Gray-Scale Filters. CVGIP Image Underst. 1992, 55, 55–72. [Google Scholar] [CrossRef]
- Hirata, N.S.T.; Barrera, J.; Terada, R.; Dougherty, E.R. The Incremental Splitting of Intervals Algorithm for the Design of Binary Image Operators. In Proceedings of the 6th International Symposium: ISMM 2002, Sydney, Australia, 3–5 April 2002; Talbot, H., Beare, R., Eds.; pp. 219–228. [Google Scholar]
- Hirata, R., Jr.; Dougherty, E.R.; Barrera, J. Aperture Filters. Signal Process. 2000, 80, 697–721. [Google Scholar] [CrossRef]
- Hirata, N.S.T.; Dougherty, E.R.; Barrera, J. Iterative Design of Morphological Binary Image Operators. Opt. Eng. 2000, 39, 3106–3123. [Google Scholar]
- Wolpert, D.H. Stacked Generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Pitas, I.; Venetsanopoulos, A.N. Order statistics in digital image processing. Proc. IEEE 1992, 80, 1893–1921. [Google Scholar] [CrossRef] [Green Version]
- Wendt, P.D.; Coyle, E.J.; Gallagher, N.C., Jr. Stack Filters. IEEE Trans. Acoust. Speech Signal Process. 1986, ASSP-34, 898–911. [Google Scholar] [CrossRef]
- Maragos, P.; Schafer, R.W. Morphological Filters: Part II: Their Relations to Median, Order Statistic, and Stack-Filters. IEEE Trans. Acoust. Speech Signal Process. 1987, ASSP-35, 1170–1184. [Google Scholar] [CrossRef] [Green Version]
- Coyle, E.J. Rank order operators and the mean absolute error criterion. IEEE Trans. Acoust. Speech Signal Process. 1988, 36, 63–76. [Google Scholar] [CrossRef]
- Coyle, E.J.; Lin, J.H. Stack Filters and the Mean Absolute Error Criterion. IEEE Trans. Acoust. Speech Signal Process. 1988, 36, 1244–1254. [Google Scholar] [CrossRef]
- Yoo, J.; Fong, K.L.; Huang, J.J.; Coyle, E.J.; Adams, G.B., III. A Fast Algorithm for Designing Stack Filters. IEEE Trans. Image Process. 1999, 8, 1014–1028. [Google Scholar] [PubMed]
- Harvey, N.R.; Marshall, S. The Use of Genetic Algorithms in Morphological Filter Design. Signal Process. Image Commun. 1996, 8, 55–71. [Google Scholar] [CrossRef]
- Yoda, I.; Yamamoto, K.; Yamada, H. Automatic Acquisition of Hierarchical Mathematical Morphology Procedures by Genetic Algorithms. Image Vis. Comput. 1999, 17, 749–760. [Google Scholar] [CrossRef]
- Quintana, M.I.; Poli, R.; Claridge, E. Morphological algorithm design for binary images using genetic programming. Genet. Program. Evolvable Mach. 2006, 7, 81–102. [Google Scholar] [CrossRef] [Green Version]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef] [Green Version]
- Viola, P.; Jones, M. Rapid object detection using a boosted cascade of simple features. In Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Kauai, HI, USA, 8–14 December 2001; Volume 1. [Google Scholar]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), San Diego, CA, USA, 20–25 June 2005; Volume 1, pp. 886–893. [Google Scholar]
- Fukushima, K.; Miyake, S. Neocognitron: A Self-Organizing Neural Network Model for a Mechanism of Visual Pattern Recognition. In Competition and Cooperation in Neural Nets; Amari, S.I., Arbib, M.A., Eds.; Springer: Berlin/Heidelberg, Germany, 1982; pp. 267–285. [Google Scholar]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation Applied to Handwritten Zip Code Recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- CS231n: Convolutional Neural Networks for Visual Recognition. Available online: https://cs231n.github.io/ (accessed on 29 July 2020).
- Julca-Aguilar, F.D.; Hirata, N.S.T. Image operator learning coupled with CNN classification and its application to staff line removal. In Proceedings of the 14th IAPR International Conference on Document Analysis and Recognition (ICDAR), Kyoto, Japan, 9–15 November 2017; pp. 53–58. [Google Scholar]
- Cireşan, D.C.; Giusti, A.; Gambardella, L.M.; Schmidhuber, J. Deep Neural Networks Segment Neuronal Membranes in Electron Microscopy Images. In Proceedings of the International Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 2843–2851. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Chen, Q.; Xu, J.; Koltun, V. Fast Image Processing with Fully-Convolutional Networks. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), IEEE Computer Society, Venice, Italy, 22–29 October 2017; pp. 2516–2525. [Google Scholar]
- Wang, C.; Xu, C.; Wang, C.; Tao, D. Perceptual Adversarial Networks for Image-to-Image Transformation. IEEE Trans. Image Process. 2018, 27, 4066–4079. [Google Scholar] [CrossRef] [Green Version]
- Ritter, G.X.; Sussner, P. An introduction to morphological neural networks. In Proceedings of the 13th International Conference on Pattern Recognition, Washington, DC, USA, 25–29 August 1996; Volume 4, pp. 709–717. [Google Scholar]
- Sussner, P.; Esmi, E.L. Constructive Morphological Neural Networks: Some Theoretical Aspects and Experimental Results in Classification. In Constructive Neural Networks; Franco, L., Elizondo, D.A., Jerez, J.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 123–144. [Google Scholar] [CrossRef]
- Zamora, E.; Sossa, H. Dendrite morphological neurons trained by stochastic gradient descent. Neurocomputing 2017, 260, 420–431. [Google Scholar] [CrossRef]
- Mondal, R.; Santra, S.; Chanda, B. Dense Morphological Network: An Universal Function Approximator. arXiv 2019, arXiv:abs/1901.00109. [Google Scholar]
- Davidson, J.L.; Hummer, F. Morphology neural networks: An introduction with applications. Circuits Syst. Signal Process. 1993, 12, 177–210. [Google Scholar] [CrossRef]
- Won, Y.; Gader, P.D.; Coffield, P.C. Morphological shared-weight networks with applications to automatic target recognition. IEEE Trans. Neural Netw. 1997, 8, 1195–1203. [Google Scholar] [PubMed]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Netzer, Y.; Wang, T.; Coates, A.; Bissacco, A.; Wu, B.; Ng, A.Y. Reading Digits in Natural Images with Unsupervised Feature Learning. In Proceedings of the NIPS 2011 Workshop on Deep Learning and Unsupervised Feature Learning, Granada, Spain, 16–17 December 2011. [Google Scholar]
- Krizhevsky, A. Learning Multiple Layers of Features from Tiny Images; Technical Report; University of Toronto: Toronto, ON, Canada, 2009. [Google Scholar]
- Fu, X.; Huang, J.; Ding, X.; Liao, Y.; Paisley, J. Clearing the Skies: A Deep Network Architecture for Single-Image Rain Removal. IEEE Trans. Image Process. 2017, 26, 2944–2956. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mondal, R.; Chakraborty, D.; Chanda, B. Learning 2D Morphological Network for Old Document Image Binarization. In Proceedings of the International Conference on Document Analysis and Recognition (ICDAR), Sydney, Australia, 20–25 September 2019; pp. 65–70. [Google Scholar]
- Real, E.; Liang, C.; So, D.R.; Le, Q.V. AutoML-Zero: Evolving Machine Learning Algorithms From Scratch. arXiv 2020, arXiv:cs.LG/2003.03384. [Google Scholar]
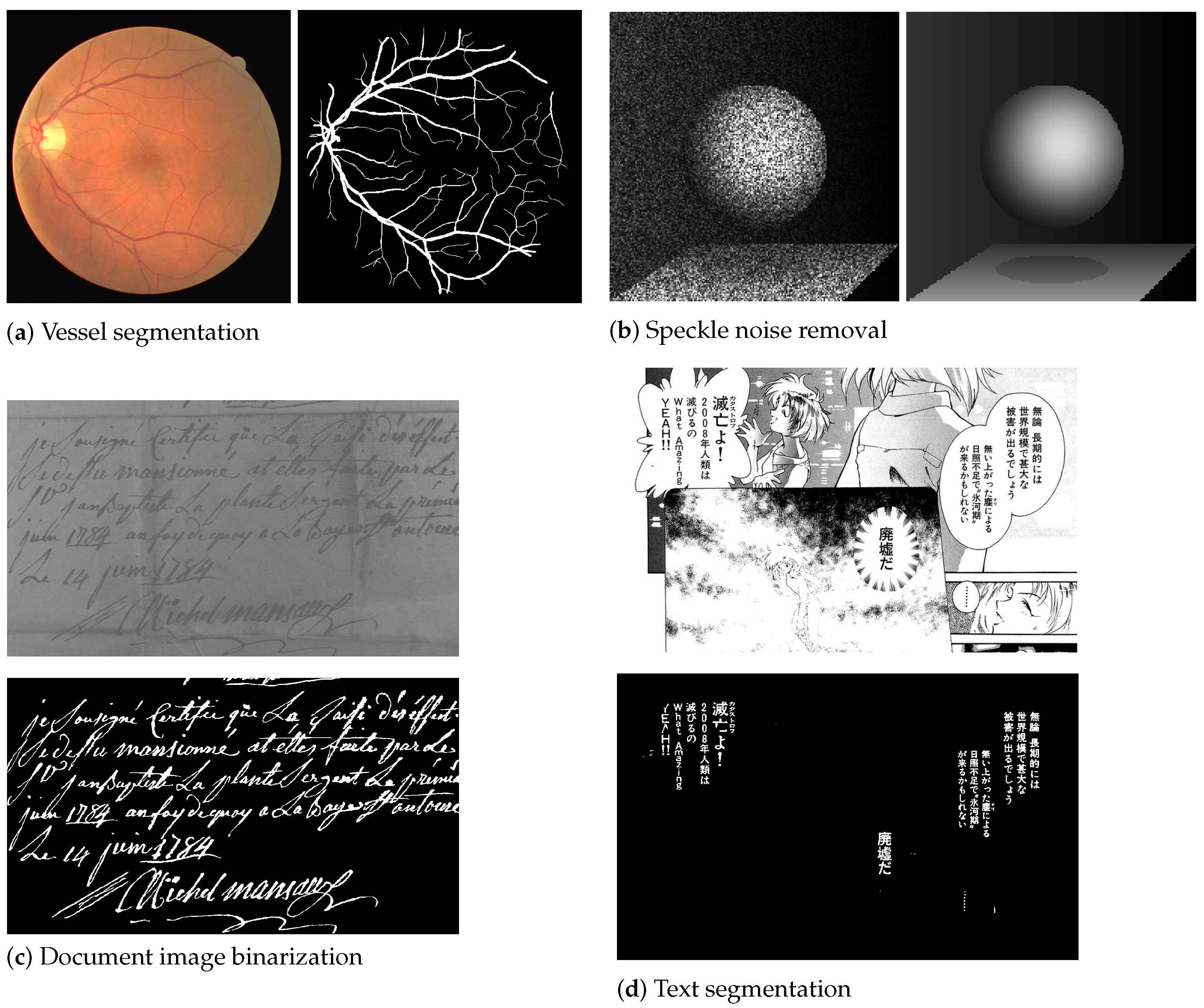


| Task | Architecture Details | Remarks |
|---|---|---|
| Defect detection in steel surface images [25]. | Two morphological layers with two nodes each, followed by a convolutional layer and an absolute difference (with respect to input image). Morphological nodes are the ones defined in Equation (19) and thus only an approximation of erosions and dilations are computed. | The ground-truth images were generated by applying white top-hat with a disk of size 5 and a black top-hat with a line of size 10 that have been verified to be useful to detect bright small spots as well as dark line-like structures that characterize possible defects. |
| Noise filtering [25] (1) Binomial noise (2) Salt-and-pepper (3) Additive Gaussian noise | (1) Two morphological layers with single node each (filter size 5 × 5). (2) 4 morphological layers with single node each. (3) Two morphological layers with two filters each plus an averaging layer. Same observation of the above cell, regarding morphological nodes. | Network results are compared with: (1) A 2 × 2 opening; (2) a closing followed by an opening by a 2 × 2 structuring element; (3) the total variation restoration. The trained networks performed better than the hand-crafted operators, except for case (3). |
| Noise filtering [28] Salt-and-pepper noise | A sequence of morphological layers with single node each, corresponding to the sequence opening-closing-opening. | Results indicate that the filtering task can be learned. |
| Edge detection [28] | A convolutional neural network with one learnable morphological pooling layer, thus a hybrid network. | An edge enhancing pre-processing is performed on the input images. The example showcases the use of morphological pooling layers. |
| Detraining [27] | Architectures with two branches, each consisting of a sequential composition of erosion and dilation nodes. The two branches are linearly combined at the end. | The networks are trained and tested on a synthetic rainy image dataset made available in [76]. One of the networks, with 16,780 parameters, presents a similar performance to the one obtained with a U-Net with 6,110,773 parameters. |
| Document binarization [77] | Erosion and dilation nodes on multi-channel inputs are defined considering a multi-channel structuring function that generates a one-channel feature map. Then a morphological block is defined as consisting of dilation and erosion nodes, followed by linear combination nodes of the channels. A network is a sequence of such blocks, with sigmoid activation at the end. | Competitive results, for instance, with those of runners-up in the ICDAR2017 Competition on Document Image Binarization are achieved. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hirata, N.S.T.; Papakostas, G.A. On Machine-Learning Morphological Image Operators. Mathematics 2021, 9, 1854. https://doi.org/10.3390/math9161854
Hirata NST, Papakostas GA. On Machine-Learning Morphological Image Operators. Mathematics. 2021; 9(16):1854. https://doi.org/10.3390/math9161854
Chicago/Turabian StyleHirata, Nina S. T., and George A. Papakostas. 2021. "On Machine-Learning Morphological Image Operators" Mathematics 9, no. 16: 1854. https://doi.org/10.3390/math9161854
APA StyleHirata, N. S. T., & Papakostas, G. A. (2021). On Machine-Learning Morphological Image Operators. Mathematics, 9(16), 1854. https://doi.org/10.3390/math9161854







