1. Introduction
The usual approach in models for time-to-event data is built on the assumption that all subjects will experience the event of interest if the follow-up time is long enough. In many studies in different areas, there are subjects insusceptible to the event of interest. We call cure rate the proportion of insusceptible subjects. Cure rate models, also known as long-term survival models, are capable to deal with this situation.
Cure rate models have had an intense research activity in last years. From the seminal contributions in [
1,
2] and the approach based on competing risks for cure rate models in [
3], we find many papers in recent years on this research area. The competing risks approach is summarized as follows. Let
M be an unobserved variable denoting the initial number of competing causes related to the occurrence of the event of interest. For instance, in cancer studies
M represents the number of carcinogenic cells at the end of treatment that can produce a detectable cancer. For
M following the Bernoulli or the Poisson distribution, we obtain the models in [
2,
3], respectively. The time for the
j-th competing cause to produce the event of interest (that is, the promotion time) is denoted by
,
. We also assume that, conditional on
M, the latent times
are independent and identically distributed with cumulative distribution function (cdf)
and survival function
, where
is the parameter vector. Under a competing risks setup, the time elapsed until the event of interest is given by
, where
is a random variable degenerate at
. Our paper is based on the competing risks approach for cure rate models.
Many cure rate models proposed in last years are formulated from different distributions for the number of competing causes
M. This research line includes the negative binomial [
4], COM-Poisson [
5], power series [
6], Yule-Simon [
7], polylogarithm [
8], modified power series [
9], zero inflated power series [
10] and zero-modified geometric [
11] distributions, among many others. In this vein, we adopt the one-parameter Bell distribution recently proposed in [
12], with probability mass function (pmf)
for
, where
is the Bell number defined as
. The first few Bell numbers are
and
. We denote
to say that
M follows a distribution with pmf in (
1). Denoting the mean and the variance of
M by
and Var
, respectively, we have that
and Var
. Since Var
, the Bell distribution accommodates overdispersed counts. For cure rate models, this distribution is interesting due to some characteristics:
The distribution has only one parameter, being an alternative to traditional discrete distributions such as Poisson and Geometric.
The probability generating function (pgf) of the distribution has a simple expression. In fact, if
, then its pgf is given by
, for
. See Proposition 1 in [
12]. This fact is relevant from the point of view of cure rate models because the population survival function depends on this function.
has a simple form. This fact is important because this probability is the cure rate of the model. The simplicity of this term allows, among other things, to reparameterize the model in terms of the cure rate.
The distribution belongs to the power series family of distributions [
13] with pmf
, where
,
, and
. Recently, ref. [
14] proposed an EM-type algorithm for a class of cure rate models based on the power series family. The maximization (M) step of the EM algorithm is decomposed in two steps involving the distribution of the number of competing causes
M and the distribution of the latent times
Z.
To the best of our knowledge, the Bell distribution has not yet been proposed to model the number of competing causes in a cure rate models context.
The remaining of the paper is organized as follows. In
Section 2, we present the cure rate rate model. Inference methods are presented in
Section 3.
Section 4 is dedicated to a simulation study covering properties of the estimators and model selection. A dataset on melanoma is analyzed in
Section 5. Closing remarks are given in
Section 6.
2. Model
Let
M be an unobserved variable denoting the initial number of competing causes related to the occurrence of an event of interest. We assume that
. Under the competing risks setup in
Section 1, from Theorem 2 in [
4], see also [
15], we have that the (improper) population survival function of the Bell cure rate (Bellcr) model is given by
It is immediate that the cure rate of the model is given by . Henceforth, we adopt the parameterization , i.e., . In this way, covariates can be directly linked to the cure rate p, allowing to compare regression coefficients among different models parameterized in terms of the cure rate.
An interesting family of cure rate models parameterized in the cure rate is studied in [
16]. Such family includes the Bernoulli cure rate (Berncr) model, also known as mixture cure model [
1,
2], the Poisson cure rate (Pocr) model, also known as the promotion time cure model [
3,
17], the logarithmic cure rate (Locr) model and the negative binomial cure rate (NBcr) model, noticing that the NBcr model has an additional parameter
q and
corresponds to the geometric cure rate (Geocr) model.
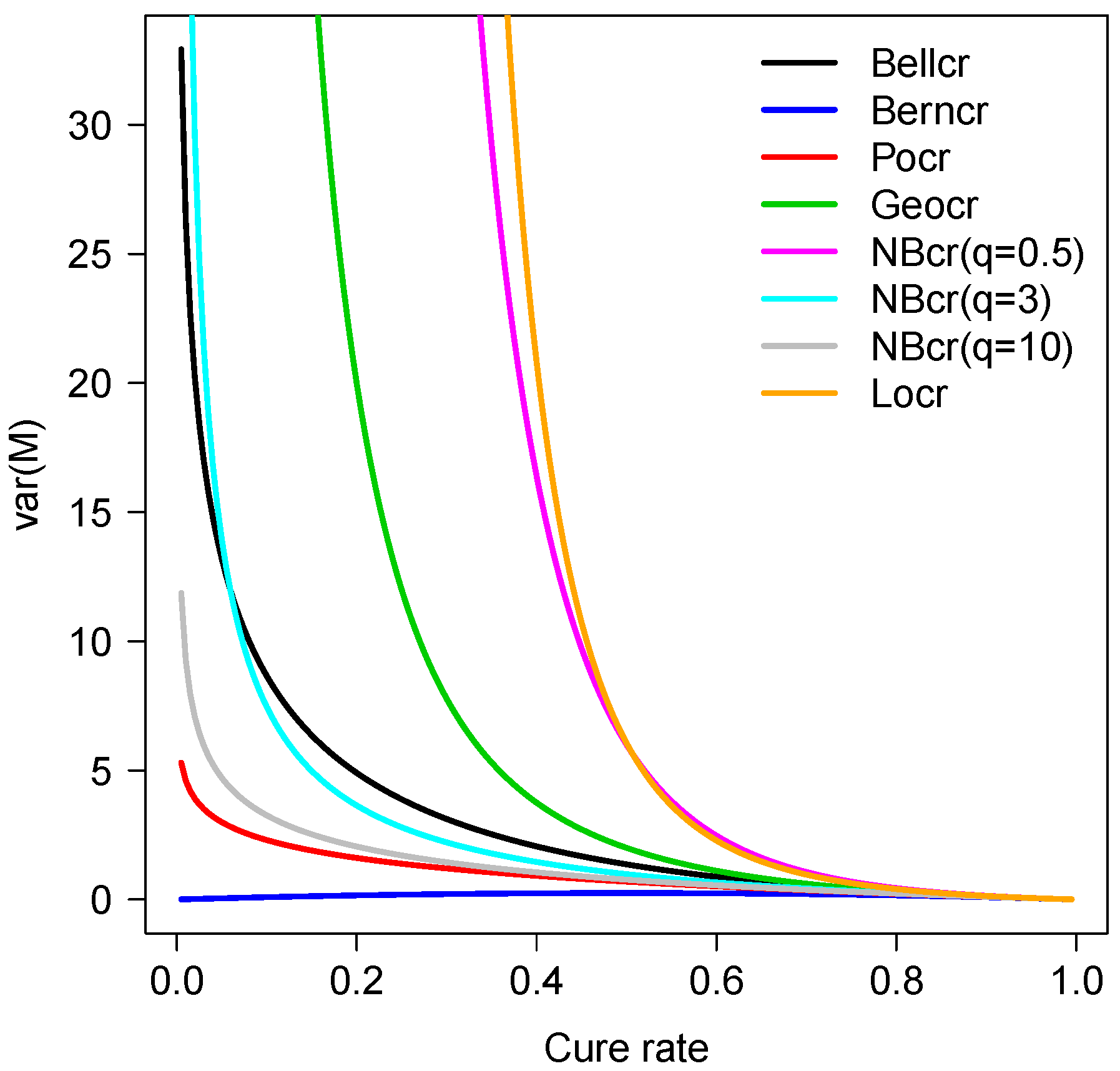
Table 1 and
Figure 1 show the variance of the number of competing causes
M in terms of the cure rate for some models. Note that the curve for the Bellcr model lies between the Geocr and Pocr models. Also, the curves for the NBcr model with
q = 0.3, 5 and 10 are close to the Locr, Bellcr and Pocr models, respectively. In fact, by applying the L’Hopital’s rule, we have
so that the proximity between the NBcr
and Pocr curves is justified.
With the parameterization in the cure rate
p, the population survival function for the Bellcr model in (
2) is recast, leading to
so that the population density and hazard functions are given by
In a sample of size
n, for the
i-th subject the covariates are represented by
,
, where the symbol “⊤” denotes the transpose operator. The cure rate
is linked to
through the logistic function, that is,
where
is the vector of regression coefficients of dimension
. Therefore, interpretations about the regression coefficients can be obtained in terms of the odds ratio for the cure probability.
3. Inference
In this section, we present some details about the estimation procedure for the parameters of the model in
Section 2. We consider a framework in which the lifetimes are subject to right censoring. Let
and
be the failure and censoring time variables for the
i-th subject, respectively. In a sample of size
n, the observed variables are
and
, where
and
denote either if a failure or a censored time was observed for the
i-th subject, respectively,
. Under the usual assumption of non-informative censoring and with
as in (
5), the log-likelihood function of
is given by
The maximum likelihood (ML) estimator of
,
say, is obtained by maximizing (
6) with respect to
. However, direct maximization is not computationally simple because some terms in (
6) involve both
and
. For this reason and taking advantage of the EM algorithm developed for the power series family of cure rate models in [
14], ML estimates in the Bellcr model are computed using this algorithm. In short, the
k-th iteration of the EM algorithm goes as follows:
E step: For
, compute
, where
with
and
comes from (
5).
M step 1: Given
, find
that maximizes
with respect to
, where
M step 2: Given
, find
that maximizes
with respect to
, where
The E and M steps are cycled until a suitable convergence criterion is attained, for instance,
, where “
” denotes the Euclidean norm and
is a specified tolerance. Maximization of the functions in (
7) and (
8) can be performed using the optim function in R language [
19].
We stress that the proposed EM algorithm procedure is general in the sense that it can accommodate different distributions for the latent time
Z in
Section 1. In this work, we assume the Weibull distribution, denoted by Wei
, because it is a suitable model in a cure rate model context. With
, the survival function for this distribution is given by
, for
,
and
.
On the other hand, the normal theory asymptotic covariance matrix of the maximum likelihood estimator
can be estimated from minus the Hessian matrix of the log-likelihood function in (
6) evaluated at
. The numDeriv R package [
20] provides a numerical approximation to this matrix. Interval estimates of the parameters are computed from the asymptotic standard errors. Computational codes are available from the authors upon request.
Finally, inference usually is made on the cure rate. However, we might also be interested in the cure rate for subjects who survived up to a certain time
, denoted by
. First, for
, from (
3) we have
. Then, omitting the dependence on the covariates and passing to the limit for
we obtain the conditional cure rate
Of course, if
in (
9),
reduces to the cure rate
p in (
5). For comparatives purposes, Remark 1 gives expressions for
under the Pocr, Locr, NBcr and Bincr models.
Remark 1. For the Pocr, Locr, NBcr and Bincr models, routine calculation shows that is given by
where
.
4. Simulation Studies
In this section, we present two simulation studies. The main goal of the first study is to assess the performance of the ML estimates for the parameters of the Bellcr model computed with the EM algorithm in
Section 3. The second study is devoted to model selection based on Vuong’s test statistic in [
21] (see
Appendix A) when the true cure rate model is the Bellcr model or may be wrongly specified. The null hypothesis states that the two compared models are undistinguishable. If the null hypothesis is rejected, the model with the highest value of the likelihood function is preferable. We pick a model with three covariates
,
and
.
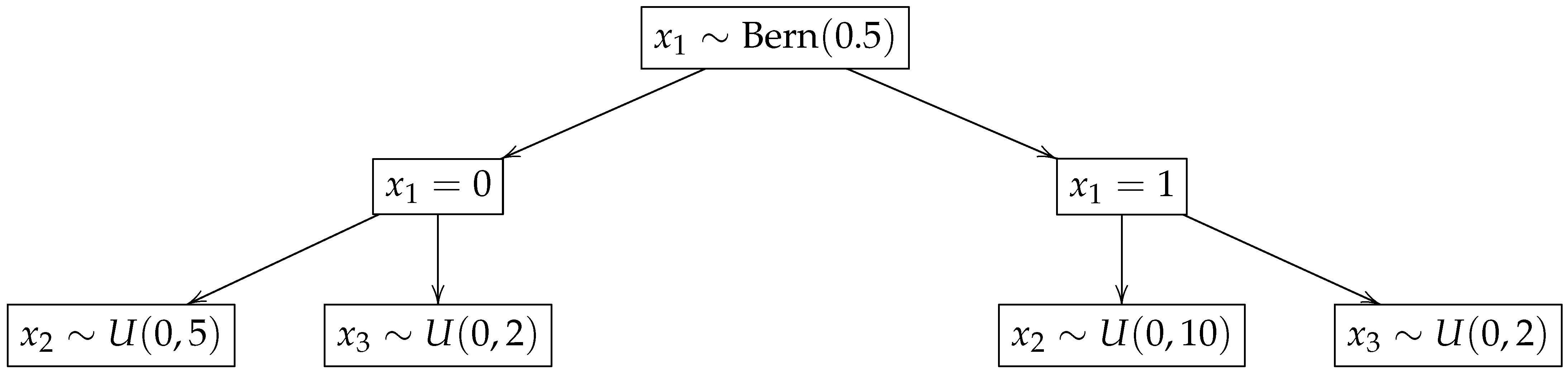
Figure 2 shows the scheme to draw the covariates.
The true value of
is computed from four combinations of values of
and cure rates
. For
, we choose
,
,
and
. Solving the equations in (
5), we get
,
,
and
, where
, for
. In the studies presented here, cure rates
are
,
and
, labeled as Cure 1, Cure 2 and Cure 3, respectively. On the other hand, to set the vector
we choose values for the expected value
and the variance Var
of the latent time
Z in
Section 1. For the Wei
distribution in
Section 3, these conditions imply that
and
is the solution to the equation
.
Table 2 showcases the true values of the parameters for the simulations.
The simulations comprise two sample sizes,
and
, and two cases for the latent time
Z in
Section 1, namely, (i)
and Var
and (ii)
and Var
. For each combination of sample size, cure rate
and
, we compute
, with
as in (
5). Next,
is drawn from the Bell
distribution. If
, the failure time is
. If
, we draw
from the Wei
distribution and the failure time is
. The censoring time
is sampled from the
distribution. A simulated dataset is formed by
,
and
,
. For the Pocr, Locr, NBcr, Geocr and Berncr models in
Section 4.2, the data generation process is similar.
Each scenario was replicated 1000 times. The average proportion of censored times ranges from 56% to 77%. The vectors of covariates , , are kept fixed throughout the replications.
4.1. Estimation
Having in mind the goal of assessing the behavior of the ML estimates of the parameters in the Bellcr model,
Table 3 reports the simulated bias for each parameter (Bias), the average of the asymptotic standard errors (SE) based on the covariance matrix in
Section 3, the root of the simulated mean squared error (RMSE) and the coverage probability of the normal theory 95% asymptotic confidence intervals (CP). In general, the estimators show a good behavior in all scenarios of our study. We see that Bias is low so that SE and RMSE are close and get closer when the sample size is 400. It is noteworthy that CP is close to the nominal value for both sample sizes, ranging from 0.939 to 0.963. Overall, we see that within the scope of our study, the estimators and the estimation algorithm in
Section 3 have a good performance.
4.2. Model Comparison
In this section, we present a simulation study aimed to test the Bellcr model against the Pocr, Locr, NBcr and Geocr models. In our comparisons, the models are compared with the Bellcr model whichever the model generating the data (True model in
Table 4 and
Table 5). The models are tested against the Bellcr model using the Vuong’s test statistic. The nominal significance level is 5%.
In
Table 4, when the data generating model is the Bellcr model, rejection rates of the Bellcr model are very low regardless of the model being compared, as expected. When the true model is the Pocr model, the highest rejection rates of the Bellcr model, between 11.4% and 24.4%, correspond to the Pocr and NBcr models. We recall the Pocr model is a limiting case of the NBcr model. In
Table 4 and
Table 5, we see null rejection rates (up to one decimal place) of the Bellcr model against the Berncr model. This is not surprising because the Berncr model (mixture cure model) is too simple to cope with the structure of the data generated in our simulation study.
When the data are drawn from the NBcr
model, rejection rates in
Table 4 are low, as expected in light of
Figure 1. The largest rejection rates of the Bellcr model are achieved when the true model is the Locr model in
Table 4 (rates between 75.8% and 80.9%) and the Geocr model in
Table 5 (rates between 15.8% and 96.2%). In all scenarios in
Table 4 and
Table 5, rejection rates of the Bellcr model are consistent with the patterns in
Figure 1.
5. Data Analysis
In this section, we conduct an analysis of a dataset on melanoma available at the timereg R package [
22]. The study includes 205 patients, with survival times observed after an operation for removal of a malignant melanoma. The observed times vary from 10 to 5565 days (from 0.03 to 15.24 years), with mean and median 5.89 and 5.49 years, respectively, and standard deviation 3.07 years. The dataset comprises 148 censored observations (72.2%), corresponding to patients who died from other causes or were still alive at the end of the study. The dataset includes the covariates ulceration status
(absent,
; present,
) and tumor thickness
(in mm, mean = 2.91, median = 1.94 and standard deviation = 2.96).
We consider the Bell cure rate model for analyzing this dataset. For comparison purposes, we also consider the Pocr, Locr, NBcr, Geocr and Bincr models. We assume the Weibull distribution for the time-to-event for the concurrent causes. First we assess the goodness of fit of the models. For such purpose, we use the Cox-Snell residual, see, e.g., [
23] and the normalized quantile residual [
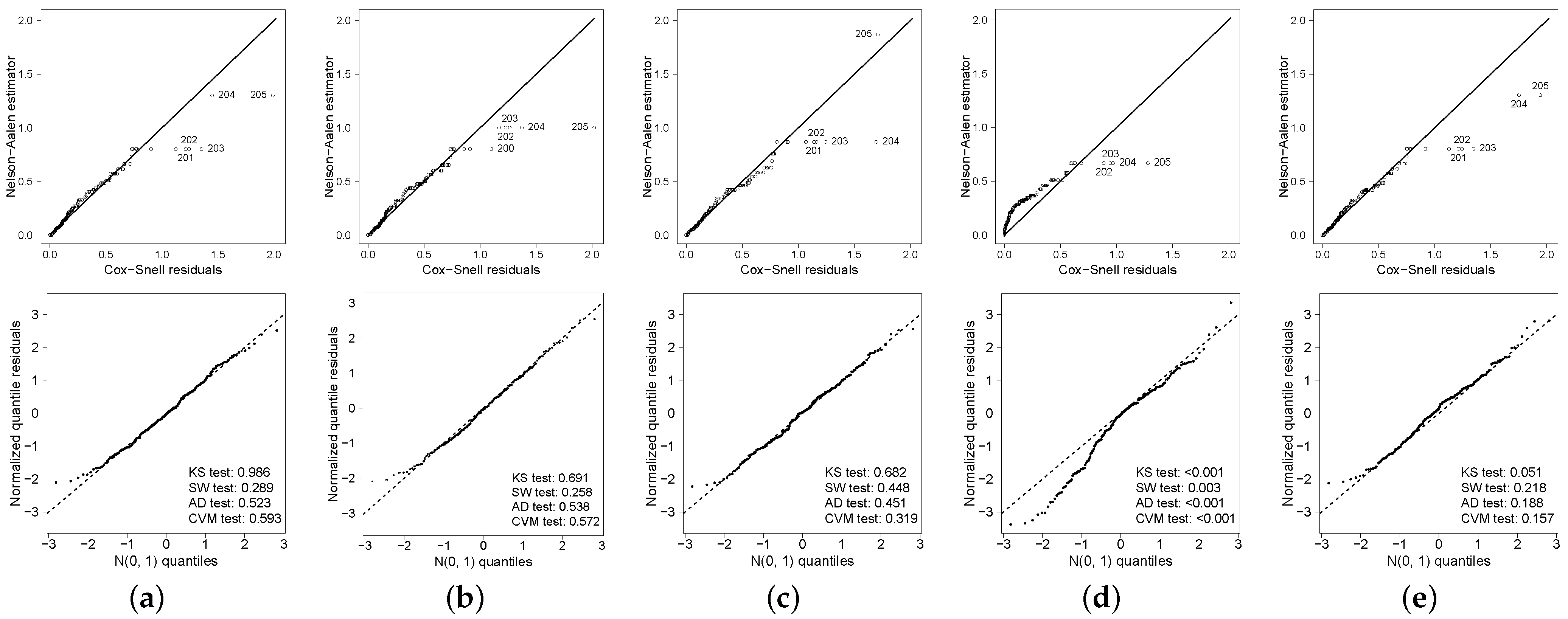
24]. In
Figure 3, we see that the Bellcr, Pocr, Locr and Geocr models yield a reasonable fit. However, the deviation from the identity line in both residuals plot is evident for the NBcr model. We omit the results for the Bincr model because the plots are similar to the ones for the NBcr model. For this reason, we disregard the NBcr and Bincr models. The Cox-Snell residuals highlight observations 200–205, which correspond to the largest censored times. On the other hand, the normalized quantile residuals do not suggest the presence of possible poorly fitted observations.
Table 6 displays parameter estimates and odds ratio for the Bellcr, Locr, Pocr and Geocr models. At a 5% significance level, the coefficients of ulceration status
and tumor thickness
are significant and the negative sign is as expected. Moreover, the estimates of
indicate that the exponential distribution for the latent times in
Section 1 is not adequate.
Note that for all the models, . Therefore, patients with ulceration have approximately their probability of being cured reduced by a quarter in relation with patients without ulceration.
Table 7 shows the Vuong’s statistic for the fitted models. At a 5% significance level, we conclude that the Bellcr model is preferred to the Pocr model. Moreover, there is no significant difference among the Bellcr and the Locr and Geocr models.
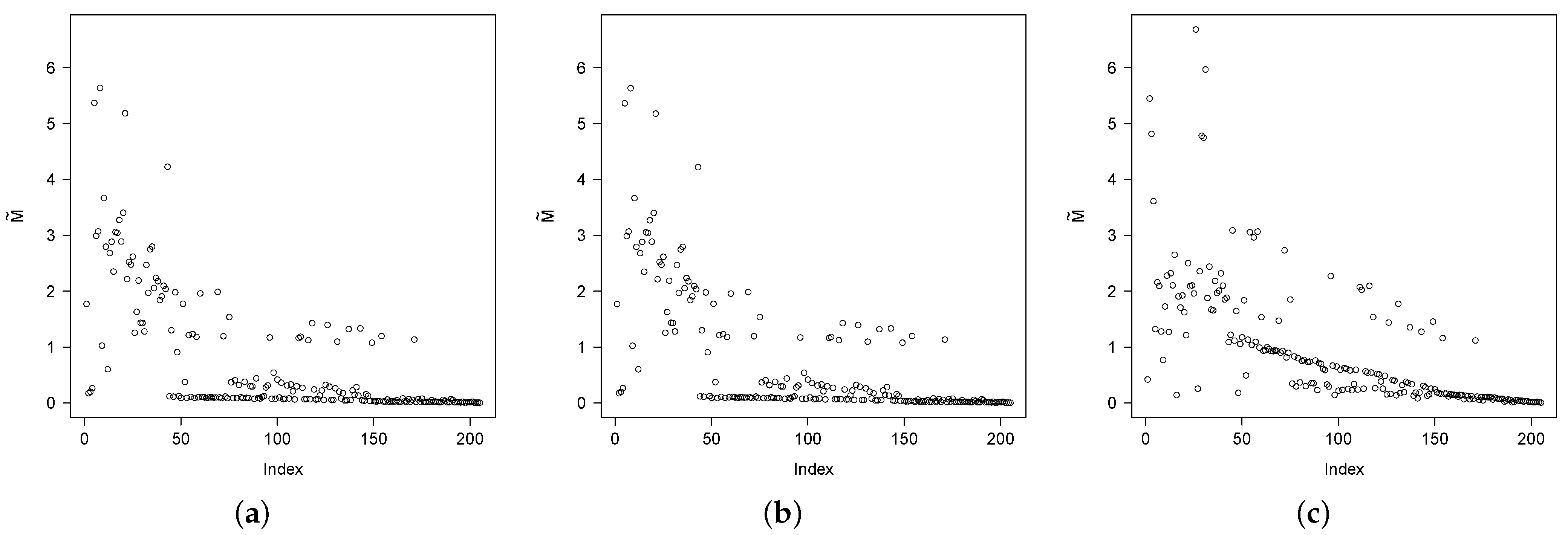
Figure 4 shows the estimates of the mean of the conditional distribution of
, say
, for
. As previously discussed, values closer to 0 suggest which individuals are cured. Note that the Bellcr and Locr models provide very similar values. For instance, the observation 6 corresponds to a patient who died after 204 days (0.56 years), with ulceration and a tumor thickness of 4.84 cm., providing
equal to 2.988, 2.985 and 2.156 for Bellcr, Locr and Geocr models, respectively. Therefore, the three models suggest that this observation has a greater number of carcinogenic cells (a susceptible individual). Similarly, the observation 149 corresponds to a patient who died after 2782 days (7.62 years), without ulceration and a tumor thickness of 1.94 cm., providing
equal to 1.076, 1.076 and 1.453 for Bellcr, Locr and Geocr models. This explains why the patient 6 fails in a time considerably lower than patient 149. In a similar way, the observation 203 has a censored time after 4688 days (12.84 years), without ulceration and a tumor thickness of 0.48 cm., resulting in
equal to 0.002, 0.002 and 0.015 for the three models. In this case, the models agree that this patients is a potentially cured individual.
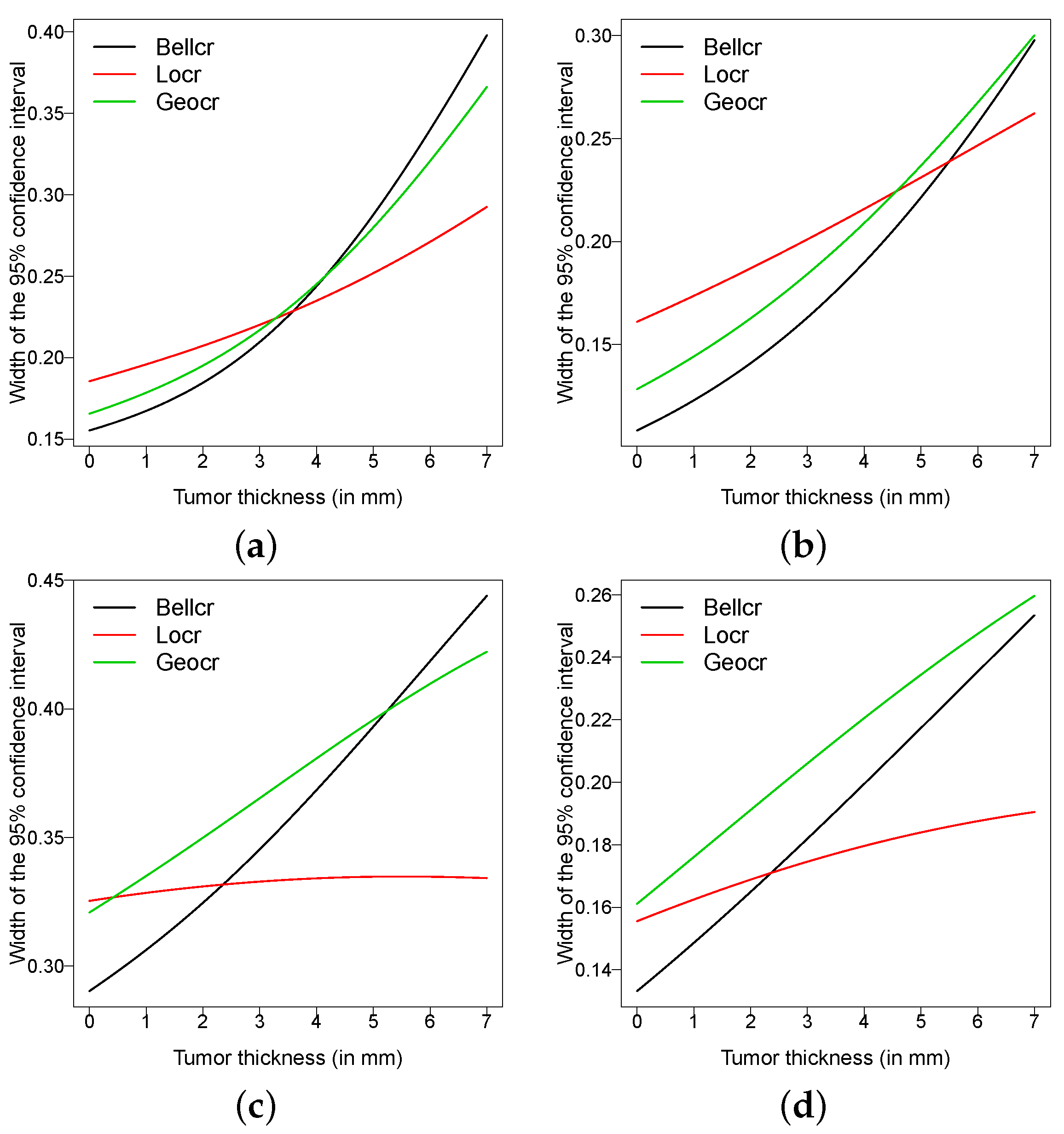
Finally,
Figure 5 presents the width of the 95% confidence intervals for the conditional cure rate in (
9) and
Figure 6 displays estimates of cure rate under the Bellcr, Locr and Geocr models. In all models, the confidence intervals are computed using the delta method [
25] (Theorem 3.4.5) using expressions of the covariance matrix of the estimators in the power series cure rate model presented in Gallardo et al. [
14]. For the Locr and Geocr models, the conditional cure rate is computed as in Remark 1. Note that the Bellcr model provides more accurate confidence intervals for some settings in
Figure 5. Finally,
Figure 6 shows the conditional cure rate in Equation (
9) for different in terms of the tumor thickness for
and
years and patients with and without ulceration.
6. Conclusions
In this paper, a cure rate model is proposed under the competing risks setup. For the number of competing causes of the event of interest, we posit the Bell distribution. This is a one-parameter distribution that accommodates overdispersed counts. [
26] emphasized that the Poisson distribution represents a strong assumption when modelling the number of competing causes. Therefore, compared to the two-parameter negative binomial distribution, the proposed model is more parsimonious. The cure rate is a parameter linked to covariates, facilitating the comparison with other models. Parameter estimates are computed through iterative steps of the EM algorithm. In order to compare different models, the test statistic proposed in [
21] is implemented. In our simulation studies, the estimation method and the test statistic have a good performance.
A dataset on melanoma is analyzed using the proposed model as well as some models from the literature. Extensions of the proposed model to accommodate other types of censoring (e.g., interval censoring) might be a theme for future work.