Revisited Carmichael’s Reduced Totient Function

Abstract

The modified Totient function of Carmichael $\lambda (.)$ is revisited, where important properties have been highlighted. Particularly, an iterative scheme is given for calculating the $\lambda (.)$ function. A comparison between the Euler $\phi$ and the reduced totient $\lambda (.)$ functions aiming to quantify the reduction between is given.

1. Introduction

More than a century ago, Robert D. Carmichael (1879–1967) [1] introduced a function $\lambda (.)$ known as Carmichael’s function. This $\lambda \left(n\right)$ is spread as the reduced totient function which can be seen as the smallest divisor of Euler’s totient function verifying Euler’s theorem. This Totient function is deeply related to prime numbers and integer orders [2,3,4,5], mainly used for primality testing. Furthermore, the reader may cross in the literature that the Carmichael function represents the exponent ($\lambda \left(n\right)$ represents the order of the largest cyclic subgroup of ${\left(Z/nZ\right)}^{*}$) of the group ${\left(Z/nZ\right)}^{*}$.

In this paper, we aim to analyse $\lambda (.)$ and we present some of its important properties. Mainly, we give in Lemma 3 a suitable iterative scheme for calculating the values of $\lambda \left(n\right)$. In addition, we prove the following estimation

$$\lambda \left(n\right)\le {\displaystyle \frac{1}{2^{N-1}}}\phi \left(n\right),N\mathrm{is} \mathrm{the} \mathrm{number} \mathrm{of} \mathrm{odd} \mathrm{prime} \mathrm{divisors} \mathrm{of}n,$$

which could be considered an indicator of reduction of the modified totient function and we can easily duduce that

$${\displaystyle \underset{n\to \infty }{lim\; sup}{\displaystyle \frac{\phi \left(n\right)}{\lambda \left(n\right)}}=+\infty .}$$

The complexity of finding the inverse function of Carmichael $\lambda (.)$ is more complex than finding the inverse of Euler function.

2. Preliminaries

In the literature, Carmichael’s new totient function named $\lambda$ is defined as follows: For the prime decomposition of a given natural integer

$$n=\prod _{i=1}^k{p}_i^{k_i},\lambda \left(n\right)=LCM\left[\lambda \left(p_1^{k_1}\right),\dots ,\lambda \left(p_k^{k_k}\right)\right],$$

where (LCM denotes the least common multiple.) we have:

$$\lambda \left(p_i^{k_i}\right)=\left\{\begin{array}{ccc}{2}^{k_i}-2\hfill & \mathrm{If}& p_i=2\mathrm{and}{k}_i>2,\hfill \\ p_i^{k_i-1}(p_i-1)\hfill & & otherwise.\hfill \end{array}\right.$$

We refer to [1,2,6,7] and references therein for the properties of the function $\lambda$.

Figure 1 and Figure 2 produce the first thousand values of $\lambda \left(p\right)$ and $\phi \left(p\right)$. The points on the top lines represent $\lambda \left(p\right)=p-1=\phi \left(p\right),$ when p is a prime number.

Figure 1. The first 1000 values of the Carmichael function.

Figure 2. The first 1000 values of the Euler function.

In this section, we show how we built the modified Totient function $\lambda$.

Euler theorem [1] states that if n and m are co-prime positive integers, then

$$m^{\phi \left(n\right)}\equiv 1\left(modn\right),$$

where $\phi (.)$ is Euler’s Totient function. It is known that for any prime number p, we have $\phi \left(p\right)=p-1$ since all the positive integers less than p are co-prime with p.

If p and q are two different primes, then

$$\left\{\begin{array}{cc}{m}^{k_1(p-1)}\equiv 1\left(modp\right)\hfill & \forall k_1\in N,gcd(m,p)=1.\hfill \\ \\ m^{k_2(q-1)}\equiv 1\left(modq\right)\hfill & \forall k_2\in N,gcd(m,q)=1.\hfill \end{array}\right.$$

The two integers $k_1$ and $k_2$ can be chosen in such a way that

$$k_1(p-1)=k_2(q-1),$$

then we obtain:

$$\left\{\begin{array}{cc}{m}^{k_1(p-1)+1}\equiv m\left(modp\right)\hfill & \forall k_1\in N,\forall m\in N.\hfill \\ \\ m^{k_2(q-1)+1}\equiv m\left(modq\right)\hfill & \forall k_2\in N,\forall m\in N.\hfill \end{array}\right.$$

We can also conclude the following

$$m^{k_1(p-1)+1}\equiv m^{k_2(q-1)+1}\equiv m\left(modpq\right).$$

(1)

In the next definition, we introduce a new function related to the Totient function of Euler given as follows:

Definition 1.

Let $n=pq$

$$\begin{array}{ccc}\lambda \left(n\right)\hfill & =& min\{k_1(p-1):k_1(p-1)=k_2(q-1)\}\hfill \\ \hfill & =& min\{k_1\phi \left(p\right):k_1\phi \left(p\right)=k_2\phi \left(q\right)\}.\hfill \end{array}$$

(2)

According to the above definition, we will have:

$$m^{\lambda \left(pq\right)+1}\equiv m\left(modpq\right),\forall m\in N,$$

(3)

and by using previous results, we can conclude the following Lemma.

Lemma 1.

Let p and q two different primes

• If $gcd(m,pq)=1$, then

  $$\left\{\begin{array}{c}{m}^{\phi \left(n\right)}\equiv 1\left(modpq\right)\\ \\ m^{\lambda \left(n\right)}\equiv 1\left(modpq\right).\end{array}\right.$$
• For all integer m, then

  $$\left\{\begin{array}{c}{m}^{\phi \left(n\right)+1}\equiv m\left(modpq\right)\\ \\ m^{\lambda \left(n\right)+1}\equiv m\left(modpq\right).\end{array}\right.$$

Let us generalize the previous Lemma for ${\displaystyle n={\Pi }_{i=1}^N{p}_i,\forall N\in N}$, but the function $\lambda \left({\displaystyle n={\Pi }_{i=1}^N{p}_i}\right)$ needs also to be generalized.

From Euler theorem, we can write

$$\left\{\begin{array}{cc}{m}^{k_i(p_i-1)+1}\equiv m\left(mod{p}_i\right)\hfill & \forall (m,k_i)\in N^2\hfill \\ \\ m^{k_i(p_i-1)}\equiv 1\left(mod{p}_i\right)\hfill & \forall k_i\in N,gcd(m,p_i)=1.\hfill \end{array}\right.$$

Then, the function $\lambda$ at ${\displaystyle n={\Pi }_{i=1}^N{p}_i}$ should be defined as follows:

$$\begin{array}{ccc}\lambda \left({\displaystyle {\Pi }_{i=1}^N{p}_i}\right)\hfill & =& min\left\{k_1(p_1-1):k_i(p_i-1)=k_1(p_1-1),i=1,2,\cdots ,N\right\}\hfill \\ & =& min\left\{k_1\phi \left(p_1\right):k_i\phi \left(p_i\right)=k_1\phi \left(p_1\right),i=1,2,\cdots ,N\right\}.\hfill \end{array}$$

Example 1.

If $n=105=3\times 5\times 7$, then

$$\lambda \left(n\right)=min\{2k_1:2k_1=4k_2=6k_3\}=12,$$

so,

$$\left\{\begin{array}{cc}{m}^{12k_0+1}\equiv m(mod3\times 5\times 7)\hfill & \forall (m,k_0)\in N^2\hfill \\ \\ m^{12k_0}\equiv 1(mod3\times 5\times 7)\hfill & \forall k_0\in N,gcd(m,3\times 5\times 7)=1.\hfill \end{array}\right.$$

The following proposition provides a recursive scheme to evaluate the $\lambda \left(n\right)$ for different situations.

Proposition 1.

$\lambda \left(n\right)$ can be calculated by a recursive way:

$$\lambda \left(p_1{p}_2\right)={\displaystyle \frac{(p_1-1)(p_2-1)}{gcd(p_1-1;p_2-1)}}.$$

(4)

$$\lambda \left(p_1{p}_2{p}_3\right)={\displaystyle \frac{\lambda \left(p_1{p}_2\right)(p_3-1)}{gcd(\lambda \left(p_1{p}_2\right);p_3-1)}}.$$

(5)

and

$${\displaystyle \lambda \left({\Pi }_{j=1}^i{p}_j\right)={\displaystyle \frac{{\displaystyle \lambda \left({\Pi }_{j=1}^{i-1}{p}_j\right)(p_i-1)}}{{\displaystyle gcd(\lambda \left({\Pi }_{j=1}^{i-1}{p}_j\right);p_i-1)}}}.}$$

(6)

Again, we generalize our Lemma 1 result for $n=p_i^k$, where $k\ge 2$, as follows:

Lemma 2.

If ${\displaystyle n={\Pi }_{i=1}^N{p}_i^{n_i}}$ and $K={max}_i\left\{n_i\right\}$, then

$$\lambda \left(n\right)=min\left\{k_1\phi \left(p_1^{n_1}\right):k_i\phi {(}_i^{n_i})=k_1\phi \left(p_1^{n_1}\right),i=1,2,\cdots ,N\right\},$$

$$\left\{\begin{array}{cc}{m}^{k\varphi \left(n\right)}\equiv 1\left(modn\right)\hfill & \forall k\in N,gcd(m,n)=1,\hfill \\ \\ m^{k\lambda \left(n\right)+K}\equiv m^K\left(modn\right)\hfill & \forall m,k\in N,\hfill \end{array}\right.$$

Proof. 

• If $gcd(n,m)=1$, then

  $$\left\{\begin{array}{c}{m}^{p_i^k-p_i^{k-1}}\equiv 1\left(mod{p}_i^k\right)\\ \\ m^{p_i^k-p_i^{k-1}+1}\equiv m\left(mod{p}_i^k\right).\end{array}\right.$$
• For $k\ge 2$, we have

  $$p_i^k-p_i^{k-1}+1=p_i^{k-1}(p_i-1)+1\ge 2^{k-1}+1\ge k.$$
• It concludes that

  –

  If $gcd(m,n)=1,$ then

  $$m^{p_i^k-p_i^{k-1}+1}\equiv m\left(mod{p}_i^k\right).$$

  –

  If $p_i|m,$ then

  $$m^{p_i^k-p_i^{k-1}+1}\equiv m^{lk+r}\equiv m^{lk}{m}^r\equiv 0\left(mod{p}_i^k\right)\ne m\left(mod{p}_i^k\right),$$

  where $p_i^k-p_i^{k-1}+1=lk+r.$

  –

  Therefore,

  $$m^{k_i(p_i^k-p_i^{k-1})+k}\equiv m^k\left(mod{p}_i^k\right),\forall m\in N,$$

  we can say that if ${\displaystyle n={\Pi }_{i=1}^N{p}_i^{n_i}}$ and $K={max}_i\left\{n_i\right\}$, then

  $$m^{k_i(p_i^k-p_i^{k-1})+K}\equiv m^K\left(mod{p}_i^{n_i}\right),\forall m\in N,\forall k_i\in N.$$

□

Proposition 2.

$$\lambda \left(p_1^{n_1}{p}_2^{n_2-1}\right)={\displaystyle \frac{(p_1^{n_1}-p_1^{n_1-1})(p_2^{n_2}-p_2^{n_2-1})}{gcd\left(p_1^{n_1}-p_1^{n_1-1};p_2^{n_2}-p_2^{n_2-1}\right)}},$$

(7)

and

$${\displaystyle \lambda \left({\Pi }_{j=1}^i{p}_j^{n_j}\right)={\displaystyle \frac{{\displaystyle \lambda \left({\Pi }_{j=1}^{i-1}{p}_j^{n_j}\right)(p_i^{n_i}-p_i^{n_i-1})}}{gcd\left({\displaystyle \lambda \left({\Pi }_{j=1}^{i-1}{p}_j^{n_j}\right);p_i^{n_i}-p_i^{n_i-1}}\right)}}.}$$

(8)

Proof. 

The proof will be given after Lemma 5. □

Lemma 3.

$${\displaystyle \lambda \left({\Pi }_{j=1}^i{p}_j^{n_j}\right)=\left(p_1^{n_1}-p_1^{n_1-1}\right)LCM\left(\left\{{\displaystyle \frac{p_k^{n_k}-p_k^{n_k-1}}{gcd(p_k^{n_k}-p_k^{n_k-1};p_1^{n_1}-p_1^{n_1-1})}}:2\le k\le i.\right\}\right)}$$

(9)

Proof. 

According to the definition of $\lambda$:

$$\begin{array}{ccc}{\displaystyle \lambda \left({\Pi }_{j=1}^i{p}_j^{n_j}\right)}\hfill & :=& min\left\{k_1(p_1^{n_1}-p_1^{n_1-1}):\exists k_j,k_1(p_1^{n_1}-p_1^{n_1-1})=k_j(p_j^{n_j}-p_j^{n_j-1}),2\le j\le i.\right\}\hfill \\ \\ & :=& min\left\{k_1(p_1^{n_1}-p_1^{n_1-1}):\forall 2\le j\le i:k_j,(p_j^{n_j}-p_j^{n_j-1})|k_1(p_1^{n_1}-p_1^{n_1-1})\right\}\hfill \end{array}$$

and using the fact that

$$Ifa|bc⟺{\displaystyle \frac{a}{gcd(a,b)}}|c,$$

we obtain

$${\displaystyle \lambda \left({\Pi }_{j=1}^i{p}_j^{n_j}\right)=min\left\{k_1(p_1^{n_1}-p_1^{n_1-1}):\forall 2\le j\le i,{\displaystyle \frac{p_j^{n_j}-p_j^{n_j-1}}{gcd(p_j^{n_j}-p_j^{n_j-1};p_1^{n_1}-p_1^{n_1-1})}}|k_1\right\},}$$

and the smallest $k_1$ satisfying the above relation is the least common multiple (LCM) of ${\displaystyle \frac{p_j^{n_j}-p_j^{n_j-1}}{gcd(p_j^{n_j}-p_j^{n_j-1};p_1^{n_1}-p_1^{n_1-1})}}$, which completes the proof. □

Lemma 4.

$${\displaystyle \lambda \left({\Pi }_{j=1}^{i+1}{p}_j^{n_j}\right)=\lambda \left({\Pi }_{j=1}^i{p}_j^{n_j}\right)\times {\displaystyle \frac{p_{i+1}^{n_{i+1}}-p_{i+1}^{n_{i+1}-1}}{gcd(p_{i+1}^{n_{i+1}}-p_{i+1}^{n_{i+1}-1};p_1^{n_1}-p_1^{n_1-1})\times gcd(A_{i+1};B_1)}}}$$

(10)

where

$$A_{i+1}={\displaystyle \frac{p_{i+1}^{n_{i+1}}-p_{i+1}^{n_{i+1}-1}}{gcd(p_{i+1}^{n_{i+1}}-p_{i+1}^{n_{i+1}-1};p_1^{n_1}-p_1^{n_1-1})}},B_1={\displaystyle \frac{{\displaystyle \lambda \left({\Pi }_{j=1}^i{p}_j^{n_j}\right)}}{p_1^{n_1}-p_1^{n_1-1}}}.$$

Proof. 

We will use the following two results:

$$LCM(a_1,\cdots ,a_{i+1})=LCM\left(LCM(a_1,\cdots ,a_i),a_{i+1}\right),$$

(11)

and

$$LCM(a,b)={\displaystyle \frac{ab}{gcd(x,y)}}.$$

(12)

According to Lemma 3 and (11), we have by setting $d_j=gcd(p_j^{n_j}-p_j^{n_j-1};p_1^{n_1}-p_1^{n_1-1})$:

$${\displaystyle \lambda \left({\Pi }_{j=1}^{i+1}{p}_j^{n_j}\right)=\left(p_1^{n_1}-p_1^{n_1-1}\right)LCM\left(LCM\left[\left\{{\displaystyle \frac{p_j^{n_j}-p_j^{n_j-1}}{d_j}}:2\le j\le i.\right\}\right];A_{i+1}\right)}$$

which is equivalent to

$${\displaystyle \lambda \left({\Pi }_{j=1}^{i+1}{p}_j^{n_j}\right)=\left(p_1^{n_1}-p_1^{n_1-1}\right)LCM\left({\displaystyle \frac{{\displaystyle \lambda \left({\Pi }_{j=1}^i{p}_j^{n_j}\right)}}{p_1^{n_1}-p_1^{n_1-1}}};A_{i+1}\right).}$$

Furthermore, according to (12), we obtain:

$${\displaystyle \lambda \left({\Pi }_{j=1}^{i+1}{p}_j^{n_j}\right)={\displaystyle \frac{{\displaystyle \lambda \left({\Pi }_{j=1}^i{p}_j^{n_j}\right)\times A_{i+1}}}{gcd\left({\displaystyle \frac{{\displaystyle \lambda \left({\Pi }_{j=1}^i{p}_j^{n_j}\right)}}{p_1^{n_1}-p_1^{n_1-1}}};A_{i+1}\right)}},}$$

which proves Lemma 4. □

Lemma 5.

$$gcd(z;xy)=gcd(z;x)gcd\left({\displaystyle \frac{z}{gcd(z;x)}};y\right).$$

(13)

Proof. 

Let $d=gcd(z;x)$, then $z=dc$ and $x=da$ where $gcd(a,c)=1.$ Thus

$$gcd(z;xy)=gcd(dc;day)=dgcd(c;ay)=d\times gcd(c;y)=gcd(z;x)gcd\left({\displaystyle \frac{z}{gcd(z;x)}};y\right).$$

□

Proof of Proposition 2. 

By applying Lemma 5 to the denominator of the expression in Lemma 4, with $x=p_1^{n_1}-p_1^{n_1-1},y=B_i$ and $z=p_{i+1}^{n_{i+1}}-p_{i+1}^{n_{i+1}-1}$ we will obtain:

$${\displaystyle \lambda \left({\Pi }_{j=1}^{i+1}{p}_j^{n_j}\right)={\displaystyle \frac{{\displaystyle \lambda \left({\Pi }_{j=1}^i{p}_j^{n_j}\right)\left(p_{i+1}^{n_{i+1}}-p_{i+1}^{n_{i+1}-1}\right)}}{gcd\left({\displaystyle p_{i+1}^{n_{i+1}}-p_{i+1}^{n_{i+1}-1};\lambda \left({\Pi }_{j=1}^i{p}_j^{n_j}\right)}\right)}}.}$$

The Carmichael and Euler functions are a very important theoretic functions having a deep relationship with prime numbers. Figure 1 and Figure 2 shows the first thousand values of $\lambda \left(n\right)$ and $\phi \left(n\right)$, respectively, where the Euler function has been defined as $\phi \left(n\right)=(p_1^{n_1}-p_1^{n_1-1}).\cdots .(p_k^{n_k}-p_k^{n_k-1})$, where $p_1^{n_1}.\cdots .p_k^{n_k}$ is the prime factorization of the integer n. □

3. Properties of $\mathbf{\lambda }(.)$

In this section, we present some properties of the new Totient function $\lambda (.)$.

• $$\forall k\in N,\forall primep:\lambda \left(p^k\right)=\phi \left(p^k\right)=p^k-p^{k-1}.$$
• If $n=2{\Pi }_{i=1}^k{p}_i^{k_i},p_i$ are odd primes and k is any positive integer, then

  $$\lambda \left(n\right)=\lambda (n/2).$$
• If $n=2p$, where p is an odd prime, then $\lambda \left(2p\right)=\phi \left(p\right)$;
• If $n=2^k,k>2$, then $\lambda \left(2^k\right)=\phi \left(2^k\right)/2$.
• If $n>5$ then $\lambda \left(n\right)$ is an even number.
• If p and q are two odd primes, and k and l are any natural numbers, then

  $$\lambda \left(p^k{q}^l\right)\le {\displaystyle \frac{1}{2}}\phi \left(p^k{q}^l\right).$$
• If $m,p,$ and q are three odd primes, and $k,l$ and s are any natural numbers, then

  $$\lambda \left(m^k{p}^l{q}^r\right)\le {\displaystyle \frac{1}{4}}\phi \left(m^k{p}^l{q}^r\right).$$
• Let ${\left(p_i\right)}_i$ be an increasing sequence of primes, then:

  $$\lambda \left(\prod _{i=1}^k{p}_i^{n_i}\right)={\displaystyle \frac{\lambda \left({\prod }_{i=1}^{k-1}{p}_i^{n_i}\right)\left(p_k^{n_k}-p_k^{n_k-1}\right)}{gcd\left[\lambda \left({\prod }_{i=1}^{k-1}{p}_i^{n_i}\right),p_k-1\right]}}.$$
• $$\lambda \left(\prod _{i=1}^k{p}_i^{n_i}\right)={\displaystyle \frac{\lambda \left({\prod }_{j=1,j\ne i}^k{p}_j^{n_j}\right)\left(p_i^{n_i}-p_i^{n_i-1}\right)}{gcd\left[\lambda \left({\prod }_{j=1,j\ne i}^k{p}_j^{n_j}\right),p_i^{n_i}-p_i^{n_i-1}\right]}}.$$

Proof. 

• From the definition of the function $\lambda \left(n\right)$, we can conclude the following:

  $$\forall k\in N,\forall primep:\lambda \left(p^k\right)=\phi \left(p^k\right)=p^k-p^{k-1}.$$
• If $n=2{\Pi }_{i=1}^k{p}_i^{k_i},p_i$ are primes and k is any integer, then $\lambda \left(n\right)=\lambda (n/2)$. Indeed,

  $$\lambda \left(n\right)={\displaystyle \frac{\lambda \left({\Pi }_{i=1}^k{p}_i^{k_i}\right)(2-1)}{GCD\left({\Pi }_{i=1}^k{p}_i^{k_i},2-1\right)}}=\lambda \left({\Pi }_{i=1}^k{p}_i^{k_i}\right).$$
• For all odd primes p, we have: $\lambda \left(2p\right)=\lambda \left(p\right)=p-1.$ Indeed,

  $$\begin{array}{ccc}\lambda \left(2p\right)\hfill & =& \lambda \left(p\right)\left(\mathrm{from}P2\right)\hfill \\ & =& \phi \left(p\right)\left(\mathrm{from}P1\right)\hfill \\ & =& p-1\left(\mathrm{from}\mathrm{def}.\mathrm{of}\phi \right(p\left)\right).\hfill \end{array}$$
• If $n=2^k,k>2$, then $\lambda \left(2^k\right)=\phi \left(2^k\right)/2$.
  We note the following

  $$m^{2^k-2^{k-1}}-1=(m^{2^{k-2}-2^{k-3}}-1)(m^{2^{k-2}-2^{k-3}}+1)(m^{2^{k-1}-2^{k-2}}+1).$$
  Therefore, for any odd number m, we have

  $$\left(m^{2^{k-2}-2^{k-3}}-1\right)\left(m^{2^{k-2}-2^{k-3}}+1\right)\equiv 0\left(mod\left(2^3\right)\right).$$
  If $k>3$, we can factor more the term

  $$m^{2^k-2^{k-1}}-1=(x^4+1)(x^2+1)(x+1)(x-1),x=m^{2^{k-3}-2^{k-4}}.$$
  By the Euler theorem, we have $m^{2^k-2^{k-1}}-1\equiv 0\left(mod\left(2^5\right)\right).$
  By induction, we can easily prove that for any odd integer m and for all integer $k>2$ the following statement is true:

  $$m^{2^{k-1}-2^{k-2}}-1=0\left(mod\left(2^k\right)\right).$$
  Thus,

  $$\lambda \left(2^k\right)=2^{k-1}-2^{k-2}=\phi \left(2^k\right)/2.$$
• For $n>5$, we have the following:
  • $\lambda \left(3\right)=2,\lambda \left(2\right)=1.$
  • $\lambda \left(4\right)=2^{2-1}(2-1)=2.$
  • $\lambda \left(5\right)=4.$
  • $\lambda \left(p\right)=p-1$, which is even for any odd prime p.
  • $\lambda \left(p^k\right)=p^{k-1}(p-1)$, which is even for any odd prime p.
  • $$\begin{array}{ccc}\lambda \left(p_1^{k_1}{p}_2^{k_2}\right)\hfill & =& {\displaystyle \frac{\lambda \left(p_1^{k_1}\right)(p_2^{k_2}-p_2^{k_2-1}}{GCD\left(\lambda \left(p_1^{k_1}\right),p_2^{k_2}-p_2^{k_2-1}\right)}}\hfill \\ \\ & =& {\displaystyle \frac{p_1^{k_1-1}(p_1-1)p_2^{k_2-1}(p_2-1)}{GCD\left(p_1^{k_1-1}(p_1-1),p_2^{k_2-1}(p_2-1)\right)}}\hfill \end{array}$$

    (a)

    For some integer l, if $2^l$ divides $GCD\left(p_1^{k_1-1}(p_1-1),p_2^{k_2-1}(p_2-1)\right)$, then $2^l|p_2^{k_2-1}(p_2-1)$.

    (b)

    $p_1-1$ is an even number.

    (a) and (b) imply that $\lambda \left(p_1^{k_1}{p}_2^{k_2}\right)$ is even.
• According to Lemma 3, we have:

  $$\begin{array}{ccc}\lambda \left(p^k{q}^l\right)\hfill & =& {\displaystyle \frac{\lambda \left(p^k\right)(q^l-q^{l-1})}{GCD\left(\lambda \left(p^k\right),q^l-q^{l-1}\right)}}\hfill \\ \\ & \le & {\displaystyle \frac{\lambda \left(p^k\right)(q^l-q^{l-1})}{2}},\mathrm{Property}5.\hfill \\ & \le & {\displaystyle \frac{\phi \left(p^k{q}^l\right)}{2}},\mathrm{Property}1.\hfill \end{array}$$
• According to Lemma 3, we have:

  $$\begin{array}{ccc}\lambda \left(m^k{p}^r{q}^s\right)\hfill & =& {\displaystyle \frac{\lambda \left(m^k{p}^r\right)(q^s-q^{s-1})}{GCD\left(\lambda \left(m^k{p}^r\right),q^s-q^{s-1}\right)}}\hfill \\ \\ & \le & {\displaystyle \frac{\lambda \left(m^k{p}^r\right)(q^s-q^{s-1})}{2}},\mathrm{Property}5.\hfill \\ & \le & {\displaystyle \frac{\phi \left(m^k{p}^r\right)(q^s-q^{s-1})}{4}},\mathrm{Property}6.\hfill \\ & \le & {\displaystyle \frac{\phi \left(m^k{p}^r{q}^s\right)}{4}}.\hfill \end{array}$$
• Obvious, it is enough to prove that $gcd\left[\lambda \left({\prod }_{i=1}^{k-1}{p}_i^{n_i}\right),p_k\right]=1$.
• Obvious.

□

Corollary 1.

$$\lambda \left(\prod _{i=1}^k{p}_i^{n_i}\right)\le {\displaystyle \frac{1}{2^{k-1}}}\phi \left(\prod _{i=1}^k{p}_i^{n_i}\right).$$

Proof. 

From properties P6 and P7, the proof can be completed by induction.

As a conclusion, we can easily prove the following limit

$${\displaystyle \underset{n\to \infty }{lim\; sup}{\displaystyle \frac{\phi \left(n\right)}{\lambda \left(n\right)}}=+\infty ,}$$

by considering the subsequence $n_k=p_1.p_2.\cdots .p_k$, where $(p_1,p_2,\dots ,p_k)$ are the first k-consecutive odd primes.

Again, since the primes are not bounded, we can conclude that

$${\displaystyle \underset{n\to \infty }{lim\; inf}{\displaystyle \frac{\phi \left(n\right)}{\lambda \left(n\right)}}=1.}$$

□

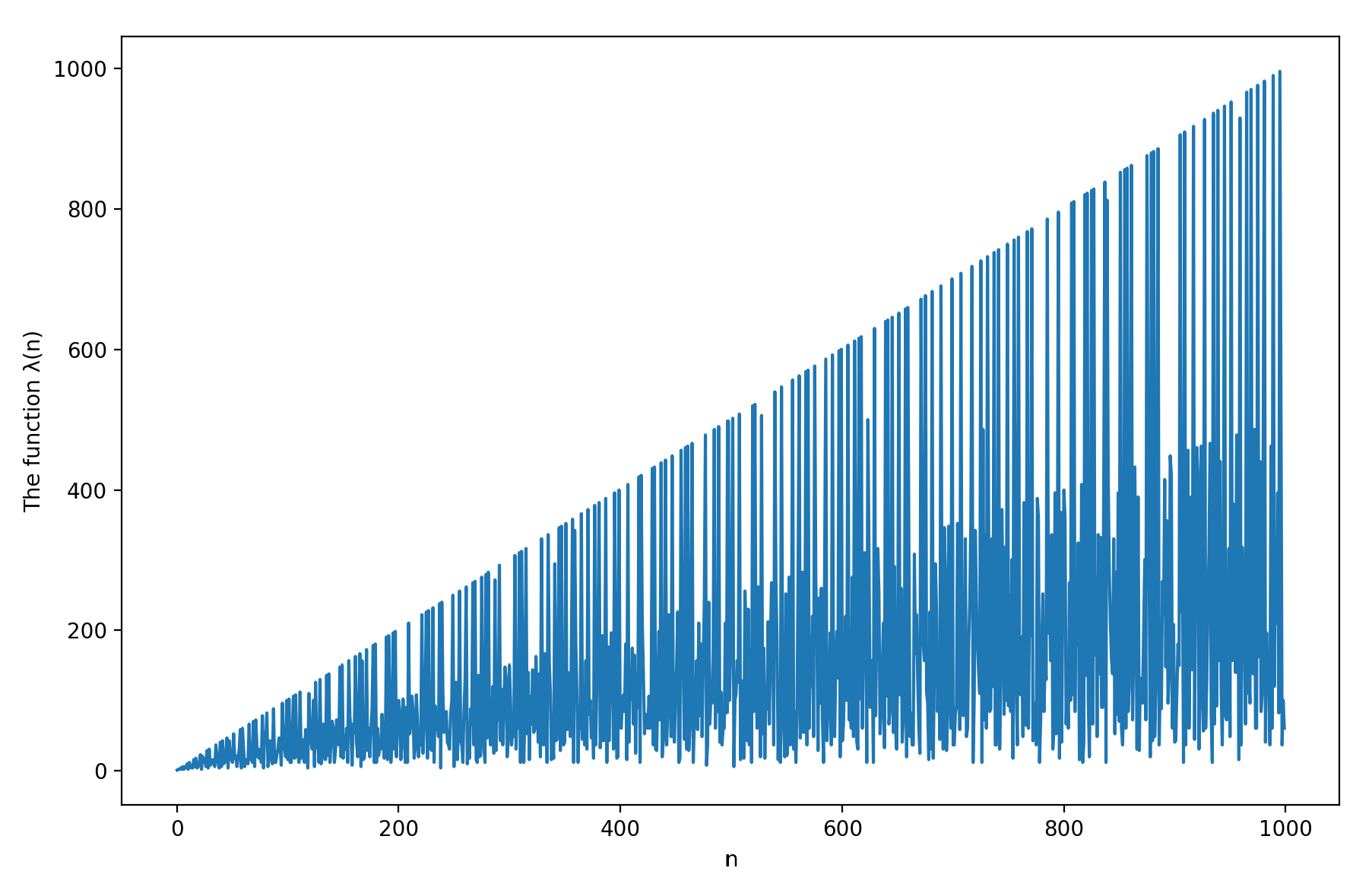
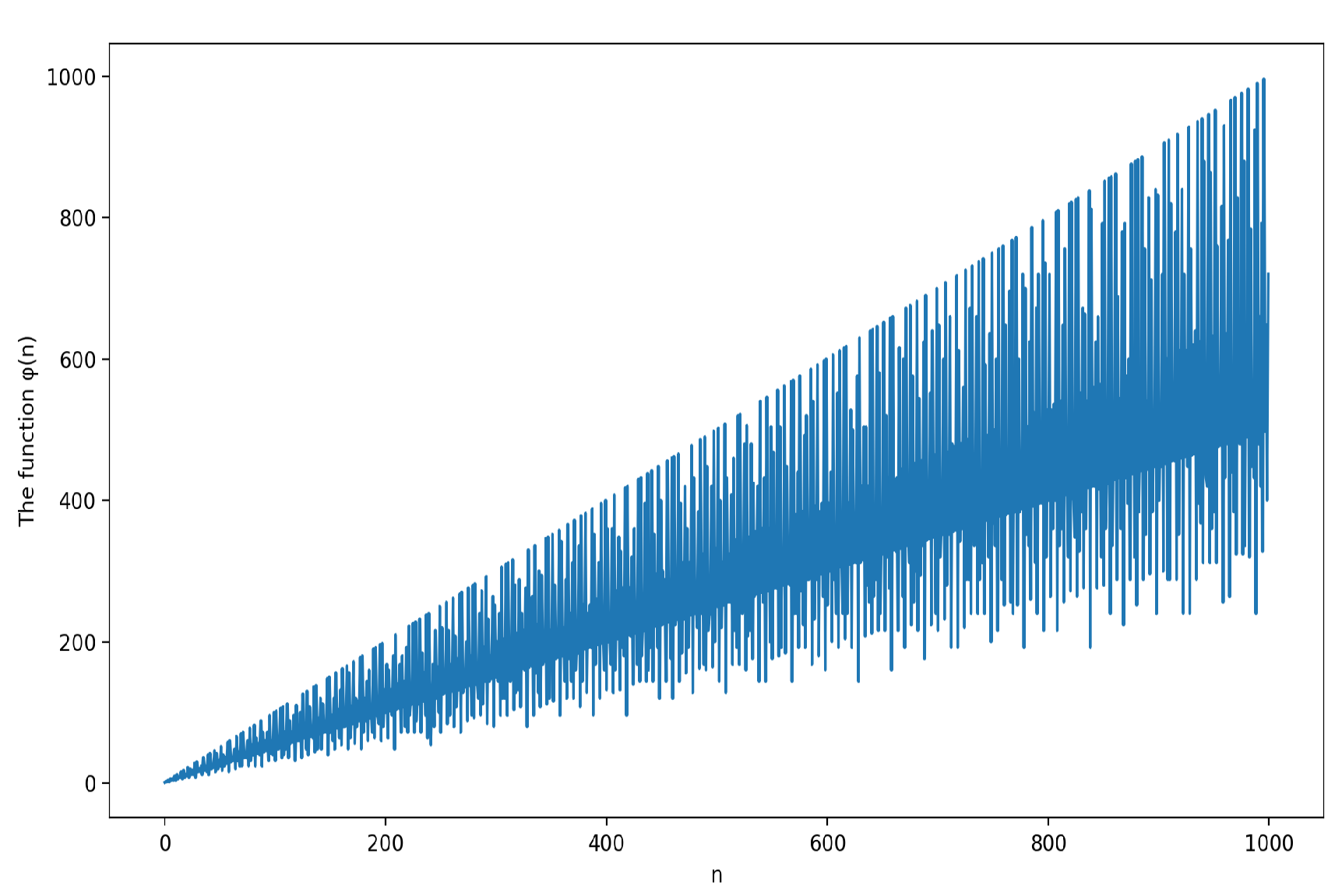
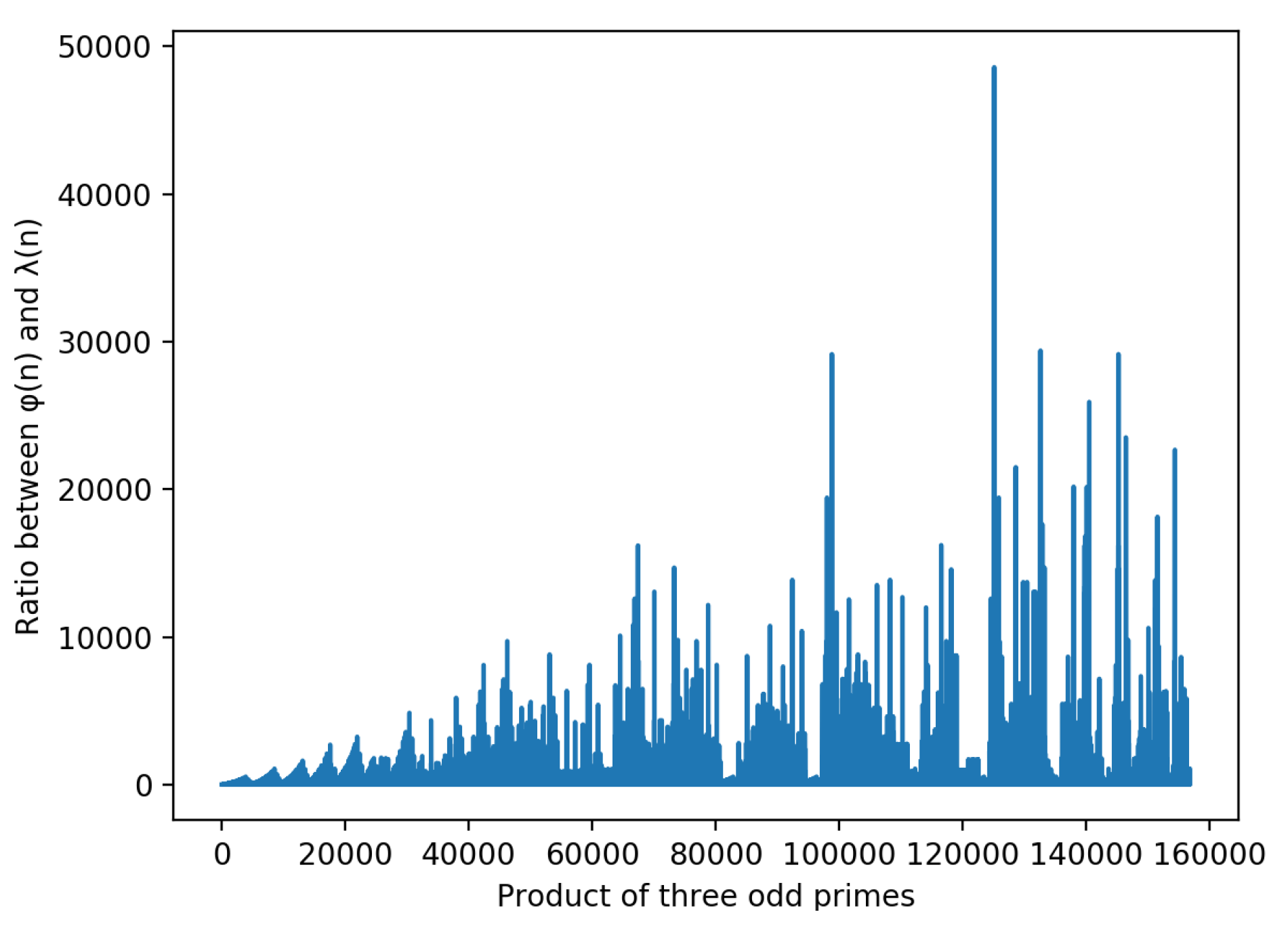
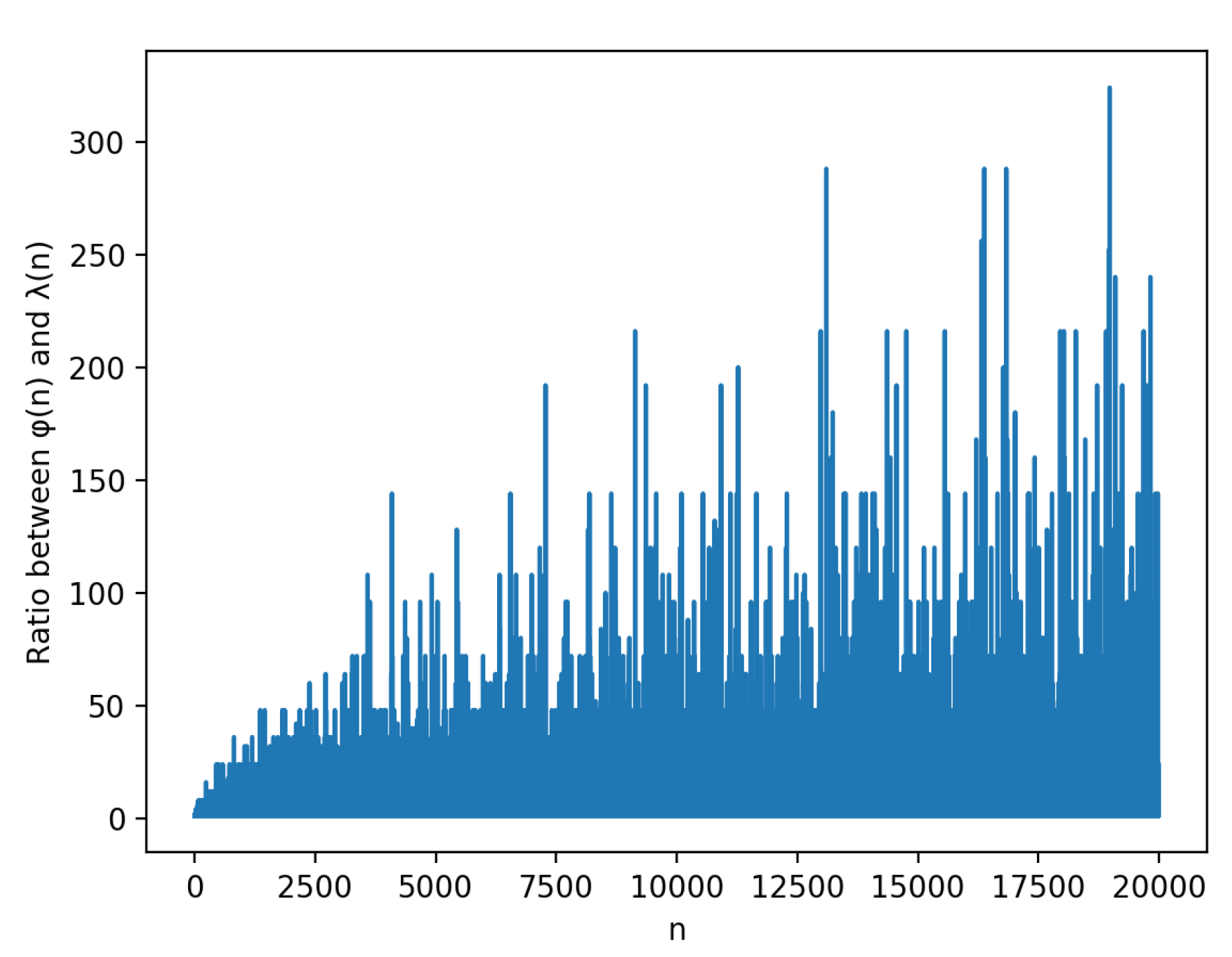
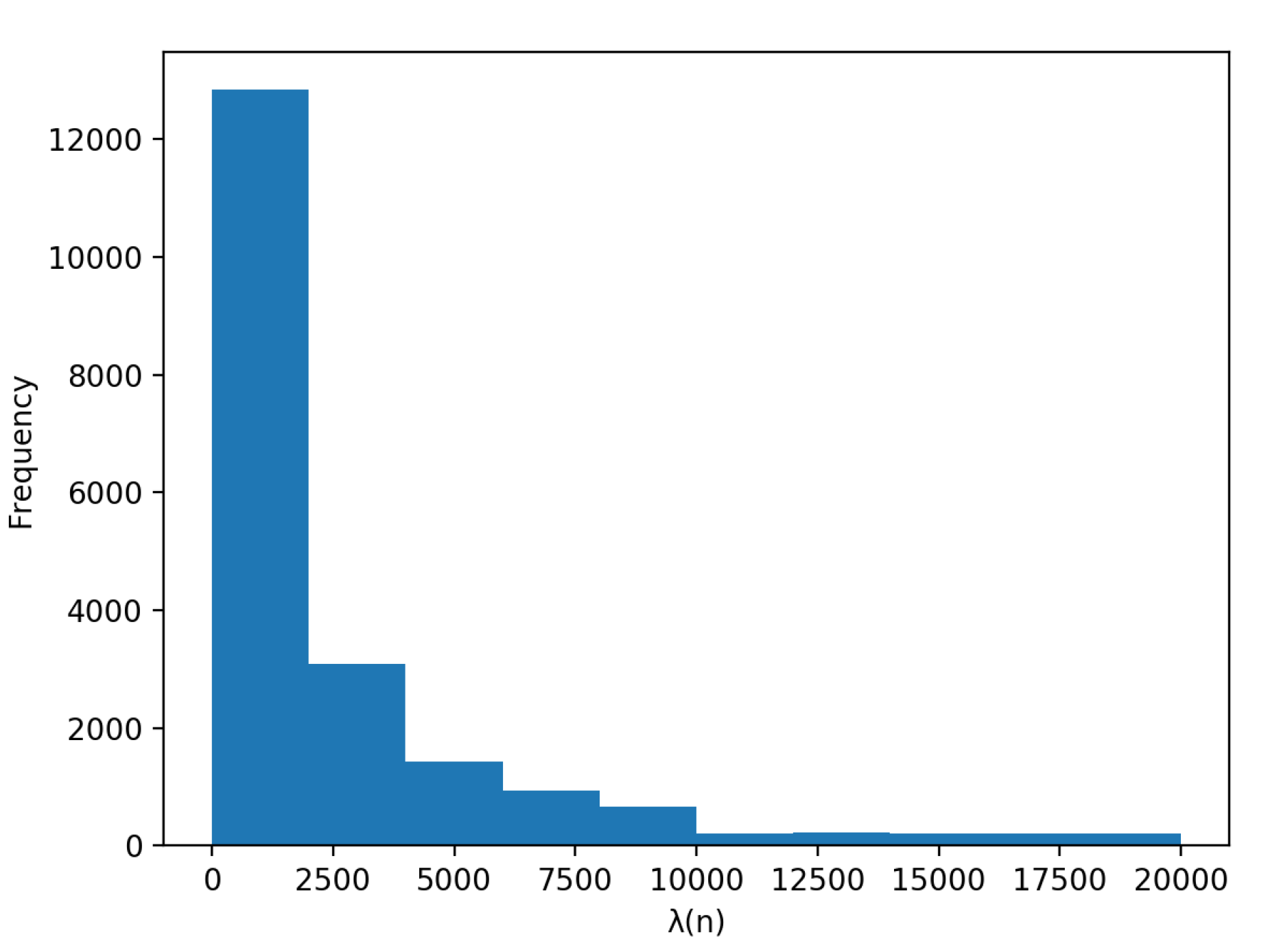
4. Computations of $\mathbf{\lambda }\left(\mathbf{n}\right)$ versus $\mathbf{\phi }\left(\mathbf{n}\right)$

In this section, we compare the magnitude of the Euler function $\phi \left(n\right)$ versus the Carmichael function $\lambda \left(n\right)$ see Table 1 and Table 2.

Table 1. Comparison between Carmichael and Euler functions for the product of two primes.

n	$3\times 5$	$5\times 7$	$5\times 29$	$5\times 61$	$11\times 31$	$17\times 97$	$37\times 73$	$73\times 109$
$\lambda \left(n\right)$	4	12	28	60	30	96	72	216
${\displaystyle \frac{\phi \left(n\right)}{\lambda \left(n\right)}}$	2	2	4	4	10	16	36	36

Table 2. Comparison between Carmichael and Euler functions for the product of three primes.

n	$3\times 5\times 7$	$5\times 13\times 97$	$7\times 31\times 61$	$11\times 31\times 71$	$13\times 19\times 113$	$37\times 73\times 109$
$\lambda \left(n\right)$	12	96	60	210	108	216
${\displaystyle \frac{\phi \left(n\right)}{\lambda \left(n\right)}}$	4	48	180	100	216	1296

Figure 3 and Figure 4 present, respectively, the ratio ${\displaystyle \frac{\phi \left(n\right)}{\lambda \left(n\right)}}$ when n is a product of two primes, respectively, three primes.

Figure 3. The Ratio between Carmichael and Euler functions for n less than 45,000.

Figure 4. The Ratio between Carmichael and Euler functions for n less than 155,000.

5. Conclusions

In this paper, we presented how we built the modified Totient function of Carmichael $\lambda (.)$. Important properties have been highlighted, particularly the given iterative scheme for calculating the $\lambda (.)$ function. Some preliminary numerical results comparing the Euler $\phi$ and the reduced totient $\lambda (.)$ functions aiming to quantify the reduction between them are given (see Table 1 and Table 2 and Figure 3, Figure 4 and Figure 5). Figure 6 and Figure 7 express the frequency of n for getting the value of $\lambda \left(n\right)$; in other words, determining the cardinal of the following set:

$$\left\{n:\lambda \left(n\right)=k\right\},k\mathrm{is}a\mathrm{given}\mathrm{positive}\mathrm{integer}.$$

Furthermore, it may be worthwhile investigating more results in Corollary 1 by finding a better upper-bound.

Figure 5. ${\displaystyle \frac{\phi \left(n\right)}{\lambda \left(n\right)}}$ for all $n\le$ 20,000.

Figure 6. The Cardinal of the Inverse of Carmichael function.

Figure 7. The Cardinal of the Inverse of Euler function.