Opinion Diversity and the Resilience of Cooperation in Dynamical Networks
Abstract
:1. Introduction
2. Materials and Methods
2.1. Computational Model
2.2. Information-Based Decision Making
- If Then Connect
- If Then Do not Connect
- If Then Connect with probability p
- If Then Connect with probability q
3. Results
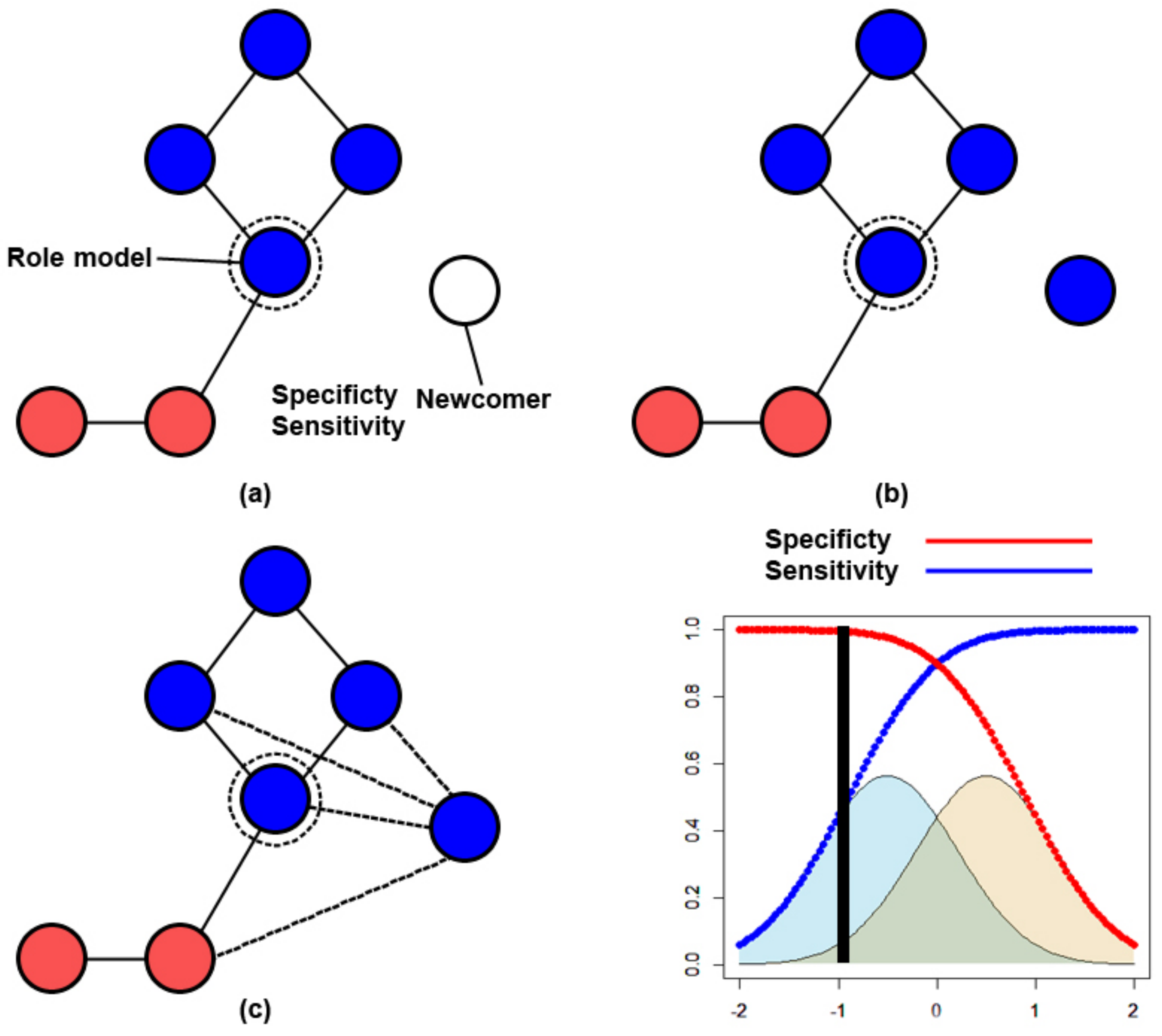
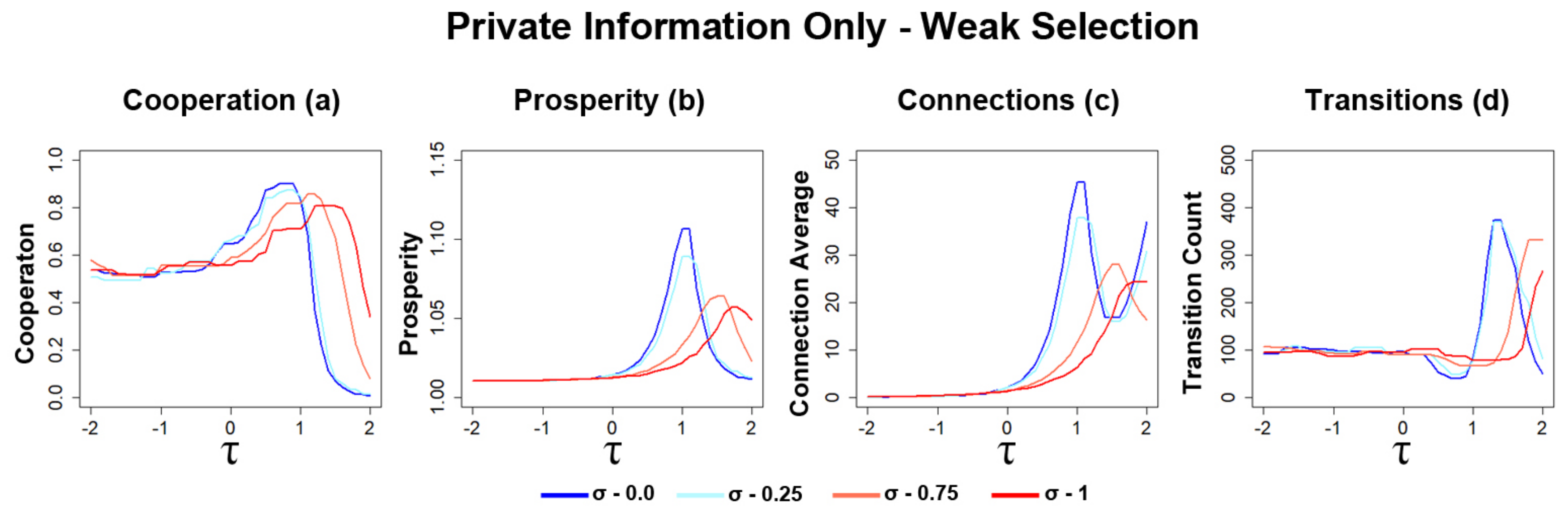
3.1. Private Information Decision Making
3.1.1. Increasing Opinion Diversity Leads to Network Changes
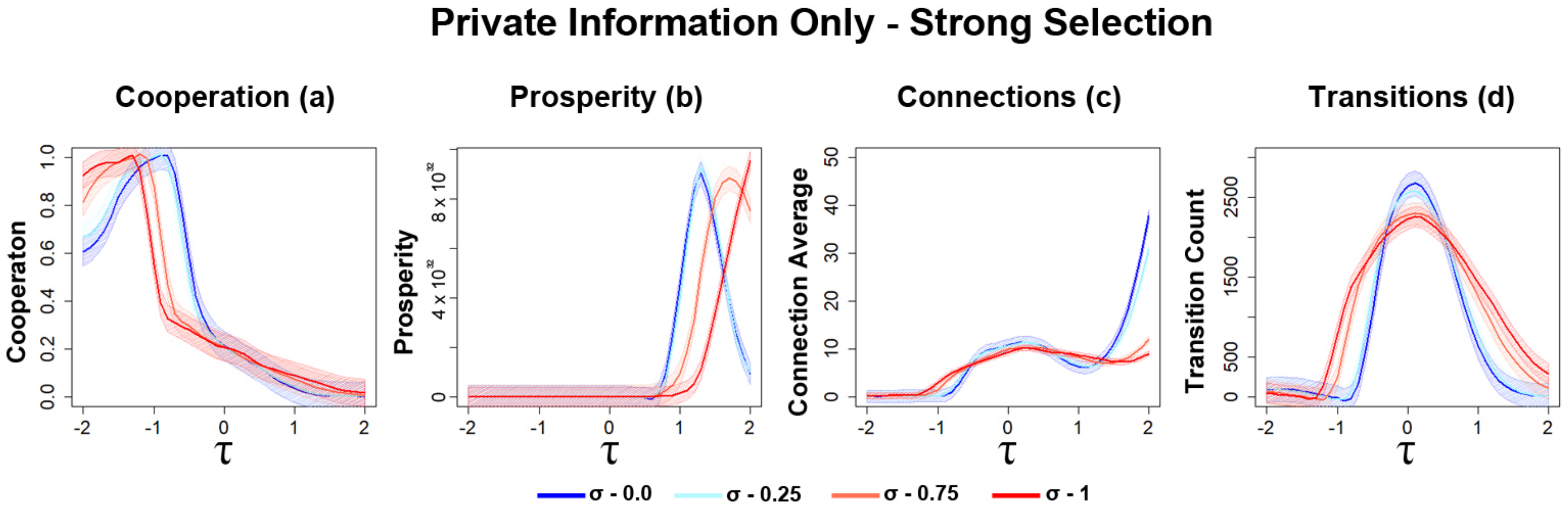
3.1.2. Increasing Selection Strength Leads to Increase in Network Instability
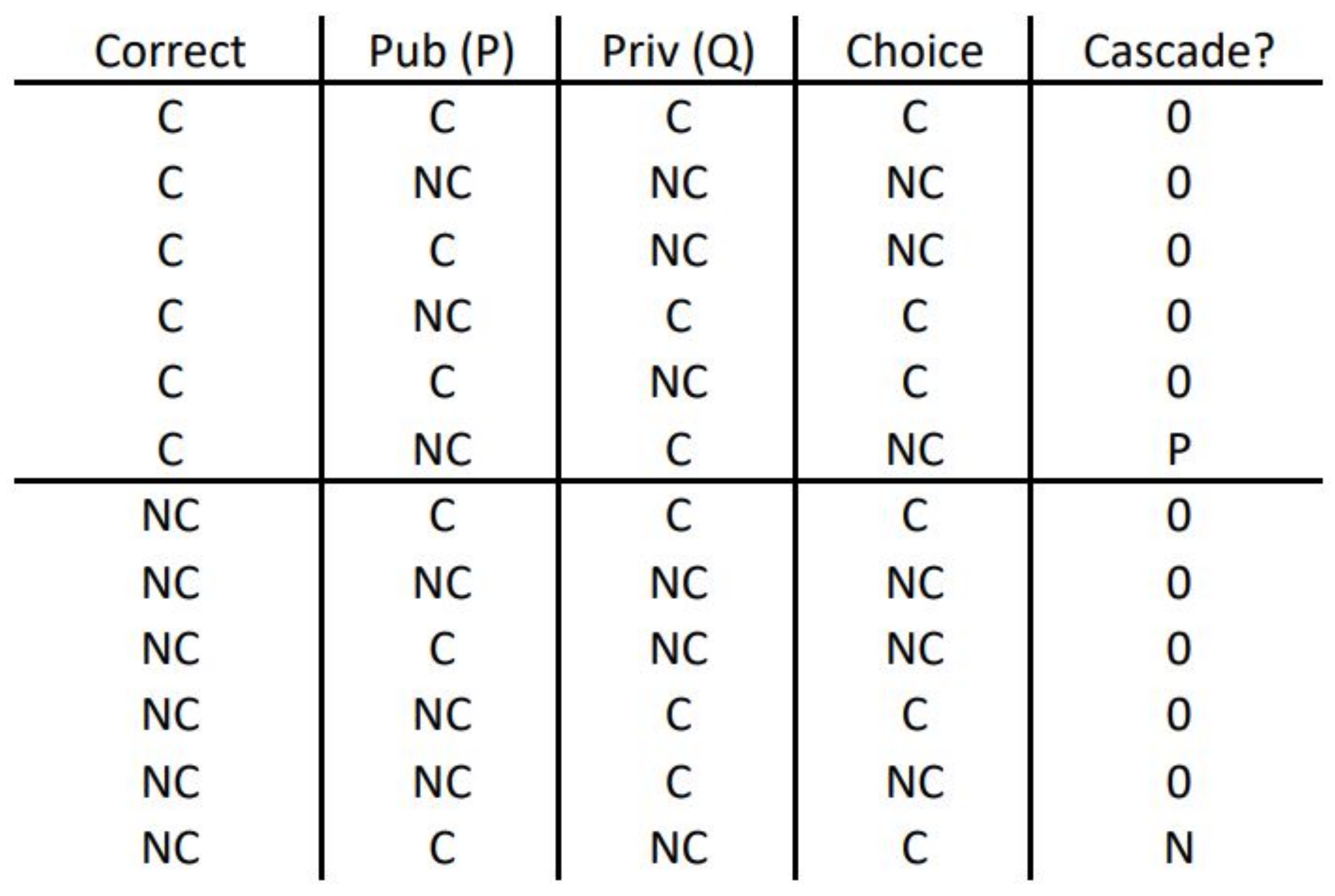
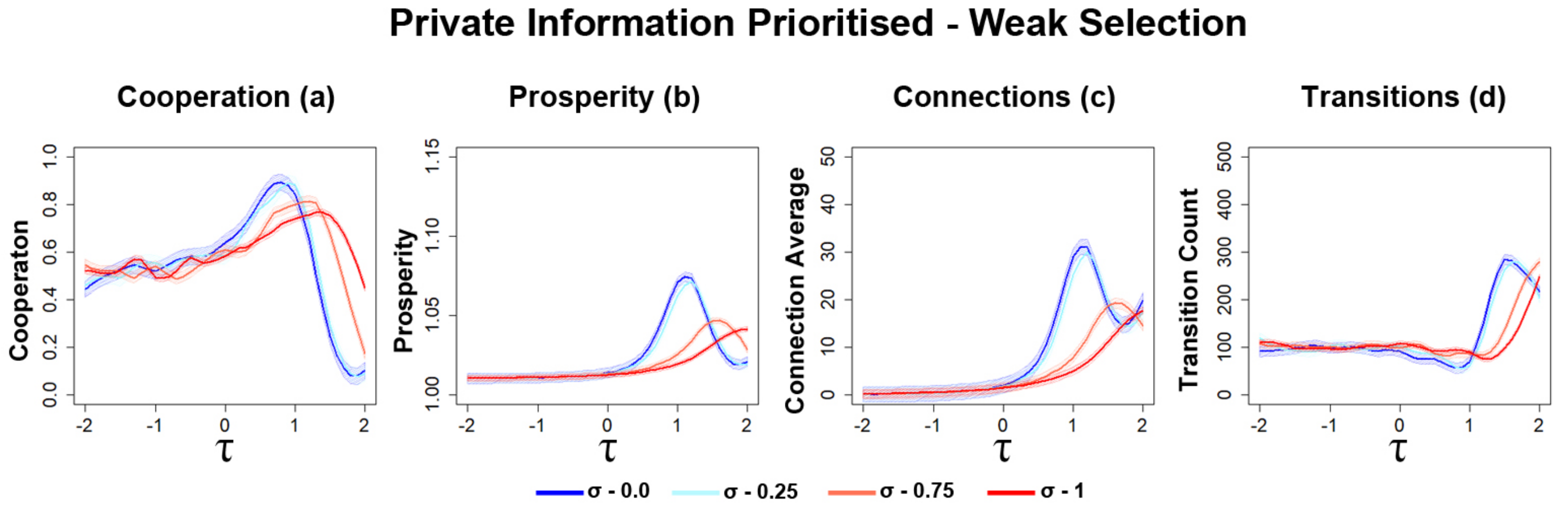
3.2. Private/Public Information Decision Making
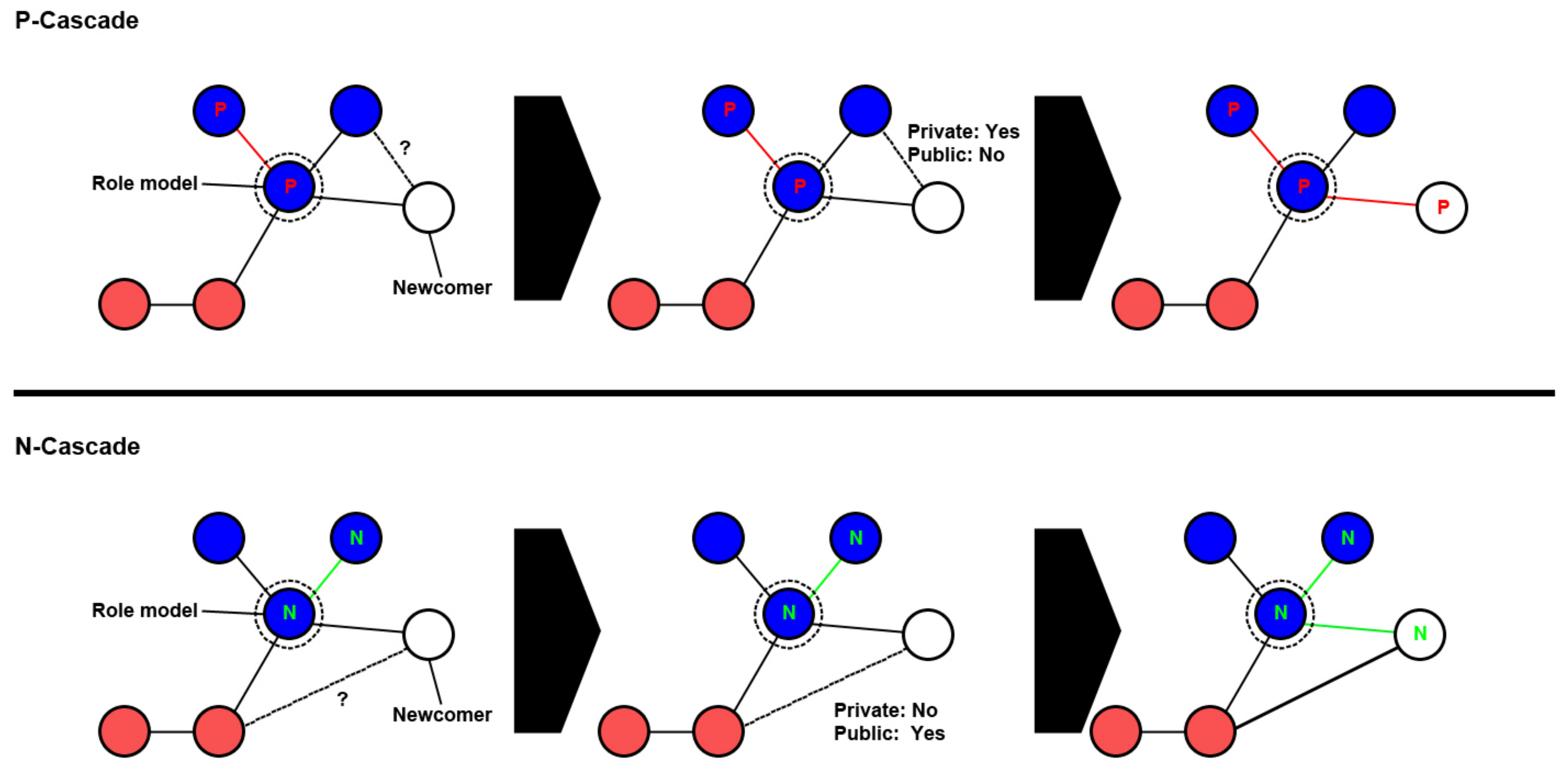
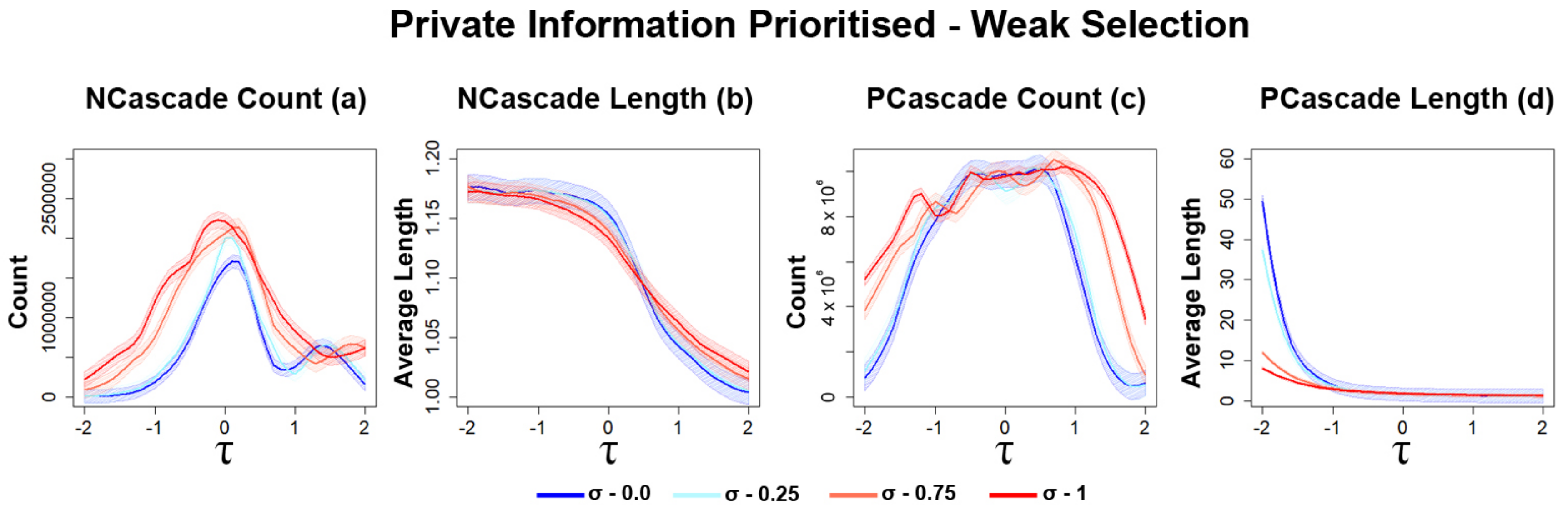
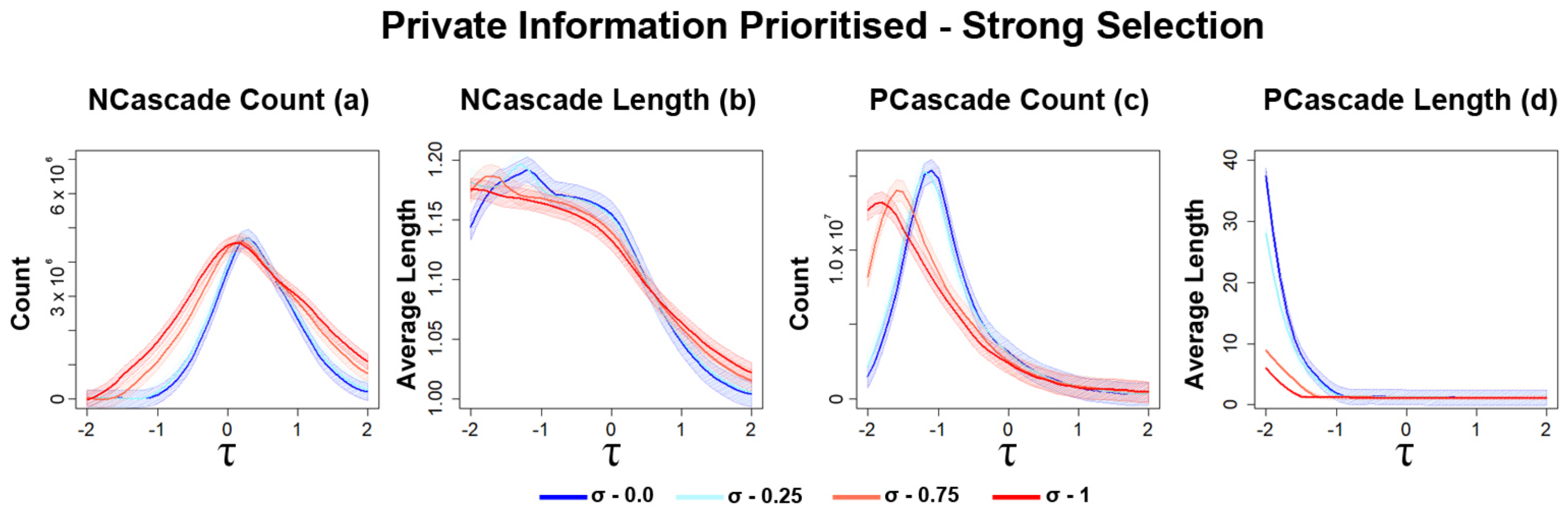
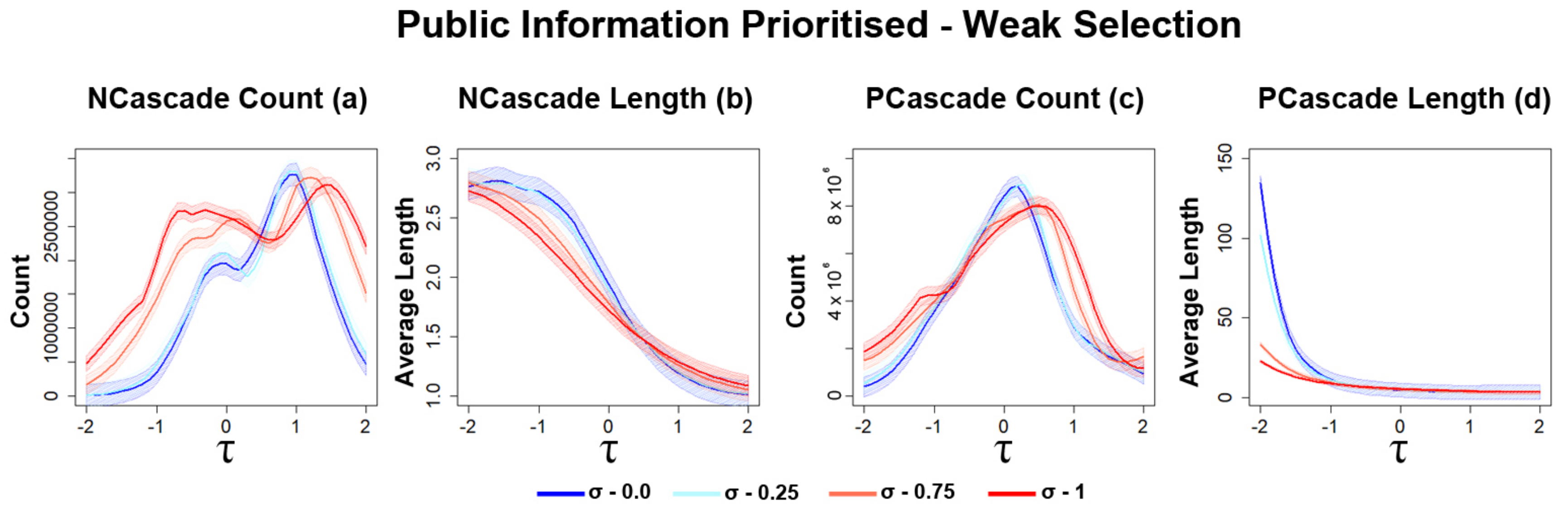
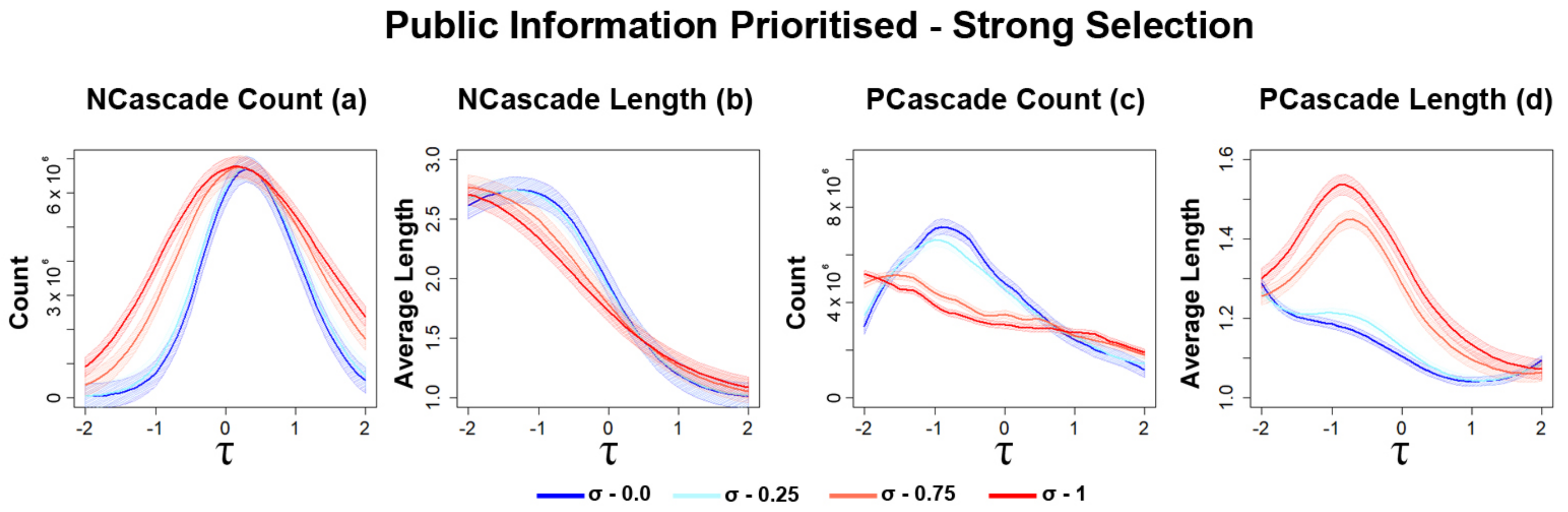
3.2.1. Opinion Diversity Affects the Frequency of Information Cascades
3.2.2. Strong Selection Results in Higher Frequency of Information Cascades
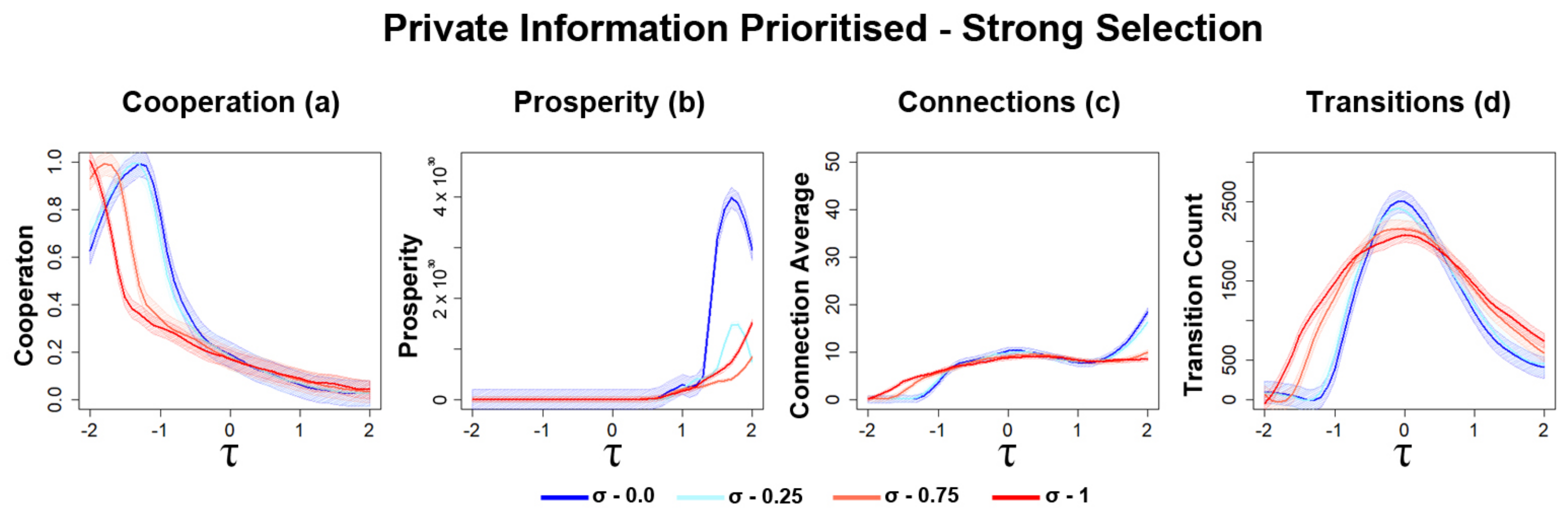
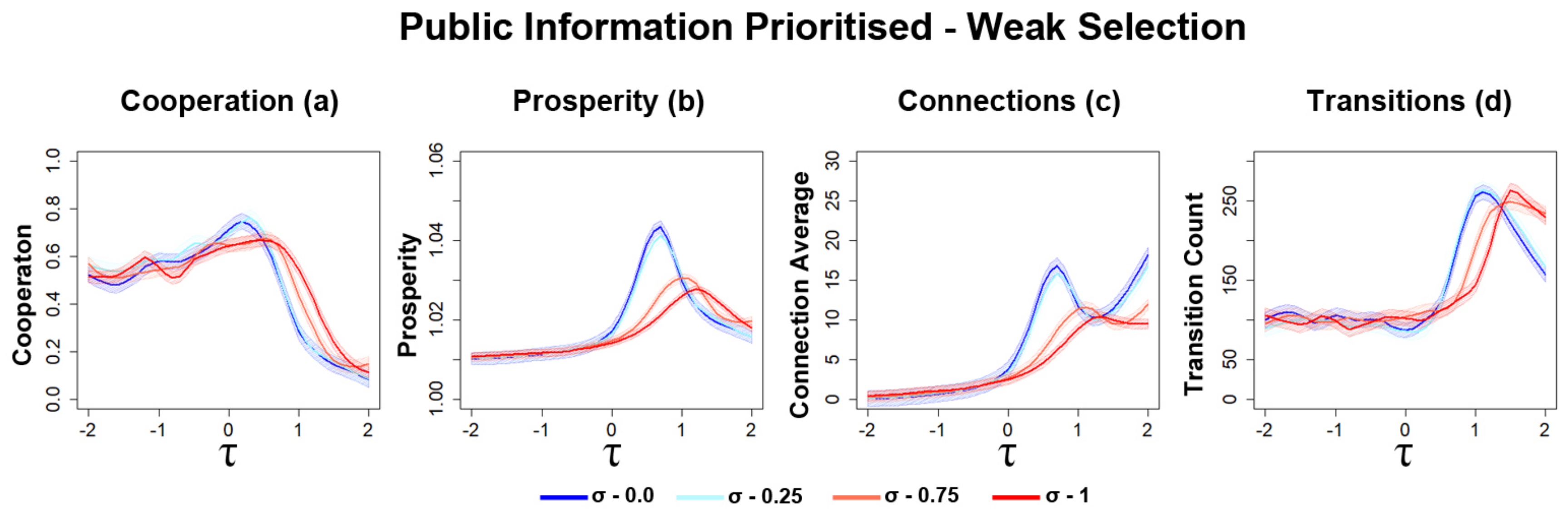
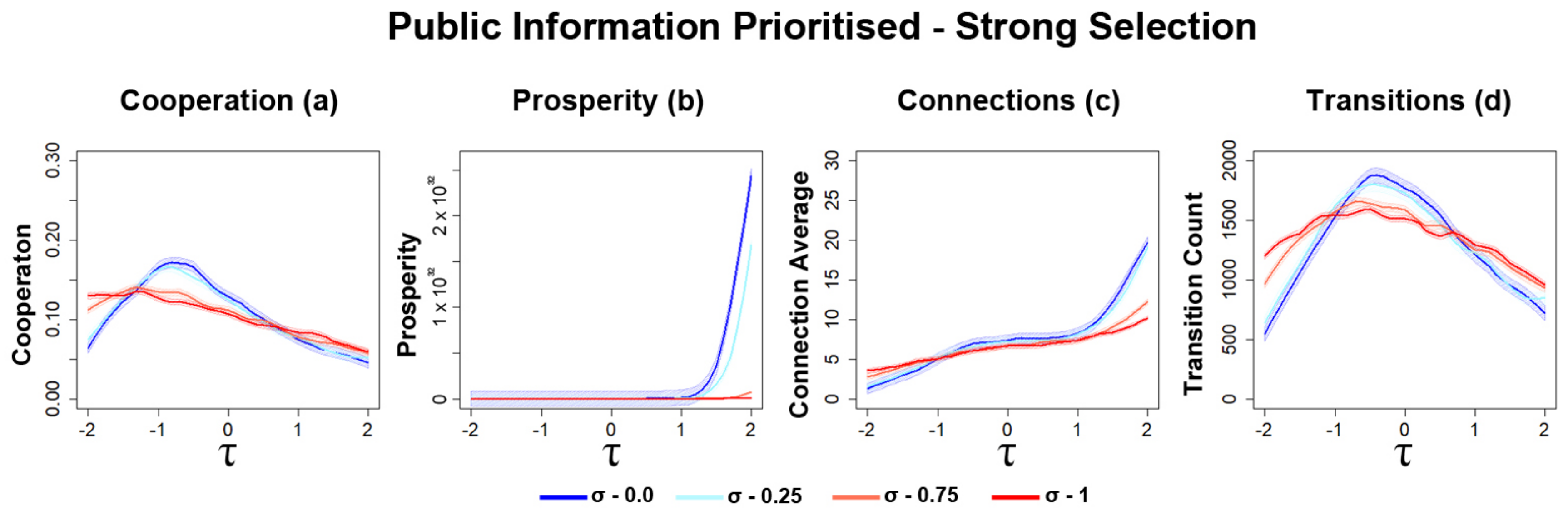
3.2.3. Opinion Diversity Can Mitigate Disruption of Networks
3.2.4. Sharp Increases in the Number of Transitions for Strong Selection
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. RStudio Functions
Appendix A.1. Standard Error Function
Appendix A.2. Graph Initialisation Function
Appendix A.3. Cooperation Plot Function
Appendix A.4. Prosperity Plot Function
Appendix A.5. Degree Plot Function
Appendix A.6. Transition Plot Function
Appendix A.7. NCascade Count Plot Function
Appendix A.8. NCascade Length Plot Function
Appendix A.9. PCascade Count Plot Function
Appendix A.10. PCascade Length Plot Function
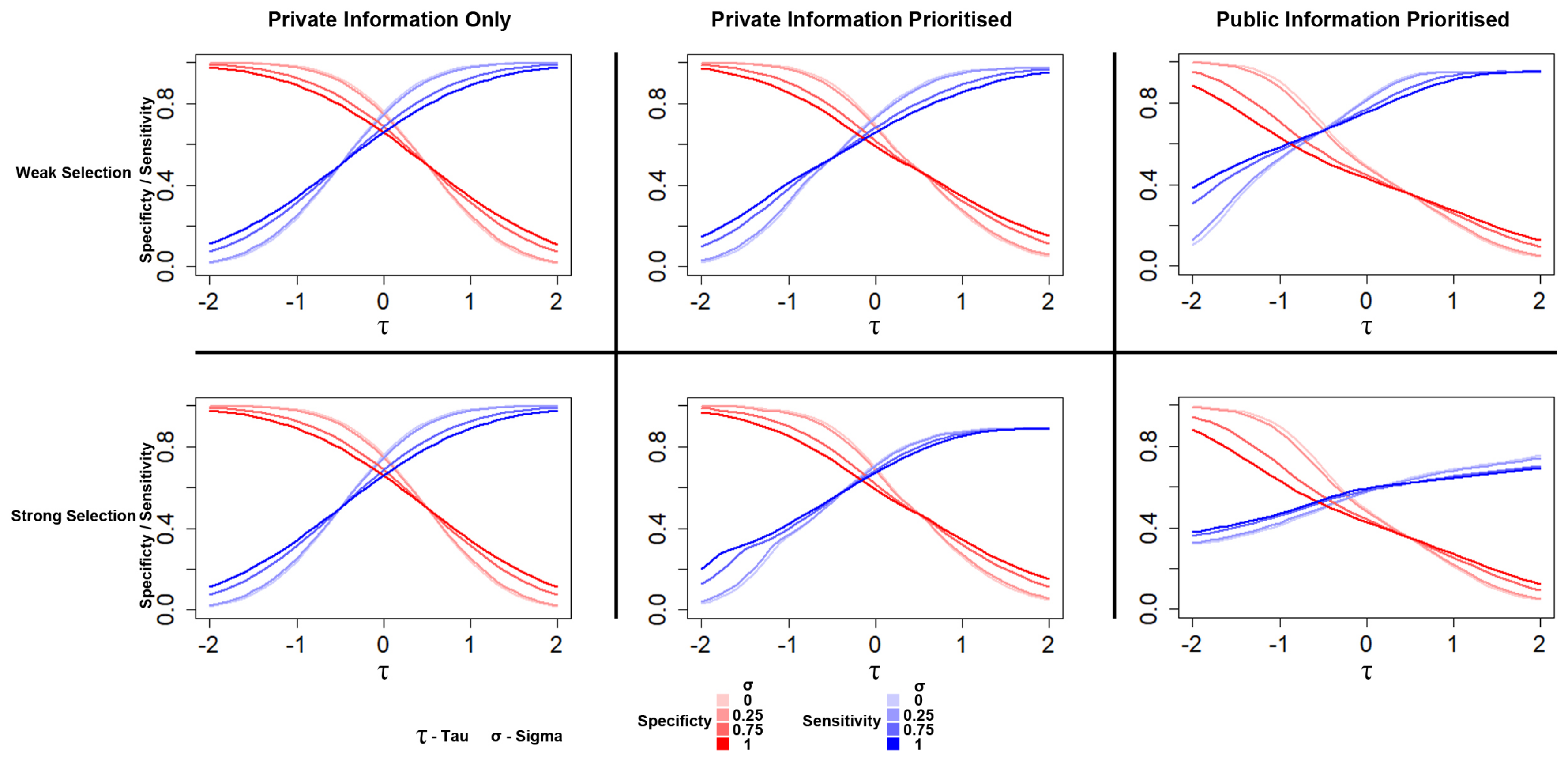
Appendix A.11. Specificity and Sensitivity Plot Function
References
- Easley, D.; Kleinberg, J. Networks, Crowds, and Markets; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Kraft-Todd, G.; Yoeli, E.; Bhanot, S.; Rand, D. Promoting Cooperation in the Field. Curr. Opin. Behav. Sci. 2015, 3, 96–101. [Google Scholar] [CrossRef]
- Rand, D.G.; Nowak, M.A. Human Cooperation. Trends Cogn. Sci. 2013, 17, 413–425. [Google Scholar] [CrossRef] [PubMed]
- Hauser, O.P.; Hendriks, A.; Rand, D.G.; Nowak, M.A. Think global, act local: Preserving the global commons. Sci. Rep. 2016, 6, 36079. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Levin, S. Crossing Scales, Crossing Disciplines: Collective Motion and Collective Action in the Global Commons. Philos. Trans. R. Soc. B Biol. Sci. 2010, 365, 13–18. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lloyd, W.F. WF Lloyd on the Checks to Population. Popul. Dev. Rev. 1980, 6, 473–496. [Google Scholar] [CrossRef]
- Nowak, M.A. Evolutionary Dynamics: Exploring the Equations of Life; Harvard University Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Leskovec, J.; Singh, A.; Kleinberg, J. Patterns of Influence in a Recommendation Network. In Pacific-Asia Conference on Knowledge Discovery and Data Mining; Springer: Berlin, Germany, 2006; pp. 380–389. [Google Scholar]
- Maharani, W.; Gozali, A.A.; Adiwijaya. Degree Centrality and Eigenvector Centrality in Twitter. In Proceedings of the 2014 8th International Conference on Telecommunication Systems Services and Applications (TSSA), Kuta, Indonesia, 23–24 October 2014; pp. 1–5. [Google Scholar]
- Wooldridge, M. Computation and the Prisoner’s Dilemma. IEEE Intell. Syst. 2012, 27, 75–80. [Google Scholar] [CrossRef]
- Bikhchandani, S.; Hirshleifer, D.; Welch, I. Learning from the Behavior of Others: Conformity, Fads, and Informational Cascades. J. Econ. Perspect. 1998, 12, 151–170. [Google Scholar] [CrossRef] [Green Version]
- Sánchez, A. Physics of Human Cooperation: Experimental Evidence and Theoretical Models. J. Stat. Mech. Theory Exp. 2018, 2018, 024001. [Google Scholar] [CrossRef] [Green Version]
- Wu, B.; Zhou, D.; Fu, F.; Luo, Q.; Wang, L.; Traulsen, A. Evolution of cooperation on stochastic dynamical networks. PLoS ONE 2010, 5, e11187. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Son, Y.J. Extended Decision Field Theory with Social-Learning for Long-Term Decision-Making Processes in Social Networks. Inf. Sci. 2020, 512, 1293–1307. [Google Scholar] [CrossRef]
- Tappin, B.M.; Pennycook, G.; Rand, D.G. Thinking Clearly About Causal Inferences of Politically Motivated Reasoning: Why Paradigmatic Study Designs Often Undermine Causal Inference. Curr. Opin. Behav. Sci. 2020, 34, 81–87. [Google Scholar] [CrossRef]
- Busu, M. Game Theory in Strategic Management-Dynamic Games. Theoretical and Practical Examples. Manag. Dyn. Knowl. Econ. 2018, 6, 645–655. [Google Scholar] [CrossRef]
- Yang, G.; Csikász-Nagy, A.; Waites, W.; Xiao, G.; Cavaliere, M. Information Cascades and the Collapse of Cooperation. Sci. Rep. 2020, 10, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Sood, V.; Redner, S. Voter model on heterogeneous graphs. Phys. Rev. Lett. 2005, 94, 178701. [Google Scholar] [CrossRef] [Green Version]
- Xue, M.; Roy, S. Averager-copier-voter models for hybrid consensus. IFAC-PapersOnLine 2016, 49, 1–6. [Google Scholar] [CrossRef]
- Avilés, L. Cooperation and non-linear dynamics: An ecological perspective on the evolution of sociality. Evol. Ecol. Res. 1999, 1, 459–477. [Google Scholar]
- Traulsen, A.; Shoresh, N.; Nowak, M.A. Analytical results for individual and group selection of any intensity. Bull. Math. Biol. 2008, 70, 1410–1424. [Google Scholar] [CrossRef] [Green Version]
- Loess: Local Polynomial Regression Fitting—RDocumentation. Available online: https://www.rdocumentation.org/packages/stats/versions/3.6.2/topics/loess (accessed on 26 April 2021).
- Tomassini, M.; Pestelacci, E. Coordination games on dynamical networks. Games 2010, 1, 242–261. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Zhao, L.; Zhang, J. Strategy Dynamics with Feedback Control in the Global Climate Dilemma Games. In Proceedings of the 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC), Bari, Italy, 6–9 October 2019; pp. 518–522. [Google Scholar]
- Pejó, B.; Biczók, G. Corona Games: Masks, Social Distancing and Mechanism Design. In Proceedings of the 1st ACM SIGSPATIAL International Workshop on Modeling and Understanding the Spread of COVID-19, Seattle, WA, USA, 3 November 2020; pp. 24–31. [Google Scholar]
- Brodie, B. Strategy in the Missile Age; Princeton University Press: Princeton, NJ, USA, 2015. [Google Scholar]
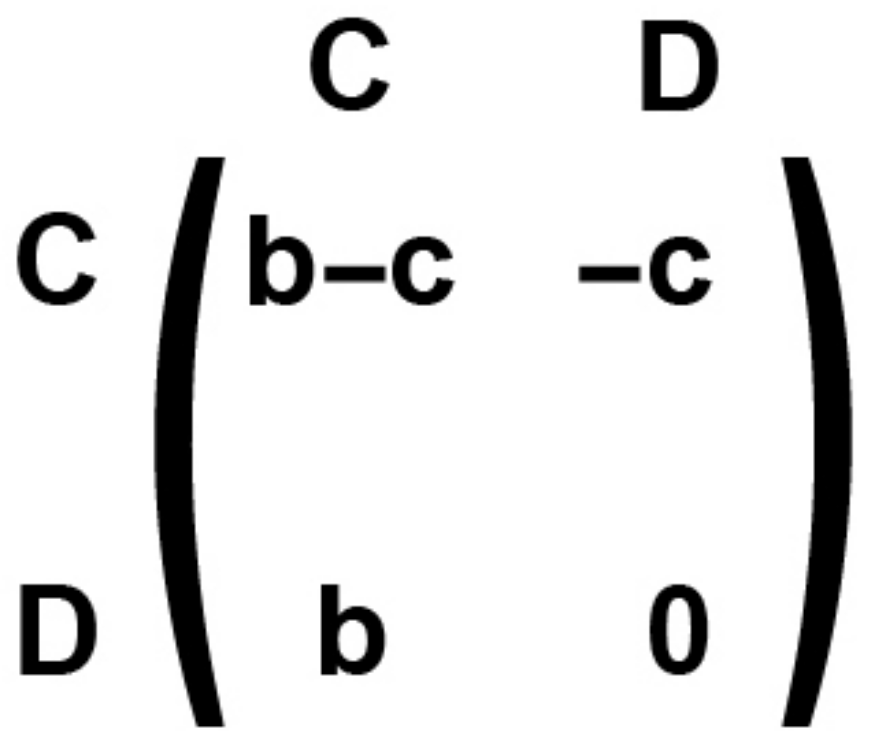
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miles, A.L.; Cavaliere, M. Opinion Diversity and the Resilience of Cooperation in Dynamical Networks. Mathematics 2021, 9, 1801. https://doi.org/10.3390/math9151801
Miles AL, Cavaliere M. Opinion Diversity and the Resilience of Cooperation in Dynamical Networks. Mathematics. 2021; 9(15):1801. https://doi.org/10.3390/math9151801
Chicago/Turabian StyleMiles, Adam Lee, and Matteo Cavaliere. 2021. "Opinion Diversity and the Resilience of Cooperation in Dynamical Networks" Mathematics 9, no. 15: 1801. https://doi.org/10.3390/math9151801
APA StyleMiles, A. L., & Cavaliere, M. (2021). Opinion Diversity and the Resilience of Cooperation in Dynamical Networks. Mathematics, 9(15), 1801. https://doi.org/10.3390/math9151801





