Abstract
This paper presents a numerical analysis of the influence of mechanical properties and the thickness of viscoelastic materials on the transient dynamic behavior of free layer damping beams. Specifically, the beams consist of cantilever metal sheets with surface viscoelastic treatment, and two different configurations are analyzed: symmetric and asymmetric. The viscoelastic material is characterized by a five-parameter fractional derivative model, which requires specific numerical methods to solve for the transverse displacement of the free edge of the beam when a load is applied. Concretely, a homogenized finite element formulation is performed to reduce computation time, and the Newmark method is applied together with the Grünwald–Letnikov method to accomplish the time discretization of the fractional derivative equations. Amplitudes and response time are evaluated to study the transient dynamic behavior and results indicate that, in general, asymmetrical configurations present more vibration attenuation than the symmetrical ones. Additionally, it is deduced that a compromise between response time and amplitudes has to be reached, and in addition, the most influential parameters have been determined to achieve greater vibration reduction.
1. Introduction
Vibration reduction is a recurrent topic in mechanical engineering. Vibration generates noise, unpleasant motions and dynamic stress that may cause the failure of a system, and may result in energy losses and structure degradation [1].
Among the different approaches that can be employed to reduce structural vibration, surface treatments are widely used by means of passive damping techniques [2,3,4,5]. Some of the most frequently used here are free layer damping (FLD) and constrained layer damping (CLD) configurations. It is known that CLD configurations provide better damping results with respect to the mass-damping relation. Numerous studies have been carried out employing CLD configurations. For example, in [6,7], a CLD beam is analyzed in order to minimize the vibration energy in the frequency domain. In [8,9], an optimization in the frequency domain is made to different parameters such as the density or thickness of different viscoelastic materials applied in a CLD plate configuration in order to maximize the modal loss factor and minimizing the displacement response. A new formulation to reduce computation time, such as an homogenized formulation for plates with a thick constrained viscoelastic core, is carried out in [10] in the frequency domain. However, FLD configurations are still a common occurrence due to being easier to procure and they have a lower economic value [11]. Therefore, this paper is focused on these configurations.
One way to mathematically characterize a viscoelastic material is with fractional models, because they allow to reproduce the damping behavior with a reduced number of parameters that, in addition, have a physical interpretation [12,13]. The definition and study of fractional calculus and its applications can be found widely in literature, for example in [13,14,15,16,17]. Several studies have been carried out using fractional derivative models in FLD applications. For example, in [11], a frequency domain study is made to an FLD plate in order to study the resonant region. In [18] Lyapunov’s direct method for dynamical systems with fractional damping is proposed. This is done in a single degree-of-freedom system first, and it is then generalized for the finite-dimensional case. Similar methodology is used in [19] in order to compare the dynamic behavior between a viscoelastic beam and a viscous one. The application of a general homogenized formulation has been presented in [20] for thick viscoelastic layered structures with the aim to reduce computation time.
There are numerous studies conducted in the time domain due to the importance of knowing the dynamic transient behavior in engineering applications. An analysis of the impact of the fractional derivative order in a viscoelastic material is done in [21] to study the transient behavior of plates. A study in both the frequency and time domain is conducted to beams, plates and shells in [22] to analyze the damping ratio under different configurations. Additionally, in [23], a transient analysis is carried out on viscoelastic beams and plates to study the effect of different boundary conditions and stiffness that those systems have on the energy dissipation. An alternative formulation to the finite element analysis is proposed in [24] to study the transient behavior of plates in order to get better results by using a higher-order shear deformation theory (HSDT). Another alternative to the classical approach of fractional calculus is presented in [25] with the goal to reduce computation time when an analysis in the time domain is conducted. Due to the high computation time that a transitory analysis can present, this new approach considers the stress of the viscoelastic material not self-dependent and dependent only on the displacements of it, reducing computation time. An alternative to the Runge–Kutta method that duplicates the number of equations to solve is carried out in [26], where non-linear equations are transformed into a fractional integro-differential equation in which the fractional operator represents a variable stiffness. Other method to extend the Kirchhoff–Love thin plate formulation into thick plates in a FLD configuration is presented in [27]. Additionally, a homogenized formulation is presented in [28] for FLD beams in which an asymmetrical and a symmetrical configuration is studied to reduce computation time.
All the mentioned studies are focused on the general behavior of a system modeled by fractional derivatives, and do not analyze the impact that the different parameters of the model have on the transient behavior of the system. The studies encountered in the time domain have an emphasis on the formulation of the problem and finding new resolution methods with the aim to reduce computation time, and they are not centered in analyzing the viscoelastic material parameters. The studies addressed on an analysis of the viscoelastic material are focused in analyzing some parameters such as the thickness of the viscoelastic layer or the fractional order derivative of the model, but none analyze all the parameters involved in the viscoelastic material model.
Thus, this article is carried out in order to get a better understanding of the viscoelastic parameters present in fractional derivative models and its influence in the time domain. Knowing which parameters are governing the transient behavior the most can prove to be very beneficial in practical applications in order to prevent unsuspected mechanical failures caused by vibrations. To that end, all parameters of a fractional derivative model need to be analyzed and not only the fractional order derivative. In addition, the viscoelastic layer thickness is studied too in order to evaluate the effect that the amount of viscoelastic material can have on the transient response and in vibration attenuation. For that, a transient analysis is performed in a FLD cantilever beam. To reduce significantly computation time, a homogenized formulation is carried out that allows to study a multilayered beam as if it was a homogeneous beam with equivalent properties, valid for symmetrical and asymmetrical configurations [28]. The Grünwald–Letnikov method is used to approximate the fractional derivatives, and the Newmark method is applied to obtain the discretized transverse displacement of the free edge of the beam when a unitary load is applied transversely on the same point.
Finally, two numerical applications are presented and discussed aimed at illustrating the conclusions derived from the analysis.
2. Homogenized Model for an FLD Beam
2.1. Homogenized Finite Element Formulation
In this section, the homogenized model used in the analysis of an FLD beam is described for both asymmetrical and symmetrical configurations. These configurations are illustrated in Figure 1. In this model, the constitutive law of the elastic material is given by
and the constitutive law of the viscoelastic material represented by a fractional model of five parameters is given by
where is spatial variable along the length of the beam , is time, is stress, is strain, is the Young’s modulus of the elastic material, is the fractional derivative operator with respect to time, and are the fractional parameters, , is the relaxation time, and and are the relaxed and the unrelaxed moduli of the viscoelastic material, respectively [16]. The deformations are small, and the Euler–Bernoulli hypothesis [29] is considered, where the curvature of each layer is considered the same,
where is the transverse displacement field. This implies that the strain distribution along the thickness is linear and the bending moments of both materials, and , can be obtained by integrating the moment of the stress with respect to the neutral axis for each material (more information about this topic can be found in any text on dynamics of solids such as [30]), to obtain
and
where represents the cross-sectional second-order moment (also known as the inertia moment of the cross-sectional area). This inertia moment is dependent on the width of the beam , the modulus of each material, the position of the neutral axis , the thickness of the elastic layer and the total thickness of the viscoelastic layer . The position of the neutral axis is considered constant along time. For the asymmetrical configuration (see Figure 1), due to the fact that beam is composed of two different materials, the position of the neutral fiber depends not only on the geometry of the transverse section but also on the material of each layer [28,31]. Taking this into account, for the asymmetrical configuration this results in
and
and for the symmetrical one, in
and
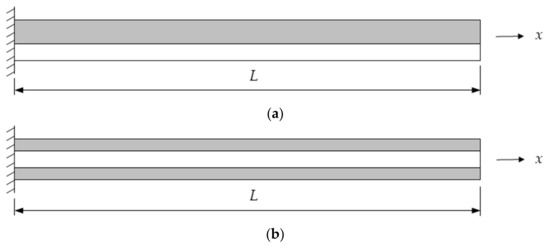
Figure 1.
Elastic (  ) and viscoelastic (
) and viscoelastic (  ) material distribution in both FLD configurations: (a) Asymmetrical configuration; (b) Symmetrical configuration.
) material distribution in both FLD configurations: (a) Asymmetrical configuration; (b) Symmetrical configuration.
 ) and viscoelastic (
) and viscoelastic (  ) material distribution in both FLD configurations: (a) Asymmetrical configuration; (b) Symmetrical configuration.
) material distribution in both FLD configurations: (a) Asymmetrical configuration; (b) Symmetrical configuration.
The total flexural moment , for both symmetrical and asymmetrical configurations, is obtained by adding the individual contribution of each material,
To be able to accomplish this addition, the operator has to be applied to Equation (4). Thus, the resultant flexural moment yields
In order to get the transverse displacement field, the combination of Equation (13) with the local equation of linear momentum [30] is required. This equation takes the following form,
where and are the density of the elastic and the viscoelastic materials, respectively, is the acceleration field, and is the transverse force density. The operator has to be applied on both sides of Equation (14), and Equation (13) has to be differentiated twice. Following these steps, the final expression results in
This last equation does not have an analytical solution, and therefore numerical resolution methods are required, which are presented next.
2.2. Numerical Integration
To obtain a finite element formulation, the weighted residual method is used (Galerkin approximation [32]) on Equation (15) for a finite volume of length , yielding
where, for the ith finite element, , , and are the mass and stiffness matrices for the elastic and viscoelastic layer, respectively, and are the nodal acceleration and displacement vectors and is the vector of the nodal external forces.
In Equation (16), the elementary mass matrices and are defined as
where the subscript is or for the elastic and viscoelastic material, respectively, and according to the elastic term of Equation (2), , represents the interpolation function matrix for the -th element and denotes the transposition operator. The interpolation functions considered are the classical used in finite element formulations [33]. Additionally, from Equation (16) the elementary stiffness matrices and are defined as
The finite element that constitutes the elementary matrices is linear composed of 2 nodes, where the transverse displacement and the rotational degrees of freedom are defined in each node. Then, the elementary mass matrix for the i-th finite element is defined by
and the elementary stiffness matrix by
in which the subscript is or for the elastic or viscoelastic material, respectively, and according to the elastic term of Equation (2), . The assembly of the global system yields
where and are the global mass and stiffness matrices, , , and are the assembled matrices for each material, and , and are the global nodal displacement, acceleration and external force vectors.
The M-K-F implicit formulation for direct integration of Equation (21) is presented next [34]. The matrix equation of motion at the time takes the form
where the displacement has to be solved. The Grünwald–Letnikov approach [13] is used to approximate the fractional derivatives. This approach proposes that for any real order and for a finite time step , the fractional derivative can be approximated by
where is the number of steps and the coefficients are the Grünwald–Letnikov parameters of order that have the following properties:
and
which gives the ‘short-memory’ property of the fractional derivative operator. The definition of these parameters applied to the fractional derivatives of order and on Equation (22) yields
and
The M-K-F method transforms Equations (27)–(29) in
and
respectively. These definitions allow to transform Equation (22) in a second-order system such as
where the equivalent mass matrix is
the equivalent stiffness matrix results
and the equivalent force vector is given by
Equation (33) can be solved given the initial displacement and the initial velocity using implicit numerical resolution methods such as Newmark method [33].
3. Description of the Model
In this section, the model used for the analysis is described. The study is carried out in an FLD cantilever beam on which a static unitary load is transversely applied on the free edge of the beam. The goal of the study is to analyze the influence that each of the parameters of the viscoelastic material model (namely , , , and ) and the thickness of the viscoelastic material have on the transverse displacement of the free edge of the beam, in order to get a better understanding of the time response and the amplitudes present during the vibration. The analysis is performed in an asymmetrical and a symmetrical configuration as the ones illustrated in Figure 1.
The beam is modelled by means of 30 linear finite elements, the interpolation functions used are cubic and the size of all the finite elements is the same, each one having 2 degrees of freedom in each node: the transverse displacement and the rotation . The choice of 30 finite elements to discretize the beam is considered enough due to the fact that in Ref. [28] a validation of the model with that number of finite elements was carried out. The elementary matrices used to assemble the system are the ones provided by Equations (19) and (20). The simulation time is not fixed because different times are required for each parameter. All studies have been performed in MATLAB, and the code generated to obtain the transient response with the formulation exposed in this article has been elaborated by the authors.
The dimensions of the beam and the properties of the elastic material are shown in Table 1. These values are taken from Ref. [28], where a study of different FLD models is carried out. The reference values of the density of the viscoelastic material and the thickness of the viscoelastic material are also taken from [28].

Table 1.
Geometry of the beam and properties of the elastic material [28].
The reference values of the viscoelastic material are taken from Ref. [35], where Jones carries out a characterization of different viscoelastic materials by means of a complex modulus E* given by
where , and are model parameters, is the fractional derivative order, is the reduced frequency, and are the loss factors at low and high frequencies, respectively, and .
In order to make an equivalence between the parameters given by the model presented in Equation (2) in the time domain with the model given by Jones in Equation (37) in the frequency domain, the Fourier transform is applied on Equation (2), where
and
where represents the Fourier transform operator. The definitions of Equations (38) and (39) applied on Equation (2) yield
where represents the ratio between the Fourier transform of and , given by and , respectively.
The model in Equation (37) used by Jones has 6 parameters. Taking into account that the coefficients of Equation (2) have to be real in the time domain, and are considered to be 0 on Equation (37), meaning that the damping is not taken into account at very low frequencies and very high frequencies. With this, the model given by Jones in Equation (37) results in a particular case of the model in Equation (2) when . It is then established the following relations between parameters: , , and .
The values considered as a reference for the study are taken from the mean values of the experimental results obtained by Jones for free layer materials. These values are gathered in the second column of Table 2.

Table 2.
Reference value and interval of study for each parameter.
The study intervals are taken between the maximum and minimum value encountered by Jones, and they can be consulted on Table 2. In each case, 11 values are studied evenly distributed within the intervals. For the thickness , which is independent of the parameters of the viscoelastic material, the range of the interval will be set to a variation of with respect to the reference value .
4. Numerical Analysis
First, the influence of each parameter of the viscoelastic material model on the dynamic behavior of the beam is studied. Next, the influence of the thickness of the viscoelastic layer is taken into account. Finally, two numerical examples are presented to illustrate the conclusions of the analysis.
In each simulation, the displacement ratio between the transverse displacement and the displacement of the stationary response is computed from Equation (21) on the free edge of the beam. For that, the displacement of the stationary response is previously calculated when there are no time dependent terms in Equation (21), which results in
Four variables are considered to characterize the transient response (see Figure 2):
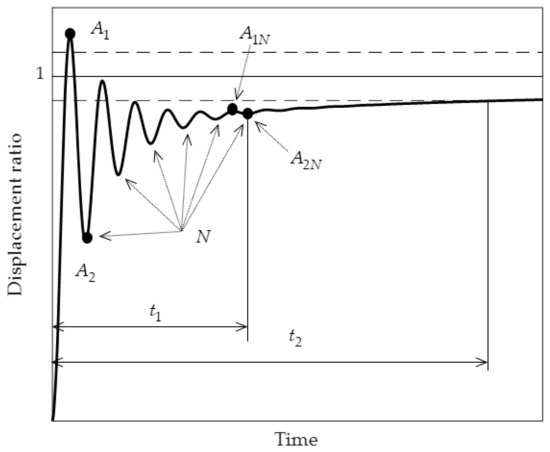
Figure 2.
Variables to analyze. The two discontinuous lines (  ) represent the interval of the stationary response, which is always 1 according to the definition of the displacement ratio .
) represent the interval of the stationary response, which is always 1 according to the definition of the displacement ratio .
 ) represent the interval of the stationary response, which is always 1 according to the definition of the displacement ratio .
) represent the interval of the stationary response, which is always 1 according to the definition of the displacement ratio .
- Amplitude ratio between the first relative maximum and the first relative minimum, . This parameter illustrates the initial intensity of the response. The higher this value, the larger the system oscillates at first, and therefore, the lower the value, the higher it is the attenuation of the vibration. This variable is important, for example, in human comfort applications.
- Amplitude ratio between the first relative maximum and the stationary response (which is always normalized to 1), . The higher this amplitude, the lesser the vibration attenuation present into the beam.
- Number of cycles to reduce the vibration. This is considered when the difference between a relative maximum and the consecutive relative minimum is the 5% of the mean value between them, i.e., the next equation is satisfied,for practical applications, it is desired a low value in the number of cycles in order to get a quicker vibration attenuation.
- Time ratio : is the time at which the system reaches the stationary value with a tolerance of and is the required time to perform the cycles previously mentioned. This ratio should be as low as possible in order to get a faster time response.
4.1. Analysis of the Influence of the Viscoelastic Material Parameters
In this section, the four variables previously described are evaluated in order to measure the influence that the material model parameters of Equation (40) have on the transient response. The interval of study of each parameter can be found in Table 2.
4.1.1. Initial Amplitude Ratio Influence
The ratio between the amplitudes of the first relative maximum and minimum is studied in this section. The results obtained for both asymmetrical and symmetrical configurations are illustrated in Figure 3.
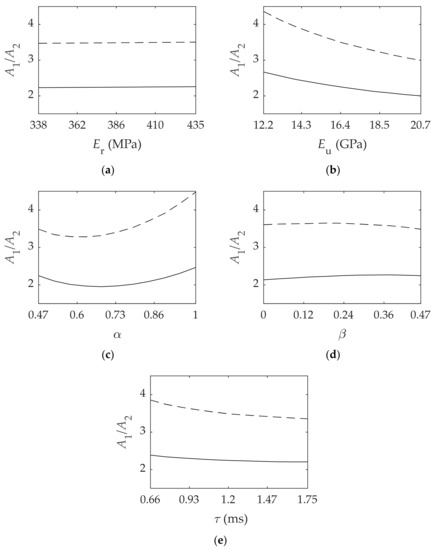
Figure 3.
Viscoelastic material parameters influence on the ratio between the first relative maximum and the first relative minimum for the asymmetrical (  ) and symmetrical (
) and symmetrical (  ) configurations. In order: (a) Relaxed modulus ; (b) Unrelaxed modulus ; (c) Fractional parameter ; (d) Fractional parameter ; (e) Relaxation time .
) configurations. In order: (a) Relaxed modulus ; (b) Unrelaxed modulus ; (c) Fractional parameter ; (d) Fractional parameter ; (e) Relaxation time .
 ) and symmetrical (
) and symmetrical (  ) configurations. In order: (a) Relaxed modulus ; (b) Unrelaxed modulus ; (c) Fractional parameter ; (d) Fractional parameter ; (e) Relaxation time .
) configurations. In order: (a) Relaxed modulus ; (b) Unrelaxed modulus ; (c) Fractional parameter ; (d) Fractional parameter ; (e) Relaxation time .
First, it can be noted that, in all cases, the asymmetrical configuration presents higher damping according to the results observed for each parameter. In the asymmetrical configuration, the neutral plane is further to the viscoelastic material and therefore it is subjected to higher deformation compared to the symmetrical configuration, implying higher damping.
Moreover, the results indicate that has not any remarkable influence on the amplitude of the first oscillation. This is a consequence of being much lower in value compared to as seen in Table 1. Additionally, and have the lowest influence on the response, and and are the parameters that have the major influence on this ratio. In addition, in general, a monotonous behavior occurs in which the ratio decreases with the parameters except with : ratio decreases first, and it reaches a minimum value at around 0.6 in both configurations, and then increases.
Quantitatively, the reference values taken for each parameter indicate that this ratio has a value of 2.25. If increases, then the ratio is reduced in 19% in the asymmetrical configuration and in 31% in the symmetrical one. Lastly, for and the differences are lower than 10% in both configurations; the symmetrical one is slightly the most affected.
4.1.2. First Maximum and Stationary Amplitude Ratio Influence
In this section, the ratio between the amplitude of the first maximum and the stationary response is computed. In Figure 4 the results obtained for asymmetrical and symmetrical configurations are represented.
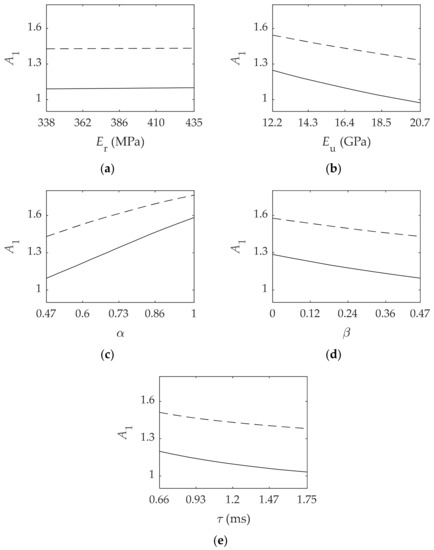
Figure 4.
Viscoelastic material parameters influence on the ratio between the amplitude of the first maximum and the stationary response for the asymmetrical (  ) and symmetrical (
) and symmetrical (  ) configurations. In order: (a) Relaxed modulus ; (b) Unrelaxed modulus ; (c) Fractional parameter ; (d) Fractional parameter ; (e) Relaxation time .
) configurations. In order: (a) Relaxed modulus ; (b) Unrelaxed modulus ; (c) Fractional parameter ; (d) Fractional parameter ; (e) Relaxation time .
 ) and symmetrical (
) and symmetrical (  ) configurations. In order: (a) Relaxed modulus ; (b) Unrelaxed modulus ; (c) Fractional parameter ; (d) Fractional parameter ; (e) Relaxation time .
) configurations. In order: (a) Relaxed modulus ; (b) Unrelaxed modulus ; (c) Fractional parameter ; (d) Fractional parameter ; (e) Relaxation time .
On the one hand, from Figure 4 it can be pointed out that, similarly to the previous parameter, the asymmetrical configuration presents more damping than the symmetrical one. Additionally, the relaxed modulus does not modify this ratio through the interval, and , and present similar trends. On the contrary, the first maximum increases with throughout the interval.
From a quantitative point of view, in the asymmetrical configuration there is an increase of 15% in this ratio for and a reduction of 22% for . In this last particular case, the amplitude is lower than 1. This means that the system does not reach the point of equilibrium when oscillating due to the viscoelastic behavior present in the beam. This effect is discussed later.
4.1.3. Number of Cycles Influence
The results of the number of cycles that the system fulfills to reduce the oscillations are illustrated in Figure 5.
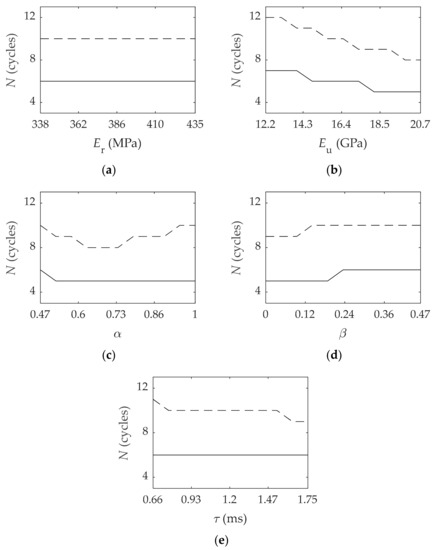
Figure 5.
Viscoelastic material parameters influence on the number of cycles for the asymmetrical (  ) and symmetrical (
) and symmetrical (  ) configurations. In order: (a) Relaxed modulus ; (b) Unrelaxed modulus ; (c) Fractional parameter ; (d) Fractional parameter ; (e) Relaxation time .
) configurations. In order: (a) Relaxed modulus ; (b) Unrelaxed modulus ; (c) Fractional parameter ; (d) Fractional parameter ; (e) Relaxation time .
 ) and symmetrical (
) and symmetrical ( 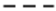 ) configurations. In order: (a) Relaxed modulus ; (b) Unrelaxed modulus ; (c) Fractional parameter ; (d) Fractional parameter ; (e) Relaxation time .
) configurations. In order: (a) Relaxed modulus ; (b) Unrelaxed modulus ; (c) Fractional parameter ; (d) Fractional parameter ; (e) Relaxation time .
In relation to the differences between the symmetrical and asymmetrical configurations, the same conclusion as in the previous cases can be drawn. In this case, the only parameter that has a remarkable influence is the unrelaxed modulus , in which is reduced from 12 to 8 in the symmetrical configuration. A similar reduction is given in the asymmetrical configuration, from 7 to 5. The influence of the other parameters is less significant, the only remarkable behavior is the one of ; it can be observed a minimum value of at around the midpoint of the interval in the symmetrical configuration, the reduction of the value is from 10 to 8.
4.1.4. Time Ratio Influence
The influence of the material parameters on the time ratio is shown in Figure 6.
Figure 6.
Viscoelastic material parameters influence on the time ratio for the asymmetrical (  ) and symmetrical (
) and symmetrical (  ) configurations. In order: (a) Relaxed modulus ; (b) Unrelaxed modulus ; (c) Fractional parameter ; (d) Fractional parameter ; (e) Relaxation time .
) configurations. In order: (a) Relaxed modulus ; (b) Unrelaxed modulus ; (c) Fractional parameter ; (d) Fractional parameter ; (e) Relaxation time .
 ) and symmetrical (
) and symmetrical (  ) configurations. In order: (a) Relaxed modulus ; (b) Unrelaxed modulus ; (c) Fractional parameter ; (d) Fractional parameter ; (e) Relaxation time .
) configurations. In order: (a) Relaxed modulus ; (b) Unrelaxed modulus ; (c) Fractional parameter ; (d) Fractional parameter ; (e) Relaxation time .
When analyzing this variable, in general the symmetrical configuration presents a lower value in the time ratio, the only exception occurs when is higher than 0.6 or is close to 0. In those cases, this variable is near to 1, meaning that both and are practically the same. The reduction of the time ratio is more significant when increasing than when reducing .
Same as with all the other studies does not have any impact in this variable.
Finally, and present a similar trend through the interval, but from a quantitative point of view the time ratio increases in 400% with in the asymmetrical configuration, whereas a 190% is increased with . These high values on the time ratio mean that although the system can reduce the vibration fast, it requires a lot more time to reach the stationary state. This is due to the system having a dynamic point of equilibrium that changes over time consequence of having a viscoelastic layer. This makes the beam to vibrate around different values in contrast to the viscous behavior where the point of equilibrium does not change over time. This effect can be observed in Figure 7 and it was discussed in other studies, such as in Refs. [19,36].
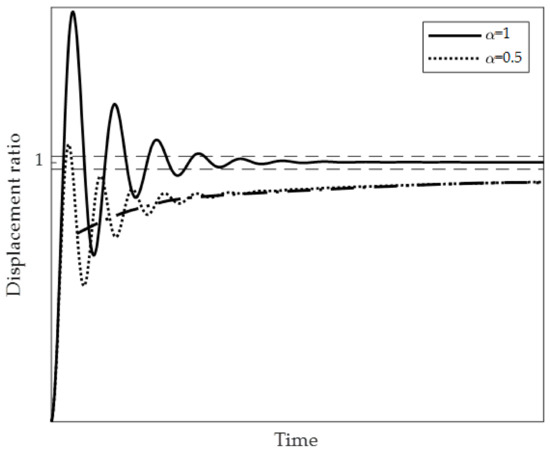
Figure 7.
Comparison between viscous and viscoelastic behaviors. Continuous line () corresponds to viscous response and dotted line ( ) to viscoelastic response. The line (  ) represents point of equilibrium changing over time and the two horizontal dashed lines (
) represents point of equilibrium changing over time and the two horizontal dashed lines (  ) represent the interval of the stationary response.
) represent the interval of the stationary response.
 ) represents point of equilibrium changing over time and the two horizontal dashed lines (
) represents point of equilibrium changing over time and the two horizontal dashed lines (  ) represent the interval of the stationary response.
) represent the interval of the stationary response.
4.2. Analysis of the Influence of the Viscoelastic Layer Thickness
After studying the influence of the material parameters, in this section, the thickness of the viscoelastic layer is discussed. The analysis is carried out in the same way as in the previous section. The interval of study can be found in Table 2 along with the viscoelastic model parameters used which corresponds to the reference values. The results obtained for each variable for both the asymmetrical and the symmetrical configurations are shown in Figure 8.
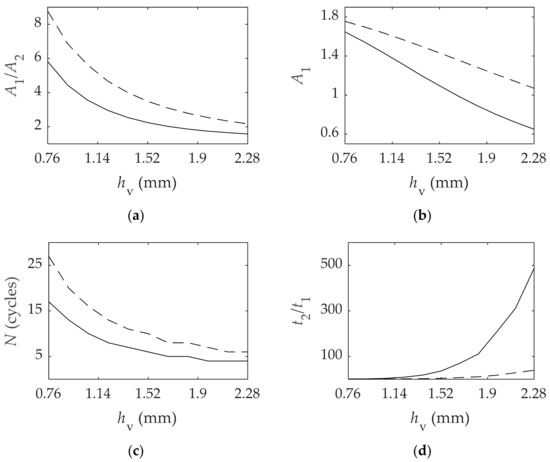
Figure 8.
Influence of the viscoelastic layer thickness of the asymmetrical (  ) and symmetrical (
) and symmetrical (  ) configurations on: (a) Ratio between the first relative maximum and the first relative minimum ; (b) Ratio between the amplitude of the first maximum and the stationary response ; (c) Number of cycles ; (d) Time ratio .
) configurations on: (a) Ratio between the first relative maximum and the first relative minimum ; (b) Ratio between the amplitude of the first maximum and the stationary response ; (c) Number of cycles ; (d) Time ratio .
 ) and symmetrical (
) and symmetrical (  ) configurations on: (a) Ratio between the first relative maximum and the first relative minimum ; (b) Ratio between the amplitude of the first maximum and the stationary response ; (c) Number of cycles ; (d) Time ratio .
) configurations on: (a) Ratio between the first relative maximum and the first relative minimum ; (b) Ratio between the amplitude of the first maximum and the stationary response ; (c) Number of cycles ; (d) Time ratio .
According to the results obtained, the asymmetrical configuration has a higher vibration attenuation compared to the symmetrical configuration, and on the contrary the time ratio is significantly higher when increases.
From a quantitative point of view, two remarkable facts can be derived. On the one hand, the amplitude ratio of the initial oscillation is reduced in 30% and in 38% in the asymmetrical and symmetrical configurations, respectively, and in both cases the reduction takes an exponential form. On the other hand, the initial amplitude is reduced in 41% in the asymmetrical configuration, and at the end of the interval is lower than 1. Another fact is that the number of cycles is significantly decreased when the amount of viscoelastic material is higher. This variation has an exponential form and in both configurations the number of cycles is reduced in 75% through the interval.
The results observed indicate that a compromise has to be reached when choosing the amount of viscoelastic material: to increase thickness results in higher vibration attenuation, but the response time increases exponentially because, as it has been previously discussed and illustrated in Figure 7, the viscoelastic behavior is more patent.
4.3. Examples of Parameter Combination
After the influence analysis, two numerical applications are presented next to better illustrate the derived conclusions. In the previous sections, the effect that each parameter has on the transient response has been studied and here, how the transient response is altered when a combination of parameters are changed is studied. First, beginning with the reference values of the viscoelastic model, some parameters are modified as shown in Table 3 in order to reduce the time ratio. Then, from these parameters, the thickness of the viscoelastic material is increased in 25% () with the aim of reducing the amplitudes. The asymmetrical configuration is chosen for these two numerical examples.

Table 3.
Comparison between reference values and the ones of Examples 1 and 2.
The response obtained for both examples are shown in Figure 9, and the results of the analyzed variables are gathered in Table 4.
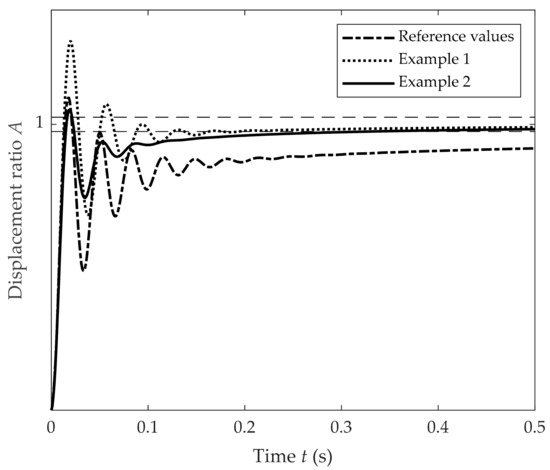
Figure 9.
Comparison between reference values, Example 1 values and Example 2 values. The two horizontal dashed lines (  ) represent the interval with regard to the normalized displacement ratio at the stationary value.
) represent the interval with regard to the normalized displacement ratio at the stationary value.
 ) represent the interval with regard to the normalized displacement ratio at the stationary value.
) represent the interval with regard to the normalized displacement ratio at the stationary value.

Table 4.
Results comparison rounded to three significant figures.
Analyzing Example 1, the most notable change in the response is in relation with the time ratio, which is reduced from 36 to 1.3. This value is higher in comparison to both examples due to the fact that the system requires too much time to reach the stationary state as seen in Figure 9. One downside of the proposed values is that the initial amplitude increases in 18%. Nevertheless, the amplitude ratio of the initial oscillation is decreased in 16%. Moreover, the number of cycles is reduced from 6 to 4.
With Example 2, the viscoelastic layer thickness has been increased in order to have a lower result of , concretely it is reduced in 18% compared to Example 1. Nevertheless, the time ratio increases from 1.30 to 3.29. This antagonism between and has been manifested in Section 4.2. This example illustrates that the vibration attenuation can be potentially improved further.
Taking the model parameters and thickness of Example 2, all the 4 variables studied present an improvement in its values in comparison with the reference values.
5. Conclusions
In this paper, the dynamic behavior of an FLD cantilever beam composed of a metallic component with a viscoelastic surface treatment has been analyzed by means of numerical methods. Specifically, the influence of the material parameters and the thickness of the viscoelastic layer on the transient response have been studied in in two different configurations: asymmetrical and symmetrical. Taking into account that the material model is represented by fractional derivatives, specific numerical methods have been performed in a finite element framework.
The results obtained have illustrated that in general an asymmetrical configuration presents more vibration attenuation. In the asymmetrical configuration, the neutral fiber is closer to the elastic material and therefore the viscoelastic material is put under more strain compared to the symmetrical configuration.
The analysis performed can give a better understanding of the viscoelastic model parameters, and it can be concluded that the dynamic behavior of a system with viscoelastic surface treatments can be potentially optimized by choosing the adequate material in practical engineering applications. To illustrate this, comparing the results obtained in Example 2 to the ones obtained with the reference values, is reduced in 37%, in 4.5%, in 50% and in 90%.
One of the main advantages that this research provides is that it allows to get a better understanding of the influence of each viscoelastic material model parameter. Knowing the effect that each viscoelastic model parameter has on the transient response can prove to be very beneficial in practical applications. The homogenized formulation employed for the analysis provides another important factor to consider by reducing computation time compared to using a plane or cubic finite element formulation due to the reduction on the degrees of freedom required.
By contrast, the formulation used is not valid for all configurations. The Euler–Bernoulli hypothesis is only correct for thin beams and cannot be employed to study thick beams. In addition, the formulation performed cannot be used to study more complex systems such as CLD beams or plates. Therefore, more research can be carried out to expand the analysis to other configurations and to keep investigating the viscoelastic properties of materials characterized by fractional derivative models.
Author Contributions
Conceptualization, M.B., F.C. and M.J.E.; methodology, M.B., F.C. and M.J.E.; software, M.B.; investigation, M.B., F.C. and M.J.E.; writing—original draft preparation, M.B.; supervision, F.C. and M.J.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially supported by the ISAVA project (PUE 2020 04, Basque Government).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rao, M.D. Recent Applications of Viscoelastic Damping for Noise Control in Automobiles and Commercial Airplanes. J. Sound Vib. 2003, 262, 457–474. [Google Scholar] [CrossRef]
- Chakraborty, B.; Ratna, D. Polymers for Vibration Damping Applications, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Sun, C.T.; Lu, Y.P. Vibration Damping of Structural Elements, 1st ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 1995. [Google Scholar]
- Nashif, A.D.; Jones, D.I.; Henderson, J.P. Vibration Damping, 1st ed.; John Wiley & Sons: New York, NY, USA, 1985. [Google Scholar]
- Elejabarrieta, M.J.; Cortés, F.; Martínez, M. Viscoelastic Surface Treatments for Passive Control of Structural Vibration, 1st ed.; Nova Science Publishers: New York, NY, USA, 2011. [Google Scholar]
- Zheng, H.; Cai, C.; Tan, X.M. Optimization of partial constrained layer damping treatment for vibrational energy minimization of vibrating beams. Comput. Struct. 2004, 82, 2493–2507. [Google Scholar] [CrossRef]
- Irazu, L.; Elejabarrieta, M.J. The influence of viscoelastic film thickness on the dynamic characteristics of thin sandwich structures. Compos. Struct. 2015, 134, 421–428. [Google Scholar] [CrossRef]
- Lall, A.K.; Nakra, B.C.; Asnani, N.T. Optimum design of viscoelastically damped sandwich panels. Eng. Optim. 1983, 6, 197–205. [Google Scholar] [CrossRef]
- Irazu, L.; Elejabarrieta, M.J. The effect of the viscoelastic film and metallic skin on the dynamic properties of thin sandwich structures. Compos. Struct. 2017, 176, 407–419. [Google Scholar] [CrossRef]
- Zarraga, O.; Sarría, I.; García-Barruetabeña, J.; Cortés, F. Homogenised formulation for plates with thick constrained viscoelastic core. Comput. Struct. 2020, 229, 106185. [Google Scholar] [CrossRef]
- Sun, W.; Yan, X.; Gao, F. Analysis of Frequency-Domain Vibration Response of Thin Plate Attached with Viscoelastic Free Layer Damping. Mech. Based Des. Struct. Mach. 2018, 46, 209–224. [Google Scholar] [CrossRef]
- Adolfsson, K.; Enelund, M.; Olsson, P. On the fractional order model of viscoelasticity. Mech. Time-Depend. Mater. 2005, 9, 15–34. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations, 1st ed.; Academic Press: Cambridge, NY, USA, 1998. [Google Scholar]
- Jannelli, A. Numerical solutions of fractional differential equations arising in engineering sciences. Mathematics 2020, 8, 215. [Google Scholar] [CrossRef] [Green Version]
- Miller, K.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations, 1st ed.; John Wiley & Sons: New York, NY, USA, 1993; pp. 19–93. [Google Scholar]
- Bagley, R.L.; Torvik, P.J. Fractional calculus—A different approach to the analysis of viscoelastically damped structures. AIAA J. 1983, 21, 741–748. [Google Scholar] [CrossRef]
- Cortés, F.; Elejabarrieta, M.J. Finite element analysis of the seismic response of damped structural systems including fractional derivative models. J. Vib. Acoust. Trans. ASME 2014, 136, 050901. [Google Scholar] [CrossRef]
- Hinze, M.; Schmidt, A.; Leine, R.I. The direct method of lyapunov for nonlinear dynamical systems with fractional damping. Nonlinear Dyn. 2020, 102, 2017–2037. [Google Scholar] [CrossRef]
- Zarraga, O.; Sarría, I.; García-Barruetabeña, J.; Cortés, F. An analysis of the dynamical behaviour of systems with fractional damping for mechanical engineering applications. Symmetry 2019, 11, 1499. [Google Scholar] [CrossRef] [Green Version]
- Zarraga, O.; Sarría, I.; García-Barruetabeña, J.; Elejabarrieta, M.J.; Cortés, F. General homogenised formulation for thick viscoelastic layered structures for finite element applications. Mathematics 2020, 8, 714. [Google Scholar] [CrossRef]
- Praharaj, R.K.; Datta, N. On the transient response of plates on fractionally damped viscoelastic foundation. Comput. Appl. Math. 2020, 39, 256. [Google Scholar] [CrossRef]
- Al-Huniti, N.; Al-Faqs, F.; Abu Zaid, O. Finite element dynamic analysis of laminated viscoelastic structures. Appl. Compos. Mater. 2010, 17, 405–414. [Google Scholar] [CrossRef]
- Kiasat, M.S.; Zamani, H.A.; Aghdam, M.M. On the transient response of viscoelastic beams and plates on viscoelastic medium. Int. J. Mech. Sci. 2014, 83, 133–145. [Google Scholar] [CrossRef]
- Shafei, E.; Faroughi, S.; Rabczuk, T. Nonlinear transient vibration of viscoelastic plates: A NURBS-Based isogeometric HSDT approach. Comput. Math. Appl. 2021, 84, 1–15. [Google Scholar] [CrossRef]
- Cunha-Filho, A.G.; Briend, Y.; de Lima, A.M.G.; Donadon, M.V. A new and efficient constitutive model based on fractional time derivatives for transient analyses of viscoelastic systems. Mech. Syst. Signal Process. 2021, 146, 107042. [Google Scholar] [CrossRef]
- Sarría, I.; García-Barruetabeña, J.; Cortés, F.; Mateos, M. Dynamic Analysis of nonlinear structural systems by means of fractional calculus. DYNA Ing. Ind. 2015, 90, 54–60. [Google Scholar] [CrossRef] [Green Version]
- Zarraga, O.; Sarría, I.; García-Barruetabeña, J.; Cortés, F. Dynamic analysis of plates with thick unconstrained layer damping. Eng. Struct. 2019, 201, 109809. [Google Scholar] [CrossRef]
- Cortés, F.; Elejabarrieta, M.J. Homogenised finite element for transient dynamic analysis of unconstrained layer damping beams involving fractional derivative models. Comput. Mech. 2007, 40, 313–324. [Google Scholar] [CrossRef]
- Gere, J.M.; Timoshenko, S. Mechanics of Materials, 4th ed.; PWS Publishing Company: Boston, MA, USA, 1996. [Google Scholar]
- Inman, D.J. Engineering Vibration, 4th ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 1996. [Google Scholar]
- Megson, T. Structural and Stress Analysis, 1st ed.; Butterworth-Heinemann: Bodmin, UK, 1996. [Google Scholar]
- Universidad de Vigo. Available online: http://www.dma.uvigo.es/files/cursos/mef/teoria.pdf (accessed on 21 April 2021).
- Bathe, K.-J. Finite Element Procedures, 1st ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 1996. [Google Scholar]
- Cortés, F.; Elejabarrieta, M.J. Finite element formulations for transient dynamic analysis in structural systems with viscoelastic treatments containing fractional derivative models. Int. J. Numer. Methods Eng. 2007, 69, 2173–2195. [Google Scholar] [CrossRef]
- Jones, D.I. Handbook of Viscoelastic Vibration Damping, 1st ed.; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- García-Barruetabeña, J.; Cortés, F.; Manuel Abete, J. Influence of nonviscous modes on transient response of lumped parameter systems with exponential damping. J. Vib. Acoust. 2011, 133, 064502. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).