A Bender’s Algorithm of Decomposition Used for the Parallel Machine Problem of Robotic Cell

Abstract

The present research addresses the single transportation robot used to alleviate problems of robotic cell scheduling of the machines. For the purpose of minimizing the make-span, a model of mixed-integer linear programming (MILP) has been suggested. Since the inefficiency exists in NP-hard, a decomposition algorithm posed by Bender was utilized to alleviate the problem in real life situations. The proposed algorithm can be regarded as an efficient attempt to apply optimality Bender’s cuts regarding the problem of parallel machine robotic cell scheduling in order to reach precise resolutions for medium and big sized examples. The numerical analyses have demonstrated the efficiency of the proposed solving approach.

1. Introduction

Computer-controlled material conveying systems used to transfer raw materials or semi-finished goods through the multiple processing stages have become standard tools in modern manufacturing processes, especially after the fourth industrial revolution. By a robotic cell we mean a cell produced including a series of tools along with a robot material control [1,2].

The use of robots in manufacturing cells is mainly preferred due to several reasons. First, manufacturing robots enable to avoid contamination, which is crucial for industries like pharmaceutical compounding, semiconductor manufacturing, etc. Second, robots can substitute human beings in inhospitable environments. For instance, robots are good alternative for operations being carried out in high temperature vacuum cells like welding and iron working, coloring or some other types of coatings that might spray noxious fumes applications. Finally, yet importantly, robots offer incomparable speed and high precision of producing considerable volumes of either a single part or some intensively related parts.

Regarding the aforementioned advantages in robotic manufacturing cells and the trend of implementing bigger and more complicated cells in robots by manufacturers, more complex decision support models are needed to produce optimal functions and to maximize the cell productivity. In respective, various combinatorial optimization problems such as decisions by cells, proper arrangement of robot moves, programming the products or resource arrangement of the robots have been addressed by researchers to enhance efficiency of these cells [3,4].

A historical study of robotic cell scheduling demonstrates that there has been a common tendency in favor of cyclic type scheduling of robotic cells aiming at maximizing throughput rate, or shortening the time to cycle through repeated move cycles in an optimal form [5]. Programming problems in the form of multi-parts is more difficult than the same problems even if we consider a few machines. The decisions that are to be made in multiple part-type involve recognizing the robot move cycle and also the parts arrangement concurrently minimizing the time required to produce the cycle [1].

It is known that usually Robotic cells entail an input/output device for sections entering and going out of the cell, units of processing able to carry out different process steps, and a one or two grippers entailing robot. It is able to transport all the parts between processing units [6,7]. Additionally, robotic cells are mainly divided by two classes: a group containing a process of inspection built into the operations of a multi-function robot (MFR), and another category lacking inspection [8].

The technical definition of minimal part set (MPS) demonstrates the most trivial part-types which are proportional to the production demands. The use of the different arrangements of part types is the same as the ones demanded [9]. As an illustration, for the production demand of 2000 constituents of Type A, 1000 B Type parts and 3000 C Type parts, the MPS could be considered like (A, A, B, C, C, C) to be produced repetitively for 1000 times [1]. The purpose of considering MPS in robot cell scheduling is to simultaneously recognize the sequence of move in robots and the arrangement of part input in MPS while minimizing the time required to cycle or the use of steady-state common cycles.

This study aims to find the optimal single cycle for robot moves and at the same time, assigning the activities to be done to the machines to help in minimizing the make span while multiple identical machines are considered. Additionally, a proper method like Benders’ decomposition (BD) should be utilized to alleviate the problem. The results indicated that more effective use of machine capacity could lead to better results of resource allocation.

2. Literature Review

Initial studies of the robotic cell optimization mostly include cells having two- and three-machines, also those with multiple part-types. Sethi [10] suggested an algorithm of polynomial time determining a cycle with optimal multi-parts considering the arrangement of robot moves. Bilge and Ulusoy [11] carried out a research on scheduling vehicles guided automatically regarding m-machine flexible production systems. The authors presented nonlinear mixed integer-programming models and a procedure of iteration to minimize make-span.

Sriskandar [12] conducted a research project on the m-machine robotic cell in several part-types form. The authors categorized problems of part sequencing along with all cycles of one-unit robot move as: (i) independent of the sequence; (ii) with formulation capability as the problem of traveling salesman (TSP); (iii) having formulation capability as a TSP and unary NP-hard; and (iv) unary NP-hard, without a TSP structure.

Soukhal and Martineau [13] investigated about the problem of the robotic cell scheduling flow shop considering a unitary transportation robot, also multiple part-types. To find a solution for the problem, a model of integer linear programming and a genetic algorithm were recommended by them. Soukhal [14] carried out a research project on the problem of two-machine flow shop scheduling presupposing transfer limits. They could reinforce the problem regarding additional constraints, such as blocking, and using NP-hard.

Some scholars such as; Carlier et al. [3] investigated about an approximate decomposition algorithm for the cell scheduling of flow shop robotic using a unitary transfer robot and a constraint of block. Kharbeche [15] supplied a novel MILP model for the problem above using a separate robot and an exact branch, and a bound algorithm was suggested thereafter. Zahrouni and Kamoun [16] investigated about different part-types robotic cells and introduced a heuristic frame. A prior researcher, Fazel-Zarandi [17], went through a project considering the two-machine robotic cell using a sequence dependent setup to load/unload every part.

What’s more, Geismar et al. [18] carried out research about cells of robots with parallel machines and robots having multiple dual grippers. Batur [19] completed a research on cells of two-machine in robots making multiple part-types scheduling problem happen. Foumani and Jenab [20] worked on the robotic CSP having two machines and identical parts presupposing busy robots’ swap ability. Elmi and Topaloglu [1] presented the problem of cyclic job shop robotic cell scheduling in the presence of multiple robots aiming at minimizing the cycle time to increase throughput rate. In a subsequent research, Elmi and Topaloglu [21] investigated about a multiple degree cyclic flow shop robotic cell scheduling in the presence of multiple robots considering time window for processing and transportation operations.

Far [22] dealt with flexible scheduling under energy constraints and optimized the electricity consumption cost of production operations within on peak and off-peak electricity tariffs. Foumani [8] worked with optimization of two-machine flow shop robotic cells in stochastic form using inspection times that are controllable: theory to practice. Xiuli [23] investigated about a multi objective algorithm with differential evolution to solve robotic cell scheduling problems using a batch processing machine: robotic CSP with batch processing machines (RCSP-BMs) requires a determination of the sequence of processing and the sequence of transferring at the same time. Fattahi [24] carried out a study on a novel hybrid particle swarm optimization and parallel variable neighborhood search algorithm to carry out flexible job shop scheduling with assembly process.

To sum up, the literature available on the problem of several-parts type cell scheduling of robots could be precisely categorized from the perspective of six following features: stage number (SN); machine number per stage (MS); pickup criterion (PCri); robot move sequence (RMS); part sequence (PS) and solution procedure for RMS and PS (Sol-Proc).

Table 1. Several-parts type robotic cell scheduling problems categorized based on studies.

Project	SN	MS	PCri	RMS	PS	Sol-Proc	Helps
Sethi et al. [10]	2, 3	1	Free	Given	✓	-	Utilization of Gilmore and Gomory algorithms.
Bilge and Ulusoy [11]	S	1	Free	✓	✓	Parallel	Model of MILP and a resolving procedure in iterative mode.
Chen et al. [25]	3, S	1	Free	Given	✓	-	An algorithm called Branch and Bound.
Hall et al. [26]	3	1	Free	✓	✓	Separate	NP-completeness in sequences specific for robot move.
Sriskandarajah [12]	S	1	Free	✓	✓	Separate	Classification of part sequences within 4 groups.
Aneja and Kamoun [27]	2	1	Free	✓	✓	Separate	O (n log n) algorithm.
Agnetis [28]	2, 3	1	Not-wait	✓	✓	Parallel	O (n log n) algorithms for the 2-machines case. Analysis of optimality in 3-machine cases.
Hurink and Knust [29]	3, S	1	Free	✓	✓	Parallel	Analyzing complexity in 2, 3 and m-machine flow shop robotic cells.
Hurink and Knust [30]	S	1	Free	✓	✓	Parallel	Probe approach regarding job shop robotic cell.
Soukhal and Martineau [13]	S	1	Free	✓	✓	Parallel	Genetic algorithm along with MILP models.
Soukhal et al. [14]	2	1	Free	✓	✓	-	Analysis of complexity regarding transportation capacity.
Carlier et al. [3]	S	1	Free	✓	✓	Separate	Genetic algorithm along with Branch and Bound in robot move sequences.
Kharbeche et al. [15]	S	1	Free	✓	✓	Parallel	Branch and Bound algorithm along with MILP model and a new lower Bound.
Zahrouni and Kamoun [16]	3	1	Free	✓	✓	Parallel	Heuristic Min MPS cycle provided by a 3-machine robotic cell.
Zarandi et al. [31]	2	1	Free	✓	✓	Parallel	Analysis of robotic flow shops extension into sequence-dependent setup time.
Elmi and Topaloglu [5]	S	M	Free	✓	✓	Parallel	New MILP models and simulated annealing (SA) algorithms. Machines with different speed at each stage and machine eligibility limits.
Majumder and Laha [4]	1,2	M	Free	✓	✓	-	A novel location algorithm for two-machine CS considering sequence-dependent setup times.
Elmi and Topaloglu [1]	S	M	Free	✓	✓	Parallel	Multi-degree cyclic problem using multiple robots.
Elmi and Topaloglu [21]	S	M	Free	✓	✓	Parallel	Cyclic job shops robotic cell scheduling problem: Ant colony optimization.
Majumder and Laha [4]	S	M	Free	✓	✓	-	Bacteria foraging optimization algorithm for robotic cell scheduling problem.
Far [22]	S	M	Free	✓	✓	-	A problem of cell scheduling having flexibility and automated guided vehicles and robots using an energy-conscious policy.
Foumani [8]	S	M	Free	✓	✓	-	Optimization in two-machine flow shop robotic cells using controllable inspection times: theory to practice.
Xiuli [23]	S	M	Free	✓	✓	-	An algorithm of multi objective differential evolution to solve robotic CSP using batch-processing machines.
Fattahi [24]	S	M	Free	✓	✓	Parallel	A hybrid particle swarm optimization model and parallel variable neighborhood location algorithm to be used with flexible job shop scheduling along with assembly processes
Current research	1	M	Free	✓	✓	Parallel	An exact method based on benders decomposition.

SN: number of stage; MS: number of machines (at each stage); PCri: criterion for pickup; RMS: sequence in robot move; PS: sequence of part; Sol-Proc: procedure of solution regarding RMS and PS.

classifies research projects dealing with problems of several-parts type robotic cell scheduling according to these six features. The table enables to demonstrate the contribution of the current study to the related literature. The existing background on robotic cell scheduling problems shows that the lack of methods to solve the problems efficiently, regarding the fact that existing mathematical programming models are solely able to resolve examples of the problems with small sizes. Accordingly, our study is the first attempt that suggests an exact method of BD for the problem being in question.

3. Problem Definition

Cells of robots can carry out processing lots involving parts with different types. According to just-in-time production, part types proportionate of each lot must meet incoming demands and be of the same quantity. For this reason, researchers emphasize n cycles containing the MPS with the same demanded proportions in robotic cell manufacturing. There have been lots of cases where robotic cells have been used repetitively or in the form of cyclic production of MPSs.

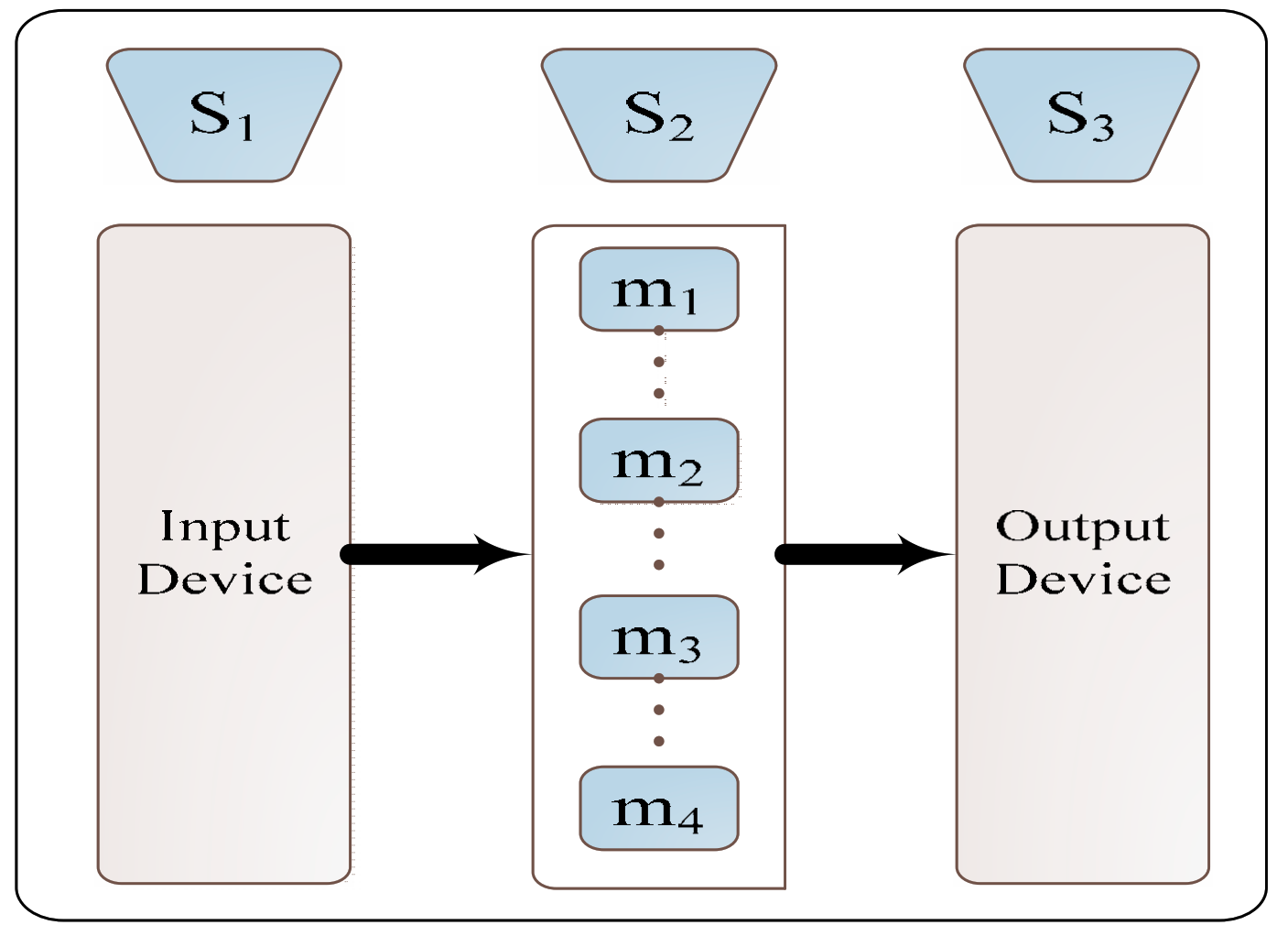
The current research focuses on the robotic manufacturing cells with identical parallel machines (see Figure 1) for the purpose of proposing least average time to manufacture one MPS within a cyclic manufacturing system.

An MPS sequence is considered as an MPS part sequence (or part sequence, in other words). An MPS (or a sequence of robot move) is known as a robot activities sequence performed along with an MPS cycle. It is believed that the difficult task is to get a minimum cycle time MPS cycle and it is two-folded. Therefore, two selections should be performed: (a) a robot move sequence identification, and (b) a sequence of part determination. This demands us to also determine a sequence of part and a sequence of robot move to result in minimization of the time for a cycle.

Following common assumptions are taken into consideration regarding the problem of multiple part parallel machine robotic cell scheduling in this paper:

• Data are considered to be deterministic.
• Input buffer always includes parts and there exists constantly a gap at the output buffer.
• There could not be seen any buffer storage within machines.
• Every part can either be on a machine or be controled by the robot.
• The robot and the machines cannot possess more than one part at any predetermined time span.
• The intended robot and the processing machines considered above never encounter breakdown and never need maintenance.
• Times for setup are regarded as something trivial.
• There isn not any preemption authorized in the processing of any operation.

The decisions that need to be given in the addressed problem are allocating the parts in the machines, parts scheduling and move sequencing of robots considering robotic cells. An MILP model has been suggested for the purpose of minimizing the makespan regarding operation completion times in the presence of parallel machine robotic cell scheduling problems. Note that makespan minimization could lead to enhance the throughput. The proposed model could be represented as follows:

A. 

Index properties

J = Parts’ amount, j ∈ {1, 2… J},

S = Stages’ amount regarding input and output, s ∈ {1, 2, 3},

M_s = Related machines’ amount at stage s, while input and output stages have a single machine, m ∈ {1, 2… Ms}

W = Operations’ amount during which the robot is busy with unloading, f ∈ {1, 2… W},

B. 

The list of Parameters utilized

P_j = Processing time standard regarding j^th part at the processing stage, through which all parts’ processing time at input and output stages (s = 1, 3 respectively) are equal to zero,

SP = Speed of handling the robot,

C. 

BM = a great many deal, the historical “Big M”.

D. 

Variables used to make decisions

X_j,j’ = 1 if j^th part calculated before ${j^{\prime }}^{th}$ part regarding processing stage, 0 if not,

Z_j,s,f = 1 if part j on stage s is the f^th operation that would be transmitted by robot to the next stage,

Y_j,s,m = 1 if machine m processes part j at stage s, 0 if not,

D_{j, s}= Time of departure of j^th part from stage s,

C_MAX = When all parts meet the output device.

E. 

Model of mathematics

$Minimize:C_{MAX}$

$${\mathrm{D}}_{\mathrm{j},2}+\mathrm{BM}\times \left(2-\left({\mathrm{Y}}_{\mathrm{j},2,\mathrm{m}}+{\mathrm{Y}}_{\mathrm{j},1,{\mathrm{m}}^{\prime }}\right)\right)\ge {\mathrm{D}}_{\mathrm{j},1}+\left(\mathrm{SP}\times \left(1+\left|\mathrm{m}-{\mathrm{m}}^{\prime }\right|\right)\right)+{\mathrm{P}}_{\mathrm{j},2}$$

(1)

$$\begin{array}{cc}\mathrm{j}\in \left\{1,2,\dots ,\mathrm{J}\right\};\mathrm{m}\in {\mathrm{M}}_2;& {\mathrm{m}}^{\prime }\in {\mathrm{M}}_1\\ \left({\sum }_{\mathrm{m}}^{{\mathrm{M}}_{\mathrm{s}}}{\mathrm{Y}}_{\mathrm{j},\mathrm{s},\mathrm{m}}\right)=1& \mathrm{j}\in \left\{1,2,\dots ,\mathrm{J}\right\};\mathrm{s}\in \left\{1,2,3\right\}\end{array}$$

(2)

$$\left({\sum }_{\mathrm{f}=1}^{\mathrm{W}}{\mathrm{Z}}_{\mathrm{j},\mathrm{s},\mathrm{f}}\right)=1\mathrm{j}\in \left\{1,2,\dots ,\mathrm{J}\right\};\mathrm{s}\in \left\{1,2\right\}$$

(3)

$$\left({\sum }_{\mathrm{j}=1}^{\mathrm{J}}{\sum }_{\mathrm{s}=1}^2{\mathrm{Z}}_{\mathrm{j},\mathrm{s},\mathrm{f}}\right)=1\mathrm{f}\in \left\{1,2,\dots ,\mathrm{W}\right\}$$

(4)

$$\left({\sum }_{\mathrm{f}=1}^{{\mathrm{f}}^{\prime }}{\mathrm{Z}}_{\mathrm{j},2,\mathrm{f}}\right)-\mathrm{BM}\times \left(1-{\mathrm{Z}}_{\mathrm{j},1,{\mathrm{f}}^{\prime }}\right)\le 0\mathrm{j}\in \left\{1,2,\dots ,\mathrm{J}\right\};{\mathrm{f}}^{\prime }\in \left\{1,2,\dots ,\mathrm{W}\right\}$$

(5)

$$\left({\displaystyle \sum }_{\mathrm{f}=1}^{{\mathrm{f}}^{\prime }}{\mathrm{Z}}_{\mathrm{j},1,\mathrm{f}}\right)-\mathrm{BM}\times \left(3-{\mathrm{Y}}_{{\mathrm{j}}^{\prime },2,\mathrm{m}}-{\mathrm{Y}}_{\mathrm{j},2,\mathrm{m}}-{\mathrm{Z}}_{{\mathrm{j}}^{\prime },2,{\mathrm{f}}^{\prime }}+{\mathrm{X}}_{\mathrm{j},{\mathrm{j}}^{\prime }}\right)\le 0$$

(6)

$$\begin{array}{c}\mathrm{j},{\mathrm{j}}^{\prime }\in \left\{1,2,\dots ,\mathrm{J}\right\},\mathrm{j}\ne {\mathrm{j}}^{\prime };\mathrm{m}\in {\mathrm{M}}_{\mathrm{s}};{\mathrm{f}}^{\prime }\in \left\{1,2,\dots ,\mathrm{W}\right\}\\ \left({\displaystyle {\displaystyle \sum }_{\mathrm{f}=1}^{{\mathrm{f}}^{\prime }}}{\mathrm{Z}}_{{\mathrm{j}}^{\prime },1,\mathrm{f}}\right)-\mathrm{BM}\times \left(4-{\mathrm{Y}}_{{\mathrm{j}}^{\prime },2,\mathrm{m}}-{\mathrm{Y}}_{\mathrm{j},2,\mathrm{m}}-{\mathrm{Z}}_{\mathrm{j},2,{\mathrm{f}}^{\prime }}-{\mathrm{X}}_{\mathrm{j},{\mathrm{j}}^{\prime }}\right)\le 0\end{array}$$

(7)

$$\begin{array}{c}\mathrm{j},{\mathrm{j}}^{\prime }\in \left\{1,2,\dots ,\mathrm{J}\right\},\mathrm{j}\ne {\mathrm{j}}^{\prime };\mathrm{m}\in {\mathrm{M}}_{\mathrm{s}};{\mathrm{f}}^{\prime }\in \left\{1,2,\dots ,\mathrm{W}\right\}\hfill \\ {\mathrm{D}}_{\mathrm{j},\mathrm{s}}+(\mathrm{BM}\times (5-{\mathrm{Y}}_{\mathrm{j},\mathrm{s},\mathrm{m}}-{\mathrm{Y}}_{{\mathrm{j}}^{\prime },{\mathrm{s}}^{\prime },{\mathrm{m}}_1^{\prime }}-{\mathrm{Y}}_{{\mathrm{j}}^{\prime },{\mathrm{s}}^{\prime }+1,{\mathrm{m}}_2^{\prime }}-{\mathrm{Z}}_{{\mathrm{j}}^{\prime },{\mathrm{s}}^{\prime },\mathrm{f}-1}-{\mathrm{Z}}_{\mathrm{j},\mathrm{s},\mathrm{f}}))\\ \ge {\mathrm{D}}_{{\mathrm{j}}^{\prime },{\mathrm{s}}^{\prime }}\\ +\left(\mathrm{SP}\times \left(\left(\left|{\mathrm{s}}^{\prime }-\left({\mathrm{s}}^{\prime }+1\right)\right|+\left|{\mathrm{m}}_1^{\prime }-{\mathrm{m}}_2^{\prime }\right|\right)+\left(\left|\left({\mathrm{s}}^{\prime }+1\right)-\mathrm{s}\right|+\left|{\mathrm{m}}_2^{\prime }-\mathrm{m}\right|\right)\right)\right)\end{array}$$

(8)

$$\mathrm{j},{\mathrm{j}}^{\prime }\in \left\{1,2,\dots ,\mathrm{J}\right\},\mathrm{j}\ne {\mathrm{j}}^{\prime };\mathrm{s},{\mathrm{s}}^{\prime }\in \left\{1,2\right\};{{\mathrm{m}}^{\prime }}_1\in {\mathrm{M}}_{{\mathrm{s}}^{\prime }};{{\mathrm{m}}^{\prime }}_2\in {\mathrm{M}}_{{\mathrm{s}}^{\prime }+1};\mathrm{m}\in {\mathrm{M}}_{\mathrm{s}};\mathrm{f}\in \left\{2,\dots ,\mathrm{W}\right\}$$

$${\mathrm{C}}_{\mathrm{MAX}}+\mathrm{BM}\times \left(2-{\mathrm{Y}}_{\mathrm{j},2,\mathrm{m}}-{\mathrm{Z}}_{\mathrm{j},2,\mathrm{W}}\right)\ge {\mathrm{D}}_{\mathrm{j},2}+\left(\mathrm{SP}\times \left(1+\left|1-\mathrm{m}\right|\right)\right)$$

(9)

$$\begin{array}{c}\mathrm{j}\in \left\{1,2,\dots ,\mathrm{J}\right\};\mathrm{m}\in {\mathrm{M}}_2\\ {\mathrm{X}}_{\mathrm{j},{\mathrm{j}}^{\prime }},{\mathrm{Y}}_{\mathrm{j},\mathrm{s},\mathrm{m}},{\mathrm{Z}}_{\mathrm{j},\mathrm{s},\mathrm{f}}\in \left\{0,1\right\}\end{array}$$

Regarding Constraint (1), a part can be processed if it only leaves input device and transports to the processing stage with the robot. On the other hand, the departing duration of any single section from the processing stage ought to be the same as or greater compared to the time of depart in input device in addition to the transfer and process times. Constraint (2) ensures a section being processed only on a single machine at every stage where input/output stages are presupposed to have a single machine with zero processing time. Constraints (3) and (4) will guarantee just one part being transferred by the robot once. Limitation (5) requires a part transmission to a stage only when it is transmitted to the stage before. Based on the requirement of Constraints (6) and (7), the processed operations’ sequence through a concurrent machine clarified regarding the robot unloading. Limitation (8) stresses on the fact that no operations of unloading can be carried out by the robot simultaneously. This constraint also identifies arrangement of unloading operations carried out through the robot. Based in the obligation which is presented through constraint (9), makespan means an equal or bigger depart time compared to the ending section unloaded as a result of processing in addition to the transfer duration.

4. Solving Methodology

4.1. Logic-Based Benders’ Decomposition (LBBD)

The BD algorithm was first suggested by Benders [32] mainly aiming at tackling problems with complicating variables yielding a problem considerably easier to be dealt with, when temporarily fixed. This method (BD), which is also known as various partitioning and outer linearization has been introduced as the most commonly utilized algorithms in exact form because it alleviates the problem and decentralizes the burden imposed by the general computation.

There have been many applications of this process observed in lots of diverse areas, involving planning and scheduling by Canto [33] and Hooker [34] and health care Luong [35].

LBBD was firstly proposed by Hooker and Yan [36] through logic circuit verification method. In this algorithm, cuts of Benders’ are calculated through the solvation of the inference dual of the slave problems through which we can consider that there is a special case for the linear programming duality. The cut introduced by Benders’ is formed to establish a bound which is valid at optimal level while initial variables have other values.

Though we can see logic-based Benders’ cuts in any form, they must be formularized in the form of linear inequalities because the major problem is an MILP. This method has been used in various combinatorial optimization problems, such as logic circuits’ verification by Hooker and Yan [36]; scheduling and planning by Hooker [36,37]; Benini [38]; Bajestani and Beck [39]; deterministic and stochastic location/fleet management by Fazel Zarandi and Beck [17]; Zarandi [31] and finally, control and queue design by Terekhov [40].

To model LBBD problem, you must initially try to divide the parts of the variables of decision into two vectors of x and y. Overall investigations show the problem as given in Equations (10)–(12):

Make the minimum    f(x; y)

(10)

$$\mathrm{s}.\mathrm{t}:(\mathrm{x};\mathrm{y})\in \mathrm{S}$$

(11)

$$\mathrm{x}\in D_x,\mathrm{y}\in D_y$$

(12)

where, f is known as a real-valued function, S is called feasible set (commonly determined by add ups of limits), and D_x and D_y are the domain amounts of x and y, consecutively. This issue could be divided into limitations only including the x or variables of master problem and limits that integrate the x and y, variables of slave problem. Because only the x variables are considered by the master problem, the set S is relaxed and also be demonstrated as $\overline{S}$. On the contrary to Benders’ decomposition theory, there are not any structural constraints (e.g., linearity) regarding the various constituents related to decomposition. As a whole, master problem could be identified in Equations (13)–(16):

Make the minimum z

(13)

$$\mathrm{s}.\mathrm{t}:\mathrm{x}\in \overline{S},$$

(14)

$$\mathrm{z}\ge {\beta }_x^k(\mathrm{x}),\mathrm{k}=1\dots \dots ...\mathrm{K}$$

(15)

$$\mathrm{x}\in D_x$$

(16)

where, z could be identified as a variable of real-valued decision, $\overline{S}$ called a relaxation of S, and ‚${\beta }_x^k\left(\mathrm{x}\right)$ is a cut of Benders’ on the objective function f (x,y) realized if fixed values of x to $x^k$ limitations (16) are derivate through solving slave problem and $x^1$, …. $x^k$ are x variables’ values regarding master problem solutions recognized during previous iterations. The slave problem regarding iteration k is as shown in Equations (17)–(19):

$$\mathrm{minimize}f(x^k,y)$$

(17)

$$\mathrm{s}.\mathrm{t}:(x^k,\mathrm{y})\in \mathrm{S},$$

(18)

$$\mathrm{y}\in D_y.$$

(19)

Solving an LBBD model refers to iteratively the master problem solving and the slave problems until a type of convergence is gained. Some master problem is worked on to be solved to optimality, making solution x^k with cost z^k in iteration k. The solution obtained, is used afterwards in order to formulate a single or more slave problems, solved one by one while producing functions of bounding (i.e., the Benders cuts) on z. Suppose that k^th solution method of master problem satisfies all bounding functions encountered, gained in iteration 1 to k, the process is known as to be converted to an optimal solution globally (i.e., z^k = f (x^k,y^k), where y^k is the slave problem solution). If not, the master problem could be put for solution again, and the iterations go on. Within the conditions’ boundary on the Benders’ cuts, it is known that converges of the process to an optimal solution in a finite amount of iterations is achieved Chu ve Xia [41].

4.2. Application of LBBD on the Problem

The proposed problem here could be decomposed into two partitions including assignment and scheduling options. The Benders’ master problem allocates parts to machines, and the slave problem comprises a group of problems with independent scheduling. Benders’ cuts that are gathered together with the master problem are known as mathematically equivalent to informal operations to avoid the related assignments. The Benders’ algorithm often leads to a solution optimally designed for the overall allocation and the scheduling problem.

4.2.1. Master Problem

Jobs are assigned to machine with regards to relaxation, while minimizing the total processing time on each machine at current processing stage. Note that robot moving times are ignored in the master problem. See Equations (20)–(25).

$$\left[MP\right]:Minimize{\mathrm{C}}_{\mathrm{MAX}}$$

(20)

Subject to:

$$\mathbf{1}\mathbf{.}\left({\sum }_{\mathrm{m}}^{{\mathrm{M}}_{\mathrm{s}}}{\mathrm{Y}}_{\mathrm{j},2,\mathrm{m}}\right)=1\mathrm{j}\in \left\{1,2,\dots ,\mathrm{J}\right\};\mathrm{s}\in \left\{1,2,3\right\}$$

(21)

$$\mathbf{2}\mathbf{.}{\mathrm{Y}}_{\mathrm{j},1,1}=1\mathrm{j}\in \left\{1,2,\dots ,\mathrm{J}\right\}$$

(22)

$${\mathrm{Y}}_{\mathrm{j},3,1}=1\mathrm{j}\in \left\{1,2,\dots ,\mathrm{J}\right\}$$

(23)

$$\mathbf{3}\mathbf{.}{\sum }_{\mathrm{j}=1}^{\mathrm{J}}{\mathrm{Y}}_{\mathrm{j},2,\mathrm{m}}\times {\mathrm{P}}_{\mathrm{j},2}\le {\mathrm{C}}_{\max }\mathrm{m}\in {\mathrm{M}}_2$$

(24)

$$\mathbf{4}\mathbf{.}Cu{t}_c\in Cutset\mathrm{c}\in \left\{1,2,\dots ,\left|\mathrm{Cutset}\right|\right\}$$

(25)

4.2.2. Slave Problem

In this step, the robot-based slave problem will find the jobs sequence and sequence of transportation activities to make the makespan minimum. Below, the slave problem will be solved iteratively to generate the related logic cut for the machine assignments (see Equations (26)–(34)).

$\left[\mathrm{SP}\right]:{\mathrm{Minimize}\mathrm{C}}_{\max }^{\mathrm{SP}}$

$$\begin{array}{cc}1.& {\mathrm{D}}_{\mathrm{j},2}\ge {\mathrm{D}}_{\mathrm{j},1}+\left(\mathrm{SP}\times \left(1+\left|\mathrm{m}-{\mathrm{m}}^{\prime }\right|\right)\right)+{\mathrm{P}}_{\mathrm{j},2}\hfill \\ & \mathrm{j}\in \left\{1,2,\dots ,\mathrm{J}\right\};\mathrm{m}\in {\mathrm{M}}_2;{\mathrm{m}}^{\prime }\in {\mathrm{M}}_1;{\overline{\mathrm{Y}}}_{\mathrm{j},2,\mathrm{m}}={\overline{\mathrm{Y}}}_{\mathrm{j},1,{\mathrm{m}}^{\prime }}=1\hfill \end{array}$$

(26)

$$2.\left({\sum }_{\mathrm{f}=1}^{\mathrm{W}}{\mathrm{Z}}_{\mathrm{j},\mathrm{s},\mathrm{f}}\right)=1\mathrm{j}\in \left\{1,2,\dots ,\mathrm{J}\right\};\mathrm{s}\in \left\{1,2\right\}$$

(27)

$$3.\left({\sum }_{\mathrm{j}=1}^{\mathrm{J}}{\sum }_{\mathrm{s}=1}^2{\mathrm{Z}}_{\mathrm{j},\mathrm{s},\mathrm{f}}\right)=1\mathrm{f}\in \left\{1,2,\dots ,\mathrm{W}\right\}$$

(28)

$$4.\left({\sum }_{\mathrm{f}=1}^{{\mathrm{f}}^{\prime }}{\mathrm{Z}}_{\mathrm{j},2,\mathrm{f}}\right)-\mathrm{BM}\times \left(1-{\mathrm{Z}}_{\mathrm{j},1,{\mathrm{f}}^{\prime }}\right)\le 0\mathrm{j}\in \left\{1,2,\dots ,\mathrm{J}\right\};{\mathrm{f}}^{\prime }\in \left\{1,2,\dots ,\mathrm{W}\right\}$$

(29)

$$\begin{array}{l}5.\left({\sum }_{\mathrm{f}=1}^{{\mathrm{f}}^{\prime }}{\mathrm{Z}}_{\mathrm{j},1,\mathrm{f}}\right)-\mathrm{BM}\times \left(1-{\mathrm{Z}}_{{\mathrm{j}}^{\prime },2,{\mathrm{f}}^{\prime }}+{\mathrm{X}}_{\mathrm{j},{\mathrm{j}}^{\prime }}\right)\le 0\\ \mathrm{j},{\mathrm{j}}^{\prime }\in \left\{1,2,\dots ,\mathrm{J}\right\},\mathrm{j}\ne {\mathrm{j}}^{\prime };\mathrm{m}\in {\mathrm{M}}_{\mathrm{s}};{\mathrm{f}}^{\prime }\in \left\{1,2,\dots ,\mathrm{W}\right\};{\overline{\mathrm{Y}}}_{{\mathrm{j}}^{\prime },2,\mathrm{m}}={\overline{\mathrm{Y}}}_{\mathrm{j},2,\mathrm{m}}=1\end{array}$$

(30)

$$\begin{array}{l}6.\left({\sum }_{\mathrm{f}=1}^{{\mathrm{f}}^{\prime }}{\mathrm{Z}}_{{\mathrm{j}}^{\prime },1,\mathrm{f}}\right)-\mathrm{BM}\times \left(2-{\mathrm{Z}}_{\mathrm{j},2,{\mathrm{f}}^{\prime }}-{\mathrm{X}}_{\mathrm{j},{\mathrm{j}}^{\prime }}\right)\le 0\\ \mathrm{j},{\mathrm{j}}^{\prime }\in \left\{1,2,\dots ,\mathrm{J}\right\},\mathrm{j}\ne {\mathrm{j}}^{\prime };\mathrm{m}\in {\mathrm{M}}_{\mathrm{s}};{\mathrm{f}}^{\prime }\in \left\{1,2,\dots ,\mathrm{W}\right\};{\overline{\mathrm{Y}}}_{{\mathrm{j}}^{\prime },2,\mathrm{m}}={\overline{\mathrm{Y}}}_{\mathrm{j},2,\mathrm{m}}=1\end{array}$$

(31)

$$\begin{array}{c}7.D_{j,s}+\left(BM\times \left(2-Z_{j^{\prime },s^{\prime },f-1}-Z_{j,s,f}\right)\right)\ge D_{j^{\prime },s^{\prime }}+(SP\times ((\left|s^{\prime }-\left(s^{\prime }+1\right)\right|+\\ \left|m_1^{\prime }-m_2^{\prime }\right|)+\left(\left|\left(s^{\prime }+1\right)-s\right|+\left|m_2^{\prime }-m\right|\right)))\\ j,j^{\prime }\in \left\{1,2,\dots ,J\right\},j\ne j^{\prime };s,s^{\prime }\in \left\{1,2\right\};m{\prime }_1\in M_{s^{\prime }};m{\prime }_2\in M_{s^{\prime }+1};m\in M_s;f\in \left\{2,\dots ,W\right\}\\ ;{\overline{Y}}_{j,s,m}={\overline{Y}}_{j^{\prime },s^{\prime },m_1^{\prime }}={\overline{Y}}_{j^{\prime },s^{\prime }+1,m_2^{\prime }}=1\end{array}$$

(32)

$$\begin{array}{cc}8.& {\mathrm{C}}_{\max }^{\mathrm{SP}}+\mathrm{BM}\times \left(2-{\mathrm{Z}}_{\mathrm{j},2,\mathrm{W}}\right)\ge {\mathrm{D}}_{\mathrm{j},2}+\left(\mathrm{SP}\times \left(1+\left|1-\mathrm{m}\right|\right)\right)\\ & \mathrm{j}\in \left\{1,2,\dots ,\mathrm{J}\right\};\mathrm{m}\in {\mathrm{M}}_2;{\overline{\mathrm{Y}}}_{\mathrm{j},2,\mathrm{m}}=1\hfill \end{array}$$

(33)

$$9.{\mathrm{X}}_{\mathrm{j},{\mathrm{j}}^{\prime }},{\mathrm{Z}}_{\mathrm{j},\mathrm{s},\mathrm{f}}\in \left\{0,1\right\}$$

(34)

Through finding the solution for the master problem, a logic-based Benders’ cut is created and it is increased onto the master problem so as, it can effectively find better solutions. The related cuts generated from the slave problem can be represented as given in Equation (35):

$$\mathit{l}\mathit{b}\mathit{c}\mathit{u}\mathit{t}\equiv \left\{{\mathrm{C}}_{\max }^{\mathrm{SP}}-\mathrm{BM}\times \left({\displaystyle \sum }_{\mathrm{m}=1}^{\mathrm{M}2}{{\displaystyle \sum }}_{j=1|{\overline{\mathrm{Y}}}_{\mathrm{j},2,\mathrm{m}}=0}^{\mathrm{J}}{\mathrm{Y}}_{\mathrm{j},2,\mathrm{m}}+{\displaystyle \sum }_{\mathrm{m}=1}^{\mathrm{M}2}{\displaystyle \sum }_{j=1|{\overline{\mathrm{Y}}}_{\mathrm{j},2,\mathrm{m}}=1}^J\left(1-{\mathrm{Y}}_{\mathrm{j},2,\mathrm{m}}\right)\right)\le {\mathrm{C}}_{\mathrm{MAX}}\right\}$$

(35)

where, all the $lbcut$ cuts would be included within the master problem due to the assigned jobs to each machine. The aforementioned cuts provide the real completion time of operations, while all transportation operations consider their optimal sequence. $lbcut$ forces the objective function of master problem to be larger-equal than objective function of dedicated parallel machine scheduling with a single robot. Thus, the master problem is guided to find different assignments. The whole process can be summarized as follows:

Initialization: $\mathit{U}\mathit{B}=\infty$, $\mathit{L}\mathit{B}=0$, $\mathit{C}\mathit{u}\mathit{t}\mathit{s}\mathit{e}\mathit{t}=\varnothing$

While$\left(\mathit{L}\mathit{B}\ne \mathit{U}\mathit{B}\right)$

(1)

Solve $\left[\mathit{M}\mathit{P}\right]$ considering $\mathit{C}\mathit{u}\mathit{t}\mathit{s}\mathit{e}\mathit{t}$, obtain solution $\left({\overline{\mathit{Y}}}_{\mathit{j},\mathit{s},\mathit{m}}\leftarrow {\mathit{Y}}_{\mathit{j},\mathit{s},\mathit{m}}\right)$,

(2)

Update $\mathit{L}\mathit{B}\leftarrow {\mathit{C}}_{\mathit{M}\mathit{A}\mathit{X}}$

(3)

Solve the $\left[\mathit{S}\mathit{P}\right]$ and obtain the solution ${\mathit{C}}_{\mathit{m}\mathit{a}\mathit{x}}^{\mathit{S}\mathit{P}}$

(4)

Update $\mathit{U}\mathit{B}\leftarrow {\mathit{C}}_{\mathit{m}\mathit{a}\mathit{x}}^{\mathit{S}\mathit{P}}$

(5)

Generate the $\mathit{l}\mathit{b}\mathit{c}\mathit{u}\mathit{t}$ as a logic-based cut

(6)

Update the set of cuts: $\mathit{C}\mathit{u}\mathit{t}\mathit{s}\mathit{e}\mathit{t}\leftarrow \mathit{C}\mathit{u}\mathit{t}\mathit{s}\mathit{e}\mathit{t}+\mathit{l}\mathit{b}\mathit{c}\mathit{u}\mathit{t}$

End While

5. Results of the Computations

To measure the empirical performance of the suggested logic-based Benders’ decomposition method, the experiments for computations were worked on based on a group of examples generated randomly. The attributed to sizes of the problem are identified through different levels of two elements of part types’ number, and parallel machines’ number at processing stage, respectively. A mixture of the aforementioned parameter levels leads to generation of five different problem categories. For each category, five different problem instances are generated and resolved by the proposed MILP.

The parameter “number of parts” is considered to vary in five classes: 10, 20, 30, 40, and 50. For the first class that includes ten parts, three machines in parallel status are taken into consideration at the processing stage. Regarding the next classes (20 to 50 parts), parallel machines’ number varies between three and five. However, the time for processing is generated uniformly in the range of [10, 100]. Moreover, it is considered that the handling speed of robot (SP) is 5 s.

The proposed decision support tools, MILP mathematical model as LBBD method, are implemented on the generated test problems being coded in C# 2012 and run on a Core (TM) i5-4590 CPU with 3.30 Gigahertz speed, 4 Gigabyte RAM and WINDOWS 64-bit operating system. Then the performance evaluation of the LBBD and the MILP are analyzed considering achieved CPU time and makespan that corresponds the time needed to solve sub problems (SP) (reported in seconds). The experimental results are then represented in

Table 2. Computational results of the suggested MILP model and implemented LBBD method.

Part		Makespan		CPU Time		Total CPU Time		GAP %	Problem
		MILP	LBBD	MILP	LBBD	MP	SP
10	3	492	492	1105.38	24.35	7.06	17.28	0	1
		421	421	1214.15	31.61	9.79	21.81	0	2
		503	503	1005.54	22.26	6.67	15.58	0	3
		516	516	1116.54	26.81	7.50	19.30	0	4
		488	488	1204.64	33.10	10.92	22.17	0	5
20	3	1058	1058	2166.72	154.75	46.42	108.32	0	6
		1114	1114	2018.33	142.29	41.26	101.02	0	7
		1104	1104	1974.87	165.67	46.38	119.28	0	8
		1046	1046	2083.77	155.15	48.09	107.05	0	9
		1083	1083	2117.33	149.31	49.27	100.03	0	10
	5	751	751	3124.12	138.85	40.26	98.58	0	11
		793	793	3101.52	130.19	36.45	93.73	0	12
		709	709	3204.96	127.73	39.59	88.13	0	13
		815	815	2961.24	139.95	46.18	93.76	0	14
		762	762	3087.57	149.11	44.73	104.37	0	15
30	3	1731	1552	3600	293.47	88.04	205.42	−10.34	16
		1803	1487	3600	301.91	90.57	211.33	−17.52	17
		1792	1563	3600	243.55	73.06	170.48	−12.77	18
		1649	1449	3600	288.47	86.54	201.92	−12.12	19
		1711	1603	3600	251.79	75.53	176.25	−6.31	20
	5	1293	947	3600	274.61	82.38	192.22	−26.75	21
		1351	1031	3600	237.89	71.36	166.52	−23.68	22
		1285	918	3600	208.06	62.41	145.64	−28.56	23
		1291	883	3600	264.44	79.33	185.10	−31.60	24
		1163	949	3600	225.71	67.71	157.99	−18.40	25
40	3	1933	1737	3600	341.18	105.7658	235.41	−10.13	26
		1967	1805	3600	327.75	95.0475	232.70	−8.23	27
		1849	1597	3600	339.51	112.0383	227.47	−13.62	28
		2013	1897	3600	349.47	104.841	244.62	−5.76	29
		1784	1617	3600	350.47	98.1316	252.33	−9.36	30
	5	1352	1149	3600	328.15	91.882	236.26	−15.01	31
		1374	1169	3600	310.59	96.2829	214.30	−14.91	32
		1289	1091	3600	325.94	107.5602	218.37	−15.36	33
		1417	1209	3600	330.07	95.7203	234.34	−14.67	34
		1286	1180	3600	343.95	103.185	240.76	−8.24	35
50	3	3094	2507	3600	851.85	255.55	596.29	−18.97	36
		3271	2376	3600	902.56	270.76	631.79	−27.36	37
		3158	2451	3600	812.93	243.87	569.05	−22.38	38
		2974	2329	3600	784.40	235.32	549.08	−21.68	39
		3052	2385	3600	806.95	242.08	564.86	−21.85	40
	5	2842	1749	3600	752.17	225.65	526.51	−38.45	41
		2937	1672	3600	811.49	243.44	568.04	−43.07	42
		2566	1659	3600	715.62	214.68	500.93	−35.34	43
		2732	1532	3600	771.91	231.57	540.33	−43.92	44
		2691	1471	3600	735.41	220.62	514.78	−45.33	45

for MILP and LBBD. Additionally, Table 2 contains the total solution times (time acquired to solve both of master problem (MP) and sub problem (SP)) or total CPU times. Regarding Table 2, it can be observed that the LBBD is capable to recognize optimal solutions of all 25 instances within acceptable time of computation, while the MILP can only solve 15 problems. For the third class of problems that include 30 parts (problem number 16 to 25) and all next classes, the proposed MILP has been run for one hour but no optimal solution has been found.

The gap obtained between proposed MILP and implemented LBBD is calculated according to Equation (36):

$$GAP=\frac{MILP-LBBD}{LBBD}\ast 100\gg \frac{1551-1731}{1731}\ast 100=-10.34$$

(36)

As it is represented in Table 2, for problem numbers 1 to 15, no gap has been reported between MILP and LBBD solutions, which clarifies the efficiency of the proposed LBBD in finding optimal solutions and in terms of makespan. Besides the proposed LBBD outperforms the MILP based on CPU time performance measure. Moreover, it is obvious that the run time achieved by proposed LBBD method for the parallel machine robotic CSP is influenced by the number of parallel machines. Hence, there can be a conclusion that as parts’ number expands regarding robotic cell, increase in parallel machines will be more effective. This fact confirms that the run time of LBBD method for problems 6–10 and 16–20 is strictly greater than that of problems 11–15 and 20–25, respectively.

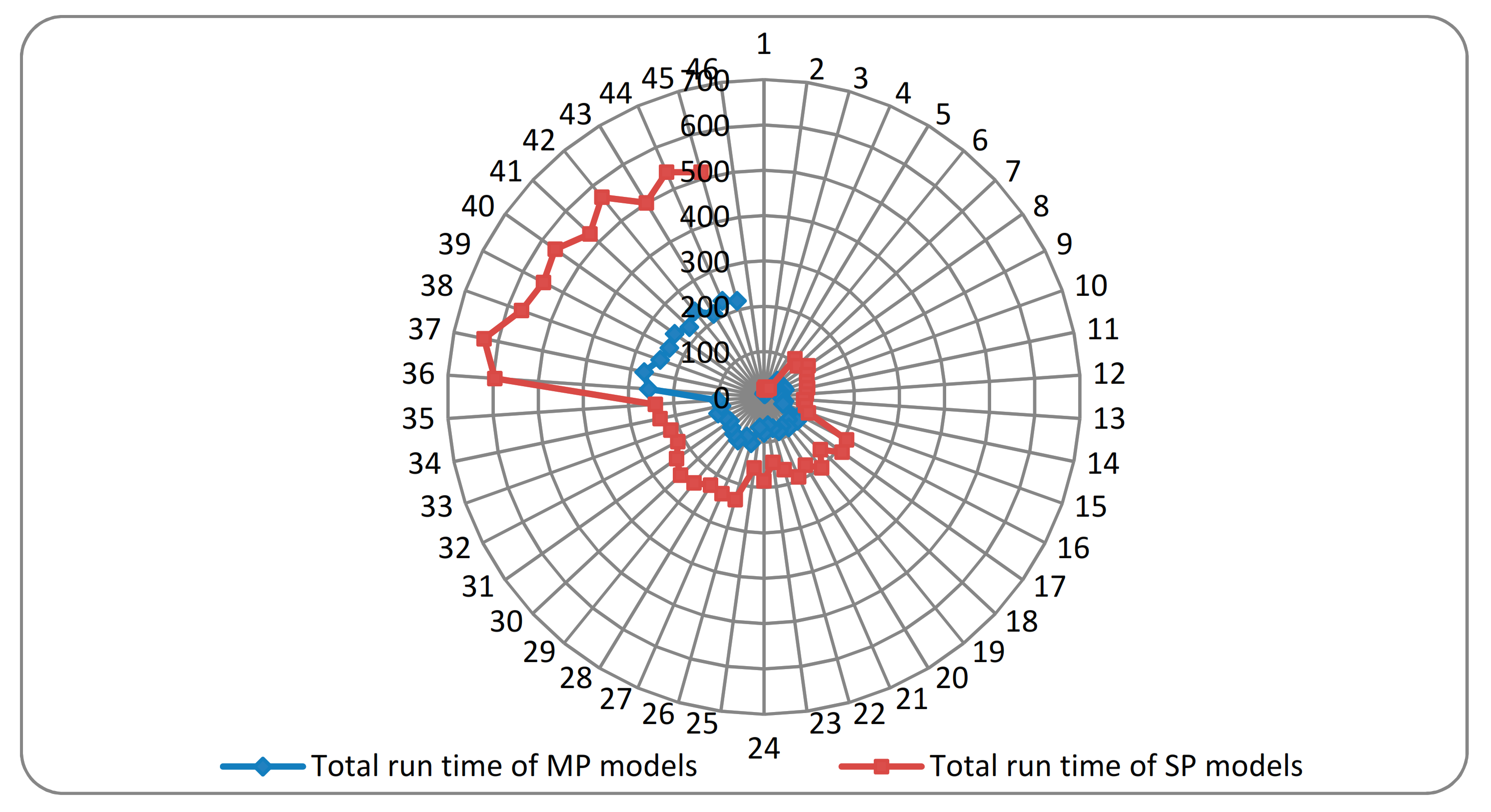
Figure 2 compares the total CPU times of solved SP (red color) and MP models (blue color) solved during the LBBD method for each problem. As an instance for problem number 45 that includes 50 parts with five parallel machines the total CPU time of solving SP models is achieved as 514 while the CPU time for obtaining solution of MP models equals to 220. Therefore, it could be seen that the total SP models run times are larger than the one for MP models. This is known as SP problem complexity as it identifies the parts’ sequence and transportation operations’ sequence, while the MP just determines the machine assignments for the parts.

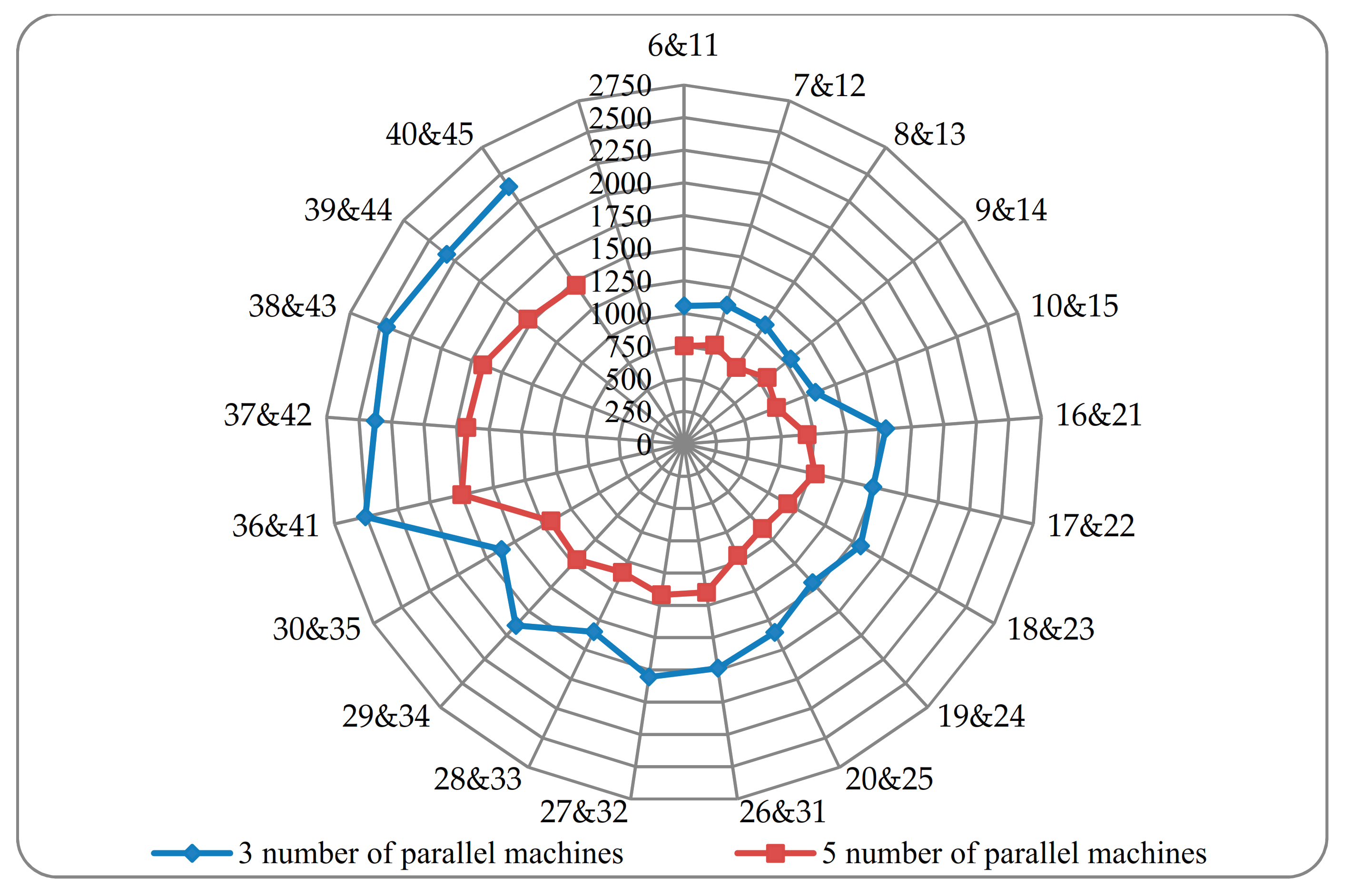
Figure 3 represents the pair wise differences between obtained makespan with three and five available parallel machines in the manufacturing cell. It is clear that the difference of achieved makespan between three and five parallel machines increases as the number of parts is made larger. For example, the terms 6 and 11 in Figure 3 defines the differences between makespan obtained in problem numbers 6 and 11 where there are three and five parallel machines. The blue and red lines specify the issue when there are three and five parallel machines in the robotic cells, respectively. There can be a conclusion that the increase of parts in robotic cells, increases the number of parallel machines to be more effective (see Table 2).

6. Conclusions

The research discusses the parallel machine problem of cell scheduling in robots using a unitary transfer robot. As the achievable background knowledge on robotic cell scheduling problems shows, the lack of efficient exact solution methods to these problems, MILP has been formulated for alleviating problems and providing a solution. The proposed MILP model contains two sub problems, i.e., (1) machine assignment sub-problem and (2) the robot moves and parts sequencing sib-problems. For the purpose of solving the proposed MILP regarding large sized problems, a Benders’ decomposition (BD) based algorithm, which aims to minimize the makespan, has been developed.

Geismar et al. [18] studied robotic cells containing parallel machines and multiple dual gripper robots: a comparative overview. An integration of parallel machines and multiple dual gripper robots has turned into permanently prevalent phenomenon regarding manufacturing in modern era with robotic cells. Meanwhile, there has not been much previous study considering the design and scheduling problems encountered by managers utilizing these cells with a complex nature. An output of applying dual grippers in multiple robots’ cells over cells with the same amount of single gripper robots is represented through numbers in the current study. The decisions for configuration are addressed through the comparison of different administrations of multi-robot cells to manifest that parts being exchanged between robots (machines shared model versus transfer stations method) enforces little burden on the throughput. On the contrary, it has been shown that processing stages’ assignment to robots is able to significantly affect cell’s throughput of potential. A pattern allowing multiple robots to cooperate avoiding the colliding incident or suffering gridlock is explained; the condition mentioned is truly operationalized with great effects on throughput. The optimal situation is believed to be analytically set, in very commonly practical conditions, to create a certain cyclic sequence of robot moves in robotic cells having one or more dual gripper robots, parallel machines and transfer stations. They developed a guaranteed algorithm to prepare a cycle containing a throughput of at least 66.7% of the optimum throughput for a cell having a single dual gripper robot. Elmi and Topaloglu [1] proposed a scheduling blocking hybrid flow shop robotic cells problem containing multiple robots. The present project deals with the robotic scheduling problem present in blocking hybrid flow shop cells considering multiple part types, unrelated parallel machines, multiple robots and machine eligibility limitations. First, a MILP model is suggested to minimize the makespan for the problem mentioned. Since the model is too complex, a SA based solution approach was proposed to resolve it. In order to enhance the SA algorithm efficiency, a new neighborhood structure based on block properties could be utilized. The actual work out of the suggested SA is measured over a set of randomly generated examples. The computational results show that the SA algorithm is effective using the employed neighborhood structure. Furthermore, the current research project showed that the appropriate varieties of robots is dependent on processing operations’ sequence to be carried out at any single stage. However, times of stochastic processing can add on the applicability of the suggested approach. Furthermore, the problem probed can be extended by taking into consideration of dual-gripper robots. Recognizing an optimal cycle for a cell with multiple dual gripper robots and arbitrary deterministic processing times still deserves much attention. It is not clearly known that an optimal cycle for a deterministic cell would be the most efficient schedule for one with stochastic processing times. Further studies may also include an investigation of robotic cells including stochastic processing times. Far et al. [22] proposed a flexible CSP containing automated guided vehicles and robots under energy-conscious policy. A flexible CSP in the presence of time-of-use electricity tariffs is worked out in this research. In order to use a type of energy-conscious policy, over on-peak period electricity consumption cost, constraints on energy consumption totality by all facilities, set up time available on each cell, part defect (pert) percentage and the total number of automated guided vehicles (AGV) are taken into consideration. In addition, an optimization of ant colony (ACO) algorithm is regarded to be used to reach a near-optimum solution of suggested MILP model aiming at minimizing the total cost of CSP model. Because literature lacks much information about this issue, a lower bound is applied along with validating the result gained. Moreover, to improve the quality of the results achieved by meta-heuristic algorithms, two hybrid genetic algorithms (HGA) and hybrid ant colony optimization (HACO) was proposed to find a solution for the model. Regarding parameter tuning algorithms, Taguchi experimental design method is applied. Then, numerically represented instances are shown to practically represent the application of the suggested methodology. The findings resulted here compared with the lower bound and as a result it confirmed that HACO was able to locate better and closer optimal solutions. In this study, for decreasing difficulty in the model, the authored ignored some issues and assumptions that we now recommend them to be considered for future studies in this area. Some of parameter of the model may be considered either as fuzzy or random.

In the proposed BD, the sub-problems of assignment are defined as the major problem and the sub-problems of parts and robot moves sequencing are exerted as the solution for this master problem and to generate logic-based Benders’ cuts. The suggested MILP model and LBBD method are tested on five categories including 50 randomly generated problem instances. The detailed experimental results represent the advantages of using decomposition methods in parallel machine robotic cell scheduling problem. It worth to mention here that the suggested BD algorithm described in this research, is the first attempt to apply optimal Benders’ cuts regarding single cell scheduling problems. The problem probed here can be extended by taking into the consideration that dual gripper robots should be investigated further in future studies. Additionally, the proposed Benders’ decomposition approach could be extended for other robotic cell scheduling problems confronted.