Adaptive Control of CO2 Production during Milk Fermentation in a Batch Bioreactor
Abstract
:1. Introduction
1.1. Basic Facts about Fermentation Process and Batch Bioreactors
1.2. Literature Review
1.3. Contributions and Novelties
- The first contribution of the presented study is the discovery of the solution for the closed-loop control of the growth of microorganisms (and, thus, control the time course of the fermentation product quantity), which will be valid for batch bioreactors. The controlled operation mode has so far been reserved only for the fed-batch and continuous bioreactors, which are much more expensive to purchase and more difficult to maintain than batch bioreactors. All today’s industrial or laboratory batch bioreactors operate without a closed-loop control system in an autonomous mode. The time course of the fermentation product quantity depends only on the initial concentrations of substances introduced into the bioreactor before the start of the fermentation process. The presented solution is based on the finding that changing the bioreactor’s temperature could be used for the closed-loop control of the fermentation product profile. This discovery was obtained from the analysis of previous studies, from simulation calculations based on the derived mathematical model, and from the laboratory experiments. Based on this finding, the structure of the closed-loop control system was defined. This structure allows the use of different control approaches.
- The second contribution of the article is the finding that adaptive control is very convenient for the control of the time course of the fermentation product in batch bioreactors. A study of various adaptive theories was made. Model reference adaptive control based on almost strictly positive real theory proved to be convenient for the implementation of the founded control structure. This control approach assures stability, easy realization, and an undemanding choice of adaptation coefficients. The proposed adaptive control system was compared with the conventional linear control system. The advantages of the developed adaptive control system are to ensure the desired course of the fermentation process even when the parameters of the mathematical model of the fermentation process are unknown. An additional and important advantage of the presented adaptive control system is that it ensures the same performance even in the case of significantly different fermentation processes.
- A new derived non-linear mathematical model which describes the impact of temperature on the fermentation process substances in batch bioreactors;
- The use of an optimization technique for mathematical model parameters estimation;
- The definition of the fundamental control structure for control of time courses of fermentation products in batch bioreactors using temperature changes;
- Implementation of conventional linear and adaptive control theories for control of the fermentation product response;
- Comparison of the efficiency of both control approaches and simulation-based numerical evaluation of both control approaches;
- Experimental confirmation of the proposed adaptive control system.
2. Materials and Methods
2.1. Studied Fermentation Process
2.2. Laboratory Equipment
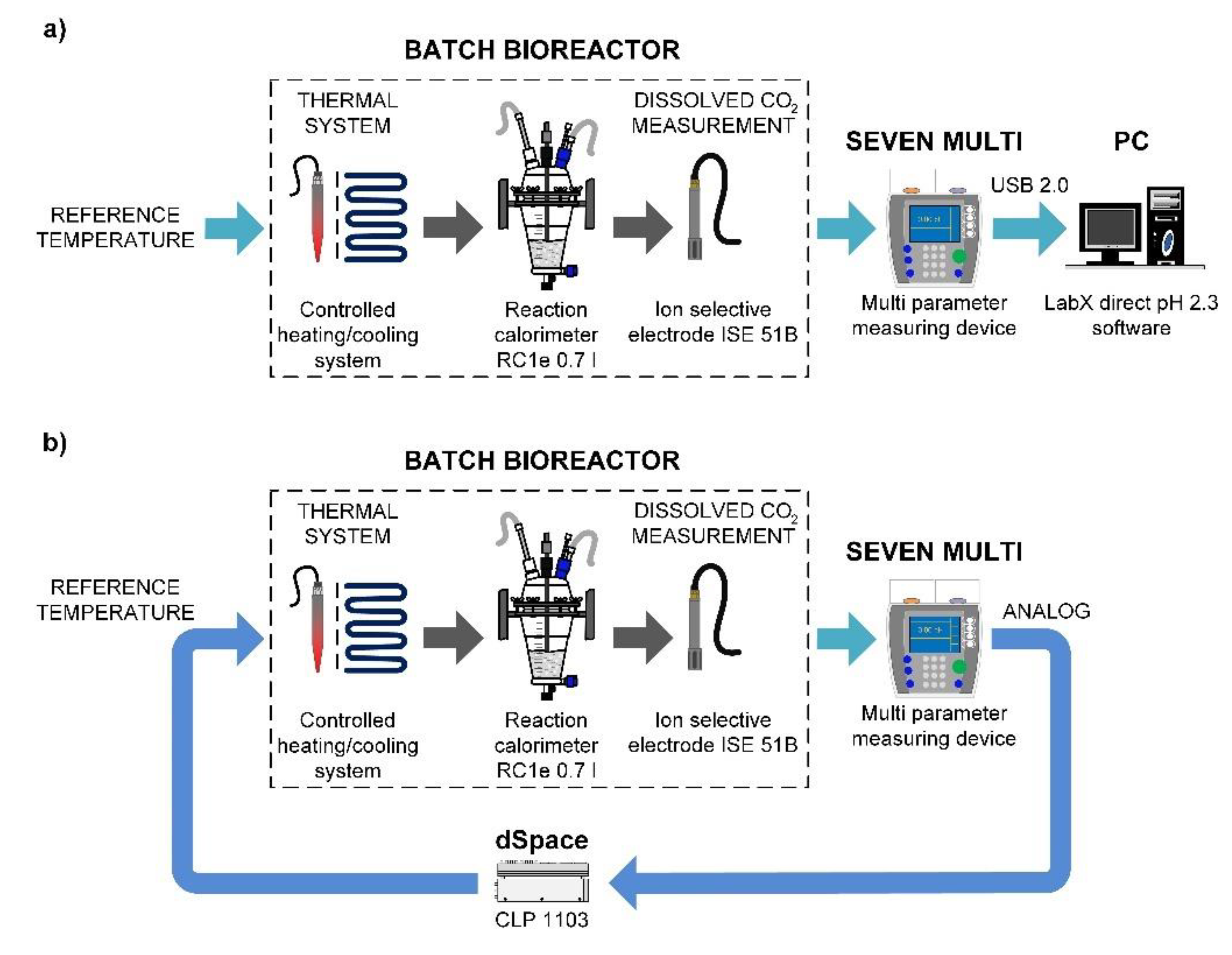
2.2.1. Batch Bioreactor
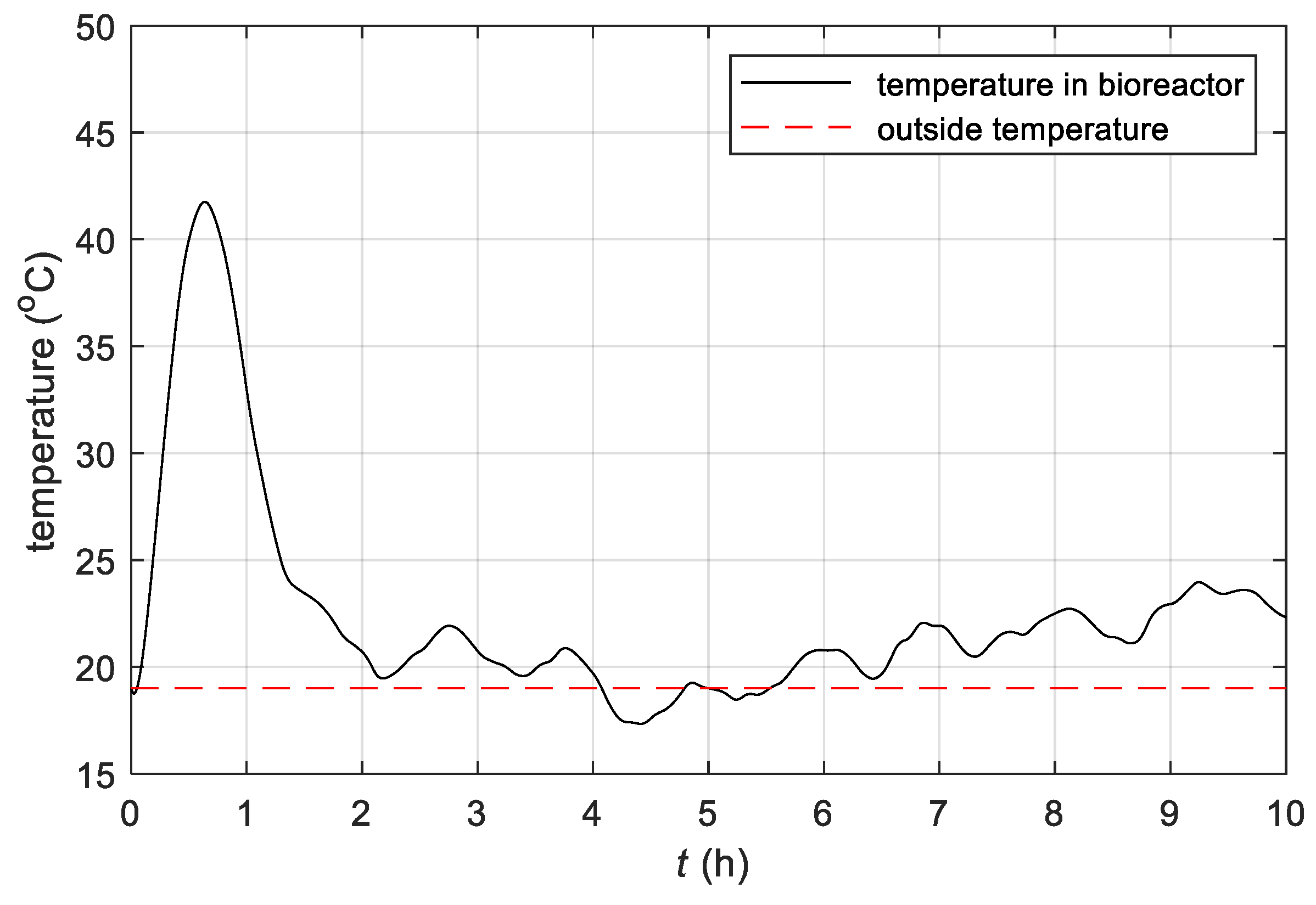
2.2.2. Heating/Cooling System
2.2.3. Dissolved CO2 Measurement
2.2.4. Equipment for Data Acquisition and Control
2.2.5. Reference Profile Generation
2.3. Laboratory Set-Ups for Parameter Estimation and Control
2.4. Mathematical Model of the Fermentation Process
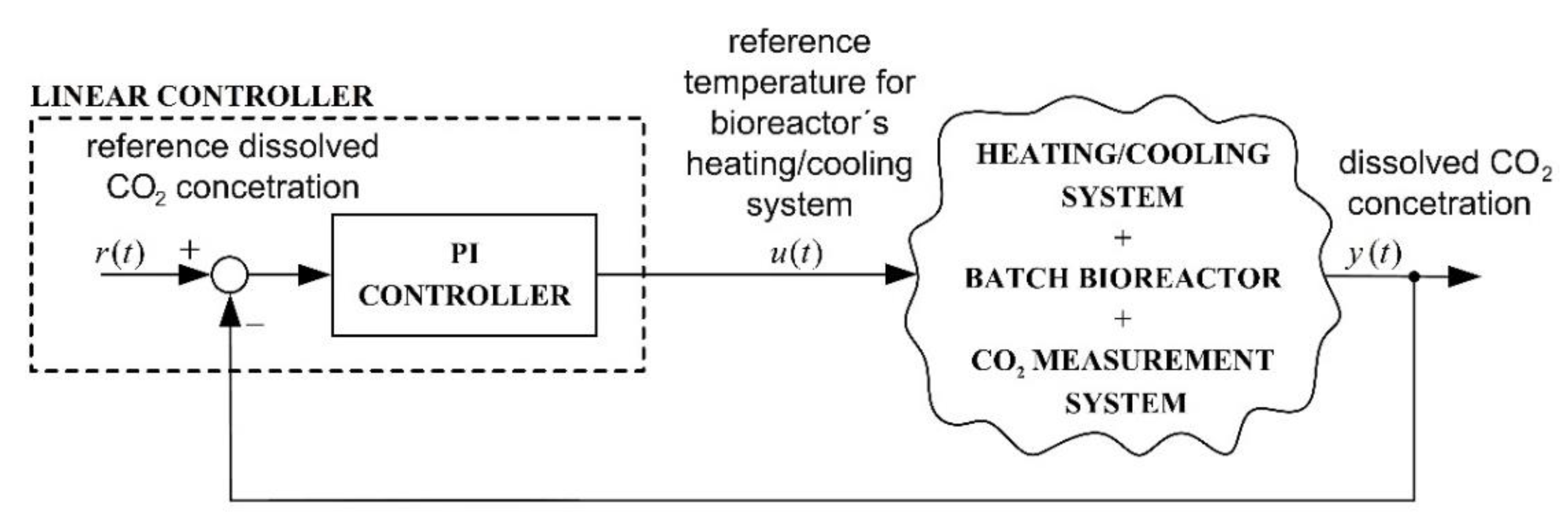
2.5. Conventional Control System with a Linear Controller
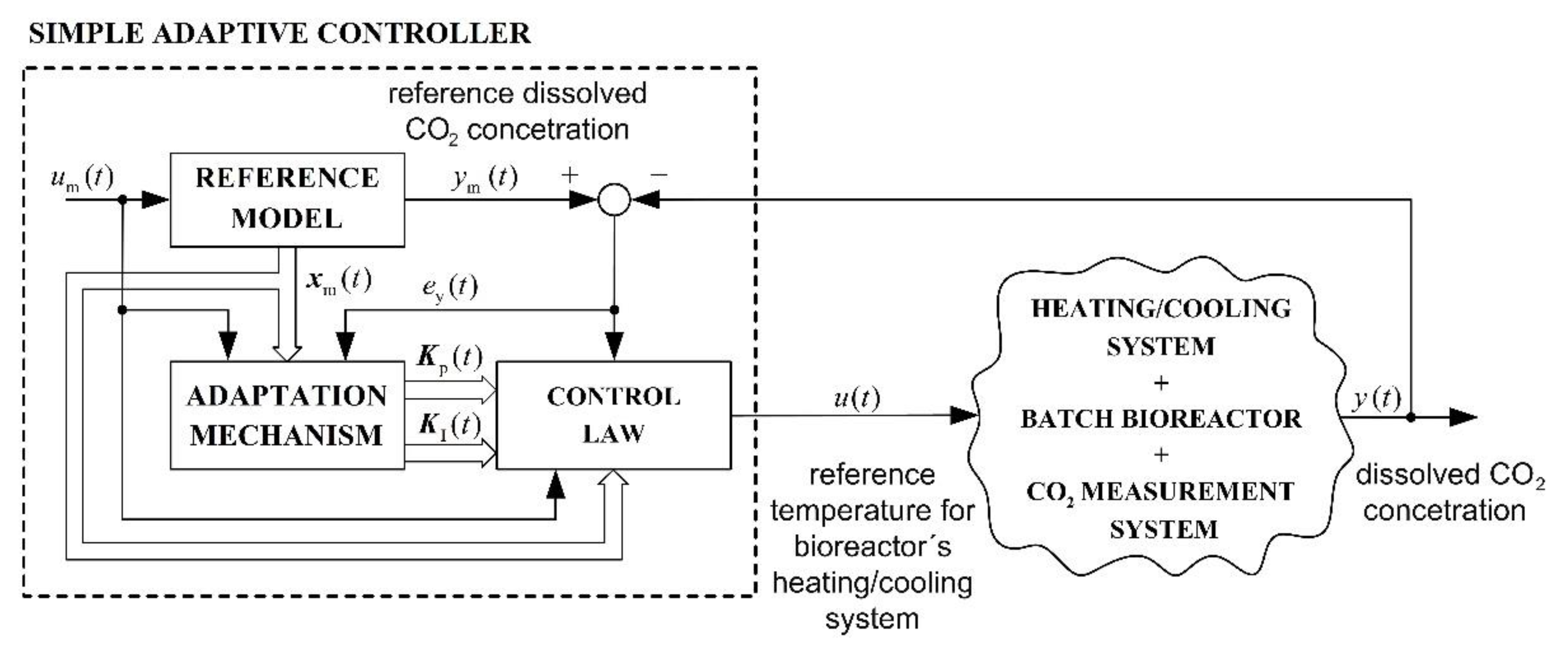
2.6. Adaptive Control System
- Adaptive control systems based on the full-state access method, which requires that all state variables of the controlled plant are measurable (MRAC-FSA) [35];
- Adaptive control systems based on the input–output description of a controlled plant, where an adaptive observer is incorporated into the controller to overcome the inability to access the entire state space vector (MRAC-AO) [36];
- Adaptive control systems, where the adaptive algorithm only requires that the controlled plant’s outputs and the reference model states are available for measurement. The asymptotic stability of this adaptive approach is assured in the case when the plant is almost strictly positive real. This adaptive approach is called model reference adaptive control for almost strictly positive real plants (MRAC-ASPR) [37].
- They are applicable to non-minimum phase systems;
- The order of the controlled plant need not be known to select the reference model and the adaptation mechanism;
- The adaptation mechanism is computationally undemanding.
3. Results
3.1. Estimation of Model Parameters
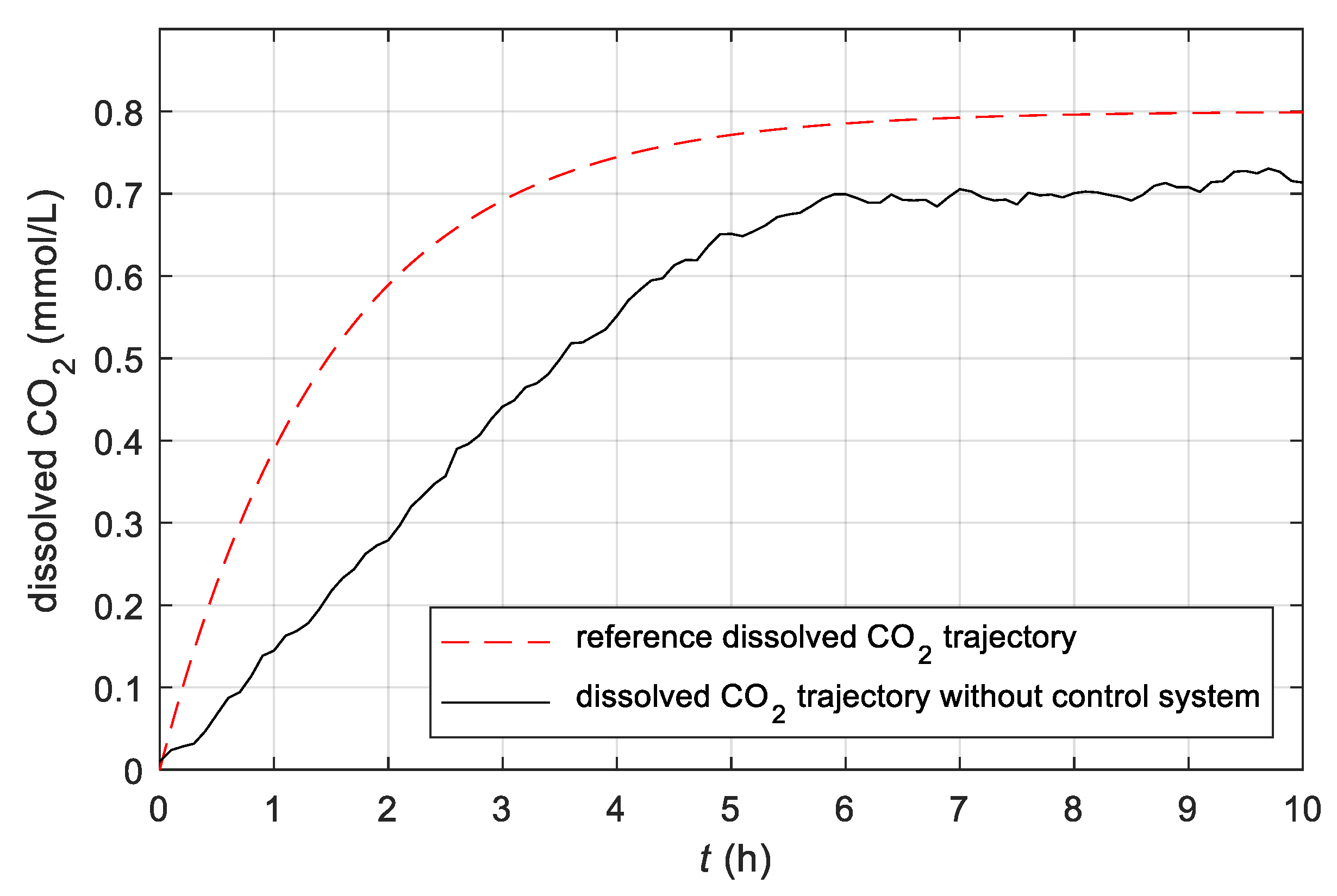
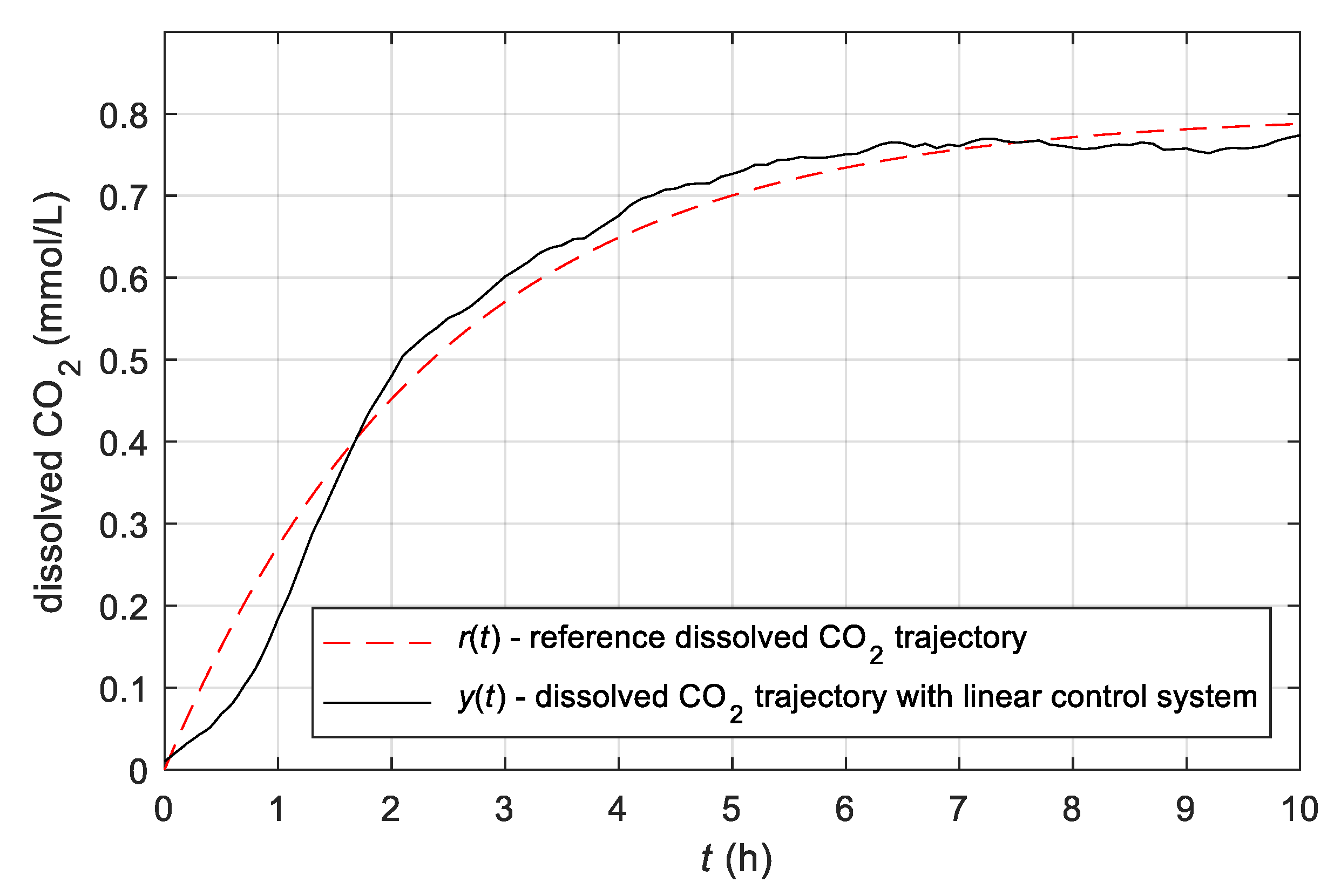
3.2. Results Obtained with the Conventional Control System
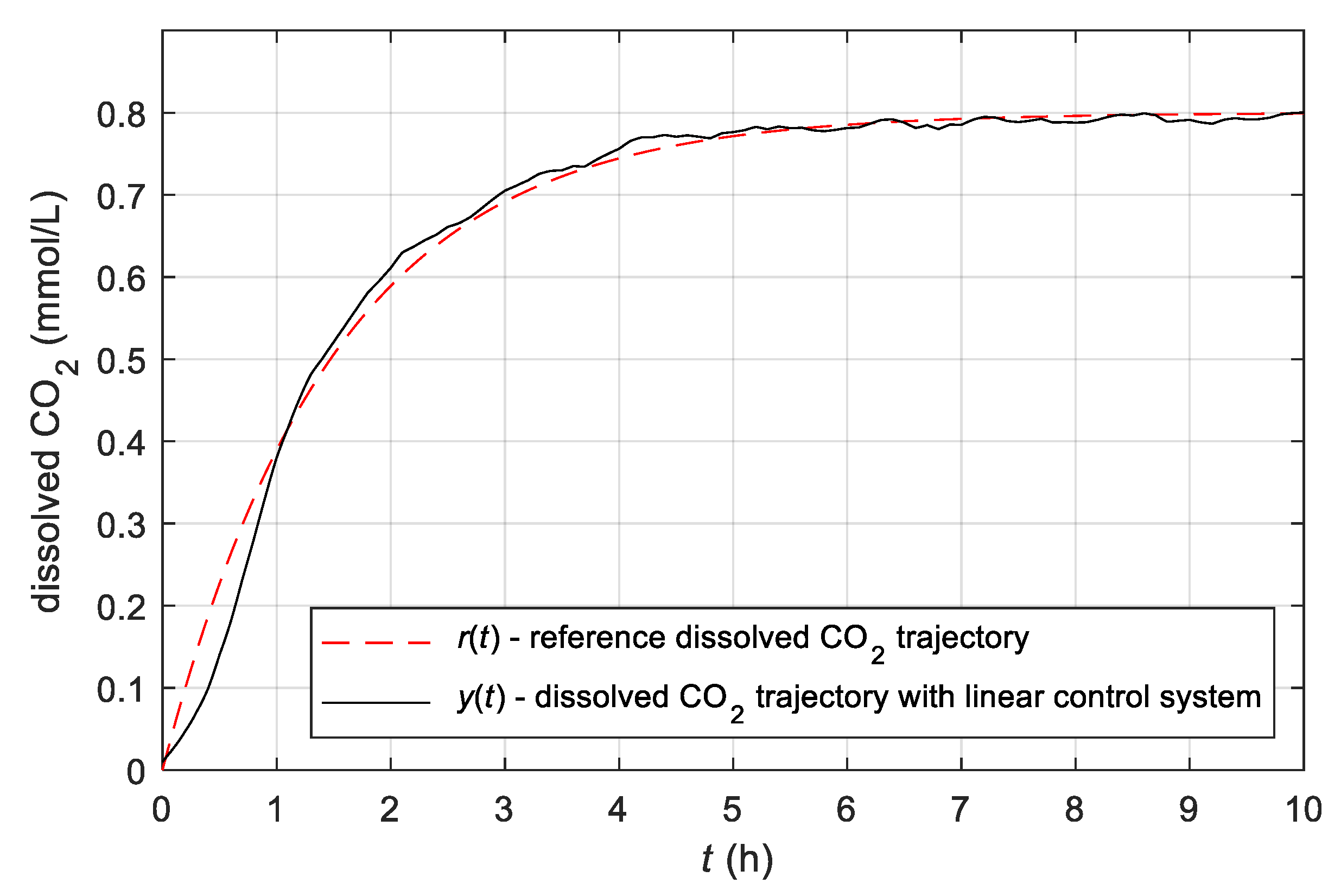
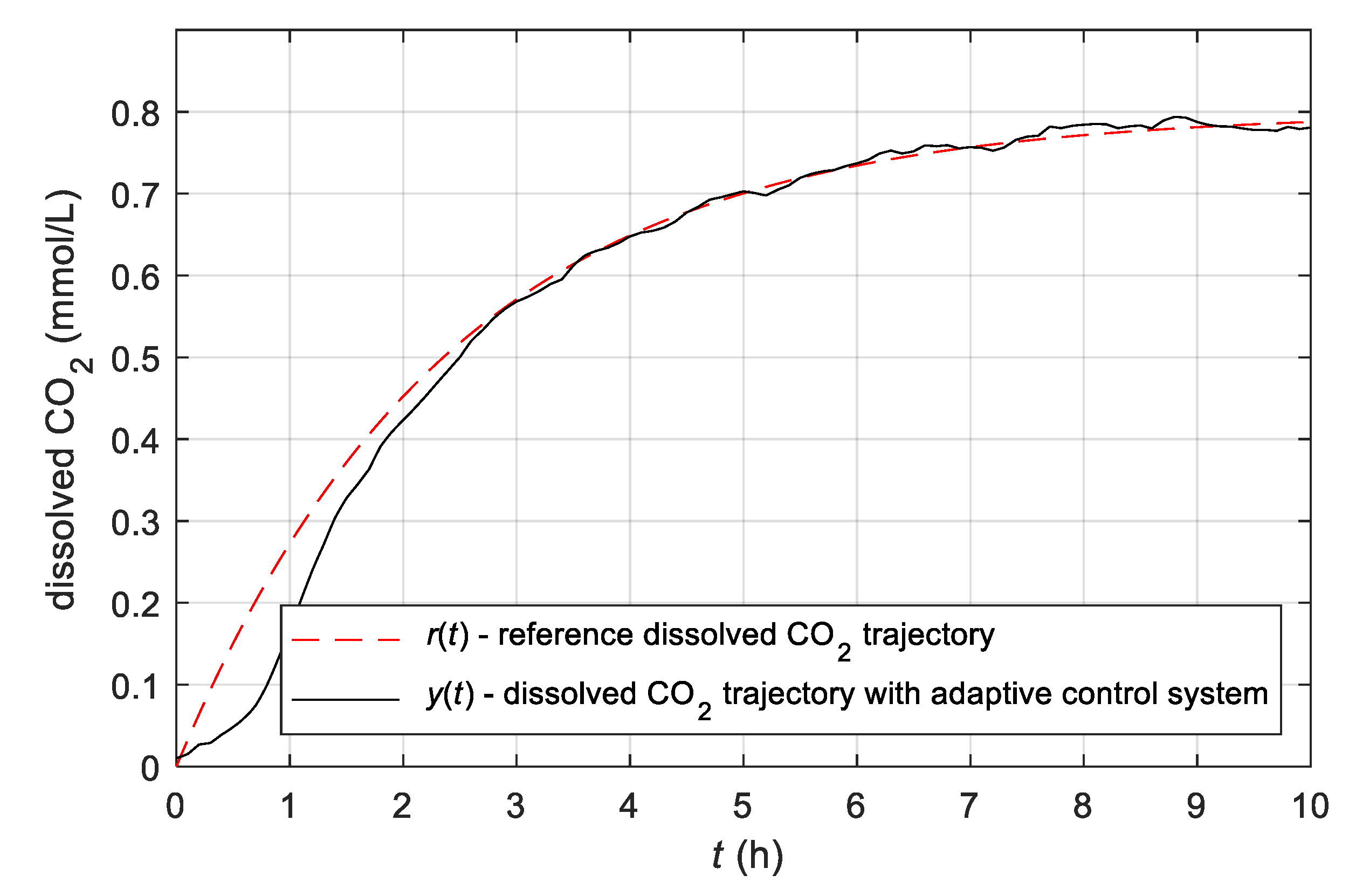
3.3. Results Obtained with the Simple Adaptive Control System
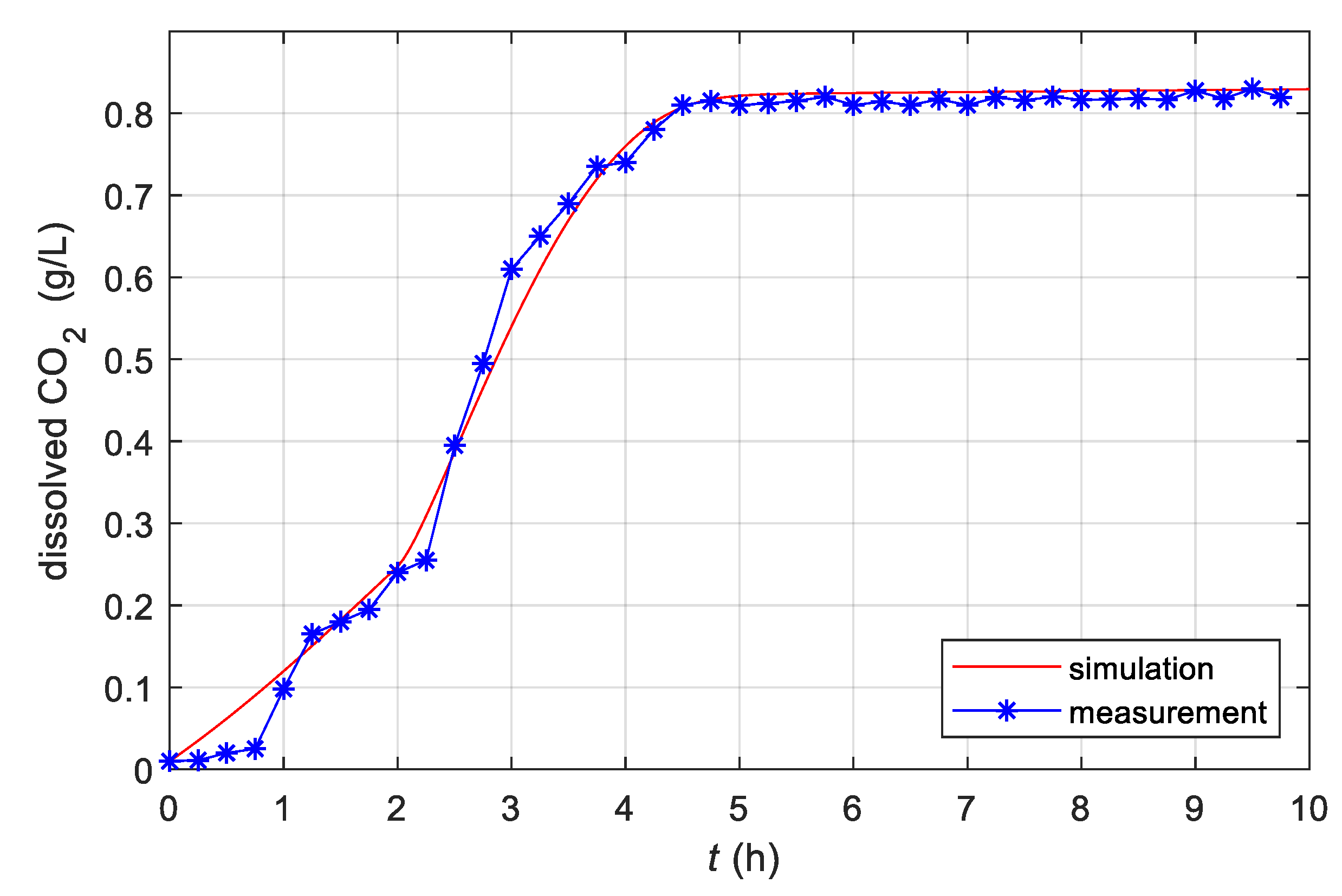
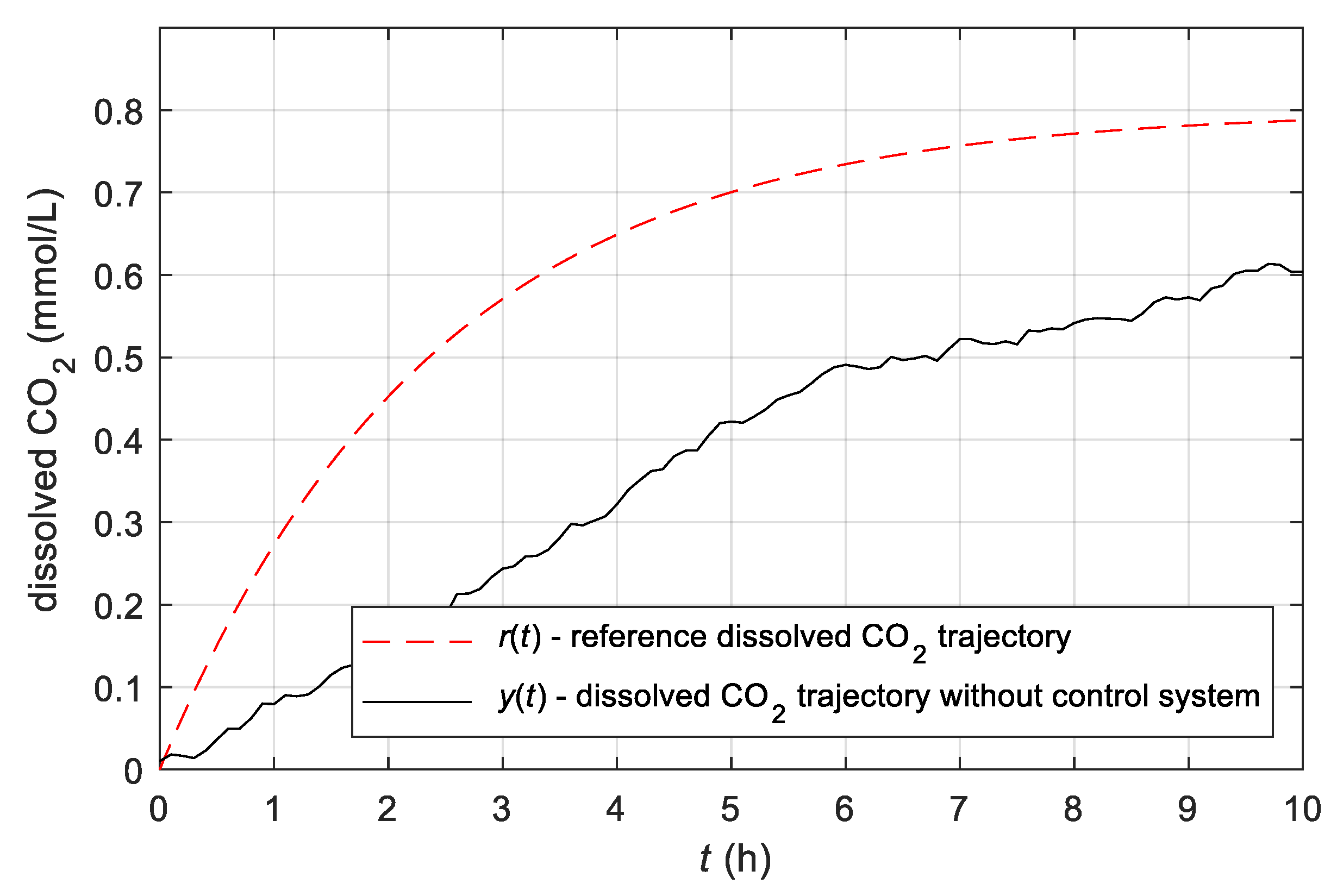
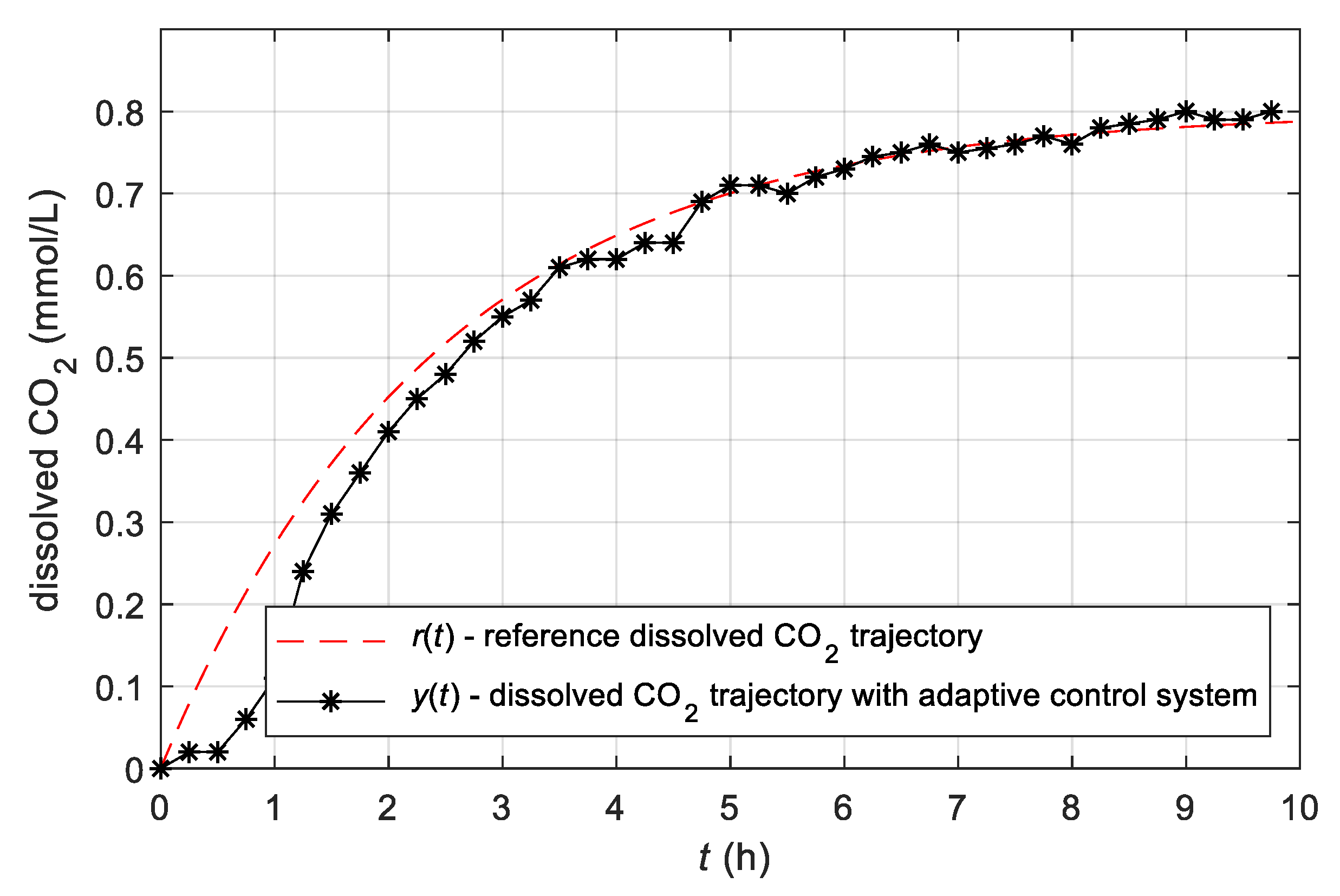
3.4. Experimental Results Obtained with the Simple Adaptive Control System
4. Discussion
5. Conclusions
- The study confirmed that by changing the temperature in the batch bioreactor, the execution of the fermentation process could be controlled;
- The author showed that the proposed minor supplementation of the batch bioreactor with a controlled heating/cooling system and CO2 measurement system enables the development of the closed-loop control system, which ensures that the time profiles of substantial biological quantities during the fermentation process will be the same as the reference profile;
- The author derived an original non-linear mathematical model of the fermentation process in the batch bioreactor, which describes the influence of temperature variations in the bioreactor on the courses of the fermentation quantities; the derived model was used for the design and synthesis of the closed-loop control systems;
- Based on the derived mathematical model, the author utilizes a conventional closed-loop control system with optimized parameters, which ensures that the course of trajectories of substantial biological quantities during the fermentation process will be the same as the course of the reference trajectories when the parameters of the mathematical model are known;
- The author reviewed various advanced control concepts and, on this basis, proposed and developed a control system based on the use of adaptive control theory. The proposed usage of the MRAC-ASPR theory for the development of the control of the growth in the fermentation process in batch bioreactor represents the main original contribution.
- It has been shown that the developed simple adaptive control system represents a very effective control for batch bioreactor operation. The advantage of the developed adaptive controller is significantly easier implementation while having the same or better performance as a conventional controller, which requires complicated and time-demanding tuning. The proposed adaptive control system was analysed theoretically and experimentally, and its advantages were confirmed with the results.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Biotechnology Market Growth & Trends. Available online: https://www.grandviewresearch.com/press-release/global-biotechnology-market (accessed on 2 April 2021).
- Shuler, M.L.; Kargi, F. Bioprocess Engineering: Basic Concepts, 2nd ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 2002. [Google Scholar]
- Cinar, A.; Parulekar, S.J.; Undey, C.; Birol, G. Batch Fermentation—Modelling, Monitoring and Control; Marcel Dekker Inc.: New York, NY, USA, 2003. [Google Scholar]
- Blanch, H.W.; Clark, D.S. Biochemical Engineering; Marcel Dekker, Inc.: New York, NY, USA, 1997. [Google Scholar]
- Henson, M.A. Exploiting cellular biology to manufacture high-value products—Biochemical reactor modelling and control. IEEE Control. Syst. Mag. 2006, 1066, 54–62. [Google Scholar]
- Goršek, A.; Ritonja, J.; Pečar, D. Mathematical model of CO2 release during milk fermentation using natural kefir grains. J. Sci. Food Agric. 2018, 98, 4680–4684. [Google Scholar] [CrossRef] [PubMed]
- Ritonja, J. Implementation of stir-speed adopted controllers onto a batch bioreactor for improved fermentation. IEEE Access 2021, 9, 16783–16806. [Google Scholar] [CrossRef]
- Coutinho, D.; Vande Wouwer, A. A robust non-linear feedback control strategy for a class of bioprocesses. IET Control. Theory Appl. 2013, 7, 829–841. [Google Scholar] [CrossRef]
- De Andrade, G.A.; Pagano, D.J.; Guzmán, J.L.; Berenguel, M.; Fernández, I.; Acién, F.G. Distributed sliding mode control of pH in tubular photobioreactors. IEEE Trans. Control. Syst. Technol. 2015, 24, 1160–1173. [Google Scholar] [CrossRef]
- Battista, H.D.; Picó-Marco, E.; Santos-Navarro, F.N.; Picó, J. Output feedback linearization of turbidostats after time scaling. IEEE Trans. Control. Syst. Technol. 2018, 27, 1668–1676. [Google Scholar] [CrossRef]
- Casenave, C.; Perez, M.; Dochain, D.; Harmand, J.; Rapaport, A.; Sablayrolles, J.-M. Antiwindup input–output linearization strategy for the control of a multistage continuous fermenter with input constraints. IEEE Trans. Control. Syst. Technol. 2020, 28, 766–775. [Google Scholar] [CrossRef]
- Li, S.; Yueyang, L. Model predictive control of an intensified continuous reactor using a neural network Wiener model. Neurocomputing 2016, 185, 93–104. [Google Scholar] [CrossRef]
- Vasičkaninová, A.; Bakošová, M.; Oravec, J.; Mészáros, A. Model predictive control of a tubular chemical reactor. In Proceedings of the 22nd International Conference on Process Control, Štrbské Pleso, Slovakia, 11–14 June 2019. [Google Scholar]
- Rodriguez, A.E.; Munoz, J.A.T.; Luna, R.; Correa, J.R.P.; Bocanegra, A.R.D.; Ramirez, H.S.; Castro, R. Robust control for cultivation of microorganisms in a high density fed-batch bioreactor. IEEE Lat. Am. Trans. 2015, 13, 1927–1933. [Google Scholar] [CrossRef]
- Estakhrouiyeh, M.R.; Vali, M.; Gharaveisi, A. Application of fractional order iterative learning controller for a type of batch bioreactor. IET Control. Theory Appl. 2016, 10, 1374–1383. [Google Scholar] [CrossRef]
- Maria, G. Model-based optimization of a fed-batch bioreactor for mAb production using a hybridoma cell culture. Molecules 2020, 25, 5648. [Google Scholar] [CrossRef]
- Grigs, O.; Galvanauskas, V.; Dubencovs, K.; Vanags, J.; Suleiko, A.; Berzins, T.; Kunga, L. Model predictive feeding rate control in conventional and single-use lab-scale bioreactors: A study on practical application. Chem. Biochem. Eng. Q. 2016, 30, 47–60. [Google Scholar] [CrossRef]
- Chitra, M.; Pappa, N. Optimal tuning of model predictive controller tuning using chicken swarm optimization for real cultivation of Escherichia coli. In Proceedings of the IEEE Second International Conference on Control, Measurement and Instrumentation (CMI), Kolkata, West Bengal, India, 8–10 January 2021. [Google Scholar]
- Rodriguez-Mata, A.E.; Luna, R.; Pérez-Correa, J.R.; Gonzalez-Huitrón, A.; Castro-Linares, R.; Duarte-Mermou, M.A. Fractional sliding mode nonlinear procedure for robust control of an eutrophying microalgae photobioreactor. Algorithms 2020, 13, 50. [Google Scholar] [CrossRef] [Green Version]
- Gharagozloo, M.H.; Ghasemi, R.; Sedighi, M. Nonlinear Model Predictive Versus Sliding Mode Controller Design for a Class of Nonlinear Non-Affine Chemical Batch Reactor Dynamics; EasyChair Preprint: Budapest, Hungary, 2020. [Google Scholar]
- Kumar, M.; Prasad, D.; Shekher Giri, B.; Sharan Singh, R. Temperature control of fermentation bioreactor for ethanol production using IMC-PID controller. Biotechnol. Rep. 2019, 22. [Google Scholar] [CrossRef] [PubMed]
- Pachauri, N.; Rani, A.; Singh, V. Bioreactor temperature control using modified fractional order IMC-PID for ethanol production. Chem. Eng. Res. Des. 2017, 122, 97–112. [Google Scholar] [CrossRef]
- Imtiaz, U.; Jamuar, S.; Sahu, J.N.; Ganesan, P.B. Bioreactor profile control by a non-linear auto regressive moving average neuro and two degree of freedom PID controllers. J. Process. Control. 2014, 24, 1761–1777. [Google Scholar] [CrossRef]
- Flores-Hernández, A.A.; Reyes-Reyes, J.; Astorga-Zaragoza, C.M.; Osorio-Gordillo, G.L.; García-Beltrán, C.D. Temperature control of an alcoholic fermentation process through the Takagi–Sugeno modeling. Chem. Eng. Res. Des. 2018, 140, 320–330. [Google Scholar] [CrossRef]
- Fonseca, R.R.; Schmitz, J.E.; Frattini, A.M.; Vasconcelos da Silva, F. A fuzzy–split range control system applied to a fermentation process. Bioresour. Technol. 2013, 142, 475–482. [Google Scholar] [CrossRef] [Green Version]
- The Importance of Real-Time CO2 Monitoring in Cell Culture. Available online: https://https://bioprocessintl.com/sponsored-content/the-importance-of-real-time-co2-monitoring-in-cell-culture/ (accessed on 8 July 2021).
- Chopda, V.R.; Holzberg, T.; Ge, X.; Folio, B.; Tolosa, M.; Kostov, Y.; Tolosa, L.; Rao, G. Real-time dissolved carbon dioxide monitoring I: Application of a novel in situ sensor for CO2 monitoring and control. Biotechnol. Bioeng. 2020, 117, 981–991. [Google Scholar] [CrossRef] [Green Version]
- Chatterjee, M.; Ge, X.; Uplekar, S.; Kostov, Y.; Croucher, L.; Pilli, M.; Rao, G. A unique noninvasive approach to monitoring dissolved O2 and CO2 in cell culture. Biotechnol. Bioeng. 2015, 112. [Google Scholar] [CrossRef]
- Arévalo, H.; Snáchez, F.; Ruiz, F.; Guerrero, D.; Patino, D.; Alméciga-Díaz, C.; Rodríguez-López, A. Gain-scheduled oxygen concentration control system for a bioreactor. IEEE Lat. Am. Trans. 2018, 16, 2689–2697. [Google Scholar] [CrossRef]
- Ritonja, J.; Goršek, A.; Pečar, D. Use of a heating system to control the probiotic beverage production in batch bioreactor. Appl. Sci. 2021, 11, 84. [Google Scholar] [CrossRef]
- Ritonja, J.; Goršek, A.; Pečar, D. Model reference adaptive control for milk fermentation in batch bioreactor. Appl. Sci. 2020, 10, 9118. [Google Scholar] [CrossRef]
- Goršek, A.; Tramšek, M. Kefir grains production—An approach for volume optimization of two-stage bioreactor system. Biochem. Eng. J. 2008, 42, 153–158. [Google Scholar] [CrossRef]
- Zosel, J.; Oelßner, W.; Decker, M.; Gerlach, G.; Guth, U. Topical review: The measurement of dissolved and gaseous carbon dioxide concentration. Meas. Sci. Technol. 2011, 22, 072001. [Google Scholar] [CrossRef]
- Isermann, R.; Lachmann, K.H.; Matko, D. Adaptive Control Systems; Prentice Hall International: New York, NY, USA, 1992. [Google Scholar]
- Landau, Y.D. Adaptive Control: The Model Reference Approach; Marcel Dekker, Inc.: New York, NY, USA, 1979. [Google Scholar]
- Narendra, K.S.; Annaswamy, A.M. Stable Adaptive System; Prentice Hall Inc.: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Kaufman, H.; Bar-Khana, I.; Sobel, K. Direct Adaptive Control. Algorithms; Springer: New York, NY, USA, 1993. [Google Scholar]
- Barkana, I. Output feedback stabilizability and passivity in nonstationary and non-linear systems. Int. J. Adapt. Control. Signal. Process. 2009, 24, 568–591. [Google Scholar]
- Barkana, I. Adaptive control? But is so simple! A tribute to the efficiency, simplicity and beauty of adaptive control. J. Intell. Robot. Syst. 2016, 83, 3–34. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. Proc. IEEE Int. Conf. Neural Netw. 1995, 4, 1942–1948. [Google Scholar]
- Mezura-Montes, E.; Coello, C.A. Constraint-handling in nature-inspired numerical optimization: Past, present and future. Swarm Evol. Comput. 2011, 1, 173–194. [Google Scholar] [CrossRef]
- Pedersen, M.E.H. Good parameters for particle swarm optimization. Hvass Lab. Cph. Den. Tech. Rep. HL1001 2010, 1551–3203. [Google Scholar]
- Particle Swarm Optimization Algorithm. Available online: https://mathworks.com/help/gads/particle-swarm-optimization-algorithm.html (accessed on 12 May 2021).


| Variable | Value |
|---|---|
| The initial value of the microorganisms’ concentration | x1(0) = 0.26 mg/L |
| The initial value of the substrate’s concentration | x2(0) = 0.89 mg/L |
| The initial value of the product’s concentration | x3(0) = 0.02 mg/L |
| The initial temperature of the bioreactor’s contents | x4(0) = 22 °C |
| Parameter | Value |
|---|---|
| The maximum microorganisms’ growth rate | μm = 0.5 h−1 |
| The product inhibition constant | Pi = 7.0 g/L |
| The substrate saturation constant | Sm = 0.42 g/L |
| The substrate inhibition constant | Si = 62.15 g/L |
| The parameter of the product yield related to microorganisms’ growth | α |
| The parameter of the product yield independent of the microorganisms’ growth | β = 0.001 h−1 |
| The coefficient of the impact of the temperature changing on the maximum microorganisms’ growth rate µm | = 0.1 (°C)−1 |
| The coefficient of the impact of the temperature changing on the parameter α | kα = 1.15 (°C)−1 |
| The temperature of the bioreactor’s contents at the beginning of the fermentation process, normally this temperature is equal to the outside temperature | ϑ0 = 22 °C |
| The time constant of the 1st-order model of the controlled heating system | = 0.1 h |
| Parameter | Value |
|---|---|
| The maximum microorganisms’ growth rate | μm = 0.23 h−1 |
| The product inhibition constant | Pi = 7.2 g/L |
| The substrate saturation constant | Sm = 0.67 g/L |
| The substrate inhibition constant | Si = 74.58 g/L |
| The parameter of the product yield related to microorganisms’ growth | α |
| The parameter of the product yield independent of the microorganisms’ growth | β = 0 h−1 |
| The coefficient of the impact of the temperature on the maximum microorganisms’ growth rate | = 0.12 (°C)−1 |
| The coefficient of the impact of the temperature on the temperature inhibition constant Pi | kα = 0.04 (°C)−1 |
| Original Fermentation Process with the Data in Table 2 (Activated Kefir Grains) | |
| conventional control system with PI-controller | J = 4.2496 |
| simple adaptive control system | J = 4.2864 |
| Modified Fermentation Process with the Data in Table 3 (Inactivated Kefir Grains) | |
| conventional control system with PI-controller | J = 9.9223 |
| simple adaptive control system | J = 9.0363 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ritonja, J. Adaptive Control of CO2 Production during Milk Fermentation in a Batch Bioreactor. Mathematics 2021, 9, 1712. https://doi.org/10.3390/math9151712
Ritonja J. Adaptive Control of CO2 Production during Milk Fermentation in a Batch Bioreactor. Mathematics. 2021; 9(15):1712. https://doi.org/10.3390/math9151712
Chicago/Turabian StyleRitonja, Jožef. 2021. "Adaptive Control of CO2 Production during Milk Fermentation in a Batch Bioreactor" Mathematics 9, no. 15: 1712. https://doi.org/10.3390/math9151712
APA StyleRitonja, J. (2021). Adaptive Control of CO2 Production during Milk Fermentation in a Batch Bioreactor. Mathematics, 9(15), 1712. https://doi.org/10.3390/math9151712






