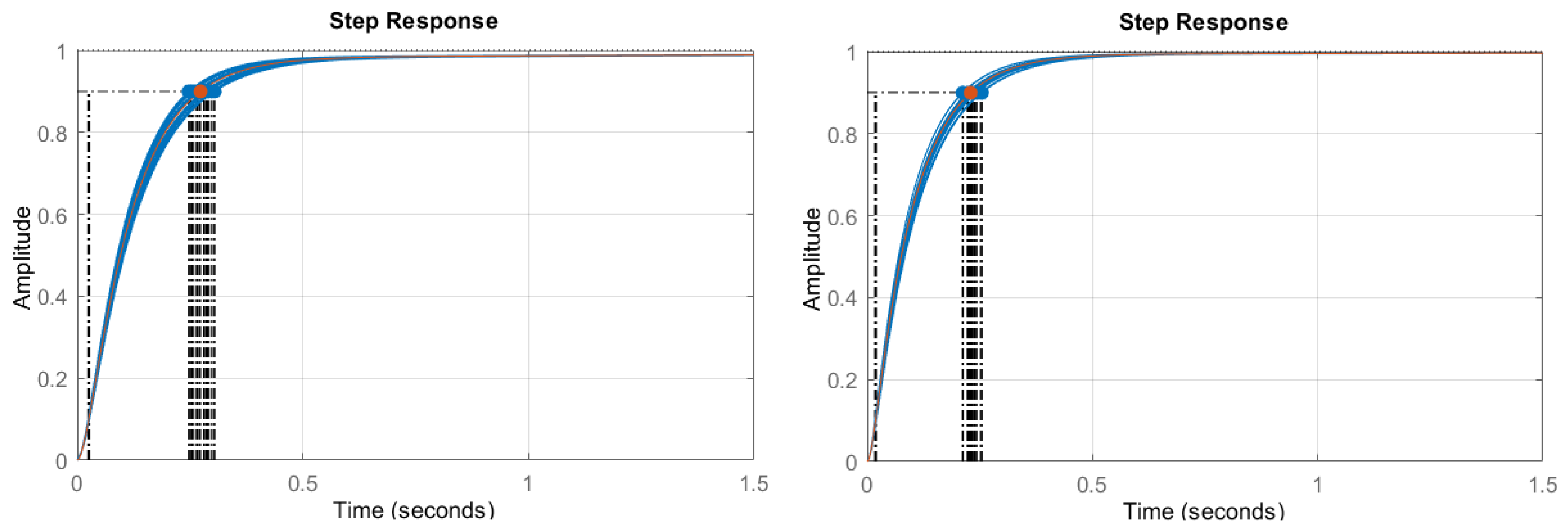
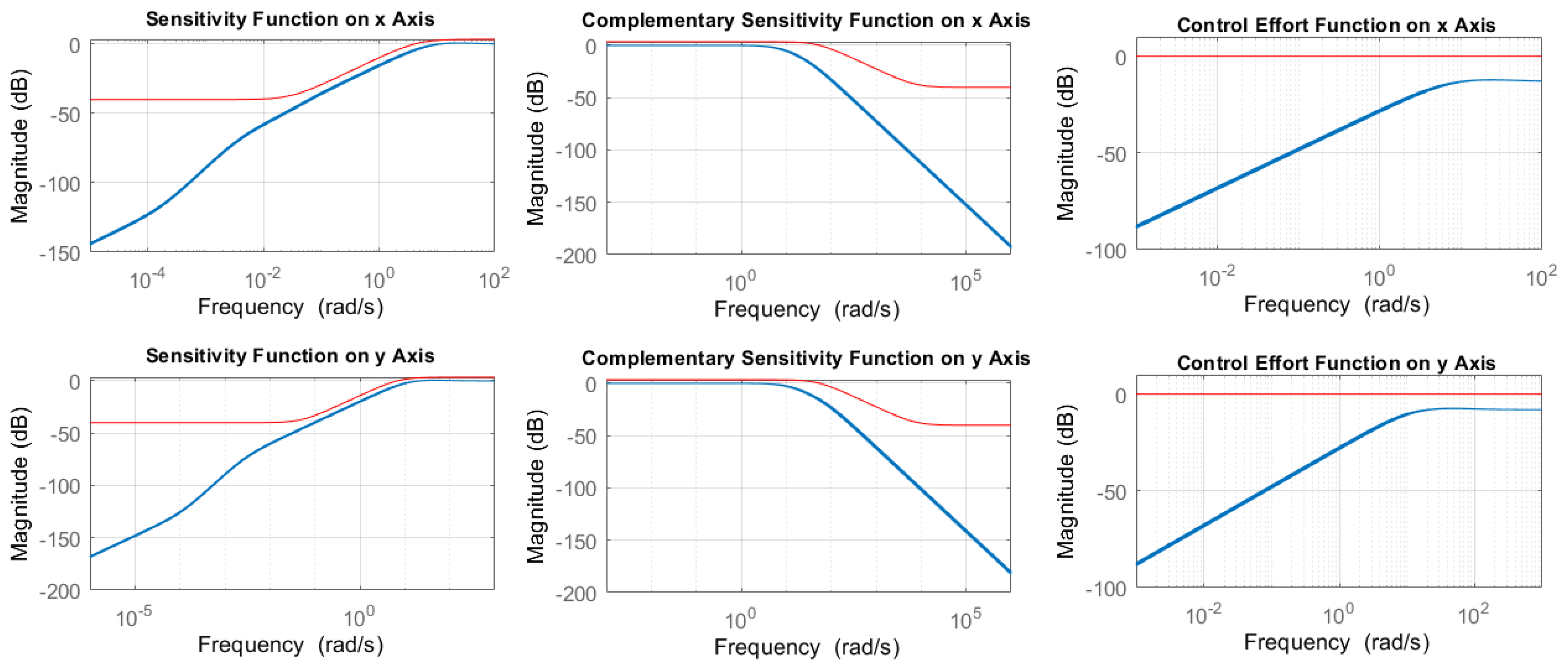
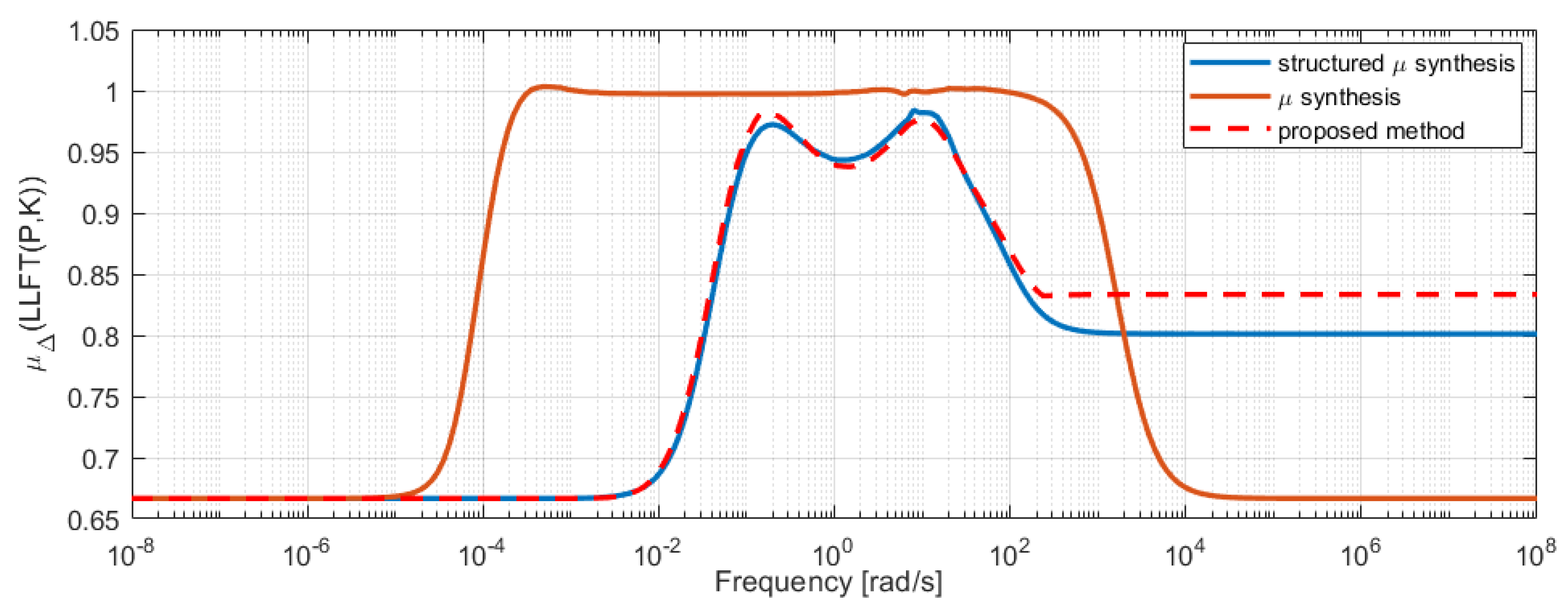
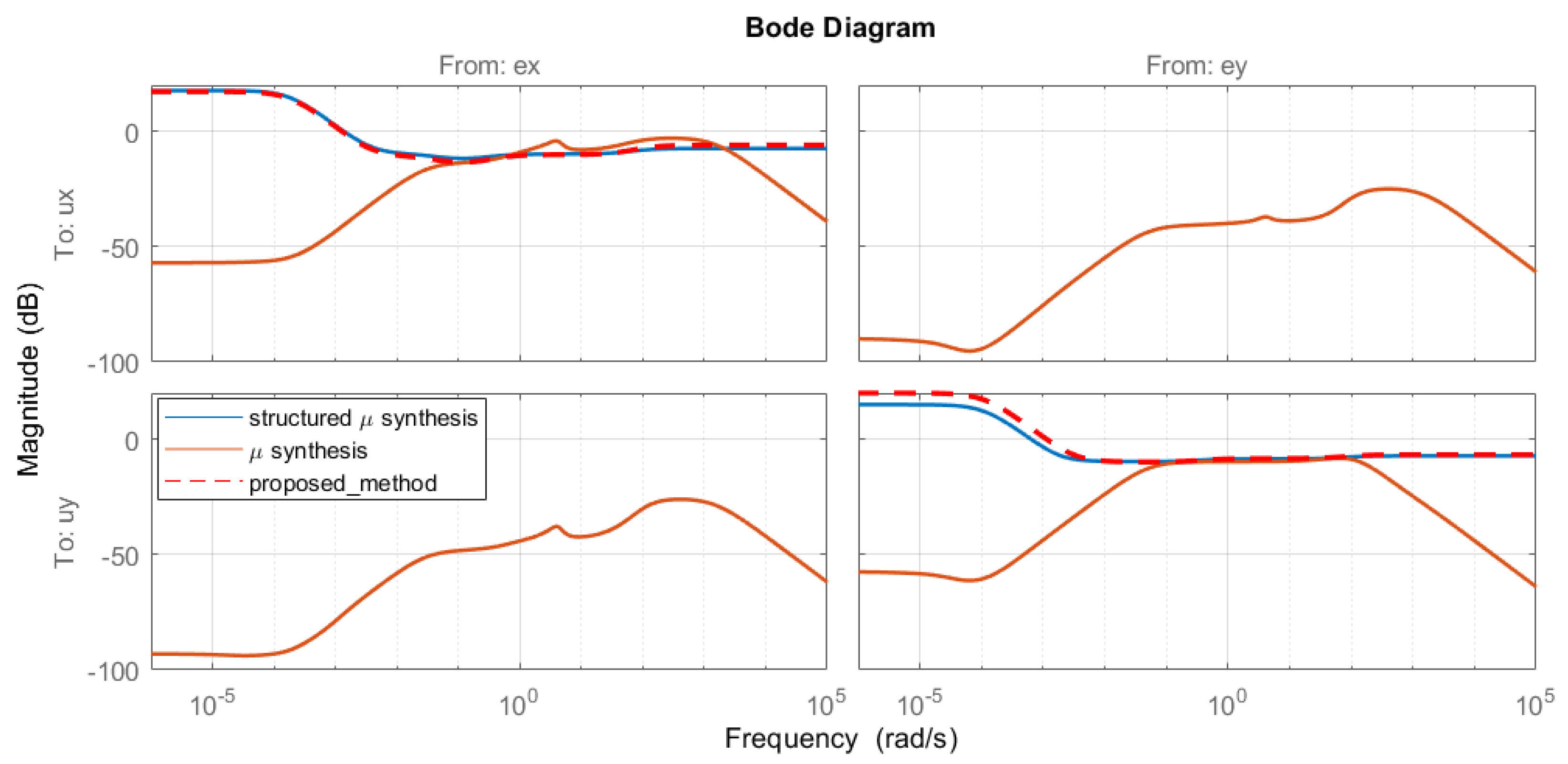
In this section we present a controller synthesis procedure which manages to find a fixed structure fractional-order controller using the -synthesis technique from the Robust Control framework, where the non-convex subproblem involved in the classical D–K iteration is replaced by a swarm optimization algorithm. First, the mathematical background comprised in fractional-order control, robust control and artificial bee colony optimization is underlined, while the fourth subsection presents the proposed design procedure using all the mechanisms briefly described.
2.1. Fractional-Order Controller
The classical integer-order calculus was extended by Riemann and Liouville to fractional-order calculus by introducing the fractional integral operator [
32]:
where
is the Euler Gamma function and the order of the integral operator is the complex parameter
. This extension develops a new area of research in the Control System domain. A commonly used definition of this operator was introduced in [
33] as:
with
and
, having the Laplace transform [
34]:
where
. One of the most common controller structures used in practice is the proportional-integral-derivative (PID) controller, having three degrees of freedom. Using fractional-order calculus, two new degrees of freedom can be added to a PID, having the notation PI
λD
μ. As such, the fractional order PID (FO-PID) has, as extra degrees of freedom, the order
of the integrator and the order
of the differentiator, with the resulting transfer function:
The time domain expression of the command signal
can be expressed using the error signal
as:
One of the major issues of such a fractional element, i.e.,
or
, is its implementation. In order to solve this problem, the Oustaloup recursive approximation (ORA) was introduced [
35], and allows the approximation of the fractional-order element with an LTI system of pre-specified order
N:
where the frequency values of the singularities are obtained based on the desired fractional order
, the integer order of the approximation
N, along with the frequency range in which the approximation is valid
. Using the following two coefficients:
the above mentioned frequencies can be computed using:
For the rest of the possible real values of
, the approximation can be easily extended as: for
by inverting the relation (
6), while for
, the components could be the integer part
and the fractional part
, with the fractional part only approximated using (
6).
2.2. Robust Control
The Robust Control framework assumes to minimize the
/
norm of the lower linear fractional transformation (
LLFT) of a plant
P and a controller
K:
where the plant
P can be written, in general form, as:
where the signals involved in the above relation will be further detailed in a more general context. One approach to solving
/
problems is using AREs, which presents several limitations that are removed by the LMI approach. However, this framework can be used to ensure nominal stability and nominal performance only, but, the plant
P must also contain an augmented model of the real process in which uncertainties are also present. There are two classic uncertainties types:
parametric, represented by
, where
is the maximum bound of the parameter for a physical variable, and
unstructured, represented by a full block
. The latter illustrates neglected or unknown dynamics uncertainties. In the mixed-scenario case, the following set is considered:
In the Robust Control field, one of the main tools used for robustness analysis is the structured singular value, defined as follows.
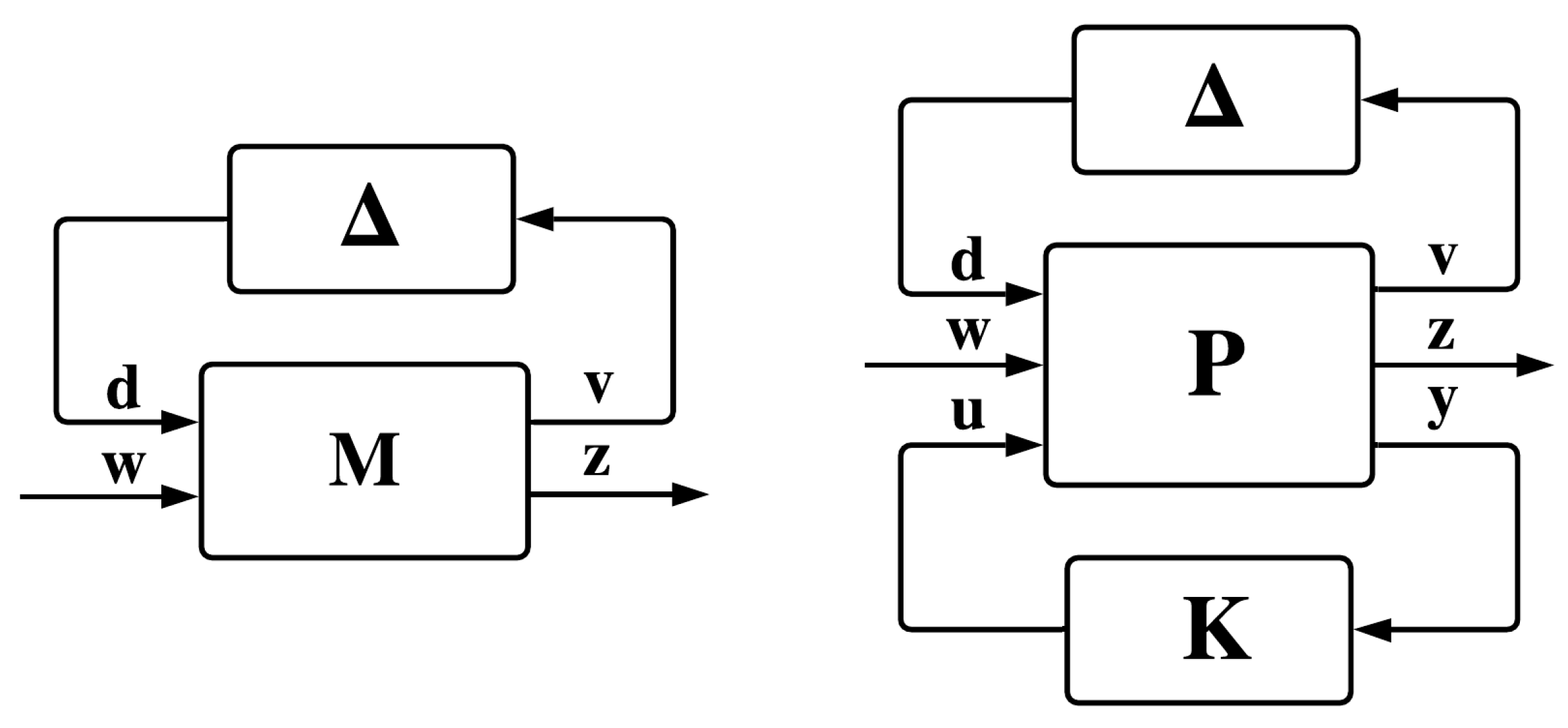
Definition 1. For a square matrix the structured singular value with respect to the set Δ is:if there exists such that the matrix is rank deficient, otherwise 0. For an LTI system described by the transfer matrix
and an upper linear fractional transformation (ULFT) connection shown in
Figure 1 (left), the structured singular value
can be defined as:
Now, considering
as being the lower linear fractional transformation (LLFT) between plant
P and controller
K, the connection illustrated in
Figure 1 (right) results. The generalized plant structure is:
where three types of input signals are present—the command input
, the performance input
, and the disturbance input
—and three types of outputs—the measurements vector
, the performances vector
, and the disturbance output
.
Besides the well-known
methods, a controller that meets robust stability and robust performance alike can be computed using the
-synthesis framework. Robust stability implies that a specific controller manages to stabilize all the processes described by the upper linear fractional transformation (
ULFT) presented in
Figure 1 (left), while robust performance implies that the controller is able to impose the desired closed-loop performance in the worst case scenario. In order to have a mathematical guarantee that a controller
K meets the robust stability and performance, the Main Loop theorem can be used. It implies that closed-loop system meets robust stability and performance if and only if the structural singular value of the
LLFT of the plant and controller, with respect to
, fulfills:
Therefore, the robust control problem can be written as:
which is not convex. More than that, the structural singular values are hard to be explicitly computed. In practice, there are various bounds which can be used to approximate the structural singular value. One of the most used approximations of the upper bound is in [
9]:
where
denotes the largest singular value, and the set
is defined as:
Based on this upper bound, a good approximation of the initial non-convex problem can be employed by solving the following quasi-convex problem:
If the scaling factor, represented by the system
D, is fixed, then the problem (
21) is nothing but a
optimization problem. On the other hand, fixing the controller
K, the
D scaling step can now be obtained by solving a Parrot problem for a desired frequency set
using the following generalized eigenvalue problem:
where from the solution
, the matrix
can be extracted using a singular value decomposition. After all Parrot problems are solved, a minimum phase system is found in order to approximate the analytical solution
. In summary, an iterative algorithm which solves the
-synthesis problem starts by setting
, with the following steps applied successively:
- 1:
Fix
D and solve the
optimal problem to find a controller
K:
- 2:
Fix the controller
K and solve the set of convex problems:
for a given frequency range
and, then, fit a stable minimum phase transfer matrix
.
Steps 1 and 2 are executed in a loop sequence until the difference between two consecutive norms is less than a prescribed tolerance or the maximum number of iterations is reached.
2.3. Artificial Bee Colony Optimization
The artificial bee colony (ABC) optimization is a nature-inspired algorithm used to minimize a cost function:
The ABC algorithm mimics the behaviour of real honeybees, where each food source represents a possible solution of the optimization problem described above. The location and the amount of nectar correspond to the design variables and the cost function, respectively. The bees are divided in two main groups: employed and unemployed bees, while the unemployed bees could be of two types as well: onlooker and scout bees. The employed bees are the ones that investigate the food source and return to the hive to inform the others by performing the waggle dance; the onlooker bees are the ones that watch the dance and decide whether or not a food source is worthy of being searched or not; the scout bees are former employed bees that have abandoned their previous food source, due to lack of nectar, and which now search for a new one. The Best Solution is represented by the food source, and the quality (or cost) of the solution is represented by the amount of nectar.
The number of employed bees coincides with number of the onlooker bees and represents the dimension of the swarm problem, denoted by
N. The employed bees start the foraging process by randomly searching an initial position
in the domain
D:
where
are random numbers. After this initialization step, the first Best Solution appears.
Each employed bee searches a new food source based on the location of the current food source
and another food source
randomly selected. The new possible position is:
where
is an array of random numbers, ⊙ is the element-wise multiplication, and
sat is the saturation function that does not allow the position to be outside the searching domain
D. Now, the position of the
ith employed bee for the next iteration will be:
which means that an employed bee will never choose a source with less nectar. If the position for the next iteration will not be changed, the abandonment counter of the
ith employed bee increments.
The onlooker bees use the information shared by each employed bee and choose a location around the position of the employed bees. The fitness value of a solution
is given by:
and the probability that
ith bee’s source will be selected by an onlooker bee is:
Now, using a roulette wheel selection method, the onlooker bee will choose a source
i and, using the same searching technique as an employed bee, a new position is computed using (
27). If the outlooker bee founds a better solution than the
ith employed bee, they change their roles, otherwise the abandonment counter for the
ith source increments. After this step, we have
N employed bees and
N unemployed bees. However, if the abandonment counter for the
ith source exceeds a threshold, the
ith employed bee becomes a scout and tries to find a new location using the relation (
26).
After every loop corresponding to employed, outlooker and scout bees, it is checked if there is a food source with a solution better than the last one. The algorithm is over when the maximum number of cycles is reached or when there is no improvement of the Best Solution after a prescribed number of cycles.
2.4. Proposed Method
The solution of the problem described in (
21) using the classical
D–
K iteration with
framework leads to a high-order controller. As a solution to this issue, a fixed structure family of controllers
can be considered, and the problem (
21) becomes:
The new problem has the disadvantage of being non-convex in terms of the parameters of the proposed controller structure. However, the problem described in (
31) will also be solved using a
D–
K iterative procedure, but the non-convex part of the problem has fewer degrees of freedom and it will be managed with an ABC optimization.
Starting with the model of the process
G, a plant
P is obtained after the augmentation step:
where the meaning of the inputs and outputs remains the same as in
Section 2.2. Considering the advantages of the fractional-order controllers, the proposed structure of the controller is:
where
is a fractional order controller from the
ith input to the
jth output and has the form:
with the tunable parameters described by the vector:
Using these considerations, the desired family of the fixed structure controllers can be described as follows:
where all parameters are stored in a single vector
describing all degrees of freedom of the tunable controller. Using the ORA mechanism, each component
has a state-space representation:
Next, we denote by
the closed-loop system represented by the lower linear fractional transformation between the augmented plant
P and controller
, which can be represented as:
where state vector, input vector and output vector of the closed-loop system are:
In Algorithm 1 the main steps necessary to obtain the parameters of the controller having the structure (
33) are presented. The inputs of the algorithm are the closed-loop plant
, containing the tunable controller parameters
, and the parameters
and
which describe the cost function that needs to be minimized using an ABC optimization, but,
must also contain the varying parameters and unmodelled dynamics. Therefore, the plant
obtained after the augmentation step with uncertainties
has the form presented in (
16). Thus, the first step made in Algorithm 1 consists in transforming the closed-loop system
in the generalized closed-loop system
described as follows:
where the new extended performance inputs and outputs are:
As mentioned in
Section 2.2, the structured singular value can be bounded using two
D-scaling factors, one for the left and one for the right scaling, denoted
and
, respectively. As it can be notice in
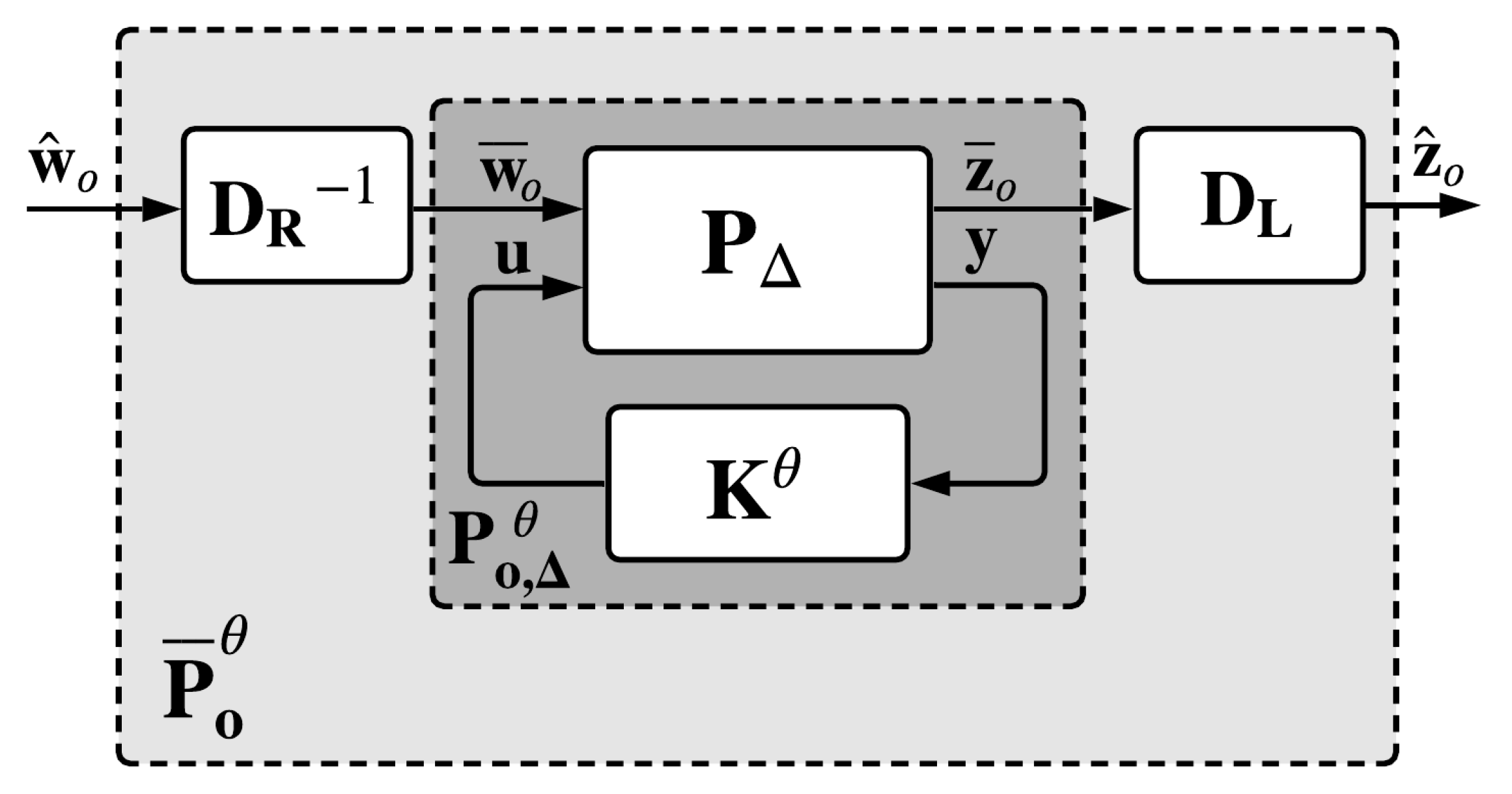
Figure 2, a new closed-loop plant
is obtained:
having the state-space representation:
All the above mentioned plants are presented in
Figure 2. First, the generalized plant
has a LLFT connection with the controller
, resulting the closed-loop plant
, having the input vector
and the output vector
. After the
D-scaling step, a new plant
is obtained, having the input vector
and the output vector
.
Before starting the
while loop of Algorithm 1, an initialization of the generalized closed-loop plant with
D-scale
is performed with the initial scale factors
and
, as seen in line 2. As noticed in line 4, the
K step is performed using this generalized plant having as degrees of freedom the tunable parameters
. In order to compute the controller parameters
, the ABC optimization will be used. The cost function to be minimized is:
where the operator
is defined by:
| Algorithm 1: Fixed Structure -Synthesis. |
![Mathematics 09 00911 i001 Mathematics 09 00911 i001]() |
The procedure
computeKstep used to obtain the controller parameters is briefly presented in Algorithm 2 and will be described below. The inputs of the algorithm are the generalized closed-loop plant with
D-scaling step
, along with the parameters
and
which describe the cost function (
44). The first step of this routine consists in computing the domain
of the cost function based on the constraints of the tunable parameters. The main limitation is represented by the fractional orders of the integral and derivative effects of the controller which must remain in
, according to ORA.
In the second step of routine Algorithm 2, an initial population is created. Let
N be the dimension of the swarm problem. This parameter can be given as input, but as a good practice, this can be chosen 100 times larger than the number of tunable parameters. The initialization step consists in randomly generating the positions
of the food sources for each employed bee in the domain
using relation (
26). After the initialization step, the first Best Solution (BS) is computed as:
Using this initial population, the main
while loop starts. In line 4, the employed bees step is performed. In this step, each employed bee searches a new position around using relation (
27), resulting
N new possible positions for the next step, denoted by
, and the proposed positions of the employed bees at step
will be:
If, for a specific food source
i, the proposed position coincides with the previous position, the abandonment counter increments.
Using the proposed solutions of the above step, each onlooker bee selects a new possible solution based on the roulette wheel selection mechanism and relation (
27), resulting a new set of proposed solutions:
. If the
ith onlooker bee has a better solution than
ith employed bee, they exchange their roles, otherwise the abandonment counter for the
ith food source increments. After this step, the new set of proposed positions for the employed bees are:
| Algorithm 2: Compute K Step. |
![Mathematics 09 00911 i002 Mathematics 09 00911 i002]() |
After performing the outlooker bees step from line 5, the abandonment counter for each active food source will be interrogated. If the abandonment counter of the
ith position exceeds a prescribed threshold, denoted by LIMIT, the employed bee becomes a scout bee and its new position is obtained using (
26). As a good practice, this paper proposed an improved mechanism of converting employed bees in scout bees. If the value of the cost function at the proposed position
is over
, this means that, in the case of a good calibration of parameters
and
, the solution corresponds to an unstable closed-loop system and can be dropped. The positions of the employed bees for the next iteration become
.
The last step of the main
while loop, presented in line 7, consists in computing the Best Solution after this new iteration:
and, then, checking if there exist any improvements after this step. In order to have a good trade-off between execution time and solution accuracy, it can be useful to establish a threshold for the number of steps when no improvement appears in Best Solution and mark if there exists such an improvement. Being a metaheuristic optimization algorithm, the runtime can be made deterministic and theoretically finite by imposing the variable
, without convergence guarantees. In practice, such methods have been successfully employed in various global optimization problems and, being that it is an offline optimization, it is not problematic for our approach.
Returning to Algorithm 1, after the K step is performed, a new parameter vector results, which leads to a new generalized closed-loop plant and to a new uncertain plant . The closed-loop plant is used to compute the next D-scale factors. From we extract a nominal plant by fixing the tunable parameters of the controller with the values determined in step 4.
The
computeDstep routine from line 7 receives as input this nominal plant and returns the left and the right
D-scale factors. Based on the poles and the transmission zeros of the nominal plant
, a set
of frequencies is generated. Then, we need to get the frequency response data for each scaling factor by solving the following generalized eigenvalue problem:
for each
, which is nothing but a Parrot problem which can be solved point by point using LMI techniques, as mentioned in
Section 2.2. Once the frequency response data points are obtained for each value in
, we need to fit two minimum phase systems, one for each scaling factor, then perform the
D-scaling step, giving a new generalized closed-loop system:
In a similar manner with the computeKstep routine, there are possible stopping criteria which can be used. First, a threshold for the maximum number of D–K iterations can be imposed. Another important stopping condition appears if the upper bound of the structural singular value is less than 1, because this fact already guarantees that the controller ensures robust stability and robust performance. In accordance with the allowed maximum number of steps, a stopping criterion could be to check if there are any improvements after a certain number of steps.