Local Inclusive Distance Vertex Irregular Graphs

Abstract

Let $G=(V,E)$ be a simple graph. A vertex labeling $f:V\left(G\right)\to \{1,2,\cdots ,k\}$ is defined to be a local inclusive (respectively, non-inclusive) d-distance vertex irregular labeling of a graph G if for any two adjacent vertices $x,y\in V\left(G\right)$ their weights are distinct, where the weight of a vertex $x\in V\left(G\right)$ is the sum of all labels of vertices whose distance from x is at most d (respectively, at most d but at least 1). The minimum k for which there exists a local inclusive (respectively, non-inclusive) d-distance vertex irregular labeling of G is called the local inclusive (respectively, non-inclusive) d-distance vertex irregularity strength of G. In this paper, we present several basic results on the local inclusive d-distance vertex irregularity strength for $d=1$ and determine the precise values of the corresponding graph invariant for certain families of graphs.

1. Introduction

All graphs considered in this paper are simple finite. We use $V\left(G\right)$ for the vertex set and $E\left(G\right)$ for the edge set of a graph G. The neighborhood $N_G\left(x\right)$ of a vertex $x\in V\left(G\right)$ is the set of all vertices adjacent to x, which is a set of vertices whose distance from x is 1. Otherwise, $N_G\left[x\right]$ denotes the set of all neighbors of a vertex $x\in V\left(G\right)$ including x, which is the set of vertices whose distance from x is at most 1. We are following the standard notation and the terminology presented in [1].

The notion of the irregularity strength was introduced by Chartrand et al. in [2]. For a given edge k-labeling $\alpha :E\left(G\right)\to \{1,2,\cdots ,k\}$, where k is a positive integer, the associated weight of a vertex $x\in V\left(G\right)$ is $w_{\alpha }\left(x\right)={\sum }_{y\in N_G\left(x\right)}\alpha \left(xy\right)$. Such a labeling $\alpha$ is called irregular if $w_{\alpha }\left(x\right)\ne w_{\alpha }\left(y\right)$ for every pair $x,y$ of vertices of G. The smallest integer k for which an irregular labeling of G exists is known as the irregularity strength of G. This parameter has attracted much attention, see [3,4,5].

Inspired by irregularity strength and distance magic labeling defined in [6] and investigated in [7], Slamin [8] introduced the concept of a distance vertex irregular labeling of graphs. A distance vertex irregular labeling of a graph is a mapping $\beta :V\left(G\right)\to \{1,2,\cdots ,k\}$ such that the set of vertex weights consists of distinct numbers, where the weight of a vertex $x\in V\left(G\right)$ under the labeling $\beta$ is defined as $w{t}_{\beta }\left(x\right)={\sum }_{y\in N_G\left(x\right)}\beta \left(y\right).$ The minimum k for which a graph G has a distance vertex irregular labeling is called the distance vertex irregularity strength of G and is denoted by $\mathrm{dis}\left(G\right)$.

In [8], Slamin determined the exact value of the distance vertex irregularity strength for complete graphs, paths, cycles and wheels, namely $\mathrm{dis}\left(K_n\right)=n$, for $n\ge 3$, $\mathrm{dis}\left(P_n\right)=⌈n/2⌉$, for $n\ge 4$, $\mathrm{dis}\left(C_n\right)=⌈(n+1)/2⌉$, for $n\equiv 0,1,2,3(mod8)$ and $\mathrm{dis}\left(W_n\right)=⌈(n+1)/2⌉$, for $n\equiv 0,1,2,5(mod8)$. Completed results for cycles and wheels are proved in [9].

Bong et al. [10] generalized the concept of a distance vertex irregular labeling to inclusive and non-inclusive d-distance vertex irregular labelings. The difference between inclusive and non-inclusive labeling depends on the way whether the vertex label is included in the vertex weight or not. The symbol d represents how far the neighborhood is considered. Thus, an inclusive (respectively, non-inclusive) d-distance vertex irregular labeling of a graph G is a mapping $\beta$ such that the set of vertex weights consists of distinct numbers, where the weight of a vertex $x\in V\left(G\right)$ is the sum of all labels of vertices whose distance from x is at most d (respectively, at most d but at least 1). The minimum k for which there exists an inclusive (respectively, non-inclusive) d-distance vertex irregular labeling of a graph G is called the inclusive (respectively, non-inclusive) d-distance vertex irregularity strength of G. The non-inclusive 1-distance vertex irregularity strength of a graph G is using Slamin’s [8] terminology known as the distance vertex irregularity strength of G, denoted by $\mathrm{dis}\left(G\right)$. For the inclusive 1-distance vertex irregularity strength, we will use notation $\mathrm{idis}\left(G\right)$.

In [10] is determined the inclusive 1-distance vertex irregularity strength for paths $P_n$, $n\equiv 0(mod3)$, stars, double stars $S(m,n)$ with $m\le n$, a lower bound for caterpillars, cycles, and wheels. In [11] is established a lower bound of the inclusive 1-distance vertex irregularity strength for any graph and determined the exact value of this parameter for several families of graphs, namely for complete and complete bipartite graphs, paths, cycles, fans, and wheels. More results on triangular ladder and path for $d\ge 1$ has been proved in [12,13].

Motivated by a distance vertex labeling [8], an irregular labeling [2] and a recent paper on a local antimagic labeling [14], we introduce in this paper the concept of local inclusive and local non-inclusive d-distance vertex irregular labelings.

A vertex labeling $f:V\left(G\right)\to \{1,2,\cdots ,k\}$ is defined to be a local inclusive (respectively, non-inclusive) d-distance vertex irregular labeling of a graph G if for any two adjacent vertices $x,y\in V\left(G\right)$ their weights are distinct, where the weight of a vertex $x\in V\left(G\right)$ is the sum of all labels of vertices whose distance from x is at most d (respectively, at most d but at least 1). The minimum k for which there exists a local inclusive (respectively, non-inclusive) d-distance vertex irregular labeling of G is called the local inclusive (respectively, non-inclusive) d-distance vertex irregularity strength of G and denoted by ${\mathrm{lidis}}_d\left(G\right)$ (respectively, ${\mathrm{ldis}}_d\left(G\right)$). If there is no such labeling for the graph G then the value of ${\mathrm{lidis}}_d\left(G\right)$ is defined as ∞. In the case when $d=1$ the index d can be omitted, thus ${\mathrm{lidis}}_1\left(G\right)=\mathrm{lidis}\left(G\right)$ (respectively, ${\mathrm{ldis}}_1\left(G\right)=\mathrm{ldis}\left(G\right)$). In this paper, we only discuss the case for inclusive labeling with $d=1$. Note that the concept of a local non-inclusive distance vertex irregular labeling has been introduced earlier in [15] with a different name. For more information about labeled graphs see [16].

In this paper, we present several basic results and some estimations on the local inclusive 1-distance vertex irregularity strength and determine the precise values of the corresponding graph invariant for several families of graphs.

2. Basic Properties

In the following observations, we give several basic properties of $\mathrm{lidis}\left(G\right)$. The first observation gives a relation between the local inclusive distance vertex irregularity strength, $\mathrm{lidis}\left(G\right)$, and the inclusive distance vertex irregularity strength, $\mathrm{idis}\left(G\right)$. The second and third observations give the requirement for giving the label of two vertices which have a common neighbor.

Observation 1.

For a graph G, it holds that $\mathrm{lidis}\left(G\right)\le \mathrm{idis}\left(G\right)$.

Observation 2.

If there exists an edge $uv$ in a graph G such that $N_G\left(u\right)-\left\{v\right\}=N_G\left(v\right)-\left\{u\right\}$, then for any local non-inclusive distance vertex irregular labeling f of a graph G holds $f\left(u\right)\ne f\left(v\right)$.

Observation 3.

If there exists an edge $uv$ in a graph G such that $N_G\left(u\right)-\left\{v\right\}=N_G\left(v\right)-\left\{u\right\}$, then $\mathrm{lidis}\left(G\right)=\infty$.

The next theorem gives a sufficient and necessary condition for $\mathrm{lidis}\left(G\right)<\infty$. Note that the graph G is not necessarily connected.

Theorem 1.

For a graph G, it holds that $\mathrm{lidis}\left(G\right)=\infty$ if and only if there exists an edge $uv\in E\left(G\right)$ such that $N_G\left[u\right]=N_G\left[v\right]$.

Proof. 

If there exists an edge $uv\in E\left(G\right)$ such that $N_G\left[u\right]=N_G\left[v\right]$, then immediately follows Observation 3 and we obtain $\mathrm{lidis}\left(G\right)=\infty$. On the other hand, if $\mathrm{lidis}\left(G\right)=\infty$ then there exist at least two vertices u and v in G that have the same weight under any vertex labeling. It is only happened if $N_G\left[u\right]=N_G\left[v\right]$. □

Immediately from the previous theorem we obtain the following result.

Corollary 1.

If there exist two distinct vertices $u,v$ in G such that ${deg}_G\left(u\right)={deg}_G\left(v\right)=\left|V\left(G\right)\right|-1$, then $\mathrm{lidis}\left(G\right)=\infty$.

Thus, for complete graphs we obtain

Corollary 2.

Let n be a positive integer. Then

$$\mathrm{lidis}\left(K_n\right)=\left\{\begin{array}{cc}1,\hfill & \mathit{if}n=1,\hfill \\ \infty ,\hfill & \mathit{if}n\ge 2.\hfill \end{array}\right.$$

Now, we present a sufficient and necessary condition for $\mathrm{lidis}\left(G\right)=1$.

Theorem 2.

Let G be a graph. Then $\mathrm{lidis}\left(G\right)=1$ if and only if for every edge $uv\in E\left(G\right)$, $deg\left(u\right)\ne deg\left(v\right)$.

Proof. 

Consider a labeling that assigns number 1 to every vertex of a graph G. Under this labeling, the weight of any vertex v in G is $wt\left(v\right)={deg}_G\left(v\right)+1$. Thus, adjacent vertices can have distinct weights if and only if they have distinct degrees. □

The chromatic number of a graph G, denoted by $\chi \left(G\right)$, is the smallest number of colors needed to color the vertices of G so that no two adjacent vertices share the same color, see [1]. The following result gives a trivial lower bound for the number of distinct induced vertex weights under any local inclusive distance vertex irregular labeling of a graph G.

Theorem 3.

For a graph G, the number of distinct induced vertex weights under any local inclusive distance vertex irregular labeling is at least $\chi \left(G\right)$.

3. Local Inclusive Distance Vertex Irregularity Strength for Several Families of Graphs

In this section, we provide the exact values of local inclusive distance vertex irregularity strengths of some standard graphs such as paths, cycles, complete bipartite graphs, complete multipartite graphs, and caterpillars. We also give results on several products of graphs, such as corona graphs, union graphs, and join product graphs.

Theorem 4.

Let $C_n$ be a cycle on n vertices $n\ge 3$. Then

$$\mathrm{lidis}\left(C_n\right)=\left\{\begin{array}{cc}\infty ,\hfill & \mathit{if}n=3,\hfill \\ 2,\hfill & \mathit{if}n\mathit{is}\mathit{even},\hfill \\ 3,\hfill & \mathit{if}n\mathit{is}\mathit{odd},n\ge 5.\hfill \end{array}\right.$$

Proof. 

Let $V\left(C_n\right)=\{v_i:i=1,2,\cdots ,n\}$ be the vertex set and let $E\left(C_n\right)=\{v_i{v}_{i+1}:i=1,2,\cdots ,n-1\}\cup \left\{v_1{v}_n\right\}$ be the edge set of a cycle $C_n$. The lower bound for the local inclusive distance vertex irregularity strength of $C_n$ follows from Theorem 3 as

$$\chi \left(C_n\right)=\left\{\begin{array}{cc}3,\hfill & \mathrm{if}n\mathrm{is}\mathrm{odd},\hfill \\ 2,\hfill & \mathrm{if}n\mathrm{is}\mathrm{even}.\hfill \end{array}\right.$$

As $C_3$ is isomorphic to $K_3$ we use Corollary 2 in this case.

For n even, we label the vertices of $C_n$ as follows

$$\begin{array}{cc}\hfill f\left(v_i\right)=& \left\{\begin{array}{cc}1,\hfill & \mathrm{if}i\mathrm{is}\mathrm{odd},\hfill \\ 2,\hfill & \mathrm{if}i\mathrm{is}\mathrm{even}.\hfill \end{array}\right.\hfill \end{array}$$

Then, for the vertex weights we obtain

$$\begin{array}{cc}\hfill w{t}_f\left(v_i\right)=& \left\{\begin{array}{cc}5,\hfill & \mathrm{if}i\mathrm{is}\mathrm{odd},\hfill \\ 4,\hfill & \mathrm{if}i\mathrm{is}\mathrm{even}.\hfill \end{array}\right.\hfill \end{array}$$

Thus, for n even we obtain $\mathrm{lidis}\left(C_n\right)=2$.

For $n=5$, we label the vertices such that $f\left(v_1\right)=f\left(v_2\right)=1$, $f\left(v_3\right)=3$ and $f\left(v_4\right)=f\left(v_5\right)=2$. Then, $w{t}_f\left(v_1\right)=4$, $w{t}_f\left(v_2\right)=w{t}_f\left(v_5\right)=5$, $w{t}_f\left(v_3\right)=6$ and $w{t}_f\left(v_4\right)=7$. Thus, $\mathrm{lidis}\left(C_5\right)=3$.

For n odd, $n\ge 7$, the vertices are labeled in the following way

$$\begin{array}{cc}\hfill f\left(v_i\right)=& \left\{\begin{array}{cc}1,\hfill & \mathrm{if}i\mathrm{is}\mathrm{odd},1\le i\le n-4,\hfill \\ 2,\hfill & \mathrm{if}i\mathrm{is}\mathrm{even},2\le i\le n-3,\hfill \\ 3,\hfill & \mathrm{if}i=n-2,n-1,n.\hfill \end{array}\right.\hfill \end{array}$$

The weights of vertices are

$$\begin{array}{cc}\hfill w{t}_f\left(v_i\right)=& \left\{\begin{array}{cc}6,\hfill & \mathrm{if}i=1,n-3,\hfill \\ 5,\hfill & \mathrm{if}i\mathrm{is}\mathrm{odd},3\le i\le n-4,\hfill \\ 4,\hfill & \mathrm{if}i\mathrm{is}\mathrm{even},2\le i\le n-5,\hfill \\ 8,\hfill & \mathrm{if}i=n-2,\hfill \\ 9,\hfill & \mathrm{if}i=n-1,\hfill \\ 7,\hfill & \mathrm{if}i=n.\hfill \end{array}\right.\hfill \end{array}$$

As adjacent vertices have distinct weights we obtain $\mathrm{lidis}\left(C_n\right)=3$ for n odd. The above explanation concludes the proof. □

Corollary 3.

Let $P_n$ be a path on n vertices $n\ge 2$. Then

$$\mathrm{lidis}\left(P_n\right)=\left\{\begin{array}{cc}\infty ,\hfill & \mathit{if}n=2,\hfill \\ 2,\hfill & \mathit{if}n\ge 3.\hfill \end{array}\right.$$

Proof. 

Let $V\left(P_n\right)=\{v_i:i=1,2,\cdots ,n\}$ be the vertex set and let $E\left(P_n\right)=\{v_i{v}_{i+1}:i=1,2,\cdots ,n-1\}$ be the edge set of a path $P_n$. The result for $n=2$ follows from Corollary 2.

For $n\ge 3$, according to Theorem 3, the $\mathrm{lidis}\left(P_n\right)$ should be more than one. Using the vertex labels for n even as in Theorem 4 and the corresponding vertex weights are

$$\begin{array}{cc}\hfill w{t}_f\left(v_i\right)=& \left\{\begin{array}{cc}3,\hfill & \mathrm{if}i=1,n,\hfill \\ 4,\hfill & \mathrm{if}i\mathrm{is}\mathrm{even},i\ne n,\hfill \\ 5,\hfill & \mathrm{if}i\mathrm{is}\mathrm{odd},i\ne 1\mathrm{and}i\ne n.\hfill \end{array}\right.\hfill \end{array}$$

Thus, $\mathrm{lidis}\left(P_n\right)=2.$ □

The following result deals with complete multipartite graphs.

Theorem 5.

Let $K_{n_1,n_2,\cdots ,n_m}$ be a complete multipartite graph, $n_i\ge 1$, $i=1,2,\cdots ,m$, $m\ge 2$. Then,

$$\begin{array}{c}\hfill \mathrm{lidis}\left(K_{n_1,n_2,\cdots ,n_m}\right)=\left\{\begin{array}{cc}\infty ,\hfill & if1=n_1=n_2,\hfill \\ 1,\hfill & if{n}_1<n_2<\cdots <n_m,\hfill \\ m,\hfill & if2\le n_1=n_2=\cdots =n_m.\hfill \end{array}\right.\end{array}$$

Proof. 

Let us denote the vertices in the independent set $V_i$, $i=1,2,\cdots ,m$ of a complete multipartite graph $K_{n_1,n_2,\cdots ,n_m}$ by symbols $v_i^1,v_i^2,\cdots ,v_i^{n_i}$.

If $1=n_1=n_2$, then the vertices $v_1^1$ and $v_2^1$ have the same degrees

$$deg\left(v_1^1\right)=deg\left(v_2^1\right)=\sum _{j=3}^m{n}_j+1=\left|V\left(K_{n_1,n_2,\cdots ,n_m}\right)\right|-1$$

and thus, by Corollary 1 we obtain $\mathrm{lidis}\left(K_{n_1,n_2,\cdots ,n_m}\right)=\infty$.

If $n_1<n_2<\cdots <n_m$, then all adjacent vertices have distinct degrees. More precisely, the degree of a vertex $v_i^j$, $i=1,2,\cdots ,m$, $j=1,2,\cdots ,n_i$ is $deg\left(v_i^j\right)={\sum }_{j=1}^m{n}_j-n_i+1$. Thus, by Theorem 2, we obtain $\mathrm{lidis}\left(K_{n_1,n_2,\cdots ,n_m}\right)=1$.

If $2\le n_1=n_2=\cdots =n_m=n$ consider a vertex labeling f of $K_{n_1,n_2,\cdots ,n_m}$ defined such that

$$f\left(v_i^j\right)=i$$

for $i=1,2,\cdots ,m$, $j=1,2,\cdots ,n$ and the corresponding vertex weights are

$$w{t}_f\left(v_i^j\right)=\frac{nm(m+1)}{2}-(n-1)i.$$

Thus, all adjacent vertices have distinct weights. Thus, $\mathrm{lidis}\left(K_{n_1,n_2,\cdots ,n_m}\right)\le m$. Using mathematical induction, it is not complicated to show that $\mathrm{lidis}\left(K_{n_1,n_2,\cdots ,n_m}\right)\ge m$. This concludes the proof. □

The following corollary gives the exact value of the studied parameter for complete bipartite graphs.

Corollary 4.

Let $K_{m,n}$, $1\le m\le n$, be a complete bipartite graph. Then

$$\mathrm{lidis}\left(K_{m,n}\right)=\left\{\begin{array}{cc}\infty ,\hfill & \mathit{if}m=n=1,\hfill \\ 2,\hfill & \mathit{if}m=n\ge 2,\hfill \\ 1,\hfill & \mathit{if}m\ne n.\hfill \end{array}\right.$$

The corona product of G and H is the graph $G\odot H$ obtained by taking one copy of G, called the center graph along with $\left|V\right(G\left)\right|$ copies of H, called the outer graph, and making the ith vertex of G adjacent to every vertex of the ith copy of H, where $1\le i\le \left|V\right(G\left)\right|$. For arbitrary graphs G, we can prove the following result.

Theorem 6.

Let r be a positive integer. Then, for $r\ge 2$ holds

$$\mathrm{lidis}(G\odot \overline{K_r})\le \mathrm{lidis}\left(G\right).$$

Moreover, if G is a graph with no component of order 1 then also $\mathrm{lidis}(G\odot K_1)\le \mathrm{lidis}\left(G\right)$.

Proof. 

If $\mathrm{lidis}\left(G\right)=\infty$ then by Theorem 1 there exists at least one edge $uv\in E\left(G\right)$ such that $N_G\left[u\right]=N_G\left[v\right]$. However, as for $r\ge 2$ or for $r=1$ if G has no component of order 1, in $G\odot \overline{K_r}$ all vertices have distinct closed neighborhood and thus $\mathrm{lidis}(G\odot \overline{K_r})<\infty$.

Now, consider that $\mathrm{lidis}\left(G\right)<\infty$ and let f be a local inclusive distance vertex irregular labeling of G. We define a labeling g of $G\odot \overline{K_r}$ such that

$$\begin{array}{cccc}\hfill g\left(v\right)=& f\left(v\right),\hfill & \hfill & \mathrm{if}v\in V\left(G\right),\hfill \\ \hfill g\left(v\right)=& 1,\hfill & & \mathrm{if}{deg}_{G\odot \overline{K_r}}\left(v\right)=1.\hfill \end{array}$$

For the vertex weights, we obtain

$$\begin{array}{cccc}\hfill w{t}_g\left(v\right)=& w{t}_f\left(v\right)+r,\hfill & \hfill & \mathrm{if}v\in V\left(G\right),\hfill \\ \hfill w{t}_g\left(v\right)=& 1+f\left(u\right),\hfill & & \mathrm{if}{deg}_{G\odot \overline{K_r}}\left(v\right)=1\mathrm{and}uv\in E(G\odot \overline{K_r}).\hfill \end{array}$$

Evidently, for $r\ge 2$ or for $r=1$ if G has no component of order 1, i.e., ${deg}_G\left(v\right)\ge 1$ for every $v\in V\left(G\right)$, we obtain that under the labeling g the vertex weights of adjacent vertices are different. □

Moreover, we can prove that the parameter $\mathrm{lidis}(G\odot \overline{K_r})$ is finite except the case when $G\odot \overline{K_r}$ contains a component isomorphic to $K_2$.

Theorem 7.

Let r be a positive integer. Then,

$$\mathrm{lidis}(G\odot \overline{K_r})\le \left|V\left(G\right)\right|$$

except the case when $r=1$ and the graph G contains a component of order 1.

Proof. 

Let us denote the vertices of a graph G by symbols $v_1,v_2,\cdots ,v_{\left|V\right(G\left)\right|}$ such that for every $i=1,2,\cdots ,\left|V\right(G\left)\right|-1$ holds

$${deg}_G\left(v_i\right)\le {deg}_G\left(v_{i+1}\right)$$

and let $v_i^j$, $j=1,2,\cdots ,r$ be the vertices of degree 1 adjacent to $v_i$, $i=1,2,\cdots ,$$\left|V\right(G\left)\right|$, in $G\odot \overline{K_r}$. Now, we define a labeling f that assigns 1 to every vertex of G. Thus, for every $i=1,2,\cdots ,\left|V\right(G\left)\right|$

$$w{t}_f\left(v_i\right)={deg}_G\left(v_i\right)+1.$$

We extend the labeling f of the graph G to the labeling g of the graph $G\odot \overline{K_r}$ in the following way

$$\begin{array}{cccc}\hfill g\left(v_i\right)=& f\left(v_i\right),\hfill & \hfill & \mathrm{if}i=1,2,\cdots ,\left|V\right(G\left)\right|,\hfill \\ \hfill g\left(v_i^j\right)=& i,\hfill & & \mathrm{if}i=1,2,\cdots ,\left|V\right(G\left)\right|,j=1,2,\cdots ,r.\hfill \end{array}$$

The induced vertex weights are

$$\begin{array}{cccc}\hfill w{t}_g\left(v_i\right)=& {deg}_G\left(v_i\right)+1+ri,\hfill & \hfill & \mathrm{if}i=1,2,\cdots ,\left|V\right(G\left)\right|,\hfill \\ \hfill w{t}_g\left(v_i^j\right)=& 1+i,\hfill & & \mathrm{if}i=1,2,\cdots ,\left|V\right(G\left)\right|,j=1,2,\cdots ,r.\hfill \end{array}$$

For $r\ge 2$ and for $r=1$ if the graph G has no component of order 1, i.e., $deg\left(v_i\right)\ge 1$ for every $i=1,2,\cdots ,\left|V\right(G\left)\right|$, we obtain that all adjacent vertices have distinct weights. □

Note that the upper bound in the previous theorem is tight, since $\mathrm{lidis}(K_n\odot K_1)=n$. Immediately, from Theorem 2, we have the following result

Theorem 8.

For $r\ge 2$ it holds $\mathrm{lidis}(G\odot \overline{K_r})=1$ if and only if $\mathrm{lidis}\left(G\right)=1$.

Moreover, when G has no component of order 1 then $\mathrm{lidis}(G\odot \overline{K_1})=1$ if and only if $\mathrm{lidis}\left(G\right)=1$.

Now, we present results for corona product of paths, cycles, and complete graphs with totally disconnected graph $\overline{K_r}$, $r\ge 1$. Combining Theorems 3 and 6, we obtain

Theorem 9.

Let $P_n$ be a path on n vertices $n\ge 2$ and let r be a positive integer. Then

$$\mathrm{lidis}(P_n\odot \overline{K_r})=2.$$

Theorem 10.

Let $C_n$ be a cycle on n vertices $n\ge 3$ and let r be a positive integer. Then

$$\mathrm{lidis}(C_n\odot \overline{K_r})=\left\{\begin{array}{cc}3,\hfill & \mathit{if}n=3\mathit{and}r=1,\hfill \\ 2,\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

Proof. 

Let

$$V(C_n\odot \overline{K_r})=\{v_i:i=1,2,\cdots ,n\}\cup \{v_i^j:i=1,2,\cdots ,n;j=1,2,\cdots ,r\}$$

be the vertex set and let

$$\begin{array}{cc}\hfill E(C_n\odot \overline{K_r})=& \{v_i{v}_{i+1}:i=1,2,\cdots ,n-1\}\cup \left\{v_1{v}_n\right\}\hfill \\ & \cup \{v_i{v}_i^j:i=1,2,\cdots ,n;j=1,2,\cdots ,r\}\hfill \end{array}$$

be the edge set of $C_n\odot \overline{K_r}$.

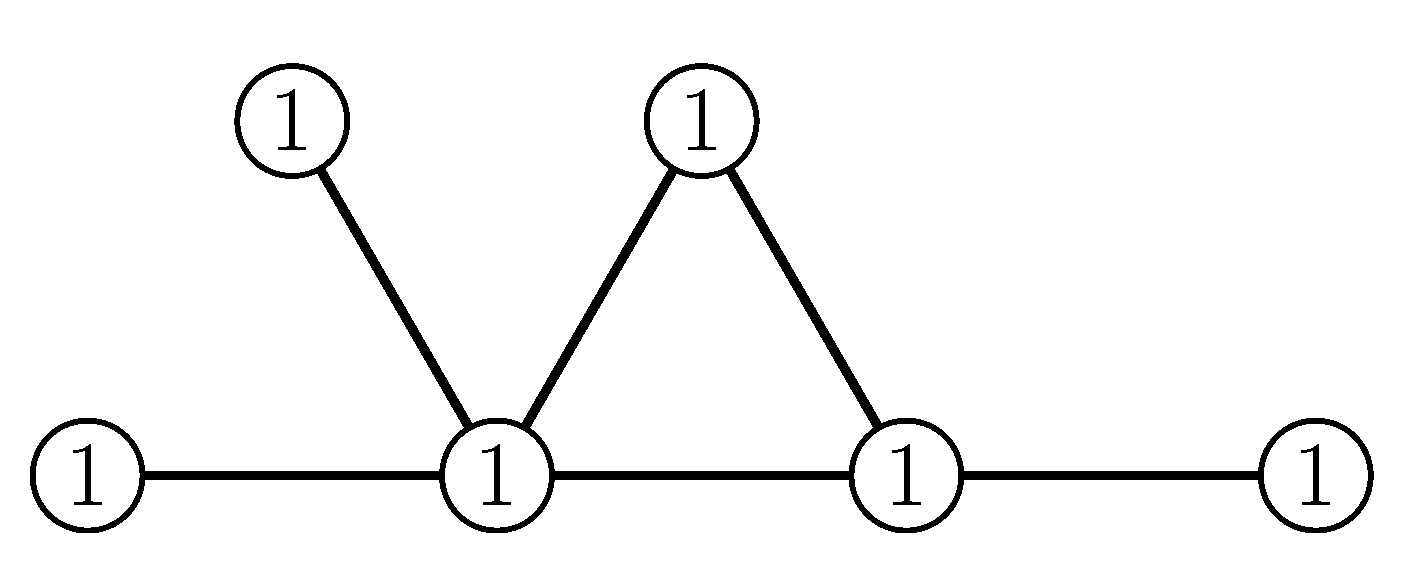
For even n the result follows from Theorems 4 and 6. For $n=3$ and $r=1$ consider the labeling illustrated on Figure 1.

For odd n and $(n,r)\ne (3,1)$, we define a vertex labeling f of $C_n\odot \overline{K_r}$ such that

$$\begin{array}{cc}\hfill f\left(v_i\right)=& \left\{\begin{array}{cc}2,\hfill & \mathrm{for}i=1,\hfill \\ 1,\hfill & \mathrm{for}i=2,3,\cdots ,n,\hfill \end{array}\right.\hfill \\ \hfill f\left(v_i^j\right)=& \left\{\begin{array}{cc}2,\hfill & \mathrm{for}i=2,4,\cdots ,n-1,n\mathrm{and}j=1,\hfill \\ 1,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\hfill \end{array}$$

The weights of vertices of degree $r+2$ are

$$\begin{array}{cc}\hfill w{t}_f\left(v_i\right)=& \left\{\begin{array}{cc}r+3,\hfill & \mathrm{for}i=3,5,\cdots ,n-2,\hfill \\ r+4,\hfill & \mathrm{for}i=1,4,6,\cdots ,n-1,\hfill \\ r+5,\hfill & \mathrm{for}i=2,n.\hfill \end{array}\right.\hfill \end{array}$$

As the weights of vertices of degree one are either 2 or 3, we obtain that adjacent vertices have distinct weights. □

Theorem 11.

Let $n,r$ be positive integers. Then

$$\mathrm{lidis}(K_n\odot \overline{K_r})=\left\{\begin{array}{cc}\infty ,\hfill & \mathit{if}n=1,r=1,\hfill \\ 1+⌈\frac{n-1}{r}⌉,\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

Proof. 

As the graph $K_1\odot \overline{K_1}$ is isomorphic to the complete graph $K_2$ we use Corollary 2 in this case.

Let $(n,r)\ne (1,1)$. Let the vertex set and the edge set of $K_n\odot \overline{K_r}$ be the following

$$\begin{array}{cc}\hfill V(K_n\odot \overline{K_r})=& \{v_i,v_i^j:i=1,2,\cdots ,n;j=1,2,\cdots ,r\},\hfill \\ \hfill E(K_n\odot \overline{K_r})=& \{v_i{v}_j:i=1,2,\cdots ,n-1;j=i+1,i+2,\cdots ,n\}\hfill \\ \hfill & \cup \{v_i{v}_i^j:i=1,2,\cdots ,n;j=1,2,\cdots ,r\}.\hfill \end{array}$$

We define a vertex labeling f of $K_n\odot \overline{K_r}$ such that

$$\begin{array}{cc}\hfill f\left(v_i\right)=& 1+⌈\frac{n-1}{r}⌉,\mathrm{if}i=1,2,\cdots ,n,\hfill \\ \hfill f\left(v_i^j\right)=& \left\{\begin{array}{cc}1+⌈\frac{i-1}{r}⌉,\hfill & \mathrm{if}i=1,2,\cdots ,n,j=1,2,\cdots ,A_i,\hfill \\ 1+⌊\frac{i-1}{r}⌋,\hfill & \mathrm{if}i=1,2,\cdots ,n,j=A_i+1,A_i+2,\cdots ,r,\hfill \end{array}\right.\hfill \end{array}$$

where for every $i=1,2,\cdots ,n$ the parameter $A_i$, $1\le A_i\le r$, is defined such that

$$i-1\equiv A_i(modr).$$

For the vertex weights, we obtain

$$\begin{array}{cc}\hfill w{t}_f\left(v_i\right)=& n(1+⌈\frac{n-1}{r}⌉)+r+i-1,\mathrm{if}i=1,2,\cdots ,n,\hfill \\ \hfill w{t}_f\left(v_i^j\right)=& \left\{\begin{array}{cc}⌈\frac{n-1}{r}⌉+2+⌈\frac{i-1}{r}⌉,\hfill & \mathrm{if}i=1,2,\cdots ,n,j=1,2,\cdots ,A_i,\hfill \\ ⌈\frac{n-1}{r}⌉+2+⌊\frac{i-1}{r}⌋,\hfill & \mathrm{if}i=1,2,\cdots ,n,j=A_i+1,A_i+2,\cdots ,r.\hfill \end{array}\right.\hfill \end{array}$$

Evidently adjacent vertices have distinct weights. Thus, as the maximal vertex label is $1+⌈\left(n-1\right)/r⌉$, the proof is completed. □

A caterpillar is a graph derived from a path by hanging any number of leaves from the vertices of the path. We denote the caterpillar as $S_{n_1,n_2,\cdots ,n_r}$, where the vertex set is $V\left(S_{n_1,n_2,\cdots ,n_r}\right)$ = $\{c_i:1\le i\le r\}\cup {\bigcup }_{i=1}^r\{u_i^j:1\le j\le n_i\}$, and the edge set is $E\left(S_{n_1,n_2,\cdots n_r}\right)=\{c_i{c}_{i+1}:1\le i\le r-1\}\cup {\bigcup }_{i=1}^r\{c_i{u}_i^j:1\le j\le n_i\}$.

Theorem 12.

For every caterpillar $S_{n_1,n_2,\cdots ,n_r}$ with at least 3 vertices holds $\mathrm{lidis}\left(S_{n_1,n_2,\cdots ,n_r}\right)\le 2$.

Proof. 

For a regular caterpillar, thus the case $n_1=n_2=\dots =n_r=n$, using Theorem 9, we obtain that $\mathrm{lidis}\left(S_{n,n,\cdots ,n}\right)=2$.

For the other cases, label the vertices of a caterpillar $S_{n_1,n_2,\cdots ,n_r}$ using the following algorithm.

Step 1:

Label all vertices with 1.

Then the weights of vertices $c_i$, $i=1,2,\cdots ,r$ are $deg\left(c_i\right)$ and all vertices of degree 1 have weight 2.

Step 2:

Find the smallest index s, $2\le s\le r-1$, such that $wt\left(c_{s+1}\right)=wt\left(c_s\right)$.

Step 3:

If such number does not exist, it means that adjacent vertices have distinct degrees and thus $\mathrm{lidis}\left(S_{n_1,n_2,\cdots ,n_r}\right)=1$. We are done.

Step 4:

If such number exists either relabel a leaf of adjacent to $c_{s+1}$ (if a leaf exists) from 1 to 2 or relabel the vertex $c_{s+2}$ from 1 to 2. Then $wt\left(c_{s+1}\right)=wt\left(c_s\right)+1$.

Note that this relabeling will not have an effect on weights of vertices $c_i$ for every $i\le s$.

Step 5:

Find the smallest index t, $s+1\le t\le r-1$, such that $wt\left(c_{t+1}\right)=wt\left(c_t\right)$.

Step 6:

If such number does not exist, it means that adjacent vertices have distinct degrees and thus $\mathrm{lidis}\left(S_{n_1,n_2,\cdots ,n_r}\right)=2$. We are finished.

Step 7:

If such number exists either relabel a leaf of adjacent to $c_{t+1}$ (if a leaf exists) from 1 to 2 or relabel the vertex $c_{t+2}$ from 1 to 2. Then $wt\left(c_{s+1}\right)=wt\left(c_t\right)+1$.

Step 8:

Return to Step 5.

After a finite number of steps, the algorithm stops and the weights of the vertices are always different from the weights of their neighbors. □

A similar algorithm can be used to obtain a result for closed caterpillars, which are graphs where the removal of all pendant vertices gives a cycle. We denote the closed caterpillar as $C{S}_{n_1,n_2,\cdots ,n_r}$, where the vertex set is $V\left(C{S}_{n_1,n_2,\cdots ,n_r}\right)$ = $\{c_i:1\le i\le r\}\cup {\bigcup }_{i=1}^r\{u_i^j:1\le j\le n_i\}$, and the edge set is $E\left(C{S}_{n_1,n_2,\cdots n_r}\right)=\{c_i{c}_{i+1}:1\le i\le r-1\}\cup \left\{c_1{c}_r\right\}\cup {\bigcup }_{i=1}^r\{c_i{u}_i^j:1\le j\le n_i\}$.

Theorem 13.

For closed caterpillar $C{S}_{n_1,n_2,\cdots ,n_r}$ holds

$$\begin{array}{cc}\hfill \mathrm{lidis}\left(C{S}_{n_1,n_2,\cdots ,n_r}\right)& =\left\{\begin{array}{cc}\infty ,\hfill & \mathit{if}r=3\mathit{and}\{n_1,n_2,n_3\}=\{n,0,0\},\mathit{where}n\ge 0,\hfill \\ 3,\hfill & \mathit{if}r=3\mathit{and}(n_1,n_2,n_3)=(1,1,1),\hfill \\ 3,\hfill & \mathit{if}r=3+6k,k\ge 1\mathit{and}\{n_1,n_2,\cdots ,n_r\}=\{1,0,\cdots ,0\},\hfill \\ \le 2,\hfill & \mathit{otherwise}.\hfill \end{array}\right.\hfill \end{array}$$

The proof of the next result for the disjoint union of graphs, follows from the fact that there are no edges between the distinct components.

Theorem 14.

Let $G_i$, $i=1,2,\cdots ,m$ be arbitrary graphs. Then

$$\mathrm{lidis}\left(\bigcup _{i=1}^m{G}_i\right)=max\{\mathrm{lidis}\left(G_i\right):i=1,2,\cdots ,m\}.$$

Immediately from the previous theorem, we obtain the following result.

Corollary 5.

Let n be a non-negative integer and let G be a graph. Then, $\mathrm{lidis}\left(G\cup n{K}_1\right)=\mathrm{lidis}\left(G\right)$.

The join $G\oplus H$ of the disjoint graphs G and H is the graph $G\cup H$ together with all the edges joining vertices of $V\left(G\right)$ and vertices of $V\left(H\right)$. Let $\Delta \left(G\right)$ denote the maximal degree of the graph G.

Theorem 15.

For any graph G holds

$$\begin{array}{c}\hfill \mathrm{lidis}(G\oplus K_1)=\left\{\begin{array}{cc}\infty ,\hfill & \mathit{if}\Delta \left(G\right)=\left|V\right(G\left)\right|-1,\hfill \\ \mathrm{lidis}\left(G\right),\hfill & \mathit{if}\Delta \left(G\right)<\left|V\right(G\left)\right|-1.\hfill \end{array}\right.\end{array}$$

Proof. 

Let w be the vertex of $K_1$. In a graph $G\oplus K_1$ the vertex w is adjacent to all vertices in G we immediately get that $\mathrm{lidis}(G\oplus K_1)\ge \mathrm{lidis}\left(G\right)$.

If $\Delta \left(G\right)=\left|V\right(G\left)\right|-1$ then in $G\oplus K_1$ there are at least two vertices of degree $\left|V\left(G\right)\right|=|V(G\oplus K_1)|-1$ and thus by Corollary 1 we have $\mathrm{lidis}(G\oplus K_1)=\infty$.

Let $\Delta \left(G\right)<\left|V\right(G\left)\right|-1$. If $\mathrm{lidis}\left(G\right)=\infty$ then by Theorem 1 there exists at least two vertices, say u and v in G such that $N_G\left[u\right]=N_G\left[v\right]$. However, these vertices have the same closed neighborhood also in the graph $G\oplus K_1$ as

$$N_{G\oplus K_1}\left[u\right]=N_G\left[u\right]\cup \left\{w\right\}=N_G\left[v\right]\cup \left\{w\right\}=N_{G\oplus K_1}\left[v\right].$$

However, this implies that

$$\mathrm{lidis}(G\oplus K_1)=\infty =\mathrm{lidis}\left(G\right).$$

Now, consider that $\mathrm{lidis}\left(G\right)<\infty$ and let f be a corresponding local inclusive distance vertex irregular graph of G. We define a labeling g of $G\oplus K_1$ in the following way

$$\begin{array}{c}\hfill g\left(v\right)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}v=w,\hfill \\ f\left(v\right),\hfill & \mathrm{if}v\in V\left(G\right).\hfill \end{array}\right.\end{array}$$

The induced vertex weights are

$$\begin{array}{c}\hfill w{t}_g\left(v\right)=\left\{\begin{array}{cc}{\displaystyle \sum _{u\in V\left(G\right)}}f\left(u\right)+1,\hfill & \mathrm{if}v=w,\hfill \\ w{t}_f\left(v\right)+1,\hfill & \mathrm{if}v\in V\left(G\right).\hfill \end{array}\right.\end{array}$$

As $\Delta \left(G\right)<\left|V\right(G\left)\right|-1$ we get that for any vertex $v\in V\left(G\right)$ is

$$w{t}_f\left(v\right)=\sum _{u\in N_G\left(v\right)}f\left(u\right)<\sum _{u\in V\left(G\right)}f\left(u\right).$$

Thus, all adjacent vertices have distinct weights. This means that g is a local inclusive distance vertex irregular labeling of $G\oplus K_1$. As vertex w is adjacent to every vertex in G we get $\mathrm{lidis}(G\oplus K_1)=\mathrm{lidis}\left(G\right)$ in this case. This concludes the proof. □

The graph in the previous theorem is not necessarily connected.

Theorem 16.

Let $G_i$, $i=1,2,\cdots ,m$, $m\ge 2$ be arbitrary graphs. Then

$$\mathrm{lidis}\left(\left(\bigcup _{i=1}^m{G}_i\right)\oplus K_1\right)=max\{\mathrm{lidis}\left(G_i\right):i=1,2,\cdots ,m\}.$$

Proof. 

The proof follows from Theorems 14 and 15. □

A wheel $W_n$ with n spokes is isomorphic to the graph $C_n\oplus K_1$. A fan graph $F_n$ is isomorphic to the graph $P_n\oplus K_1$, while a generalized fan graph is isomorphic to the graph $k{P}_n\oplus K_1$. The following results are immediate corollaries of the previous theorems.

Corollary 6.

Let $W_n$ be a wheel on $n+1$ vertices $n\ge 3$. Then

$$\mathrm{lidis}\left(W_n\right)=\left\{\begin{array}{cc}\infty ,\hfill & \mathit{if}n=3,\hfill \\ 2,\hfill & \mathit{if}n\mathit{is}\mathit{even},\hfill \\ 3,\hfill & \mathit{if}n\mathit{is}\mathit{odd},n\ge 5.\hfill \end{array}\right.$$

Corollary 7.

Let $F_n$ be a fan on $n+1$ vertices $n\ge 2$. Then

$$\mathrm{lidis}\left(F_n\right)=\left\{\begin{array}{cc}\infty ,\hfill & \mathit{if}n=2,\hfill \\ 2,\hfill & \mathit{if}n\ge 3.\hfill \end{array}\right.$$

Corollary 8.

Let $k{P}_n\oplus K_1$ be a generalized fan graph, $k,n\ge 2$. Then

$$\mathrm{lidis}(k{P}_n\oplus K_1)=2.$$

If $\mathrm{lidis}\left(G\right)=\infty$ then by Theorem 1 there exist at least two vertices, say u and v in G such that they have the same closed neighborhood $N_G\left[u\right]=N_G\left[v\right]$. Thus, we immediately get

$$\begin{array}{cc}\hfill N_{G\oplus \overline{K_r}}\left[u\right]=& N_G\left[u\right]\cup \{w_i:i=1,2,\cdots ,r\}\hfill \\ \hfill =& N_G\left[v\right]\cup \{w_i:i=1,2,\cdots ,r\}=N_{G\oplus \overline{K_r}}\left[v\right],\hfill \end{array}$$

where $w_i$, $i=1,2,\cdots ,r$, are the vertices of $\overline{K_r}$. Thus, $\mathrm{lidis}(G\oplus \overline{K_r})=\infty$ for every positive integer r. Now we will deal with the case when $\mathrm{lidis}\left(G\right)<\infty$ and $r\ge 2$.

Theorem 17.

Let $r\ge 2$ be a positive integer and let G be not isomorphic to a totally disconnected graph. If $\mathrm{lidis}\left(G\right)<\infty$ and $r\ge \left|V\right(G\left)\right|·\mathrm{lidis}\left(G\right)$ then $\mathrm{lidis}(G\oplus \overline{K_r})=\mathrm{lidis}\left(G\right)$.

Proof. 

Let us denote the vertices $\overline{K_r}$ by the symbols $w_i$, $i=1,2,\cdots ,r$ and let $r\ge 2$. Thus, $V(G\oplus \overline{K_r})=V\left(G\right)\cup \{w_i:i=1,2,\cdots ,r\}$. In a graph $G\oplus \overline{K_r}$ all the vertices $w_i$, $i=1,2,\cdots ,r$ are adjacent to all vertices in G thus we immediately get that $\mathrm{lidis}(G\oplus \overline{K_r})\ge \mathrm{lidis}\left(G\right)$.

Let $\mathrm{lidis}\left(G\right)<\infty$ and let f be a corresponding local inclusive distance vertex irregular labeling of G. We define a labeling g of $G\oplus \overline{K_r}$ in the following way

$$\begin{array}{c}\hfill g\left(v\right)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}v=w_i,i=1,2,\cdots ,r,\hfill \\ f\left(v\right),\hfill & \mathrm{if}v\in V\left(G\right).\hfill \end{array}\right.\end{array}$$

Then, the vertex weights are

$$\begin{array}{c}\hfill w{t}_g\left(v\right)=\left\{\begin{array}{cc}{\displaystyle \sum _{u\in V\left(G\right)}}f\left(u\right)+1,\hfill & \mathrm{if}v=w_i,i=1,2,\cdots ,r,\hfill \\ w{t}_f\left(v\right)+r,\hfill & \mathrm{if}v\in V\left(G\right).\hfill \end{array}\right.\end{array}$$

Evidently, under the labeling g, all adjacent vertices in $V\left(G\right)$ have distinct weights. We need also to prove that no vertex in $V\left(G\right)$ has the same weight as in $V\left(\overline{K_r}\right)$. Consider that

$$r\ge \left|V\right(G\left)\right|·\mathrm{lidis}\left(G\right).$$

As G is not isomorphic to a totally disconnected graph then for the weight of any vertex v in $V\left(G\right)$ we have

$$\begin{array}{cc}\hfill w{t}_g\left(v\right)=& w{t}_f\left(v\right)+r\ge 1+\left|V\left(G\right)\right|·\mathrm{lidis}\left(G\right)>1+\sum _{u\in V\left(G\right)}f\left(u\right)=w{t}_g\left(w_i\right)\hfill \end{array}$$

for every $i=1,2,\cdots ,r$. Thus, g is a local inclusive distance vertex irregular graph of $G\oplus \overline{K_r}$ and hence $\mathrm{lidis}(G\oplus \overline{K_r})\le \mathrm{lidis}\left(G\right)$. □

Note that for small r the previous theorem is not necessarily true. Consider the graph G illustrated on Figure 2, evidently $\mathrm{lidis}\left(G\right)=1$. However, $\mathrm{lidis}(G\oplus \overline{K_3})=2$.

4. Conclusions

In this paper, we introduced the local inclusive distance vertex irregularity strength of graphs and gave some basic results and also some constructions of the feasible labelings for several families of graphs. We still have some open problems and conjecture as follows:

Problem 1.

Find $\mathrm{lidis}\left(K_{n_1,n_2,\cdots ,n_m}\right)$ for general case, which is for the case $n_1\le n_2\le \cdots \le n_m$, where $m>2$.

Problem 2.

Characterize graphs for which $\mathrm{lidis}(G\odot \overline{K_r})=\mathrm{lidis}\left(G\right)$.

Conjecture 1.

For arbitrary tree T with $T\ne K_2$, $\mathrm{lidis}\left(T\right)=1$ or 2.