Cognitive Conflict in Technological Environment: Cognitive Process and Emotions through Intuitive Errors in Area, Perimeter and Volume

Abstract

This study was conducted among 28 seventh-grade students. They worked in groups in an activity with modeling features; the activity consisted of three tasks dealing with an intuitive error, namely, same A–same B. The data source was nine video recordings of three groups across the three activities. The results obtained from analyses of students’ discussions and interactions indicate that they moved through three central stages: the intuitive error stage, the revealing of the intuitive error connected with cognitive conflict and the stage of overcoming the intuitive errors. In each of the three stages in the three tasks, we identified similar emotion features among the three groups across the three tasks. In the intuitive error stage, the participants were characterized by confidence, comfort and enjoyment. In revealing the intuitive errors, we identified several indicators and signs of non-comfortable situations by revealing the errors in the three tasks, such as a high sound or sad tone of voice, physical movements such as moving closer to the computer screen and other physical indicators such as opening the mouth and putting a hand on the head or the face. After overcoming and understanding the sources of the errors, the participants showed confidence that was clear in their facial signs, joy and smiles, loud tone and eye contact between students and the teacher, or between students.

1. Introduction

Making mistakes is considered as one element in the learning process, and some mistakes and errors are affected by the intuitive thinking of students. According to intuitive theory, formwork addressed that students’ conceptions and reasoning processes in solving mathematical tasks are affected by three intuitive rules [1], which we will elaborate on later. Exploring students’ cognitive process underlying the impact of intuitive rules could contribute to designing an effective environment to support students in overcoming their intuitive interference [2]. Overcoming intuitive errors connected with conceptual change occurs through a conflict between the exciting knowledge and the new knowledge [3]. However, some researchers hesitated in the process of change due to the emotions that combined with it. For example, Dreyfus et al. [4] found that conflict makes unsuccessful students feel endangered and worried, and that they attempt to avoid it. In order to be aware of learners through these processes, we need to know more about emotions that combine the conflict process and conceptual change.

The emotion and cognition relationship is examined in mathematics in a different context (e.g., [5,6,7]). The connection is emphasized by different researchers. For example, Izard and Ackerman [8] declared that emotions are the cornerstone of human behavior, stimulating human activity in general and mathematical activity in particular. Additionally, Op’ t Eynde et al. [9] considered emotions as a part of students’ solution to mathematical problems, as they determine the cognitive strategies used by students and influence their motivation. Emotions change during mathematics learning and differ from context to context as they affect and are affected during students’ learning about mathematics [10], specifically, in critical points such as when learners have a conflict between their existing knowledge and new knowledge.

In the current study, we followed students’ cognitive process and their emotions during cognitive conflict. We used the context of area and volume. We used technology-rich learning environments. Technology plays an increasingly important role in 21st century education, and the emotions learners experience in these environments are pivotal for their cognitive and affective learning gains [11]. Moreover, understanding emotions in technology-based learning environments has become a vital goal across different research communities [12].

2. Theoretical Background

This section will present the first review about intuitive reasoning and rules, cognitive conflict and emotions among learning and technology in teaching mathematics.

2.1. Intuitive Errors

Epstein [13] indicated there is considerable disagreement about whether feelings are an essential aspect of intuition. Due to that, among many definitions of intuition, many definitions are entirely cognitive and do not include emotions or feelings. In contrast, other definitions emphasize feelings as an essential aspect of intuition. For that, Epstein [13] chose to define intuition as follows: “Intuition involves a sense of knowing without knowing how one knows”, and “Intuition involves a sense of knowing based on unconscious information processing” (p. 296). Fischbein [14] indicated several significant characteristics of intuitive reasoning: immediate, self-evident characteristics, that is, they are obtained without a sense of justification of their correctness, and they are accompanied by a sense of security and deep inner conviction—no formal or empirical proof required; obsessive-compulsive disorder characteristics—they force themselves on the way of thinking in choosing hypotheses and solutions; diffusion (expansion) characteristics—beyond empirical vision, and even if the situation is not empirically proven, they have global attributes.

Intuitive rules theory addresses intuitive rules that individuals develop in themselves that impact their solutions to an extensive range of topics in science and mathematics [15]. Stavy and Tirosh [1] found that students tend to react according to three intuitive rules: more A–more B; same A–same B; and everything can be divided. In the current study, we focused on the same A–same B rule, which is defined as follows: “When students are presented with comparison tasks in which two objects are equal in a certain quantity (A1 = A2) but differ in another quantity (B1 is not equal to B2), they often claim that B1 = B2 because A1 = A2” [16] (p. 422).

Intuitive rules related to the concepts of area, perimeter and volume were examined among several studies (e.g., [17,18]). In two different studies, [17,19] found that students claimed that the same perimeters must have the same area and vice versa. In presenting the situation where one side in a square is lengthened and the other is shortened by the same amount, the students claimed that the perimeter and area of the created rectangle are equal to the perimeter and area of the original square. Tirosh and Stavy [18] reported that almost all students from grades five to nine incorrectly claimed that if the surface area of two cylinders (made from rotating the same rectangle and folding) is equal, they are equal.

2.2. Cognitive Conflict

Cognitive conflict can be defined as an imbalance created when the new knowledge contradicts the existing knowledge [20]. Cognitive conflict is related to the learning process that Piaget [21] described as assimilation-disequilibrium-accommodation when the learner fails to assimilate (conflicting) the new knowledge into the cognitive schemas they have acquired. A mental inequality is created that motivates the learner to accommodate existing agreements to fit the new knowledge.

Cognitive conflict is considered a teaching tool that attempts to help students overcome their existing misconceptions and perceptual change to mathematical topics and concepts [22]. Waston [23] used cognitive conflict as a tool for teaching an average subject. Furthermore, it is considered an effective tool for perceptual change in decimal numbers [24,25]. Yuwono and Sumadji [26] examined the application of cognitive conflict strategies carried out by lecturers among low-ability students in trigonometry courses. In applying cognitive conflict strategies, their mistakes were shown, and then the teachers acted against them with at least one example of denial. They reported that the strategy effectively overcame students’ thinking difficulties with a high level of effectiveness. Cognitive conflict has also been proposed to support learning the proof [27]. Many empirical findings highlight the ineffectiveness of cognitive conflict in conceptual changing [28,29]. Therefore, different recommendations were highlighted to streamline cognitive conflict, recommending that students must be actively involved while applying the prior knowledge they acquired and have some epistemological beliefs and reasoning ability to apply them, and the activity they learned must be exciting and preventative for them [30,31]. Other recommendations emphasized the importance of confrontation between students so that social interaction and argumentation were elevated to the process of perceptual change [32,33].

Shahbari and Peled [3] examined the realization of changing reference infractions; they reported conceptual change and a better understanding of changing reference among sixth-grade students in the experimental group who engaged in an activity based on modeling and realistic mathematics education principles.

2.3. Emotions among Learning

As an essential theoretical basis for our study, we used Philip’s [34] definition of emotions:

[Emotions are] feelings or states of consciousness, distinguished from cognition. Emotions change more rapidly and are felt more intensely than attitudes and beliefs. Emotions may be positive (e.g., the feeling of “aha”) or negative (e.g., the feeling of panic). Emotions are less cognitive than attitudes [34] (p. 259).

Emotions are the cornerstone of human behavior, as they stimulate human activity in general and mathematical activity in particular [8]. Emotions are the system of states that the student experiences when exposed to situations that require sufficient skill to solve them, as they are related to ideas and behavior [35]. The emotional aspect is considered one of the most critical factors affecting the teaching process in learning mathematics. Our feelings are the basis for our actions and our behavior, as they are a catalyst for human activity [8].

The affective state of the student influences their mathematical performance. Pekrun et al. [36] stated that the literature points at positive affective states as assisting general, flexible and creative ways of solving problems. However, negative states assist and encourage more inflexible and analytical thinking methods. Pekrun et al. [37] reported that positive and negative emotions positively and negatively predicted success achievement. Additionally, Lehman et al. [38] indicated that students with little or no anxiety scored higher than students with some or high anxiety. Additionally, Ashcraft and Faust [39] reported, in their study, that the least anxious students were always the fastest and most accurate in completing mental computational tasks, while the most anxious students were slower and most vulnerable to errors.

Emotions and thinking are not separate entities; they are fused—people cannot think without emotions [40]. Moreover, students’ ideas, emotions and actions are shaped by interactional practices’ dynamic [35]. Amran and Bakar [41] found that there is a correlation between positive emotion and memory in learning mathematics. In particular, they indicated that students who are more likely to prefer positive emotions in learning mathematics could have a better memory compared to those with negative emotions. Similarly, Di Leo and her colleagues [42] indicated that positive emotions, such as enjoyment, can facilitate the learning process more than negative emotions, such as frustration. Daher, Swidan and Shahbari [43] reported that students’ positive emotions and positions will be cultivated through collaborative work with a technological tool.

Emotions sometimes apparent as facial expressions and body language, but part of their nature is the unobservable individual experience [44]. For example, indicators for “worry” can be observed by different body actions such as biting or tapping the fingers, or touching and holding the nose [45]. Indicators of excitement can observe as speaking faster, making eye contact, gleeful wiggling of legs [41]. Indicators of surprise can observe as an arched appearance of the shape of the eyebrows or raising the upper eyelids [46].

2.4. Technology in Teaching Mathematics

Technology is used more widely in the classroom. Smaldino and colleagues’ [47] study showed that technology enhances the teaching process and enables students to learn more effectively in predominantly specialized classes, making learning more enjoyable and more attractive to students, as indicated by the results of the study. They concluded that in integrated learning environments, students and teachers benefit from technology. The use of technology enhances students’ learning capabilities and stimulates them more than traditional learning methods, and thus students are more focused on the educational process [48].

Technology can be effective at the level of software, such as the use of dynamic features in GeoGebra or design software such as Scratch, and at the level of data representation, with features such as those in Excel [49]. The use of dynamic software, such as GeoGebra, provides students with an interactive learning environment, allowing them to investigate and validate mathematical hypotheses and solutions [50]. For that, GeoGebra can support students through problem solving [51].

3. Research Goal and Questions

The current research examined the cognitive processes and students’ accompanying feelings during intuitive errors, revealing and overcoming them.

Research questions:

• What are the characteristics of the cognitive processes that appear when students interact with activities in a technological environment related to intuitive errors?
• What are the students’ emotions’ characteristics during the emergence and overcoming of the intuitive errors in a technological environment?

4. Method

4.1. Participants

This study was conducted among 28 seventh-grade students. They were considered middle achievement students according to their mathematics teacher. They worked in groups of 4–5 students each. According to their desire, their distribution into groups promoted more accessible discussions and interactions with each other.

4.2. Procedure

The students were required to fill out the first questionnaire, and then they worked in the same group on three tasks included in the chocolate molds activity that we will present in the next section. Each task was presented during one lesson (45 min), with one lesson per week. Overall, the tasks were presented over three weeks. After one month from engaging in the third task, the students were required to answer the second questionnaire.

4.3. The Chocolate Molds Activity

This activity discusses the intuitive errors related to the intuitive role of same A–same B in areas and volumes. The author designed the activity, and the first task and the third task were developed based on another advanced version of tasks presented by Stavy et al. [16], and Tsamir [15], respectively.

4.3.1. Activity Context

The Chocolate Factory, which manufactures chocolate, is considered one of the most important and famous factories in chocolate production. Its products are known for their high cocoa content and quality. In addition to the concern for its products’ taste, the factory relies on a permanent change in its shapes. It constantly renews the molds used for pouring chocolate to produce new products that attract consumers.

Adopting new molds puts factory workers in confusion about the price of the products—that is, whether they should hold the same amount of chocolate or differ.

The factory’s workers required advice about the capacity of some molds which they performed some procedures on.

4.3.2. Task 1

Foldable rectangular molds were bought. The rectangle will be folded in two ways, once linear and once in width (after rotating). After the molds are produced, they will be filled with chocolate. Will the two molds accommodate the same amount?

4.3.3. Task 2

Candy ropes are used as a frame to surround the chocolate. Different frames are all rectangular from the same candy rope. Inside each frame, chocolate cubes are added in a stack (from one layer only). Do all the frames need the same number of chocolate cubes?

4.3.4. Task 3

Some change will be made to the cube template so that four sides (the two parallel sides from the top and the two parallel sides from the bottom) are enlarged by a quarter, and another four sides are reduced (the two parallel sides from the side and the two opposite sides) by a quarter (see figure). Will the resulting object contain the same amount of chocolate and the same amount of chocolate drink?

4.4. Data Sources

The data sources were collected from video recordings. Three groups of the study sample were recorded through video and audio during the three tasks performed in the math lessons. That means we depended on nine video recordings, each one 45 min in length.

4.5. Data Analyses

The observations were analyzed in two stages. In each stage, a different theory was used. In the first stage, we analyzed the cognitive processes according to grounded theory [52] and considered the cognitive stages as presented in Shahbari and Peled [3]. The stages of students’ resolution were traced before, during and after the cognitive conflict. The second stage analyzed the students’ emotions according to the historical-cultural theory of Radford [40]. This theory examines the students’ emotions by analyzing their expressive physical gestures and signals and the various verbal symbols during the learning process.

Table 1. Examples of analyses of the participants’ emotions.

Category	Examples of Sub-Categories	Examples from Participant Discussions and Behaviors
Positive emotions	Confidence	Shaking head as accepting
	Enjoyment	Specific words such as “OHH”, “YEAH”
	Comfort	Relaxed tone of voice Smiling
Negative emotions	Confusion	Putting a hand on the head or the face
	Non-comfortable	Loud voice or sad tone of voice

exemplifies the analysis process of the participants’ emotions.

5. Finding

We identified three intuitive mistakes among almost all of the students in the three groups. In each task, we identified three main phases, the error phase, the occurrence of cognitive conflict and overcoming the errors. Each phase is accompanied by different emotions. We present the cognitive process and emotions process combined in each phase with examples from students’ discussions.

5.1. Cognitive and Emotion Processes during the Intuitive Error in the Three Tasks

We identified that students worked according to the intuitive role in the three tasks, same A–same B. In the cylinder tasks, students claimed that the same surface is the same volume. All groups agreed that the volume of the cylinders is equal (the amount of chocolate in the two cylinders is equal); that is, because the dimensions are the same (the rectangle), the volume will be equal (as shown in Episode 1). The same occurred in the second task, where students claimed that the same circumference is the same area. There was consensus among the students in the three groups that the number of chocolate cups is equal because of the same rope of candy (see Episode 2). Additionally, students claimed that if the four sides extended by a quarter, and the other four sides shrunk by a quarter, the volume would be the same in the original cup and the new box. Participants in the three groups indicated that the amount of the chocolate would be equal in the two cups and the box, as presented in Episode 3.

Episode 1: The intuitive error, same area–same volume:

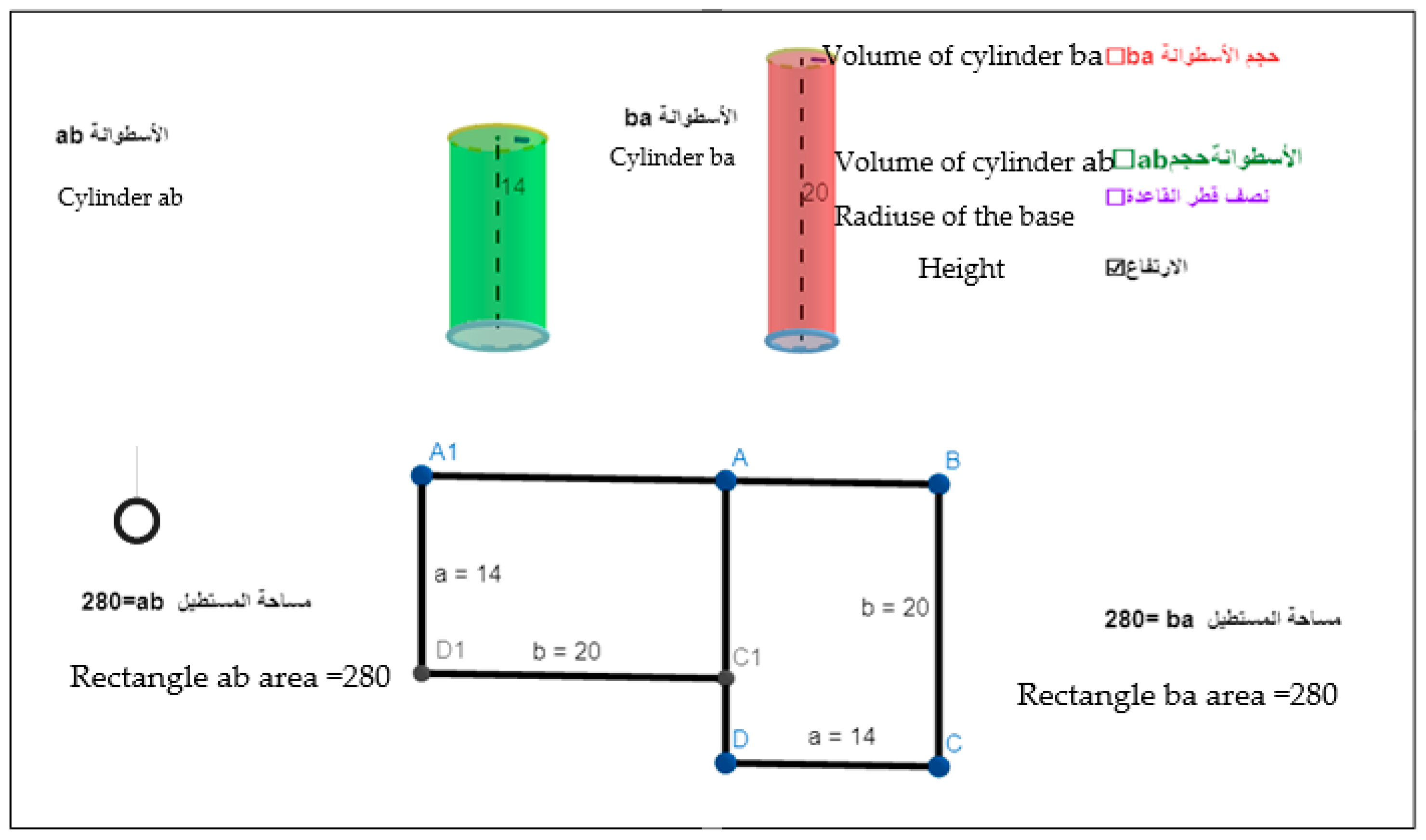
• (5) Adam: I think the amount of the chocolate will be the same in the two cylinders; We made them by the same rectangle (looks to the other students in the group)
• (7) Ahmad: it will be the same amount (with his eyes on the computer screen, and shakes his head); in one case it will be thin or wide, but the same amount.
• (21) Ahmad: Yeah, look how…, the cylinders (while the applet builds the cylinders)

The two students, Adam and Ahmad, answered that the amount (the volume) will be equal in the two cylinders. We did not identify any disagreement from the other students. Adam (5) justified his answer because the cylinders were produced from the same rectangle.

Episode 2: Making the intuitive error—same circumference–same area:

• (105) Adam: the same rope is the same circumference; the cups cover the shape we Produce (in a confident tone)
• (107) Ahmad: the number of the cups is the area (looking to other students with comfortable and confident tone)
• (109) Ahmad: Sure, it is equal, the rope has not changed. I am sure
• (111) Adel: We can frame different shape, but it still the same rope; yes I think so (shakes his head)
• (112) Ahmad: it is the same circumference in all shapes, maybe sometimes we need to divide the cups, it will not be a whole number
• (113) Adam: it did not matter, you will have the complementing parts

The students agree that the number of cups is the area of the shapes that they produced from the same rope, as shown in Adam’s (105) and Ahmad’s (107) speech. They also agreed that the area is equal because they used the same candy rope or the same circumference, as shown in Ahmad’s (109, 112) and Adel’s (111) speech.

Episode 3: Making the intuitive error—dynamic referent in volume:

• (206) Mohammed: how we know, we do not have the dimensions of the cup or the box
• (207) Rami: it does not matter; we know that the cup has equal lengths
• (208) Sameer: we do the same process increased four sides and increased four sides by quarter.
• (209) Rami: I think the seam extended and curtailed in the same mount
• (210) Mohammed: I think we will have errors like the other activities we did (smiles)
• (211) Rami: I think no; this time, they are equal. (shakes his head with confident tone)

Mohamed (206) first declared that he needed more information for solving the problem. Rami (207, 209) and Samier (208) were convinced that the amount would not change. Mohammed (210) connected this task to the previous tasks; he did not provide any explanations. However, the others were confident that the volume is equal, as Rami (211) declared.

The participants in the three groups across the three intuitive errors were characterized by confidence, comfort and enjoyment, and sometimes excitement, when applying the applet; we did not identify negative emotions or emotions connecting to confusion. We identified excitement from their tone of voice using specific words such as “OHH” and “YEAH” and physical indicators such as their looks and interactivity such as clipping. For example, through Episode 1, Ahmad shook his head in acceptance to Adam’s (5) claim, and then Ahmed (21) was excited while activating the applet that built the cylinders; he said “Yeah”, emphasized his excitement with an indication to the computer screen and said to the other group members, “Look how…”. Ahmad speaks with a loud tone of voice, impulsive speed of response and execution and physical indicators that appear through clapping when completing a task (Figure 1). This is in addition to the relaxed and confident tone identified in the second episode in Adam’s (105) and Ahmad’s (107) speech, and in Rami’s (211) speech in the third episode.

5.2. Cognitive Processes and Emotions during Revealing the Intuitive Errors in the Three Tasks

In the three tasks, the students in all groups revealed that they had mistaken their solutions. In the first task, students inserted the dimension of the two cylinders; then, the cylinders were built by the applet in a three-dimensional view with the volume of each one. Students emphasized that there is a mistake in the calculation of the volumes. They tried to insert the data again, as shown in Episode 4. In the second task, students obtained different areas or different numbers of cups. They used several circumferences by using several ropes and always obtained different areas (see Episode 5). The same occurred in the third task, where the participants revealed that the volume is different, although when extending and reducing the same amount of sides, the students tried different cases and always obtained a different volume (see Episode 6)

Episode 4: Revealing the intuitive error, same area–same volume:

• (83) Ahmad: Ha; the size is not the same thing? (with a surprised tone) (see Figure 2)
• (84) Adam: what? 102? 56? (he means the volume of the cylinders; he talks with a surprised tone)
• (85) Adel: However, how? why are they different? (he means the cylinders’ volume, he looks at the other students and talks in a low and sad tone)
• (86) Ahmad: How this happen, it the exact dimensions (he points to the computer screen)
• (87) Adel: The same rectangle. Each time we rounded differently; why the volume different.

All of the students faced the error that the volume is different in the two cylinders. They expressed their surprise at the result; they asked how and why, and they emphasized (86, 87) that the same rectangle was made the cylinder.

Episode 5: Revealing the intuitive error—same circumference–same area:

• (155) Ahamd: It is different! (with a surprised tone, deeply looking at the screen computer and then to other students) (see Figure 3)
• (156) Adam: oh, all of them! (with a surprised tone), they (the different rectangle) not equal
• (157) Ahmed: Haa, it means we are wrong (knocks with his hand on the table).
• (158) Adel: uh, may we try a different length of the rope? (with a non-confident tone)
• (159) Ahmed: Ok; I changed (changed the rope length)
• (160) Adel: uh, it does not matter; the area is not equal (with a surprised tone)
• (161) Adam: It is different; all of them (rectangles).

The participants revealed that they were wrong, and the same circumference did not produce the same area, as presented in their speech (155–161).

Episode 6: Revealing the intuitive error—dynamic referent in volume:

• (210) Adam: it is impossible to be wrong (deeply looking at the computer screen (see Figure 4)
• (211) Adel: it is different in all of them (with a surprised tone)
• (213) Ahmad: I do not understand (with an uncomfortable tone)

Episode 6 showed that all students (210, 211 and 212) think it is strange to obtain different volumes.

In this phase, we identified several indicators and signs of non-comfortable and confusing situations by revealing the errors in the three tasks. These included a loud voice or a sad tone of voice, physical movements such as moving closer to the computer screen and other physical indicators such as opening the mouth and putting a hand on the head or the face. For example, in Episode 4, we identified surprising and sad tones while revealing that the two cylinders’ volumes are different. Adel (85) spoke in a low and sad tone while asking why the two cylinders’ volumes are different; he moved closer to the computer screen, deeply looking at (see Figure 5). Additionally, in the second task, in Episode 5, all the students spoke in a surprised tone; Ahmad (157) knocked with his hand at the table with a non-comfortable movement; and Adel (160) said that the area of the rectangles is not equal while he was putting his two hands on his head (see Figure 6). In the third task, in Episode 6, we also identified a surprised and non-comfortable tone; Ahmad (213) expressed his understanding of why the volumes of the cup and the box are different by putting his hand on his face (see Figure 7).

5.3. Cognitive Processes and Emotions during Overcoming Intuitive Errors in the Three Tasks

In the three tasks, after the phase, students verified that the calculations are correct, and they tried to think about the error’s sources. In the first task, the students inserted different data, and they always obtained the result that the volume of the wide cylinder is bigger than the long cylinder (see Episode 7). In the second task, after trying different lengths of ropes, students overcame their error. They understood that the logic of the area changed (see Episode 8). In the last task, after trying different cases, the participants revealed that the box’s volume is smaller than the cup. The three groups’ participants succeeded at knowing, at first, that the box is smaller by 1\16 than the box. Then, they succeeded in generalizing their conclusion. They found that after using the applet, they could calculate the two volumes of the box and the cup. The applet revealed the multiplication of the three dimensions of the box, which helped them overcome their error (see Episode 9).

Episode 7: Overcoming the intuitive error, same area–same volume:

• (101) Adel: always the volumes are different (indicates to computer screen and then looks to the other students)
• (103) Adam: the thin one is always smaller (the volume of the thin cylinder is smaller than the wide one)
• (104) Adel: the radius here (the thin cylinder) is smaller than this (the wide cylinder)
• (105) Ahmad: Ahh, the area here is bigger (the bases of the wide cylinder, with loud tone)
• (106) Adam: but here (the thin cylinder), the highest is bigger
• (107) Ahmad: but the radius we squired! (in confident tone talking to Adam)
• (109) Adam: Ah, this will affect more in the volume (with a smile)

Adam (103) revealed that the thin cylinders are smaller than the wide ones. Adel (104) revealed the reasons that are related to the radius. This affects the bases’ area of the cylinder according to Ahmad (105), and because the radius is squared (Ahmad (107)), it has a greater effect than the height of the thin cylinder (Adam (109)).

Episode 8: Overcoming the intuitive error—same circumference–same area:

• (170) Muhammad: Compare this rectangle and this rectangle. Sure, that they will not have the same area.
• (171) Rami: why you are sure? (looks to Muhammed)
• (172) Sameer: It is so thin (indicating one of the rectangles) it will include a small Number of cups, but here (another rectangle), it will include more
• (174) Muhammed: Yes, it is clear (shakes his head)
• (176) Rami: look, it is the biggest area (with a confident tone)
• (177) Muhammed: it is square; try another length (request from Rami)
• (178) Rami: you see (produced different rectangles) the biggest is the square
• (181) Sameer: always the square is the biggest area for the same circumference
• (182) Rami: I think it is logic (shakes his head); if we closed the sides, there would be a small area. The square is the shape that we keep each of the parallel sides with the same distance.
• (183) Muhammed: Yes, so it includes more units (with a confident tone)
• (184) Rami: it is means the same area.

The participants concluded that the same circumference did not mean the same area (Muhammed (170) and Sameer (172)). They also concluded that the biggest area is always the square (Muhammed (177) and Sameer (181)). Furthermore, they provided a logical explanation that each parallel side is the most far-off one from another in the square, which means a big area, as shown in Rami’s (182,183) speech.

Episode 9: Overcoming the intuitive error—dynamic referent in volume:

• (262) Lean: how much it smaller, it is different each time (serious tone)
• (263) Noor: the difference is to do subtraction between them
• (265) Maise: in all the cases, it is the same number, look here (the difference between the volume), Ah, it always the same (opens her mouth)
• (266) Noor: yes, it does not matter the dimensions. It always the same result (shakes his head)
• (268) Maise: I think it because always the multiplication of these sides (the one which was extended, and the one which was reduced)
• (269) Noor: Ah, look this (the side that is constant) and always the multiplication of these sides are 15\16 (loud tone)
• (270) Maise: it misses 1\16, so it always smaller 1\16
• (272) Lean: yes, it does not matter what the sides are
• (273) Maise: but it is a quarter?
• (274) Noor: may we can try fifth (short pause) it 1\25 smaller
• (275) Maise: May try sixth? (with an excited tone)
• (276) Noor: it is 1\36
• (277) Maise: I think seventh is 1\49 (excited tone and smiling)
• (278) Lean: OHH, yes. We found the method! (knocks on the table with smiling)

The participants concluded that the cup’s volume is always bigger than the box as Lean (262) declared; then, they concluded that it is always 1\16 of the box, as Maise (276) declared. Then, they tried to find the difference in the volume of the cup and the box when they were extended by a fifth, sixth and seventh (274–277). Noor (278) succeeded in generalizing their understanding; he said we found the method, where he means finding the differences between the volumes of the cups and the boxes.

Through overcoming and understanding the sources of the errors, the participants showed confidence that was clear in their facial signs, joy and smiles, and in the eye contact between students and the teacher, or between students, as well as through shaking their heads as acceptance, and a confident and loud tone. For example, in Episode 7, Ahmad (107) talked in a confident tone, and Adam (109) was smiling when they understood why the two cylinders’ volumes are different. In Episode 8, we identified head shaking as acceptance in Muhammed (174), a sign that the area of the same circumference is different, and in Rami (182) as acceptance that the square is the biggest area among all the rectangles with the same circumference. We also identified a confident tone in Rami (176) and Muhammed (183). In Episode 9, Maise (277) expressed her excitement by an excited tone and smiling when she found that when the volume was decreased or increased by a seventh, the difference will be 1\49 (see Figure 8). Moreover, Lean (278) knocked on the table, smiling when she looked at her classmate, and summarized their discussion by saying that “we found the method” (see Figure 9).

6. Discussion

The current study examined the cognitive processes and the students’ accompanying feelings during the intuitive errors to reveal and overcome them. The current study focused on the intuitive role of same A–same B by providing tasks based on modeling features and designed in a technological environment. The findings reveal that students solved the tasks with the effect of the intuitive role of same A–same B. While solving the first task, they emphasized that the same surface of the cylinder leads to the same volume. In the second task, they agreed that the same perimeter contributes to the same area. Similar to the third task, they indicated that if we enlarged four sides by a quarter and shrunk the other four sides by a quarter, the new box’s volume equals the original square. These findings align with other studies [18,19,53,54].

The findings also reveal three cognitive processes through engagement in the tasks: the occurrence of the intuitive errors, revealing the intuitive errors and overcoming the intuitive errors. All students in different groups collaborated in the tasks that interested them, which was considered an essential factor in causing cognitive conflict and succeeding in the conceptual changes [30]. From a cognitive perspective, the students exhibited and used their exciting knowledge; they revealed their errors and were convinced that their exciting knowledge was not correct; and, finally, they considered critical steps for conceptual change [3]. Moreover, designing the tasks in the technological environment provided the opportunity for different mathematical representations of the cylinders, rectangles and boxes. These representations were important in communicating their mathematical ideas and thinking, as emphasized in different studies, e.g., [55].

We identified common emotions that characterize intuition through cognitive processes, which were positive and negative emotions. We identified the positive emotions (e.g., enjoyment, confidence) among students before and after revealing the errors they made. While they were affected by their intuitive thinking, they were not aware of their errors; thus, they felt stultified in their solving. The same thing occurred after they overcame their errors and accepted the new knowledge, where they returned to having positive feelings. The negative feelings (e.g., confusing, non-comfortable) were identified when they revealed that their solution was not correct and did not understand why it was not right. These results are similar to those of Tulis and Ainley [56], who reported that emotions were identified more often after success, whereas negative emotions were identified more often after failure experiences. The changes in students’ emotions through the engagements in the activities support Di Leo and her colleagues’ [42] findings that there is a transition in students’ emotions through problem solving.

This study’s results indicate that emotional experience activates students to redirect their behavior and try alternative cognitive strategies to solve the problem. Specifically, the negative emotions that students have required more cognitive resources; these results support Pekrun and his colleagues [36], who emphasized that negative emotions trigger learning more than positive emotions. As we reported in the Finding section, students’ emotions were combined with a specific tone of voice, some students through the stage of revealing and overcoming their errors. Talking aloud indicated their non-comfortable emotions or expressions of confusion, and, in the second case, as expression and clarification of their new understanding; in two cases, we identified that talking aloud was directed at students themselves to think for themselves [57]. The students’ negative and positive emotions were reflected in their speech tone, and these results are consistent with other studies’ results, e.g., the results in [53] that indicated different tones of voice such as sad, dislike tone and angry tone, through a problem solving situation.

The negative emotions that accompanied the revealing of intuitive errors passed quickly by the use of technological tools. The use of technology, specifically the use of applets, allowed presenting different cases in a limited time; due to that, the students did not have to calculate the volumes of cylinders, rectangles or boxes. Therefore, the students’ efforts were focused on revealing the errors and in the resolutions. In addition, the technological environment did not prevent students’ confrontation and social interaction and argumentation, as suggested by Mercer [32]. However, the students did not engage in a concrete activity such as in Shahbari and Peled [3]. The design of the applets provided the opportunity for activating the students in the different stages of the cognitive process and was helpful in the application of cognitive conflict strategies. The role of technology in the current study was as a motivational force that motivated students to correct their errors; as Tulis, Steuer and Drese [58] emphasized, learning from one’s own errors requires motivational forces in order to correct these errors. Therefore, the current study will stand in line with many studies (e.g., [49,51]) that reported the effectiveness of technology in mathematics teaching and learning.

7. Implication

The current study examined the cognitive process in making intuitive errors, revealing and overcoming these errors and the emotions accompanied by these processes. The main implication is connected to mathematics teachers’ awareness and responses to these processes. Mathematics teachers are familiar with the intuitive rules and their effect on the students at two levels: cognitive and emotional. The current study will help teachers specifically consider students’ emotional, as well as cognitive, experiences. Teachers aware of their students’ thinking and emotions will help them overcome their intuitive errors by providing an effective environment that helps their students to overcome their errors by themselves. In addition, teachers are more empathetic to the changes in their students’ emotions. Teachers’ awareness of students’ different emotions affected students’ cognitive process and facilitated the change from intuitive to formal thinking. Teachers need to be aware of the voice tone of the students, which will be a sign of different emotions that students did not control. In addition, we recommend using technological tools, and designing appropriate applets that facilitate the process of revealing and overcoming intuitive errors.