Abstract
In this work, numerical estimations of a nonlinear hyperbolic bioheat equation under various boundary conditions for medicinal treatments of tumor cells are constructed. The heating source components in a nonlinear hyperbolic bioheat transfer model, such as the rate of blood perfusions and the metabolic heating generations, are considered experimentally temperature-dependent functions. Due to the nonlinearity of the governing relations, the finite element method is adopted to solve such a problem. The results for temperature are presented graphically. Parametric analysis is then performed to identify an appropriate procedure to select significant design variables in order to yield further accuracy to achieve efficient thermal power in hyperthermia treatments.
1. Introduction
Recent research developments have shown that the problem of heating transfers in skin tissues is an incredibly complicated problem. There are many controversial parameters found in this field. To describe the current status [1], at temperatures above 60 °C, the time needed to check irreversible damages decreases rapidly, while, at temperatures around 40–45 °C, irreversible tissue damage happens after only prolonged exposures. A human body behaves differently under different environmental conditions (e.g., different air temperatures, humidity levels, and wind velocities). Thermotherapy operations, such as laser tissues welding [2], hyperthermy [3], and lasers operations [4], have been openly used in modern medicine. Since the temperature distribution in the living tissues depends on complex phenomena, like metabolic heating generations and blood circulation, investigators have expanded some formulations. In clinical therapy, various contemporary thermotherapeutic techniques have been widely used for microwave, laser, ultrasound, and radiofrequency technologies. First, using an objective thermal lens, the laser focuses on the tumor. One of the main challenges in the treatment process is to provide adequate thermal power to diseased tissue without affecting healthy tissue. Therefore, it is important to consider the impact of temperature and stress fields on heat treatment kinetics. Van and Gybels [5] demonstrated that deformation due to heating and cooling can also contribute to a feeling of discomfort. Therefore, exact predictions of the Sun, mechanical reaction, and thermal damage in organic tissues are required for the treatment planning and development of new clinical heating systems. In 1948, Pennes [6] investigated the thermal behavior of skin temperature in the forearm. The investigation included many phenomenological mechanizations, such as metabolic heat generation, radiation, blood perfusion, thermal conduction, and phases change. In biological tissues, the phase changes occur in wide ranges. The adjusted Penne’s bioheat models are presented by various techniques of numerical approach available in the literature: the homotopy perturbation method [7], the Legendre wavelet Galerkin approach, the finite element approaches, the Galerkin approach, and the approach of variations and iterations [8,9], as well as the finite-decomposition approach [10]. Hobiny et al. [11] presented analytical estimations of temperature in biological tissue under TPL bioheat model with experimental verifications. Dillenseger and Esneault [12] studied temperature improvement over time by using the approach of finite differences in the case where the body temperature is abnormally low. Hobiny and Abbas [13] studied the temperature increment and variations of thermal damages in living tissues due to mobile heating sources. Zhu et al. [14] considered the rate process models for the resulting thermal injury and the sedimentations of lighting energy in tissues by using the diffusion theory. Diaz et al. [15] applied the finite element scheme to solve the thermos-diffusions model type in the biological tissues to determine the thermal damages. Alzahrani and Abbas [16] investigated the analytical solution of thermal damage in living tissue due to laser irradiations. In considering the study of real phenomenon regarding thermal transfers in finite mediums, the linear/nonlinear models of heat transfers have been expanded, and their numerical or analytical solutions have been solved by several authors [17,18,19,20,21,22,23,24,25,26,27,28,29].
This work explores the numerical solutions of the thermal injury of biological tissue using a nonlinear bioheat theory in the living tissue. Due to the nonlinearity of the governing relations, the finite element method is used in order to determine solutions for this problem. The numerical outcomes for temperature behaviors are provided graphically. Furthermore, a comparison is made with the results obtained in the presence and absence of delay times. Additionally, comparisons between the nonlinear and linear influences on bioheat transfers are made when the nonlinear parameter are zeroes.
2. Mathematical Model
We consider that the medium is a semi-infinite living tissue under thermal insulation. Based on Cattaneo [30], with the delay time , the bioheat relation in skin tissues can be given by the following equation [31,32]:
where is the thermal delay time, is the mass density of tissues, is the temperature of blood, is the time, is the temperature of tissue, is the tissue-specific heat, is the tissue thermal conductivity, and represents the thermal generated per unit volume of tissue due to the absorption of electromagnetic radiations, which is expressed by the following equation [7]:
where is the transmitted power, and are the antenna constants, is the probe radius, is the distance of tissues from external surface, and refers to the blood perfusion heat source, which is expressed as follows:
where is the blood perfusion rate dependent on temperature, is the mass density of blood, and is the specific heat of blood. Depending on the anatomical structure of the biological living tissue containing blood vessels, this point will extend with the increasing temperature of the local tissues. The perfusion rate of blood with the temperature of local tissues is presumed as in [33] as follows:
where is the reference blood perfusions rate, is the constant associated with blood perfusions, is the initial temperature of normal tissues, and is the heat generated by metabolics process. Mitchell et al. [33] noticed that the metabolic heat generations is a function of the temperature of local tissues and is expressed as follows:
where is the associated metabolic constant and is the metabolic heat source reference.
3. Application
The appropriate initial and boundary conditions are defined by the following:
For its adaptations, the non-dimensional variables can be expressed by the following:
In terms of this nondimensional parameters (8), the formulation (1) as well the initial (6) and the boundary (7) conditions can be inserted as (the scripts have been abandoned for its suitability) as follows:
4. Numerical Scheme
In this section, the highly nonlinear formulation of bioheat transfer based upon thermal delay time in biological tissues is summarized using the finite element method (FEM). This technique is a powerful approach that is primarily used to obtain the numerical solution of complex problem and the finite element method is the selected method for nonlinear systems in several fields. The finite element scheme is applied here to obtain the solution of nonlinear formulation (9) under the initial condition (10) and the boundary (11) condition. Abbas and his colleagues [34,35,36,37,38,39,40,41,42] presented solutions for various problems under deference generalized thermoelasticity models. The finite element formulation of nonlinear bioheat transfer can be obtained by using the standard procedure. The non-dimension weak formulations of bioheat model are derived. The set of independent test functions resulting in the temperature is specified. The governing formulation is multiplied by independent weighting functions and then the boundary conditions are used to integrate over the spatial domain. The applications of integration by parts and the use of the divergence theorem to decrease the order of the spatial derivative paves the way for the application of the boundary condition. Using the Galerkin procedure, the unknown temperature and the corresponding test function are approximated by the same shape function.
where refers to the shape function and refers to the node numbers per element. The quadratic element with three nodes is used. In this problem, a one-dimensional quadratic element is used, and we suppose that the local coordinates in the range are used for the master element, which can be defined as follows:
Furthermore, the time derivatives of the unknown variables should be determined by the implicit approaches. Thus, the weak formulations for the finite element scheme corresponding to the basic Equation (9) can be written as follows:
Symbolically, the discredited equation of Equation (15) can be given as follows:
where ,
, .
By using the implicit method for time, Equation (16) can be expressed as follows:
5. Numerical Results
The temperature distribution in a biological tissue under nonlinear bioheat transfer models was investigated. For numerical computation, exemplary values of thermal properties for biological tissue are given below (as in [43]):
The calculations were made by the MATLAB software (R2018a), and the outcomes are graphically presented. The impacts of the external heating sources on the skin’s surface were integrated. In this study, it was considered that is the normal temperature and a slab of tissues is 0.05 m thick. The grid sizes were refined and, consequently, the values of various parameters were stabilized. Further refinement of mesh sizes over 18,000 elements did not change the values considerably, therefore the mesh sizes were accepted as the grid sizes for computing purposes. In Figure 1 and Figure 2, the computations are carried out when , and the variations of temperature are presented graphically. The dotted lines represent the nonlinear bioheat model, while the solid lines represent the linear bioheat model. Comparing the figures of the solutions obtained with the linear and nonlinear models, one observes important phenomena, as in Figure 1 and Figure 2. Figure 3 and Figure 4 display the influences of thermal delay time on the temperature distribution. As expected, the thermal delay time has a major impact on the temperature distributions. Figure 1 and Figure 3 show the temperature variations with respect to the distances at min. It is observed from the graphs that the temperature increases from the normal temperature to the maximum values on the tissue surface. A timeline of the surface temperature is presented in Figure 2 and Figure 4. It was observed that after starting from the normal temperature temperature increases with time until the highest temperature values are obtained. Finally, Figure 5 and Figure 6 display the effects of the rate of blood perfusion under bioheat model with one relaxation time on the temperature variation. The higher the rate of blood perfusion, the greater the convective heat loss due to faster blood flow.
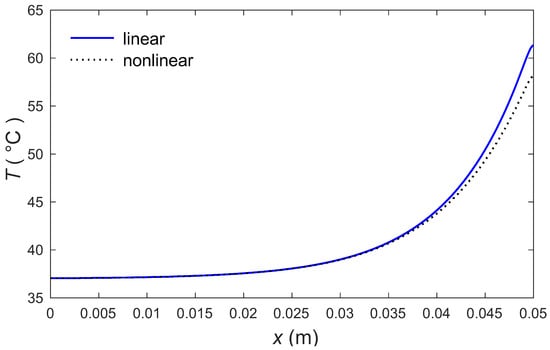
Figure 1.
Temperature profile in skin tissues due to linear and nonlinear models.
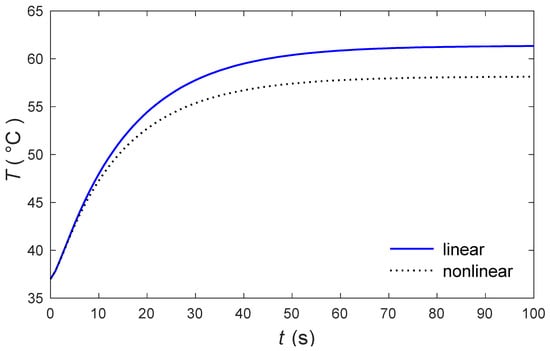
Figure 2.
The skin surface temperature through the time under nonlinear and linear models.
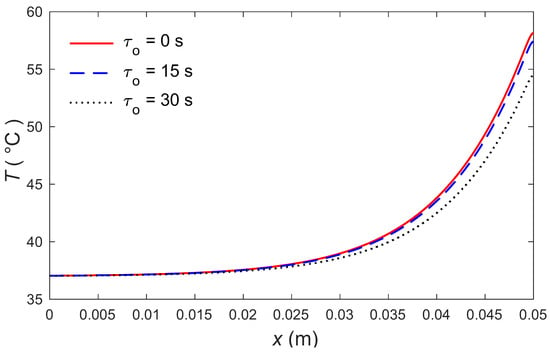
Figure 3.
Temperature distributions along the distance for several values of .
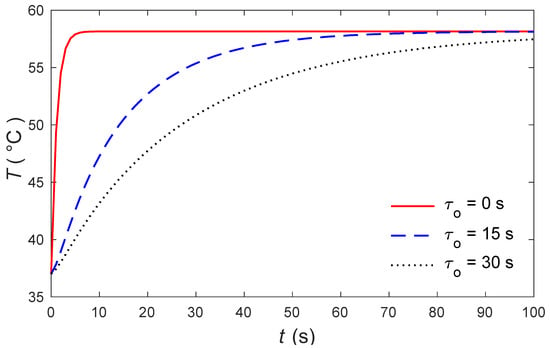
Figure 4.
The skin surface temperature over time for several values of .
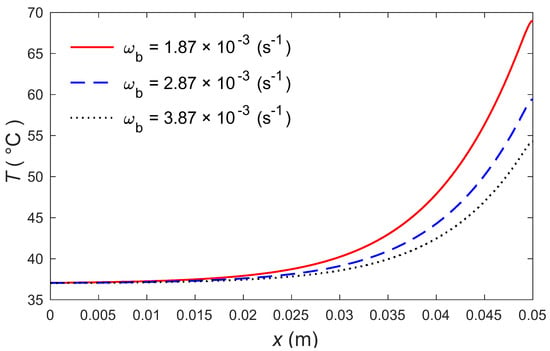
Figure 5.
Temperature distributions according to distance for three values of .
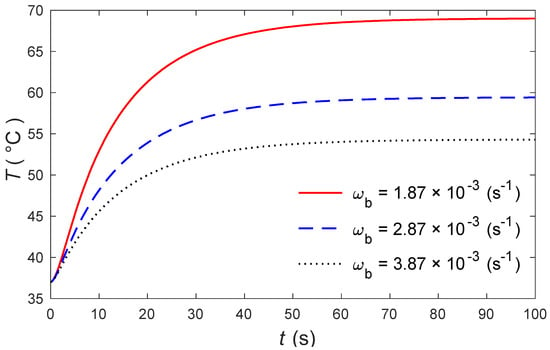
Figure 6.
The skin surface temperature over time for different values of .
6. Conclusions
Based on a highly nonlinear bioheat model of skin tissues, temperature behaviors were studied when applying thermotherapy. Numerical solutions were derived for the nonlinear bioheat with one relaxation time under an external heat source. The finite element method was applied to solve the second-order nonlinear differential equation by using a quadratic element. The theoretical outcomes can be used as confirmation tools in order to examine practical operations like laser treatment.
Author Contributions
Conceptualization: A.H., I.A. and M.M.; methodology: M.M. and I.A.; validation: A.H., I.A. and M.M.; formal analysis: A.H., I.A. and M.M.; investigation: A.H. and I.A.; resources: I.A.; data curation: A.H., I.A. and M.M.; writing—original draft preparation: A.H., I.A. and M.M.; writing—review and editing: A.H.; visualization: I.A. and M.M.; supervision: A.H., I.A. and M.M.; project administration: I.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Huang, X.; Jain, P.K.; El-Sayed, I.H.; El-Sayed, M.A. Plasmonic photothermal therapy (PPTT) using gold nanoparticles. Lasers Med. Sci. 2008, 23, 217. [Google Scholar] [CrossRef]
- Gabay, I.; Abergel, A.; Vasilyev, T.; Rabi, Y.; Fliss, D.M.; Katzir, A. Temperature-controlled two-wavelength laser soldering of tissues. Lasers Surg. Med. 2011, 43, 907–913. [Google Scholar] [CrossRef]
- Mahjoob, S.; Vafai, K. Analytical characterization of heat transport through biological media incorporating hyperthermia treatment. Int. J. Heat Mass Transf. 2009, 52, 1608–1618. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, J.; Zhang, Y. Dual-phase lag effects on thermal damage to biological tissues caused by laser irradiation. Comput. Biol. Med. 2009, 39, 286–293. [Google Scholar] [CrossRef]
- Van Hees, J.; Gybels, J. C nociceptor activity in human nerve during painful and non painful skin stimulation. J. Neurol. Neurosurg. Psychiatry 1981, 44, 600–607. [Google Scholar] [CrossRef] [Green Version]
- Pennes, H.H. Analysis of tissue and arterial blood temperatures in the resting human forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [CrossRef]
- Gupta, P.K.; Singh, J.; Rai, K. Numerical simulation for heat transfer in tissues during thermal therapy. J. Therm. Biol. 2010, 35, 295–301. [Google Scholar] [CrossRef]
- Kumar, P.; Kumar, D.; Rai, K. A numerical study on dual-phase-lag model of bio-heat transfer during hyperthermia treatment. J. Therm. Biol. 2015, 49, 98–105. [Google Scholar] [CrossRef]
- Yadav, S.; Kumar, D.; Rai, K.N. Finite Element Legendre Wavelet Galerkin Approch to Inward Solidification in Simple Body Under Most Generalized Boundary Condition. Z. Für Nat. A 2014, 69, 501–510. [Google Scholar] [CrossRef]
- Gupta, P.K.; Singh, J.; Rai, K.; Rai, S. Solution of the heat transfer problem in tissues during hyperthermia by finite difference–decomposition method. Appl. Math. Comput. 2013, 219, 6882–6892. [Google Scholar] [CrossRef]
- Hobiny, A.; Alzahrani, F.; Abbas, I. Analytical Estimation of Temperature in Living Tissues Using the TPL Bioheat Model. with Experimental Verification. Mathematics 2020, 8, 1188. [Google Scholar] [CrossRef]
- Dillenseger, J.-L.; Esneault, S. Fast FFT-based bioheat transfer equation computation. Comput. Biol. Med. 2010, 40, 119–123. [Google Scholar] [CrossRef] [Green Version]
- Hobiny, A.D.; Abbas, I.A. Theoretical analysis of thermal damages in skin tissue induced by intense moving heat source. Int. J. Heat Mass Transf. 2018, 124, 1011–1014. [Google Scholar] [CrossRef]
- Zhu, D.; Luo, Q.; Zhu, G.; Liu, W. Kinetic thermal response and damage in laser coagulation of tissue. Lasers Surg. Med. 2002, 31, 313–321. [Google Scholar] [CrossRef]
- Díaz, S.H.; Nelson, J.S.; Wong, B.J. Rate process analysis of thermal damage in cartilage. Phys. Med. Biol. 2002, 48, 19. [Google Scholar] [CrossRef] [Green Version]
- Alzahrani, F.S.; Abbas, I.A. Analytical solutions of thermal damage in living tissues due to laser irradiation. Waves Random Complex Media 2019, 1–14. [Google Scholar] [CrossRef]
- Ghazanfarian, J.; Saghatchi, R.; Patil, D. Implementation of Smoothed-Particle Hydrodynamics for non-linear Pennes’ bioheat transfer equation. Appl. Math. Comput. 2015, 259, 21–31. [Google Scholar] [CrossRef]
- Li, L.; Liang, M.; Yu, B.; Yang, S. Analysis of thermal conductivity in living biological tissue with vascular network and convection. Int. J. Therm. Sci. 2014, 86, 219–226. [Google Scholar] [CrossRef]
- Ellahi, R.; Alamri, S.Z.; Basit, A.; Majeed, A. Effects of MHD and slip on heat transfer boundary layer flow over a moving plate based on specific entropy generation. J. Taibah Univ. Sci. 2018, 12, 476–482. [Google Scholar] [CrossRef] [Green Version]
- Selvi, C.; Srinivas, A.; Sreenadh, S. Peristaltic transport of a power-law fluid in an elastic tube. J. Taibah Univ. Sci. 2018, 12, 687–698. [Google Scholar] [CrossRef] [Green Version]
- Jha, B.K.; Musa, M.K. The combined effects of anisotropic porous medium and stably stratified fluid on free convective flow through an annulus. J. Taibah Univ. Sci. 2018, 12, 678–686. [Google Scholar] [CrossRef] [Green Version]
- Saeed, T.; Abbas, I.; Marin, M. A gl model on thermo-elastic interaction in a poroelastic material using finite element method. Symmetry 2020, 12, 488. [Google Scholar] [CrossRef] [Green Version]
- Hobiny, A.; Alzahrani, F.; Abbas, I.; Marin, M. The Effect of Fractional Time Derivative of Bioheat Model. in Skin Tissue Induced to Laser Irradiation. Symmetry 2020, 12, 602. [Google Scholar] [CrossRef]
- Alzahrani, F.; Hobiny, A.; Abbas, I.; Marin, M. An Eigenvalues Approach for a Two-Dimensional Porous Medium Based Upon Weak, Normal and Strong Thermal Conductivities. Symmetry 2020, 12, 848. [Google Scholar] [CrossRef]
- Saeed, T.; Abbas, I.A. The Effect of Fractional Time Derivative on Two-Dimension Porous Materials Due to Pulse Heat Flux. Mathematics 2021, 9, 207. [Google Scholar] [CrossRef]
- Khan, A.A.; Bukhari, S.R.; Marin, M.; Ellahi, R. Effects of chemical reaction on third-grade MHD fluid flow under the influence of heat and mass transfer with variable reactive index. Heat Transf. Res. 2019, 50. [Google Scholar] [CrossRef]
- Abbas, I.A.; Marin, M. Analytical solution of thermoelastic interaction in a half-space by pulsed laser heating. Phys. E Low-Dimens. Syst. Nanostructures 2017, 87, 254–260. [Google Scholar] [CrossRef]
- Marin, M.; Vlase, S.; Paun, M. Considerations on double porosity structure for micropolar bodies. Aip Adv. 2015, 5, 037113. [Google Scholar] [CrossRef] [Green Version]
- Marin, M. Generalized solutions in elasticity of micropolar bodies with voids. Rev. Acad. Canar. Cienc. Folia Canar. Acad. Sci. 1996, 8, 101–106. [Google Scholar]
- Cattaneo, C. A form of heat conduction equation which eliminates the paradox of instantaneous propagation. Compte Rendus 1958, 247, 431–433. [Google Scholar]
- Xu, F.; Seffen, K.; Lu, T. Non-Fourier analysis of skin biothermomechanics. Int. J. Heat Mass Transf. 2008, 51, 2237–2259. [Google Scholar] [CrossRef]
- Ahmadikia, H.; Fazlali, R.; Moradi, A. Analytical solution of the parabolic and hyperbolic heat transfer equations with constant and transient heat flux conditions on skin tissue. Int. Commun. Heat Mass Transf. 2012, 39, 121–130. [Google Scholar] [CrossRef]
- Mitchell, J.W.; Galvez, T.L.; Hengle, J.; Myers, G.E.; Siebecker, K.L. Thermal response of human legs during cooling. J. Appl. Physiol. 1970, 29, 859–865. [Google Scholar] [CrossRef]
- Abbas, I.A.; Youssef, H.M. Two-temperature generalized thermoelasticity under ramp-type heating by finite element method. Meccanica 2013, 48, 331–339. [Google Scholar] [CrossRef]
- Abbas, I.A.; Youssef, H.M. A Nonlinear Generalized Thermoelasticity Model. of Temperature-Dependent Materials Using Finite Element Method. Int. J. Thermophys. 2012, 33, 1302–1313. [Google Scholar] [CrossRef]
- Abbas, I.A.; Othman, M.I.A. Generalized thermoelasticity of the thermal shock problem in an isotropic hollow cylinder and temperature dependent elastic moduli. Chin. Phys. B 2012, 21, 014601. [Google Scholar] [CrossRef]
- Kumar, R.; Abbas, I.A. Deformation due to thermal source in micropolar thermoelastic media with thermal and conductive temperatures. J. Comput. Theor. Nanosci. 2013, 10, 2241–2247. [Google Scholar] [CrossRef]
- Abbas, I.A.; Youssef, H.M. Finite element analysis of two-temperature generalized magneto- thermoelasticity. Arch. Appl. Mech. 2009, 79, 917–925. [Google Scholar] [CrossRef]
- Mohamed, R.; Abbas, I.A.; Abo-Dahab, S. Finite element analysis of hydromagnetic flow and heat transfer of a heat generation fluid over a surface embedded in a non-Darcian porous medium in the presence of chemical reaction. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 1385–1395. [Google Scholar] [CrossRef]
- Abbas, I.A. Finite element analysis of the thermoelastic interactions in an unbounded body with a cavity. Forsch. Im Ing. 2007, 71, 215–222. [Google Scholar] [CrossRef]
- Abbas, I.A.; Abo-Dahab, S. On the numerical solution of thermal shock problem for generalized magneto-thermoelasticity for an infinitely long annular cylinder with variable thermal conductivity. J. Comput. Theor. Nanosci. 2014, 11, 607–618. [Google Scholar] [CrossRef]
- Abbas, I.A. Generalized magneto-thermoelasticity in a nonhomogeneous isotropic hollow cylinder using the finite element method. Arch. Appl. Mech. 2009, 79, 41–50. [Google Scholar] [CrossRef]
- Askarizadeh, H.; Ahmadikia, H. Analytical analysis of the dual-phase-lag model of bioheat transfer equation during transient heating of skin tissue. Heat Mass Transf. 2014, 50, 1673–1684. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).