Closed-Form Solution for Circular Membranes under In-Plane Radial Stretching or Compressing and Out-of-Plane Gas Pressure Loading

Abstract

The large deflection phenomenon of an initially flat circular membrane under out-of-plane gas pressure loading is usually involved in many technical applications, such as the pressure blister or bulge tests, where a uniform in-plane stress is often present in the initially flat circular membrane before deflection. However, there is still a lack of an effective closed-form solution for the large deflection problem with initial uniform in-plane stress. In this study, the problem is formulated and is solved analytically. The initial uniform in-plane stress is first modelled by stretching or compressing an initially flat, stress-free circular membrane radially in the plane in which the initially flat circular membrane is located, and based on this, the boundary conditions, under which the large deflection problem of an initially flat circular membrane under in-plane radial stretching or compressing and out-of-plane gas pressure loading can be solved, are determined. Therefore, the closed-form solution presented in this paper can be applied to the case where the initially flat circular membrane may, or may not, have a uniform in-plane stress before deflection, and the in-plane stress can be either tensile or compressive. The numerical example conducted shows that the closed-form solution presented has satisfactory convergence.

1. Introduction

A thin elastic film is, in mechanics, called a “membrane” when used as a structure or a structural component, because it usually has no resistance to bending and is usually in a stress state of full tension. Elastic membrane structures, or structural components, often exhibit large deflection phenomena when subjected to out-of-plane loads, giving rise to the nonlinear equations that are usually difficult to be solved analytically. Among them, the problem of axisymmetric deformation and deflection of an initially flat circular membrane fixed at its perimeter (attached at its perimeter to a stiff ring) and subjected to uniform out-of-plane loads has been widely concerned by scholars. This problem is usually called circular membrane problem for short, and Hencky is the first scholar to deal with this problem analytically [1]. Chien [2] and Alekseev [3], respectively, corrected a mistake in the solution presented originally by Hencky. This solution is usually called the well-known Hencky solution and is often cited in some related studies [4,5,6,7,8,9,10]. The well-known Hencky solution has been modified several times to improve its computational accuracy and adaptability, including modifying the out-of-plane equilibrium equation [11], in-plane equilibrium equation [12], and geometric equations [13], as well as extending the adaptability to the cases with a tensile or compressive pre-stress [14,15,16]. The analytical solutions are necessary in the field of mechanical properties characterization for freestanding thin films, or thin-film/substrate systems based on pressured bulge or blister tests [8,14,15,17,18,19,20,21,22], and can provide these technical applications with a required analytical relationship between loads and stress or deflection, or an analytical relationship between radius and deflection of a blister that is gradually getting larger (which is usually difficult to achieve by a numerical analysis). Therefore, the well-known Hencky solution, as well as its modified solutions, are often used in this field to explain the results of bulge or blister tests, by which the mechanical properties of freestanding thin films, or thin film/substrate systems, can be characterized.

The well-known Hencky solution, as well as its modified solutions, are actually suitable for uniform lateral loading, where the direction of the loads applied to the deflected membrane is constant and is always perpendicular to the plane in which the membrane before deflection is located. However, in bulge or blister tests, the bulging or blistering thin film is loaded usually by gas pressure, where the direction of the loads applied to the deflected thin film continuously alters and is always perpendicular to the deflected thin film, usually named uniform normal loading. Therefore, if the well-known Hencky solution or its modified solutions is used to explain the results of bulge or blister tests, then this actually means that only the vertical (lateral) component of the applied gas pressure is taken into account and the horizontal component of the applied gas pressure is neglected. Obviously, in order to reduce the analytical errors during bulge or blister tests, it is necessary to develop an analytical solution which is suitable for the circular membrane problem under gas pressure loading, i.e., the problem of axisymmetric deformation and deflection of an initially flat circular membrane, fixed at its perimeter and subjected to gas pressure. Fichter [23] dealt with the circular membrane problem under gas pressure loading analytically, where the horizontal component of the applied gas pressure, which was neglected in the well-known Hencky solution, was included. However, Fichter failed to consider the case where the circular membrane was pre-stressed. In blister tests for characterizing thin film/substrate systems, the thin film adhering to its substrate is often pre-stressed, i.e., it often has a so-called residual stress due to the changes in processing conditions, such as humidity, temperature, or the sequence of fabrication procedures. In bulge tests for characterizing freestanding thin films, the pre-stress may also be present due to the error in preparation of test samples, or the different temperature when preparing and loading test samples.

It should be said that, long before Fichter, Campbell [24] dealt with the problem of circular membrane under uniform pressure and considered the case where the circular membrane was pre-stressed. Unfortunately, there are three shortcomings in Campbell’s work. First of all, from the in-plane equilibrium equation established by Campbell, it can be seen that the horizontal component of the applied gas pressure, which is neglected in the well-known Hencky solution, was still not included. This means that the solution obtained by Campbell is still not suitable for the circular membrane problem under gas pressure loading. Secondly, based on the linear division of resultant stress /strain into initial stress/strain and incremental stress/strain, Campbell let the incremental stress and strain satisfy the generalized Hooke’s theorem, resulting in an inconsistent definition of incremental strain with initial strain. Thirdly, it is unreasonable that the initial stress is considered only in the out-of-plane equilibrium equation and excluded from the in-plane equilibrium equation. In fact, it is difficult to divide resultant strain into initial strain and incremental strain in practical problems, while in classical theory of elasticity, the physical relations of stress and strain for isotropic linear elastic materials, the so-called generalized Hooke’s theorem, are derived from the basic assumptions and definitions of theory of elasticity. In other words, the stress and strain in the generalized Hooke’s theorem refer to the resultant stress and strain of a point on a deformed elastomer, emphasizing the state of stress and strain for any point on the deformed elastomer.

In fact, as far as the solution to the circular membrane problem with pre-stress is concerned, it is not necessary to divide resultant stress/strain into initial stress/strain and incremental stress/strain. In order to make the solution process clear and easy to understand, this paper strictly follows the classical theory of elasticity to solve the circular membrane problem under gas pressure loading analytically and presents a new closed-form solution of the problem under consideration. The originality of this study is mainly reflected in the following two points. In comparison with Fichter’s study [23], this study takes pre-stress into account, while Fichter’s study does not. In comparison with Campbell’s study [24], this study establishes the correct membrane equations from the perspective of mechanics and determines the reasonable boundary conditions according to the physical phenomena; while Campbell, from the perspective of mathematics, modified the Hencky’s membrane equations [1] (suitable for the case without pre-stress) and directly used the boundary conditions, suitable for the case without pre-stress. In addition, this study not only presents the correct membrane equations considering gas pressure loading and pre-stress, but also presents universal boundary conditions that are suitable for the case, without or with pre-stress, and even with tensile pre-stress or with compressive pre-stress. Therefore, the closed-form solution presented in this paper is suitable for the case where the gas pressure loaded circular membrane may, or may not, have pre-stress, and the pre-stress can be either tensile or compressive.

Since in the existing literature there is no such closed-form solution as the one presented in this paper, which considers pre-stress and gas pressure loading, the mechanical properties characterization based on pressured bulge or blister tests [8,14,15,17,18,19,20,21,22] has to use the well-known Hencky solution or its modified solutions, which are suitable for uniform lateral loading, rather than the gas pressure loading. Therefore, with the closed-form solution presented in this paper, the above-mentioned mechanical properties characterization does not have to continue to rely on the well-known Hencky solution or its modified solutions. This is also the significance of this study. The paper is organized as follows. In the following section, the membrane equations are established, the universal boundary conditions are derived, and the closed-form solution for stress and deflection is presented. In Section 3, some important issues, such as the effectiveness and convergence of the presented closed-form solution and the difference between the existing solution and the presented closed-form solution, are discussed, and a simple experiment is conducted. Concluding remarks are given in Section 4.

2. Membrane Equation and Its Solution

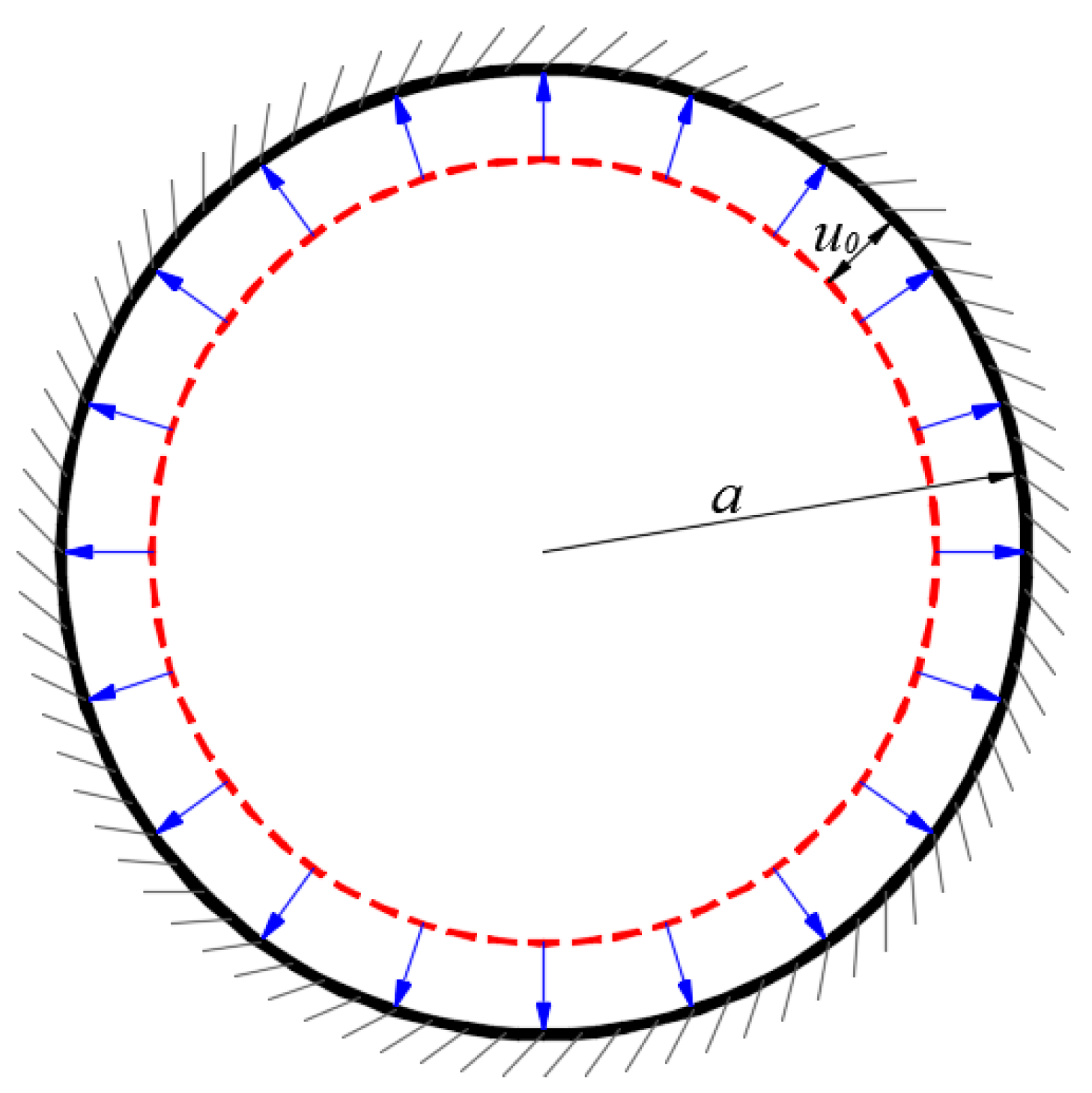
An initially flat, rotationally symmetric, linearly elastic, stress-free circular membrane with Poisson’s ratio $\nu$, Young’s modulus of elasticity E, thickness h is stretched (or compressed) radially in the plane in which the initially flat circular membrane is located, and then is fixed at the edge of radius a, resulting in an exact radial plane displacement u₀ at the radius a, as shown in Figure 1 (exemplified only by the case of stretching), where the dotted line represents the initially flat stress-free (un-stretched) circular membrane. The in-plane stress or strain of the plane-radially stretched circular membrane structure, shown in Figure 1, is uniformly distributed, and at any point on the circular membrane, the circumferential stress or strain is equal to the radial stress or strain, which is confirmed by a detailed derivation that follows. We here focus on the problem of axisymmetric deformation of this plane-radially stretched circular membrane, under the action of gas pressure q, as shown in Figure 2, where the dot dashed line represents the geometric intermediate plane of the plane-radially stretched circular membrane, or the initially flat stress-free (un-stretched) circular membrane, i.e., the plane bisecting the thickness of the plane-radially stretched circular membrane, or the initially flat stress-free (un-stretched) circular membrane. Obviously, relative to the stress caused by the gas pressure q, the in-plane stress before the action of the gas pressure q could be called initial stress or pre-stress. Thus the plane-radially stretched circular membrane is usually called the circular membrane with initial stress, or more briefly the pre-stressed circular membrane. In fact, the initially flat circular membrane could also be plane-radially compressed (shrunk), which could be thought of as being negatively stretched and corresponds to the case of u₀ < 0. Therefore, the so-called initial stress or pre-stress could be less than zero, equal to zero, or greater than zero, corresponding to compressing case (u₀ < 0), classic case (u₀ = 0), and stretching case (u₀ > 0), respectively.

To solve the axisymmetric deformation problem shown in Figure 2 analytically, we employ a cylindrical polar coordinate system (r, φ, w), where r and φ denote the radial and circumferential coordinates of the polar coordinate system (r, φ), w denotes the cylindrical coordinate, the origin of the cylindrical polar coordinate system (r, φ, w) is placed in the centroid of the geometric intermediate plane of the initially flat circular membrane, the polar coordinate plane (r, φ) is placed in the plane in which the geometric intermediate plane is located, the positive direction of the w-axis corresponds to the deflecting direction of the pre-stressed circular membrane, and w also denotes the deflection or transverse displacement of any point on the geometric intermediate surface of the deflected pre-stressed circular membrane, as shown in Figure 2. The so-called geometric intermediate surface of the deflected pre-stressed circular membrane refers to the curved surface that bisects its thickness, and is actually the one after the geometric intermediate plane of the initially flat pre-stressed circular membrane is deflected under the action of gas pressure q. Therefore, after ignoring the change in thickness of the membrane during axisymmetric deformation, the problem of axisymmetric deformation of the initially flat pre-stressed circular membrane under gas pressure q can be simplified into a deflection problem of its geometric intermediate plane under gas pressure q.

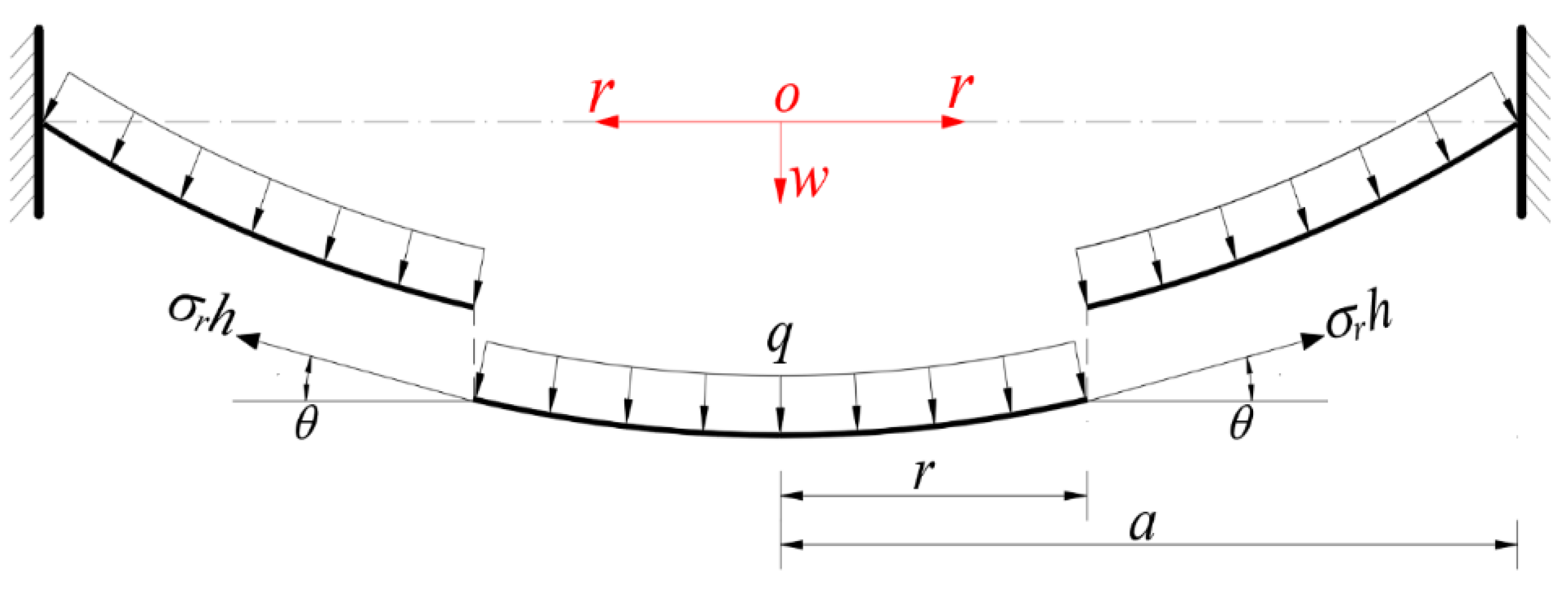
The geometric intermediate surface of the deflected pre-stressed circular membrane, which is endowed with all materials and their mechanical responses, is taken away a free body from its central portion, to study the static equilibrium problem of this free body under the joint action of the gas pressure q and the membrane force σ_rh acted on the boundary of the free body, just as it is shown in Figure 3, where σ_r denotes radial stress, h denotes the thickness of the membrane, and θ is the slope angle of the deflected pre-stressed circular membrane, which varies with radial coordinate r. Right here there are two vertical (transverse) forces whose direction is perpendicular to the polar coordinate plane, i.e., the total vertical force πr²q (0 ≤ r ≤ a) of the gas pressure q [23] and the total vertical force 2πrσ_rhsinθ that is produced by the membrane force σ_rh. Therefore, from the condition of the resultant force being zero at the direction perpendicular to the polar coordinate plane we may have

$$2\pi r{\sigma }_{r}h\sin \theta =\pi r^{2}q.$$

(1)

Equation (1) is the usually so-called out-of-plane equilibrium equation, where

$$\sin \theta =-\mathrm{d}w/\mathrm{d}r.$$

(2)

Substituting Equation (2) into Equation (1), one has

$$\frac{1}{2}rq+{\sigma }_{r}h\frac{\mathrm{d}w}{\mathrm{d}r}=0.$$

(3)

In the horizontal direction parallel to the polar coordinate plane, for any infinitesimal element taken away from the geometric intermediate surface of the deflected pre-stressed circular membrane, there are two kinds of horizontal forces: one is from the membrane force, including the horizontal component of radial membrane force ${\sigma }_{r}h$ and the circumferential membrane force ${\sigma }_{t}h$ (here ${\sigma }_t$ is the circumferential stress), and the other is from the horizontal component of the gas pressure q acted on the infinitesimal element. The so-called in-plane equilibrium equation can be obtained by summing the horizontal forces on the infinitesimal element, which is seen to be [23].

$${\sigma }_{t}h=\frac{\mathrm{d}}{\mathrm{d}r}\left(r{\sigma }_{r}h\right)-qr\frac{\mathrm{d}w}{\mathrm{d}r}.$$

(4)

Suppose that $e_r$ is the radial strain, $e_t$ is the circumferential strain, $u(r)$ is the radial displacement at r, and $w(r)$ is the transversal displacement at r. Then the usually so-called geometric equations, i.e., the relations of the strain and displacement, may be written as

$$e_r=\frac{\mathrm{d}u}{\mathrm{d}r}+\frac{1}{2}{(\frac{\mathrm{d}w}{\mathrm{d}r})}^2$$

(5)

and

$$e_t=\frac{u}{r}.$$

(6)

Furthermore, the relations of the stress and strain, i.e., the usually so-called physical equations, satisfy the generalized Hooke’s law due to the membrane assumed to be linearly elastic, and can be written as

$${\sigma }_r=\frac{E}{1-{\nu }^2}(e_r+\nu e_t)$$

(7)

and

$${\sigma }_t=\frac{E}{1-{\nu }^2}(e_t+\nu e_r).$$

(8)

Substituting Equations (5) and (6) into Equations (7) and (8) yields

$${\sigma }_r=\frac{E}{1-{\nu }^2}[\frac{\mathrm{d}u}{\mathrm{d}r}+\frac{1}{2}{(\frac{\mathrm{d}w}{\mathrm{d}r})}^2+\nu \frac{u}{r}]$$

(9)

and

$${\sigma }_t=\frac{E}{1-{\nu }^2}[\frac{u}{r}+\nu \frac{\mathrm{d}u}{\mathrm{d}r}+\frac{\nu }{2}{(\frac{\mathrm{d}w}{\mathrm{d}r})}^2].$$

(10)

By means of Equations (9), (10) and (4), one has

$$\frac{u}{r}=\frac{1}{Eh}\left({\sigma }_{t}h-\nu {\sigma }_{r}h\right)=\frac{1}{Eh}\left[\frac{\mathrm{d}}{\mathrm{d}r}\left(r{\sigma }_{r}h\right)-\nu {\sigma }_{r}h-qr\frac{\mathrm{d}w}{\mathrm{d}r}\right].$$

(11)

After substituting the u in Equation (11) into Equation (9), the usually so-called consistency equation can be written as

$$3r\frac{\mathrm{d}}{\mathrm{d}r}\left({\sigma }_{r}h\right)+r^2\frac{{\mathrm{d}}^2}{\mathrm{d}{r}^2}\left({\sigma }_{r}h\right)+\frac{Eh}{2}{\left(\frac{\mathrm{d}w}{\mathrm{d}r}\right)}^2-\left[r\frac{{\mathrm{d}}^{2}w}{\mathrm{d}{r}^2}+\left(\nu +2\right)\frac{\mathrm{d}w}{\mathrm{d}r}\right]qr=0.$$

(12)

Equations (3), (4) and (12) are three equations for the solutions of ${\sigma }_r$, ${\sigma }_t$ and $w$.

Based on the following solution to the problem of the plane-radially stretching of the initially flat, stress-free circular membrane, the boundary conditions, under which Equations (3), (4) and (12) can be solved, can be determined. For the case where the initially flat, stress-free circular membrane is plane-radially stretched and produces a radial plane displacement u₀ at r = a, obviously $\mathrm{d}w/\mathrm{d}r=0$. Therefore, substituting $\mathrm{d}w/\mathrm{d}r=0$ into Equation (4) yields

$$\frac{\mathrm{d}}{\mathrm{d}r}(r{\sigma }_r)-{\sigma }_t=0.$$

(13)

Equation (13) is the classic in-plane equilibrium equation which is suitable for the problem of the axisymmetric deformation of the transversely loaded circular membrane. Further, substituting $\mathrm{d}w/\mathrm{d}r=0$ into Equation (5) yields

$$e_r=\frac{\mathrm{d}u}{\mathrm{d}r}.$$

(14)

Substituting Equations (14) and (6) into Equations (7) and (8), one has

$${\sigma }_r=\frac{E}{1-{\nu }^2}(\frac{\mathrm{d}u}{\mathrm{d}r}+\nu \frac{u}{r})$$

(15)

and

$${\sigma }_t=\frac{E}{1-{\nu }^2}(\frac{u}{r}+\nu \frac{\mathrm{d}u}{\mathrm{d}r}).$$

(16)

By substituting Equations (15) and (16) into Equation (13) and using the condition of dw/dr = 0, we can obtain a Euler equation that contains only the radial displacement u

$$r^2\frac{{\mathrm{d}}^{2}u}{\mathrm{d}{r}^2}+r\frac{\mathrm{d}u}{\mathrm{d}r}-u=0.$$

(17)

As is known, the general solution of Equation (17) may be written as

$$u=C_{1}r+C_2/r,$$

(18)

where C₁ and C₂ are two undetermined constants. According to the physical characteristics of the axisymmetric in-plane deformation of the plane-radially stretched or compressed circular membrane, the conditions for determining C₁ and C₂ are

$$u=0 \mathrm{at} r=0$$

(19)

and

$$u=u_0 \mathrm{at} r=a.$$

(20)

Obviously, the radial displacement u is finite at r = 0, therefore it can be found from Equation (19) that C₂ has to be equal to zero. Further, with C₂ = 0 we can, from Equation (20), obtain C₁ = u₀/a. Therefore, the special solution of Equation (17) is

$$u=\frac{u_0}{a}r.$$

(21)

Substituting Equation (21) into Equations (6) and (14)–(16), it is found that

$$e_r=e_t=\frac{u_0}{a}=e_0$$

(22)

and

$${\sigma }_r={\sigma }_t=\frac{E}{1-\nu }\frac{u_0}{a}={\sigma }_0.$$

(23)

Here, ${\sigma }_0$ denotes the so-called initial stress or pre-stress in the initially flat, plane-radially stretched or compressed circular membrane, and $e_0$ is the initial strain. Equations (22) and (23) indicate that the result of plane-radially stretching or compressing an initially flat, stress-free circular membrane is that the stress or strain in the plane-radially stretched or compressed circular membrane is uniformly distributed, i.e., at all points on the membrane the stress or strain is the same, especially the circumferential stress ${\sigma }_t$ is equal to the radial stress ${\sigma }_r$ and the circumferential strain $e_t$ is equal to the radial strain $e_r$. Therefore, after the plane-radially stretched or compressed circular membrane is fixed at the edge of radius a, the membrane remains flat and has a uniform in-plane stress ${\sigma }_0$ and strain $e_0$. Thus, the boundary conditions for solving Equations (3), (4) and (12) can finally be written as

$$\frac{\mathrm{d}w}{\mathrm{d}r}=0 \mathrm{at} r=0,$$

(24)

$$e_t=\frac{u}{r}=\frac{1}{Eh}\left[\frac{\mathrm{d}}{\mathrm{d}r}\left(r{\sigma }_{r}h\right)-\nu {\sigma }_{r}h-qr\frac{\mathrm{d}w}{\mathrm{d}r}\right]=e_0=\frac{1-\nu }{E}{\sigma }_0 \mathrm{at} r=a$$

(25)

and

$$w=0 \mathrm{at} r=a.$$

(26)

Here, the uniform in-plane stress ${\sigma }_0$ is the so-called pre-stress, which is usually used as a parameter to describe a circular membrane problem with pre-stress (in place of the parameter u₀, the radial plane displacement).

Now, let us introduce the following nondimensionalization

$$Q=\frac{aq}{hE},W=\frac{w}{a},S_r=\frac{{\sigma }_r}{E},S_t=\frac{{\sigma }_t}{E},S_0=\frac{{\sigma }_0}{E},x=\frac{r}{a},$$

(27)

and transform Equations (3), (4), (12) and (24)–(26) into

$$\frac{1}{2}xQ+S_r\frac{\mathrm{d}W}{\mathrm{d}x}=0,$$

(28)

$$\frac{\mathrm{d}}{\mathrm{d}x}(x{S}_r)-S_t-xQ\frac{\mathrm{d}W}{\mathrm{d}x}=0,$$

(29)

$$3x\frac{\mathrm{d}}{\mathrm{d}x}(S_r)+x^2\frac{{\mathrm{d}}^2}{\mathrm{d}{x}^2}(S_r)+\frac{1}{2}{(\frac{\mathrm{d}W}{\mathrm{d}x})}^2-Qx\left[x\frac{{\mathrm{d}}^2}{\mathrm{d}{x}^2}(W)+(\nu +2)\frac{\mathrm{d}W}{\mathrm{d}x}\right]=0,$$

(30)

$$\frac{\mathrm{d}W}{\mathrm{d}x}=0 \mathrm{at} x=0,$$

(31)

$$(1-\nu \left)\right(S_r-S_0) + x\frac{d{S}_r}{dx}-Qx\frac{dW}{dx}=0 \mathrm{at} x=1$$

(32)

and

$$W=0 \mathrm{at} x=1.$$

(33)

Obviously, the stress and deflection are both finite at $x=0$, therefore $S_r$ and W can be expanded into the power series in x

$$S_r(x)={\displaystyle \sum _{i=0}^{\infty }{c}_i{x}^i}$$

(34)

and

$$W(x)={\displaystyle \sum _{i=0}^{\infty }{d}_i{x}^i}.$$

(35)

After substituting Equations (34) and (35) into Equations (28) and (30), it is found, by using the mathematical software Maple 2018, that $c_i\equiv 0$ and $d_i\equiv 0$ when i is odd, and when i is even, the coefficients $c_i$ and $d_i$ can be expressed into the polynomial function with regard to the coefficient $c_0$, which is, respectively, listed in Appendix A (for $c_i$) and Appendix B (for $d_i$).

The remaining two coefficients $c_0$ and $d_0$ are two undetermined constants depending on the specific problem addressed and can be determined by using the boundary conditions of Equations (32) and (33) as follows. From Equations (34) and (35), the boundary condition of Equation (32) gives

$$(1-\nu ){\displaystyle \sum _{i=0}^{\infty }{c}_i}+{\displaystyle \sum _{i=1}^{\infty }i{c}_i}-Q{\displaystyle \sum _{i=1}^{\infty }i{d}_i}=(1-\nu )S_0.$$

(36)

Substituting all expressions of $c_i$ and $d_i$ (i = 2, 4, 6, …) into Equation (36), we can obtain an equation that contains only the undetermined constant $c_0$. Therefore, $c_0$ can be determined by solving this univariate equation for $c_0$, and as a result, the expression of $S_r$ can also be determined. Further, from Equation (35) the condition of Equation (33) gives

$$d_0={\displaystyle \sum _{i=1}^{\infty }{d}_i}.$$

(37)

Obviously, at this time, all the coefficients $d_i$ are known, because $d_i\equiv 0$ when i is odd and when i is even $d_i$ can be determined with the known $c_0$. Therefore, after substituting all the known coefficients $d_i$ into Equation (37), the remaining undetermined constant $d_0$ can finally be determined, and also the expression of $W$ can be determined. Furthermore, with the known expressions of $S_r$ and $W$, the expression of $S_t$ can easily be determined by using Equation (29).

At this point, the problem addressed here has been analytically solved perfectly, and its closed-form solutions for stress and deflection has been given.

3. Results and Discussions

Firstly, let us see whether the analytical solution obtained in Section 2 meets Equation (24) or Equation (31), the boundary condition that has not been used yet during the derivation, that is, $\mathrm{d}w/\mathrm{d}r=0$ at $r=0$. The dimensional form of the deflection $w(r)$ can be written as, from Equations (27) and (35)

$$w(r)={\displaystyle \sum _{i=0}^{\infty }\frac{d_i}{a^{i-1}}{r}^i},$$

(38)

and the first derivative on both sides of Equation (38) is

$$\frac{\mathrm{d}w}{\mathrm{d}r}={\displaystyle \sum _{i=1}^{\infty }\frac{i{d}_i}{a^{i-1}}{r}^{i-1}}.$$

(39)

Obviously, from Equation (39) it can be found that $\mathrm{d}w/\mathrm{d}r\equiv d_1$ at $r=0$. However, from Section 2, we know that $d_1\equiv 0$ due to $d_i\equiv 0$ (i = 1, 3, 5, …). Thus, $\mathrm{d}w/\mathrm{d}r\equiv 0$ at $r=0$, which indicates that the analytical solution obtained in Section 2 can automatically meet Equation (24) or Equation (31) and is reliable to some extent.

Now, let us consider a circular membrane with Poisson’s ratio $\nu =0.45$, Young’s modulus of elasticity $E=7.84 \mathrm{MPa}$, thickness $h=0.2 \mathrm{mm}$ and radius $a=70 \mathrm{mm}$, as a numerical example to illustrate how to use the closed-form solution presented in Section 2. Suppose that the circular membrane is subjected to a gas pressure q = 0.008 MPa and is pre-stressed with ${\sigma }_0=-0.2 \mathrm{MPa}$, ${\sigma }_0=0 \mathrm{MPa}$ and ${\sigma }_0=0.2 \mathrm{MPa}$, respectively. For convenience of operation, the infinite power series in Equations (36) and (37) have to be truncated to n terms, that is,

$$(1-\nu ){\displaystyle \sum _{i=0}^n{c}_i}+{\displaystyle \sum _{i=1}^{n}i{c}_i}-\frac{aq}{hE}{\displaystyle \sum _{i=1}^{n}i{d}_i}=(1-\nu )\frac{{\sigma }_0}{E}$$

(40)

and

$$d_0={\displaystyle \sum _{i=1}^n{d}_i}.$$

(41)

Equations (40) and (41) are used to determine the specific numerical values of the undetermined constants $c_0$ and $d_0$ for this three circular membrane problems. Here, a so-called asymptotic approximant is used to find the more accurate numerical values of the undetermined constants $c_0$ and $d_0$. To this end, the parameter n in Equations (40) and (41) has to take its value from a relatively small number (usually from n = 4). A pair of numerical values of the undetermined constants $c_0$ and $d_0$ can first be obtained by using Equations (40) and (41) with n = 4, and the second pair of numerical values of the undetermined constants $c_0$ and $d_0$ can also be obtained by using Equations (40) and (41), with n = 6 (skip n = 5 because $c_i\equiv 0$ and $d_i\equiv 0$ when i is odd). Continue the numerical value calculation of the undetermined constants $c_0$ and $d_0$ with n = 8, if the difference between the numerical values of $c_0$ or $d_0$, which are obtained with n = 4 and n = 6, is not as small as you wish. If the difference between the numerical values of $c_0$ or $d_0$, which are obtained with n = 6 and n = 8, is as small as you wish, stop the numerical value calculation of the undetermined constants $c_0$ and $d_0$, otherwise, continue the numerical value calculation with the next value of the parameter n until the difference between the obtained numerical values of $c_0$ or $d_0$ is small enough as you wish.

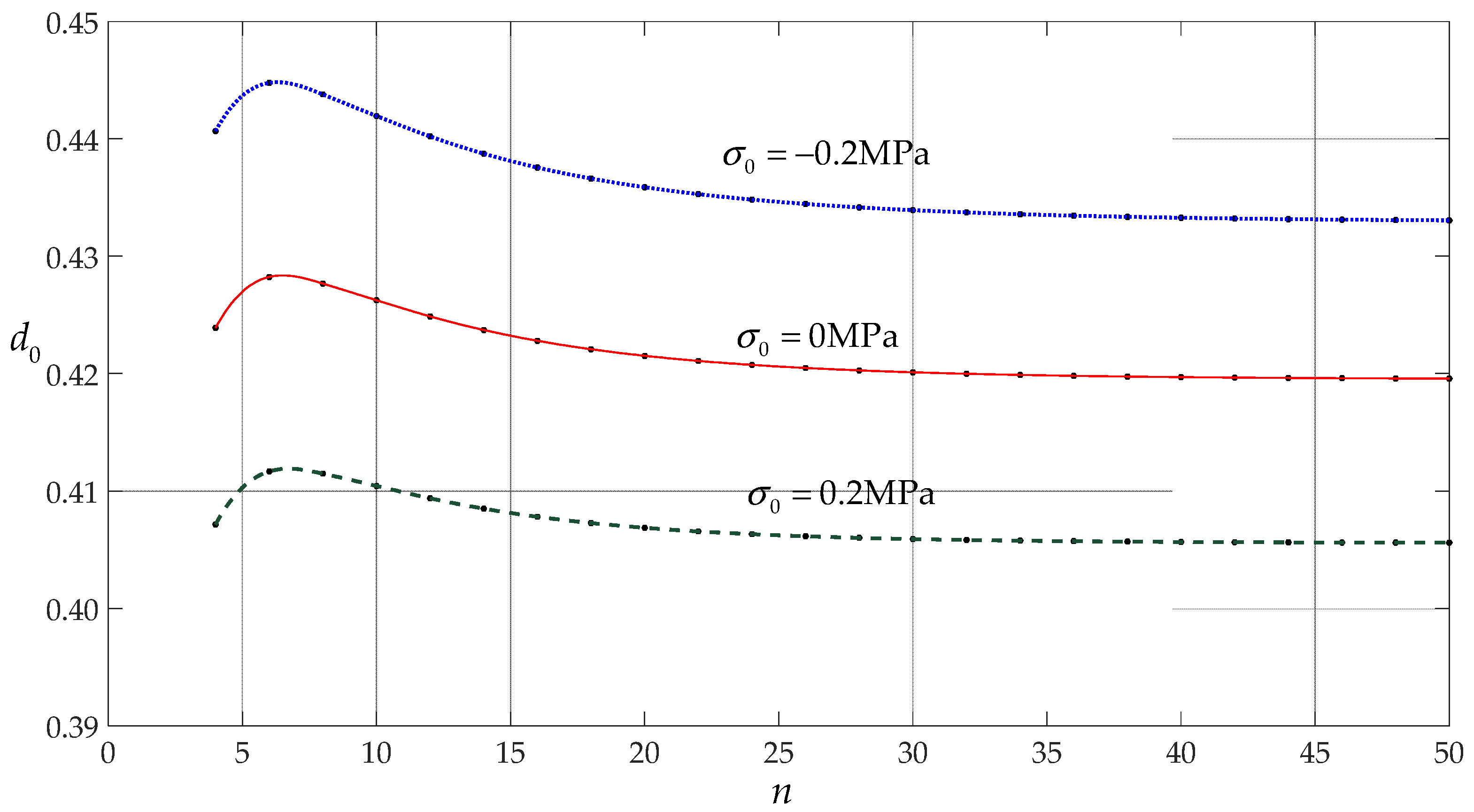
The obtained numerical values of the undetermined constants $c_0$ and $d_0$ under different parameter n and pre-stress σ₀ are listed in

Table 1. Numerical values of c₀ under different parameter n and pre-stress σ₀.

n	c0 (σ0 = −0.2 MPa)	c0 (σ0 = 0 MPa)	c0 (σ0 = 0.2 MPa)
4	0.033575757	0.036718983	0.040895160
6	0.034571798	0.037437982	0.041351580
8	0.034937506	0.037668787	0.041471936
10	0.035090915	0.037752220	0.041506960
12	0.035160346	0.037784376	0.041517690
14	0.035193278	0.037797245	0.041521070
16	0.035209381	0.037802520	0.041522156
18	0.035217421	0.037804718	0.041522510
20	0.035221493	0.037805644	0.041522626
22	0.035223579	0.037806037	0.041522665
24	0.035224656	0.037806206	0.041522678
26	0.035225216	0.037806279	0.041522682
28	0.035225508	0.037806310	0.041522684
30	0.035225662	0.037806324	0.041522684
32	0.291048183	0.294766104	0.299135074
34	0.291111023	0.294823088	0.299173082
36	0.291160458	0.294866648	0.299201321
38	0.291199517	0.294900099	0.299222391
40	0.291230497	0.294925891	0.299238168
42	0.291255153	0.294945846	0.299250020
44	0.291274833	0.294961334	0.299258948
46	0.291290585	0.294973386	0.299265689
48	0.291301202	0.294982788	0.299270792
50	0.291303222	0.294990139	0.299274660

and

Table 2. Numerical values of d₀ under different parameter n and pre-stress σ₀.

n	d0 (σ0 = −0.2 MPa)	d0 (σ0 = 0 MPa)	d0 (σ0 = 0.2 MPa)
4	0.191259377	0.170013719	0.148629681
6	0.190695512	0.169946392	0.148823819
8	0.190025293	0.169675311	0.148764097
10	0.189609686	0.169517042	0.148725927
12	0.189376490	0.169439316	0.148709778
14	0.189249321	0.169403143	0.148703640
16	0.189180665	0.169386685	0.148701407
18	0.189143746	0.169379280	0.148700612
20	0.189123924	0.169375968	0.148700331
22	0.189113288	0.169374491	0.148700233
24	0.189107580	0.169373833	0.148700199
26	0.189104516	0.169373541	0.148700187
28	0.189102870	0.169373411	0.148700183
30	0.189101985	0.169487693	0.148700182
32	0.433731681	0.419987899	0.405828941
34	0.433578999	0.419888878	0.405769100
36	0.433455904	0.419810953	0.405723345
38	0.433356458	0.419749529	0.405688320
40	0.433275966	0.419701040	0.405661478
42	0.433210705	0.419662710	0.405640887
44	0.433157713	0.419632375	0.405625077
46	0.433114625	0.419608340	0.405612927
48	0.433079546	0.419589278	0.405603582
50	0.433050957	0.419574146	0.405596390

. It may be seen, from Table 1 and Table 2, that the difference between the numerical values of $c_0$ or $d_0$, which are obtained with n = 48 and n = 50, is very small. Their convergence trend is shown in Figure 4 and Figure 5. It may be seen, from Figure 4 or Figure 5, that as the parameter n is increased, the data sequence for ${\sigma }_0=0.2 \mathrm{MPa}$ converge rapidly to the theoretical values (unknown exact values) of the undetermined constants $c_0$ or $d_0$, whereas the data sequence for ${\sigma }_0=0 \mathrm{MPa}$ converge relatively slowly, and the convergence rate of the data sequence for ${\sigma }_0=-0.2 \mathrm{MPa}$ is the slowest of the three cases. This means that the pre-stress ${\sigma }_0$ has an effect on the convergence rate. Meanwhile, it may also be seen, from Figure 4 or Figure 5, that the pre-stress ${\sigma }_0$ also has an effect on the size of the unknown exact values of the undetermined constants $c_0$ and $d_0$, that is, it affects the determination of the theoretical values of the undetermined constants $c_0$ and $d_0$.

The very good convergence exhibited in Figure 4 and Figure 5 allows the undetermined constants $c_0$ and $d_0$ to take 0.291303222 and 0.433050957 as the approximations for the case of ${\sigma }_0=-0.2\mathrm{MPa}$, 0.294990139 and 0.419574146 for ${\sigma }_0=0\mathrm{MPa}$, and 0.299274660 and 0.405596390 for ${\sigma }_0=0.2\mathrm{MPa}$ (see Table 1 and Table 2). Thus, the special solutions of the deflection $w(r)$ and radial stress ${\sigma }_r(r)$ can finally be determined. The geometry of the deflected circular membrane along the radius of the circular membrane is depicted in Figure 6, and the distribution of radial stress along the radius of the circular membrane is shown in Figure 7.

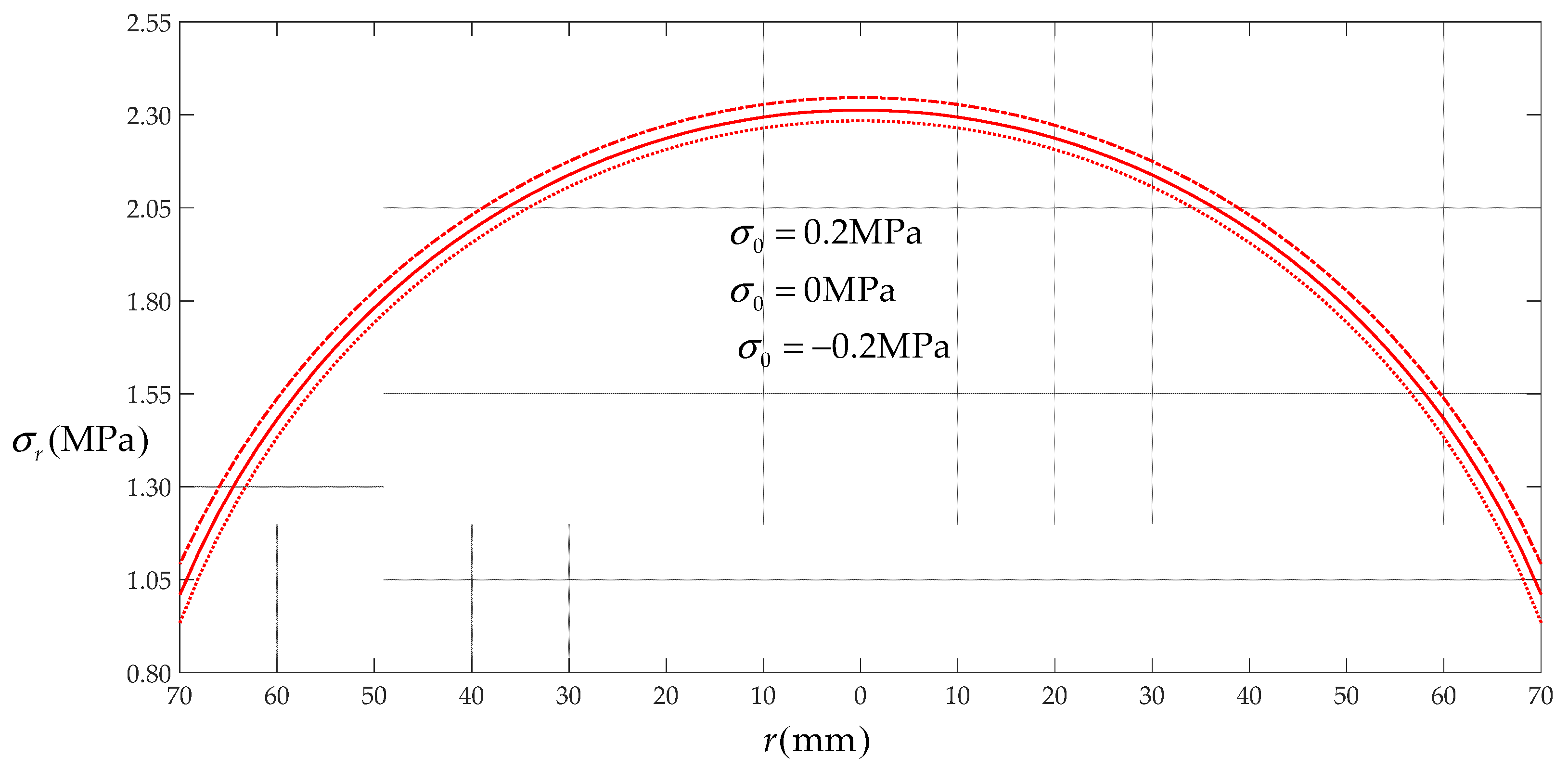
Now, let us show the difference between the solution presented in this paper and the solutions presented by Fichter [23] and Campbell [24]. Figure 8 and Figure 9 show the variations of the deflection $w(r)$ and radial stress ${\sigma }_r(r)$ with the radius r, where the solution 1 refers to the solution presented by Fichter [23], the solution 2 refers to the solution presented by Campbell [24], and the solution 3 refers to the solution presented in this paper.

From Figure 8b and Figure 9b, it may be seen that when ${\sigma }_0=0 \mathrm{MPa}$ the deflection or stress curve by solution 3 (which is presented by this paper) basically coincides with the curve by solution 1 (which is presented by Fichter [23]). This proves to some extent that the process of solving in Section 2 of this paper is correct and the closed-form solution presented is reliable, because solution 3 should be returned to solution 1 when the pre-stress is equal to zero. However, it may also be seen from Figure 8 and Figure 9 that the deflection and stress curves by solution 2 (which is presented by Campbell [24]) are far from the curves by solution 1 or 3, especially the stress curve (the maximum relative error of solution 2 to solution 1 or 3 is about 25% for ${\sigma }_0=-0.2 \mathrm{MPa}$, 24% for ${\sigma }_0=0 \mathrm{MPa}$ and 23% for ${\sigma }_0=0.2 \mathrm{MPa}$). This means that if solution 1 is reliable, then solution 3 should also be reliable, and therefore solution 2 must be unreliable.

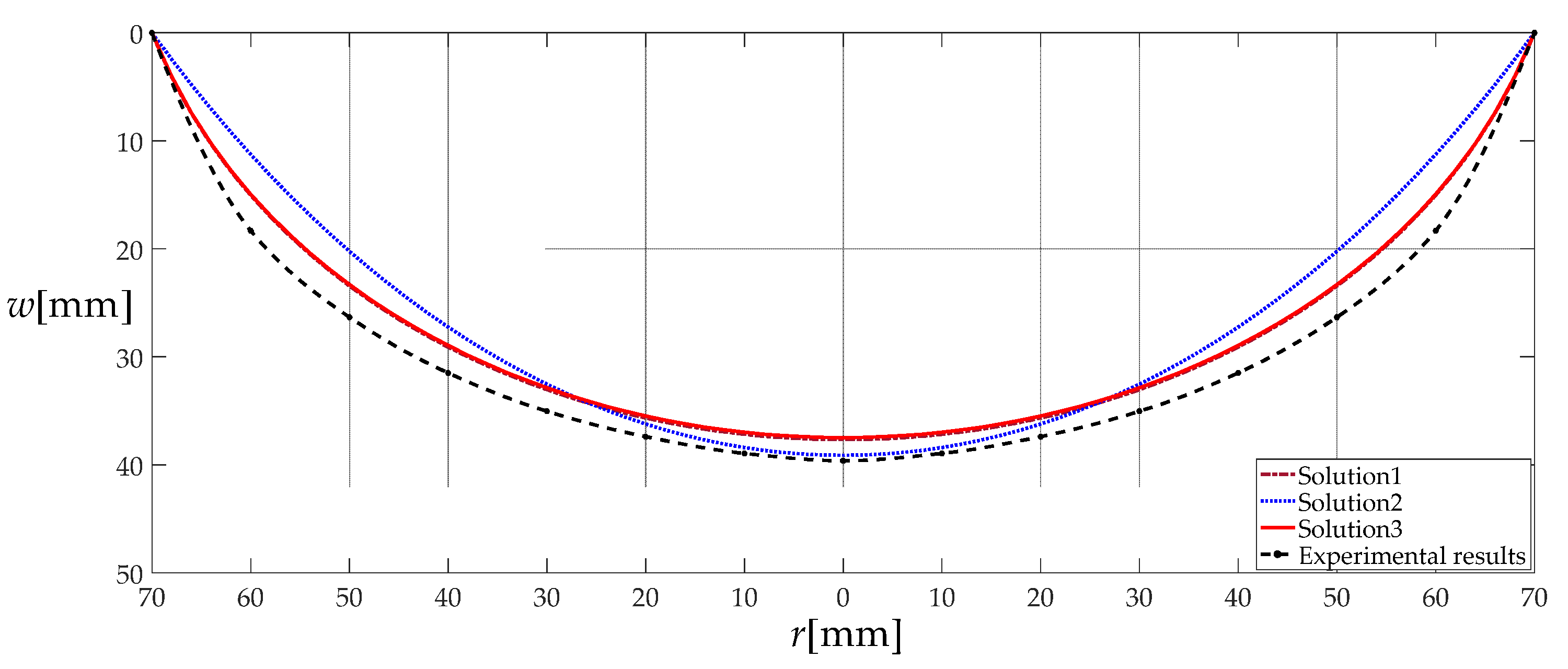
Now, let us consider a simple experiment to test the accuracy of the solutions presented by Fichter [23], Campbell [24] and this paper. An initially flat stress-free circular natural latex thin film with Young’s modulus of elasticity E = 0.941 MPa, Poisson’s ratio $\nu =0.43$, thickness h = 0.8, and radius a = 70 mm is subjected to the action of gas pressure q = 0.008 MPa, as shown in Figure 10. A non-contact laser displacement sensor (ZSY Group Ltd., London, UK) is employed to measure the membrane deflection. The measured membrane deflection along the radius of the circular membrane is shown in Figure 11, where solution 1 refers to the solution presented by Fichter [23], solution 2 by Campbell [24], and solution 3 by this paper. From Figure 11, it may be seen that within r = 20 mm the Campbell’s solution outperforms the solutions presented by Fichter [23] and by this paper, but it becomes worse and worse as r becomes bigger, especially on the scale of r = 40–60 mm. This is because the Campbell’s solution uses Hencky’s in-plane equilibrium equation [1,24], thus neglecting the horizontal component of the applied gas pressure q, performing poorly on both sides.

Table 3. The measured and calculated results of deflection and relative errors.

r (mm)	Measured Results (mm)	Calculated Results by Solution 2 and Relative Errors to Measured Results		Calculated Results by Solution 3 or 1 and Relative Errors to Measured Results
		Results (mm)	Error	Results (mm)	Error
0	39.52	39.02	1.27%	37.85	4.22%
10	38.94	38.40	1.39%	36.98	5.02%
20	37.39	36.21	3.13%	35.48	5.11%
30	35.03	32.53	7.16%	32.86	6.20%
40	31.49	27.14	13.81%	28.94	8.09%
50	26.43	20.07	24.06%	23.42	11.39%
60	18.32	11.13	39.25%	15.12	17.47%

shows the measured and calculated results of deflection and the relative errors of calculation to measurement. It may be seen from Figure 11 or Table 3 that the overall effect of the closed-form solution presented in this paper is better than that of Campbell’s solution [24].

4. Concluding Remarks

In this study, the problem of axisymmetric deformation and deflection of an initially flat circular membrane under in-plane radial stretching or compressing and out-of-plane gas pressure loading is solved analytically, and a new closed-form solution of the problem is presented. From this study, the following conclusions can be drawn.

From Table 1 and Table 2 or Figure 4 and Figure 5, it may be seen that the initial in-plane stress or pre-stress will affect the convergence of the undetermined constants $c_0$ and $d_0$, and the greater the pre-stress, the faster the undetermined constants $c_0$ and $d_0$ converge. Therefore, in order to make sure that a more accurate numerical value can be obtained for the undetermined constants $c_0$ and $d_0$, the parameter n in Equations (40) and (41) must start from a relatively small number and eventually reach a number as large as possible, especially when the pre-stress is negative or zero.

From Figure 8, Figure 9 and Figure 11, it may be seen that the difference between the solution presented by Campbell [24] and the solution presented in this paper is not very significant for deflection calculation (see Figure 8) but is quite significant for stress calculation (see Figure 9). However, the shape of the deflection curve calculated by the solution presented by Campbell [24] is too different from the experimental results (see Figure 11 or Table 3), which will affect some technical applications, such as using closed-form solutions to predict the shape of orbiting inflatable reflectors [23]. Therefore, the solution presented by Campbell [24] is generally unreliable and should not be recommended.

From the derivation of the boundary conditions in Section 2, it may be seen that the derived boundary conditions, Equations (24)–(26), can be called universal boundary conditions, because the case of ${\sigma }_0=0$ in Equation (25) corresponds to the circular membrane without pre-stress, ${\sigma }_0>0$ corresponds to the circular membrane with tensile pre-stress, and ${\sigma }_0<0$ corresponds to the circular membrane with compressive pre-stress. Therefore, the closed-form solution obtained in Section 2 can be applied to the case where the initially flat circular membrane may or may not have a uniform in-plane stress before deflection, and the in-plane stress can be either tensile or compressive.

The closed-form solutions are often found to be necessary in many technical applications, such as the above-mentioned shape prediction of the orbiting inflatable reflector [23], and the characterization of mechanical properties of freestanding thin films, or thin-film/substrate systems based on pressured bulge or blister tests [8,14,15,17,18,19,20,21,22], while a numerical analysis is helpless in these technical applications due to the rigid demand for analytical relationships. The closed-form solutions of stress and deflection presented in this paper can provide these technical applications with a required analytical relationship between deflection or stress and loads or blister radius. However, it may also be seen from Figure 11 or Table 3 that the computational accuracy of this closed-form solution is still not very satisfactory and needs further improvement.