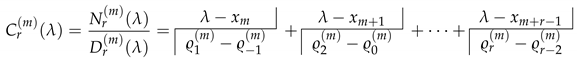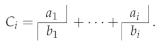The Legacy of Peter Wynn
Abstract
| Contents | ||
| Introduction.......................................................................................................................... | 2 | |
| The Discovery....................................................................................................................... | 4 | |
| Mathematical Background.................................................................................................. | 7 | |
| The Shanks Transformation and the ε-algorithms.................................................... | 7 | |
| Padé Approximation..................................................................................................... | 9 | |
| Continued Fractions...................................................................................................... | 9 | |
| Rational Interpolation................................................................................................... | 11 | |
| The Legacy............................................................................................................................. | 11 | |
| Main Documents........................................................................................................... | 11 | |
| Complex Analysis and Continued Fractions..................................................... | 11 | |
| Interpolation.......................................................................................................... | 17 | |
| The ε-algorithm..................................................................................................... | 24 | |
| Project for a Book.................................................................................................. | 32 | |
| Algebra................................................................................................................... | 33 | |
| Software.................................................................................................................. | 35 | |
| Unpublished Typewritten Documents........................................................................ | 36 | |
| Other Documents.......................................................................................................... | 36 | |
| Drafts on Analysis................................................................................................ | 36 | |
| Drafts on Algebra.................................................................................................. | 37 | |
| Personal Documents............................................................................................. | 38 | |
| References............................................................................................................................. | 40 | |
| References of Peter Wynn............................................................................................ | 40 | |
| Translations by Peter Wynn......................................................................................... | 44 | |
| General Bibliography.................................................................................................... | 44 | |
1. Introduction
2. The Discovery
I have just now read your recent remembrance of Peter Wynn appearing in Numerical Algorithms. I was charmed—thank you for that. But I am also very much interested because, serendipitously, I have just today “inherited” from a retired colleague several rather heavy boxes of Wynn’s papers which had been left with my colleague for safekeeping (or convenience) some years earlier.I have not yet opened the boxes, but I will begin examining the contents soon. The reason I am writing you is to ask if you would be willing to answer a couple of questions, which I pose below.As I begin looking at the material, I could find (1) drafts of papers that might be of interest to mathematicians, (2) personal items that might be of interest to family or friends, (3) miscellany that would be of little interest to anyone, or (4) items for which I am at a loss to know whether to keep or discard […]Here are my questions to you:In case I find material that looks as if it might have some mathematical import, would you be willing to take look at it, or could you suggest someone who would be?
I have opened two of the four boxes, looking thoroughly through the contents of one of them.FIRST BOXThe first box was a smaller one containing several hundreds of pages of handwritten notes and a few other random items. In this and the next message, I have attached several of the smaller items that might be indicative of material to come. Nothing is dated so I have no idea whether this material simply anticipates papers that have been completed and published or represents new work. In addition, not much is paginated, so I generally presume that the order in which pages appear is the order in which they were completed and assembled. Some of this material was left with Dr. Berriozábal here in San Antonio after Peter had visited Mexico and there are some suggestions (e.g., written accounts of receipts) that suggest that some of the material was produced while he was living in Mexico. Whether this was after his last publication in 1981, I do not know.To Do List:The first document above appears to be a list of various topics he wished to address, mainly through the construction of relevant notes.Projects:This document lists a number of projects that he had planned and may well have completed. Whether these “projects” have found their way into the literature as published papers, I do not know. I’ve copied a snapshot from the document and you will note that some of the items have been denoted with a “D__”. Perhaps this is Peter’s shorthand for “Done” or fait accompli. I didn’t see in his publications any that specifically included, for example, “stratified commutative ring” or “Bürmann series”, so perhaps this represents some work that hasn’t yet been published, but will appear somewhere in his collection of notes. I did find the beginnings of what looks to be a monograph on Interpolation Theory–the first in his list of projects and one that doesn’t seem to have been completed at that time.Duplicate List:This may reflect a list of some of the items that Peter included in his boxes of documents.The next messages will include 2 larger documents, one a bibliography and the other a more extensive list of documents.Other items in this first box include the aforementioned piece of a monograph on Interpolation Theory, as well as a couple of hundred pages of paginated notes of another document. In that case, I see pages 70–300+ so I can’t be sure of the initial title. There is another paginated treatment of a topic (I don’t recall exactly what at the moment), a book review, and some hundreds of other pages of notes that do not appear to fit together well.SECOND BOXI’ll mention here that the second box, one that originally held a dozen reams of office paper, now holds about 20 kg of handwritten notes. I have not yet examined these notes in detail, and when I do, I want to be careful not to disturb the assembly of any documents.Bibliography:This is likely not anything that you would use. I imagine Peter kept this bibliography simply for reference purposes.List of documents:This seems to be a list of documents and/or things he felt he needed to do, such as copy this or Xerox that. I don’t know if it has any intrinsic value, but it might reflect documents included among his papers.
We liked his visits. Each time he came it was without much notice and we would just go out to eat. For me I was so very busy for so many years and so was Manny [her husband Manuel] that a surprise visit took creativity to get the three of us together, but we did it for Peter. He liked nice places. And I loved hearing he and Manny talk old times. He would also talk about living in Mexico which he loved.He was such a mystery to me because he was pretty much alone and he liked it that way.I do not recall meeting Peter when we were in New Orleans which was August 1975 to June 1976 […]What I do recall is that after we married I was sorting and clearing papers for Manny from our apartment which he had lived in for many years and I came across a letter from Peter written around the time Manny and I met. In that letter I gathered Peter was a bachelor friend of Manny who was not the marrying kind and he was commenting that Manny had met “the one”. He was happy for Manny but it seemed to me Peter was happy being alone. Now that I think of it I don’t think I ever got to know who Peter was. He had a wonderful smile. He liked to laugh and joke and was very very blond.
[…] The photos are valuable. I met Peter when he was a much older man but still had that incredibly beautiful smile and lots and lots of hair!Each time he came to the US for many years, he would call Manny and we would go to dinner. If I recall correctly, it was mostly on Peter’s nickel and as I stated to Sandy [F.A.N.] we went to nice restaurants, although Manny may have won some times and we would go to our famous Luby’s Cafeteria—always the frugal Manny.I do not recall Peter in New Orleans when I lived there with Manny the first nine months of our marriage. I left San Antonio to join him as he was waiting and hoping to join UTSA. The New Orleans scholars community from the four universities and colleges there met socially and regularly at people’s homes but I do not recall Peter in any of that circle. It could have been that he was no longer in New Orleans. This was August 1975 to June 1976.This morning when I read your note the words that rang in my head is how youth is wasted on the young. I wish I had paid more attention and had retained the conversations with Peter, but at that time my life was incredibly full and so was Manny’s. There were times when I had to make major changes in my schedule to join Manny and Peter and I always did and looked forward to those dinners. My questions to Peter were always about Mexico and his life there. That is what I wish I could recall more. I just know that he was very happy there. I do not recall what his conversations with Manny were all about and now Manny is forgetting a lot of things.On one of these trips which had to occur every six months, I believe, because that is how he kept his US citizenship active he said he had some boxes with him and asked if we could store them for him for safekeeping. I recall his taking them out of his car. When I looked at them again seriously in recent years I saw how big the boxes were and soon learned how heavy they were. Yet, I seem to recall Peter carrying them by himself. Maybe a Dolly helped. I just know he trusted us with them.One of my last year’s resolutions was to clean the garage and I did. It took some weeks but with some help I did it. Peter’s boxes were the only things that were still in there without any resolution. We had been telling each other for a couple of years that Peter had probably died since we did not hear from him anymore. He quit coming. Manny and I would comment from time to time that we still had those boxes and that we needed to do something about them.A year ago when the boxes were the last unsettled things in the garage I told our gardener who was helping me with the project the story of the boxes. He said what if it is money. Since it had been so long that Peter had left the boxes with us I gave myself permission to open them. Hilario, my helper, even wondered if they were full of money! I only opened two boxes and all I saw were reams of papers with math problems. Pages and pages and pages. When Sandy [F.A.N.] helped us with Manny’s papers after he retired I decided to ask him to go over the papers and determine what they were. Manny looked at them but had no idea what the material was. When Sandy [F.A.N.] took the boxes out I saw how at least one of them had folders of some kind so the papers were not only sheets of math problems. I hope someone who has Peter’s interest and his career uppermost in their mind will continue to review it and possibly record it for posterity.To close, thank you again for honoring Peter’s work.
3. Mathematical Background
3.1. The Shanks Transformation and the -Algorithms
3.2. Padé Approximation
3.3. Continued Fractions
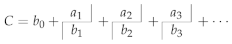
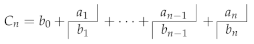
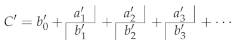
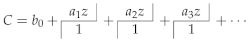
3.4. Rational Interpolation
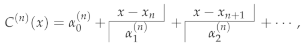
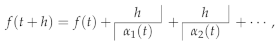
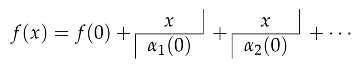
4. The Legacy
4.1. Main Documents
4.1.1. Complex Analysis and Continued Fractions
- 1
- Bürmann series over a fieldThese titled notes (52 pages) are devoted to Bürmann series. They are mentioned in documents {26–28}, and were probably written at the same time as {14}, since both titles are listed together.The Bürmann series of a function f is a generalized form of a Taylor series in which, instead of a series in powers of , we have a series in powers of the analytic function . It is used in the reversion of series which consists, starting from , in expressing w as . The problem was considered by Joseph Louis Lagrange (1736–1813) in 1770 [120] and generalized by Hans Heinrich Bürmann (?–1817). A report on Bürmann’s theorem by Joseph-Louis Lagrange and Adrien-Marie Legendre (1752–1833) appeared in Rapport sur deux mémoires d’analyse du professeur Bürmann, Mémoires de l’Institut National des Sciences et Arts: Sciences Mathématiques et Physiques, vol. 2, pages 13–17 (1799). An exhaustive treatment of this topics is given in Reference [121] (pp. 55 ff.). The Lagrange-Bürmann series, as it is often called, also allows for two functions f and g, both holomorphic in the neighborhood of a point, to be expanded in a power series of the other one in two overlapping regions. Series reversion related to Hankel determinants, continued fractions, and combinatorics as explained in Section 6.10.4 of Reference [113] about combinatorics; also see Reference [122]. Wynn wrote:This paper is directed towards the transformation of series expansions [...]The general results derived are illustrated by application to a problem concerning the transformation of asymptotic relationships.Notation. Let be fixed finite integer.(1) With w a fixed point in , the finite part of the complex plane, an open set of points in with limit point at w, , and mappings of into ,means that as z tends through to w.(2) Let M be a nonvoid set of points in . For each , let be as in (1) and .means that for each , . [We have] and where for all .The main problem considered has a simple form as follows: let [This notation means that j runs from 1 to n. The notation means that j goes from 0 to n] with and, with fixed, let be such thatDetermine for whichIn the general form of the problem are mappings with for all ; for each , is such thatthe mapping satisfies the relationshipand for whichare to be determined.Then, Wynn described three variants of the problem corresponding to various properties of the function a. The particular case of polynomials is treated. The text ends by:The function is inverse to . maps the segment onto a curve , symmetric about the real axis, enclosing its nonpositive part, containing the real point , the imaginary points , and having as asymptotes the lines , being the open domain bounded by , a maps bijectively onto the unit open disc.
- 2
- On Stability FunctionsThe handwritten paper On stability functions (mentioned in {26} as “Paper, latest version”) contains 187 pages with a bibliography at the end. Its first section is an introduction and a presentation of the notations:This paper is concerned with functions of the formwhere , andwhere is a nondecreasing function of bounded variation for such that all momentsfor exist.A function f of this form will be called an F-function. If the context permits, the notation or, where convenience dictates, , will be used. The function s in the representation (1) plays a significant role in the theory of the function f. A function of the form (2) with as described will be called an S-function; again the notations or will be used.The mapping properties of F- and S-functions, in particular, will be investigated.Then, Wynn stated that an F-function f is real for finite negative values of z with for all sufficiently small negative values of z, is asymptotically represented as z tends to zero over an open set in the sector with the limit point 0, and that the function f can be asymptotically represented by a series of the form (formula scratched) which generates an associated continued fraction whose even convergents map the closed infinite left half-plane into the closed unit disc if and only if f is an F-function. The proof is given with a reference to his paper (Reference [98]) for details. An example of an F-function is , and Wynn added:The study of F-functions was motivated by the following consideration: With A a bounded linear operator, the solution of the differential equationwith prescribed, satisfies the relationshipfor If and the eigenvalues of A lie in , those of lie in . remains bounded and, indeed, decreases to zero as n increases indefinitely. An approximation to the solution of Equation (9) may be obtained by use of a Taylor series method based upon use of an approximate identitySetting and taking the and to be the denominator and numerator coefficients of powers of z in , where , with fixed, is a convergent of the continued fraction associated with the exponential series, and setting , the special form of the approximate identity (11) applied to Equation (10) yields the relationshipfor As a consequence of the mapping properties of described above, the eigenvalues of lie in , and the remarks concerning the behaviour of apply with equal force to : the exact and approximate solutions of Equation (9) behave in the same way. The practical details of the way in which relation (12) is implemented are not of immediate concern; any method for the approximate solution of Equation (9) based upon use of recursion (12) is stable.Let us remember that the convergent of the associated continued fraction to a series is its Padé approximant. Since the computation of Padé approximants to the exponential function are highly numerically unstable (see References [123,124]) one can doubt the practical usefulness of the procedure mentioned.Other examples of F-functions are given. Wynn claimed that they open up the possibility of constructing stable schemes for the approximate solution of certain nonlinear differential equations. A characterisation of F-functions which is independent of the continued fraction theory is given. Based on the proof of this result, Wynn asserted that it is possible to demonstrate the existence of functions with mapping properties less specific than those of F-functions. Indeed, a number of F-functions can be derived from a given F-function. This remark reminds the way some totally monotone sequences can be derived from a totally monotone one as explained in Reference [125]. Then, Wynn proved that F-functions are closed with respect to multiplication. Meromorphic F-functions are then considered.The next part of the work deals with variation diminishing functions. Let be a sequence of real numbers. The transformation given by , (it seems that n should be replaced by j), is said to be variation diminishing if the number of changes of sign of the is less than or equal to the number of changes of sign of the . Wynn wrote: Transformations of this type underly the theory of many smoothing operations, and also occur in the numerical solution of certain partial differential equations by iterative methods, and he referred to Reference [126]. Several results are proved.The next section of this manuscript is devoted to interpolation. Wynn wrote:It is possible to construct a rational F-function whose derivative values agree with those of a generating F-function up to prescribed orders not only at the origin but at a prescribed sequence of points in ; furthermore this rational function may be derived by the use of purely algebraic methods of rational function interpolation.A theorem is proved and recurrences for the coefficients occurring in the interpolating rational F-function are given. A long discussion, where orthogonal polynomials play a role, follows. The algebraic problem of determining a rational function with denominator and numerator of degrees equal to m and respectively, which satisfies the interpolation conditions may be solved by a recursive process which is described and justified in his Appendix 3 Extremal solutions of the Pick-Nevanlinna problem. It could be of interest to code and test this algorithm, and to compare it with the other existing ones.Exponential fitting forms the topic of the following section. Since differential systems of the form (9) constitute a very restricted class, Wynn now considered the system . Linearizing it yields where J is the Jacobian matrix of f. Assuming its nonsingularity, we haveAssuming that the eigenvalues of J are distinct, and … what follows is not clearly stated and it seems that one page of the manuscript is missing. Anyway, Wynn constructed a rational function such that its derivatives of prescribed orders agree with those of at the points , and he wrote:It is eminently desirable that a method for the construction of general rational functions mapping into and having prescribed orders of contact with the exponential function at the origin and other specified points in should be made available. This is precisely the service offered by Section [not identified] of this paper. In Theorem 4 [not identified], the F-function producing the interpolation data is taken to be the exponential function; the results of that theorem then show that the required function is obtained simply by means of rational function interpolation.A section on meromorphic F-functions follows in which the properties of the corresponding continued fractions they generate are studied. The even and odd convergents are examined.The first Appendix has the title The asymptotic expansion of positive real functions. Appendix two is on The construction of functions belonging to certain classes. It deals with a general theory of the derivation of functions of the formfrom others of the same form. In a previous Appendix (without a number) Wynn already treated the same problem for S-functions. The third Appendix, already mentioned above, considers the Pick-Nevanlinna problem in a wider setting. Let us remember that this problem consists in finding a holomorphic function that interpolates the data subject to the constraint for all ; see Reference [127]. Wynn wrote:It is clear from the above conspectus of results from the Pick-Nevanlinna theory, that the solution of the problem of determining a rational function which satisfies the mapping and interpolation conditions described above differs from that of constructing a rational function which satisfies interpolation conditions alone in at least two respects: in the solution of the first problem a combination of function-theoretic and algebraic methods is involved, while in that of the second, algebraic methods are exclusively deployed; furthermore, each stage of the solution of the first problem results, not in the construction of a single interpolating function as is the case for the second problem, but in that of a family of functions with the required properties.Developments and theoretical results follow. A bibliography of 26 items ends the paper. One can wonder why Wynn never published it.
- 3
- The Hamburger-Pick-Nevanlinna problemThis manuscript contains 179 pages but with many portions scratched (it probably contains a mixing of a draft of a paper, notes and rough notes all cited in {26,28}).Let be finite positive integers, let be finite real numbers, let be distinct real argument values, be the corresponding finite positive integers, and sets of finite real valued coefficients, let be distinct argument values in , be the corresponding finite positive integers, and sets of finite complex valued coefficients. The problem is to determine a function G which satisfies the asymptotic relationshipas tends to infinity in a sector of the form , and satisfies also the asymptotic relationship foras tends to over an open set contained in with limit point at , for , and moreover satisfies the interpolation conditions for , and finally maps into (or ?). According to Wynn The proof of the principal theorem of this section is largely based upon results, due to M. Riesz, in the theory of linear functionals. Since this part is a draft in quite bad shape, we will not pursue its analysis.The document contains another interesting sectionMatrix criteriaIn this section Akhiezer’s treatment of the simple Pick-Nevanlinna problem is extended to the diminished Hamburger-Pick-Nevanlinna problem; conditions that are necessary and sufficient for the solubility of the latter problem are established and, assuming this problem to be nondegenerate, inclusion discs for its solutions are located.As a preliminary, a Hermitian matrix is constructed from the data which leads to an extension of a theorem on the existence of inclusion discs for the values of all solutions to the Hamburger problem and the simple Pick-Nevanlinna problem.Wynn concluded:The results of the above theorem are exclusively concerned with the diminished version of the Hamburger-Pick-Nevanlinna problem. It is possible to extend the method of proof to the treatment of the Hamburger-Pick-Nevanlinna problem itself, to examine the structure of the rational function solutions to this problem and its diminished form, and to describe the relative positions of the inclusion discs deriving from a sequence of subordinate problems. These matters are, however, more conveniently dealt with methods described in the following section, in which explicit expressions for the general solutions to the interpolation problems concerned are described.Unfortunately, this following section of the manuscript is not under a form which allows to give a clear account of it.
- 4
- Continued fraction transformations of the Euler-Mclaurin seriesThe document is 202 pages long. It dates from December 1976. The first part of the document is in a quite good shape (probably a draft of the paper mentioned in {26}, with an abstract and a bibliography) with some corrections done with a pencil. Not all pages have been written with the same pen. Some of them are missing or not in the right order since all of them are not numbered (they could be some additional notes on integral transform and analytic continuation). Moreover, references to some formulas are missing, and some authors quoted in the text are not listed into the bibliography given at the end. An in-depth study of this document is needed to fully understand it if possible to exploit it.It begins by a long abstract from which we extract the main points.Results concerning the convergence of forward diagonal sequences of quotients in the Padé table are given. In particular, it is shown that, if (*) , being a bounded nondecreasing real valued function such that all moments (*) exist, and () then all forward diagonal sequences of Padé quotients derived from the series converge uniformly over any bounded region in the z-plane not containing any point of the nonnegative real axis to () , being the le Roy or sum of the given series for all finite z in the sector .This result extends results given by various authors, and it can also be extended to the case where the lower limit in (*) and () is replaced by . These results are applied to the delayed Euler-Mclaurin series(, and being ) regarded as a series expansion in ascending powers of . Convergence results for the Padé approximants of this series are derived, and also for the same series in which single zeros are inserted between its successive terms. Applications to Stirling’s asymptotic expansion of the logarithm of the gamma function, and to the asymptotic expansion of the generalised Riemann zeta-function are presented.
- 5
- Convergence and truncation error bounds for associated continued fractionsThis is a short document (13 pages), probably only the notes mentioned in {26}.In this work, he proposes to give a convergence theorem for the functions , where, presumably, is the th convergent of Thiele’s continued fraction. He begins to prove other results (not reproduced herein since they contain too many erasures) upon which the proof of the theorem is based. It is:Theorem 3. Let be a fixed interval of the finite real axis, and be a bounded nondecreasing real valued function for , and not a step function with a finite number of salti. Let be fixed andThen , andwhereAccording to what precedes, it seems that the sign that looks like × in has to be replaced by . We do not know if this result had been later rediscovered by other researchers. Thus, it was interesting to reproduce it here.
4.1.2. Interpolation
- 6
- Functional InterpolationThis very well handwritten manuscript has 52 pages and seems to be the paper mentioned several times in all the list of documents, projects and activities, with a bibliography with a last reference dating from 1984. The first section is Interpolation and extrapolation with a subsection 1.1–Procrustean technique. This word was already used by Wynn in the title of the published paper of Reference [2] where he introduced a particular form of the -algorithm for extrapolation at infinity by a rational function in n (see Reference [113]). It describes situations where different properties are fitted to an arbitrary standard. In the Greek myth, Procrustes was a son of Poseidon. He compelled travelers to lie on a bed, he cut off their legs that were longer than bed, and stretched the feet of those who were too small. The manuscript begins by:Most general theories arise from investigations of particular problems, and in this respect the theory to be described is not exceptional. By way of motivation, the problem of deriving an extrapolation method from an interpolatory formula and its converse are considered.It is first supposed that an interpolatory function of complex variablesis available for which (a) ; throughout the paper is the sequence ; is the sequence ; I is ) and (b) for certain distributions of the andexists. The function serves as the basis of an extrapolation method: given the sequence the number obtained by setting in is an estimate of . (The numbers used are suggested by the process producing the sequence : the choice is natural; the choice arises, for example, in Romberg’s method of integration [2 references] in which the number of integration subranges is doubled at each stage, being a polynomial in .)Then, Wynn illustrates the method by taking as the quotient of two polynomials of degree i in . Subject to certain existence conditions, the coefficient of in the denominator is 1, and that in the numerator is which can be expressed as the quotient of two determinants involving . In this case . Replacing by , the determinantal formula for gives the extrapolated limit. These numbers can be recursively computed by Thiele’s reciprocal difference algorithm (see (3) in Section 3.4), and they can be displayed in a two dimensional array for which Wynn does not use the usual notation but a new one, and he writes:[The process] involves numbers which may be set at the intersections of the full rows and columns and of the half rows and columns of a chipped triangular array in which the row index i ranges over ( is the sequence is ) and the column index j over the range , the number being missing. The numbers are constructed from the initial vales (the dash is used to indicate a displacement operation acting upon numbers with two suffixes, whose effect is illustrated by the relationships and ) by use of the relationshipfor where is the difference operator and is similarly defined. With[it holds]And he concludes with his personal sense of humor:We have called an extrapolation method of the above type a Procrustean technique [2], although in fitting function values to a sequence, i.e. the bed to the victim, we are a little kinder than Procrustes is reputed to have been.He continues:If in formula (1) is fixed and one of the is very large, [not defined] is approximately equal to : if is fixed and the are fixed and finite, . This observation may be made in terms of the behaviour of as tends to infinity, the other remaining finite; expressed in terms of the it is that, under suitable conditions, .There should be an error in what Wynn wrote. Since he states that is fixed, should be replaced by (remark of one of the reviewers). Wynn concludes that this property is, for example, satisfied by the ratio of determinants expressing which, thus, tends to as tends to infinity.The second subsection is named 1.2–Interpolatory functions. He claims that The steps taken in the above derivation of an extrapolation method from an interpolatory formula may be reversed. Then, he shows how to reverse the recursive rule given in the preceding subsection.[…] set and . Suppose that a function of complex variablesfor which as , obtained either from an interpolatory or from an extrapolation method or in some other way is available. Set[…] Thus in view of the property attributed to just described, as over Z (: [Z is an open set of points in ] is an interpolatory function. If the may be computed by means of a recursive process, appropriate modification yields a process for computing numerical values of the .Then, Wynn develops the particular case of the extrapolation estimate , and he obtains a set of rational functions . He proves that as . Imposing the further conditionit follows thatThe interpolatory function derived from the extrapolation estimate is . He proves that as . ThenSetting now and , .In this result, the conditions of the simple case in whichmay be imposed upon e and f. Now is a constant, independent of and is the difference . In this case, is the quotient of two ith degree polynomials in z, the rational function from which the extrapolation limit was derived. The above process now reduces to an algorithm for rational function interpolation due to Brezinski [128] of which a generalisation has been proposed by Cordellier [129].The discussion of interpolatory formulæ and extrapolation methods is terminated by the remark that under appropriate conditions cyclic derivation of extrapolation methods from interpolatory formulæ and conversely may be repeated indefinitely.Section 2 of this document is entitled Approximants of general order. In the simple case (8), is a ratio of two polynomials of degree i. In this Section, he proposes to study the more general system of approximants . The first subsection is Nonuniform approximation. Under the condition (8), the relationship (7) reduces to : approximation is uniform, the form of the function being the same for all relevant . Wynn notices that a suitable choice of the functions in the non simplified case, non uniform approximation is possible.The next subsection is Remainder term formulæ. Wynn explains thatIn certain circumstances an interpolation property of the form (7) holding at points induces on the function possessing it a corresponding property of approximation over a set containing the points. By imposing severe restrictions upon the functions e and f it is possible in a few lines to exhibit the as approximations to a function defined over Z, and to provide associated remainder terms.He imposes the conditionswith for all y in Z. By a straightforward (as he writes) adaptation of an argument of Nörlund [130] (Ch. 15, §3), Wynn obtains the expression of the error.The following subsection is on Algorithms for approximation evaluation in which Wynn gives formulæ for the recursive computation of the approximant values for a fixed . After quite long developments involving Lagrange forms and divided differences, Wynn shows that his relationship (3) can be applied with to yield starting from two different sets of initializations. However, in (3), the are intermediate computations which can be eliminated, and he arrives at the rulewhere . The initializations are in the row by row order or in the column order withandRecursive relations for the ’s and the ’s are also given. Using divided differences, they are also expressed in Newton form. Determinantal formulæ are related to the recursive rules given.It is showed that particular cases for the and the give back the usual Lagrange interpolation formula, the Neville-Aitken scheme, and Newton series. The work of Stoer on interpolation by rational functions [131] and the variant of the -algorithm due to Claessens [132] are also recovered as special cases.The next subsection is named Termination. When is a polynomial or rational function of , termination of the algorithms previously given is proved.The following subsection treats Confluence that is when some argument values coincide. Wynn examines what happens to the previous formulæ and recursions. In that case, for ,and formulæ for the computation of the coefficients and are given. They implement a truncated composition of polynomials. The ’s are the coefficients of the Newton series representations of the corresponding Lagrange forms, which are confluent forms of the functional divided differences. They are related to the , but all details are too complex to be given herein.Then, comes a subsection on Zero finding algorithms. Under suitable conditions, the above algorithm for the truncated composition of polynomials can be used for the inversion of formal power series. MoreoverIn so doing it serves as the basis of a number of algorithms for determining the zeros of a function and motivates the use of the approximants for the same purpose. Setting and , being the function under treatment, relationships of the form (31,32) hold with are Taylor series coefficients, and .[…] Taking the points and to be confluent, the Lagrange forms […] arewhere . Newton’s process is obtained from by equating the latter to zero after setting . The third order process is obtained from in the same way. Applying relationship (3) to the initial values with (since ) and using as just described, the further third order process is obtained.The artifice described above is capable of further application.For example, if , leads to the method regula falsi . If , then Wynn obtains two combinations of Newton’s method and regula falsiIn the same way, an nth order single point iteration process can be obtained. The subsection ends byThe last subsection of this document is entitled Extensions of the Lagrange-Bürmann expansion. Wynn claims that The above treatment of the confluent case offers an interpretation of the theory of this paper. He first gives the Lagrange-Bürmann expansion of in powers of where belongs to a close contour in the complex plane. Then, he obtains an algorithm for determining the coefficients in the Lagrange-Bürmann expansion and in an asymptotic version of it from the Taylor series coefficients of and at the point . The case of confluence is also treated.In addition, in this case, we do not know why Wynn never published this work since it was ready to be submitted.
- 7
- Interpolation by the use of rational functionsThis handwritten complete paper of 90 pages with a bibliography of 27 items, the last one dated 1979, is present in the projects and in the Lists of documents, and it was never published. It seems to be related to the previous manuscript {6}.In the Section 1 of this document, titled The Thiele-Nörlund interpolation theory, Wynn reminds how to construct rational interpolating functions in which the numerator and the denominator have degree s, and with a numerator of degree and a denominator of degree s and such that for , where the and the are assumed to be complex numbers. After having constructed the reciprocal differences by Thiele process (this is the -algorithm (3), where now r and m are arbitrary indexes)for with and , it holdsThe successive numerators and denominators are recursively computed bywithWynn asserts that conditions to ensure that all rational functions can be constructed by the above scheme and that they have the required interpolation properties can be formulated in terms of determinants, and that determinantal formulæ can also be given for the numbers and the functions involved, and he claims that Such formulae are made more concise by the use of a special notation. It takes 6 pages to establish these notations. After quoting a remark in German by Nörlund [130] (Ch. 15, p. 420) that Wynn finds perhaps a little exuberant, he writes that:It is the principal purpose of this paper to point out that, using another very simple relationship (namely, in particular, that, if is replaced by , becomes many results suggested by the behaviour of reciprocal differences may be obtained for convergents.These procedures are described in Section 2 of this document, titled The σ- and μ-algorithms. After explaining how to obtain them, Wynn writesTheorem 1. Let be a fixed finite complex number unequal to . Set for […] Numbers can be constructed from the initial values by use of the relationshipwith and, in particular,forThen, the document becomes unclear. It seems that replacing in the above recurrence, by (this is the unclear point), and renaming ’s the ’s, Wynn obtains . A proof of this result is given.Section 3 of this document is entitled Interpolation and extrapolation. It is interesting to quote its introduction which contains general comments by Wynn on these topics.The simple observation that, if the argument values are replaced by functions the reciprocal differences become interpolating functions has already produced the -algorithm of relationship (16), the simplest and most economical method, subject to the stated conditions, for evaluating these functions; the observation also leads directly, as will be shown below, to new interpolatory theory. Once made, the observation is trivial, and its implications are not difficult to work out; perhaps its most interesting feature is that it has not been made before. The simple relationship between reciprocal differences and rational interpolating functions was not so much discovered as forced upon the author’s attention while working out the consequences of principles underlying the process of interpolation and the transformation of divergent series. These two subjects have recently became increasingly important in computational mathematics; new theory in what once might have been considered dead subjects is constantly being developed (mention may be made of recent generalisations of polynomial interpolation described in [135,136,137,138]); it is highly probable that the principles concerned will find further applications, and for this reason they are now outlined.It is difficult to summarize what follows without quoting large parts of the document. Moreover, some notations and their inferences are not clear enough. Basically, Wynn comes back to the link between interpolation and extrapolation already discussed in the document {6}, that he named Functional Interpolation. In particular, he considered the following extended -algorithm (which contains the -algorithm and some other extensions [128])with . He considers the particular case , which corresponds to the -algorithm. He reminds that, when applied to the partial sums of a formal power series, this algorithm furnishes the Padé approximants belonging to the lower half, diagonal included, of the Padé table, and that he derived (no reference) various determinantal formulæ from a more general form of approximating fractions given by Jacobi [139]. He also mentions that, in its special form, the problem was also studied by Frobenius [140] and Padé [141], and he adds the following remark in which he explains how he obtained his -algorithmWhile idly investigating the formulæ resulting from the choice in the relationship (25) […] the author noted that expressions obtained for the numbers were equivalent to extrapolatory determinantal expressions, simplified versions of those due to Jacobi and used by Frobenius, previously published by Schmidt [142] and republished by Shanks [112]. In this way the -algorithm was discovered.Then, Wynn notices that (25) has been used by Claessens with , and applied to the partial sums of the Newton interpolation series, for obtaining rational interpolating functions [132], and he explains the theoretical basis of this algorithmClaessens was led to the discovery of the extended -algorithm by the consideration of interpolatory continued fractions not of Thiele form, but of a form introduced by Kronecker [143] in connection with a process initiated by Rosenhain [144] and Borchardt [145] for constructing the resolvent of two polynomials from systems of their numerical values.If all the tend to a common value x, the interpolation fractions tend to the Padé approximants and the extended -algorithm (25) tends to the usual one. When , (25) gives back the -algorithm studied by Wynn in Reference [2].The following Section is on Lozenge algorithms, which are algorithms relating quantities located at the four corners of a lozenge in a table where the lower index indicates a columns and the upper index a descending diagonal. The -algorithm and its generalizations [146], the -algorithm, and the algorithms numbered by Wynn (23) (see the manuscript {6}), (16) and (25) (see above in this manuscript) enter into this class. They share some algebraic properties when, instead of applying them to a sequence , they are applied to , when in (25) is multiplied by a constant, and when a fractional linear transformation is applied to the elements with an even lower index (property named homographic invariance). In these algorithms, the quantities with an odd lower index are only intermediate results with no interest for their purpose. They can be eliminated and a new rule relating five quantities disposed at the center and at the extremities of a cross are obtained. The first algorithm to have been treated in that way is the -algorithm for which Wynn obtained this cross rule [48]. Concerning this rule, he writes in the document under consideration Despite the author’s pianissimo protests, this relationship and others of its kind have been referred to by various writers as Wynn identities. This extended cross rule and the homographic invariance property were independently presented by Cordellier in his Doctoral Thesis [147]. They were also published by the same author in Reference [129] without, of course, knowing this unpublished document by Wynn. On the contrary, Wynn was knowing Cordellier’s results through his correspondence with C.B., and he indeed refers to Reference [129] for the extension of his cross rule. The homographic invariance for the ’s and the ’s presented above is treated. In the same document, Wynn also discusses the possible breakdown of these relations when a denominator becomes zero. Singular rules for continuing the computations in the case of only one isolated singularity are given. They extend the singular rules he gave in References [20,36] for the usual -algorithm. All these results are gathered into Theorem 2 in which Wynn also gives the cross rule for formulæ (16) and (25). If the relationship is satisfied between the , then the cross rule also holds as described with the five ’s replaced by . Then, if an extended cross rule holds between five numbers as explained above, Wynn looks at which conditions a recurrence relationship of the form (25) holds between them.The following Section deals with Invariance properties. Denoting by the reciprocal differences obtained by Thiele’s formula (that is the -algorithm given by (3)) from the argument and functions values , and setting and with , Wynn proves thatIf , a property for is also given. These invariance properties have their counterparts for the convergents .Section 4 is on Confluent algorithms. Up to now, all the have been assumed to be distinct. Now Wynn sets and allows h to tend to zero. The functions evolve, in particular, to a confluent form and become the successive convergents of the continued fraction corresponding to the Taylor series . The coefficients of this continued fraction may be expressed in terms of Thiele’s reciprocal derivatives. He refers to Reference [130] (Ch. 15) for the corresponding theory, and explains that the confluent forms of the algorithms of formulæ (16) arewith and . Determinantal formulæ for these ’s are given. The functions are treated similarly. Complete proofs are given.
4.1.3. The -Algorithm
- 8
- Sequel to the abstract theory of the -algorithmIn February 1971, when he was working at the Centre de Recherches Mathématiques of the Université de Montréal, Wynn published a report on the abstract theory of the -algorithm [69]. In the boxes he left with his friends, we found a document with the title Notes on sequel to the abstract theory of the ε-algorithm. All topics treated are in the noncommutative case. It probably corresponds to the rough notes indicated in {26}. It consists of 153 pages including numerous corrections and additions as well as strikethrough passages, and pages from Reference [69] intercalated. In the lists, a corresponding paper is also mentioned, but, unfortunately, we have not found it yet.The document begins with a discussion about the application of Euclid’s algorithm to rational functions in a ring with a zero and a unit element. Another one on noncommutative continued fractions follows. Recurrence relations for the numerators and the denominators of their successive convergents are given. They are the same as the usual ones. Wynn claims that:the theory of continued fractions may be used to recover the original rational function from the sequence of polynomials produced by means of Euclids’ algorithm. […] The above theorem offers a method for determining the rational function of the form equivalent to a given function .Then, he discusses Euclid’s algorithm for formal power series with coefficients over a ring. Wynn proves that they have two sided reciprocal series. It is difficult to extract some results from this part without much work. Then, he considers systems of continued fractions derived from a single power series. Notions on -regularity and semi-normality are introduced. Applying a recursive algorithm whose rule is that of the vector -algorithm, that is , but without giving the definition of the inverse, to the partial sums of a semi-normal series he proves that for a certain value of r. Other theoretical results are given, but they are difficult to exploit. Then, pages 93–96 of Reference [69] are reproduced which leads to think that what precedes is a complement to that report. Wynn then shows that both halves of the Padé table can be constructed via this algorithm under certain assumptions. A cross-rule is given for each half.Pages on vector continued fractions follow. Arithmetic operations upon vectors and formal power series with vector coefficients are first explained. But the pages, the concepts (vector valued rational functions, McLeod isomorphism [148], …), and the results are so entangled that it seems difficult to extract something coherent. There are pages on Euclid’s algorithm for formal power series with vector valued coefficients, a vector -algorithm, and the vector -algorithm. However, an interesting result is given but it needs to be verified. Let us give it after a simplification of the notations. Summations are over :Theorem. If the finite dimensional vectors of the sequence satisfy a system of relationships of the formwhere the are real numbers, then the series is generated by a vector values rational function . If vector value rational functions can be constructed from the initial valuesby means of the recursionfor , thenLooking at the proof, which is not complete, one can understand that the words the series is generated by the rational function means thatwhere .The vector valued Padé table is presented. Then, Wynn gives some elementary results in the theory of ε-algorithm as applied to sequences of elements of a ring. In particular, a cross rule is obtained. Rational functions with coefficients over a ring are discussed.Then, Wynn studies the application of the -algorithm to a sequence of numbers satisfying an inhomogeneous linear difference equation. He proves the following result (notations slightly changed)Theorem. Let the numbers satisfy the recursion and no recursion of a similar form with r replaced by a smaller integer; set . It is not possible that both D and H are both factors of zero.It is then proved that, for such a sequence, for all m. Other results of a lower interest are given. Then, Wynn looks at the properties of the hierarchies of -arrays, as defined in Reference [79], that are obtained for such sequences. Since pages 23–28 of his report from the Université de Montréal corresponding to the paper of Reference [79] are inserted here between the pages of the manuscript, and preceded by If followed by a difference equation, what precedes can be considered as an addition to them. Using the vector-matrix isomorphism of McLeod [148], Wynn writes that, for recursions involving vectors, it is a relatively simple matter to derive results analogous to those of the preceding section. Further notes end the document.
- 9
- How to find the centre of a spiralThis handwritten document contains 49 pages that correspond to the slides for a talk. There are parts in the text separated by numbers in bold from 1 to 30 in large square boxes (see {28}). Its title could be How to find the centre of a spiral, and it was delivered by Wynn after 1987 since a book dating 1987 is quoted. After there are 30 pages where the same content is detailed and illustrated very carefully, probably some notes to copy and distribute.The document gives an interesting new interpretation of extrapolation by the -algorithm.We start with a fixed complex number . If the modulus of is less than 1, lies inside the unit circle. If the modulus of is greater than 1, lies outside the unit circle.Next, we form the successive powers of . They lie on a spiral in the complex plane. The argument of is twice , the argument of is three times and so on. If the modulus of is less than 1, the powers of tend to zero and the spiral contracts to the origin. If the modulus of is greater than 1, the spiral expands away from the origin.Then, we multiply each of the points by a constant complex number b. This does no more than rotate the spiral through and magnify or diminish it by a factor of . But a contracting spiral remains contracting and an expanding spiral remains expanding.Lastly we add a constant C to each of the transformed points and produce membersof a first order spiral sequence. In the case in which , the sequence converges to C and the spiral upon which its members lie contracts toward C. In the case in which , the spiral expands away from C. If is finite, .Already we may pose a problem in connection with first order spiral sequences. It is known that three successive members and of a sequence have the formbut the values of and k are unknown. Find the value of C alone. If we can solve this problem then what we are able to do is fit a first order spiral sequence to the subsequence and and find its centre.Then, Wynn shows that the problem can be solved by computing by a rule which is that of the -algorithm (without mentioning its name). He gave the formulæ for and . Then, he computes , and shows that it holds . Thus, the spiral has been fitted without the determination of the values of b and . Then, he considers three other members and having the formAnother spiral can be fitted through these three numbers, and a similar computation leads to . He mentions that is identical to the one computed before. The same process can be continued with and , and so on. For each value of the upper index, the center of the spiral can be computed by the rulefrom , and This is the -algorithm [3]. Wynn mentions that, if are successive members of the same first order spiral sequence, that is for , then for all i. This set of sequences is the kernel of the sequence transformation which is, in fact, Aitken’s process. Then, Wynn considers a second spiral entangled into the first one.The members of a second order spiral sequence have the representation. This sequence has two forms: either(a) only one geometric term accompanied by a linear function of i is present andor(b) two geometric terms accompanied by constant coefficients are present andIn the latter case a second order spiral sequence may be regarded as a first order spiral sequence whose members are represented by whose center moves on a further first order spiral upon which the points lie.In these forms, the kernel of the transformation is recognized.Then, Wynn considers nth order spirals with the satisfying the same formula but now with the condition , and he discusses their various special forms. The center C of such spirals can be obtained via the -algorithm which, starting from , delivers . Since he writes that: There is no time to give a proof of this result this confirms that these notes were written for lectures. The same process is repeated with , and it gives . As before, the two schemes have some in common, and, if are successive members of the same nth order spiral, then, for all m, . This is a known property of the -algorithm since the sequence belongs to the kernel of the transformation .If the parameters and in the equation of the first order spiral are real, the , still lie on a spiral in the complex plane, but the numbers themselves lie on the real axis. In that case, the are also real.Then, Wynn explains how the process for finding the centres of spirals which we have described serve as the basis of a method for obtaining estimates of the limit of a sequence. Starting from and , the center of the corresponding first order spiral is an estimate of the limit. Then, from and , a second estimate is obtained, and so on. Now, from , the center of the second order spiral passing through these numbers furnishes another estimate of the limit. The process can be repeated by increasing the number of terms of the sequence used in the construction of the successive spirals. And Wynn writes This method of estimating the limit of a sequence is known as the ε-algorithm [...]A question now arises: does this method work? Wynn gives two numerical examples: partial sums of the series which converge to , and those of the series ( represents the binomial coefficient) which tends to . He tentatively explains the success of the process:Perhaps a happier interpretation is to suggest that a great deal of information lies lurking in the first few members of a sequence: we have only to think of a way of getting it out. This interpretation serves us a little better when we come to consider the transformation of divergent sequences.In saying that, Wynn is too much optimistic. Indeed, the behavior of a sequence can completely change after a certain number of terms, and change again later. As proved in Reference [149], an algorithm to accelerate the convergence of all sequences cannot exist. It is the same even for restricted classes of sequences [150]. Then, Wynn gives examples of divergent series and explains that the reasons why the -algorithm works in these examples are found in the classical theory of continued fractions.After that, he describes the use of the algorithm in the solution of the fixed point problem . He explains graphically the convergence of the Picard iterates, and what the notion of order of convergence of a sequence is. Since Newton’s and higher order methods require the use of the derivatives of f, he explains how this drawback can be avoided. He starts from an initial estimate of the fixed point, sets , performs the iterations for , and finds the center of the spiral constructed from these iterates, and restarts the Picard iterates from . When , this is exactly Steffensen’s method which has order 2. Wynn claims that under suitable conditions . Let us mention that this claim has never been proved.Then, Wynn explains that the -algorithm can be applied to sequences of functions, of vectors, of a field or of any mathematical system over which addition, subtraction and the formation of an inverse are defined, and that the theory of continued fractions has been developed for such cases.The continuous case of the preceding method is considered. It is aimed at the estimation of . In what precedes, i is replaced by t and by , and he names an rth order spiral function, the expressionWynn proposes to estimate by fitting a spiral function to at one value x of t, and to take its center as this estimate. For that purpose, he assumes that are given for , but that the value of x itself is unknown. For finding the center C of the nth order spiral function, Wynn gives the following lozenge algorithm (defined in References [88,89]):with and , he obtains , and writes This method of estimating the limit of a function is known as the ω-algorithm. He adds:This method has application in estimating the end-point of the trajectory of an aerodynamic vehicle, given its position, velocity components, etc. […]Since Texas is an oil-producing state the last problem we consider is that of the owner of a well producing oil with cast price c per barrel who wishes to determine(a) the price P par barrel which maximizes his profitand(b) his profit at the optimal price P.We now describe a solution and hasten to say that the economic part of the argument is taken directly from the mid nineteenth century French economist Cournot who considered the problem of the owner of a spring producing mineral water at zero cost per bottle.After giving the solution of this problem, Wynn proposes some references for those who are interesting in studying the matter further. Among them, the book of Antoine Augustin Cournot (1801–1877) [151]. As said before, at the end, there are 30 particularly nicely written pages with figures about spirals (see Figure 3), implementation schemes for the and the algorithms, an illustration of Picard iterates, numerical results, illustrations for the order of convergence, details about the problem of oil pricing policy, and references. It seems that these pages were ready to be copied for distribution to participants. Since the application was about an oil problem in Texas, this document could have been prepared for a seminar at the University of Texas at San Antonio.Let us mention that the interpretation of the scalar and vector Aitken’s process and -algorithm by means of spirals was independently rediscovered in 2014 by Berlinet [152], together with other interesting geometrical analyses of them.We did some numerical experiments with the spirals introduced by Wynn, and, in particular, we wanted to test his drawing reproduced in Figure 3. Remember that, according to Wynn’s nomenclature, a first order spiral has the form (our notation) , and that a second order spiral can have two forms (a) or (b) . If the -algorithm is applied to a first order spiral, then, , which is Aitken’s process. Applied to a second order spiral of form (a) or (b), this algorithm gives , while the iterated process (that is the process applied to the sequence ) does not possess this property.Wynn’s drawing of Figure 3 corresponds to the case (b). He wanted to illustrate the fact that can be written as , with , which he described as the spiral with center moving on spiral .In our numerical experiments, we always took . In Figure 4, we show two first order spirals with : the one on the left is obtained with , and it converges to C, the one on the right is with and does not converge or diverge since .Now, we consider second order spirals of forms (a) and (b). We took, for the form (a), , and, for the form (b), . All spirals are converging to C since and . Figure 5 shows the corresponding second order spirals: (a) on the left and (b) on the right.In Figure 6, we see the results obtained by the process applied to second order spirals: (a) on the left and (b) on the right. Comparing these curves with those of Figure 5 shows that, in fact, Aitken’s process acts as if it was suppressing one of the spirals of the curve (which contains two of them) since the sequence still looks like another spiral, and is not reduced to a single point as in the case where only one spiral was present.Indeed, if has the form (b) with , we have . It is easy to see thatwhich shows the gain brought by Aitken’s process by almost suppressing the role played by , the most important one.If has the form (a), that is , then . Aitken’s process leads towhich shows the acceleration brought by suppressing the leading error term.In Figure 7, we see the results obtained by the iterated process applied twice to second order spirals: (a) on the left and (b) on the right. Thus, the iterated process does not gives the exact value of C, which should be a single point and not a curve although is a spiral (see Figure 6), while (), in exact arithmetic, gives exactly C. However, the iterated process has a faster convergence, and it also has the form of a spiral.Spirals with different values of the parameters can have various shapes. It is sufficient, for instance, to change one sign in or . We intend to deepen this subject in a forthcoming paper.
4.1.4. Project for a Book
- 10
- Book on -algorithmThis 120 pages document is clearly a preparatory work for a book. Looking at its contents, it is probably the Resumé of book on the -algorithm, mentioned by Wynn in {26}, and also at the end of his document {28}, with an O (ongoing) in front of the name. In this manuscript, he stated in detail what he intended to treat. It contains an incredible succession of theorems whose proofs are not given, and comments and explanations between them are missing. It is divided into chapters.Chapter 1: Theorem concerning determinants. It contains identities for compound determinants, Schweins’ lemmata, simple and extended Hankel determinants.Chapter 2: Prediction based upon a linear model. Its sections are on exponential extrapolation (that is, the Aitken process), and extrapolation using a linear recursion (that is the Shanks transformation).Chapter 3: The epsilon algorithm. The sections are on the auxiliary numbers , the fundamental formulæ, and the algebraic theory of the epsilon algorithm (invariance properties and the cross rule).Chapter 4: The Padé table. Sections are on the Padé quotients and the Padé table.Chapter 5: The epsilon algorithm and the Padé table. The first section is on the even order epsilon numbers and the Padé table. The second section studies the epsilon array associated with a rational function. The next one is on the extended epsilon array, that is the second half of the Padé table. Recursions for primitive Padé quotients are then given.Chapter 6: Continued fractions. The chapter begins by the general theory (definitions, recurrences, equivalence transformation, contraction and extension, the Euler-Minding formulæ). The second section is about continued fractions derived from power series (corresponding and associated continued fractions). Then, the connection between continued fractions and the Padé table is studied. The continued fractions of the even order epsilon array are then discussed, and again those derived from power series. Transformations of corresponding continued fractions are presented, and a method of deriving an associated continued fraction is explained.Chapter 7: The epsilon algorithm and orthogonal polynomials. Definition, determinantal formula, associated polynomials, recurrence relationships in the case of formal orthogonality are first given. The -algorithm and Bauer’s bridge are presented.Chapter 8: The convergence behaviour of the row and column sequences of the Padé table. There is a section on Hadamard’s theory of the Taylor series, and two sections on the convergence of the rows and columns of the Padé table. Another section deals with the construction and convergence of the even order epsilon-array.Chapter 9: The convergence of the sequence . It presents Samuel Lubkin’s lemmata, and consequences.Chapter 10: Some analysis. The chapter gives classical results on functions of a real variable, definition and properties of the Stieltjes integral, theorems of choice, orthogonal polynomials derived from a positive distribution, the problem of moments, the Hausdorff moment problem, completely monotonic functions, complex variable theory.Chapter 11: Integral transforms. The first section is on the Riesz-Herglotz theorem, followed by one on Hamburger-Nevanlinna functions. Then, Wynn gives results on the Laplace transform, the Stieltjes inversion formula, the Riesz-Herglotz-Wall functions.Chapter 12: Power series. The chapter begins by the series generated by Hamburger-Nevanlinna and Stieltjes functions. Then, asymptotic series are discussed. The next section is on the transformation of divergent power series (Borel integrals and Watson-Nevanlinna lemma).Chapter 13: The convergence of associated and corresponding continued fractions. The first section considers the associated continued fractions generated by Hamburger-Nevanlinna functions. It is followed by a study of nested circular value regions. Convergence criteria expressed in terms of the coefficients of the continued fraction and of those of the series are then given. The next section is on what Wynn names theorems of access (logarithmic derivatives and Laplace transforms). The equivalence between the method of Borel and the use of continued fractions is then discussed. A characterisation of Stieltjes fractions is proposed.Chapter 14: The diagonal sequences of the Padé table and the even order ε-array. Wynn begins by the structure of the Padé table associated with a Hamburger-Nevanlinna and a Stieltjes function. The convergence of the diagonals of the Padé table for such functions is discussed, and, then, the construction and the convergence of the diagonal sequences of the even order epsilon array. There is a section on the Padé table derived from a Stieltjes series. A comparison between the epsilon algorithm and the generalised Euler transformation is proposed. Then, Wynn considers the epsilon algorithm and the transformation of trigonometric series, and that of operational formulæ in numerical analysis.Chapter 15: The operator epsilon algorithm. The chapter treats noncommutative continued fractions and orthogonal polynomials, the operator -algorithm, the noncommutative version of Bauer’s bridge. Wynn gives a fundamental theorem concerning operator valued orthogonal polynomials.Chapter 16: The vector epsilon algorithm. McLeod’s isomorphism and Clifford algebra are explained. Then, come the vector valued and the functional Padé tables.Chapter 17: The first confluent form of the epsilon algorithm: the rational function limit and the continued fraction limit. This chapter has two sections where these topics are treated.Chapter 18: The second confluent form of the epsilon algorithm: the definition of an integral as the limit of a continued fraction. After defining this second confluent form, Wynn explains the connection between both forms. Then, he treats the rational function and the continued fractions integrals. Euler integration ends the chapter.Chapter 19: The rational function integral. The degenerate theory in treated in the first section, and the general theory in the second one. A special convergence result is then given.Chapter 20: The continued fraction integral. The chapter begins by the degenerate theory before coming to a remarkable equivalence.Chapter 21: The third and fourth confluent forms of the epsilon algorithm. The fourth one is given but not the third one.Chapter 22: A partial differential equation associated with the epsilon algorithm. The first section is about a so-called -array. Then, partial differential equations are derived for it. The cases of the epsilon algorithm and that of the Padé surface are then treated. The following section is about self conjugate systems of partial differential equations for symmetric algorithms. Adjoint partial differential equations are discussed, and special solutions of the partial differential equation of the Padé surface are given.Chapter 23: Error analyses of the epsilon algorithm. The chapter begins by a perturbation analysis. Then, the convergence and stability of the epsilon algorithm are studied. The singular rule for the algorithm is given.This preparatory work for a book is in an advanced form since the results are well positioned in it. It only remains to link them by explanations and to give the proofs of the theoretical results (or the corresponding references to the literature).
4.1.5. Algebra
- 11
- Theory of stratified commutative fieldThis document presents a total of 266 pages. These notes, mentioned in many of the lists of Wynn, seem in a final form because they contain no erasures.After defining his notations for the ranges of the indexes, Wynn writes (all indexes are in ):Definition. A stratified commutative ring, or S-ring, is a system S of numbers arranged into strata such that(i) the members of form an additive Abelian group;(ii) commutative and associative multiplication is defined between elements of the various : with , and for such products;(iii) multiplication is distributive with respect to addition within appropriate strata: with , , addition on the left being within , that on the right within .A number belonging to the above system is an S-number and the to which it belongs is its stratum.is the class of S-rings.It is not assumed in the above definition that addition and subtraction between disparate strata should be possible, although in special cases this may be so. It is so, for example, when all are the same additive Abelian group; S is then simply a commutative ring. More generally, it is also possible between congruent strata if when , m being a prescribed integer.Two special S-rings are described, and then:The above examples serve to draw attention to a salient feature of theory to follow. It will be shown that the end results of certain computations involving S-numbers are members of fixed strata–for example that certain bilinear forms with S-number coefficients are expressible as linear sums of squares with coefficients that are S-numbers.The rest of the document cannot be summarized without going into detail. It is a purely theoretical work. No practical application is given, and there are no references to the literature.
- 12
- Stratified field, determinantal identities and LU decomposition in such fieldThis document of 105 pages probably follows the preceding document {11}. It contains theoretical notes about determinantal identities and LU decomposition over stratified commutative ring. He defines the so-called P-numbers that, in fact, have the same definition of the S-number of the document {11}. He defines the P-array and the P-matrices that are different in their definition. Several result were proved, concerning, for instance Jacobi’s theorem on the adjugate, product of determinants, Sylvester’s and Schweins’ determinantal identities, and so on. A LU decomposition is also proposed. This document, purely theoretical, is in almost good shape, and it seems to be complete since the numbered pages correspond to what Wynn indicates in {26}.
- 13
- Equations in field extensionsThis theoretical document, without title, contains 37 pages numbered from 1 to 37. Probably it is also intended to follow the work {11}, since inside there are references to that theory. It is perhaps what Wynn called Last notes (see {26}).
- 14
- Factorisations of a triangular matrixThis document contains 43 pages of well written notes with this title. This work is mentioned in {26–28}, together with the notes {1} on Bürmann series.As usual in many of his works, Wynn begins by introducing a plethora of notations which makes the results more difficult to apprehend. However, we need to give some of them.[…] (2a) indicates that the integer i should take the values . (b) If the lower limit j is unity, it and the subsequent semi-colon are omitted, thus is an abbreviation for . Conjoint descriptions are separated by a vertical bar, thus is an abbreviation for . […]For is the jth order determinant formed from the array whose th row contains the elements for ; when .A bunch of results are then presented but without any explanation on their purpose. However, it seems that the final goal is the following one:Notation. A being a lower triangular matrix with elements , is, for , the jth order determinant formed from the array whose th row contains the elements . Also, […]Theorem. Let be the elements of a nonsingular lower triangular matrix, and those of its inverse. ThenProof. The formulais obtained from the system of equationsThe result is correct when . A short inductive proof based upon the use of the formula, suffices to show that the result is true as stated.The last page of the document is a list of possible applications, not all of them being intelligible. But Wynn also mentions: Examine band matrix decomposition for deriving from differential equation; Partial sum transformation . Convergence acceleration; Integral transform of transformation as in motivation of -algorithm; Band matrix decomposition of and Newton series extension; Extension of Bernoulli polynomials , etc.
4.1.6. Software
- 15
- Numal in FORTRANNumal was a library of numerical algorithms written in Algol 60 and developed by members of the Mathematical Center in Amsterdam. Remember that Wynn belonged to this Center from 1960 to 1964. During his stay in München, he privately participated actively to the development of Algol 60 and used it for his programmes (see, i.e., References [33,44,55]). When he was in North America, he supervised a translation of the library into a FORTRAN version suitable for mini-computers and wrote a detailed documentation. As he wrote […]the translation it self was carried out almost single-handedly by H.T. Lau. It is interesting to remark that Hang T. Lau made the same for C-language and Java, and published two books on that, respectively in 1994 and in 2003. According to the Wynn explanation, this is a translation into Fortran of a Numerical Algorithms Library written in Algol 60. Its table of contents shows that it covers the main domains of numerical analysis: computer arithmetic, linear algebra, polynomials, series, numerical solution of differential equations, numerical integration, Fourier series, zero finding algorithms, minimisation, parameter estimation and special functions. The document found, submitted on 11 February 1981 has 29 pages and a preface, and it is the first part of this work and it is entitled 0. Introduction and Summary. The titles and contents of the other parts are given. This part begins by a comparison of the respective merits of Algol and FORTRAN. Then, Wynn describes the modifications he did and the improvements he brought. He also explains how the translation was performed and that the FORTRAN versions of the Algol procedures are far longer because the petty restrictions with which FORTRAN is afflicted cannot directly be overcome. Finally, he describes the machine and compiler dependent features which had to be taken into consideration.
4.2. Unpublished Typewritten Documents
- 16
- Commuting Cayley numbersThis is a one page note but complete with abstract and references. It can be downloaded from our website. A necessary and sufficient conditions are given for α and β, belonging to a division algebra of generalized Cayley numbers, to satisfy the relationship . References and the AMS subject classifications are given. Cayley numbers, also known as octonions, are elements of the 8-dimensional normed division algebra over the field of real numbers. It is the only 8-dimensional real alternative algebra without zero divisors. The Cayley algebra is an algebra with unique division and with an identity; it is alternative, non-associative and non-commutative.Octonions were discovered by John Thomas Graves (1806–1870) in December 1843, two months after the discovery of quaternions by Hamilton. Graves communicated his discovery to Hamilton in a letter dated 4 January 1844 but it was only published in 1848 after having been rediscovered by Arthur Cayley (1821–1895) in 1845. Since then they have been called Cayley numbers; see Reference [153]. Wynn already discussed them in several of his publications [65,66,69,99].
- 17
- On rational approximations to the exponential functionThis is a 8 pages paper that can be downloaded from our website. In the personal document {25}, this paper is mentioned as to appear in 1981 or after. It seems that it was never published. It is on the precise locations for the roots with large modulus of the equation . Notice that the approximants were given in closed form by Padé [141].
4.3. Other Documents
4.3.1. Drafts on Analysis
- 18
- Connections between various classes of functions of a complex variableThe first page of this document of 18 pages only contains the title. It seems to be a copy of Wynn’s original notes, and unfortunately it is incomplete since it contains only pages 8–14, 21–25, 28–32. Only the first two theorems are exploitable:Th 1. maps Re into iffwhere , bounded nondecreasing over .Th 2. maps Re into and as in (for fixed) iffwhere , bounded nondecreasing over such that all moments exist.The following pages are not in a sufficiently good shape to be analyzed.
- 19
- Generalization of the - and -algorithm integration processesUnfortunately these notes (may be a copy of the original) start from the page numbered 8 and, thus, it is difficult to analyze them. Perhaps the other pages have not yet been found in the boxes left by Wynn. As the title explains, they contain an attempt to generalize the - and -algorithm integration processes. This generalization consists in considering , where is approximately constant (slowly varying), and , and he assumes that the sequence such that is known. Then, he introduces many notations and conditions upon them, but after 20 pages, no clear conclusion follows from this work.In the same document, there is the original review of 11 pages written by Wynn himself of his paper in Reference [106]. It appeared, shortened, in Zentralblatt MATH, as Zbl 0531.40002. Wynn almost surely put these pages together since they both concern the computation of integrals of the form .
- 20
- Extraction of totally monotone sequences from convergents of a continued fractionThis document is a partial copy (pages 31–35) of original notes. There are some pages on an attempt to extract a totally oscillating sequence from the successive convergents of a continued fractionIf with , then tends to , and the sequence is totally monotone. No other interesting result can be extracted from this partial document.Then, there are 2 pages of rough notes on “Auxiliary sequence transformation before application of the ε-algorithm”, which could be related to what precedes, and 3 pages on “Transformation of monotonic sequences by means of the ε-algorithm”, which seem to be independent of the topic.
4.3.2. Drafts on Algebra
- 21
- Interpolation TheoryThis is an unfinished document of 60 pages, not numbered but in a good shape, entitled Interpolation theory. It is probably a part of a monograph (an important project) referenced in several documents (see {26,28}).Wynn wrote:The following notes concern interpolation in a field by the use of polynomials and rational functions, the interpolatory argument values being assumed to be discrete. The notes serve both as a basis for subsequent more general theory concerning interpolation in the presence of confluent arguments and as a framework for the theory of the transformation of Schweins’ series.I. Notations, definitions and classes of matrices and mappingsII. Formulae from the calculus of finite differencesIII. Matrix formulations of finite difference formulaeIV. Interpolation by the use of polynomials and rational functionsOnly the part I. has been found. It is a list of notations and it is too vague to be of interest. A Schweins’ series is related to minor identities for quasi-determinants of noncommutative matrices; see, for example, Reference [154]. Schweins obtained it in 1825 for the quotient of two n-rowed determinants which differ only in one column [155].
- 22
- Linear equations in a commutative ringThis untitled document of 38 pages (numbered from the 9th one) begins by a first list of 7 topics he wanted to treat. Then, 8 pages that look like two tables of contents with several topics covered follow. After that, these items are detailed and, hopefully, Wynn also inserted in front of them the number of the pages where each subitem can be found. In the first page, Wynn inserted also a sketch of the following notes {23}.The first section begins by1. Linear equations in a commutative ring.It is proposed to study the systems of solutions of equations of the formwhere, W being a prescribed commutative ring, , and I being a system of numbers in W, the above equation is to be interpreted in the sense that exists for which .The other main sections are:2. Systems of numbers3. Divisibility4. Numerator systems5. Solution systems6. Square free ideals7. The ideal reductionA complete analysis of this first section, also if it looks quite complete, seems to be difficult.
- 23
- MappingThis only theoretical handwritten draft of 81 pages (there is a page 18 followed by page 18’) and is about what Wynn named Aggregates. A sketch of these notes can be found in {22}. It is quite difficult to understand what it is about since the manuscript is not entirely well written, and seems not to have been finished.Let . A nonvoid aggregate in is composed of a nonvoid set and a system of nonvoid sets defined for each . Then, other definitions and properties follow. Parts of the document are on mappings and classes of aggregates. There is no indication of the purpose of this work, and, searching on internet, nothing similar or related was found.
- 24
- Factor relationships of the formThis is a long theoretical text of 115 pages, entitled Factor relationships of the form , where , and d are mapping systems. At the beginning, there is a sketch of the topics that are developed in the sequel.After introducing a lot of notations, Wynn treated the existence of domains of constancy and intersection mapping systems. Then, there is a section on invariance of spaces with respect to sequence rearrangement, one on the properties of domains of constancy, another one on properties of prequotient spaces with respect to domains of constancy and intersection systems, a section giving complete factorisation results, and one on spaces of ordered pairs of mapping systems.
4.3.3. Personal Documents
- 25
- Curriculum vitæ of Peter WynnThis document is a typewritten curriculum vitæ by Wynn himself (born 1 September 1931; Hoddesdon, Herts (U.K.)). Then, he reports his education, his professional experience from 1952 to 1980 (thus, it does not contain his positions after that). In this curriculum, we can see that he occupied several positions in different countries in the World. Moreover, we were able to confirm his date and place of birth with certainty. This curriculum contains a bibliography with publications from 1956 to 1981. In this bibliography, Wynn mentioned two references that we did not know: a paperOn rational approximations to the exponential function, 1981, to appear, which was found in the boxes and is reproduced at the end of this paper, and a monograph, Numal in Fortran. 0, Comunicaciones Técnicas, Universidad Nacional Autónoma de México, Instituto de Investigaciones en Matemáticas Aplicadas y en Sistemas (IIMAS), México.The number of the reports written by Wynn were 48.0–48.11. Certainly it is a completed project (he mentioned it in {28}, with an O) and, looking into the web, we found that the report 48.0 was published in Serie azul, monografías–Instituto de Investigaciones en Matemáticas Aplicadas y en Sistemas. UNAM, México, 1981, Pag. 1–93. On the URL https://biblat.unam.mx/en/buscar/wynn-p/ (accessed on 30 April 2021) the part 48.0 is cited (93 pages). We found the number 48.0 in one of the boxes (see {15}).
- 26
- Lists of documentsIn each of the two opened boxes, we found a list of documents (one of them with the title Duplicate list. They are probably the lists of documents (xerox copies, handwritten notes and papers, reviews, and so on) that Wynn holds, and that he inserted into the boxes, since we also found a (sometime) partial correspondence mixed with the documents found and analyzed in this paper. There are plenty of what Wynn named “rough notes”. Among these rough notes, we find the ones showed in Figure 8, that lead us to think he was looking for a determinantal expression for the even vectors obtained by the vector -algorithm.Since the text could be difficult to read, we reproduce below what Wynn wrote:Rough notes on extensions of determinantal relationships, algorithmic recursions, etc. to noncommutative, possibly nonassociative elements, by use of linear algebraic equations.Rough notes of derivation of expressions representing -algorithm vectors by differentiation of scalar expressions involving inner product.Rough notes on expression in closed form of vectors produced by vector -algorithm & other forms.Thus, one can wonder if Wynn was trying to express the vectors computed by his vector -algorithm as ratios of some kind of (generalized) determinants. Such a result would be of great interest for the understanding of this algorithm, but, unfortunately, it has not been obtained yet. In any case, these rough notes are difficult to read and understand!
- 27
- List of activitiesThis is a list of activities that have to be accomplished: construct notes and Resumé on different topics. The activities are structured in subitems of an itemized list (from (A) to (J)). Are they separated subjects or the skeleton of a book or for other papers? It is difficult to say. The itemized main topics are: Preparatory algebraic theory; Polynomials and rational functions; Interpolation theory; Moment problem and stability functions; Anti-derivative theory; An array of functions; Functions defined by an integral transform; the Euler-Maclaurin and Boole series; Sequence transformations (a subtopic is about auxiliary transformation before application of the -algorithm, a problem addressed in Reference [156]). The item (J) Low priority seems to contains activities having another scope (documentation for Algol programmes, preparation of talks, and another Resumé).This document was probably written after 1981 since Reference [109] is mentioned.
- 28
- List of projectsThere are 3 pages containing a list of projects. Some of them were probably realized (those preceded by a D) and some of them, with an O, perhaps meaning Ongoing. But we are not sure that some other remained in the state of projects, although some of them are preceded by a D. Among this list, we find: theory of stratified commutative ring, functional interpolation, variants of the remainder terms in the Euler Maclaurin and Boole series, auxiliary sequence transformation before application of the -algorithm (such a pre-processing or preconditioning as already evoked in References [56,72]), extension of determinantal identities and algorithmic recursions to noncommutative and nonassociative forms by use of linear algebraic equations, numerical experiments in nonassociative algebras, numerical experiments in optimisation, vector -algorithm, etc., the analytic continuation of functions defined by an integral transform. And, finally, there is a mention of a book on the -algorithm.
- 29
- Bibliography of various authorsIt is a list of references by various authors, probably a list of Xerox copied papers.
- 30
- Reviews of Wynn for zbMATHThis document contains two papers published in the journal Ukrainskii Matematicheskii Zhurnal (Ukrainian Mathematical Journal) in Russian. The first one is authored by R. I. Mikhal’chuk & M. S. Syavavko and its title (in English) is A continual analog of continued fraction (Vol. 34, No. 5, pp. 559–564, September–October (1982), doi: 10.1007/BF01093130 for English translation). The second one is the paper by Y.R. Batyuk & M.S. Syavavko entitled Integral continued fractions, Dokl. Akad. Nauk Ukrain. SSR Ser.A7, 6–8 (1984), also in Russian. This is not strange since Wynn knew Russian (and also German, Duch, Spanish, and some French) and translated two books in this language [110,111]. There are also four handwritten reviews written for zbMATH. The first two are related to the papers (Zbl 0579.40001, Zbl 0571.40003) on continued fractions previously indicated, and the last one (Zbl 0554.65003) to a paper by Naoyuki Tokuda (A new application of Lagrange-Bürmann expansions. I. General principle, Z. Angew. Math. Phys. 34, 697–727 (1983)). Wynn, during his stay in Mexico, was a very active mathematical reviewer for zbMATH (145 reviews) by analyzing papers and books published from 1971 to 2011, some of them in Russian. The last one, very detailed, contains a review of a paper on rational function interpolation and the -algorithm, but it is not present in zbMATH.The first three handwritten reviews have been shortened when published in zbMATH.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
References of Peter Wynn
- Wynn, P. A note on Salzer’s method for summing certain convergent series. J. Math. Phys. 1956, 35, 318–320, MR0086910, Zbl 0075.12802, Submitted 19 July 1955. [Google Scholar] [CrossRef]
- Wynn, P. On a procrustean technique for the numerical transformation of slowly convergent sequences and series. Math. Proc. Camb. Philos. Soc. 1956, 52, 663–671, MR0081979, Zbl 0072.33802, Submitted 31 October 1955. [Google Scholar] [CrossRef]
- Wynn, P. On a device for computing the em(Sn) transformation. Math. Tables Aids Comput. 1956, 10, 91–96, MR0084056, Zbl 0074.04601. [Google Scholar] [CrossRef]
- Wynn, P. On a cubically convergent process for determining the zeros of certain functions. Math. Tables Aids Comput. 1956, 10, 97–100, MR0081547, Zbl 0073.10703. [Google Scholar] [CrossRef][Green Version]
- Wynn, P. Central difference and other forms of the Euler transformation. Quart. J. Mech. Appl. Math. 1956, 9, 249–256, MR0080782, Zbl 0074.29004, Submitted 28 July 1955. [Google Scholar] [CrossRef]
- Wynn, P. On the propagation of error in certain non-linear algorithms. Numer. Math. 1959, 1, 142–149, MR0107988, Zbl 0087.32502, Submitted 26 February 1959. [Google Scholar] [CrossRef]
- Wynn, P. A sufficient condition for the instability of the q-d algorithm. Numer. Math. 1959, 1, 203–207, MR0109426, Zbl 0096.09501, Submitted 25 March 1959. [Google Scholar] [CrossRef]
- Wynn, P. Converging factors for continued fractions, I. Numer. Math. 1959, 1, 272–307, MR0116158, Zbl 0092.05101, Submitted 25 March 1959. [Google Scholar] [CrossRef]
- Wynn, P. Converging factors for continued fractions, II. Numer. Math. 1959, 1, 308–320, MR0116158, Zbl 0092.05101, Submitted 25 March 1959. [Google Scholar] [CrossRef]
- Wynn, P. Über einen Interpolations-algorithmus und gewisse andere Formeln, die in der Theorie der Interpolation durch rationale Funktionen bestehen. Numer. Math. 1960, 2, 151–182, MR0128597, Zbl 0222.65007, Submitted 31 July 1959. [Google Scholar] [CrossRef]
- Wynn, P. The rational approximation of functions which are formally defined by a power series expansion. Math. Comp. 1960, 14, 147–186, MR0116457, Zbl 0173.18803, Submitted 5 November 1959. [Google Scholar] [CrossRef]
- Wynn, P. Confluent forms of certain non-linear algorithms. Arch. Math. 1960, 11, 223–236, MR0128068, Zbl 0096.09502, Submitted 5 October 1959. [Google Scholar] [CrossRef]
- Wynn, P. A note on a confluent form of the ε-algorithm. Arch. Math. 1960, 11, 237–240, MR0128069, Zbl 0096.09601, Submitted 27 March 1959. [Google Scholar] [CrossRef]
- Wynn, P. On the tabulation of indefinite integrals. BIT 1961, 1, 286–290, Zbl 0114.07003. [Google Scholar] [CrossRef]
- Wynn, P. L’ε-algoritmo e la tavola di Padé. Rend. Mat. Roma 1961, 20, 403–408, MR0158206, Zbl 0104.34205. [Google Scholar]
- Wynn, P. The epsilon algorithm and operational formulas of numerical analysis. Math. Comp. 1961, 15, 151–158, MR0158513, Zbl 0102.33205. [Google Scholar] [CrossRef]
- Wynn, P. On repeated application of the epsilon algorithm. Rev. Fr. Trait. Inf. Chiffres 1961, 4, 19–22, MR0149145, Zbl 0102.33301. [Google Scholar]
- Wynn, P. A comparison between the numerical performances of the Euler transformation and the ε-algorithm. Rev. Fr. Trait. Inf. Chiffres 1961, 4, 23–29, Zbl 0102.33302. [Google Scholar]
- Wynn, P. The numerical transformation of slowly convergent series by methods of comparison, Part I. Rev. Fr. Trait. Inf. Chiffres 1961, 4, 177–210, MR0162350, Zbl 0113.04601. [Google Scholar]
- Wynn, P. A sufficient condition for the instability of the ε-algorithm. Nieuw Arch. Wiskd. 1961, 9, 117–119, MR0139252, Zbl 0154.40305. [Google Scholar]
- Wynn, P. Upon the Expression of an Integral as the Limit of a Continued Fraction; Report DR 24/61; Sticht. Math. Centrum. Rekenafd.: Amsterdam, The Netherlands, 1961; Available online: https://ir.cwi.nl/pub/9537 (accessed on 30 April 2021).
- Wynn, P. A note on a method of Bradshaw for transforming slowly convergent series and continued fractions. Am. Math. Mon. 1962, 69, 883–889, MR0146559, Zbl 0112.28902. [Google Scholar] [CrossRef][Green Version]
- Wynn, P. Upon a second confluent form the ε-algorithm. Proc. Glasgow Math. Assoc. 1962, 5, 160–165, MR0139253, Zbl 0118.32502, Submitted 21 July 1961. [Google Scholar] [CrossRef]
- Wynn, P. Acceleration techniques for iterated vector and matrix problems. Math. Comp. 1962, 16, 301–322, MR0145647, Zbl 0105.10302. [Google Scholar] [CrossRef]
- Wynn, P. A comparison technique for the numerical transformation of slowly convergent series based on the use of rational functions. Numer. Math. 1962, 4, 8–14, MR0136500, Zbl 0138.09901, Submitted 17 July 1961. [Google Scholar] [CrossRef]
- Wynn, P. Numerical efficiency profile functions. Koninkl. Nederl. Akad. Wet. 1962, 65A, 118–126, MR0139257, Zbl 0105.10002, Submitted 30 September 1961. [Google Scholar] [CrossRef]
- Wynn, P. The numerical efficiency of certain continued fraction expansions, IA. Koninkl. Nederl. Akad. Wet. 1962, 65A, 127–137, MR0139254, Zbl 0105.10003, Submitted 30 September 1961. [Google Scholar] [CrossRef]
- Wynn, P. The numerical efficiency of certain continued fraction expansions, IB. Koninkl. Nederl. Akad. Wet. 1962, 65A, 138–148, MR0139255, Zbl 0105.10003, Submitted 30 September 1961. [Google Scholar] [CrossRef]
- Wynn, P. On a connection between two techniques for the numerical transformation of slowly convergent series. Koninkl. Nederl. Akad. Weten. 1962, 65A, 149–154, MR0139256, Zbl 0138.09902, Submitted 30 September 1961. [Google Scholar] [CrossRef]
- Wynn, P. Una nota su un analogo infinitesimale del q-d algoritmo. Rend. Mat. Roma 1962, 21, 77–85, MR0144127, Zbl 0107.28203, Submitted 11 September 1961. [Google Scholar]
- Wynn, P. A note on fitting certain types of experimental data. Stat. Neerl. 1962, 16, 145–150, MR0150517. [Google Scholar] [CrossRef]
- Wynn, P. Note on the solution of a certain boundary-value problem. BIT 1962, 2, 61–64, MR0155445, Zbl 0105.32103. [Google Scholar] [CrossRef]
- Wynn, P. An arsenal of Algol procedures for complex arithmetic. BIT 1962, 2, 232–255, MR0166945, Zbl 0113.11605. [Google Scholar] [CrossRef][Green Version]
- Wynn, P. The numerical transformation of slowly convergent series by methods of comparison. Part II. Rev. Fr. Trait. Inf. Chiffres 1962, 5, 65–88, MR0149146, Zbl 0221.65007. [Google Scholar]
- Wynn, P. Acceleration technique in numerical analysis with particular reference to problems in one independent variable. In Information Processing 1962, Proceedings of the IFIP Congress 62, Munich, Germany, 27 August–1 September 1962; Popplewell, C.M., Ed.; North-Holland: Amsterdam, The Netherlands, 1963; pp. 149–156, Zbl 0146.14201. [Google Scholar]
- Wynn, P. Singular rules for certain non-linear algorithms. BIT 1963, 3, 175–195, MR0166946, Zbl 0123.11101. [Google Scholar] [CrossRef]
- Wynn, P. Note on a converging factor for a certain continued fraction. Numer. Math. 1963, 5, 332–352, MR0166902, Zbl 0117.10802. [Google Scholar] [CrossRef]
- Wynn, P. On a connection between the first and the second confluent forms of the ε-algorithm. Niew. Arch. Wisk. 1963, 11, 19–21, MR0149147, Zbl 0116.33101, Submitted 29 October 1962. [Google Scholar]
- Wynn, P. Continued fractions whose coefficients obey a non-commutative law of multiplication. Arch. Rat. Mech. Anal. 1963, 12, 273–312, MR0145231, Zbl 0122.30604, Submitted 13 August 1962. [Google Scholar] [CrossRef]
- Wynn, P. A numerical study of a result of Stieltjes. Rev. Fr. Trait. Inf. Chiffres 1963, 6, 175–196, MR0157470, Zbl 0116.09202. [Google Scholar]
- Wynn, P. Converging factors for the Weber parabolic cylinder function of complex argument, IA. Proc. Kon. Nederl. Akad. Weten. 1963, 66, 721–736, MR0158514, Zbl 0235.65015, Submitted 29 June 1963. [Google Scholar] [CrossRef]
- Wynn, P. Converging factors for the Weber parabolic cylinder function of complex argument, IB. Proc. Kon. Nederl. Akad. Weten. 1963, 66, 737–754, MR0158515, Zbl 0235.65015, Submitted 29 June 1963. [Google Scholar] [CrossRef]
- Wynn, P. Partial differential equations associated with certain non-linear algorithms. Z. Angew. Math. Phys. 1964, 15, 273–289, MR0166944, Zbl 0252.65096, Submitted 1 September 1963. [Google Scholar] [CrossRef][Green Version]
- Wynn, P. General purpose vector epsilon-algorithm Algol procedures. Numer. Math. 1964, 6, 22–36, MR0166947, Zbl 0113.32609, Submitted 12 July 1963. [Google Scholar] [CrossRef]
- Wynn, P. On some recent developments in the theory and application of continued fractions. SIAM J. Numer. Anal. Ser. B 1964, 1, 177–197, MR0178269, Zbl 0143.17804, Submitted 4 November 1963. [Google Scholar] [CrossRef]
- Wynn, P. Four lectures on the numerical application of continued fractions. In Alcune Questioni di Analisi Numerica; Ghizzetti, A., Ed.; Series: C.I.M.E. Summer Schools; Springer: Heidelberg, Germany, 1965; Volume 35, pp. 111–251, Zbl 0202.43904. [Google Scholar] [CrossRef]
- Wynn, P. A note on programming repeated application of the epsilon-algorithm. Rev. Fr. Trait. Inf. Chiffres 1965, 8, 23–62, Errata, 156, MR0181081, Zbl 0132.36903. [Google Scholar]
- Wynn, P. Upon systems of recursions which obtain among the quotients of the Padé table. Numer. Math. 1966, 8, 264–269, MR0215499, Zbl 0163.39502, Submitted 5 May 1965. [Google Scholar] [CrossRef]
- Wynn, P. On the convergence and stability of the epsilon algorithm. SIAM J. Numer. Anal. 1966, 3, 91–122, MR0207180, Zbl 0299.65003, Submitted 16 September 1965. [Google Scholar] [CrossRef]
- Wynn, P. Upon a Conjecture Concerning a Method for Solving Linear Equations, and Certain Other Matters; MRC Technical Summary Report 626; University of Wisconsin: Madison, WI, USA, 1966. [Google Scholar]
- Wynn, P. Complex Numbers and Other Extensions to the Clifford Algebra with an Application to the Theory of Continued Fractions; MRC Technical Summary Report 646; University of Wisconsin: Madison, WI, USA, 1966. [Google Scholar]
- Wynn, P. Upon the Diagonal Sequences of the Padé Table; MRC Technical Summary Report 660; University of Wisconsin: Madison, WI, USA, 1966. [Google Scholar]
- Wynn, P. Upon an Invariant Associated with the Epsilon Algorithm; MRC Technical Summary Report 675; University of Wisconsin: Madison, WI, USA, 1966. [Google Scholar]
- Wynn, P. On the computation of certain functions of large argument and parameter. BIT 1966, 6, 228–259, MR0203912, Zbl 0196.48301. [Google Scholar] [CrossRef]
- Wynn, P. An arsenal of Algol procedures for the evaluation of continued fractions and for effecting the epsilon algorithm. Rev. Fr. Trait. Inf. Chiffres 1966, 9, 327–362, MR0203963. [Google Scholar]
- Wynn, P. Accelerating the Convergence of a Monotonic Sequence by a Method of Intercalation; MRC Technical Summary Report 674; University of Wisconsin: Madison, WI, USA, 1967. [Google Scholar]
- Wynn, P. A general system of orthogonal polynomials. Quart. J. Math. Oxf. 1967, 18, 81–96, MR0210963, Zbl 0185.30001, Submitted 8 September 1966. [Google Scholar] [CrossRef]
- Wynn, P. Transformations to accelerate the convergence of Fourier series. In Gertrude Blanch Anniversary Volume; Wright Patterson Air Force Base, 1967; pp. 339–379; MRC Technical Summary Report 673; Mond, B., Blanch, G., Eds.; University of Wisconsin: Madison, WI, USA, 1966; MR0215553, Zbl 0242.65004. [Google Scholar]
- Wynn, P. A Note on the Convergence of Certain Noncommutative Continued Fractions; MRC Technical Summary Report 750; University of Wisconsin: Madison, WI, USA, 1967. [Google Scholar]
- Wynn, P. Upon the Padé table derived from a Stieltjes series. SIAM J. Numer. Anal. 1968, 5, 805–834, MR0239734, Zbl 0175.36102, Submitted 22 March 1968, Revised 5 July 1968. [Google Scholar] [CrossRef]
- Wynn, P. Vector continued fractions. Linear Algebra Appl. 1968, 1, 357–395, MR0231848, Zbl 0164.18503, Submitted 5 March 1968. [Google Scholar] [CrossRef]
- Wynn, P. Upon the definition of an integral as the limit of a continued fraction. Arch. Rat. Mech. Anal. 1968, 28, 83–148, MR0221152, Zbl 0162.37202, Submitted 24 May 1967. [Google Scholar] [CrossRef]
- Wynn, P. Zur Theorie der mit gewissen speziellen Funktionen verknüpften Padéschen Tafeln. Math. Z. 1969, 109, 66–70, MR0243242, Zbl 0175.36103, Submitted 17 April 1968. [Google Scholar] [CrossRef]
- Wynn, P. Five Lectures on the Numerical Application of Continued Fractions; Orientation Lecture Series 5; Mathematical Research Center, University of Wisconsin: Madison, WI, USA, 1970; 183p. [Google Scholar]
- Wynn, P. Upon a Recursive System of Flexible Rings Permitting Involution; Report CRM-50; Centre de Recherches Mathématiques, Université de Montréal: Montréal, QC, Canada, 1970. [Google Scholar]
- Wynn, P. Upon the Inverse of Formal Power Series over Certain Algebra; Report CRM-53; Centre de Recherches Mathématiques, Université de Montréal: Montréal, QC, Canada, 1970. [Google Scholar]
- Wynn, P. Upon a Hierarchy of Epsilon Arrays; Technical Report 46; Louisiana State University: New Orleans, LA, USA, 1970. [Google Scholar]
- Wynn, P. A note on the generalised Euler transformation. Comput. J. 1971, 14, 437–441, Erratum in 1972, 15, 175; MR0321266, Zbl 0227.65002, doi:10.1093/comjnl/15.2.175-a. [Google Scholar] [CrossRef]
- Wynn, P. The Abstract Theory of the Epsilon Algorithm; Report CRM-74; Centre de Recherches Mathématiques, Université de Montréal: Montréal, QC, Canada, 1971. [Google Scholar]
- Wynn, P. Upon a Class of Functions Connected with the Approximate Solution of Operator Equations; Report CRM-103; Centre de Recherches Mathématiques, Université de Montréal: Montréal, QC, Canada, 1971. [Google Scholar]
- Wynn, P. A note Upon Totally Monotone Sequences; Report CRM-139; Centre de Recherches Mathématiques, Université de Montréal: Montréal, QC, Canada, 1971. [Google Scholar]
- Wynn, P. A transformation of series. Calcolo 1971, 8, 255–272, MR0303675, Zbl 0236.65006, Submitted 1 September 1971. [Google Scholar] [CrossRef]
- Wynn, P. Difference-differential recursions for Padé quotients. Proc. Lond. Math. Soc. 1971, 3, 283–300, MR0313682, Zbl 0221.40005, Submitted 4 May 1970. [Google Scholar] [CrossRef]
- Wynn, P. Upon the generalized inverse of a formal power series with vector valued coefficients. Compos. Math. 1971, 23, 453–460, MR306224, Zbl 0239.15003, Submitted 13 January 1971. Available online: www.numdam.org/item/CM_1971__23_4_453_0 (accessed on 30 April 2021).
- Wynn, P. Über orthonormale Polynome und ein assoziiertes Momentproblem. Math. Scand. 1971, 29, 104–112, MR0308406, Zbl 0231.30037, Submitted 27 April 1971. [Google Scholar] [CrossRef][Green Version]
- Wynn, P. On an extension of a result due to Pólya. J. Reine Angew. Math. 1971, 248, 127–132, MR0289771, Zbl 0219.30002, Submitted 22 November 1969. [Google Scholar] [CrossRef]
- Wynn, P. Convergence acceleration by a method of intercalation. Computing 1972, 9, 267–273, MR0315861, Zbl 0248.65003, Submitted 6 August 1971. [Google Scholar] [CrossRef]
- Wynn, P. Invariants associated with the epsilon algorithm and its first confluent form. Rend. Circ. Mat. Palermo 1972, 21, 31–41, MR0346367, Zbl 0268.65076, Submitted January 1972. [Google Scholar] [CrossRef]
- Wynn, P. Hierarchies of arrays and function sequences associated with the epsilon algorithm and its first confluent form. Rend. Mat. Roma Ser. VI 1972, 5, 819–852, MR0355405, Zbl 0278.65002, Submitted 15 May 1972. [Google Scholar]
- Wynn, P. A Note on a Partial Differential Equation; Report CRM-22; Centre de Recherches Mathématiques, Université de Montréal: Montréal, QC, Canada, 1972. [Google Scholar]
- Wynn, P. Sur les suites totalement monotones. CR Acad. Sci. Paris 1972, 275A, 1065–1068, MR0310480, Zbl 0251.40001, Accepted 6 November 1972. [Google Scholar]
- Wynn, P. Transformation de séries à l’aide de l’ε-algorithm. CR Acad. Sci. Paris 1972, 275A, 1351–1353, MR0311068, Zbl 0257.65005, Accepted 18 December 1972. [Google Scholar]
- Wynn, P. Upon a convergence result in the theory of the Padé table. Trans. Am. Math. Soc. 1972, 165, 239–249, MR0293106, Zbl 0236.30013, Received 26 October 1970, Revised 21 May 1971. [Google Scholar] [CrossRef]
- Wynn, P. A Convergence Theory of Some Methods of Integration; Report CRM-193; Centre de Recherches Mathématiques, Université de Montréal: Montréal, QC, Canada, 1972. [Google Scholar]
- Wynn, P. The Partial Differential Equation of the Padé surface; Report CRM-197; Centre de Recherches Mathématiques, Université de Montréal: Montréal, QC, Canada, 1972. [Google Scholar]
- Wynn, P. The Algebra of Certain Formal Power Series; Report CRM-216; Centre de Recherches Mathématiques, Université de Montréal: Montréal, QC, Canada, 1972. [Google Scholar]
- Wynn, P. On Some Extensions of Euclid’s Algorithm, and Some Consequences Thereof; Report CRM; Centre de Recherches Mathématiques, Université de Montréal: Montréal, QC, Canada, 1972. [Google Scholar]
- Wynn, P. Upon some continuous prediction algorithms. I. Calcolo 1973, 9, 197–234, MR0362820, Zbl 0248.65007, Submitted 20 June 1972. [Google Scholar] [CrossRef]
- Wynn, P. Upon some continuous prediction algorithms. II. Calcolo 1973, 9, 235–278, MR0362821, Zbl 0281.65001, Submitted 20 June 1972. [Google Scholar] [CrossRef]
- Wynn, P. On the zeros of certain confluent hypergeometric functions. Proc. Am. Math. Soc. 1973, 40, 173–183, MR0318529, Zbl 0268.33004, Submitted 7 July 1972, Revised 26 October 1972. [Google Scholar] [CrossRef]
- Wynn, P. Accélération de la convergence de séries d’opérateurs en analyse numérique. CR Acad. Sci. Paris 1973, 276A, 803–806, MR0317519, Zbl 0268.65001, Accepted 12 March 1973. [Google Scholar]
- Wynn, P. On the intersection of two classes of functions. Rev. Roum. Math. Pures Appl. 1974, 19, 949–959, MR0390195, Zbl 0302.30011. [Google Scholar]
- Wynn, P. Extremal properties of Padé quotients. Acta Math. Hung. 1974, 25, 291–298, MR0352431, Zbl 0323.30043, Submitted 14 July 1972. [Google Scholar] [CrossRef]
- Wynn, P. Sur l’équation aux dérivées partielles de la surface de Padé. CR Acad. Sci. Paris 1974, 278A, 847–850, MR0341910, Zbl 0276.35015. [Google Scholar]
- Wynn, P. A Numerical Method for Estimating Parameters in Mathematical Models; Report CRM-443; Centre de Recherches Mathématiques, Université de Montréal: Montréal, QC, Canada, 1974. [Google Scholar]
- Wynn, P. Some recent developments in the theories of continued fractions and the Padé table. Rocky Mt. J. Math. 1974, 4, 297–324, MR0340880, Zbl 0302.65005, Submitted 8 February 1973. [Google Scholar] [CrossRef]
- Wynn, P. How to integrate without integrating. In Proceedings of the Euromech 58 Conference on Padé Method and Its Applicatons in Mechanics, Toulon, France, 12–14 May 1975. Unpublished. [Google Scholar]
- Wynn, P. Upon a class of functions connected with the approximate solution of operator equations. Ann. Mat. Pura Appl. 1975, 104, 1–29, MR0387553, Zbl 0315.65015, Submitted 10 October 1972. [Google Scholar] [CrossRef]
- Wynn, P. Distributive rings permitting involution. Math. Balk. 1975, 5, 299–318, Report CRM-281; Centre de Recherches Mathématiques, Université de Montréal: Montréal, QC, Canada, 1973; MR0506478, Zbl 0381.17001. [Google Scholar]
- Wynn, P. The algebra of certain formal power series. Riv. Mat. Univ. Parma 1976, 2, 155–176, MR0447220, Zbl 0369.16002, Submitted 28 August 1974. Available online: www.rivmat.unipr.it/fulltext/1976-2/1976-2-155.pdf (accessed on 30 April 2021).
- Wynn, P. An Array of Functions; Report; School of Computer Science, McGill University: Montreal, QC, Canada, 1976. [Google Scholar]
- Wynn, P. A Continued Fraction Transformation of the Euler-MacLaurin Series; Report; School of Computer Science, McGill University: Montreal, QC, Canada, 1976. [Google Scholar]
- Wynn, P. A convergence theory of some methods of integration. J. Reine Angew. Math. 1976, 285, 181–208, MR0415119, Zbl 0326.40005, Submitted 22 March 1974. [Google Scholar] [CrossRef]
- Wynn, P. The calculus of finite differences over certain systems of numbers. Calcolo 1977, 14, 303–341, MR0503568, Zbl 0379.65005, Submitted 30 August 1976. [Google Scholar] [CrossRef]
- Wynn, P. The transformation of series by the use of Padé quotients and more general approximants. In Padé and Rational Approximation. Theory and Applications; Saff, E.B., Varga, R.S., Eds.; Academic Press: New York, NY, USA, 1977; pp. 121–144, MR0473660, Zbl 0368.41014. [Google Scholar] [CrossRef]
- Wynn, P. The evaluation of singular and highly oscillatory integrals by use of the anti-derivative. Calcolo 1978, 15, 1–123, Report; School of Computer Science, McGill University: Montreal, QC, Canada, 1976; Zbl 0531.40002, Submitted 17 July 1977. [Google Scholar]
- Wynn, P. The work of E.B. Christoffel on the theory of continued fractions. In E.B. Christoffel: The Influence of His Work on Mathematics and the Physical Sciences; Butzer, P.L., Fehér, F., Eds.; Birkhäuser Verlag: Basel, Switzerland, 1981; pp. 190–202, MR0661065, Zbl 0476.30004, Submitted 9 October 1979. [Google Scholar] [CrossRef]
- Wynn, P. Remark upon developments in the theories of the moment problem and of quadrature, subsequent to the work of Christoffel. In E.B. Christoffel: The Influence of His Work on Mathematics and the Physical Sciences; Butzer, P.L., Fehér, F., Eds.; Birkhäuser Verlag: Basel, Switzerland, 1981; pp. 731–734, MR0661114, Zbl 0484.41040, Submitted 28 April 1980. [Google Scholar] [CrossRef]
- Wynn, P. The convergence of approximating fractions. Bol. Soc. Mat. Mex. 1981, 26, 57–71, MR0742016, Zbl 0479.40004. [Google Scholar]
Translations by Peter Wynn
- Khintchine, A.Y. Continued Fractions; Translated from Russian by Peter Wynn; P. Noordhoff N.V.: Groningen, The Netherlands, 1963. [Google Scholar]
- Khovanskii, A.N. The Application of Continued Fractions and their Generalizations to Problems in Approximation Theory; Translated from Russian by Peter Wynn; P. Noordhoff N.V.: Groningen, The Netherlands, 1963. [Google Scholar]
General Bibliography
- Shanks, D. Non-linear transformations of divergent and slowly convergent sequences. J. Math. Phys. 1955, 34, 1–42. [Google Scholar] [CrossRef]
- Brezinski, C.; Redivo-Zaglia, M. Extrapolation and Rational Approximation. The Works of the Main Contributors; Springer Nature: Cham, Switzerland, 2020. [Google Scholar]
- Brezinski, C.; Redivo-Zaglia, M. The genesis and early developments of Aitken’s process, Shanks’ transformation, the ε-algorithm, and related fixed point methods. Numer. Algorithms 2019, 80, 11–133. [Google Scholar] [CrossRef]
- Brezinski, C.; Redivo-Zaglia, M. Extrapolation Methods. Theory and Practice; North-Holland: Amsterdam, The Netherlands, 1991. [Google Scholar]
- Lorentzen, L.; Waadeland, H. Continued Fractions with Applications; North-Holland: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Sidi, A. Practical Extrapolation Methods. Theory and Applications; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Weniger, E.J. Nonlinear sequence transformations for the acceleration of convergence and the summation of divergent series. Comput. Phys. Rep. 1989, 10, 189–371. [Google Scholar] [CrossRef]
- Wimp, J. Sequence Transformations and Their Applications; Academic Press: New York, NY, USA, 1981. [Google Scholar]
- Lagrange, J.L. Nouvelle méthode pour résoudre les équations littérales par le moyen des séries. Mém. Acad. R. Sci. Berl. 1770, 24, 251–326. [Google Scholar]
- Henrici, P. Applied and Computational Complex Analysis; Wiley: New York, NY, USA, 1974; Volume 1. [Google Scholar]
- Bacher, R.; Lass, B. Développements limités et réversion des séries. Enseign. Math. 2006, 52, 267–293. [Google Scholar]
- Moler, C.; van Loan, C. Nineteen dubious ways to compute the exponential of a matrix. SIAM Rev. 1978, 20, 801–836. [Google Scholar] [CrossRef]
- Moler, C.; van Loan, C. Nineteen dubious ways to compute the exponential of a matrix, twenty-five years later. SIAM Rev. 2003, 45, 3–49. [Google Scholar] [CrossRef]
- Brezinski, C. Génération de suites totalement monotones et oscillantes. CR Acad. Sci. Paris 1975, 280A, 729–731. [Google Scholar]
- Schoenberg, I.J. On smooting operations and their generating functions. Bull. Am. Math. Soc. 1953, 59, 199–230. [Google Scholar] [CrossRef]
- Donoghue, W.F. Monotone Matrix Functions and Analytic Continuation; Springer: New York, NY, USA; Berlin/Heidelberg, Germany, 1974. [Google Scholar]
- Brezinski, C. Généralisation des extrapolations polynomiales et rationnelles. RAIRO 1972, R1, 61–66. [Google Scholar]
- Cordellier, F. Utilisation de l’invariance homographique dans les algorithmes de losange. In Padé Approximation and Its Applications Bad Honnef 1983; Werner, H., Bünger, H.J., Eds.; Lecture Notes in Mathematiques; Springer: Berlin, Germany, 1984; Volume 1071, pp. 62–94. [Google Scholar]
- Nörlund, N.E. Vorlesung über Differenzenrechnung; Springer: Berlin/Heidelberg, Germany, 1937. [Google Scholar]
- Stoer, J. Über zwei Algorithmen zur Interpolation mit rationalen Funktionen. Numer. Math. 1961, 3, 285–304. [Google Scholar] [CrossRef]
- Claessens, G. A useful identity for the rational Hermite interpolation table. Numer. Math. 1978, 29, 227–231. [Google Scholar] [CrossRef]
- Brezinski, C. Sur un algorithme de résolution des systèmes non linéaires. CR Acad. Sci. Paris 1971, 272 A, 145–148. [Google Scholar]
- Gekeler, E. Über den ε-Algorithmus von Wynn. ZAMM 1971, 51, 53–54. [Google Scholar]
- Håvie, T. Generalized Neville type extrapolation schemes. BIT 1979, 19, 204–213. [Google Scholar] [CrossRef]
- Lyche, T. A Newton form for trigonometric Hermite interpolation. Nord. Tids. Inf. Beh. (BIT) 1979, 19, 229–235. [Google Scholar] [CrossRef]
- Mühlbach, G. The general Neville-Aitken algorithm and some application. Numer. Math. 1978, 31, 97–110. [Google Scholar] [CrossRef]
- Mühlbach, G. The general recurrence relation for divided differences and the general Newton interpolation algorithm with application to trigonometric interpolation. Numer. Math. 1979, 32, 393–408. [Google Scholar] [CrossRef]
- Jacobi, C.G.J. Über die Darstellung einer Reihe gegebener Werthe durch einer gebrochnen rationale Funktion. J. Reine Angew. Math. 1845, 30, 127–156. [Google Scholar]
- Frobenius, G. Ueber Relationen zwischen den Näherungsbruchen von Potenzreihen. J. Reine Angew. Math. 1881, 90, 1–17. [Google Scholar]
- Padé, H. Sur la représentation approchée d’une fonction par des fractions rationnelles. Ann. Sci. L’École Norm. Supérieure 1892, 9, 3–93. [Google Scholar] [CrossRef]
- Schmidt, R.J. On the numerical solution of linear simultaneous equations by an iterative method. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1941, 7, 369–383. [Google Scholar] [CrossRef]
- Kronecker, L. Zur Theorie der Elimination einer Variablen aus zwei Algebraischen Gleichungen. Monat. Kön. Preuss. Akad. Wiss. Berl. 1881, 535–600. [Google Scholar]
- Rosenhain, G. Neue Darstellung der Resultante der Elimination von z aus zwei algebraischen Gleichungen f(z) = 0 und ϕ(z) = 0 vermittelst der Werthe welche fie Funktionen f(z) und ϕ(z) für gegebne Werthe von z annehmen. J. Reine Angew. Math. 1846, 30, 157–165. [Google Scholar]
- Borchardt, C.W. Ueber eine Interpolation entsprechende Darstellung der Eliminations-Resultante. J. Reine Angew. Math. 1860, 57, 111–121. [Google Scholar]
- Brezinski, C. Review of methods to accelerate the convergence of sequences. Rend. Mat. Roma. 1974, 7, 303–316. [Google Scholar]
- Cordellier, F. Interpolation Rationnelle et autres Questions: Aspects Algorithmiques et Numériques. Thèse de Doctorat d’État ès Sciences Mathématiques, Université des Sciences et Techniques de Lille, Lille, France, 1989. [Google Scholar]
- McLeod, J.B. A note on the ε-algorithm. Computing 1971, 7, 17–24. [Google Scholar] [CrossRef]
- Delahaye, J.P.; Germain-Bonne, B. Résultats négatifs en accélération de la convergence. Numer. Math. 1980, 35, 443–457. [Google Scholar] [CrossRef]
- Delahaye, J.P. Sequence Transformations; Springer: Berlin, Germany, 1988. [Google Scholar]
- Cournot, A.A. Recherches sur les Principes Mathématiques de la Théorie des Richesses; L. Hachette: Paris, France, 1838; Available online: https://gallica.bnf.fr/ark:/12148/bpt6k6117257c.texteImage (accessed on 30 April 2021).
- Berlinet, A.F. Geometric approach to the parallel sum of vectors and application to the vector ε-algorithm. Numer. Algorithms 2014, 65, 783–807. [Google Scholar] [CrossRef]
- Koecher, M.; Remmert, R. Cayley numbers or alternative division algebras. In Numbers; Ewing, J.H., Ed.; Springer: New York, NY, USA, 1991. [Google Scholar]
- Krob, D.; Leclerc, D. Minor identities for quasi-determinants and quantum determinants. Commun. Math. Phys. 1995, 169, 1–23. [Google Scholar] [CrossRef]
- Schweins, F. Theorie der Differenzen und Differentiale, der Gedoppelten Verbindungen, der Producte mit Versetzungen, der Reihen, der Wiederholenden Functionen, der Allgemeinsten Facultäten und der Fortlaufenden Brüche; Verlag der Universitäts—Buchhandlung von C.F. Winter: Heidelberg, Germany, 1825; Available online: https://babel.hathitrust.org/cgi/pt?id=mdp.39015068512063 (accessed on 30 April 2021).
- Brezinski, C.; Delahaye, J.P.; Germain-Bonne, B. Convergence acceleration by extraction of linear subsequences. SIAM J. Numer. Anal. 1983, 20, 1099–1105. [Google Scholar] [CrossRef]


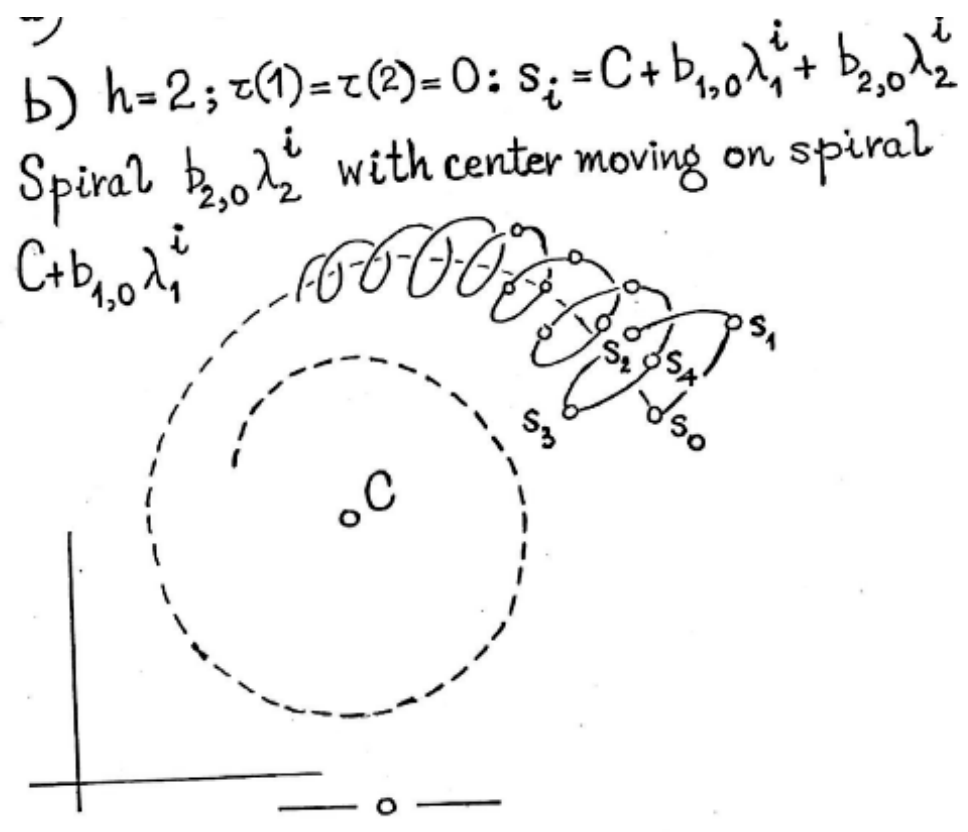
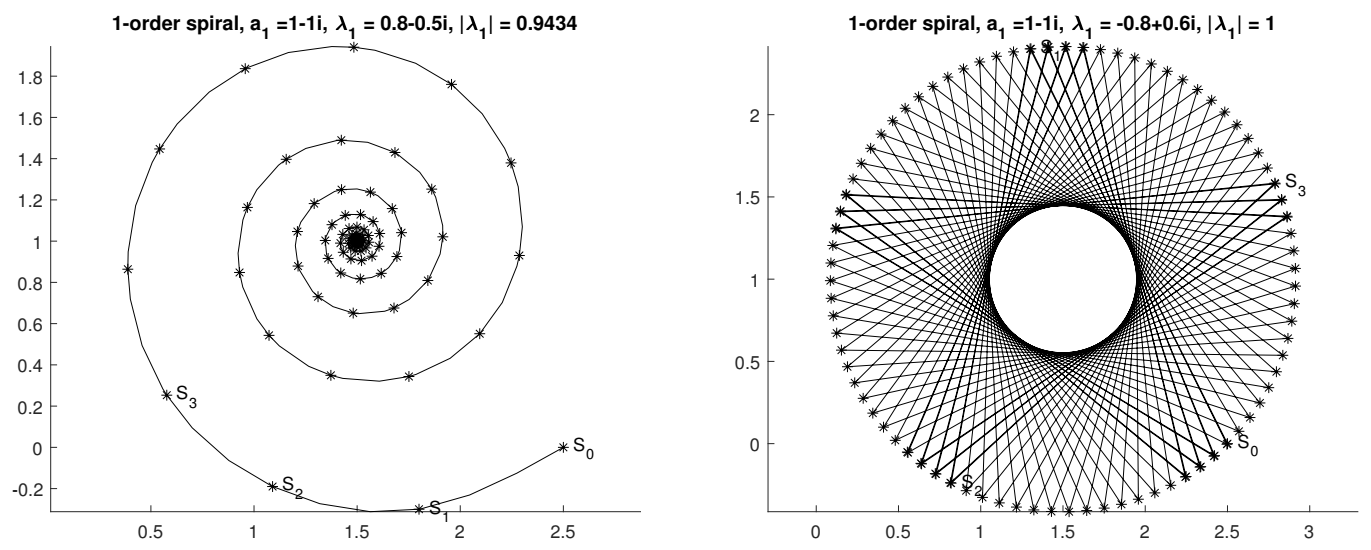
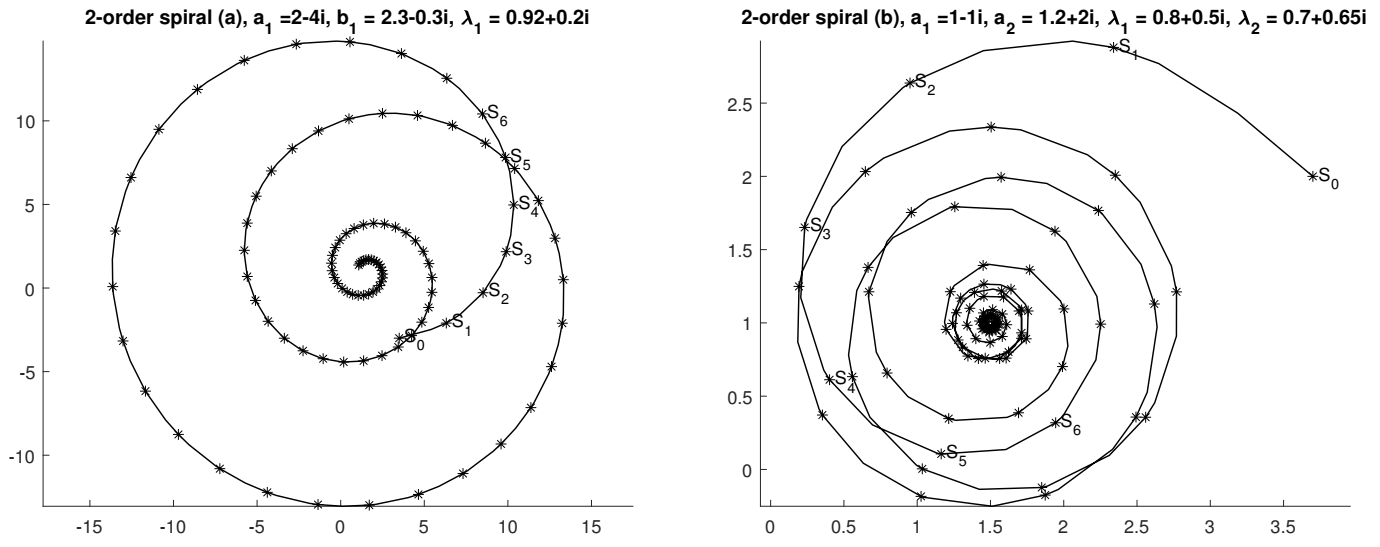
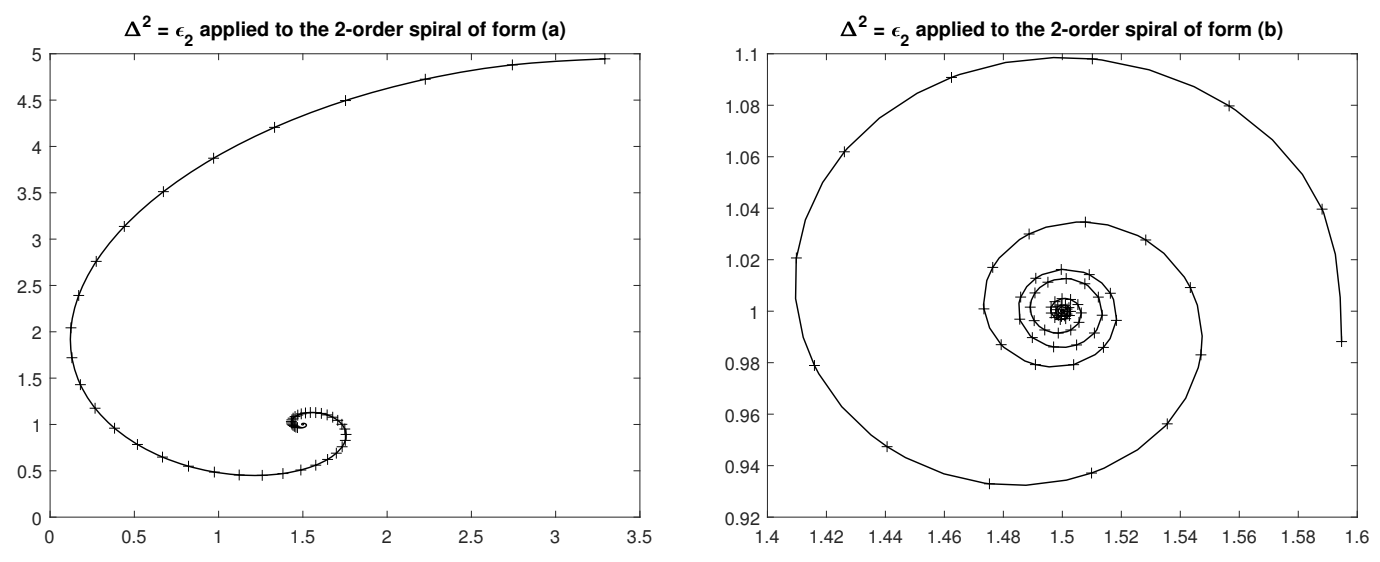
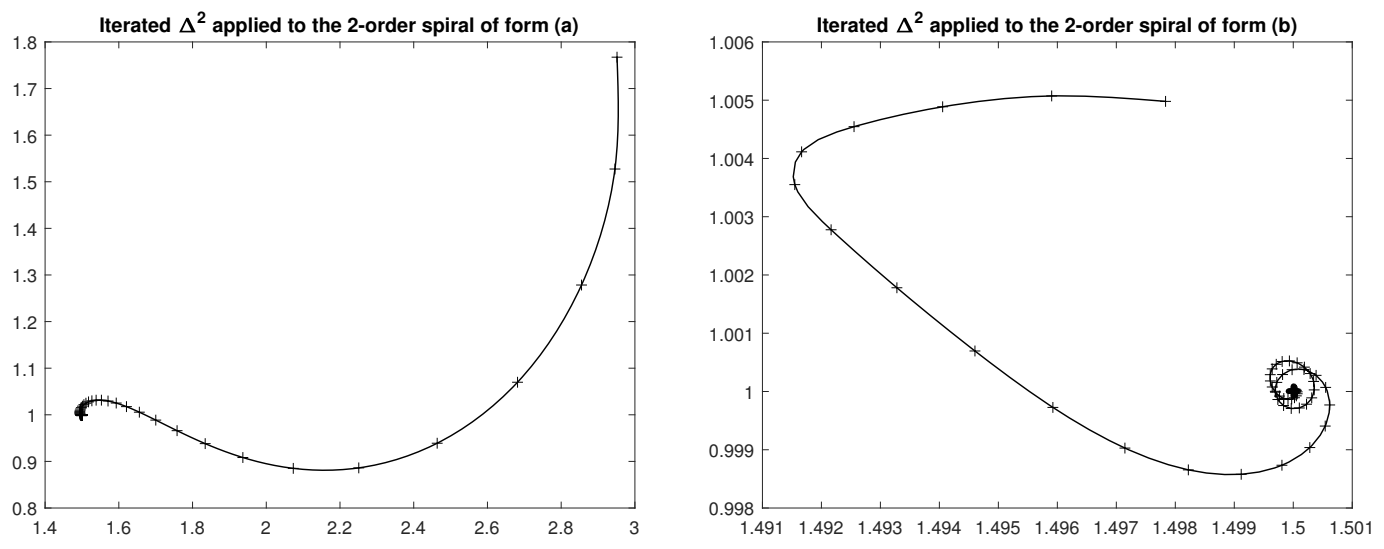

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brezinski, C.; Norman, F.A.; Redivo-Zaglia, M. The Legacy of Peter Wynn. Mathematics 2021, 9, 1240. https://doi.org/10.3390/math9111240
Brezinski C, Norman FA, Redivo-Zaglia M. The Legacy of Peter Wynn. Mathematics. 2021; 9(11):1240. https://doi.org/10.3390/math9111240
Chicago/Turabian StyleBrezinski, Claude, F. Alexander Norman, and Michela Redivo-Zaglia. 2021. "The Legacy of Peter Wynn" Mathematics 9, no. 11: 1240. https://doi.org/10.3390/math9111240
APA StyleBrezinski, C., Norman, F. A., & Redivo-Zaglia, M. (2021). The Legacy of Peter Wynn. Mathematics, 9(11), 1240. https://doi.org/10.3390/math9111240