Using a Fuzzy Inference System to Obtain Technological Tables for Electrical Discharge Machining Processes
Abstract
1. Introduction
2. State of the Art
3. Methodology
| Algorithm 1. Methodology for obtaining the technological tables. FIS—fuzzy inference system. |
|
4. Results and Discussion
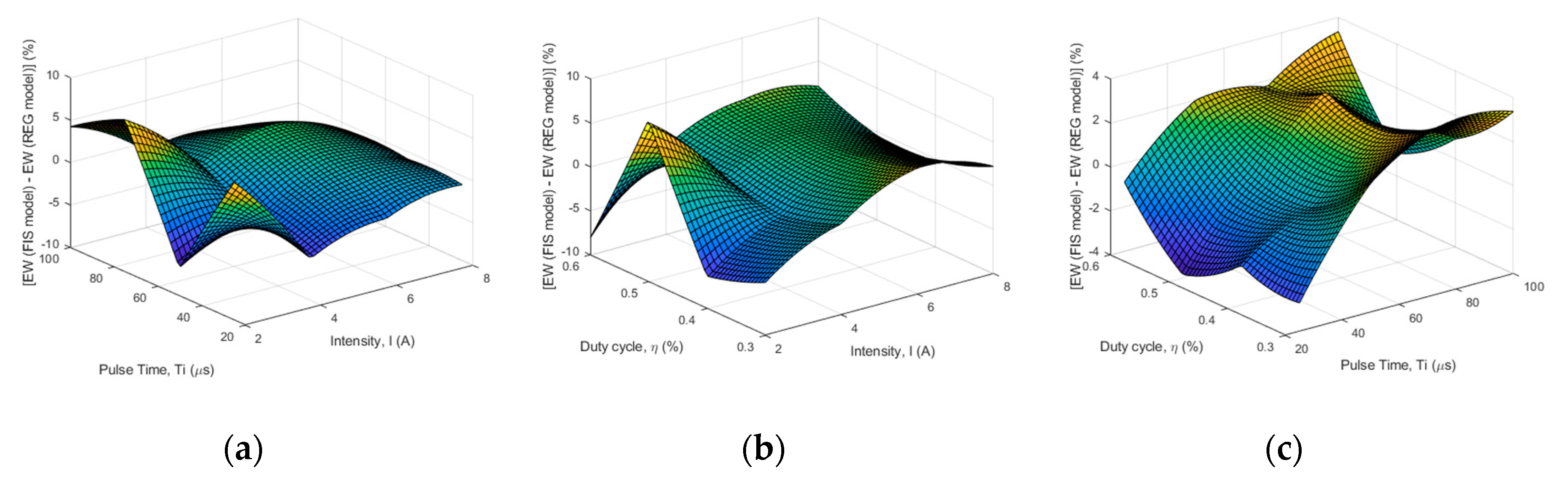
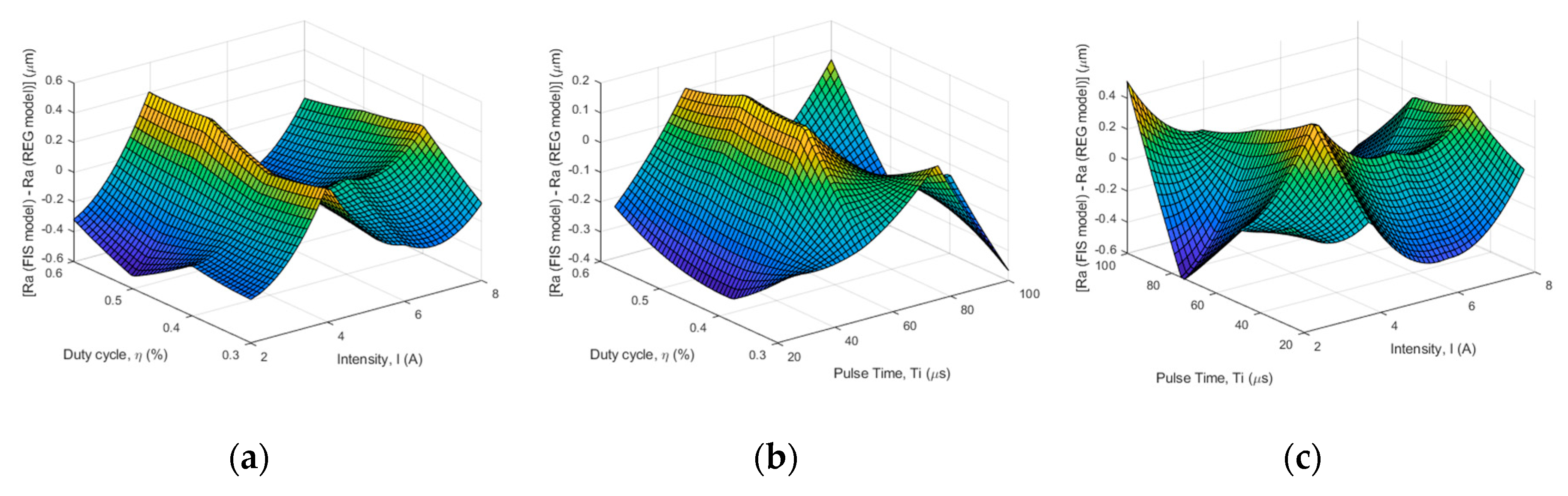
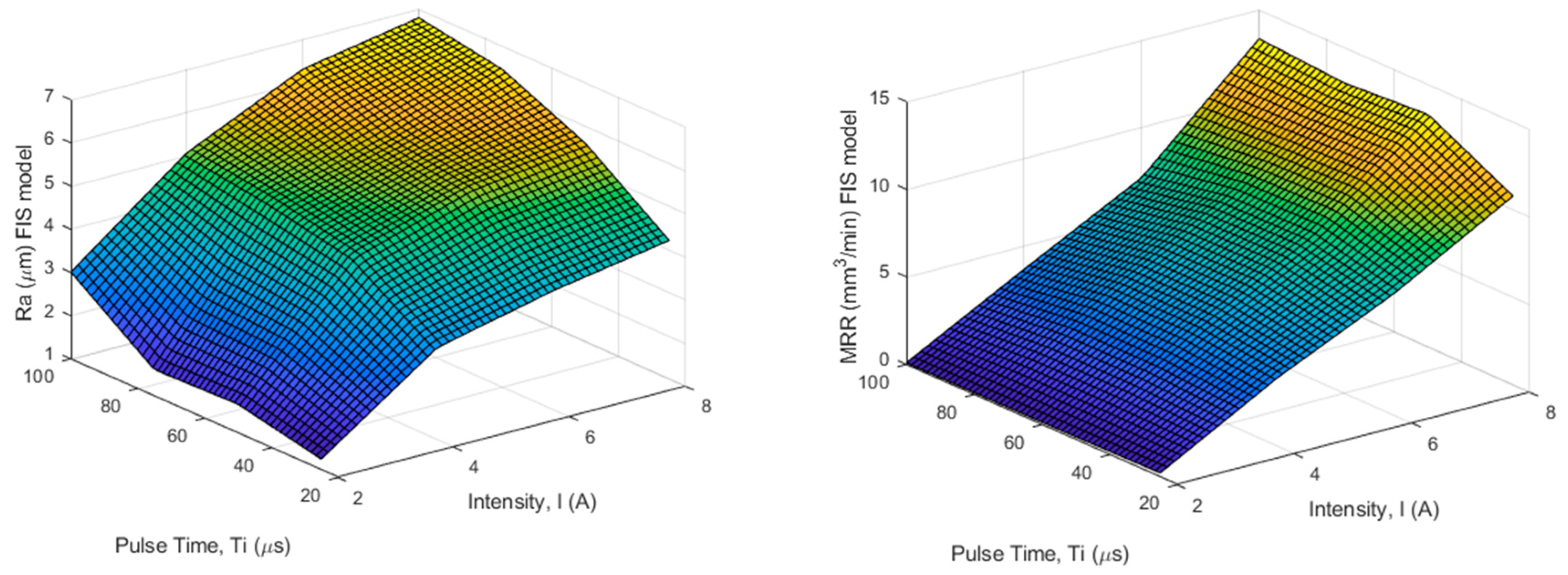
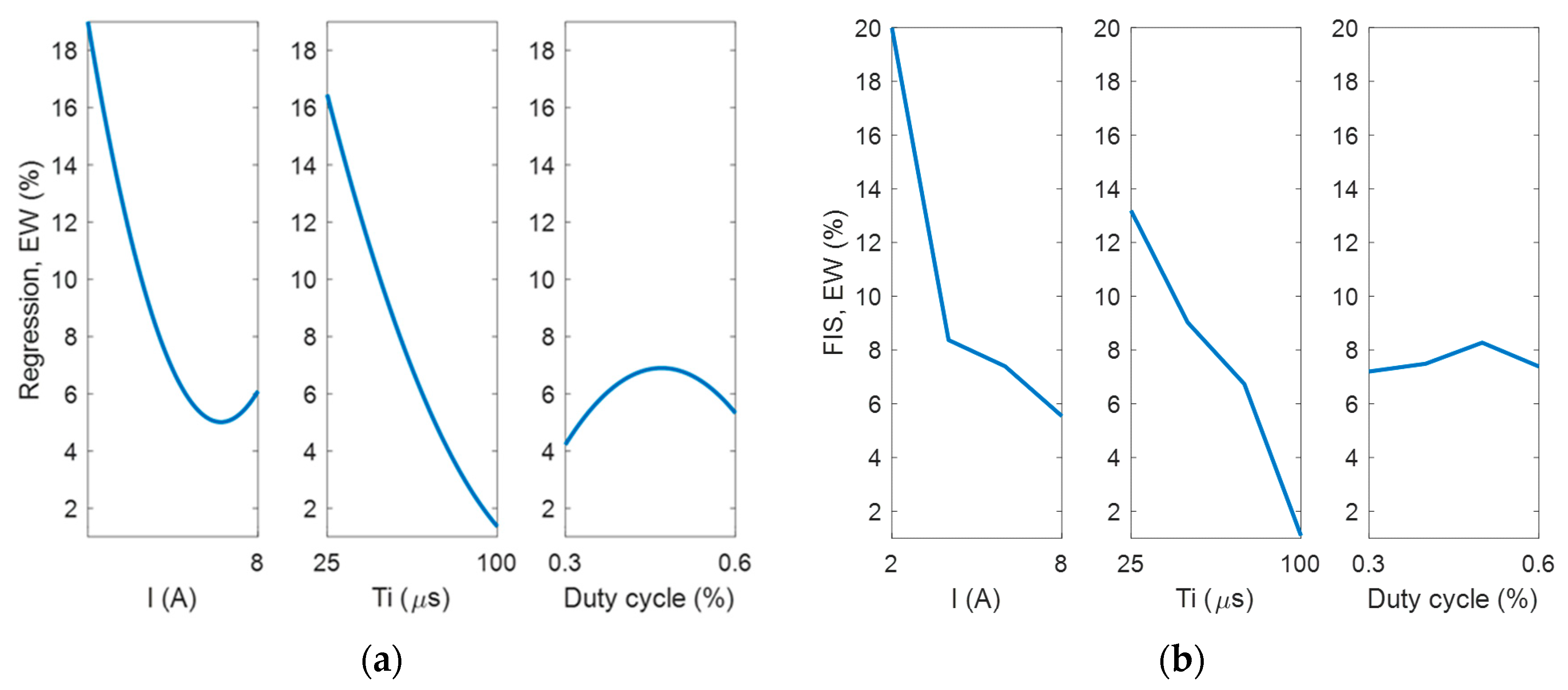
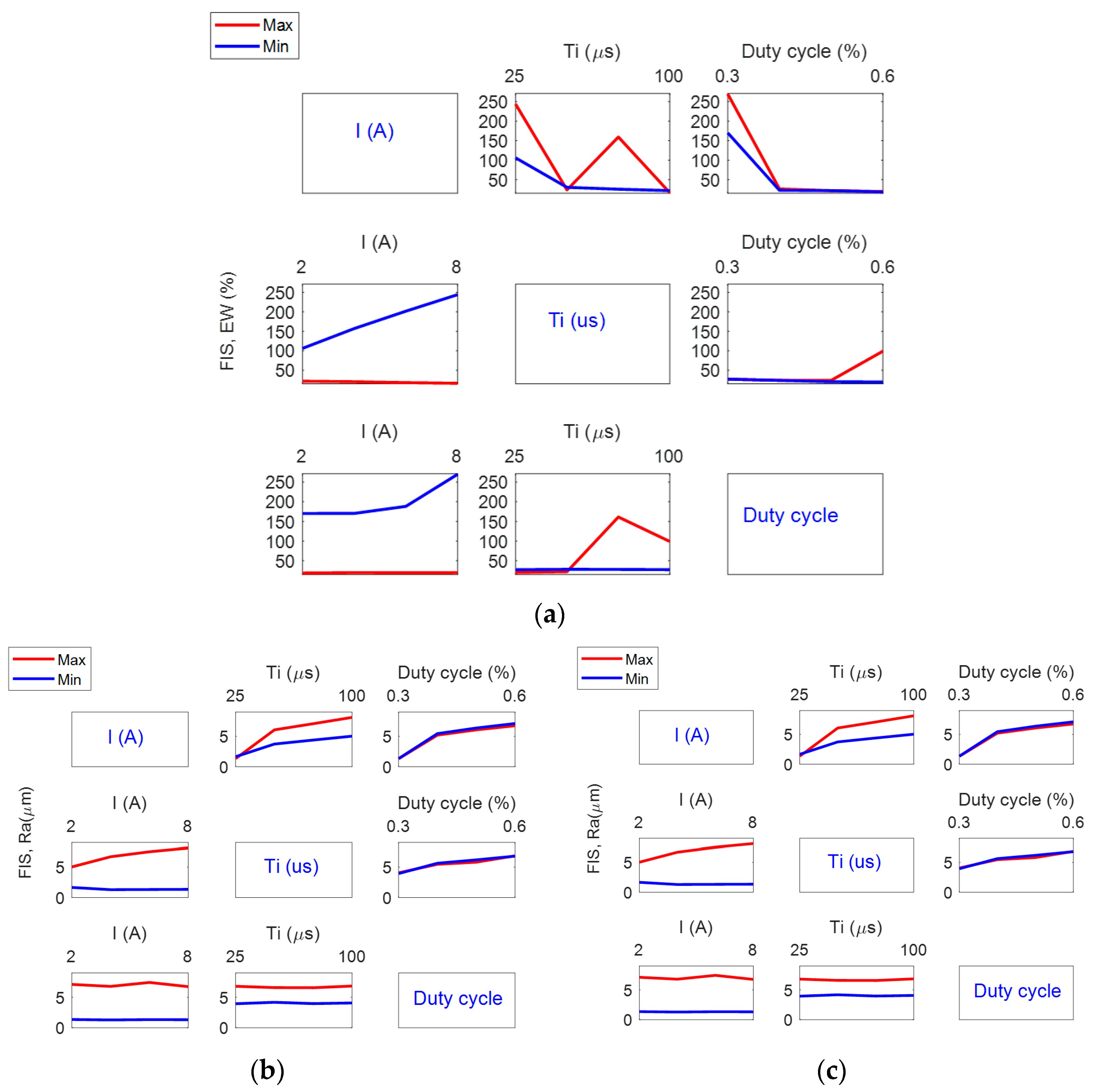
4.1. Analysis of Experimentation Using the FIS
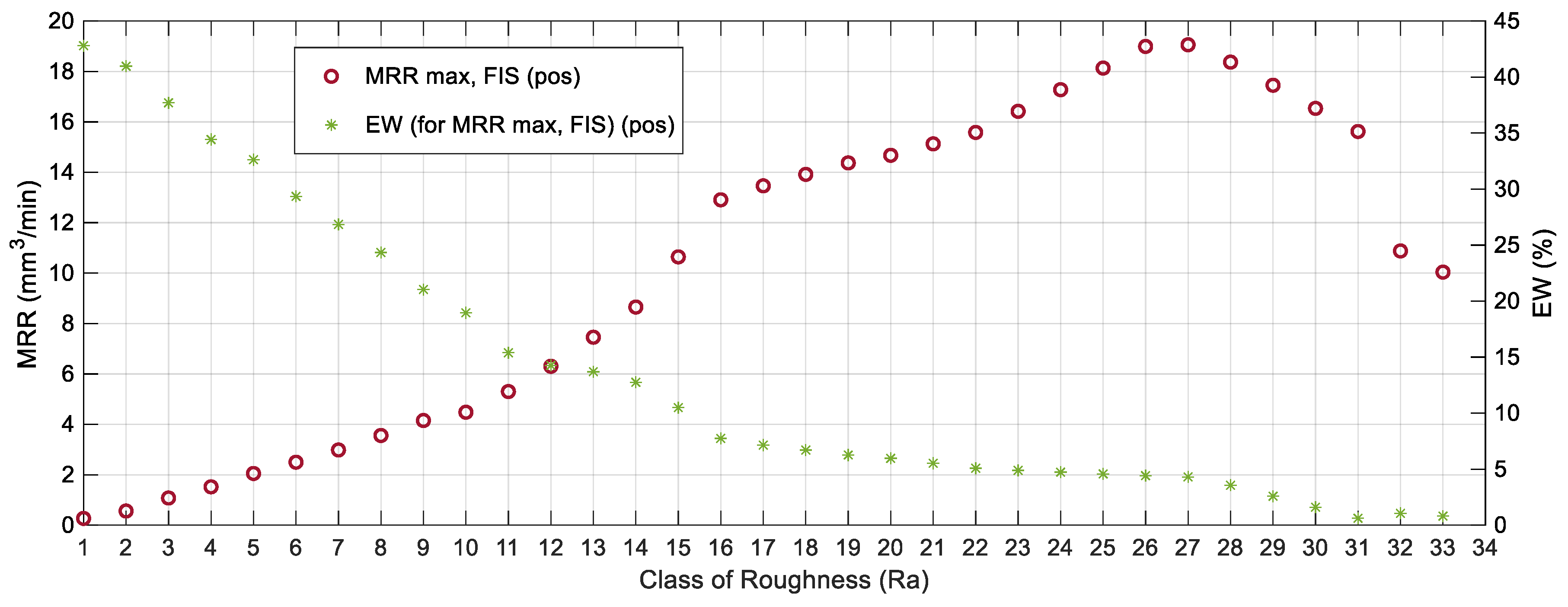
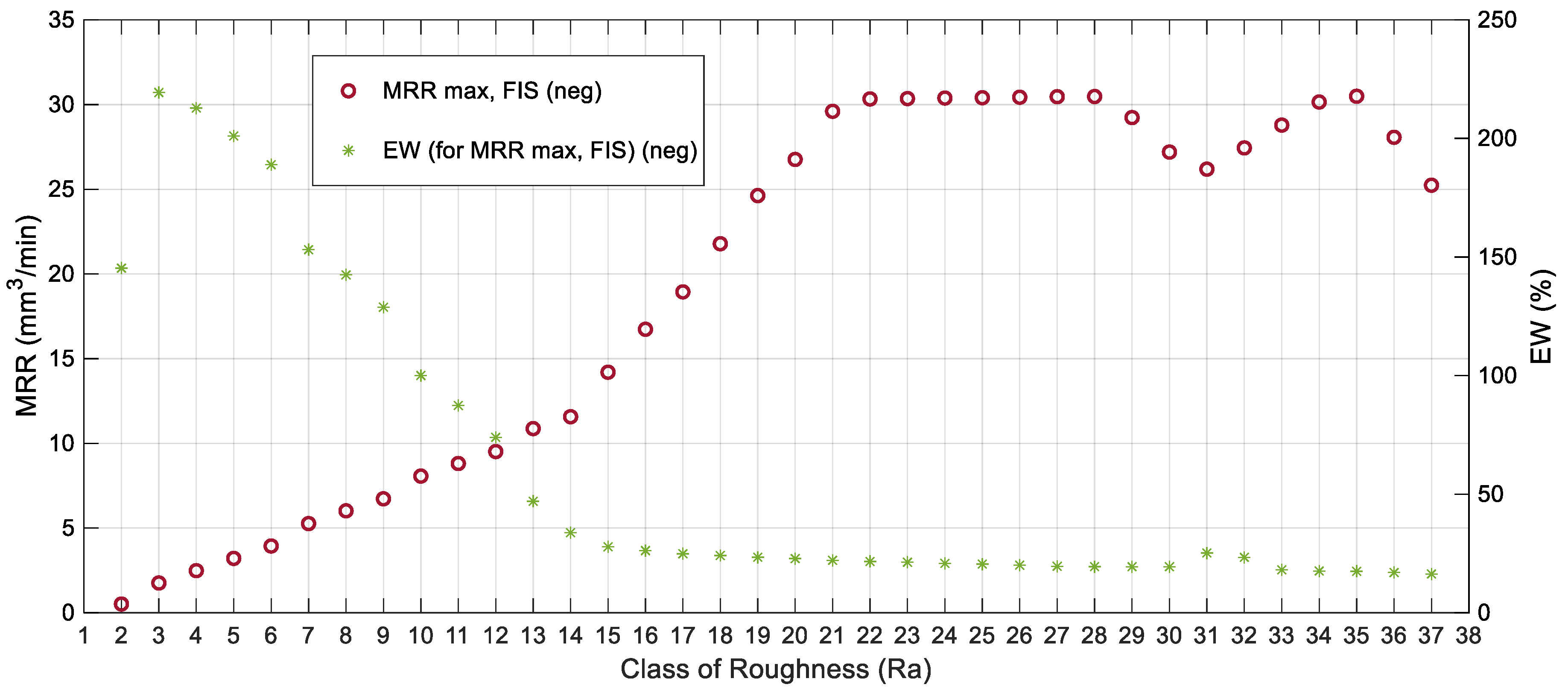
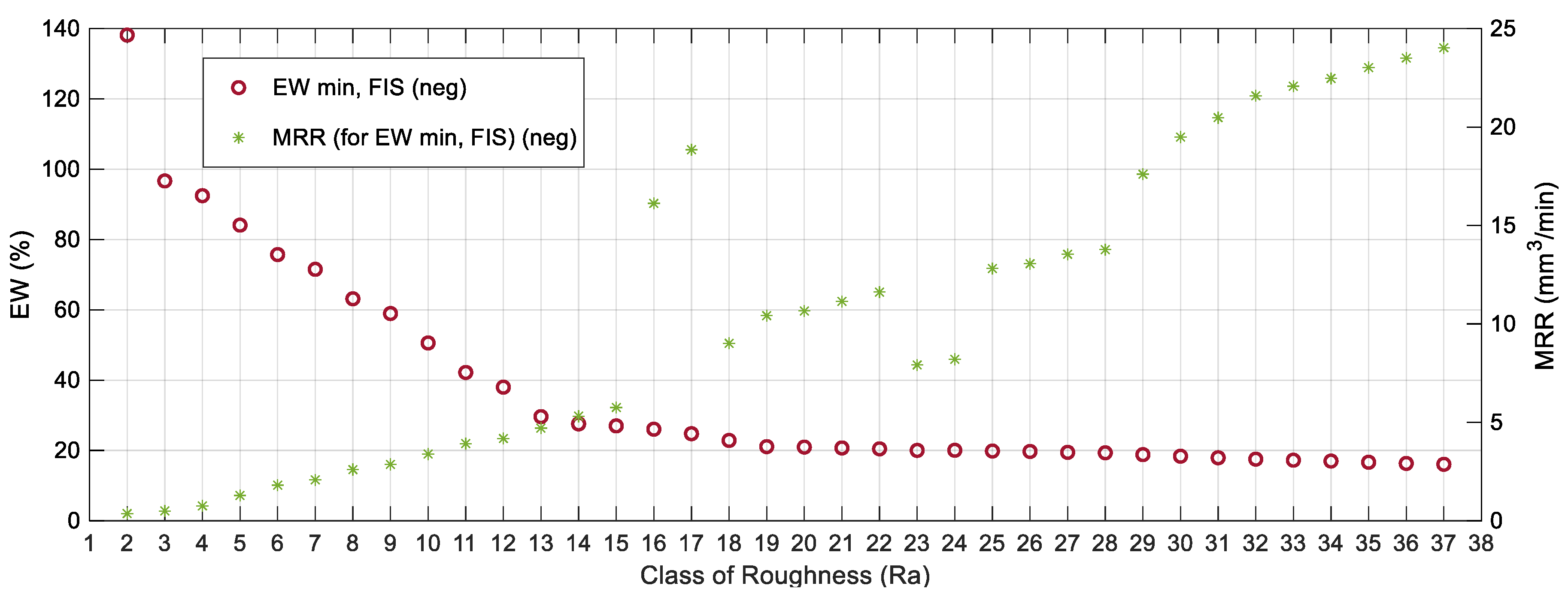
4.2. Development of the Technological Tables
5. Conclusions
Funding
Conflicts of Interest
Appendix A
| Positive Polarity (+) | |||||||
|---|---|---|---|---|---|---|---|
| E | Ra (µm) | MRR (mm3/min) | EW (%) | E | Ra (µm) | MRR (mm3/min) | EW (%) |
| 1 | 1.39 | 0.1778 | 35.81 | 33 | 1.17 | 0.2650 | 42.84 |
| 2 | 3.34 | 3.0897 | 10.66 | 34 | 3.15 | 4.2338 | 15.45 |
| 3 | 3.66 | 5.0825 | 11.69 | 35 | 3.78 | 7.7099 | 9.61 |
| 4 | 4.22 | 7.4984 | 11.68 | 36 | 4.18 | 11.5649 | 9.31 |
| 5 | 1.57 | 0.1331 | 20.74 | 37 | 1.46 | 0.1792 | 14.94 |
| 6 | 4.20 | 3.7383 | 9.14 | 38 | 4.52 | 4.8556 | 10.68 |
| 7 | 4.70 | 6.3535 | 8.58 | 39 | 5.12 | 9.1444 | 7.93 |
| 8 | 4.71 | 6.6319 | 11.26 | 40 | 5.62 | 14.5645 | 6.77 |
| 9 | 2.01 | 0.0846 | 0.44 | 41 | 1.47 | 0.1332 | 41.45 |
| 10 | 5.01 | 3.3606 | 4.32 | 42 | 4.83 | 4.6985 | 8.08 |
| 11 | 5.84 | 6.4197 | 6.76 | 43 | 5.31 | 8.5279 | 6.41 |
| 12 | 6.57 | 9.8827 | 3.92 | 44 | 6.35 | 13.6608 | 3.21 |
| 13 | 2.73 | 0.0884 | 3.02 | 45 | 3.11 | 0.0852 | 16.31 |
| 14 | 5.01 | 2.8219 | 3.21 | 46 | 5.19 | 3.9846 | 0.43 |
| 15 | 6.18 | 6.7786 | 0.84 | 47 | 5.96 | 7.3741 | 0.30 |
| 16 | 7.41 | 10.0405 | 0.81 | 48 | 6.80 | 13.8606 | 2.32 |
| 17 | 1.34 | 0.2297 | 37.33 | 49 | 1.33 | 0.2907 | 42.54 |
| 18 | 3.12 | 3.6482 | 16.26 | 50 | 3.17 | 5.1434 | 15.52 |
| 19 | 3.72 | 6.3632 | 11.44 | 51 | 3.85 | 9.0528 | 12.44 |
| 20 | 4.24 | 9.9951 | 9.80 | 52 | 4.21 | 13.1599 | 7.44 |
| 21 | 1.88 | 0.1520 | 18.76 | 53 | 1.37 | 0.1808 | 17.86 |
| 22 | 4.28 | 4.0843 | 8.58 | 54 | 4.36 | 5.7782 | 11.63 |
| 23 | 5.37 | 7.2087 | 8.92 | 55 | 4.94 | 10.4558 | 8.42 |
| 24 | 5.57 | 11.9972 | 5.72 | 56 | 5.41 | 15.6323 | 5.04 |
| 25 | 1.75 | 0.1169 | 4.80 | 57 | 1.62 | 0.1328 | 5.19 |
| 26 | 4.79 | 4.2463 | 6.15 | 58 | 4.69 | 5.3637 | 5.90 |
| 27 | 5.81 | 7.6840 | 6.31 | 59 | 5.21 | 9.8216 | 3.60 |
| 28 | 6.56 | 12.2552 | 6.47 | 60 | 6.23 | 19.1347 | 4.39 |
| 29 | 2.91 | 0.1056 | 9.32 | 61 | 1.90 | 0.1031 | 2.05 |
| 30 | 4.95 | 3.3520 | 2.52 | 62 | 5.10 | 3.9857 | 5.15 |
| 31 | 6.65 | 6.9094 | 1.13 | 63 | 6.33 | 8.4132 | 1.30 |
| 32 | 6.78 | 12.7827 | 1.63 | 64 | 7.08 | 15.3894 | 0.37 |
| Negative Polarity (−) | |||||||
|---|---|---|---|---|---|---|---|
| E | Ra (µm) | MRR (mm3/min) | EW (%) | E | Ra (µm) | MRR (mm3/min) | EW (%) |
| 1 | 1.57 | 0.4961 | 96.67 | 33 | 1.70 | 0.6719 | 107.46 |
| 2 | 3.59 | 4.7944 | 28.23 | 34 | 3.66 | 7.9205 | 29.72 |
| 3 | 4.29 | 6.6012 | 25.90 | 35 | 4.26 | 12.5716 | 25.79 |
| 4 | 4.76 | 10.4203 | 21.09 | 36 | 5.23 | 18.9419 | 21.67 |
| 5 | 1.31 | 0.3048 | 158.27 | 37 | 1.31 | 0.4777 | 154.88 |
| 6 | 5.43 | 7.4086 | 25.33 | 38 | 4.56 | 9.5215 | 27.75 |
| 7 | 5.84 | 10.3921 | 22.60 | 39 | 5.52 | 15.1031 | 21.94 |
| 8 | 6.77 | 14.3346 | 19.05 | 40 | 7.10 | 19.9893 | 19.59 |
| 9 | 1.39 | 0.3060 | 181.88 | 41 | 1.36 | 0.3882 | 221.58 |
| 10 | 5.47 | 7.7107 | 19.97 | 42 | 5.49 | 11.3645 | 26.01 |
| 11 | 6.90 | 11.5521 | 20.97 | 43 | 6.49 | 16.7606 | 21.72 |
| 12 | 7.44 | 17.7658 | 18.06 | 44 | 7.76 | 23.8823 | 18.76 |
| 13 | 1.58 | 0.3257 | 197.44 | 45 | 1.33 | 0.2949 | 263.67 |
| 14 | 6.24 | 9.9400 | 20.35 | 46 | 5.90 | 12.3596 | 24.44 |
| 15 | 7.36 | 16.1073 | 19.36 | 47 | 7.23 | 19.5421 | 297.77 |
| 16 | 8.04 | 20.0082 | 16.99 | 48 | 8.33 | 23.8906 | 16.04 |
| 17 | 1.62 | 0.5149 | 104.63 | 49 | 1.29 | 0.3546 | 245.89 |
| 18 | 3.82 | 6.2876 | 30.88 | 50 | 3.80 | 11.8064 | 29.33 |
| 19 | 4.53 | 10.5888 | 25.27 | 51 | 4.33 | 18.7034 | 24.92 |
| 20 | 4.83 | 13.1696 | 22.11 | 52 | 5.24 | 30.3120 | 21.93 |
| 21 | 1.28 | 0.4136 | 158.90 | 53 | 1.33 | 0.3144 | 291.16 |
| 22 | 4.90 | 9.7806 | 24.26 | 54 | 5.06 | 12.7525 | 26.09 |
| 23 | 6.06 | 12.7843 | 22.21 | 55 | 5.86 | 19.7280 | 21.70 |
| 24 | 6.30 | 22.1590 | 21.45 | 56 | 6.50 | 30.4760 | 19.38 |
| 25 | 1.28 | 0.3693 | 181.61 | 57 | 1.30 | 0.3561 | 248.44 |
| 26 | 5.51 | 9.2448 | 23.96 | 58 | 5.35 | 12.7624 | 26.15 |
| 27 | 6.26 | 13.5873 | 20.01 | 59 | 6.27 | 21.7225 | 21.94 |
| 28 | 7.27 | 21.4791 | 17.64 | 60 | 6.99 | 24.9210 | 19.47 |
| 29 | 1.36 | 0.3159 | 224.40 | 61 | 1.39 | 0.2823 | 320.70 |
| 30 | 6.24 | 11.3532 | 23.00 | 62 | 6.16 | 13.5013 | 25.88 |
| 31 | 6.93 | 17.2709 | 21.05 | 63 | 7.52 | 23.2371 | 171.94 |
| 32 | 7.90 | 22.7672 | 16.83 | 64 | 7.83 | 30.4894 | 17.49 |
References
- Torres, A.; Luis, C.J.; Puertas, I. EDM machinability and surface roughness analysis of TiB2 using copper electrodes. J. Alloys Compd. 2017, 690, 337–347. [Google Scholar] [CrossRef]
- Salcedo, A.T.; Puertas, I.; Luis Pérez, C.J. Analytical Modelling of Energy Density and Optimization of the EDM Machining Parameters of Inconel 600. Metals 2017, 7, 166. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Sugeno, M. Fuzzy Systems, Modeling and Control; Springer-Science+Businees Media: New York, NY, USA, 1998. [Google Scholar]
- Takagi, T.; Sugeno, M. Fuzzy Identification of Systems and Its Applications to Modeling and Control. IEEE Trans. Syst. ManCybern. 1985, SMC-15, 116–132. [Google Scholar] [CrossRef]
- Luis, C.J.; Puertas, I. Methodology for developing technological tables used in EDM processes of conductive ceramics. J. Mater. Process. Technol. 2007, 189, 301–309. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Taniguchi, T.; Eciolaza, L.; Campos, V.; Palhares, R.; Sugeno, R.M. Fuzzy Control Systems: Past, Present and Future. IEEE Comput. Intell. Mag. 2019, 14, 56–68. [Google Scholar] [CrossRef]
- Mamdani, E.H. Application of fuzzy algorithms for control of simple dynamic plant. In Proceedings of the Institution of Electrical Engineers; Institution of Engineering and Technology (IET): Stevenage, UK, 1974; Volume 121, pp. 1585–1588. [Google Scholar]
- Mamdani, E.H. Application of Fuzzy Logic to Approximate Reasoning Using Linguistic Synthesis. IEEE Trans. Comput. 1976, C-26, 1182–1191. [Google Scholar] [CrossRef]
- Mouralova, K.; Hrabec, P.; Benes, L.; Otoupalik, J.; Bednar, J.; Prokes, T.; Matousek, R. Verification of Fuzzy Inference System for Cutting Speed while WEDM for the Abrasion-Resistant Steel Creusabro by Conventional Statistical Methods. Metals 2020, 10, 92. [Google Scholar] [CrossRef]
- Aamir, M.; Tu, S.; Tolouei-Rad, M.; Giasin, K.; Vafadar, A. Optimization and Modeling of Process Parameters in Multi-Hole Simultaneous Drilling Using Taguchi Method and Fuzzy Logic Approach. Materials 2020, 13, 680. [Google Scholar] [CrossRef]
- Alarifi, I.M.; Nguyen, H.M.; Naderi Bakhtiyari, A.; Asadi, A. Feasibility of ANFIS-PSO and ANFIS-GA Models in Predicting Thermophysical Properties of Al2O3-MWCNT/Oil Hybrid Nanofluid. Materials 2019, 12, 3628. [Google Scholar] [CrossRef]
- Wang, C.-N.; Nguyen, V.T.; Chyou, J.-T.; Lin, T.-F.; Nguyen, T.N. Fuzzy Multicriteria Decision-Making Model (MCDM) for Raw Materials Supplier Selection in Plastics Industry. Mathematics 2019, 7, 981. [Google Scholar] [CrossRef]
- Kang, H.; Cho, H.-C.; Choi, S.-H.; Heo, I.; Kim, H.-Y.; Kim, K.S. Estimation of Heating Temperature for Fire-Damaged Concrete Structures Using Adaptive Neuro-Fuzzy Inference System. Materials 2019, 12, 3964. [Google Scholar] [CrossRef] [PubMed]
- Tayyab, M.; Sarkar, B.; Yahya, B.N. Imperfect Multi-Stage Lean Manufacturing System with Rework under Fuzzy Demand. Mathematics 2019, 7, 13. [Google Scholar] [CrossRef]
- Faisal, N.; Kumar, K. Optimization of Machine Process Parameters in EDM for EN 31 Using Evolutionary Optimization Techniques. Technologies 2018, 6, 54. [Google Scholar] [CrossRef]
- Lin, Y.-C.; Wang, Y.-C.; Chen, T.-C.T.; Lin, H.-F. Evaluating the Suitability of a Smart Technology Application for Fall Detection Using a Fuzzy Collaborative Intelligence Approach. Mathematics 2019, 7, 1097. [Google Scholar] [CrossRef]
- Cavallaro, F. A Takagi-Sugeno Fuzzy Inference System for Developing a Sustainability Index of Biomass. Sustainability 2015, 7, 12359–12371. [Google Scholar] [CrossRef]
- Versaci, M. Fuzzy approach and Eddy currents NDT/NDE devices in industrial applications. Electron. Lett. 2016, 52, 943–945. [Google Scholar] [CrossRef]
- Versaci, M.; Calcagno, S.; Cacciola, M.; Morabito, F.C.; Palamara, I.; Pellicanò, D. Chapter 7: Innovative Fuzzy Techniques for Characterizing Defects in Ultrasonic Nondestructive Evaluation. In Ultrasonic Nondestructive Evaluation Systems, Industrial Application Issues; Burrascano, P., Callegari, S., Montisci, A., Ricci, M., Versaci, M., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 200–232. [Google Scholar]
- Sun, X.; Jia, X. A Fault Diagnosis Method of Industrial Robot Rolling Bearing Based on Data Driven and Random Intuitive Fuzzy Decision. IEEE Access 2019, 7, 148764–148770. [Google Scholar] [CrossRef]
- Postorino, M.N.; Versaci, M. A Geometric Fuzzy-Based Approach for Airport Clustering. Adv. Fuzzy Syst. 2014, 2014, 201243. [Google Scholar] [CrossRef]
- Cheng, L.; Liu, W.; Hou, Z.G.; Huang, T.; Yu, J.; Tan, M. An Adaptive Takagi–Sugeno Fuzzy Model-Based Predictive Controller for Piezoelectric Actuators. IEEE Trans. Ind. Electron. 2017, 64, 3048–3058. [Google Scholar] [CrossRef]
- Bagua, H.; Guemana, M.; Hafaifa, A. Gas Turbine Monitoring using Fuzzy Control approaches: Comparison between Fuzzy Type 1 and 2. In Proceedings of the 2018 International Conference on Applied Smart Systems (ICASS’2018), Médéa, Algeria, 24–25 November 2018. [Google Scholar]
- Goswamia, R.; Joshib, D. Performance Review of Fuzzy Logic Based Controllers Employed in Brushless DC Motor. Procedia Comput. Sci. 2018, 132, 623–631. [Google Scholar] [CrossRef]
- Liu, X.; Gao, Z.; Chen, M.Z. Takagi–Sugeno Fuzzy Model Based Fault Estimation and Signal Compensation with Application to Wind Turbines. IEEE Trans. Ind. Electron. 2017, 64, 5678–5689. [Google Scholar]
- Lin, Y.Y.; Chang, J.Y.; Lin, C.T. A TSK-Type-Based Self-Evolving Compensatory Interval Type-2 Fuzzy Neural Network (TSCIT2FNN) and Its Applications. IEEE Trans. Ind. Electron. 2014, 61, 447–459. [Google Scholar] [CrossRef]
- Biglarbegian, M.; Melek, W.W.; Mendel, J.M. Design of Novel Interval Type-2 Fuzzy Controllers for Modular and Reconfigurable Robots: Theory and Experiments. IEEE Trans. Ind. Electron. 2011, 58, 1371–1384. [Google Scholar] [CrossRef]
- Dereli, T.; Baykasoglu, A.; Altun, K.; Durmusoglu, A.; Burhan, T. Industrial applications of type-2 fuzzy sets and systems—A concise review. Comput. Ind. 2011, 62, 125–137. [Google Scholar] [CrossRef]
- Lei, Y.; Yang, B.; Jiang, X.; Jia, F.; Li, N.; Nandi, A.K. Applications of machine learning to machine fault diagnosis: A review and roadmap. Mech. Syst. Signal Process. 2020, 138, 106587. [Google Scholar] [CrossRef]
- Shabgard, M.R.; Badamchizadeh, M.A.; Ranjbary, G.; Amini, K. Fuzzy approach to select machining parameters in electrical discharge machining (EDM) and ultrasonic-assisted EDM processes. J. Manuf. Syst. 2013, 32, 32–39. [Google Scholar] [CrossRef]
- Sibalija, T.V. Particle swarm optimisation in designing parameters of manufacturing processes: A review (2008–2018). Appl. Soft Comput. 2019, 84, 105743. [Google Scholar] [CrossRef]
- Datta, S.; Biswal, B.B.; Mahapatra, S.S. Optimization of Electro-Discharge Machining Responses of Super Alloy Inconel 718: Use of Satisfaction Function Approach Combined with Taguchi Philosophy. Mater. Today Proc. 2018, 5 Pt 1, 4376–4383. [Google Scholar] [CrossRef]
- Babu, K.N.; Karthikeyan, R.; Punitha, A. An integrated ANN—PSO approach to optimize the material removal rate and surface roughness of wire cut EDM on INCONEL 750. Mater. Today Proc. 2019, 19 Pt 2, 501–505. [Google Scholar] [CrossRef]
- Al-Ghamdi, K.; Taylan, O. A comparative study on modelling material removal rate by ANFIS and polynomial methods in electrical discharge machining process. Comput. Ind. Eng. 2015, 79, 27–41. [Google Scholar] [CrossRef]
- Devarasiddappa, D.; George, J.; Chandrasekaran, M.; Teyi, N. Application of Artificial Intelligence Approach in Modeling Surface Quality of Aerospace Alloys in WEDM Process. Procedia Technol. 2016, 25, 1199–1208. [Google Scholar] [CrossRef]
- Maher, I.; Ling, L.H.; Ahmed, A.D.S.; Hamdi, M. Improve wire EDM performance at different machining parameters—ANFIS modelling. IFAC-PapersOnLine 2015, 48, 105–110. [Google Scholar] [CrossRef]
- Joshi, K.K.; Behera, R.K.; Kumar, R.; Mohapatra, S.K.; Patro, S.S. Machinability Assessment of Inconel 800HT and its prediction using a hybrid fuzzy controller in EDM. Mater. Today Proc. 2019, 18 Pt 7, 5270–5275. [Google Scholar] [CrossRef]
- Torres, A.; Puertas, I.; Luis, C.J. Modelling of surface finish, electrode wear and material removal rate in electrical discharge machining of hard-to-machine alloys. Precis. Eng. 2015, 40, 33–45. [Google Scholar] [CrossRef]
- Bhadauria, G.; Jha, S.K.; Roy, B.N.; Dhakry, N.S. Electrical-Discharge Machining of Tungsten Carbide (WC) and its composites (WC-Co)—A Review. Mater. Today Proc. 2018, 5 Pt 3, 24760–24769. [Google Scholar] [CrossRef]
- The MathWorks, Inc. Fuzzy Logic Toolbox™User’s Guide; The MathWorks, Inc.: Natick, MA, USA, 1999. [Google Scholar]
- UNE-EN ISO 4287:1999, Geometrical Product Specifications (GPS)-Surface Texture: Profile Method—Terms, Definitions and Surface Texture Parameters; AENOR: Madrid, Spain, 1999.
- Versaci, M.; Calcagno, S.; Cacciola, M.; Morabito, F.C.; Palamara, I.; Pellicanò, D. Chapter 6: Standard Soft Computing Techniques for Characterization of Defects in Nondestructive Evaluation. In Ultrasonic Nondestructive Evaluation Systems, Industrial Application Issues; Burrascano, P., Callegari, S., Montisci, A., Ricci, M., Versaci, M., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 175–199. [Google Scholar]
- Egaji, O.A.; Griffiths, A.; Hasan, M.S.; Yu, H.N. A comparison of Mamdani and Sugeno fuzzy based packet scheduler for MANET with a realistic wireless propagation model. Int. J. Autom. Comput. 2015, 12, 1–13. [Google Scholar] [CrossRef]
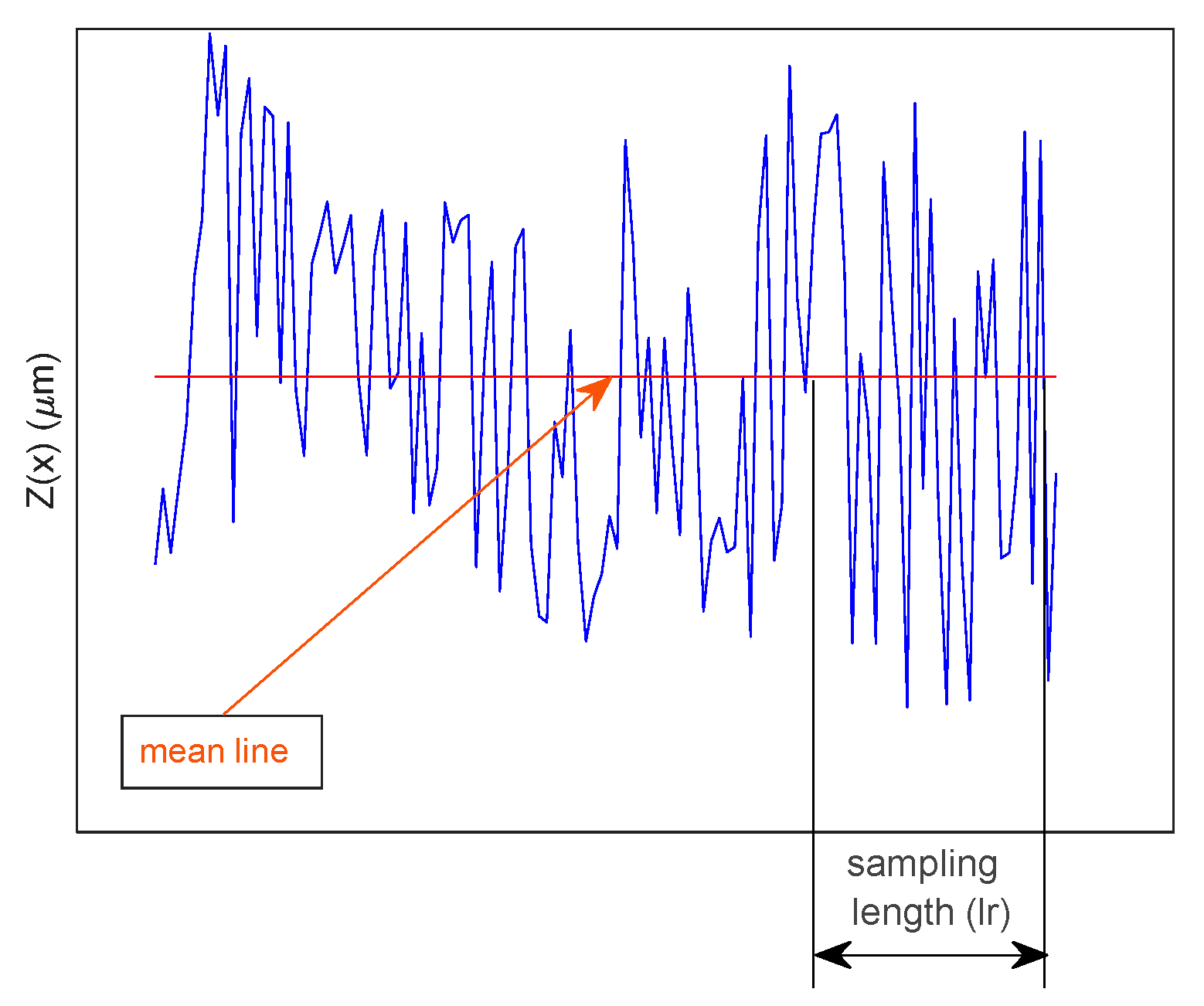

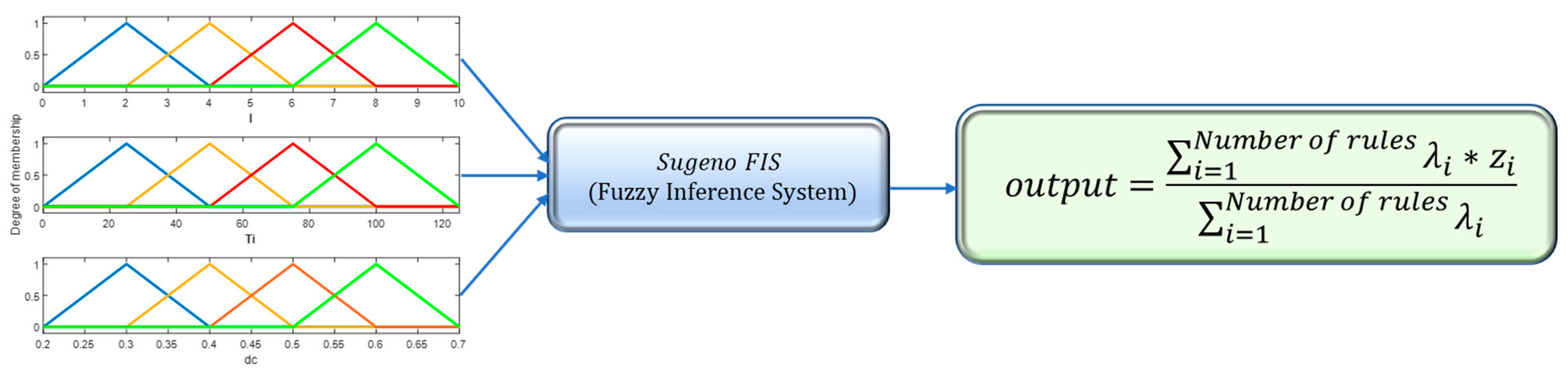
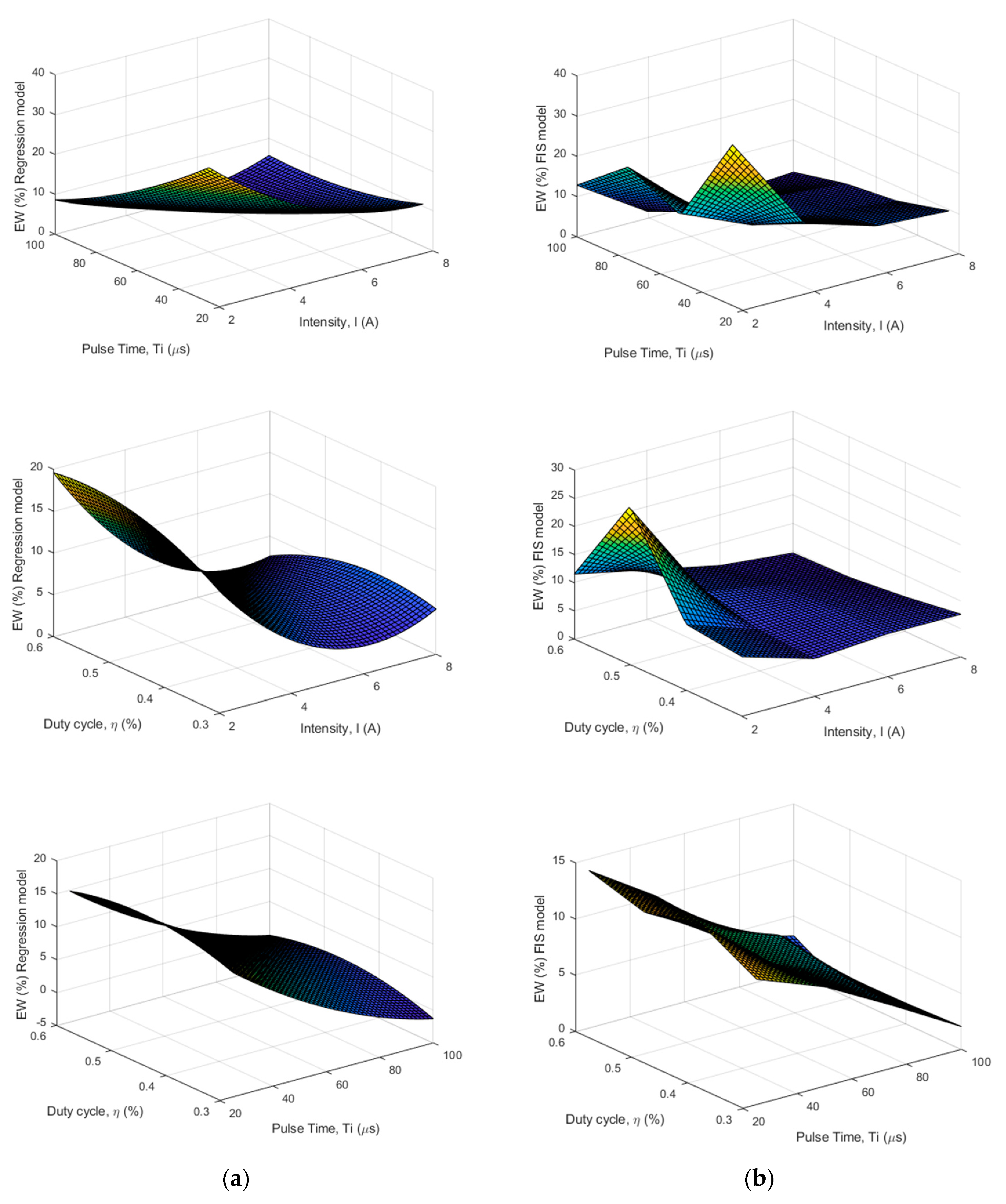


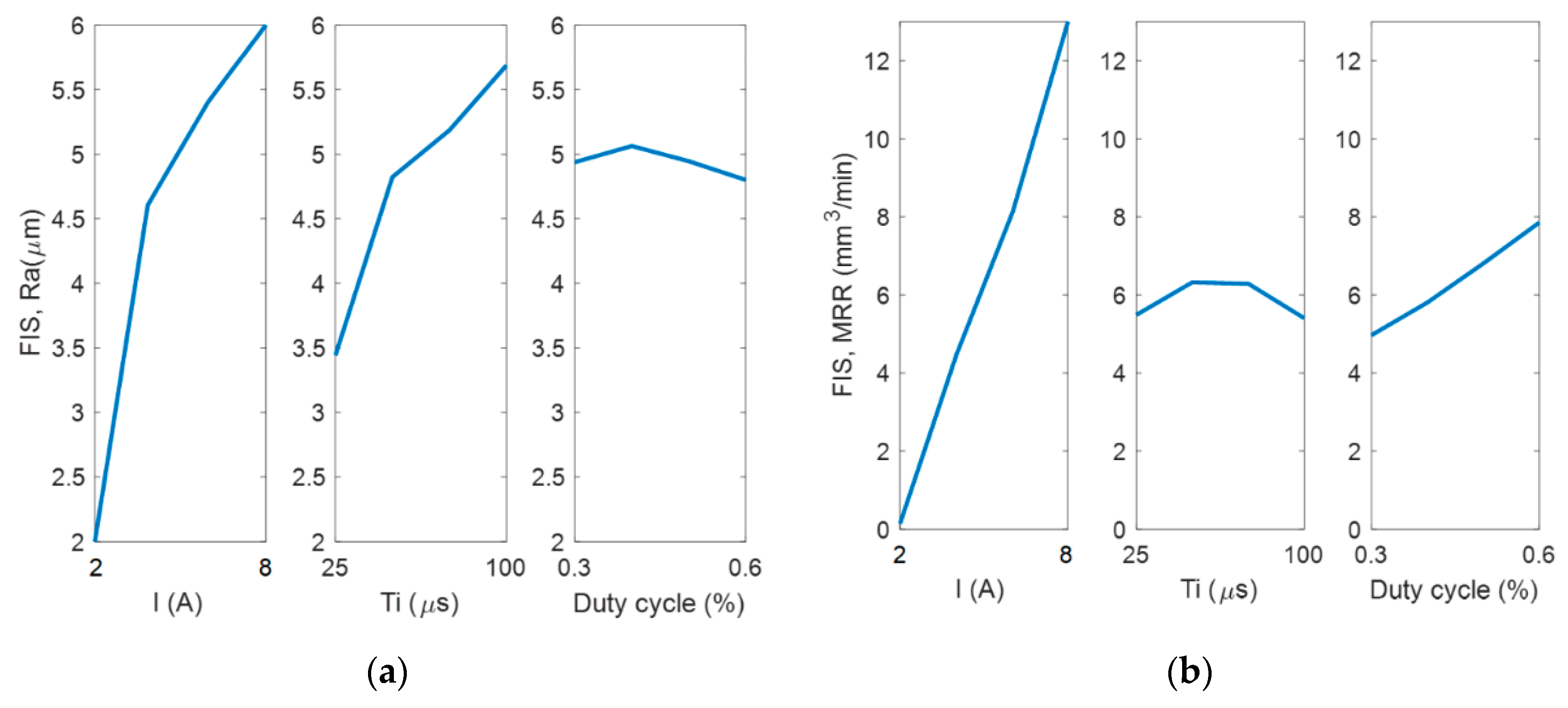
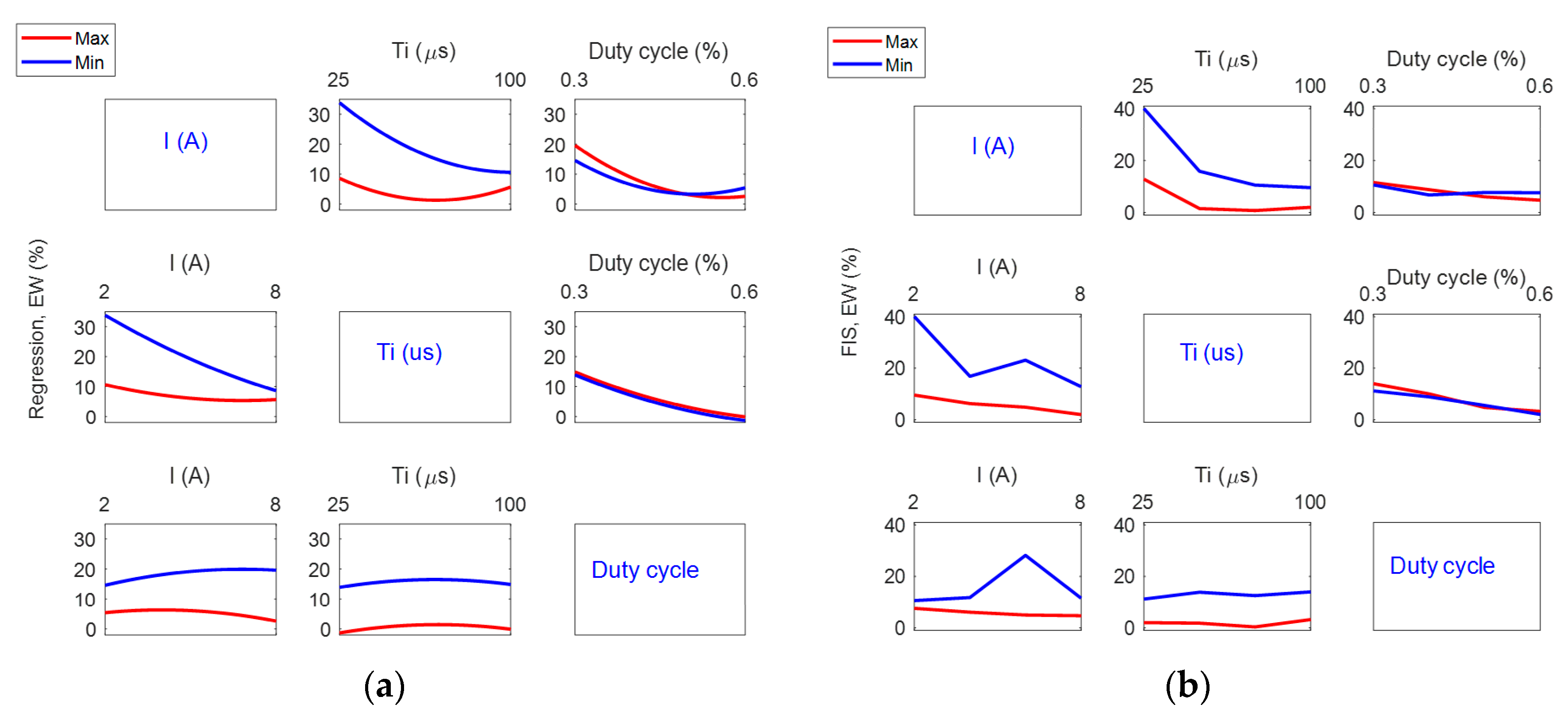
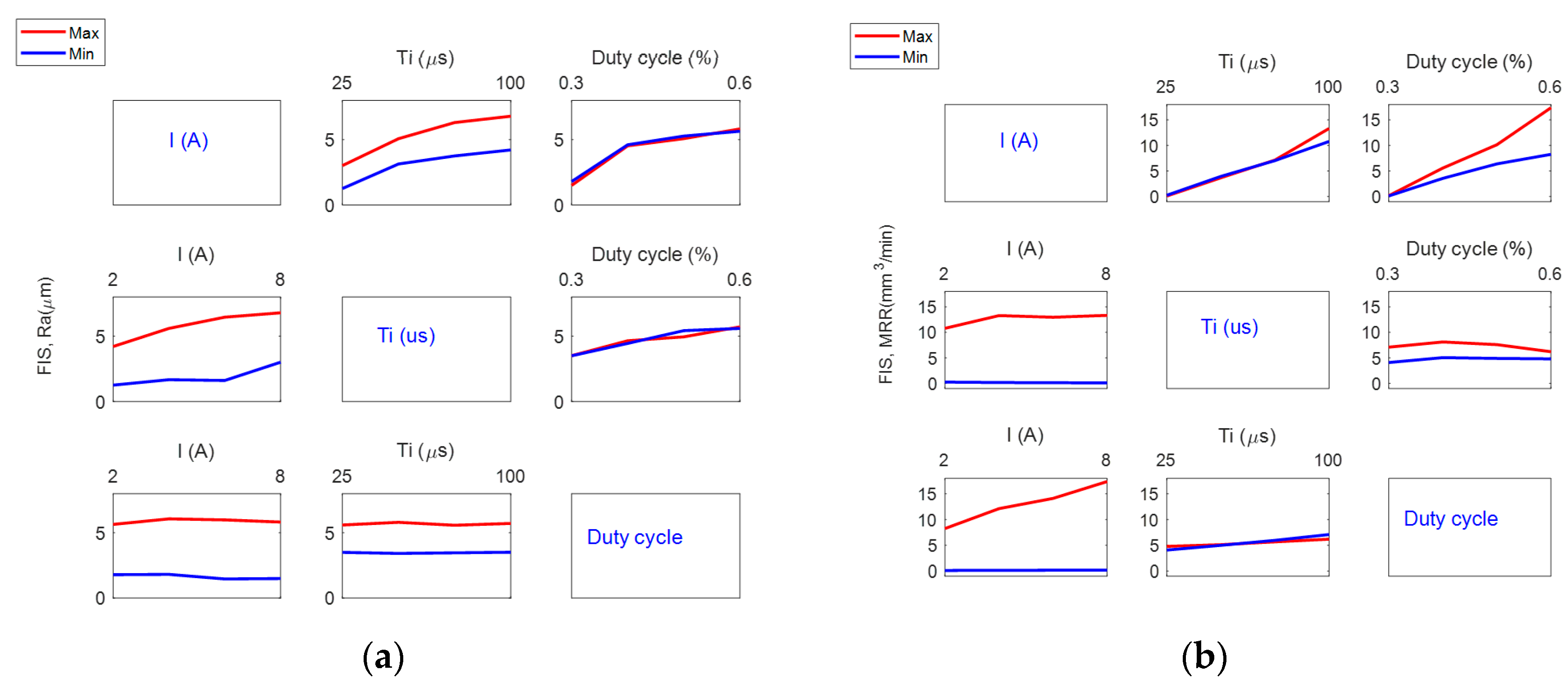
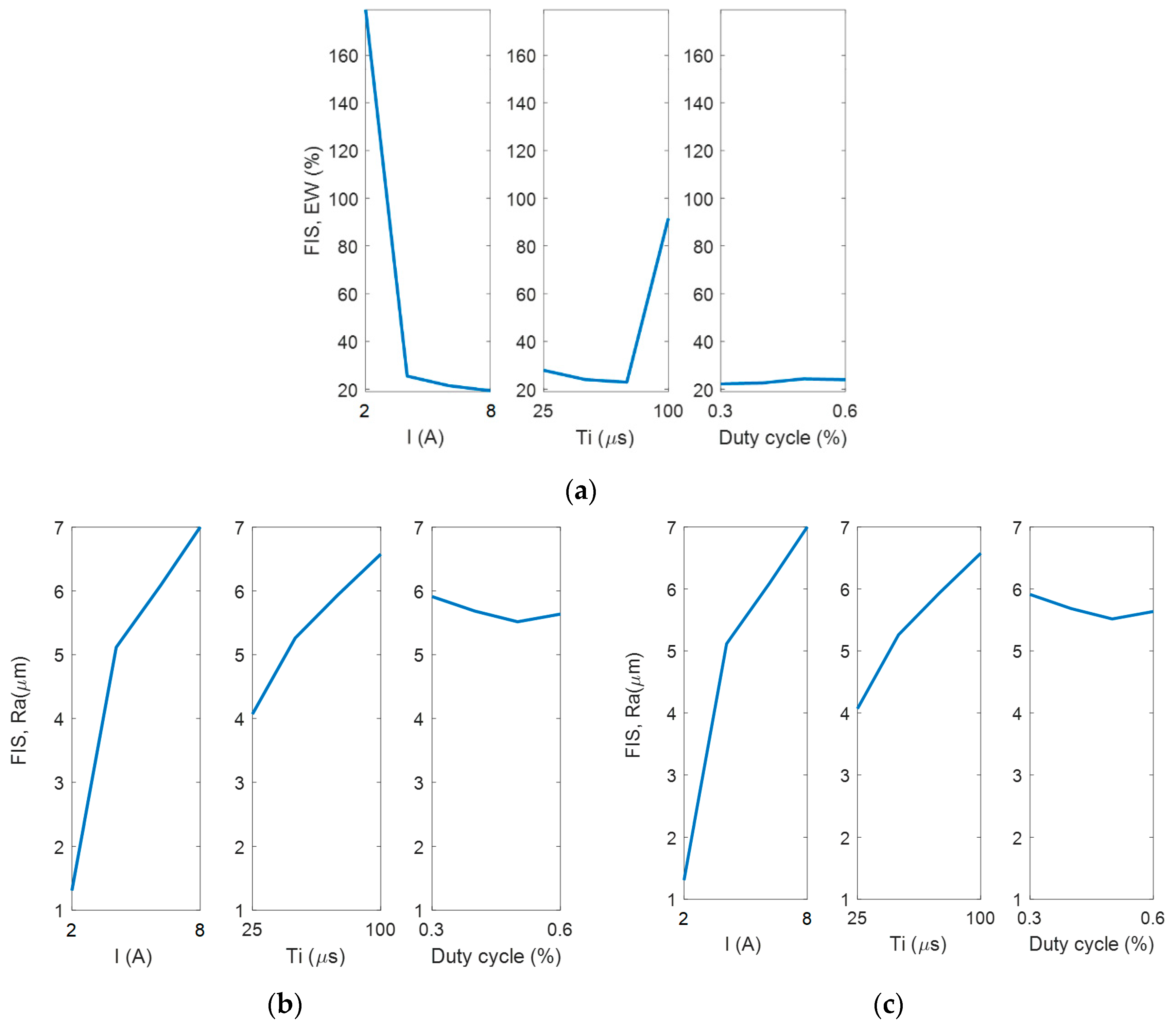

| Design Factors | Levels and Values | |||||||
|---|---|---|---|---|---|---|---|---|
| Positive Polarity | Negative Polarity | |||||||
| 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | |
| Current intensity | 2 | 4 | 6 | 8 | 2 | 4 | 6 | 8 |
| Pulse time | 25 | 50 | 75 | 100 | 25 | 50 | 75 | 100 |
| Duty cycle | 0.3 | 0.4 | 0.5 | 0.6 | 0.3 | 0.4 | 0.5 | 0.6 |
| Positive Polarity (+) | Negative Polarity (−) | ||||||
|---|---|---|---|---|---|---|---|
| E | Ra (µm) | MRR (mm3/min) | EW (%) | E | Ra (µm) | MRR (mm3/min) | EW (%) |
| 1 | 1.39 | 0.1778 | 35.81 | 1 | 1.57 | 0.4961 | 96.67 |
| 2 | 3.34 | 3.0897 | 10.66 | 2 | 3.59 | 4.7944 | 28.23 |
| 63 | 6.33 | 8.4132 | 1.30 | 63 | 7.52 | 23.2371 | 171.94 |
| 64 | 7.08 | 15.3894 | 0.37 | 64 | 7.83 | 30.4894 | 17.49 |
| Positive Polarity (+) | Negative Polarity (−) | ||
|---|---|---|---|
| Class of Roughness | Intensity (A) | Duty Cycle (%) | EW | |||||
|---|---|---|---|---|---|---|---|---|
| Class of Roughness | Lower Value (μm) | Ra Value (μm) | Upper Value (μm) | Intensity (A) | Pulse Time (μs) | Duty Cycle (%) | EW Min (%) | MRR |
|---|---|---|---|---|---|---|---|---|
| Class of Roughness | Lower Value (μm) | Ra Value (μm) | Upper Value (μm) | Intensity (A) | Pulse Time (μs) | Duty Cycle (%) | MRR Max | EW (%) |
|---|---|---|---|---|---|---|---|---|
| . | ||||||||
| . | . | . | ||||||
| . |
| Class of Roughness | Lower Value (μm) | Ra Value (μm) | Upper Value (μm) | Intensity (A) | Pulse Time (μs) | Duty Cycle (%) | EW Min (%) | MRR |
|---|---|---|---|---|---|---|---|---|
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luis Pérez, C.J. Using a Fuzzy Inference System to Obtain Technological Tables for Electrical Discharge Machining Processes. Mathematics 2020, 8, 922. https://doi.org/10.3390/math8060922
Luis Pérez CJ. Using a Fuzzy Inference System to Obtain Technological Tables for Electrical Discharge Machining Processes. Mathematics. 2020; 8(6):922. https://doi.org/10.3390/math8060922
Chicago/Turabian StyleLuis Pérez, C. J. 2020. "Using a Fuzzy Inference System to Obtain Technological Tables for Electrical Discharge Machining Processes" Mathematics 8, no. 6: 922. https://doi.org/10.3390/math8060922
APA StyleLuis Pérez, C. J. (2020). Using a Fuzzy Inference System to Obtain Technological Tables for Electrical Discharge Machining Processes. Mathematics, 8(6), 922. https://doi.org/10.3390/math8060922




