Global Stability Analysis of Fractional-Order Quaternion-Valued Bidirectional Associative Memory Neural Networks
Abstract
1. Introduction
2. Formulation of the Problem and Fundamentals
2.1. Quaternion Algebra
2.2. Caputo Fractional-Order Derivative
2.3. Problem Formulation
2.4. Fundamentals
3. Main Results
3.1. Real-Imaginary Separate-Type Activation Functions
3.2. The Activation Functions Cannot Be Expressed through Separation of the Real and Imaginary Parts
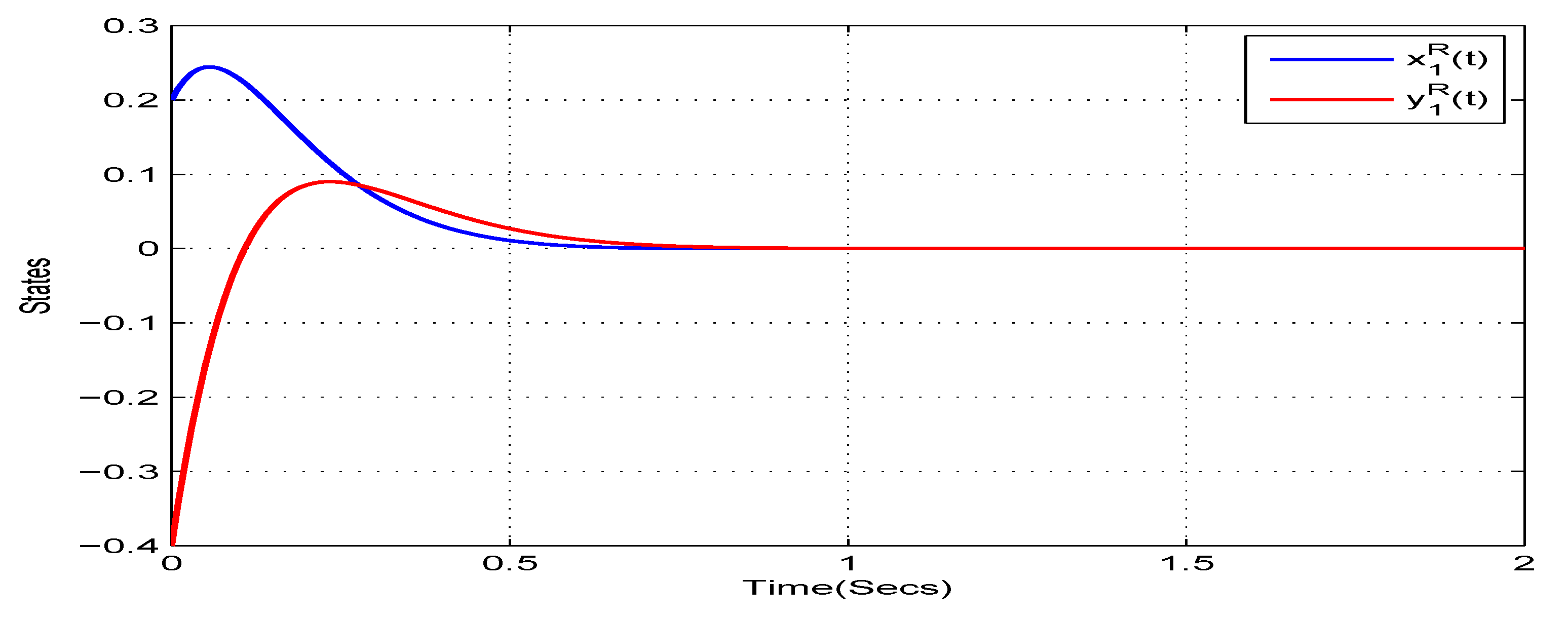
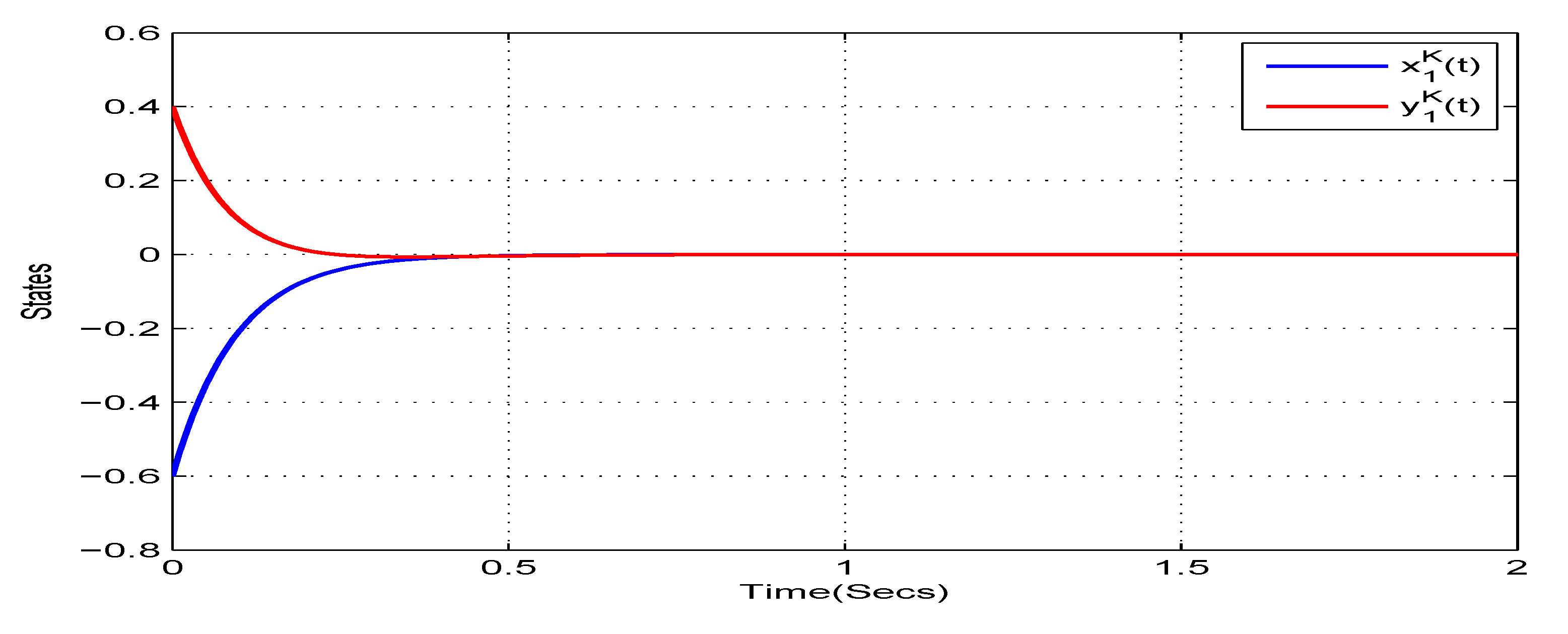
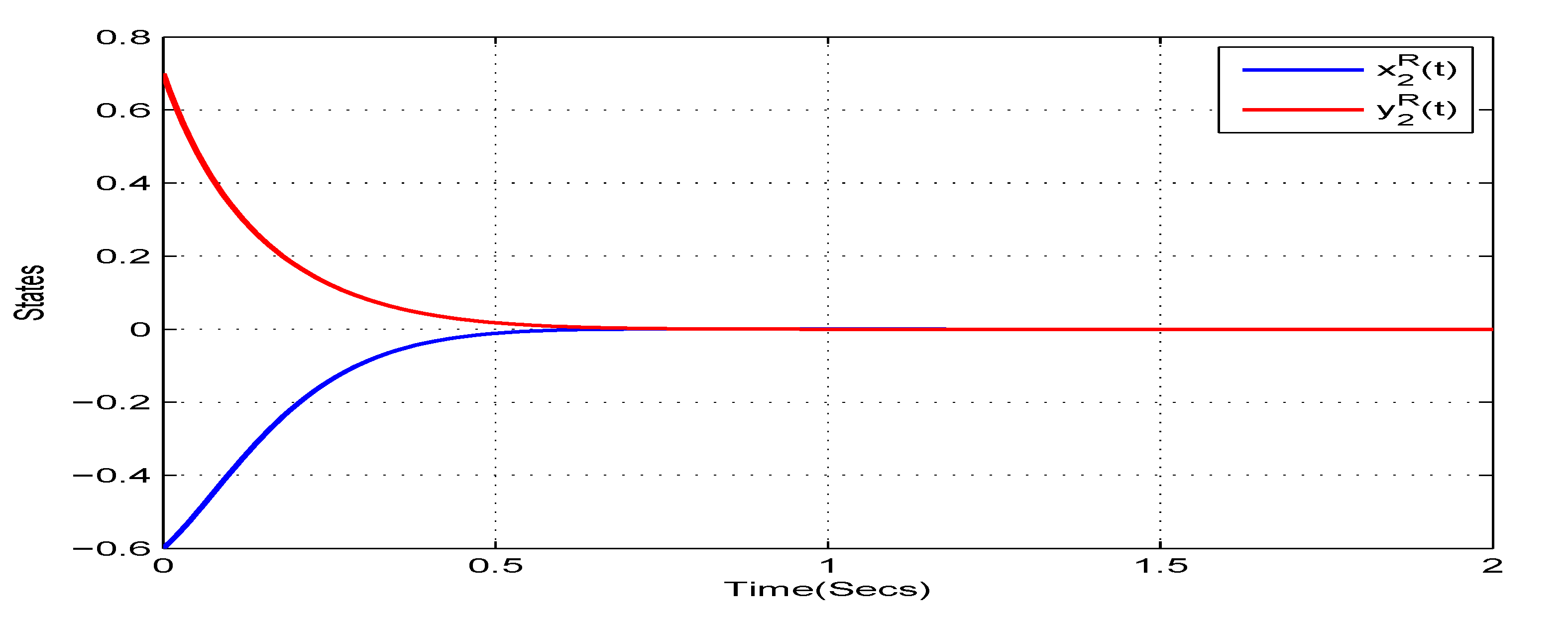
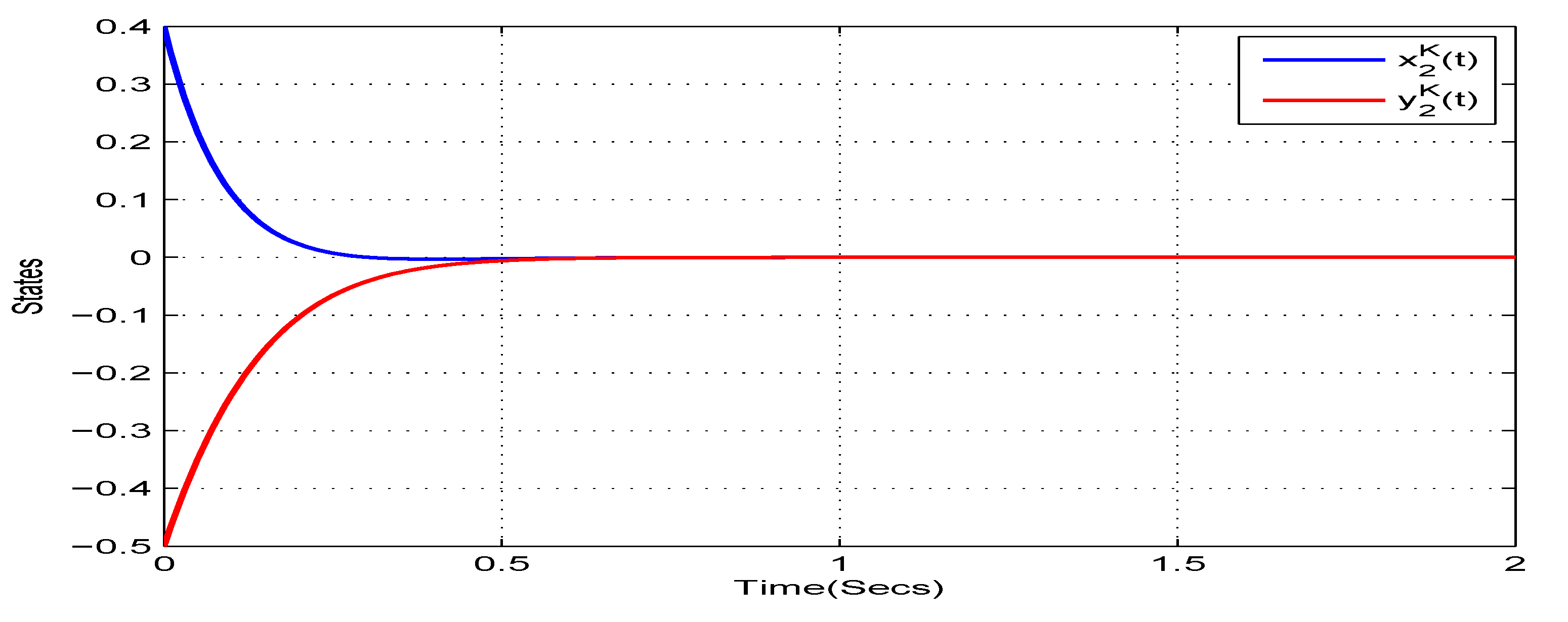
4. Illustrative Examples
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Feng, C.; Plamondon, R. On the stability analysis of delayed neural networks systems. Neural Netw. 2001, 14, 1181–1188. [Google Scholar] [CrossRef]
- Kwon, O.M.; Lee, S.M.; Park, J.H.; Cha, E.J. New approaches on stability criteria for neural networks with interval time-varying delays. Appl. Math. Comput. 2012, 218, 9953–9964. [Google Scholar] [CrossRef]
- Kwon, O.M.; Park, J.H. New delay-dependent robust stability criterion for uncertain neural networks with time-varying delays. Appl. Math. Comput. 2008, 205, 417–427. [Google Scholar] [CrossRef]
- Liu, L.; Deng, F. Stability analysis of time-varying delayed stochastic Hopfield neural networks in numerical simulation. Neurocomputing 2018, 316, 294–305. [Google Scholar] [CrossRef]
- Wang, T.; Zhao, S.; Zhou, W.; Yu, W. Finite-time state estimation for delayed Hopfield neural networks with Markovian jump. Neurocomputing 2015, 156, 193–198. [Google Scholar] [CrossRef]
- Samidurai, R.; Sriraman, R. Robust dissipativity analysis for uncertain neural networks with additive time-varying delays and general activation functions. Math. Comput. Simulat. 2019, 155, 201–216. [Google Scholar] [CrossRef]
- Kosko, B. Adaptive bidirectional associative memories. Appl. Opt. 1987, 26, 4947–4960. [Google Scholar] [CrossRef]
- Wang, G.; Cao, J.; Xu, M. Stability analysis for stochastic BAM neural networks with Markovian jumping parameters. Neurocomputing 2009, 72, 3901–3906. [Google Scholar] [CrossRef]
- Li, X. Exponential stability of Cohen-Grossberg-type BAM neural networks with time-varying delays via impulsive control. Neurocomputing 2009, 73, 525–530. [Google Scholar] [CrossRef]
- Liu, B.W. Global exponential stability for BAM neural networks with time-varying delays in the leakage terms. Nonlinear Anal. Real World Appl. 2013, 14, 559–566. [Google Scholar] [CrossRef]
- Wang, T.; Zhu, Q. Stability analysis of stochastic BAM neural networks with reaction-diffusion, multi-proportional and distributed delays. Phys. A Stat. Mech. Appl. 2019, 533, 121935. [Google Scholar] [CrossRef]
- Bao, H.; Park, J.H.; Cao, J. Non-fragile state estimation for fractional-order delayed memristive BAM neural networks. Neural Netw. 2019, 119, 190–199. [Google Scholar] [CrossRef] [PubMed]
- Xiao, J.; Wen, S.; Yang, X.; Zhong, S. New approach to global Mittag-Leffler synchronization problem of fractional-order quaternion-valued BAM neural networks based on a new inequality. Neural Netw. 2020, 122, 320–337. [Google Scholar] [CrossRef] [PubMed]
- Pratap, A.; Raja, R.; Cao, J.; Rihan, F.A.; Seadawy, A.R. Quasi-pinning synchronization and stabilization of fractional-order BAM neural networks with delays and discontinuous neuron activations. Chaos Soliton. Fract. 2020, 131, 109491. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, L. Global stability analysis for delayed complex-valued BAM neural networks. Neurocomputing 2016, 173, 2083–2089. [Google Scholar] [CrossRef]
- Wang, Z.; Guo, Z.; Huang, L.; Liu, X. Dynamical behavior of complex-valued Hopfield neural networks with discontinuous activation functions. Neural Process. Lett. 2017, 45, 1039–1061. [Google Scholar] [CrossRef]
- Sriraman, R.; Samidurai, R. Global asymptotic stability analysis for neutral-type complex-valued neural networks with random time-varying delays. Int. J. Syst. Sci. 2019, 50, 1742–1756. [Google Scholar] [CrossRef]
- Samidurai, R.; Sriraman, R.; Cao, J.; Tu, Z. Effects of leakage delay on global asymptotic stability of complex-valued neural networks with interval time-varying delays via new complex-valued Jensen’s inequality. Int. J. Adapt. Control Signal Process. 2018, 32, 1294–1312. [Google Scholar] [CrossRef]
- Tu, Z.; Cao, J.; Alsaedi, A.; Alsaadi, F.E.; Hayat, T. Global Lagrange stability of complex-valued neural networks of neutral type with time-varying delays. Complexity 2016, 21, 438–450. [Google Scholar] [CrossRef]
- Gunasekaran, N.; Zhai, G. Stability analysis for uncertain switched delayed complex-valued neural networks. Neurocomputing 2019, 367, 198–206. [Google Scholar] [CrossRef]
- Gunasekaran, N.; Zhai, G. Sampled-data state-estimation of delayed complex-valued neural networks. Int. J. Syst. Sci. 2020, 51, 303–312. [Google Scholar] [CrossRef]
- Zhang, W.; Cao, J.; Chen, D.; Alsaadi, F.E. Synchronization in fractional-order complex-valued delayed neural networks. Entropy 2018, 20, 54. [Google Scholar] [CrossRef]
- Li, L.; Wang, Z.; Lu, J.; Li, Y. Adaptive synchronization of fractional-order complex-valued neural networks with discrete and distributed delays. Entropy 2018, 20, 124. [Google Scholar] [CrossRef]
- Nitta, T. Solving the XOR problem and the detection of symmetry using a single complex-valued neuron. Neural Netw. 2003, 16, 1101–1105. [Google Scholar] [CrossRef]
- Goh, S.L.; Chen, M.; Popovic, D.H.; Aihara, K.; Obradovic, D.; Mandic, D.P. Complex-valued forecasting of wind profile. Renew. Energy 2006, 31, 1733–1750. [Google Scholar] [CrossRef]
- Hamilton, W.R. On quaternions. Proc. R. Ir. Acad. 1847, 3, 1–16. [Google Scholar]
- Zhang, F. Quaternions and matrices of quaternions. Linear Algebra Appl. 1997, 251, 21–57. [Google Scholar] [CrossRef]
- Matsui, N.; Isokawa, T.; Kusamichi, H. Quaternion neural network with geometrical operators. J. Intell. Fuzzy Syst. 2004, 15, 149–164. [Google Scholar]
- Isokawa, T.; Kusakabe, T.; Matsui, N.; Peper, F. Quaternion neural networks and its application. In International Conference on Knowledge-Based and Intelligent Information and Engineering Systems; LNAI-2774 (KES2003); Springer: Berlin/Heidelberg, Germany, 2003; pp. 318–324. [Google Scholar]
- Karney, C.F.F. Quaternions in molecular modeling. J. Mol. Graphics Model. 2007, 25, 595–604. [Google Scholar] [CrossRef]
- Bolboacă, S.D.; Jäntschi, L. Helical structure of linear homopolymers. Mater. Res. Proc. 2018, 8, 35–51. [Google Scholar]
- Buchholz, S.; Le Bihan, N. Polarized signal classification by complex and quaternionic multi-layer perceptrons. Int. J. Neural Syst. 2008, 18, 75–85. [Google Scholar] [CrossRef] [PubMed]
- Marques, J.M.C.; Pereira, F.B.; Llanio-Trujillo, J.L.; Abreu, P.E.; Alberti, M.; Aguilar, A.; Pirani, F.; Bartolomei, M. A global optimization perspective on molecular clusters. Philos. Trans. R. Soc. A 2017, 375, 20160198. [Google Scholar] [CrossRef] [PubMed]
- Jäntschi, L.; Bolboacă, S.D. Conformational study of C-24 cyclic polyyne clusters. Int. J. Quantum Chem. 2018, 118, e25614. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, D.; Lu, J. Global exponential stability for quaternion-valued recurrent neural networks with time-varying delays. Nonlinear Dyn. 2017, 87, 553–565. [Google Scholar] [CrossRef]
- Li, H.L.; Jiang, H.; Cao, J. Global synchronization of fractional-order quaternion-valued neural networks with leakage and discrete delays. Neurocomputing 2020, 385, 211–219. [Google Scholar] [CrossRef]
- Liu, J.; Jian, J. Global dissipativity of a class of quaternion-valued BAM neural networks with time delay. Neurocomputing 2019, 349, 123–132. [Google Scholar] [CrossRef]
- You, X.; Song, Q.; Liang, J.; Liu, Y.; Alsaadi, F.E. Global μ-stability of quaternion-valued neural networks with mixed time-varying delays. Neurocomputing 2018, 290, 12–25. [Google Scholar] [CrossRef]
- Xiao, J.; Zhong, S. Synchronization and stability of delayed fractional-order memristive quaternion-valued neural networks with parameter uncertainties. Neurocomputing 2019, 363, 321–338. [Google Scholar] [CrossRef]
- Rajchakit, G.; Chanthorn, P.; Kaewmesri, P.; Sriraman, R.; Lim, C.P. Global Mittag-Leffler stability and stabilization analysis of fractional-order quaternion-valued memristive neural networks. Mathematics 2020, 8, 422. [Google Scholar] [CrossRef]
- Yang, X.; Li, C.; Song, Q.; Chen, J.; Huang, J. Global Mittag-Leffler stability and synchronization analysis of fractional-order quaternion-valued neural networks with linear threshold neurons. Neural Netw. 2018, 105, 88–103. [Google Scholar] [CrossRef]
- Qi, X.; Bao, H.; Cao, J. Exponential input-to-state stability of quaternion-valued neural networks with time delay. Appl. Math. Comput. 2019, 358, 382–393. [Google Scholar] [CrossRef]
- Song, Q.; Chen, X. Multistability analysis of quaternion-valued neural networks with time delays. IEEE Trans. Neural Netw. Learn. Syst. 2018, 12, 5430–5440. [Google Scholar] [CrossRef] [PubMed]
- Tu, Z.; Zhao, Y.; Ding, N.; Feng, Y.; Zhang, W. Stability analysis of quaternion-valued neural networks with both discrete and distributed delays. Appl. Math. Comput. 2019, 343, 342–353. [Google Scholar] [CrossRef]
- Tu, Z.; Yang, X.; Wang, L.; Ding, N. Stability and stabilization of quaternion-valued neural networks with uncertain time-delayed impulses: Direct quaternion method. Phys. A Stat. Mech. Appl. 2019, 535, 122358. [Google Scholar] [CrossRef]
- Oldham, K.B.; Spanier, J. The Fractional Calculus; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Syam, M.I.; Al-Refai, M. Fractional differential equations with Atangana-Baleanu fractional derivative: Analysis and applications. Chaos Soliton. Fract. 2019, 2, 100013. [Google Scholar] [CrossRef]
- Pratap, A.; Raja, R.; Cao, J.; Rajchakit, G.; Lim, C.P. Global robust synchronization of fractional order complex-valued neural networks with mixed time-varying delays and impulses. Int. J. Control. Autom. Syst. 2019, 17, 509–520. [Google Scholar]
- Bao, H.; Park, J.H.; Cao, J. Synchronization of fractional-order complex-valued neural networks with time delay. Neural Netw. 2016, 81, 16–28. [Google Scholar] [CrossRef]
- Pratap, A.; Raja, R.; Alzabut, J.; Dianavinnarasi, J.; Cao, J.; Rajchakit, G. Finite-time Mittag-Leffler stability of fractional-order quaternion-valued memristive neural networks with impulses. Neural Process. Lett. 2020, 51, 1485–1526. [Google Scholar] [CrossRef]
- Camacho, N.A.; Duarte-Mermoud, M.A.; Gallegos, J.A. Lyapunov-functions for fractional order systems. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2951–2957. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, X.; Chen, J.; Guo, R.; Zhou, S. Further stability analysis for delayed complex-valued recurrent neural networks. Neurocomputing 2017, 251, 81–89. [Google Scholar] [CrossRef]
- Subramanian, K.; Muthukumar, P. Existence, uniqueness and global asymptotic stability analysis for delayed complex-valued Cohen-rossberg BAM neural networks. Neural Comput. Appl. 2018, 29, 565–584. [Google Scholar] [CrossRef]






© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Humphries, U.; Rajchakit, G.; Kaewmesri, P.; Chanthorn, P.; Sriraman, R.; Samidurai, R.; Lim, C.P. Global Stability Analysis of Fractional-Order Quaternion-Valued Bidirectional Associative Memory Neural Networks. Mathematics 2020, 8, 801. https://doi.org/10.3390/math8050801
Humphries U, Rajchakit G, Kaewmesri P, Chanthorn P, Sriraman R, Samidurai R, Lim CP. Global Stability Analysis of Fractional-Order Quaternion-Valued Bidirectional Associative Memory Neural Networks. Mathematics. 2020; 8(5):801. https://doi.org/10.3390/math8050801
Chicago/Turabian StyleHumphries, Usa, Grienggrai Rajchakit, Pramet Kaewmesri, Pharunyou Chanthorn, Ramalingam Sriraman, Rajendran Samidurai, and Chee Peng Lim. 2020. "Global Stability Analysis of Fractional-Order Quaternion-Valued Bidirectional Associative Memory Neural Networks" Mathematics 8, no. 5: 801. https://doi.org/10.3390/math8050801
APA StyleHumphries, U., Rajchakit, G., Kaewmesri, P., Chanthorn, P., Sriraman, R., Samidurai, R., & Lim, C. P. (2020). Global Stability Analysis of Fractional-Order Quaternion-Valued Bidirectional Associative Memory Neural Networks. Mathematics, 8(5), 801. https://doi.org/10.3390/math8050801






