Kane’s Method-Based Simulation and Modeling Robots with Elastic Elements, Using Finite Element Method
Abstract
1. Introduction
2. A Brief Overview of the Applied Formalism in (FEA) of (MBS)
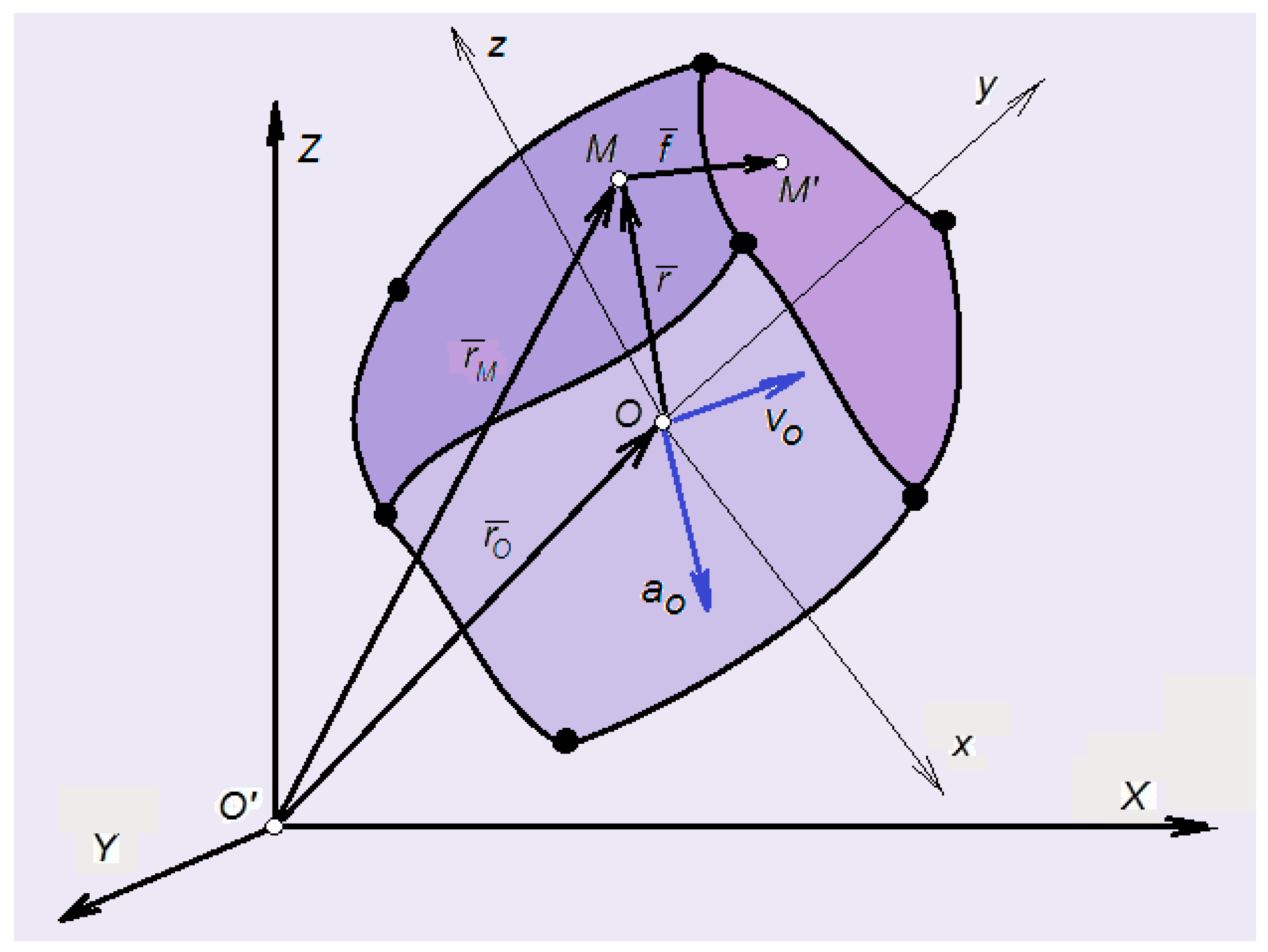
3. Preliminary Kinematics and Kinetics of Finite Elements
4. Kane’s Formalism Applied to MBS
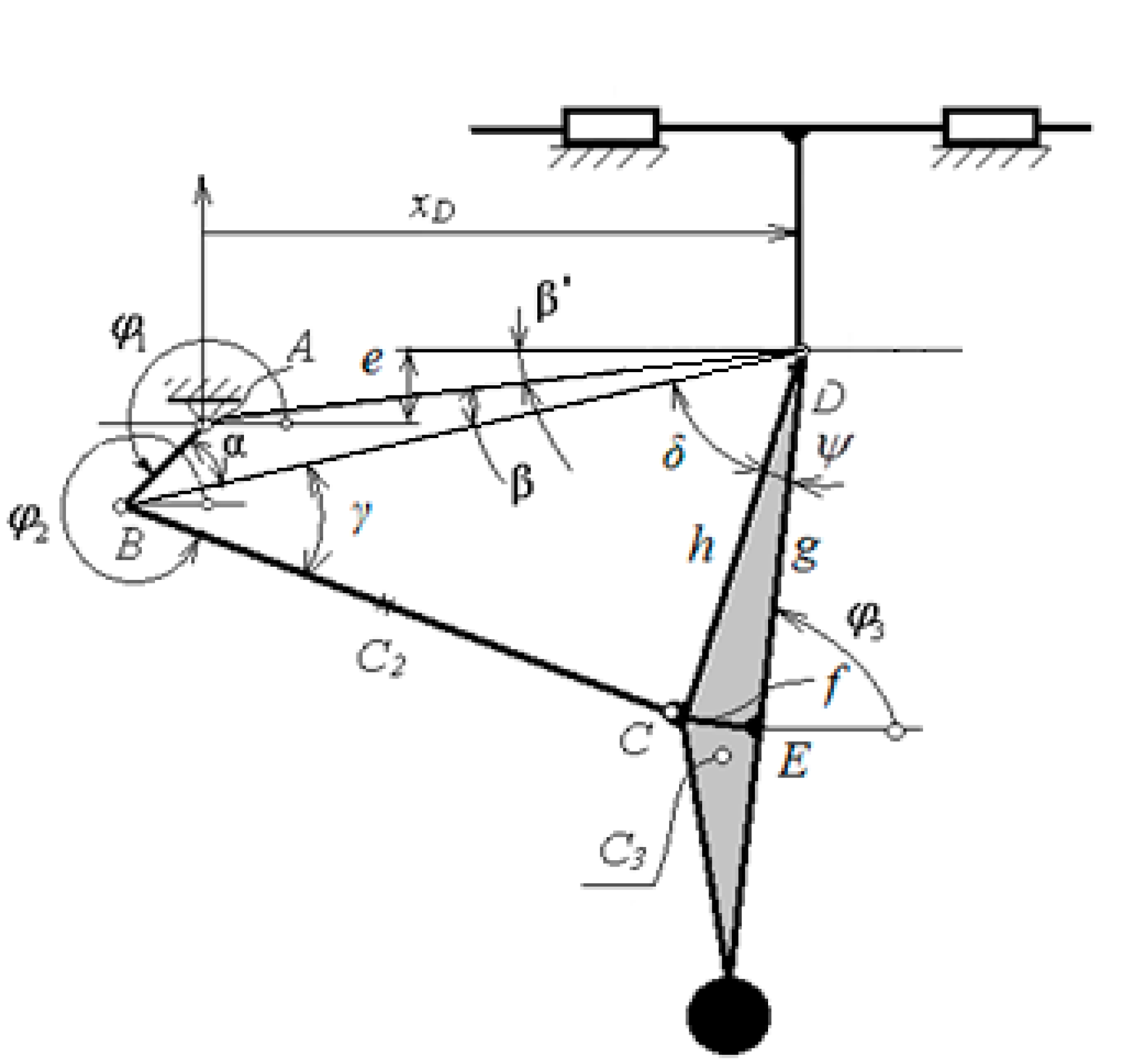
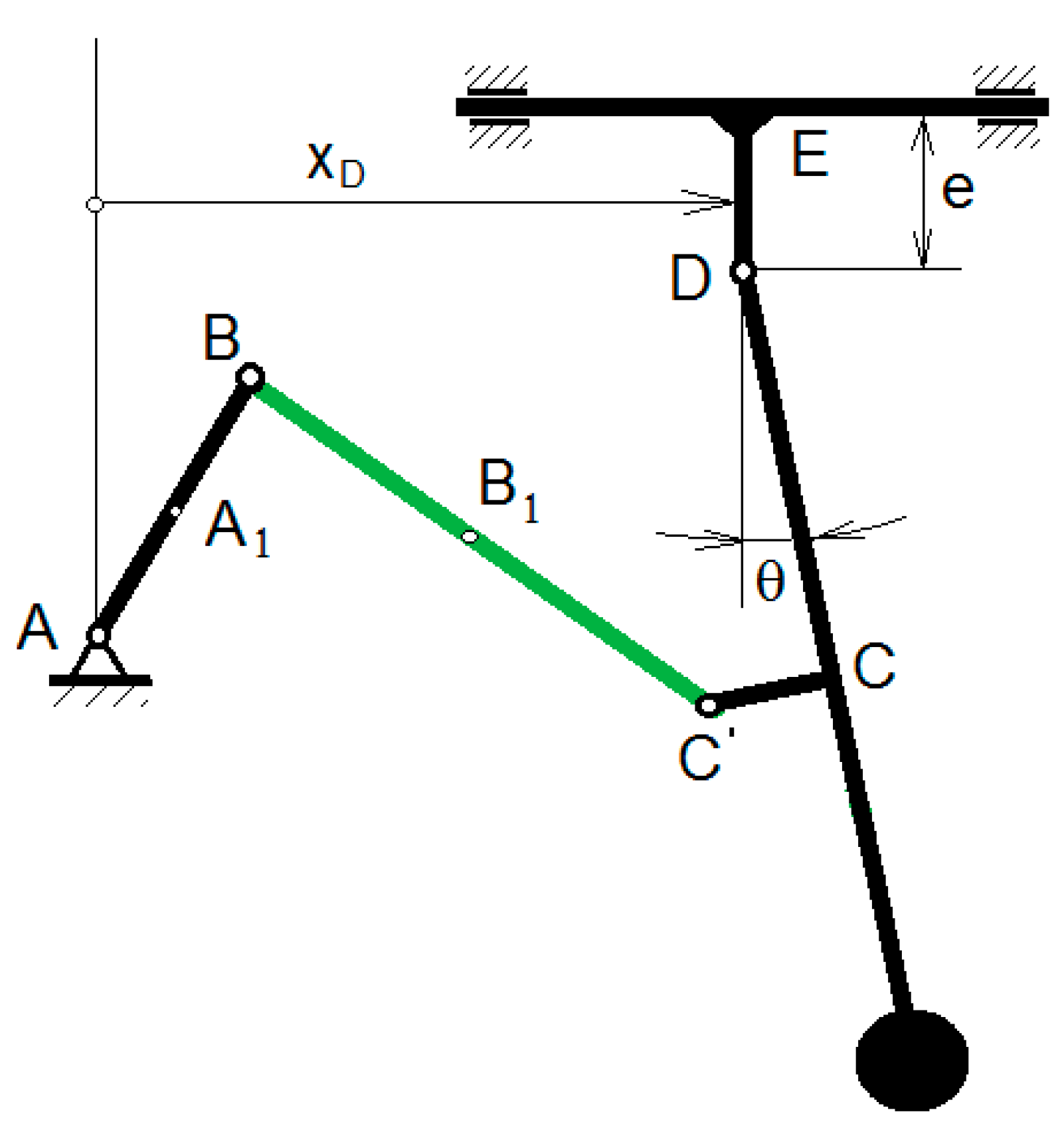
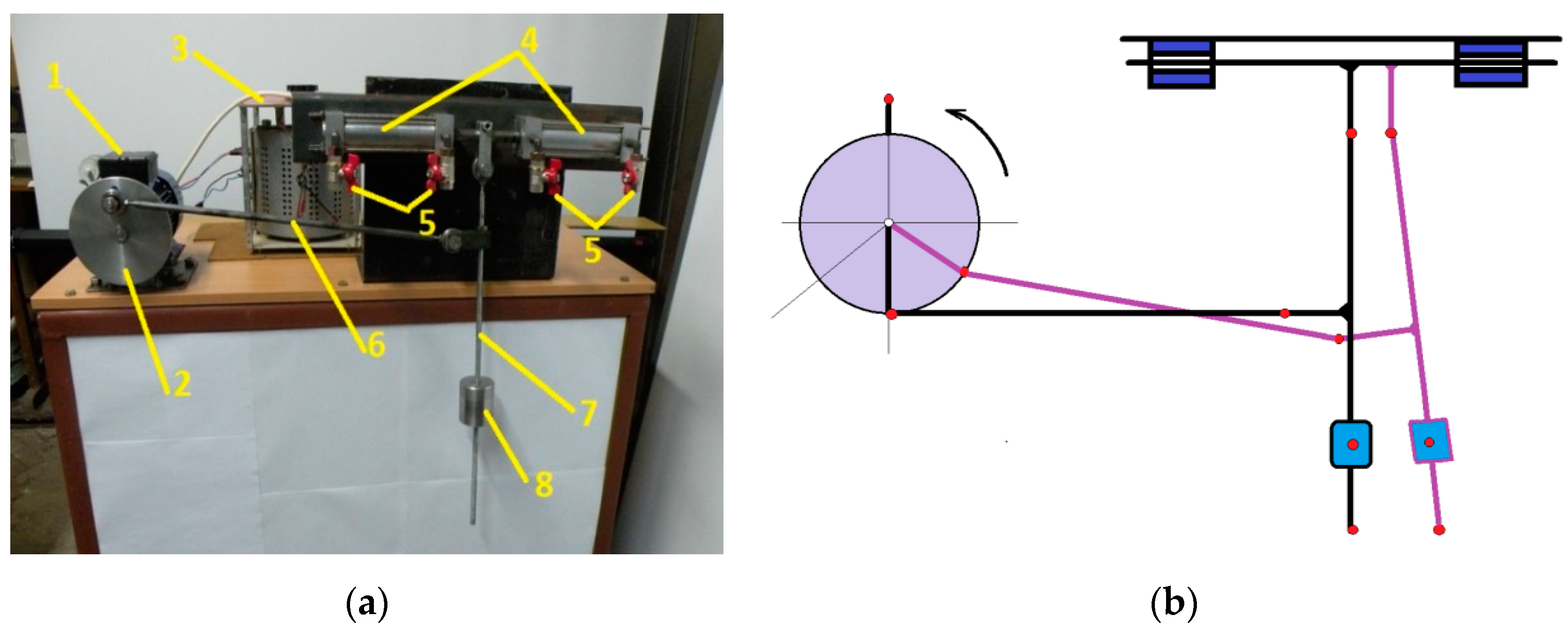
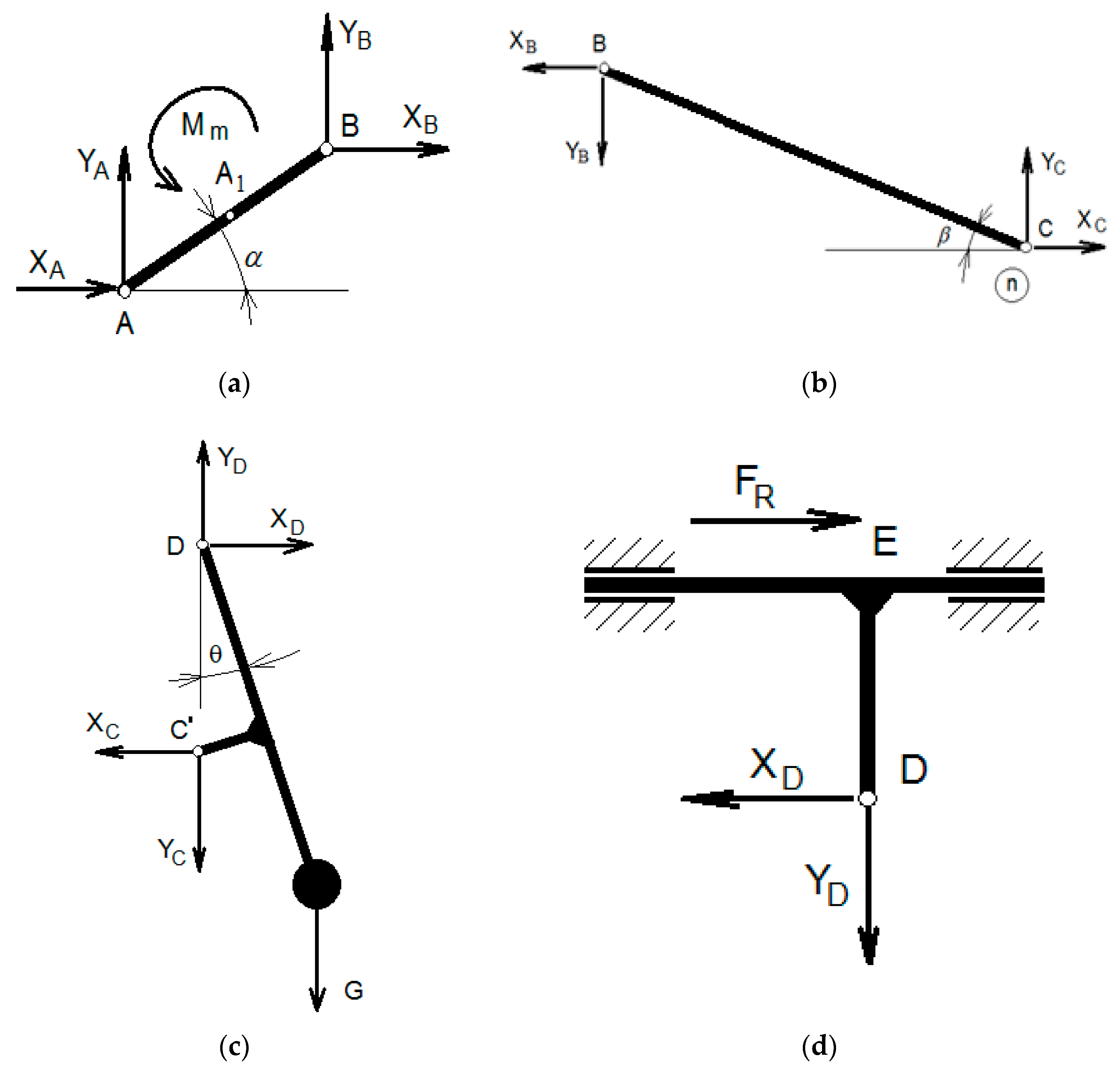
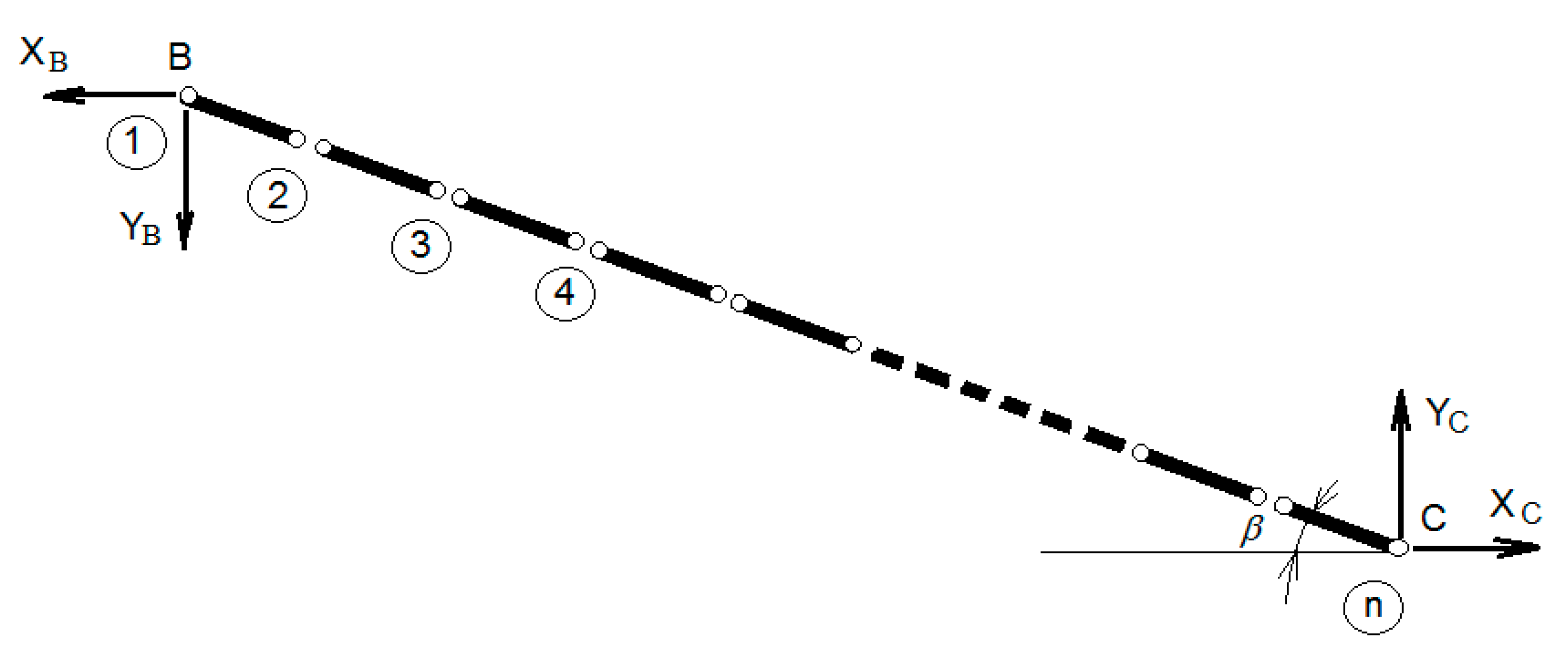
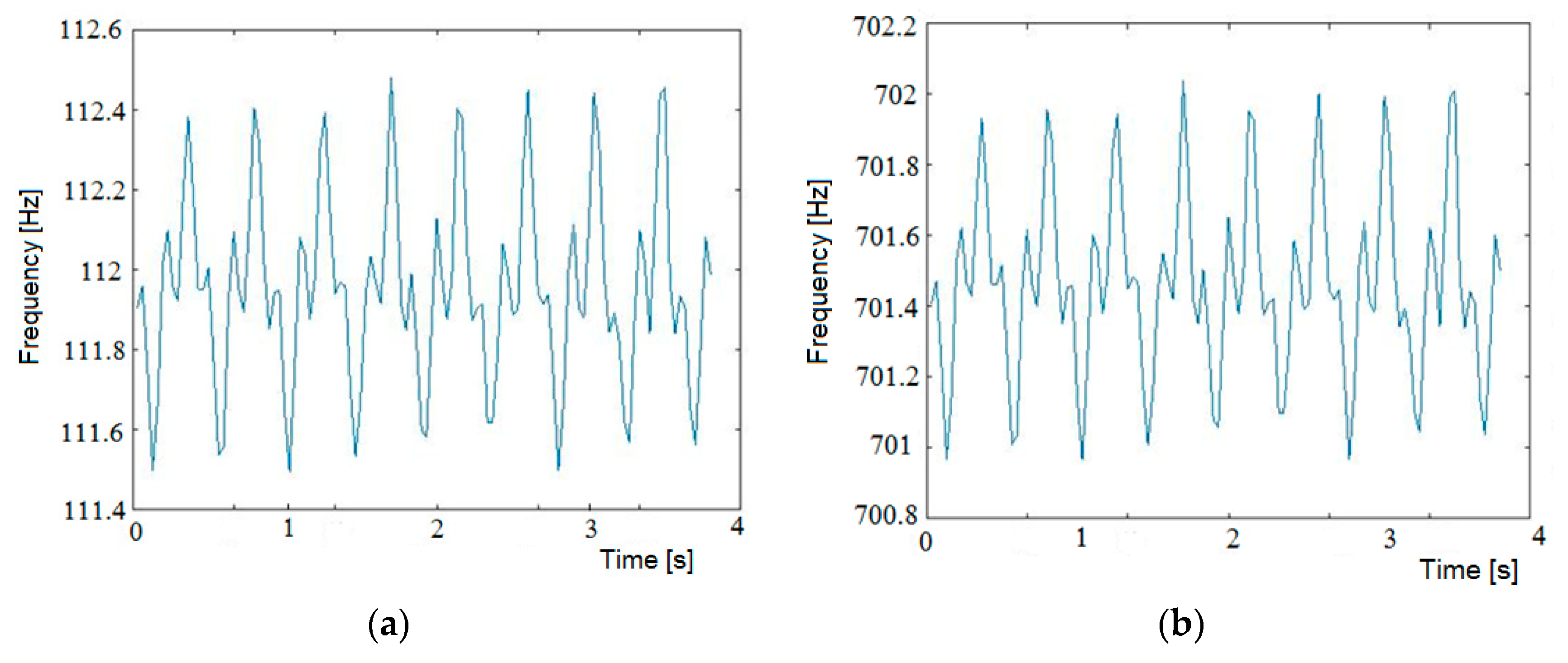
5. An Application to a Two Degrees of Freedom Mechanism Used in a Wind Water Pump
6. Conclusions and Discussions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Kane’s Equations
Appendix B
References
- Negrean, I.; Crișan, A.-D.; Vlase, S. A New Approach in Analytical Dynamics of Mechanical Systems. Symmetry 2020, 12, 95. [Google Scholar] [CrossRef]
- Hussain, Z.; Azlan, N.Z. KANE’S Method for Dynamic Modeling. In Proceedings of the IEEE International Conference on Automatic Control and Intelligent Systems (I2CAC, IS), Shah Alam, Malaysia, 22 October 2016; pp. 174–179. [Google Scholar]
- Tu, T.W. First-order form, Lagrange’s form, and Gibbs-Appell’s form of Kane’s Equations. Acta Mech. 2016, 227, 1885–1901. [Google Scholar] [CrossRef]
- Li, X.; Sun, H.X.; Liao, L.J.; Song, J.Z. Simulation and Comparison Research of Lagrange and Kane Dynamics Modeling for The 4-DOF Modular Industrial Robot. In Proceedings of the 5th International Conference on Advanced Design and Manufacturing Engineering (ICADME), Shenzhen, China, 19–20 September 2015; Volume 39, pp. 251–254. [Google Scholar]
- Ursu-Fisher, N. Elements of Analitical Mechanics; House of Science Book Press: Cluj-Napoca, Romania, 2015. [Google Scholar]
- Bagci, C. Elastodynamic Response of Mechanical Systems using Matrix Exponential Mode Uncoupling and Incremental Forcing Techniques with Finite Element Method. In Proceedings of the Sixth Word Congress on Theory of Machines and Mechanisms, New Delhi, India, 15–20 December 1983; p. 472. [Google Scholar]
- Erdman, A.G.; Sandor, G.N.; Oakberg, A. A General Method for Kineto-Elastodynamic Analysis and Synthesis of Mechanisms. J. Eng. Ind. ASME Trans. 1972, 94, 1193–1205. [Google Scholar] [CrossRef]
- Phillips, J.R.; Amirouche, F. A momentum form of Kane’s equations for scleronomic systems. Math. Comput. Model. Dyn. Syst. 2018, 24, 143–169. [Google Scholar] [CrossRef]
- Nukulwuthiopas, W.; Laowattana, S.; Maneewarn, T. Dynamic modeling of a one-wheel robot by using Kane’s method. In Proceedings of the 2002 IEEE International Conference on Industrial Technology, IEEE ICIT’ 02, Bangkok, Thailand, 11–14 December 2002; pp. 524–529. [Google Scholar]
- Bahgat, B.M.; Willmert, K.D. Finite Element Vibrational Analysis of Planar Mechanisms. Mech. Mach. Theory 1976, 11, 47. [Google Scholar] [CrossRef]
- Cleghorn, W.L.; Fenton, E.G.; Tabarrok, K.B. Finite Element Analysis of High-Speed Flexible Mechanism. Mech. Mach. Theory 1981, 16, 407. [Google Scholar] [CrossRef]
- Nath, P.K.; Ghosh, A. Kineto-Elastodynamic Analysis of Mechanisms by Finite Element Method. Mech. Mach. Theory 1980, 15, 179. [Google Scholar] [CrossRef]
- Thompson, B.S.; Sung, C.K. A survey of Finite Element Techniques for Mechanism Design. Mech. Mach. Theory 1986, 21, 351–359. [Google Scholar] [CrossRef]
- Gerstmayr, J.; Schöberl, J. A 3D Finite Element Method for Flexible Multibody Systems. Multibody Syst. Dyn. 2006, 15, 305–320. [Google Scholar] [CrossRef]
- Marin, M.; Ellahi, R.; Chirilă, A. On solutions of saint-venant’s problem for elastic dipolar bodies with voids. Carpath. J. Math. 2017, 33, 219–232. [Google Scholar]
- Pennestri, E.; de Falco, D.; Vita, L. An Investigation of the Inuence of Pseudoinverse Matrix Calculations on Multibody Dynamics by Means of the Udwadia-Kalaba Formulation. J. Aerosp. Eng. 2009, 22, 365–372. [Google Scholar]
- Vlase, S.; Marin, M.; Öchsner, A.; Scutaru, M.L. Motion equation for a flexible one-dimensional element used in the dynamical analysis of a multibody system. Contin. Mech. Thermodyn. 2019, 31, 715–724. [Google Scholar] [CrossRef]
- Vlase, S. Dynamical Response of a Multibody System with Flexible Elements with a General Three-Dimensional Motion. Rom. J. Phys. 2012, 57, 676–693. [Google Scholar]
- Vlase, S.; Dănăşel, C.; Scutaru, M.L.; Mihălcică, M. Finite Element Analysis of a Two-Dimensional Linear Elastic Systems with a Plane “Rigid Motion”. Rom. J. Phys. 2014, 59, 476–487. [Google Scholar]
- Piras, G.; Cleghorn, W.L.; Mills, J.K. Dynamic finite-element analysis of a planar high-speed, high-precision parallel manipulator with flexible links. Mech. Mach. Theory 2005, 40, 849–862. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, J.; Shen, Y. Simultaneous optimal structure and control design of flexible linkage mechanism for noise attenuation. J. Sound Vib. 2007, 299, 1124–1133. [Google Scholar]
- Gibbs, J.W. On the fundamental formulae of dynamics. Am. J. Math. 1879, 2, 49–64. [Google Scholar] [CrossRef]
- Appell, P. Sur une forme générale des equations de la dynamique. J. Reine Angew. Math. 1900, 1900, 310–319. [Google Scholar]
- Negrean, I.; Kacso, K.; Schonstein, C.; Duca, A. Mechanics. Theory and Applications; UT Press: Cluj-Napoca, Romania, 2012. [Google Scholar]
- Negrean, I.; Crișan, A.-D. Synthesis on the Acceleration Energies in the Advanced Mechanics of the Multibody Systems. Symmetry 2019, 11, 1077. [Google Scholar] [CrossRef]
- Mirtaheri, S.M.; Zohoor, H. The Explicit Gibbs-Appell Equations of Motion for Rigid-Body Constrained Mechanical System. In Proceedings of the RSI International Conference on Robotics and Mechatronics ICRoM, Tehran, Iran, 23–25 October 2018; pp. 304–309. [Google Scholar]
- Mehrjooee, O.; Dehkordi, S.F.; Korayem, M.H. Dynamic modeling and extended bifurcation analysis of flexible-link manipulator. Mech. Based Des. Struct. Mach. 2019, 48, 87–110. [Google Scholar] [CrossRef]
- Korayem, M.H.; Dehkordi, S.F. Motion equations of cooperative multi flexible mobile manipulator via recursive Gibbs-Appell formulation. Appl. Math. Model. 2019, 65, 443–463. [Google Scholar] [CrossRef]
- Shafei, A.M.; Shafei, H.R. A systematic method for the hybrid dynamic modeling of open kinematic chains confined in a closed environment. Multibody Syst. Dyn. 2017, 38, 21–42. [Google Scholar] [CrossRef]
- Amini, S.; Dehkordi, S.F.; Fahraji, S.H. Motion equation derivation and tip-over evaluations for K mobile manipulators with the consideration of motors mass by the use of Gibbs-Appell formulation. In Proceedings of the 5th RSI International Conference on Robotics and Mechatronics (IcRoM), Tehran, Iran, 25–27 October 2017. [Google Scholar]
- Korayem, M.H.; Dehkordi, S.F. Derivation of dynamic equation of viscoelastic manipulator with revolute-prismatic joint using recursive Gibbs-Appell formulation. Nonlinear Dyn. 2017, 89, 2041–2064. [Google Scholar] [CrossRef]
- Shafei, A.M.; Korayem, M.H. Theoretical and experimental study of dynamic load-carrying capacity for flexible robotic arms in point-to-point motion. Optim. Control. Appl. Methods 2017, 38, 963–972. [Google Scholar] [CrossRef]
- Haug, E.J. Extension of Maggi and Kane Equations to Holonomic Dynamic Systems. J. Comput. Nonlinear Dyn. 2018, 13, 121003. [Google Scholar] [CrossRef]
- Amengonu, Y.H.; Kakad, Y.P. Dynamics and control for Constrained Multibody Systems modeled with Maggi’s equation: Application to Differential Mobile Robots Part II. In Proceedings of the 27th International Conference on Cadcam, Robotics and Factories of the Future, London, UK, 22–24 July 2014; Volume 65, p. 012018. [Google Scholar]
- Ladyzynska-Kozdras, E. Application of the Maggi equations to mathematical modeling of a robotic underwater vehicle as an object with superimposed non-holonomic constraints treated as control laws. Mechatron. Syst. Mech. Mater. 2012, 180, 152–159. [Google Scholar] [CrossRef]
- de Jalon, J.G.; Callejo, A.; Hidalgo, A.F. Efficient Solution of Maggi′s Equations. J. Comput. Nonlinear Dyn. 2012, 7, 021003. [Google Scholar] [CrossRef]
- Malvezzi, F.; Matarazzo Orsino, R.M.; Hess Coelho, T.A. Lagrange’s, Maggi’s and Kane’s equations to the dynamic modelling of serial manipulator. In Proceedings of the XVII International Symposium on Dynamic Problems of Mechanics, DINAME 2017, São Sebastião, Brazil, 5–10 March 2017. [Google Scholar]
- Vlase, S.; Negrean, I.; Marin, M.; Scutaru, M.L. Energy of Accelerations Used to Obtain the Motion Equations of a Three-Dimensional Finite Element. Symmetry 2020, 12, 321. [Google Scholar] [CrossRef]
- Wang, J.T.; Huston, R.L. Kane’s equations with undetermined multipiers-application to constrained multibody systems. ASME J. Appl. Mech. 1987, 54, 424–429. [Google Scholar] [CrossRef]
- Wang, J.T.; Huston, R.L. Computational methods in constrained multibody dynamics: Matrix formalisms. Comput. Struct. 1988, 29, 331–338. [Google Scholar] [CrossRef]
- Kane, T.R.; Levinson, D.A. Multibody dynamics. ASME J. Appl. Mech. 1983, 50, 1071–1078. [Google Scholar] [CrossRef]
- Anderson, K. Recursive Derivation of Explicit Equations of Motion for the Efficient Dynamic/Control Simulation of Large Multibody Systems. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1990. [Google Scholar]
- Rosenthal, D. An order n formulation for robotic systems. J. Astronaut. Sci. 1990, 38, 511–529. [Google Scholar]
- Banerjee, A. Block-diagonal equations for multibody elastodynamics with geometric stiffness and constraints. J. Guid. Control Dyn. 1993, 16, 1092–1100. [Google Scholar] [CrossRef]
- Blajer, W. A geometric unification of constrained system dynamics. Multibody Syst. Dyn. 1997, 1, 3–21. [Google Scholar] [CrossRef]
- Blajer, W. A geometrical interpretation and uniform matrix formulation of multibody system dynamics. Z. Angew. Math. Mech. 2001, 81, 247–259. [Google Scholar] [CrossRef]
- Anderson, K.; Critchley, J. Improved order-N performance algorithm for the simulation of constrained multi-rigid-body dynamic systems. Multibody Syst. Dyn. 2003, 9, 185–212. [Google Scholar] [CrossRef]
- Kane, T.R.; Levinson, D.A. Formulation of Equations of Motion for Complex Spacecraft. J. Guid. Control 1980, 3, 99–112. [Google Scholar] [CrossRef]
- Kane, T.R.; Levinson, D.A. Use of Kane’s Dynamical Equations in Robotics. Int. J. Robot. Res. 1983, 2, 3–21. [Google Scholar] [CrossRef]
- Bajodah, A.H.; Hodges, D.H.; Chen, Y.-H. New Form of Kane’s Equations of Motion for Constrained Systems. J. Guid. Control Dyn. 2003, 26, 79–88. [Google Scholar] [CrossRef]
- Meghdari, F. Fahimi Dynamic Modeling of Multi-Elastic Body Systems using Kane’s Method and Congruency Transformations. Tech. Mech. 1999, 19, 127–140. [Google Scholar]
- Zhao, J.; Zhao, R.; Xue, Z.; Yu, K. A new modeling method for flexible multibody systems. Multibody Syst. Dyn. 2015, 35, 179–190. [Google Scholar] [CrossRef]
- Scutaru, M.L. Models for the study of mechanical response of the solids and systems of solids. Ph.D. Thesis, Transylvania University, Lexington, KY, USA, 2014. [Google Scholar]
- Marin, M.; EM Craciun, E.M.; Pop, N. Considerations on mixed initial-boundary value problems for micropolar porous bodies. Dyn. Syst. Appl. 2016, 25, 175–196. [Google Scholar]
- Itu, C.; Oechsner, A.; Vlase, S.; Marin, M. Improved rigidity of composite circular plates through radial ribs. Proc. Inst. Mech. Eng. Part L J. Mater.-Des. Appl. 2019, 233, 1585–1593. [Google Scholar] [CrossRef]
- Nastac, S.; Debeleac, C.; Vlase, S. Hysteretically Symmetrical Evolution of Elastomers—Based Vibration Isolators within alpha-Fractional Nonlinear Computational Dynamics. Symmetry 2019, 11, 924. [Google Scholar] [CrossRef]
| Number of Finite Elements | Lagrange | Gibbs–Appell | Kane |
|---|---|---|---|
| 5 | 288 | 120 | 10 |
| 10 | 528 | 220 | 20 |
| 15 | 768 | 320 | 30 |
| 20 | 1008 | 420 | 40 |
| 25 | 1248 | 520 | 50 |
| 30 | 1488 | 620 | 60 |
| 40 | 1968 | 820 | 80 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vlase, S.; Negrean, I.; Marin, M.; Năstac, S. Kane’s Method-Based Simulation and Modeling Robots with Elastic Elements, Using Finite Element Method. Mathematics 2020, 8, 805. https://doi.org/10.3390/math8050805
Vlase S, Negrean I, Marin M, Năstac S. Kane’s Method-Based Simulation and Modeling Robots with Elastic Elements, Using Finite Element Method. Mathematics. 2020; 8(5):805. https://doi.org/10.3390/math8050805
Chicago/Turabian StyleVlase, Sorin, Iuliu Negrean, Marin Marin, and Silviu Năstac. 2020. "Kane’s Method-Based Simulation and Modeling Robots with Elastic Elements, Using Finite Element Method" Mathematics 8, no. 5: 805. https://doi.org/10.3390/math8050805
APA StyleVlase, S., Negrean, I., Marin, M., & Năstac, S. (2020). Kane’s Method-Based Simulation and Modeling Robots with Elastic Elements, Using Finite Element Method. Mathematics, 8(5), 805. https://doi.org/10.3390/math8050805








