A New Solution to Well-Known Hencky Problem: Improvement of In-Plane Equilibrium Equation

Abstract

In this paper, the well-known Hencky problem—that is, the problem of axisymmetric deformation of a peripherally fixed and initially flat circular membrane subjected to transverse uniformly distributed loads—is re-solved by simultaneously considering the improvement of the out-of-plane and in-plane equilibrium equations. In which, the so-called small rotation angle assumption of the membrane is given up when establishing the out-of-plane equilibrium equation, and the in-plane equilibrium equation is, for the first time, improved by considering the effect of the deflection on the equilibrium between the radial and circumferential stress. Furthermore, the resulting nonlinear differential equation is successfully solved by using the power series method, and a new closed-form solution of the problem is finally presented. The conducted numerical example indicates that the closed-form solution presented here has a higher computational accuracy in comparison with the existing solutions of the well-known Hencky problem, especially when the deflection of the membrane is relatively large.

1. Introduction

Membrane structures or structural components have played important roles in many fields of engineering or technology, for example, the MEMS (Micro-Electro-Mechanical Systems) devices [1], heat transfer enhancement applications [2], characterization of mechanical properties [3,4], and civil engineering [5,6]. Mathematical modelling is often necessary to study the mechanical behavior of structures [7,8]. However, the large deflection phenomenon of the membrane usually gives rise to some nonlinear differential equations. The boundary value problems of these somewhat intractable nonlinear equations are usually difficult to deal with analytically [9,10,11,12,13,14,15]. Therefore, analytical solutions for membrane problems are available in a few cases, but it is usually easy to find the numerical solutions obtained by, for example, the iterative or shooting method in the existing literature. In practice, however, analytical solutions are often found to be necessary.

Hencky, a famous German scientist, originally dealt with the problem of axisymmetric deformation of a peripherally fixed circular membrane under uniformly distributed transverse loads and presented its closed-form solution in the form of power series [16]. A computational error in [16] was corrected by Chien [17] and Alekseev [18], respectively. This problem is usually called the well-known Föppl–Hencky membrane problem, or simply the well-known Hencky problem, and its solution is called the well-known Hencky solution. This solution is the first solution for circular membrane problems and is often cited in relevant studies [6,13,19,20,21]. During the derivation of the well-known Hencky solution, however, the so-called small rotation angle assumption of the membrane—that is, suppose that the rotation angle $\theta$ of the membrane is so small that $\sin \theta \approx \tan \theta$—was adopted, which limits the applicability of the solution to the deflection of the membrane. Consequently, we gave up the small rotation angle assumption of the membrane and used $\sin \theta =\sqrt{1+1/{\tan }^2\theta }$ to establish the out-of-plane equilibrium equation, re-solved the well-known Hencky problem, and presented the closed-form solution without the small rotation angle assumption in [21]. However, the effect of the deflection on the in-plane equilibrium equation was not considered during the derivation of the solution presented in [21], and this still limits the applicability of solution to the deflection of membrane, which will be seen from the numerical example conducted in Section 3.

In this study, the well-known Hencky problem was re-solved by simultaneously considering the improvement of the out-of-plane and in-plane equilibrium equations, and a more refined closed-form solution of well-known Hencky problem was presented. The numerical example conducted indicates that the solution presented here has a higher computational accuracy in comparison with the existing solutions. The detailed derivation of the basic equations was arranged in the next section, in which the out-of-plane equilibrium equation is established under the condition of $\sin \theta =\sqrt{1+1/{\tan }^2\theta }$, the in-plane equilibrium equation is, for the first time, improved by considering the effect of deflection on the equilibrium between radial stress and circumferential stress, the resulting nonlinear differential equation is successfully solved by using the power series method, and finally, a new closed-form solution of the well-known Hencky problem is presented. In Section 3, a numerical example is conducted for the identification of the validity of the closed-form solution presented and the applicability of solution to the deflection of membrane. Section 4 features the concluding remarks.

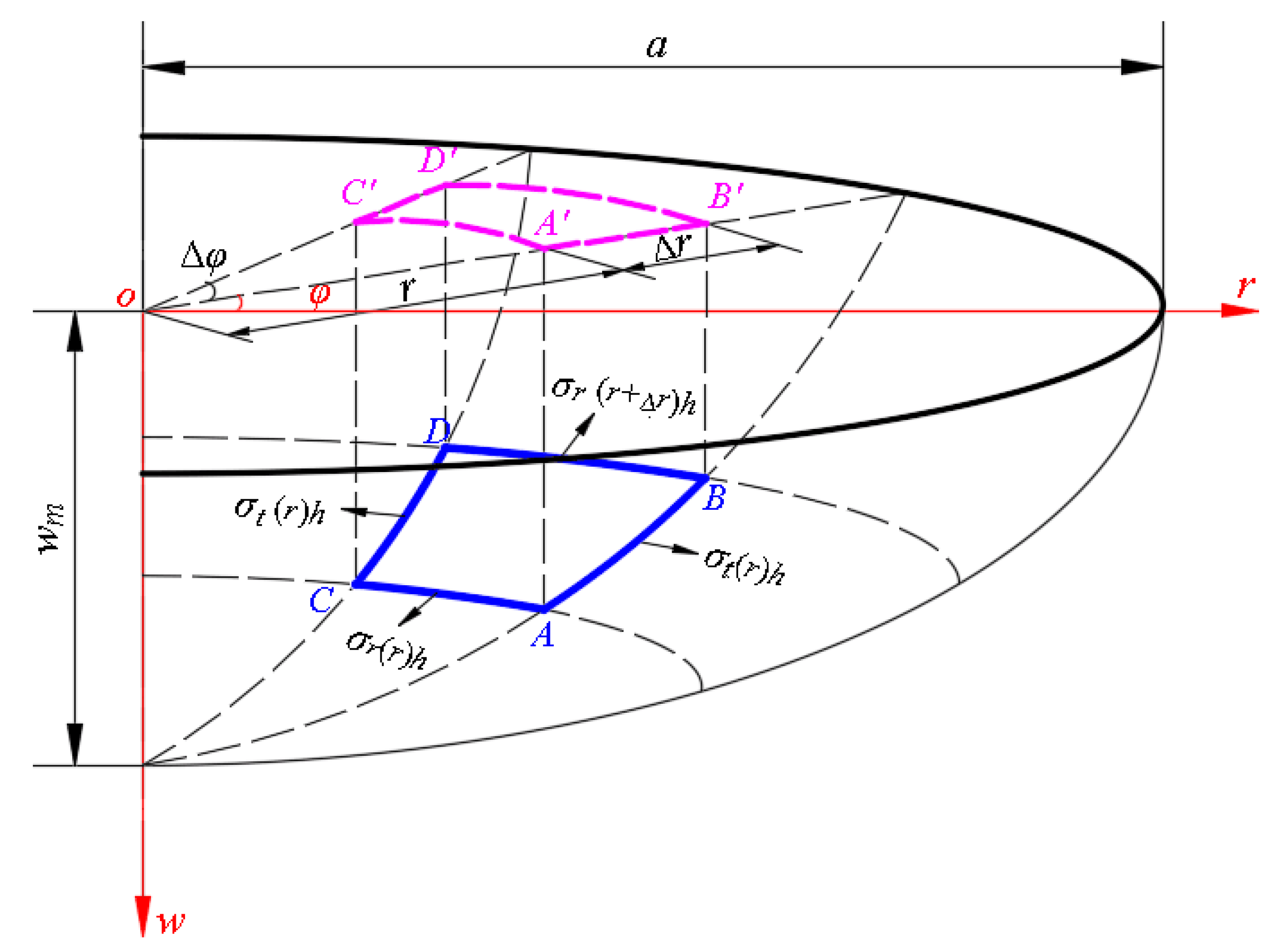
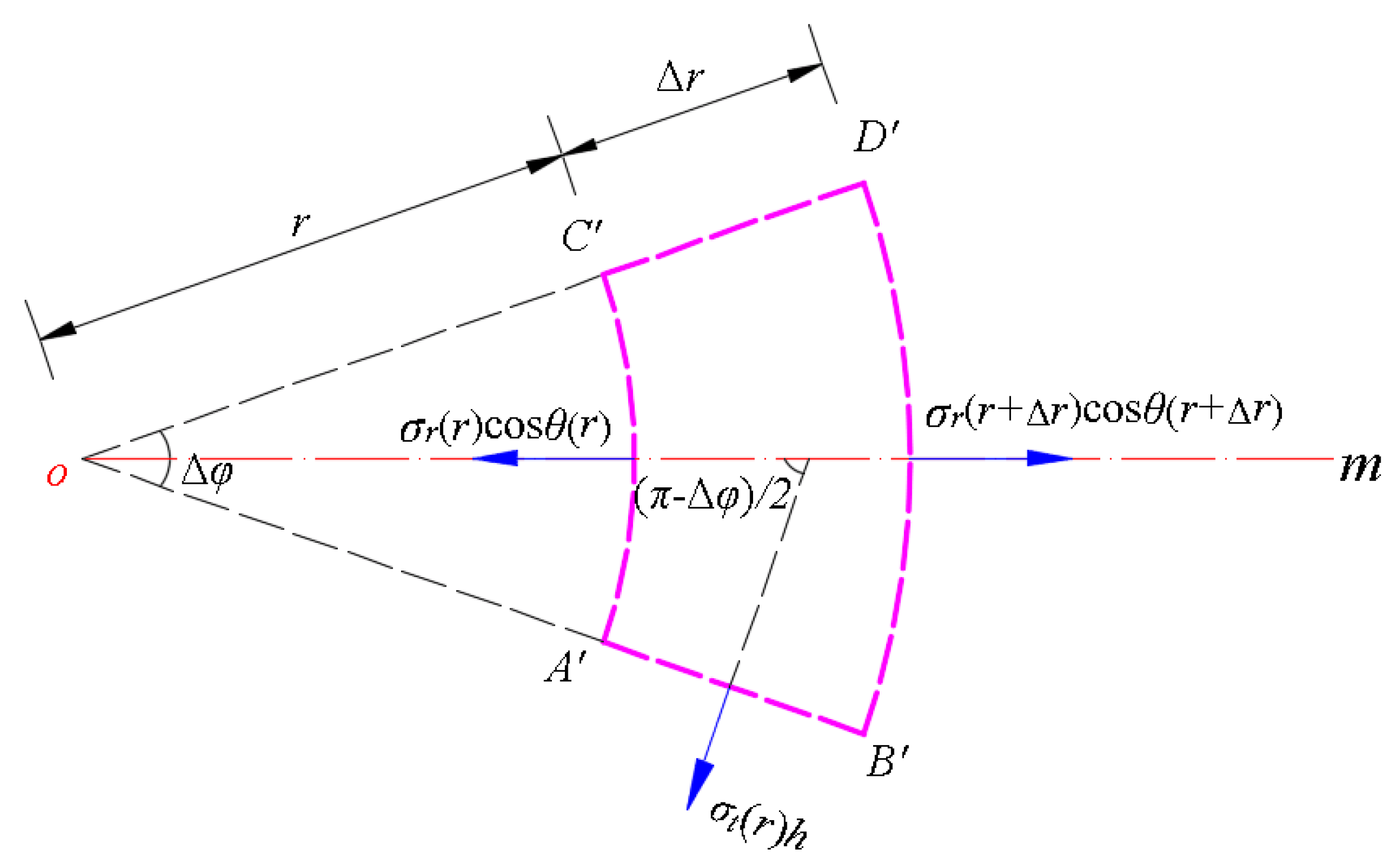
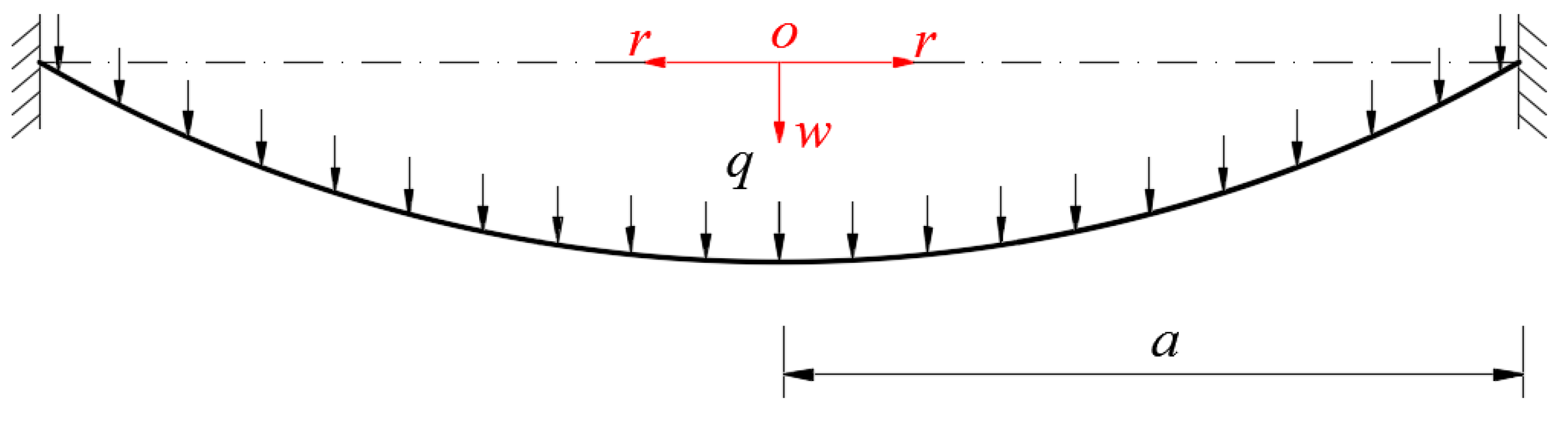
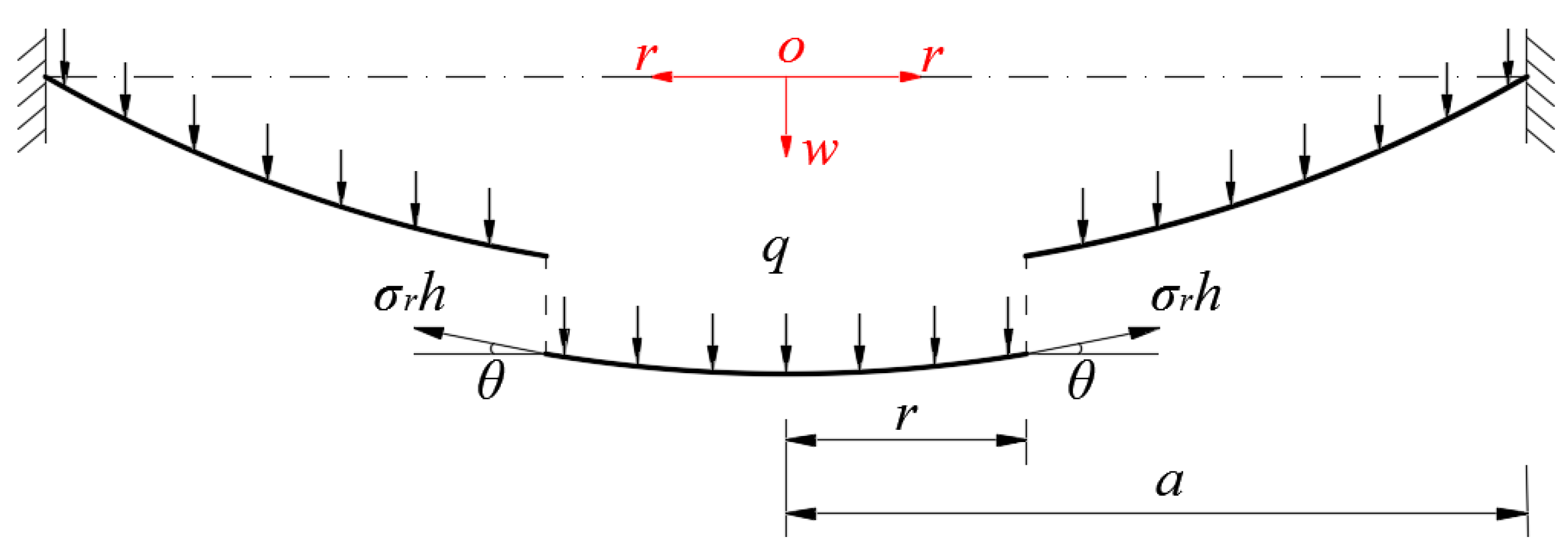
2. Membrane Equation and Its Solution

A rotationally symmetric, linearly elastic, initially-flat circular membrane with Poisson’s ratio $\nu$, Young’s modulus of elasticity $E$, radius $a$ and thickness $h$ is peripherally clamped. The uniformly distributed transverse loads $q$ is quasi-statically applied onto the surface of the membrane, as shown in Figure 1, where $r$ is the radial coordinate in a cylindrical coordinate system $(r,\phi ,w)$ (where the polar coordinate plane $(r,\phi )$ is located in the plane in which the geometric middle plane of the initially-flat circular unstretched membrane is located) and $w$ is the transverse coordinate of the cylindrical coordinate system as well as the transverse displacement of the membrane.

We take a piece of circular membrane with radius $0\le r\le a$ in the central portion of the deformed circular membrane to study the static equilibrium problem of this piece of the deformed circular membrane under the joint actions of the external loads $q$ within $r$ and the total force $2\pi r{\sigma }_{r}h$ produced by the membrane force ${\sigma }_{r}h$ acting on the boundary $r$, as shown in Figure 2, where ${\sigma }_r$ denotes the radial stress and $\theta$ denotes the slope angle of the deformed membrane. Clearly, there are two vertical forces, that is, the total force $\pi r^{2}q$ (in which $0\le r\le a$) of the external loads $q$ and the total vertical membrane force $2\pi r{\sigma }_{r}h\sin \theta$ that is produced by the membrane force ${\sigma }_{r}h$. The so-called out-of-plane equilibrium equation is

$$2\pi r{\sigma }_{r}h\sin \theta =\pi r^{2}q,$$

(1)

where

$$\sin \theta =1/\sqrt{1+1/{\tan }^2\theta }=1/\sqrt{1+1/{(-\mathrm{d}w/\mathrm{d}r)}^2}.$$

(2)

Substituting Equation (2) into Equation (1), one obtains

$$\frac{1}{2}rq\sqrt{1+1/{(\mathrm{d}w/\mathrm{d}r)}^2}={\sigma }_{r}h.$$

(3)

While in the horizontal plane which is parallel to the initially flat circular membrane, there are two horizontal forces, the circumferential membrane force ${\sigma }_{t}h$ and the horizontal component of the radial membrane force ${\sigma }_{r}h$, where ${\sigma }_t$ denotes the circumferential stress. The classic in-plane equilibrium equation, i.e., $\mathrm{d}(r{\sigma }_r)/\mathrm{d}r-{\sigma }_t=0$, is modified and replaced by

$$\frac{\mathrm{d}}{\mathrm{d}r}(r{\sigma }_r)-{\sigma }_t[1+{(-\frac{\mathrm{d}w}{\mathrm{d}r})}^2]=0.$$

(4)

The effect of deflection on the equilibrium between radial stress and circumferential stress is thus taken into account, and for brevity, the detailed derivation of Equation (4) is arranged in Appendix A. Suppose that we denote the radial strain by $e_r$, circumferential strain by $e_t$, radial displacement by $u(r)$, and the transversal displacement by $w(r)$. The relations between the strain and displacement for the large deflection problem, that is, the so-called geometric equations, may be written as

$$e_r=\frac{\mathrm{d}u}{\mathrm{d}r}+\frac{1}{2}{(\frac{\mathrm{d}w}{\mathrm{d}r})}^2$$

(5)

and

$$e_t=\frac{u}{r}.$$

(6)

Moreover, the relations of the stress and strain, that is, the so-called physical equations, are still assumed to satisfy linear elasticity and can be written as

$${\sigma }_r=\frac{E}{1-{\nu }^2}(e_r+\nu e_t)$$

(7)

and

$${\sigma }_t=\frac{E}{1-{\nu }^2}(e_t+\nu e_r).$$

(8)

Substituting Equations (5) and (6) into Equations (7) and (8) yields

$${\sigma }_r=\frac{E}{1-{\nu }^2}[\frac{\mathrm{d}u}{\mathrm{d}r}+\frac{1}{2}{(\frac{\mathrm{d}w}{\mathrm{d}r})}^2+\nu \frac{u}{r}]$$

(9)

and

$${\sigma }_t=\frac{E}{1-{\nu }^2}[\frac{u}{r}+\nu \frac{\mathrm{d}u}{\mathrm{d}r}+\frac{\nu }{2}{(\frac{\mathrm{d}w}{\mathrm{d}r})}^2].$$

(10)

By means of Equations (9) and (10), one has

$$\frac{u}{r}=\frac{1}{E}({\sigma }_t-\nu {\sigma }_r).$$

(11)

After substituting the u of Equation (11) into Equation (9), then the so-called consistency equation can be written as

$$(1+\nu )({\sigma }_t-{\sigma }_r)+r(\nu \frac{\mathrm{d}{\sigma }_r}{\mathrm{d}r}-\frac{\mathrm{d}{\sigma }_t}{\mathrm{d}r})+\frac{E}{2}{(\frac{\mathrm{d}w}{\mathrm{d}r})}^2=0.$$

(12)

Equations (3), (4) and (12) are three equations for the solutions of ${\sigma }_r$, ${\sigma }_t$ and $w(r)$. Then, the boundary conditions, under which Equations (3), (4) and (12) may be solved, are

$$\frac{\mathrm{d}w}{\mathrm{d}r}=0\mathrm{at}r=0,$$

(13)

$$u=\frac{r}{E}({\sigma }_t-\nu {\sigma }_r)=0\mathrm{at}r=a$$

(14)

and

$$w=0\mathrm{at}r=a.$$

(15)

Let us employ the following nondimensionalization

$$Q=\frac{aq}{hE},W=\frac{w}{a},S_r=\frac{{\sigma }_r}{E},S_t=\frac{{\sigma }_t}{E},x=\frac{r}{a},$$

(16)

and transform Equations (3), (4) and (12)–(15) into

$$(4S_r^2-x^2{Q}^2){(\frac{\mathrm{d}W}{\mathrm{d}x})}^2-x^2{Q}^2=0,$$

(17)

$$\frac{\mathrm{d}}{\mathrm{d}x}(x{S}_r)-S_t[1+{(\frac{\mathrm{d}W}{\mathrm{d}x})}^2]=0,$$

(18)

$$(1+\nu )(S_t-S_r)+x(\nu \frac{\mathrm{d}{S}_r}{\mathrm{d}x}-\frac{\mathrm{d}{S}_t}{\mathrm{d}x})+\frac{1}{2}{(\frac{\mathrm{d}W}{\mathrm{d}x})}^2=0,$$

(19)

$$\frac{\mathrm{d}W}{\mathrm{d}x}=0\mathrm{at}x=0,$$

(20)

$$S_t-\nu S_r=0\mathrm{at}x=1$$

(21)

and

$$W=0\mathrm{at}x=1.$$

(22)

In view of the physical phenomenon that the values of stress and deflection are both finite at $x=0$, $S_r(x)$, $W(x)$ and $S_t(x)$ can be expanded into the power series of the $x$, i.e., let

$$S_r(x)={\displaystyle \sum _{i=0}^{\infty }{b}_i{x}^i},$$

(23)

$$W(x)={\displaystyle \sum _{i=0}^{\infty }{c}_i{x}^i}$$

(24)

and

$$S_t(x)={\displaystyle \sum _{i=0}^{\infty }{d}_i{x}^i}.$$

(25)

After substituting Equations (23)–(25) into Equations (17)–(19), it is found that $b_i\equiv 0$, $c_i\equiv 0$ and $d_i\equiv 0$ (i = 1,3,5,…), while the coefficients $b_i$, $c_i$ and $d_i$ (i = 2,4,6,…) can be expressed into the polynomial with regard to the coefficients $b_0$ and $c_0$, besides $d_0\equiv b_0$ (see Appendix B).

The coefficients $b_0$ and $c_0$, as the undetermined constants depending on the concrete problem, can be determined by using the boundary conditions of Equations (21) and (22). Substituting Equations (23)–(25) into Equations (21) and (22) gives

$${\displaystyle \sum _{i=0}^{\infty }{d}_i}-\nu {\displaystyle \sum _{i=0}^{\infty }{b}_i}=0$$

(26)

and

$${\displaystyle \sum _{i=0}^{\infty }{c}_i}=0.$$

(27)

Please note that Equations (26) and (27) contain only the undetermined constants $b_0$ and $c_0$, because $d_0\equiv b_0$ and the coefficients $b_i$, $c_i$ and $d_i$ (i = 2,4,6,…) were expressed into the polynomial with regard to the coefficients $b_0$ and $c_0$ at this time. Therefore, for the problem in which the values of $a$, $h$, $E$, $\nu$ and $q$ are known beforehand, the undetermined constants $b_0$ and $c_0$ can be determined by simultaneous solutions of Equations (26) and (27), and furthermore, with the known $b_0$ and $c_0$ the other coefficients $b_i$, $c_i$, $d_i$ (i = 2,4,6,…) and $d_0$ can be easily determined. The problem dealt with here is thus solved.

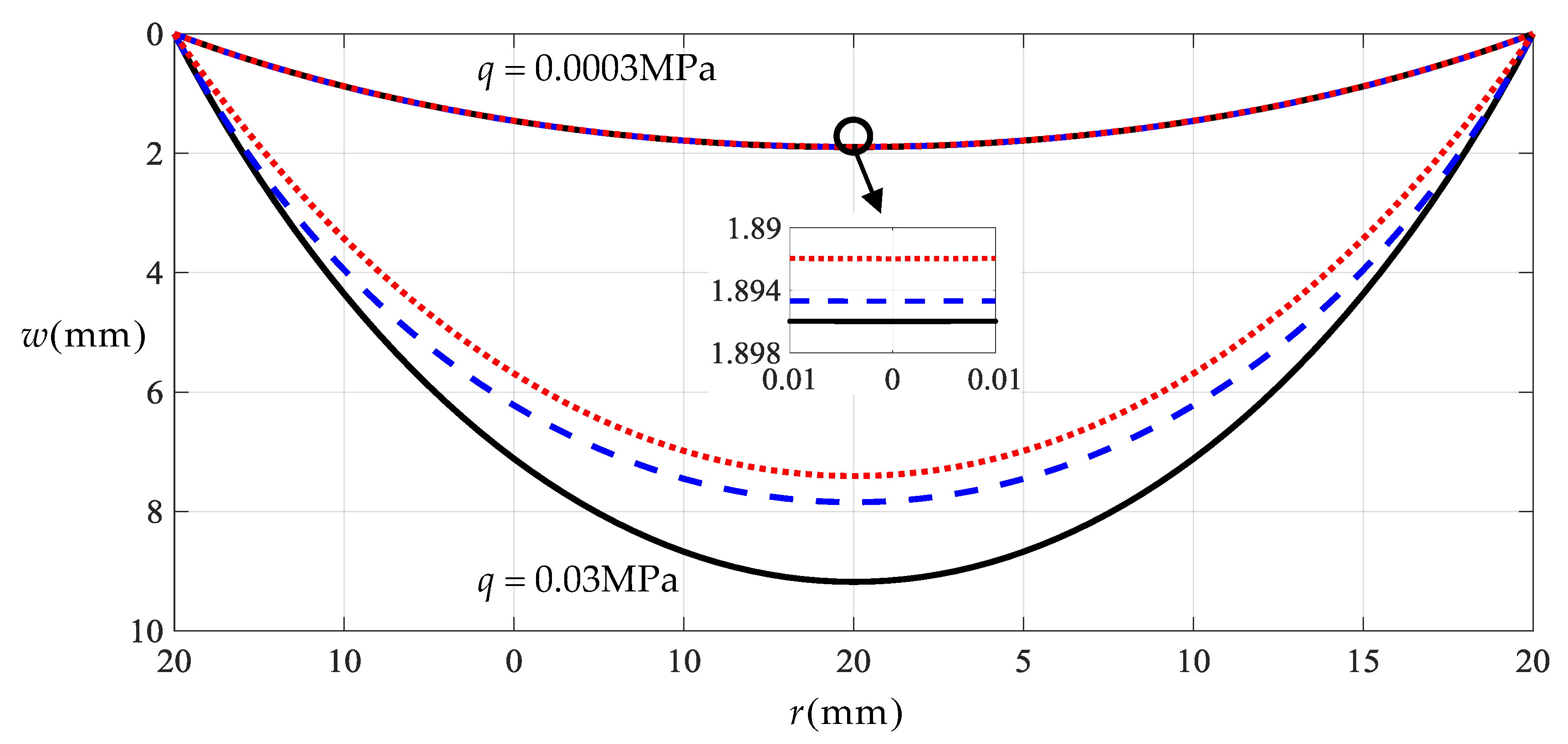
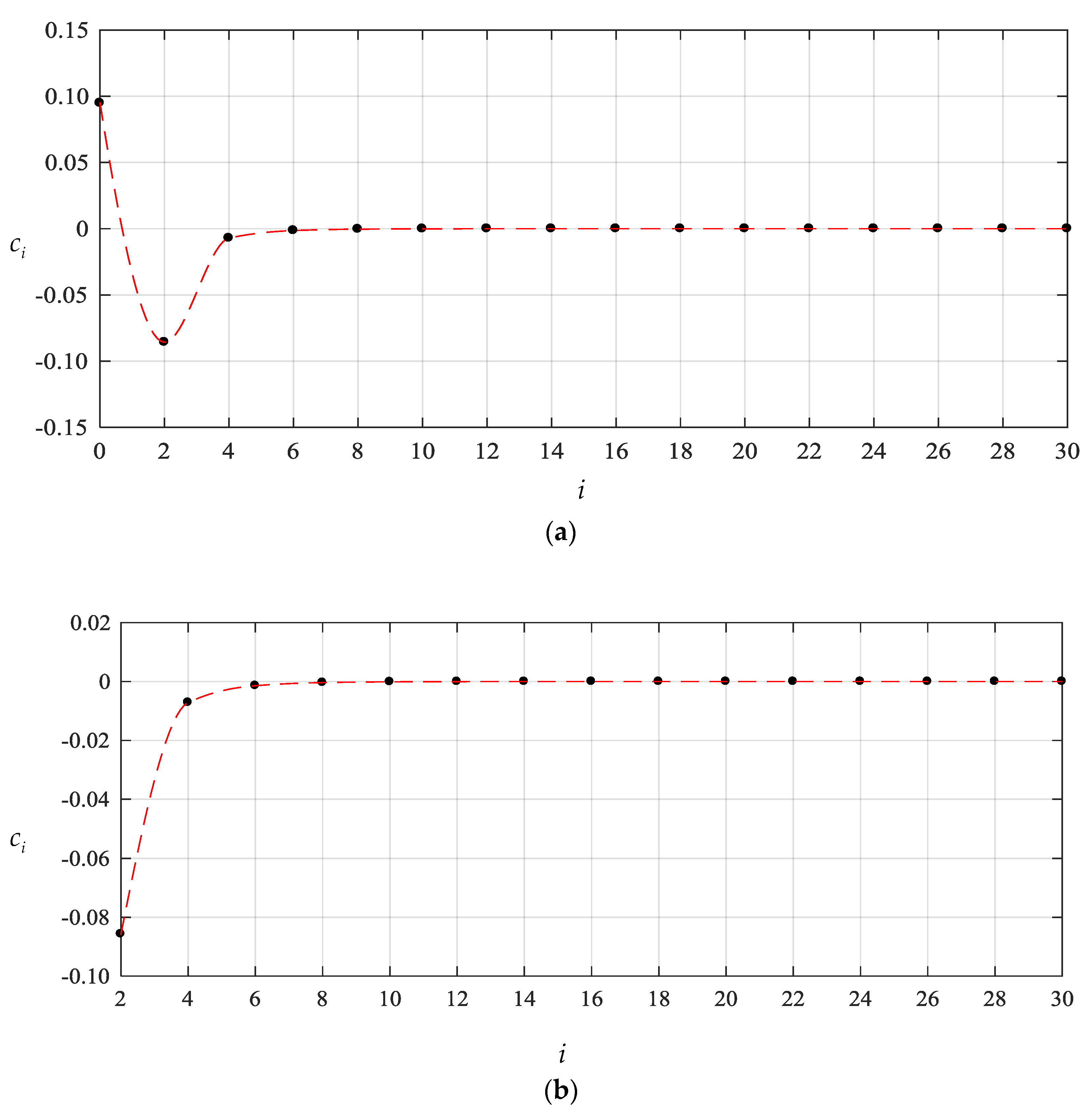
3. Results and Discussion

Let us firstly discuss the effectiveness of the solution obtained in Section 2. From the derivation of Section 2 of this paper and reference [21], we may see that only the in-plane equilibrium equation is modified to replace the classic in-plane equilibrium equation (i.e., $\mathrm{d}(r{\sigma }_r)/\mathrm{d}r-{\sigma }_t=0$). However, if we let $\mathrm{d}w/\mathrm{d}r=0$, then Equation (4) in this paper will become $\mathrm{d}(r{\sigma }_r)/\mathrm{d}r-{\sigma }_t=0$, i.e., the classic in-plane equilibrium equation which was adopted in reference [21]. This indicates that the solution presented here can regress into the solution presented in reference [21]. Furthermore, from the characteristic of axisymmetric deformation of the circular membrane, it is not difficult to understand that $\mathrm{d}w/\mathrm{d}r=0$ at $r=0$, i.e., the boundary condition Equation (13), which has not been used yet during the derivation in Section 2. Now, let us see whether the closed-form solution obtained in Section 2 meets the boundary condition of Equation (13), i.e., $\mathrm{d}w/\mathrm{d}r=0$ at $r=0$. From Equations (16) and (24) the dimensional form of the deflection $w(r)$ can be written as

$$w(r)={\displaystyle \sum _{i=0}^{\infty }\frac{c_i}{a^{i-1}}}{r}^i.$$

(28)

Then, the first derivative on both sides of Equation (28) is

$$\frac{\mathrm{d}w}{\mathrm{d}r}={\displaystyle \sum _{i=1}^{\infty }\frac{i{c}_i}{a^{i-1}}{r}^{i-1}}.$$

(29)

Therefore, it is obvious that $\mathrm{d}w/\mathrm{d}r\equiv 0$ at $r=0$ because $\mathrm{d}w/\mathrm{d}r=c_1$ at $r=0$ while $c_1\equiv 0$. This indicates that the closed-form solution obtained in Section 2 meets the physical phenomenon of axisymmetric deformation of the circular membrane. As a result, these two aspects discussed above, to some extent, reflect the effectiveness of the closed-form solution presented here.

Let us consider a circular rubber membrane with radius $a=20\mathrm{mm}$, thickness $h=0.2\mathrm{mm}$, Young’s modulus of elasticity $E=7.84\mathrm{MPa}$, Poisson’s ratio $\nu =0.47$ and under the action of transverse uniformly distributed loads $q$, as an example, to discuss the applicability of solution to the deflection of membrane. Figure 3 shows the variations of the deflection $w$ with the radius $r$ when $q$ takes 0.0003 MPa and 0.03 MPa, respectively, where the solid lines represent the results obtained by the solution presented in Section 2, the dashed lines represent the results obtained by the solution presented in [21], and the dotted lines represent the results obtained by well-known Hencky solution [19].

From Figure 3 it may be observed that the solid line is very close to the dashed line and dotted line when $q$ takes 0.0003 MPa. This also indicates that both the closed-form solution presented here and the one presented [21] are valid, if viewed from the perspective of the well-known Hencky solution. On the other hand, along with the increase of the transverse uniformly distributed loads $q$, the deflection of the deformed membrane will also increase. Therefore, when $q$ takes 0.03 MPa, from Figure 3, we may also see that the dashed line has a certain distance from the dotted line, while the solid line has a distinct distance from the dashed line. This indicates that the small rotation angle assumption adopted in the derivation of the well-known Hencky solution limits the applicability of the solution to the deflection of the membrane, the solution after giving up the small rotation angle assumption—that is, the solution presented in [21]—can be applied to the relatively large deflection, while compared with the solution presented in [21], the solution presented in this study can be applied to the larger deflection of the membrane. When $q$ takes 0.03 MPa, the maximum deflection is about 9.18 mm, 7.85 mm and 7.41 mm, respectively, which are calculated by the solution presented here, the solution presented in [21], and the well-known Hencky solution. The error between the maximum deflections calculated by the well-known Hencky solution and the one by the solution presented in [21] is about 5.94%, which is brought by the so-called small rotation angle assumption adopted in the derivation of the well-known Hencky solution. In particular, the error between the maximum deflection calculated by the solution presented in [21] and the one by the solution presented here is about 16.94%, which is brought about by the effect of the deflection ignored in the derivation of the classic in-plane equilibrium equation. It must be noted that such an error exceeds the allowable error of civil engineering, 15%, while the allowable error of instrument design is usually less than 3%, precision measurement usually less than 1%, including some characterizations of mechanical properties by bulge or blister test techniques [3,4,5,6,9,10].

The above discussions show that the applicability of the closed-form solution presented here to the deflection of membranes has been greatly improved, in comparison with the solution presented in [21] and the well-known Hencky solution. However, the convergence of the presented power series solution still needs to be discussed. The investigation into the convergence has to, perhaps, be arranged here, due to the fact that the coefficients $b_i$, $c_i$, $d_i$ (i = 2,4,6,…) are expressed into the somewhat intractable polynomial with regard to the coefficients $b_0$ and $c_0$ (see Appendix B) and thus there is no way to discuss the convergence of the general solutions for $S_r(x)$, $W(x)$ and $S_t(x)$. In other words, here we can prove only the convergence of the special solutions for $S_r(x)$, $W(x)$ and $S_t(x)$, rather than that of its general solutions, although the convergence of the general solutions, perhaps, receives the greatest attention because the special solution will converge as long as the general solution converges.

From the derivation in Section 2, we know that the general solutions for $S_r(x)$, $W(x)$ and $S_t(x)$ are the power series with regard to the nondimensional independent variable x (see Equations (23)–(25)), where the domain of the independent variable is $0\le x\le 1$ and all the coefficients $b_i$, $c_i$ and $d_i$ (i = 2,4,6,…) are expressed into the polynomial with regard to the coefficients $b_0$ and $c_0$, besides $b_i\equiv 0$, $c_i\equiv 0$, $d_i\equiv 0$ (i = 1,3,5,…) and $d_0\equiv b_0$. Moreover, we also know that the undetermined constants $b_0$ and $c_0$ should be determined by simultaneous solutions of Equations (26) and (27). It seems obvious that the special solution for $S_r(x)$, $W(x)$ and $S_t(x)$ can easily be obtained as long as the undetermined constants $b_0$ and $c_0$ can be determined. However, when solving a specific definite problem it may be found that we have to substitute the partial sum of former n terms of Equations (23)–(25), rather than Equations (23)–(25), into Equations (21) and (22), otherwise the resulting Equations (26) and (27) will contain three infinite series and thus will be difficult to solve. Therefore, it seems that the undetermined constants $b_0$ and $c_0$ determined by Equations (26) and (27) will depend on the value of terms n and different n will determine the different value of $b_0$ and $c_0$. Hence, the discussion on convergence should contain two aspects: the variation of $b_0$ and $c_0$ with terms n, and the variation of $b_i$ and $c_i$ with i for every value of terms n.

To this end, we start the numerical computation of $b_0$ and $c_0$ from $n=4$, that is, start from the partial sum of the former four terms of Equations (23)–(25), and recalculate the case of q = 0.0003 MPa of the above numerical example. The obtained different numerical values of $b_0$ and $c_0$, are listed in

Table 1. The values of b₀–b₆, b₈–b₁₄, b₁₆–b₂₂ and b₂₄–b₃₀.

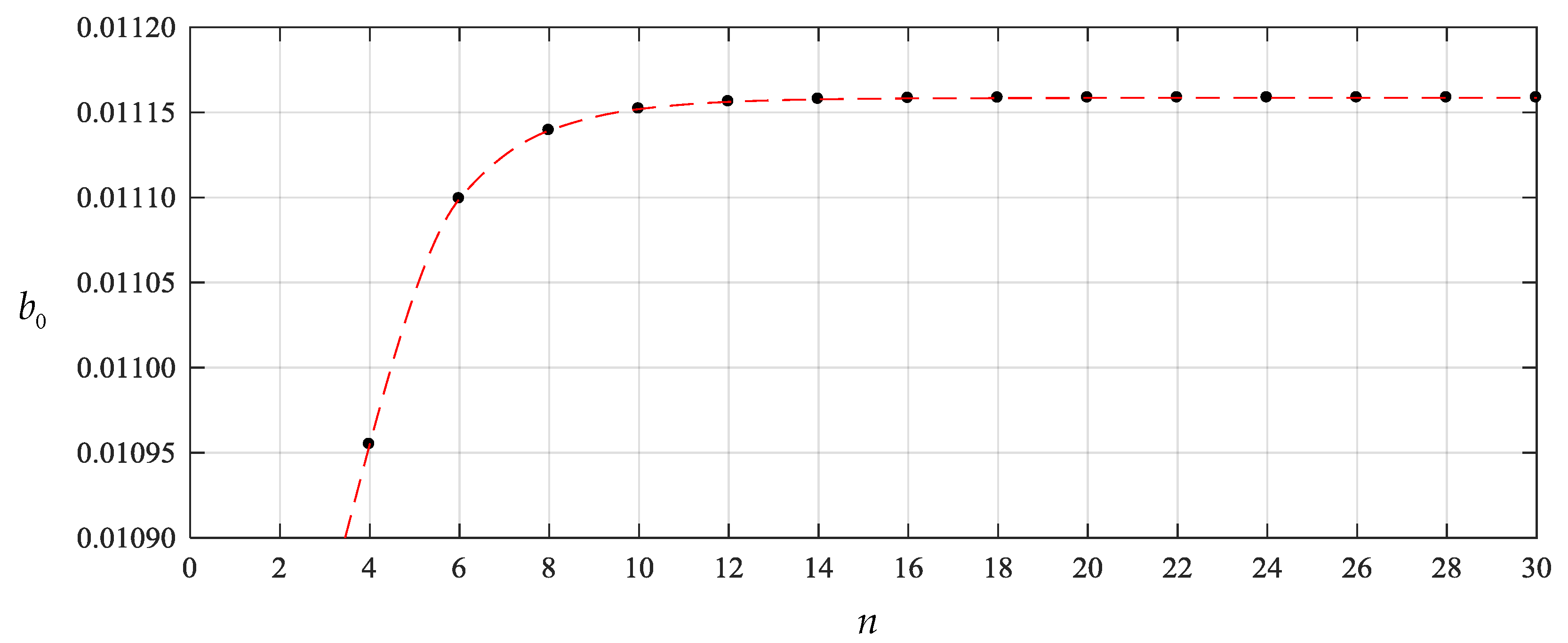
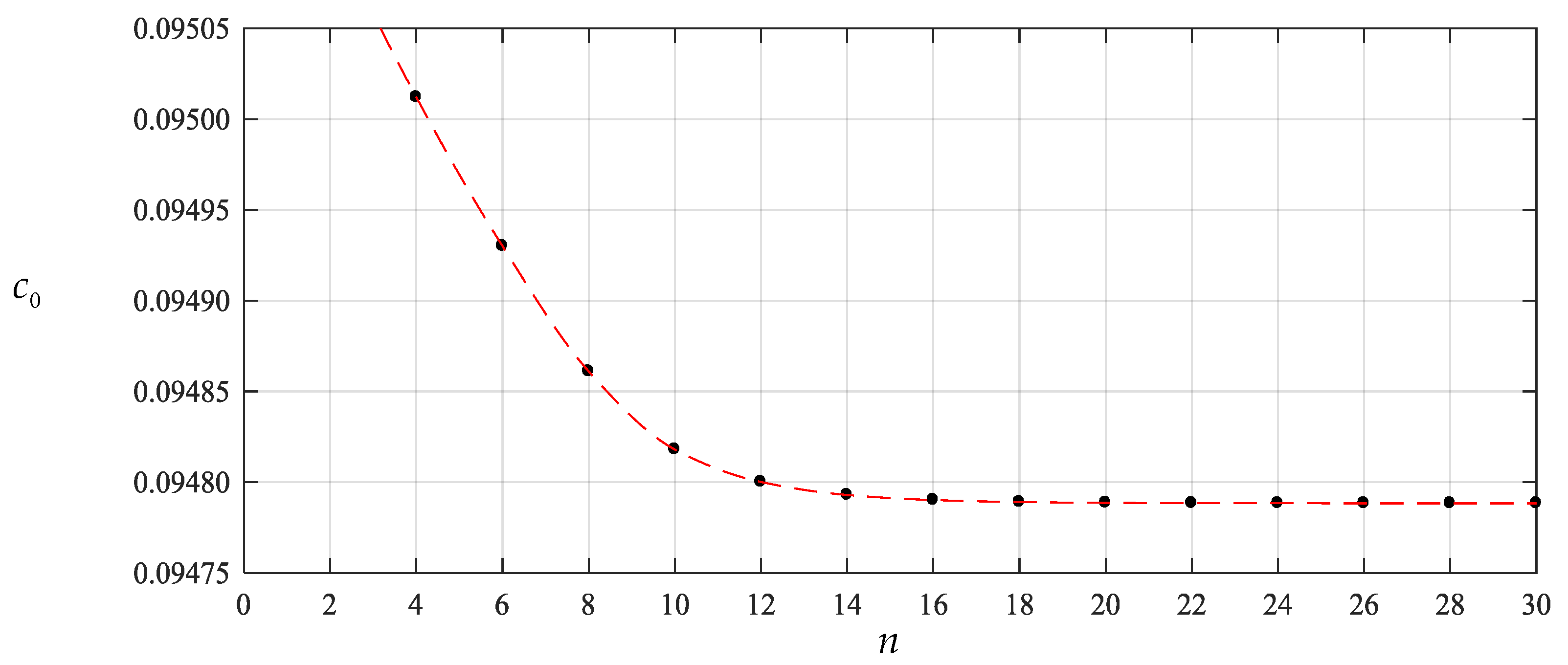
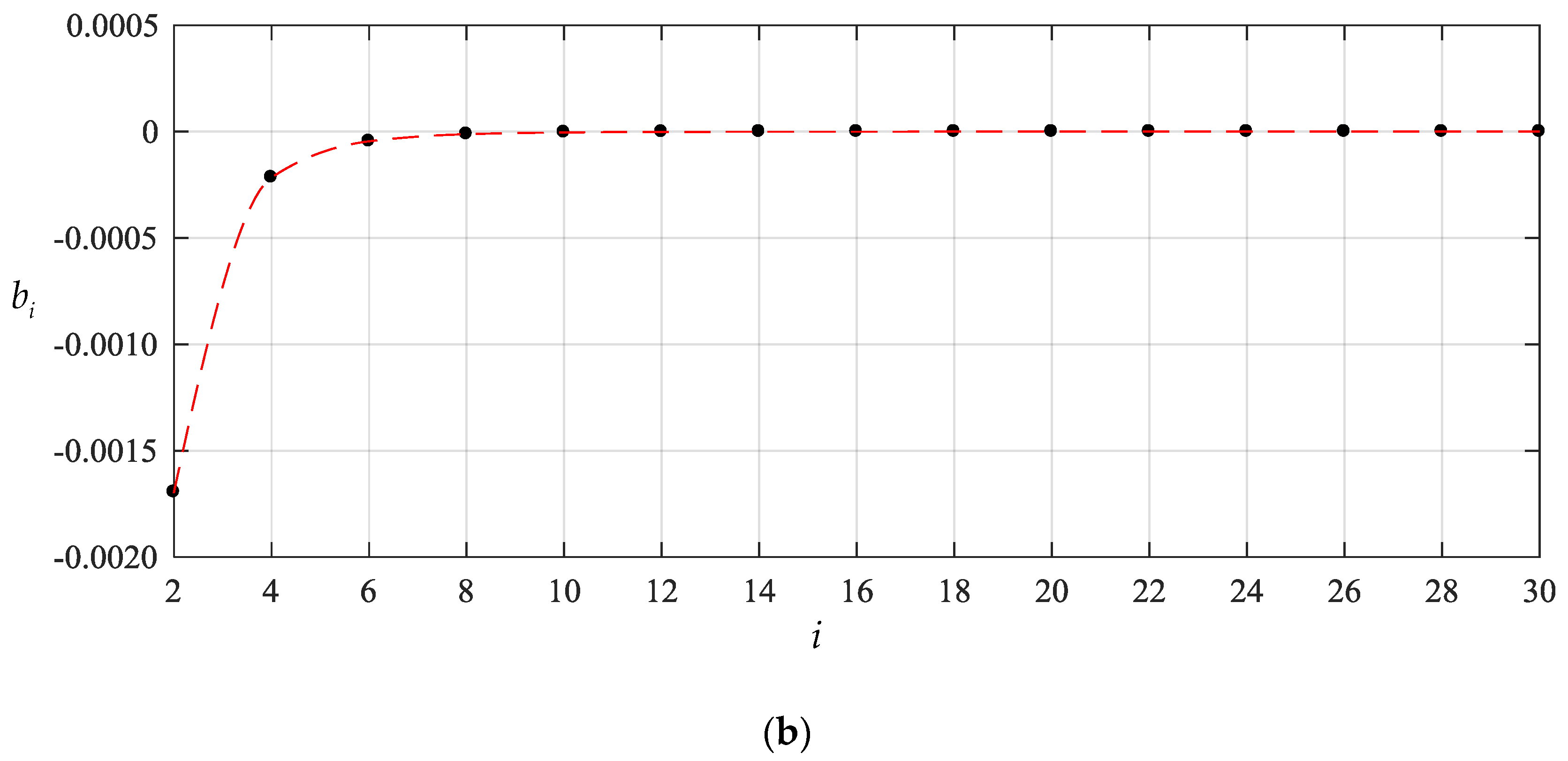
n	b0	b2	b4	b6
4	1.0954809 × 10−2	−1.7614908 × 10−3	−2.3599430 × 10−4	―
6	1.1099103 × 10−2	−1.7141283 × 10−3	−2.2121798 × 10−4	−4.7183462 × 10−5
8	1.1139261 × 10−2	−1.7012775 × 10−3	−2.1730552 × 10−4	−4.5871671 × 10−5
10	1.1151884 × 10−2	−1.6972670 × 10−3	−2.1609292 × 10−4	−4.5467874 × 10−5
12	1.1156122 × 10−2	−1.6959237 × 10−3	−2.1568767 × 10−4	−4.5333218 × 10−5
14	1.1157603 × 10−2	−1.6954547 × 10−3	−2.1554628 × 10−4	−4.5286270 × 10−5
16	1.1158134 × 10−2	−1.6952864 × 10−3	−2.1549554 × 10−4	−4.5269429 × 10−5
18	1.1158329 × 10−2	−1.6952247 × 10−3	−2.1547697 × 10−4	−4.5263264 × 10−5
20	1.1158401 × 10−2	−1.6952018 × 10−3	−2.1547007 × 10−4	−4.5260973 × 10−5
22	1.1158428 × 10−2	−1.6951932 × 10−3	−2.1546747 × 10−4	−4.5260111 × 10−5
24	1.1158439 × 10−2	−1.6951899 × 10−3	−2.1546648 × 10−4	−4.5259783 × 10−5
26	1.1158443 × 10−2	−1.6951887 × 10−3	−2.1546610 × 10−4	−4.5259657 × 10−5
28	1.1158444 × 10−2	−1.6951882 × 10−3	−2.1546596 × 10−4	−4.5259608 × 10−5
30	1.1158445 × 10−2	−1.6951880 × 10−3	−2.1546590 × 10−4	−4.5259590 × 10−5
n	b8	b10	b12	b14
8	−1.1940058 × 10−5	―	―	―
10	−1.1796657 × 10−5	−3.4390107 × 10−6	―	―
12	−1.1748940 × 10−5	−3.4213780 × 10−6	−1.0729630 × 10−6	―
14	−1.1732316 × 10−5	−3.4152393 × 10−6	−1.0706309 × 10−6	−3.5319449 × 10−7
16	−1.1726354 × 10−5	−3.4130384 × 10−6	−1.0697950 × 10−6	−3.5287054 × 10−7
18	−1.1724172 × 10−5	−3.4122330 × 10−6	−1.0694891 × 10−6	−3.5275200 × 10−7
20	−1.1723361 × 10−5	−3.4119336 × 10−6	−1.0693754 × 10−6	−3.5270795 × 10−7
22	−1.1723055 × 10−5	−3.4118209 × 10−6	−1.0693326 × 10−6	−3.5269137 × 10−7
24	−1.1722939 × 10−5	−3.4117781 × 10−6	−1.0693164 × 10−6	−3.5268507 × 10−7
26	−1.1722895 × 10−5	−3.4117617 × 10−6	−1.0693101 × 10−6	−3.5268266 × 10−7
28	−1.1722878 × 10−5	−3.4117553 × 10−6	−1.0693077 × 10−6	−3.5268172 × 10−7
30	−1.1722871 × 10−5	−3.4117529 × 10−6	−1.0693068 × 10−6	−3.5268136 × 10−7
n	b16	b18	b20	b22
16	−1.2079246 × 10−7	―	―	―
18	−1.2074584 × 10−7	−4.2508129 × 10−8	―	―
20	−1.2072852 × 10−7	−4.2501239 × 10−8	−1.5294069 × 10−8	―
22	−1.2072200 × 10−7	−4.2498646 × 10−8	−1.5293029 × 10−8	−5.6007703 × 10−9
24	−1.2071952 × 10−7	−4.2497661 × 10−8	−1.5292633 × 10−8	−5.6006106 × 10−9
26	−1.2071857 × 10−7	−4.2497283 × 10−8	−1.5292482 × 10−8	−5.6005494 × 10−9
28	−1.2071820 × 10−7	−4.2497137 × 10−8	−1.5292423 × 10−8	−5.6005256 × 10−9
30	−1.2071806 × 10−7	−4.2497080 × 10−8	−1.5292400 × 10−8	−5.6005165 × 10−9
n	b24	b26	b28	b30
24	−2.0808221 × 10−9	―	―	―
26	−2.0807972 × 10−9	−7.8239857 × 10−10	―	―
28	−2.0807875 × 10−9	−7.8239463 × 10−10	−2.9717720 × 10−10	―
30	−2.0807839 × 10−9	−7.8239312 × 10−10	−2.9717659 × 10−10	−1.1385721 × 10−10

and

Table 2. The values of c₀–c₆, c₈–c₁₄, c₁₆–c₂₂ and c₂₄–c₃₀.

n	c0	c2	c4	c6
4	9.5012072 × 10−2	−8.7325363 × 10−2	−7.6867089 × 10−3	―
6	9.4930058 × 10−2	−8.6190091 × 10−2	−7.2958154 × 10−3	−1.4651512 × 10−3
8	9.4861056 × 10−2	−8.5879367 × 10−2	−7.1914770 × 10−3	−1.4289971 × 10−3
10	9.4818023 × 10−2	−8.5782156 × 10−2	−7.1590654 × 10−3	−1.4178443 × 10−3
12	9.4800124 × 10−2	−8.5749571 × 10−2	−7.1482256 × 10−3	−1.4141226 × 10−3
14	9.4792979 × 10−2	−8.5738190 × 10−2	−7.1444425 × 10−3	−1.4128247 × 10−3
16	9.4790167 × 10−2	−8.5734105 × 10−2	−7.1430850 × 10−3	−1.4123591 × 10−3
18	9.4789066 × 10−2	−8.5732609 × 10−2	−7.1425880 × 10−3	−1.4121887 × 10−3
20	9.4788634 × 10−2	−8.5732053 × 10−2	−7.1424033 × 10−3	−1.4121253 × 10−3
22	9.4788465 × 10−2	−8.5731844 × 10−2	−7.1423338 × 10−3	−1.4121015 × 10−3
24	9.4788399 × 10−2	−8.5731765 × 10−2	−7.1423074 × 10−3	−1.4120924 × 10−3
26	9.4788373 × 10−2	−8.5731734 × 10−2	−7.1422972 × 10−3	−1.4120890 × 10−3
28	9.4788362 × 10−2	−8.5731722 × 10−2	−7.1422933 × 10−3	−1.4120876 × 10−3
30	9.4788358 × 10−2	−8.5731718 × 10−2	−7.1422918 × 10−3	−1.4120871 × 10−3
n	c8	c10	c12	c14
8	−3.6121541 × 10−4	―	―	―
10	−3.5721690 × 10−4	−1.0174043 × 10−4	―	―
12	−3.5588553 × 10−4	−1.0124963 × 10−4	−3.1069854 × 10−5	―
14	−3.5542159 × 10−4	−1.0107873 × 10−4	−3.1005500 × 10−5	−1.0015532 × 10−5
16	−3.5525519 × 10−4	−1.0101745 × 10−4	−3.0982432 × 10−5	−1.0006703 × 10−5
18	−3.5519429 × 10−4	−1.0099502 × 10−4	−3.0973990 × 10−5	−1.0003472 × 10−5
20	−3.5517166 × 10−4	−1.0098669 × 10−4	−3.0970852 × 10−5	−1.0002272 × 10−5
22	−3.5516314 × 10−4	−1.0098355 × 10−4	−3.0969672 × 10−5	−1.0001820 × 10−5
24	−3.5515990 × 10−4	−1.0098236 × 10−4	−3.0969223 × 10−5	−1.0001648 × 10−5
26	−3.5515866 × 10−4	−1.0098190 × 10−4	−3.0969051 × 10−5	−1.0001582 × 10−5
28	−3.5515818 × 10−4	−1.0098172 × 10−4	−3.0968984 × 10−5	−1.0001557 × 10−5
30	−3.5515799 × 10−4	−1.0098166 × 10−4	−3.0968959 × 10−5	−1.0001547 × 10−5
n	c16	c18	c20	c22
16	−3.3561200 × 10−6	―	―	―
18	−3.3548675 × 10−6	−1.1579367 × 10−6	―	―
20	−3.3544020 × 10−6	−1.1577544 × 10−6	−4.0875404 × 10−7	―
22	−3.3542269 × 10−6	−1.1576858 × 10−6	−4.0872695 × 10−7	−1.4697409 × 10−7
24	−3.3541603 × 10−6	−1.1576597 × 10−6	−4.0871665 × 10−7	−1.4696999 × 10−7
26	−3.3541348 × 10−6	−1.1576497 × 10−6	−4.0871270 × 10−7	−1.4696842 × 10−7
28	−3.3541249 × 10−6	−1.1576458 × 10−6	−4.0871116 × 10−7	−1.4696781 × 10−7
30	−3.3541211 × 10−6	−1.1576444 × 10−6	−4.0871058 × 10−7	−1.4696758 × 10−7
n	c24	c26	c28	c30
24	−5.3655393 × 10−8	―	―	―
26	−5.3654764 × 10−8	−1.9838915 × 10−8	―	―
28	−5.3654520 × 10−8	−1.9838817 × 10−8	−7.4153521 × 10−9	―
30	−5.3654427 × 10−8	−1.9838779 × 10−8	−7.4153369 × 10−9	−2.7977182 × 10−9

, also including the values of $b_i$ and $c_i$ corresponding to every value of $b_0$ and $c_0$. The variation of $b_0$ and $c_0$ with terms n are shown in Figure 4 and Figure 5 separately, and the variation of $b_i$ and $c_i$ with i are, only for $n=30$, shown in Figure 6 and Figure 7, respectively. From Figure 4 and Figure 5 or Table 1 and Table 2 we may see that the undetermined constants $b_0$ and $c_0$ converge reasonably well. From Figure 6 and Figure 7 or Table 1 and Table 2 we may also see that the coefficients $b_i$ and $c_i$ converge reasonably well, which indicates that the power series solutions $S_r(x)$ and $W(x)$ converge reasonably well because of $0\le x\le 1$. Furthermore, from Figure 4 and Figure 5 we may see that the undetermined constants $b_0$ and $c_0$ are already very close to their exact values when $n=18$. So, only the coefficients $b_i$, $c_i$ and $d_i$ (i = 2,4,6,…,18), which are expressed into the polynomial with regard to $b_0$ and $c_0$, are shown in Appendix B.

4. Concluding Remarks

In this paper, the well-known Hencky problem was re-solved by simultaneously considering the improvement of the out-of-plane and in-plane equilibrium equations. From this study, the following conclusions can be drawn.

The well-known Hencky solution applies only to the case where the deflection of the membrane is relatively small.

Compared with the well-known Hencky solution, the solution after improving the out-of-plane equilibrium equation can be applied to the case where the deflection of the membrane is relatively large.

However, compared with the well-known Hencky solution and the solution that only the out-of-plane equilibrium equation is improved, the solution that the out-of-plane and in-plane equilibrium equations are simultaneously improved can be applied to the larger deflection of the membrane.

The large deflection phenomenon of the membrane is possible in many fields of engineering or technical application, for example, the delamination studies for the characterization of the surface and interfacial or thin-film/substrate mechanical properties by a so-called pressurized blister test, where the maximum deflection of the blistering thin film may reach half the radius of the circular blistering thin film, or even larger. Clearly, such a large deflection is not applicable to the solutions in existing literature. Therefore, in this sense, the work presented here should be of positive significance to these fields of technical applications.