Abstract
Resources planning is an important task in a supply chain in order to achieve a good result. The better the utilization of resources, especially scarce resources, the better the performance of a supply chain. This research focuses on allocating two scarce resources, i.e., berth and quay cranes (QCs), to ships that call at a container terminal in a maritime supply chain. As global container shipments continue to grow, improving the efficiency of container terminals is important. A two-stage approach is used to find the optimal/near-optimal solution, in which the first stage is devoted to generating alternative ship placement sequences as inputs to the second stage that subsequently employs an event-based heuristic to place ships, resolve overlaps of ships, and assign/adjust QCs so as to develop a feasible solution. For identifying a better approach, various heuristics/metaheuristics, including first-come first-served (FCFS), particle swarm optimization (PSO), improved PSO (PSO2), and multiple PSO (MPSO), have been employed in the first stage, respectively. The experimental results show that combining the MPSO with the event-based heuristic leads to a better result.
1. Introduction
A supply chain consists of a series of steps to deliver products or services to end customers. These steps include activities of storing, moving and transforming raw materials into finished products that are further transported and distributed to end users. Relevant entities in a supply chain include producers, vendors, warehouses, transportation companies, distribution centers, container terminals, customs, retailers, etc. This research focuses upon the transportation activity in a container terminal of a maritime supply chain.
Transportation is one of the major activities in a supply chain. Materials and products can be transported via air, water or land. This research is specifically focused on transportation by sea, i.e., maritime transport. This kind of transport is important for international trading due to a relatively lower unit transportation cost resulting from a larger volume of delivery at one time. Maritime transportation is important for many countries, especially island countries. Among various kinds of maritime transportation, container transport is found to be especially important as global container shipments continue to grow and this kind of transport has been the mainstream transport in a maritime supply chain. However, container transport depends on container terminals which are the main working fields for loading/unloading containers to/from container ships. To achieve an efficient maritime supply chain, improving the operational efficiency of a container terminal is necessary and important [1].
A container terminal includes three main areas: seaside, yard and landside [2]. The seaside operations are considered to be the most critical as they relate to berth and quay crane (QC), two scarce resources affecting the performance of a container terminal considerably. The seaside operational area includes three well-known operational problems, namely the berth allocation problem (BAP), quay crane assignment problem (QCAP) and quay crane scheduling problem (QCSP) [3,4,5], which are faced by container terminal planners every day. To achieve a good performance for a container terminal, better resolution of these seaside operational problems is necessary [5]. This subject has thus been focused upon in this research.
Specifically, the research focuses on dealing with BAP and QCAP simultaneously. The BAP is a problem of planning how to best use berths whereas the QCAP is the problem of planning how to best use QCs. The two kinds of resources are essential for ships calling in to a container terminal. However, it is found that the two problems have different variants that should be firstly understood before solving them. Basically, the BAP can have the four variants: static and discrete BAP (SDBAP), static and continuous BAP (SCBAP), dynamic and discrete BAP (DDBAP), and dynamic and continuous BAP (DCBAP). The “static” means to consider arrived ships only whereas the “dynamic” means to also take incoming ships into account. The “discrete” means to use a quay as a number of fixed sections each of which can accommodate one ship at a time, whereas the “continuous” means to use a quay as a continuous line that can accommodate as many ships as possible at one time. On the other hand, the QCAP can have four variants: time-invariant QCAP (specific), time-invariant QCAP (number), variable-in-time QCAP (specific), variable-in-time QCAP (number). The “time-invariant” means no change on assigned QCs to a ship whereas the “variable-in-time” means that further changes on assigned QCs to a ship are allowed. The “specific” means the need to specify the identity of an assigned QC whereas the “number” means that only the number of QCs assigned is specified. This research focuses on the DCBAP and variable-in-time QCAP (number) simultaneously. These variants of BAP and QCAP are further detailed in the Section 2.1.1 and Section 2.1.2, respectively.
Some approaches are available for resources planning, including mathematical models, heuristics and metaheuristics. As a kind of exact approach, mathematical models aim to find the optimal solution. However, they tend to become computationally intractable when dealing with a large problem, due to Non Polynomial (NP)-complete [6,7,8]. Thus, heuristics/metaheuristics have become alternatives. Simple heuristics are popular in industry due to their simplicity and computational efficiency. In particular, first-come first-served (FCFS) is one of the most popularly used simple heuristics. However, simple heuristics are found incapable of finding the optimal/near optimal solution due to their simplicity and only one visit into the solution space. Advanced heuristics, such as the metaheuristics, have thus been increasingly used to deal with various problems, including container terminal operational problems. Essentially, metaheuristics are kind of high-level procedures or heuristics that can find, generate, or select a heuristic to find an optimal/near-optimal solution, based on incomplete or imperfect information or limited computational capacity [9]. In terms of advantage, metaheuristics can address the simplicity problem of simple heuristics while avoiding the computationally intractable problem of exact approaches. To deal with seaside operational problems, metaheuristics such as ant colony optimization [10], genetic algorithms (GAs) [8,11,12,13,14,15,16,17], particle swarm optimization (PSO) [18,19] have been used, in which GAs have been the mainstream approach [20]. However, particle swarm optimization has never been used to deal with the DCBAP and variable-in-time QCAP (number) simultaneously.
Proposed by Kennedy and Eberhart in 1995 [21], PSO is a kind of evolutionary and population-based metaheuristic as it employs a swarm of particles to search a solution space iteratively. The PSOs are found with the advantages of ease to implement and tune due to fewer parameters [22]. This approach has been mostly used to deal with combinative optimization problems (COPs) [23], such as assignment problems [24], scheduling problems [1,25,26,27,28,29], and BAP and QCAP [5]. However, [5] focused on the DCBAP, instead of the dynamic and continuous BAP (DCBAP).
The objective of this research was to propose a PSO-based approach for dealing with the DCBAP and variable-in-time QCAP (number) simultaneously. In this research, a two-stage procedure is used in which the first stage uses a heuristic/metaheuristic to generate alternative ship placement sequences as inputs to the second stage. Subsequently, the second stage employs an event-based heuristic to place ships, adjust QCs, and resolve overlaps of ships one by one in order to develop feasible solutions. The QCs released from a leaving ship are reassigned to berthed ships to best utilize QC capacity. To find the best approach, different methods including FCFS, PSO, PSO2, and multiple PSO (MPSO) have been respectively used in the first stage to investigate the best combination with the event-based heuristic used in the second stage. Our experimental results showed that the combination of MPSO with the event-based heuristic has the best result in terms of total cost.
The rest of this research is organized as follows. Section 2 includes a literature review of the continuous BAP (CBAP) and the simultaneous CBAP and QCAP. Section 3 formulates an integer programming (IP) model for the two problems. Section 4 introduces the basic formulas of PSO and develops the MPSO. Section 5 conducts some experiments. Section 6 has a conclusion and suggestion for a future research direction.
2. Literature Review
2.1. The Classification of Berth Allocation Problem (BAP) and Quay Crane Assignment Problem (QCAP)
2.1.1. BAP Classification
Figure 1 shows that the “arrival time of ship” and the “configuration of quay” are two factors characterizing the BAP into four variants: static and discrete BAP (SDBAP), static and continuous BAP (SCBAP), dynamic and discrete BAP (DDBAP), and dynamic and continuous BAP (DCBAP) [5]. The static BAP only considers arrived ships whereas the dynamic version also takes incoming ships into consideration. The quay configuration is the factor featuring the BAP as a discrete or continuous version. The discrete version separates a quay into a fixed number of sections, each only accommodating one ship at a time; whereas the continuous version uses the quay as a continuous line to accommodate as many ships as possible at one time. This research focuses on the DCBAP.
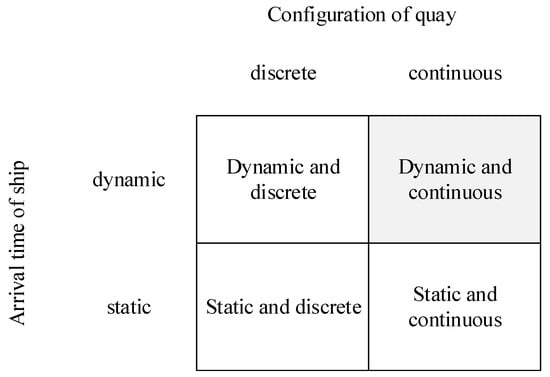
Figure 1.
The berth allocation problem (BAP) variants.
2.1.2. QCAP Classification
Figure 2 shows that the “QC identification” and “QC adjustment” are two factors characterizing the QCAP into four variants: time-invariant QCAP (specific), time-invariant QCAP (number), variable-in-time QCAP (number), and variable-in-time QCAP (specific). The factor “QC identification” means whether to identify each QC assigned to a ship. If “yes,” the QCAP is attributed as QCAP (specific); otherwise, it is attributed as QCAP (number) [27]. The factor “QC adjustment” means whether to allow further adjustment on assigned QCs to a ship. If yes, this QCAP is termed as variable-in-time QCAP; otherwise, it is termed as time-invariant QCAP [1]. Figure 3a shows a variable-in-time QC assignment in which the assigned number of QCs to the ship k has been changed from 1 to 3; whereas Figure 3b shows a time-invariant QC assignment with 1fixed QC assigned to the ship k. Obviously, the ship k can be completed earlier due to a variable-in-time QC adjustment.
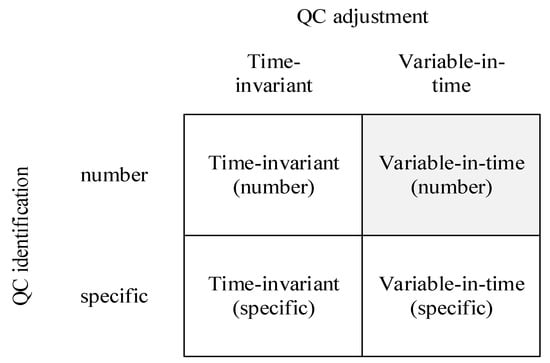
Figure 2.
The quay crane assignment problem (QCAP) variants.
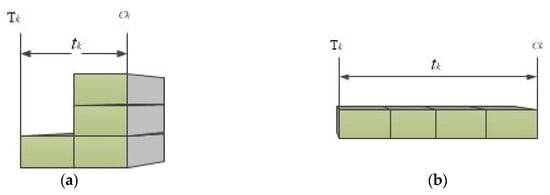
Figure 3.
(a) Variable-in-time quay crane (QC) assignment; (b) time-invariant QC assignment.
2.2. Relevant Studies
Some studies have focused on the BAP only. Lim [30] regarded the CBAP as a 2D cutting stock problem and proposed a heuristic to solve this problem. That heuristic aims to minimize the total length required in a wharf to accommodate all calling ships. However, it assumed fixed times for calling ships. Kim and Moon [6] used a simulated annealing (SA) metaheuristic to assign wharf space for calling ships with constraints taking into consideration. They concluded the SA could find the optimal solution. However, this study also assumed fixed handling times for ships. Wang and Lim [17] used a stochastic beam search to solve the CBAP. The authors claimed that the approach was able to outperform some state-of-the-art metaheuristics and the traditional deterministic beam search in terms of accuracy and efficiency. Lee and Chen [31] solved the dynamic and discrete BAP by using a neighborhood-search optimization heuristic, taking factors including FCFS rule, clearance distance between ships, and possible ship shifting into consideration. They claimed considering these factors could lead to a better decision. Zhen et al. [32] developed another two-stage model to deal with the CBAP, in which arrival and handling times of ships were treated as uncertainties. An initial schedule was generated and then adjusted in the second stage with the objective to minimize the total penalty cost deviating from the initial schedule. In addition, the authors proposed a metaheuristic to deal with a big problem. Hsu [9] proposed an improved shuffled frog-leaping algorithm (ISFLA) to deal with the DCBAP. The results showed the ISFLA outperformed the FCFS and the basic SFLA in terms of solution quality. Reference [18] focused on the DDBAP, which assigns ships to discrete berth positions and minimizes the total waiting times and handling times for all ships. A mixed integer programming (MIP) model was firstly formulated for the DDBAP. However, due to NP-hard, the authors further proposed a PSO-based approach to deal with this problem. Reference [19] focused on solving the continuous BAP (BAPC) by proposing a PSO. The PSO had been compared with GA. The results showed that the PSO works better in terms of accuracy and computational time.
However, the above studies are found only to have focused on the BAP, in which the handling times of ships are assumed. These studies neglected the fact that the handling times of a ship are mainly determined by the number of QCs assigned to the ship. It is better to solve the BAP and QCAP at the same time in order to achieve a better overall performance because of considering their interrelationship.
An increasing number of studies have considered both BAP and QCAP simultaneously and they are reviewed as follows. Park and Kim [7] formulated the two problems as an IP model. Then, they solved the two problems with a two-phase procedure. The first phase uses a sub-gradient technique to assign berthing position, berthing time, and QCs for a ship. The second phase uses a dynamic programming technique to identify the QCs assigned to each ship. However, that study did not consider QC interference on handling time. The Imai et al. [33] also proposed a two-stage approach to solve the two problems. The first stage focused on generating an initial plan that is further adjusted in the second stage to become a feasible solution. Sparsely-located or overlapped ships were repositioned in the second stage. However, this study also neglected QC interference on handling time. In Meisel and Biewirth [34] the authors proposed the consideration of QC interference on handling time. A decreasing QC marginal productivity had been considered when solving the simultaneous CBAP and QCAP. The author also used a two-stage procedure. The first stage used the hybrid approach, which combined squeaky wheel optimization (SWO) with Tabu search, to generate alternative ship assignment sequences as inputs to the second stage. Then, in the second stage another heuristic was used to assign berthing location and QCs for calling ships. The proposed approach was found to outperform that proposed by Park and Kim [7] in terms of cost. The authors demonstrated the impacts of QC interference on the total cost. Chang et al. [10] proposed a hybrid parallel GA (HPGA) to solve the CBAP together with the QCAP, taking factors including energy consumption and rolling horizon into consideration. The solutions found were further evaluated by a simulation model. The experiments confirmed the derived results were better than those obtained from the approach proposed in Chang et al. [35]. Zhang et al. [36] formulated the CBAP and QCAP as an MIP model. Then, they proposed a sub-gradient optimization algorithm to solve the two problems, taking factors including QC cover range and limited QC adjustments into consideration. The handling time of a ship was determined by the number of QCs assigned. However, that study also neglected the QC interference. Raa et al. [4] proposed an enriched MILP model for the simultaneous BAP and QCAP, taking factors including vessel priorities, preferred berthing locations and handling times into consideration. The objective was to minimize total penalty cost consisting of sub-costs of handling delay, deviation from the desired berth location, and the QC changes. Their experimental results showed that the proposed model resulted in a better decision. Yang et al. [37] proposed an integrated MIP to deal with the BAP and QCAP simultaneously. The objective was to minimize service time and total number of QC shifts. A nested loop-based evolutionary algorithm (NLEA) which includes two inner loops and one outer loop was proposed. The inner loop 1 uses a GA to find a BAP solution while loop 2 employs a heuristic-based GA to find a QCAP solution. The outer loop was mainly used to explore alternative solutions. Türkoğvllari et al. [38] separated a QCAP as a type of either “number” or “specific”. A MIP was firstly developed to deal with the combination of BAP and QCAP (number), abbreviated as BACAP. However, at most that MIP can handle 60 ships to optimality and it cannot deal with the combination of BAP and QCAP (specific), abbreviated as BACASP. To deal with the BACASP, the authors proposed using a post-processing algorithm with the optimal solution from the BACAP as an input. However, this algorithm requires a sufficient condition. If not satisfied, a cutting plane algorithm was proposed to cut plane(s) to reach that condition. However, these approach are still unable to perform variable-in-time QC assignment.
Our literature review shows that the assigned number of QCs, berthing location, and QC interference are factors affecting the handling time of a ship, and thus these factors should be considered when dealing with the simultaneous DCBAP and DQCAP (number).
3. Formulation of a Mathematical Model for Simultaneous DCBAP and QCAP
3.1. Problem Definition
Definition 1.
The problemPis defined as a simultaneous dynamic and continuous berth allocation problem (DCBAP) and variable-in-time quay crane assignment problem (QCAP) (number) with the aim of finding a feasible berth plan that includes six-tuples:
L: the length of a quay;
T: the planning horizon H = {1,…,H}, where H is the total number of time segments;
V: a finite set of calling vessels; V , where N is the total number of calling ships;
Ç: a finite set of berthing constraints;
Þ: a set of plans with assignments of berthing positions, start berthing times and numbers of QCs assigned for ships at each time interval; , where are decision variables. The is the berthing position on L assigned to the ship k under the constraint, , where is the length of ship k. The is the start berthing time assigned to the ship j under the constraint, (estimated arrival time of ship k). The is the number of QCs assigned to the ship k at the time segment t, ;
Z: an objective function mapping to a time/cot value Z;
The objective of the problem P is to find a or () that minimizes the objective function value Z, in which is a feasible solution, while is the optimal solution subjecting to Ç. For each ship k a berthing position is assigned. The problem P is an NP-hard problem.
3.2. The Estimation of Handling Time for a Ship
Estimating the handling time for a ship is essential to create a berthing plan. Meisel and Bierwirth [32] proposed Equation (1) to estimate the minimum handling time for a ship, taking berth deviation, QC interference, and QC capacity into consideration.
where
| the QC capacity required for the ship k | |
| the maximum number of QCs assignable to ship k | |
| the berth deviation of a ship k from its desired berthing position | |
| the berth deviation factor | |
| the interference exponent of QCs |
In this research, we define the berth deviation () as Equation (2),
where
- is the actual berthing position of ship k
- is the desired berthing position of the ship k
and, we define the QC capacity required for the ship k () as Equation (3).
where
: the total number of loading and unloading containers for ship k
: the working rate of a QC (QCs/hour)
Now, we transform Equation (1) to Equation (4) that is used in this research for estimating the minimum handling time required for a ship k at the time period j. Here, is a decision variable indicating the number of QCs assigned to ship k at the time period j.
where
| the total number of containers to be handled for the ship k | |
| the number of QCs assigned to the ship k | |
| the berth deviation | |
| the berth deviation factor |
The completion time of the ship k can be estimated by Equation (5),
where is the start berthing time of the ship k.
3.3. Berthing Plan
For a traditional 2D berthing plan, it lacks a dimension to represent the number of QCs assigned to a ship. Thus, this research uses a 3D berthing plan (Figure 4) with the X axis representing the time dimension; the Y axis representing the space dimension; and the Z representing the number of QC assigned to a ship. Then, each 3D object represents a ship occupying some grid squares on the X−Y plane with each square being only assigned to one ship, or it will lead to an infeasible plan.
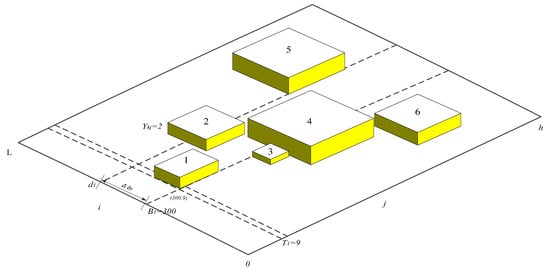
Figure 4.
A three-dimensional (3D) berthing plan.
The formation of a 3D berthing plan requires two tasks. The first task is the assignment of a coordinate on the X−Y plane for the lower-left hand corner of a ship (a 3D object). This coordinate indicates berthing time and the berthing position for the ship. The second task is the assignment of a number of QCs to the ship. Note that when performing the two tasks spatial constraints such as the quay length and the length of a ship should be considered to avoid forming an infeasible solution.
3.4. Mathematical Model
This section formulates a mathematical model for the simultaneous DCBAP and variable-in-time DQCAP (number). Before formulating this model, we first introduce the assumptions, parameters, indices, and decision variables required.
Assumptions
- Each ship is handled continuously until it is completed.
- Inter-ship clearance distance is included in ship length.
- A ship departs immediately when handling completed.
Indices
| i | a berth position; i . |
| j | a time segment; j . |
| k | a ship number; k . |
| q, | QC number; q, . |
Parameters
| L H T N Q C1 C2 | the quay length (meters) the total number of segments (each is one hour) within the planning horizon the set of time periods, T = {1,…,H} the total number of calling ships within the planning horizon the total number of QCs the length of ship k the minimum number of QC assignable to ship k the maximum number of QC assignable to ship k the expected arrival time of ship k the total number of loading and unloading containers for ship k at this port the desired berthing position of ship k the interference exponent of QCs (0 the berth deviation factor; the increase rate of QC capacity/one berth deviation ( the cost rate of handling time (Twenty foot equivalent units (TEUs)/hour) the cost rate of waiting time |
Decision variables
| the number of QCs assigned to ship k at the time period j | |
| the berthing position of ship k ( | |
| the beginning berthing time of ship k ( |
The mathematical model for the simultaneous DCBAP and DQCAP (number) is formulated as follows. It is a kind of mixed integer linear programing (MILP) model.
Equation (6) is the objective function minimizing the total cost (Z) composed of increased costs of handling and waiting for all ships, where is the increased waiting cost of ship k and is the increased handling time of ship k. Constraint (7) stipulates that a grid square can only be assigned to one ship or not assigned. Constraint (8) stipulates that the number of QCs assigned to a ship in a time period cannot exceed maximum number of available QCs. Constraint (9) stipulates the number of QCs assigned to a ship is limited to the range []. Constraint (10) prevents a ship from berthing over the quay boundary. Equation (11) indicates the berthing position of a ship k to be the minimum one of among {, where . Equation (12) requires that the berthing time of a ship k cannot be before its ETA. Equation (13) indicates the start berthing time of a ship k to be the minimum one of among , where . Equation (14) are binary constraints for decision variables .
4. Multiple Particle Swarm Optimization (MPSO)
4.1. PSO
Proposed by Kennedy and Eberhart [21], PSO employs a group of particles to find the optimal/near-optimal solution in a solution space. For a d-dimensional space, given Xi = [xi,1,…,xi,d] as the position and Vi = [vi,1,…,vi,d] as the velocity of a particle i at the time t, and pi = [pi,1,…,pi,d] as the best position of particle i and pg = [pg,1,…,pg,d] as the position of the global best particle g, the velocity of particle i at the time t + 1 is updated by Equation (15).
where
vi,d(t) = wvi,d(t) + c1r1(pi,d(t) − xi,d(t)) + c2r2(pg,d(t) − xi,d(t))
vi,d: the current velocity of the particle i; which is within the range [vmin,vmax].
w: an inertia weight typically set to a fixed value within the range [0,1].
c1, c2: acceleration coefficients usually set to the value 2.0.
r1, r2: random values selected from the interval [0,1].
The next position of the particle i is determined by Equation (16).
xi,d(t + 1) = xi,d(t) + vi,d(t)
4.2. The MPSO
4.2.1. Position Representation for a Particle
Figure 5 shows the position presentation for a particle to search a D-dimensional solution space. In this research we let D = n, where n is the total number of calling ships. In this position scheme, each (k = 1,…,n) indicates the placement sequence of n ships.
Figure 5.
The encoding scheme of a particle position.
To be feasible, each should be an integer, thus we employ a rank order value (ROV) technique to transform real values into ranking numbers (integers) in an increasing order. For example, the real vector [0.2,0.6,0.7,0.4] will be transformed into the ranking set [1,3,4,2] which indicates a placement sequence for ships 1,2,3 and 4.
4.2.2. The Two-Stage Procedure
Figure 6 shows the main logic flow for solving the simultaneous DCBAP and variable-in-time DQCAP (number). These procedure includes two stages. The first stage (steps 1 to 4) focuses on developing alternative ship placement sequences. The second stage (steps 5 to 12) is dedicated to assigning a berthing position to each ship, while resolving overlapped ships and adjusting QCs for ships using an event-based simulation approach, with spatial constraints taking into account. We detail each of these steps as follows:
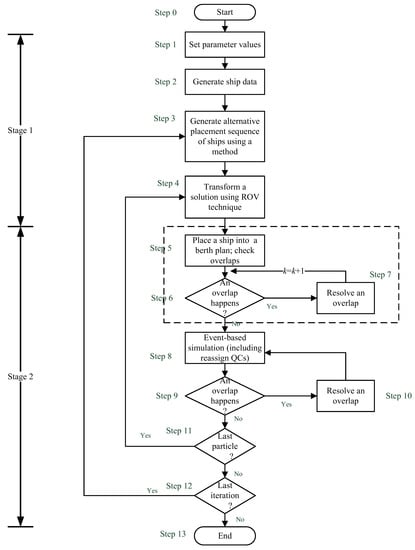
Figure 6.
The algorithm of the two-stage procedure.
Step 1: Set parameter values such as n, H, , iteration, l_iter, etc.
Step 2: Generate ship data including aj, dj, lj and j for n calling ships. Estimate the hj for each ship j based on j and using Equation (1).
Step 3: Generate alternative placement sequences of ships such as a heuristic (FCFS) or metaheuristic (PSO, MPSO, etc.).
Step 4: Transform a solution into the discrete domain using the ROV technique; Set k = 1; s = 1.The s indicates a placement order of a ship and the k indicates the difference from the s.
Step 5: Place the ship j at the placement order s into the berthing plan, with the coordinates of the lower-left and upper-right corners being positioned at the (, ) = (aj, cj) and (, ) = (aj + hj, cj + lj), respectively.
Step 6: Check whether the ship j at the placement order s has overlapped with the ship at the placement order sk using Equation (17). If “Yes” then go to Step 7; otherwise, go to Step 8.
Step 7: Resolve an overlap through cost estimation. Set k = k + 1 and go to Step 6.
Step 8: Perform event-based simulation while adjusting and reassigning QCs to ships (determines ) based on berthing and departure events of ships.
Step 9: Check any overlap after QC adjustment? If “Yes” go to Step 10; otherwise go to Step 11.
Step 10: Resolve an overlap of ships and then go to Step 11.
Step 11: Check whether this is the last particle? If “Yes” go to Step 12; otherwise go to step 4.
Step 12: Check whether this is the last iteration? If “Yes” go to Step 13; otherwise go to Step 3.
Stop 13: End.
4.2.3. Details of the Main Tasks in the Second Stage
The tasks to be dealt in the second stage are detailed as follows.
• Assign berthing positions for ships
An optimal berthing plan, which is based on each ship’s ETA and desired berthing position (dj) with the maximum QCs (), is first initialized for all ships. However, this optimal berthing plan may be infeasible due to limited resources of time and quay space that cannot satisfy all ships’ needs and thus result in overlaps of ships. Detecting and resolving these overlaps of ships are necessary to develop a feasible solution. These are detailed as follows.
• Detect an overlap of ships
Figure 7 shows a berthing plan with an overlap of ships j and k. Given a = (, ) and a’ = (,) are coordinates of lower-left hand corners of ships j and k respectively; while c = (,) and c’ = (,) are coordinates of upper-right hand corners. Then, Equation (17) gives the sufficient and necessary conditions of overlap for the two ships j and k. If any one of the conditions is not satisfied, then the two ships j and k are free of overlap.
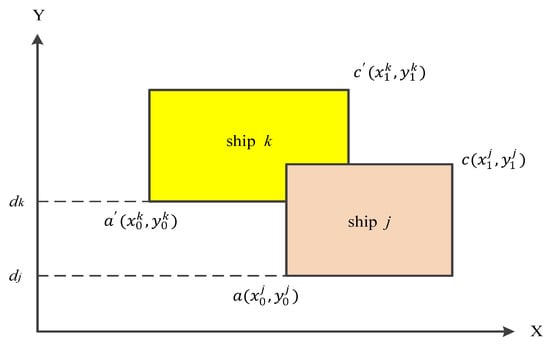
Figure 7.
The coordinates of the corner points of ships j and k.
• Resolve an overlap of ships
In this research, repositioning one of the overlapped ships is the main approach for resolving an overlap. As shown in Figure 8, the ship j is overlapped with the ship k and repositioning one of them can resolve this overlap. In this research, the ship being selected to repositioning is termed as “target ship” that is allowed to be moved towards the three directions including up (+Y), down (−Y), and right (+X), one at a time. However, as shown in Figure 8, moving the target ship j towards either +Y or −Y will increase handling time for the target ship j due to a deviation from its desired berthing position (assume that , is the desired berthing position of the ship j). The increased handling time is due to a longer moving distance for a container.
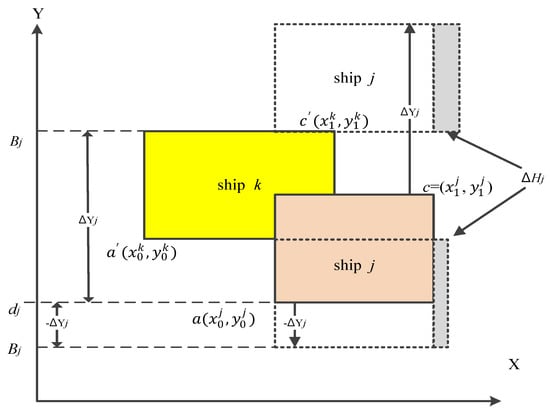
Figure 8.
Increasing the target ship j’s handling time when moving towards +Y/−Y.
In Figure 8, the indicates the increased handling time when moving the target ship j towards the +Y/−Y; the is the distance deviating from the ship j’s desired berthing position. Equation (18) is used for calculating the .
After this reposition, the coordinates of the lower-left hand and upper-right hand corners of the target ship j will become as a = (, + ) and c = (, + ), respectively. Equation (19) is used for estimating the increased cost of handling times for the target ship j. The C2 is a cost rate of handling time.
Figure 9 shows that moving the target ship j towards the +X direction will increase the ship’s waiting time (cost). The increased waiting time is estimated by Equation (20).
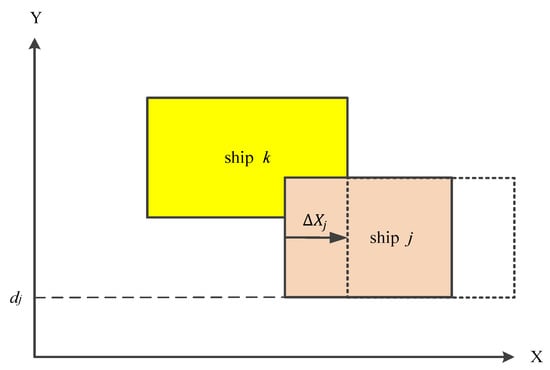
Figure 9.
Increasing the target ship j’s waiting time when moving towards +X.
After this reposition, the coordinates of the lower-left hand and upper-right hand corners of the target ship j will become as a = ( + , ) and c = (, ), respectively. The increased waiting cost of this target ship j is estimated by Equation (21), where is the cost rate of waiting time.
Estimations and prioritization of the three moving directions are required to determine the best and feasible direction.
• Adjustment of QCs
Reassigning released QCs from leaving ships to berthed ships can better utilize QCs. Referring to [4], we develop an event-based simulation based on discrete events.
Each ship has the three events: “arrive,” “berth,” and “departure.” If a ship arrives it may not berth immediately. It may lead to waiting time. If berths are available, a berth is selected and a number of QCs is assigned to the ship. A ship is assumed to depart immediately if handling is completed. In addition, we define a stage as a time interval, denoted as [t(),t()], where t() and t() are event times of two consecutive events, denoted as E( and , respectively. For example, the stage 1 is formed by [t(),t()], where t() and t() are event times of the two events E(1) and E(2). Given n calling ships, there exist 2n events and stages.
To simulate the berthing and departure of ships, it needs to identify discrete events one by one. Equation (22) is used to find the next event.
which subjects to the following conditions in Equation (23).
In Equation (22), the is the ETA of the ship while the is the expected departure time of ship k estimated at the stage . The A is a set of ships to berth; and the B is a set of berthed ships. For discrete simulation, finding the next event is necessary. This can also help to identify the owner (ship) and the type of event. For example, given the as the next event, then we can identify that the ship 3 is the event owner and this is a berthing event because the ship 3 . When dealing with a “departure” event, the number of QCs assigned to a ship should subject to the two QC constraints, Equations (8) and (9). For a “departure” event, the release QCs from a ship can be assigned to berthed ships, subjecting to the two QC constraints. In Equation (23), the C is a set of completed ships.
Equations (4) and (5) can be used to estimate the of a ship k at a stage j. However, due to QC adjustment the number of QCs assigned to a ship k at two consecutive stage, such as j and j + 1, may be different. Thus, due to discrete simulation, if the ship k has a QC adjustment then its should be updated by using Equation (24).
where
| the number of QCs assigned to ship k at the stage ; | |
| the number of QCs assigned to ship k at the stage ; |
The MPSO is one of the methods employed in step 3 of the first stage to generate alternative sequences of ship placements.
4.2.4. The Features of the MPSO
As an improved PSO, the MPSO includes the following features.
Multiple Groups of Particles
The first difference between the MPSO and the PSO is the use of multiple particle groups, which enables particles to search around elites in the swarm so as to diversify research in the solution space. Figure 10 illustrates three particle groups searching in the solution space currently. Each of the groups has a best particle that creates a search area.
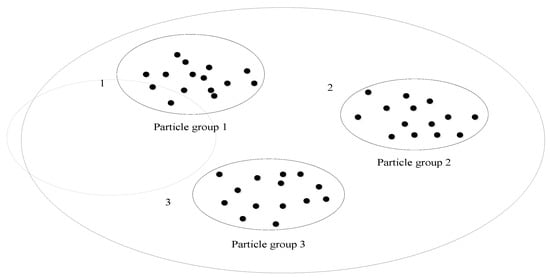
Figure 10.
Multiple groups of particle searching in the solution space.
Regrouping Mechanism
A reshuffle mechanism is used for the MPSO to regroup particles at the beginning of each iteration. Then, non-best particles in a group will search around the best particle in this group. The reshuffle mechanism can also change the number of particle groups as well as the best particle in a group. In a D-dimensional solution space, the position of a particle i at the time t is denoted as = () which corresponds to a solution in the solution space. The goodness of a position can be indicated by a Z value of an objective function. Given P particles and m groups, the MPSO groups particles in this way: the best particle is assigned to the group 1; the 2nd best to the group 2; the mth best to the group m; the m + 1th best then to the group 1 again, and so on. Finally, each of the groups contains n = P/m particles, and the particles of a same group are ordered increasingly, according to the Z values of the particles (for a problem of minimizing Z).
Self-Adaptive Velocity
One main feature of the MPSO is the use of a set of discrete operators to develop adaptive movements for particles, including distance measuring operator (~), adaptive distance operator (), and next position operator ().
The distance measuring operator (~) measures the distance between two position vectors of particles. Given and as two position vectors of particles o and j. Of a same group assume o is the target particle attracting particles i and j to search around. If we denote as the total distance vector between the particles o and j, then , and each element k in is determined by the operations defined in Equation (25).
The distance between the two particles o and j is denoted as and derived by Equation (26).
Subsequently, the total distance vector is refined by the adaptive distance operator () based on an adaptive velocity vector using Equation (27) to find an adaptive velocity for the particle i.
Each element (k = 1,…,D) in the (t) is a binary value (0 or 1) and the adaptive velocity for a particle i is derived through the operations in Equation (28).
The is used to adaptive the moving velocity of the particle j and it depends on two values, , through the operations defined in Equation (29).
In Equation (26), [0,1]; the is a random number and the is a threshold controlling the probability used to generate the binary value 1 into . To enable a bigger flying distance for a farther particle to approach the target particle quickly, is determined by Equations (30).
Having determined the we can determine the next position, of the particle j using the next position operator () and Equation (31).
The operator “” works as follows. First, it takes the first non-zero value out from the and replaces the value (that has a same position and segment and position as the non-zero value) in the Second, the replaced value takes the position of the non-zero value in the . Third, repeat the first and second steps until there is no non-zero value in the . Finally, the operator copies the current as the .
Figure 11 illustrates three particles , and of a same group and their positions are = [4,3,2,1], = [4,1,3,2], and = [1,2,3,4], respectively. The particle is the best particle attracting other particles of a same group to search around it. The particles o and i are closer as = 3 while = 4. To search around the particle o quickly, the particle j requires a bigger velocity to approach the particle o while the particle i requires a smaller velocity to avoid flying over the optima. However, no particle is allowed flying to the best particle directly due to a waste of local search.
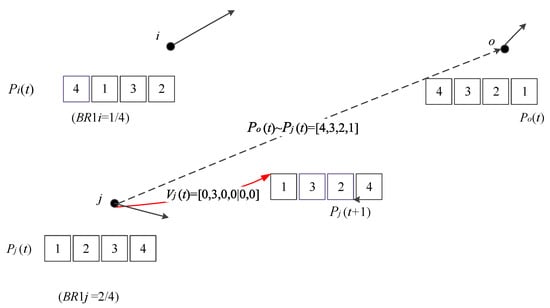
Figure 11.
Particles p1 and p2 fly toward the target particle o.
Based on Equation (23), we can derive for the particle j at the time t as follows.
In this case, we can derive the = 4 and = 2/4 for the particle j based on Equation (26) and Equation (30), respectively. With this and assume that = [0,1,0,0], then according to Equation (27) we can determine the as follows.
The next position of the particle j is finally derived as follows using Equation (31).
This example shows that an non-zero element in the will cause an exchange of two elements in the . At the time t + 1, the two particles o and j are closer due to a shorter distance = 2 and this will lead to the generation of a = [0,0,0,0] that can prevent the particle j from directly flying to the particle o.
Intelligent Movement of a Particle
When moving a particle, the MPSO uses the following intelligent mechanisms:
- Direct-fly prevention: the direct-fly prevention is a mechanism stopping a particle from flying to the target particle in the next step because such a move will waste one local search. Specifically, the MPSO will measure the current distance between a particle j and a target particle o. If the distance between them is satisfied with the condition, , the MPSO then stops generating binary value 1 for the of the particle j as additional one binary value 1 added to the will trigger a direct-fly.
- Neighborhood search: while imposed by the direct-fly prevention, a particle will stay at its current position, which will waste one local search. For improvement, the function, exchange (p1,p2), is used for neighborhood search by exchanging two randomly-selected position elements in the position vector of a particle.
The Self-Adaptive Variant of a Particle
Mutations (chaotic) can be used to avoid a solution to be trapped in a local optimum. In the MPSO, it includes two kinds of mutations to mutate a particle. They are detailed as follows.
- Swap Mutation (SM): in this mutation two values of two positions (p1 < p2) are first randomly selected and then swapped.
- Thoros Mutation (TM): in this mutation three values of three positions p1, p2, and p3 (where p1 < p2 < p3) are first selected randomly, and then the value of p1 becomes the value of p2, the original value of p2 becomes the value of p3, and the original value of p3 becomes the value of p1. Compared with the SM, the TM has a greater variant due to more mutated values.
Figure 12 shows the logical flow of mutation. The mutation depends on a generated random number RN( ) and a mutation rate ; if RN( ) < then trigger mutation; Otherwise, abort mutation. If going into mutation process, the similarity degree between and is firstly estimated by using Equation (32), where D indicates the total number of same elements between the particles o and j. The lower the indicates the two particles have a higher similarity and thus the TM is used; otherwise, the SM is used.
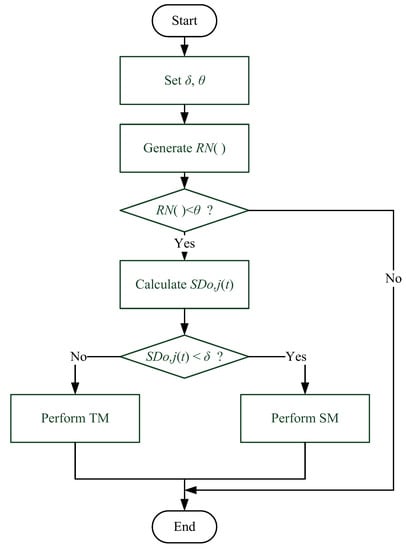
Figure 12.
The algorithm of mutation in the multiple particle swarms optimization (MPSO).
A particle with a smaller is assumed to require a bigger variant due to being at an unfavorable position. Therefore, if a particle is with then the TM is used to have a big variant; otherwise, the SM is used to have a small variant. The parameter , a threshold used to control the choice of TM or SM.
4.3. The Main Flow Logic of MPSO
Algorithm 1 shows the main logic flow of the MPSO.
| Algorithm 1. The logic flow of MPSO. | |
| 1 | Set parameter values (N, Rm, P, m, iterations, l_iter, etc.) |
| 2 | Initial positions for particles using rank order values (ROVs) |
| 3 | FOR (int t = 1; t <= iterations; t++){ |
| 4 | Calculate the Z values for all particles using Equation (6). |
| 5 | Rank particles according to their FVs |
| 6 | Generate groups m(t) for particles. |
| 7 | FOR (int li = 1;li< = l_iter; li++) |
| 8 | FOR (int j = 1; j <= m(t); j++) |
| 9 | FOR (int k = 1;k <= the_number_of_particles_in_j; k++) |
| 10 | IF particle k is not the best particle in the subgroup j |
| 11 | Move the particle k one step toward the best particle in j |
| 12 | Calculate Z value using Equation (6). |
| 13 | IF Z value of this movement is improved |
| 14 | Store the Z value for this particle k |
| 15 | Store the current position for this particle k |
| 16 | ELSE |
| 17 | Move the particle k toward the global best particle in the swarm |
| 18 | Calculate Z value using Equation (6). |
| 19 | IF Z value of this movement is improved |
| 20 | Store the Z value for this particle k |
| 21 | Store the current position for this particle k |
| 22 | ELSE |
| 23 | Change the particle k to a random position |
| 24 | END IF |
| 25 | END IF |
| 26 | Compare the solution to the global best solution |
| 27 | IF better |
| 28 | Store the solution as the global best solution |
| 29 | END IF |
| 30 | Perform the self-adaptive variant for the particle k |
| 31 | END IF |
| 32 | END FOR k |
| 33 | END FOR j |
| 34 | END FOR li |
| 35 | END FORt |
5. Numerical Example
Java language was used for programming the FCFS, PSO, PSO2, and MPSO for comparison to investigate their effectiveness. These approaches were used in the first stage of the two-stage procedure. In the second stage of the two-stage procedure a same simulation-based heuristic was used. Each comparison is based on a set of same inputs.
In this research, the simple heuristic FCFS was used due to likely less waiting time.
Section 5.1 lists the parameter values used of experiments. Section 5.2 shows the results of an experiments (N = 15). Section 5.3 shows the results of some experiments with N = 15, 20, 25, and 30.
5.1. Parameters Setting for Experiments
Table 1 shows the setting of parameters for experiments.

Table 1.
The parameters setting for the four approaches for experiments.
The t indicates the number of iterative runs. For the PSO, the w is an inertial weight of velocity; the p is a number of total particles; the c1 and c2 are two coefficients; the r1 and r2 are two random numbers; the vmax and vmin are maximum and minimum velocities, respectively. For the MPSO, the θ is a mutation rate; the δ (δ ∈ [0,1]) is a threshold controlling the use of either TM or SM; the Rm is a mutation rate; and the Rc is a crossover rate. PSO. For PSO2, the w1, w2, and w3, as with the values used in [4], are coefficients of weights; the T0 is an initial temperature; the Te is the final temperature; the β is a falling rate of temperature.
In addition, we set planning horizon to 1 week (H = 168 h). As a result, the ETAs of ships are with the interval [0,168] (hours). The quay length (L) is set to 800 m. The length of a ship k (lk) is set within the interval [100,200] (meters). The desired berthing location of a ship k (dk) then should be within the interval [0, L‒lk]. The total number of loading and unloading containers of a ship k () is within the interval [80,2000]. In the quay side there are 8 QCs in total. Table 2 shows the parameters of costs used for the FCFS, PSO, PSO2 and MPSO. The C1 and C2 are set to USD 1000/hour.

Table 2.
The original data of ships (N = 15).
5.2. A Small-Size Example
Table 2 shows the ship data randomly generated by computer for a small-size experiment (N = 15).
The first column No indicates the placement order of ship. The second column SID indicates the ship’s id. The column lj indicates the length of ship j, the column aj indicates the ETA of ship j, the column dj indicates the desired berthing position of ship j, the column Cj indicates the total number of loading and unloading containers of the ship j. The columns X0 and Y0 indicate the coordinates of the lower-left corner (X0,Y0) of a ship while the columns X1 and Y1 indicate the coordinates of the upper-right corner (X1,Y1) of a ship.
Figure 13 shows the berthing plan of 15 calling ships based on the original ship data in Table 3. We can find this is an infeasible berthing plan due to 6 overlaps of ships. Thus, resolving these overlaps of ships by using the two-stage solution procedure with different heuristics/meta-heuristics is necessary.
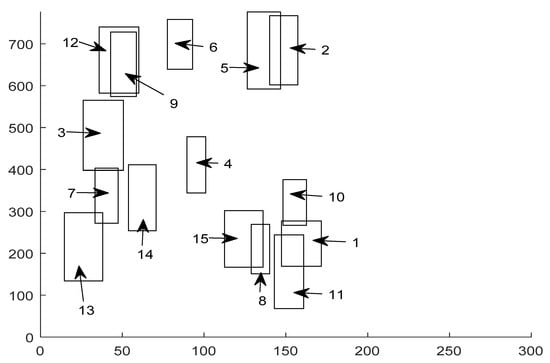
Figure 13.
The berthing plan based on the original ship data.

Table 3.
Summary data of different approaches.
Figure 14 shows the best berthing plans obtained from different approaches used in the first stage in the two-stage solution procedure. Figure 14a is the berthing plan obtained from the FCFS heuristic. Figure 14b is the best solution obtained from the PSO. Figure 14c is the best berthing plan obtained from the PSO2. Finally, Figure 14d shows the best berthing plan obtained from the MPSO. Details data obtained from these approaches are listed in Table 3 as shown below.
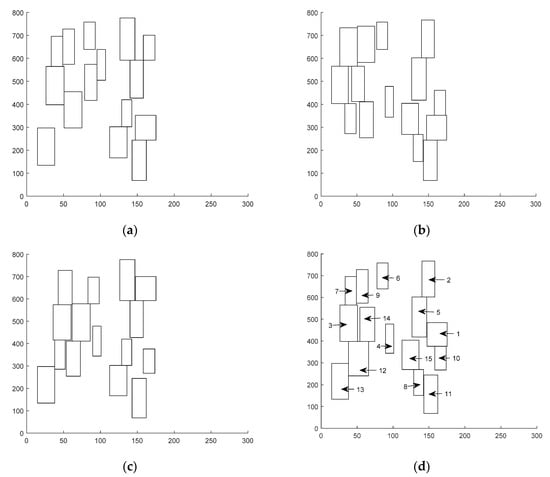
Figure 14.
(a) Berthing plan (FCFS); (b) berthing plan (PSO); (c). berthing plan (PSO2); (d) berthing plan (MPSO).
From Table 3 we know that the MPSO outperforms the FCFS, PSO and PSO2 in terms of total costs (Z) including two sub-costs: increased waiting time (ΔWC) and increased handling times (ΔHC).
Table 4 shows the ship data and the coordinate data of the berthing plan in Figure 14d obtained from the MPSO, after repositioning target ships to avoid overlapping with other ships by using the two-stage approach.

Table 4.
The coordinates of the calling ships (N = 15) after resolving overlaps of ships.
From Figure 13 we found that there exist 6 overlaps of ships, thus repositioning some target ships are necessary for making a feasible solution.
In Table 4, after comparing this table with Table 2, we have highlighted the ships with changed coordinates. These ships and changed coordinates are in bolded face. Firstly, it is noted that there are 4 calling ships with no any change on their coordinates. They are ships 3,4,13 and 6. Referring to Table 6, it is found that these ships are assigned with the maximum QCs ( 3) in their all working stages. These information help us to ensure that these ships get zero increased waiting cost as well as handling cost ( = 0) because they are at their best positions (i.e., the desired berthing positions) and with the best amount of QCs assigned. Due to being at the optimal situation, these ships face no increased cost. Furthermore, it is noted that the remaining 11 ships have changed coordinates, including ships 8, 10,1,15,9,7,12,11,2,14, and 5. These changes are adaptable to resources constraints. For example, some of these ships, including 10, 9 and 12, are found with the condition aj < X0, which indicates that these ships to have been moved toward the +X direction and thus face increased waiting times (their 0). In addition, some of these ships, including 8,10,1,15,9,7,12,11,2,14 and 5, are found with increased handling costs ( 0). These increases may come from two sources: one is the deviation from their respective desired berthing positions and another the adjustments of their QCs (variable-in-time QC assignment). The two reasons can change (increase or shorten) their required handling times. For example, ships 5 and 15 are found to be deviating from their berthing positions and this introduce increased handling times for them. In addition, from Table 6 we see that some other ships such as 8,10,1,9,7,12,11,2, and 14 which have QC adjustments and this introduces additional increased handling times for these ships. Take ship 8 in Table 6 as an example; ship 8 berths at 128.8 with 2 QCs initially assigned but this number of QCs has been increased to 3 when ship 15 completes its job and releases its QCs at the time point 136.1. Similarly, those ships with < Y0 are identified to have been moved toward the +Y direction (such as the ship 1) while those ships with > Y0 are identified to have been moved towards the −Y direction (such as ship 12).
Table 5 shows the QC assignment for each ships at each stage, which is a variable-in-time QC assignment based on available QCs. In this case, a total number of 8 QCs (Q = 8) is set.

Table 5.
The number of QCs assigned to each ship.
The column “No” indicates the stage No; the column “Fm” and “To” indicates “from” and “To” which indicates a duration of a stage; The column “SID” indicates a “ship ID”; the column “S” indicates the “state” of a ship with the value of 2 indicating a “berthing event” of the ship and the value of 3 indicating a “departure event” of the ship. In the MPSO, at the first stage all ships are default to have the maximum QC assignment ( = 3) initially. But, at the second stage this number of QCs assignment may be adjusted to conform to QC constraints, i.e., Equations (7) and (8). In addition, the released QCs from a leaving ship will be reallocated to berthed ships to best utilize available QC capacity but such reallocations should also conform to the two QC constraints. We give a detailed explanation on Table 5. At first, all ships are A (where A is a set of ships to berth). At stage 1, [0,14.6], until to the time point 14.6 the first ship (SID = 13) arrives and berths immediately because quay space and QCs are available. The ship 13 gets 3 QCs in this stage and now becomes a berthed ship (where B is a set of berthed ships). The S = 2 indicates that a “berthing event” occurs. Following this, at stage 2, with the duration [14.6,26.1], the ship 3 (SID = 3) arrives and berths at the time point 26.1 and gets 3 QCs assigned. This is also a “berthing event” (S = 2). So, now ships 13 and 3 . At stage 3, with the duration [26.1,33,3], the ship 7 (SID = 7) arrives and berths at the time point 33.3. However, ship 7 is only get 2 QCs assigned due the QC constraints (i.e., the total number of QCs in this case is 8). At the stage 3 all the QCs assigned to these berthed ships (including 13, 3 and 7) is subject to the constraints, Equation (8). Now, we have 3 berthed ships. At stage 4, with the duration [33.3,38], all these berthed ships are loading and unloading containers, but at the time point 38 the first ship (ship 13) is completed and it triggers a leaving event (S = 3). The ship 13 then leaves and the working duration for this is [14.6,38]. Now, ship 13 C (where C is a set of completed ships) ships 3 and 7 are two remaining berthed ships. The other stages in Table 5 are explained in the same way. Finally, at the last stage 30, with the working duration [173.8,175.3], ship 1 leaves at the time point 175.3. Table 5 shows the simulation results obtained from the second stage with QCs assigned/adjusted conforming to the two QCs constraints. The Table 5 provides a solution to the variable-in-time QCAP (number).
5.3. Experiments
In this section, more experiments are performed to investigate the effectiveness of different approaches used in the first stage of the two-stage procedure. Table 6 shows the experimental results.

Table 6.
The results obtained from different methods used in the first stage.
In Table 6, the “Z” column indicates the objective function value and the “T” column indicates the computational times for each experiment. In addition, Figure 15a to Figure 15d shows the comparison of total cost for different approaches under different numbers of calling ships (n = 15, 20, 25, and 30).
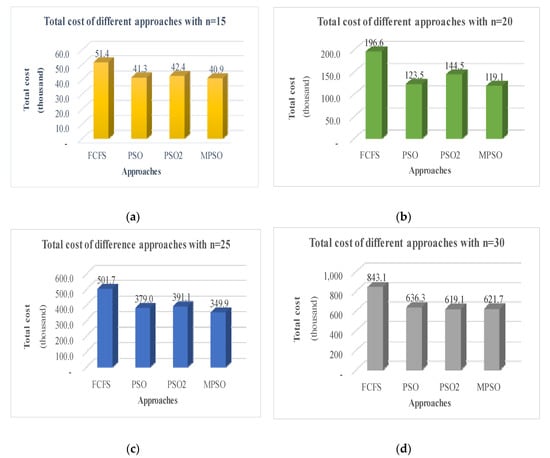
Figure 15.
(a) Comparisons of total costs (n = 15); (b) comparisons of total costs (n = 20); (c) comparisons of total costs (n = 25); (d) comparisons of total costs (n = 30).
Figure 15a shows the total costs of 4 approaches employed in the first stage of the two-stage procedure for a problem with 15 ships (n = 15), from which we note that the MPSO has the least cost (40,861.5). Figure 15b also shows the MPSO with least average cost (119,148.9) for the problem with 20 ships (n = 20). Furthermore, Figure 15c also shows the MPSO with the least average cost (349,932.6) for the problem with 25 ships (n = 25). Finally, Figure 15d shows that the MPSO has a slight higher average cost (621,650.8) than the PSO2 that has the least average cost (619,124.2) for the problem with 30 ships (n = 30). This result may come from the bias experimental samples generated by the computer automatically. However, in this research, the total number of experimental instances that MPSO performs equally or better than the PSO2 in 36 (out of the 40 samples), thus we consider the MPSO in general can find a better solution than the PSO2, especially in problem sizes n = 15,20 and 25.
5.4. Analysis and Discussion
We summarize and discuss the findings as follows:
- (1)
- This research has, respectively, employed FCFS, PSO, PSO2, and MPSO in the first stage of the two-stage procedure and it is found that these approaches lead to different results. The MPSO is found to outperform the other approaches in terms of the total cost defined in the objective function.
- (2)
- The tuning of the total number of iterative runs can also control the computational times. The more the iterative runs the more the computational times.
- (3)
- Although having less computational cost, the FCFS is incapable of finding a high-quality solution due to its simplicity. This disadvantage increases when the solution space increases. The FCFS cannot improve the solution continuously.
- (4)
- It is found that moving a target toward either the +Y or −Y direction is less costly than towards the +X direction. This leads to the better use of available quay space. Thus, the cost values of C1 and C2 can inference the selection of a moving direction for a target ship.
- (5)
- As the least-cost direction has a high priority to be selected for a target ship, it is expected that our approach is likely to find, at least, a near-optimal solution. This cost estimation mechanism plays an essential role for this finding.
- (6)
- From Table 6, as the computational times to find the solutions for these approaches are found to be acceptable, these approaches are considered as applicable for practical usage.
- (7)
- Our approach is different from some proposed in past studies. For example, it differs from [39] in which the marginal decreasing capacity of QCs was not considered. This research differs from studies [5,18,19], which are PSO-based research. The [5] focused on a discrete version of BAP instead of a continuous version. The [18,19] only focused on the BAP, which did not consider the QCAP.
- (8)
- In [5] the proposed approach, PSO2, assigns a random number of QCs to a ship initially. However, this initial assignment cannot guarantee the best assignment of QCs to a ship as it did not use the . In this research, the MPSO assigns an initial number of QCs to a ship based on the , which promises the best assignment. The best number is to be adjusted if not conforming to the two QC constraints, Equations (8) and (9), to ensure a feasible solution. The experimental results show that the MPSO outperforms the PSO2 proposed in [5].
- (9)
- However, one limitation of the MPSO is that it cannot identify each QC assigned to a ship though it allows QC adjustment, i.e., it is the type of variable-in-time QCAP (number) instead of variable-in-time QCAP (specific) that is more specific and convenient for practical usage. Thus, there is room to improve the MPSO further.
- (10)
- One lack of this research is the comparison of the MPSO to GAs that have been widely used for solving seaside operational problems. This can be treated as a future research direction. Nevertheless, this research has achieved a preliminary result.
- (11)
- Although we have reached the preliminary conclusion that the MPSO outperforms the other approaches, extensive experiments are still required to consolidate this conclusion further.
- (12)
- One concern raised by a maritime supply chain is the damage and pollution to our environment, thus environmental protection is a concern. To pursuit higher efficiency for container terminal operations, some recent ideas have even proposed to allow speeding up ships so that they can arrive at a port earlier to make a better plan for resource usage (such as better use of quay space). However, speeding up a ship can introduce more air pollution that can damage our environment. In this research, speeding up a ship is not considered, as our approach does not allow a ship to move toward the −X direction (which requires a ship to speed up its speed). Thus, our approach has the merit of protecting our environment, while trying to better use resources including quay space and berths.
6. Conclusions
A hybrid approach combining multiple particle swarm optimization (MPSO) with an event-based simulation heuristic is proposed in this research to deal with the DCBAP and the variable-in-time QCAP (number) through a two-stage procedure. Both arrived and incoming ships are considered and assigned to a quay used as a continuous line to accommodate these ships. The handling time of each ship is determined by the number of QCs assigned to this ship with QC interference being taken into consideration and the number of QCs assigned to a ship is further adjustable.
The first stage uses a heuristic/metaheuristic to generate alternative ship placement sequences as inputs to the second stage that includes an event-based simulation heuristic to place ships into the berth plan, assign/adjust QCs and resolve overlaps of ships for developing feasible solutions. Finally, the best solution is outputted. Among FCFS, PSO, PSO2, and MPSO, the MPSO is found to be the best, in terms of total cost, when used in the first stage to work with the simulation-based heuristic in the second stage.
The DCBAP and the QCAP are two problems commonly faced by container terminal planners daily. A better solution for the two problems is necessary due to their considerable impacts on the productivity of a container terminal. The main contributions of this research are listed as follows:
- (1)
- We have formulated the two problems as a mathematical model. Based on this model, a two-stage procedure was proposed to solve the two problems by including heuristics and metaheuristics.
- (2)
- A resolution of the conflict of ships is developed based on the concept of moving a target towards the least direction. This mechanism can lead to the finding of the optimal/near optimal solutions.
- (3)
- We have implemented this two-stage procedure by using java programing language to facilitate the generation of solutions. Our experiments show that our approach can find the optimal/near-optimal solution with acceptable computation times.
In future research, improving the MPSO to deal with the simultaneous DCBAP and variable-in-time QCAP (specific) can be focused. This type of combined problem is more difficult to solve but indeed more helpful for practical usage. The use of other metaheuristics such as GAs in the first stage of the two-stage approach and a comparison to the MPSO can be performed in future research. Finally, extending this research to the area of QCSP can be further considered.
Author Contributions
H.-P.H. acquired funding, guided the research direction, developed the algorithm and found the solutions; C.-N.W. summarized and analyzed the data, revised and edited this paper. All authors have contributed to this research. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Ministry of Science and Technology of Taiwan under the grant MOST 107-2410-H-992-037 as well as the Kaohsiung University of Science and Technology.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhen, L.; Yu, S.; Wang, S.; Sun, Z. Scheduling quay cranes and yard trucks for unloading operations in container ports. Ann. Oper. Res. 2019, 273, 455–478. [Google Scholar] [CrossRef]
- Bierwirth, C.; Meisel, F. A survey of berth allocation and quay crane scheduling problems in container terminals. EJOR 2010, 202, 615–627. [Google Scholar] [CrossRef]
- Vis, I.F.A.; Koster, R.D. Transshipment of container at a container terminal: An overview. EJOR 2003, 147, 1–16. [Google Scholar] [CrossRef]
- Raa, B.; Dullaert, W.; Schaeren, R.V. An enriched model for the integrated berth allocation and quay crane assignment problem. Expert Syst. Appl. 2011, 38, 14136–14147. [Google Scholar] [CrossRef]
- Hsu, H.P. A HPSO for solving dynamic and discrete berth allocation problem and dynamic quay crane assignment problem simultaneously. Swarm Evol. Comput. 2016, 27, 156–168. [Google Scholar] [CrossRef]
- Kim, K.H.; Moon, K.C. Berth scheduling by simulated annealing. Transp. Res. Part B 2003, 37, 541–560. [Google Scholar] [CrossRef]
- Salido, M.A.; Mario, R.M.; Barber, F. A decision support system for managing combinatorial problems in a container terminal. Knowl.-Based Syst. 2011, 29, 63–74. [Google Scholar] [CrossRef]
- Hsu, H.P.; Chiang, T.L. An Improved Shuffled Frog-Leaping Algorithm for Solving the Dynamic and Continuous Berth Allocation Problem (DCBAP). Appl. Sci. 2019, 9, 4682. [Google Scholar] [CrossRef]
- Leonora, B.; Dorigo, M.; Gambardella, L.M.; Gutjahr, W.J. A survey on metaheuristics for stochastic combinatorial optimization. Nat. Comput. Int. J. 2009, 8, 239–287. [Google Scholar]
- Liang, C.J.; Huang, Y.F.; Yang, Y. A quay crane dynamic scheduling problem by hybrid evolutionary algorithm for berth allocation planning. Comput. Ind. Eng. 2009, 56, 1021–1028. [Google Scholar] [CrossRef]
- Han, X.L.; Lu, Z.Q.; Xi, L.F. A proactive approach for simultaneous berth and quay crane scheduling problem with stochastic arrival and handling time. EJOR 2010, 207, 1327–1340. [Google Scholar] [CrossRef]
- Chang, D.F.; Jiang, Z.H.; Yan, W.; He, J.L. Integrating berth allocation and quay crane assignments. Transp. Res. Part E 2010, 46, 975–990. [Google Scholar] [CrossRef]
- Liang, C.J.; Guo, J.Q.; Yang, Y. Multi-objective hybrid genetic algorithm for quay crane dynamic assignment in birth allocation planning. J. Intell. Manuf. 2011, 22, 471–479. [Google Scholar] [CrossRef]
- Imai, A.; Etsuko, N.; Papadimitriou, S. Marine container terminal configurations for efficient handling of mega-containerships. Transp. Res. Part E Logist. Transp. Rev. 2013, 49, 141–158. [Google Scholar] [CrossRef]
- Rodriguez-Molins, M.; Ingolotti, L.; Barber, F.; Salido, M.A.; Sierra, M.R.; Puente, J. A genetic algorithm for robust berth allocation and quay crane assignment. Prog. Artif. Intell. 2014, 2, 177–192. [Google Scholar] [CrossRef]
- Hsu, H.P. A Hybrid GA with Variable Quay Crane Assignment for Solving Berth Allocation Problem and Quay Crane Assignment Problem Simultaneously. Sustainability 2019, 11, 2018. [Google Scholar] [CrossRef]
- Wang, F.; Lim, A. A stochastic beam search for the berth allocation problem. Decis. Support Syst. 2007, 42, 2186–2196. [Google Scholar] [CrossRef]
- Ting, C.J.; Wu, K.C.; Chou, H. Particle swarm optimization algorithm for the berth allocation problem. Expert Syst. Appl. 2014, 41, 543–1550. [Google Scholar] [CrossRef]
- Babazadeh, A.; Shahbandi, A.G.; Ganji, S.S.; Joharianzadeh, M. A PSO algorithm for continuous berth allocation problem. Int. J. Shipp. Transp. Logist. 2015, 7, 479. [Google Scholar] [CrossRef]
- Bierwirth, C.; Meisel, F. A follow-up survey of berth allocation and quay crane scheduling problems in container terminals. Eur. J. Oper. Res. 2015, 244, 675–689. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Piscataway, NJ, USA, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Allahverdi, A.; Al-Anzi, F.S. A PSO and a Tabu search heuristics for the assembly scheduling problem of the two-stage distributed data application. Comput. Oper. Res. 2006, 33, 1056–1080. [Google Scholar] [CrossRef]
- Zhou, P.F.; Kang, H.G. Study on Berth and Quay-crane Allocation under Stochastic Environments in Container Terminal. Syst. Eng.-Theory Pract. 2008, 28, 161–169. [Google Scholar] [CrossRef]
- Lin, S.Y.; Horng, S.J.; Dao, T.W.; Huang, D.K.; Fahn, C.S.; Lai, J.L.; Chen, R.J.; Kuo, I.H. Efficient bi-objective personnel assignment algorithm based on a hybrid particle swarm optimization model. Expert Syst. Appl. 2010, 37, 7825–7830. [Google Scholar] [CrossRef]
- Zhen, L.; Hu, H.; Wang, W.; Shi, X.; Ma, C. Cranes scheduling in frame bridges based automated container terminals. Transp. Res. Part C Emerg. Technol. 2018, 97, 369–384. [Google Scholar] [CrossRef]
- Liu, B.; Wang, L.; Jin, Y.H. An effective hybrid PSO-based algorithm for flow shop scheduling with limited buffers. Comput. Oper. Res. 2008, 35, 2791–2806. [Google Scholar] [CrossRef]
- Yuan, X.H.; Wang, L.; Yuan, Y.B. Application of enhanced PSO approach to optimal scheduling of hydro system. Energy Convers. Manag. 2008, 49, 2966–2972. [Google Scholar] [CrossRef]
- Zhou, D.W.; Gao, X.A.; Liu, G.H.; Mei, C.L.; Jiang, D.; Liu, Y. Randomization in particle swarm optimization for global search ability. Expert Syst. Appl. 2011, 38, 15356–15364. [Google Scholar] [CrossRef]
- Lee, D.H.; Wang, H.Q. Integrated discrete berth allocation and quay crane scheduling in port container terminals. Eng. Optim. 2010, 42, 747–761. [Google Scholar] [CrossRef]
- Lim, A. The berth scheduling problem. Oper. Res. Lett. 1998, 22, 105–110. [Google Scholar] [CrossRef]
- Lee, Y.; Chen, C.Y. An optimization heuristic for the berth scheduling problem. EJOR 2009, 196, 500–508. [Google Scholar] [CrossRef]
- Zhen, L.; Hay, L.H.; Chew, E.P. A decision model for berth allocation under uncertainty. EJOR 2011, 212, 54–68. [Google Scholar] [CrossRef]
- Imai, A.; Nishimura, E.; Paradimitrious, S. Corrigendum. The dynamic berth allocation problem for a container port. Transp. Res. Part B 2005, 39, 197. [Google Scholar] [CrossRef][Green Version]
- Meisel, F.; Bierwirth, C. Heuristic for the integration of crane productivity in the berth allocation problem. Transp. Res. Part E 2009, 45, 196–209. [Google Scholar] [CrossRef]
- Chang, D.F.; Yan, W.; Chen, C.H.; Jiang, Z.H. A berth allocation strategy using heuristics algorithm and simulation optimization. Int. J. Comput. Appl. Technol. 2008, 32, 272–281. [Google Scholar] [CrossRef]
- Zhang, C.R.; Zheng, L.; Zhang, Z.H.; Shi, L.Y.; Armstrong, A.J. The allocation of berths and quay cranes by using a sub-gradient optimization technique. Comput. Ind. Eng. 2010, 58, 40–50. [Google Scholar] [CrossRef]
- Yang, C.; Wang, X.; Li, Z. An optimization approach for coupling problem of berth allocation and quay crane assignment in container terminal. Comput. Ind. Eng. 2012, 62, 119–128. [Google Scholar] [CrossRef]
- Türkoğvllari, Y.B.; Taşkın, Z.C.; Aras, N.; Altınel, K. Optimal berth allocation and time-invariant quay crane assignment in container terminals. Eur. J. Oper. Res. 2014, 235, 88–101. [Google Scholar] [CrossRef]
- Park, Y.M.; Kim, K.H. A scheduling method for Berth and Quay cranes. OR Spectr. 2003, 25, 1–13. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).