Abstract
In this article, we obtain general bounds and closed formulas for the secure total domination number of rooted product graphs. The results are expressed in terms of parameters of the factor graphs involved in the rooted product.
1. Introduction
Recently, many authors have considered the following approach to the problem of protecting a graph [1,2,3,4,5,6,7]: suppose that one “entity” is stationed at some of the vertices of a (simple) graph G and that an entity at a vertex can deal with a problem at any vertex in its closed neighbourhood. In general, an entity could consist of a robot, an observer, a legion, a guard, and so on. Informally, we say that a graph G is protected under a given placement of entities if there exists at least one entity available to handle a problem at any vertex. Various strategies (or rules for entities placements) have been considered, under each of which the graph is deemed protected. As we can expect, the minimum number of entities required for protection under each strategy is of interest. Among these strategies we cite, for instance, domination [8,9], total domination [10], secure domination [1], secure total domination [2], Roman domination [6,7], Italian domination, [11] and weak Roman domination [5]. The first four strategies are described below.
The simplest strategies of graph protection are the strategy of domination and the strategy of total domination. In such cases, the sets of vertices containing the entities are dominating sets and total dominating sets, respectively. Typically, a vertex in a graph dominates itself and its neighbouring vertices. A set is said to be a dominating set of G if every vertex in is dominated by at least one vertex in S, while S is said to be a total dominating set if every vertex is dominated by at least one vertex in .
The minimum cardinality among all dominating sets of G is the domination number of G, denoted by . The total domination number, denoted by , is defined by analogy. These two parameters have been extensively studied. For instance, we cite the following books, [8,9,10].
Let be the open neighbourhood of and let . In the case of the secure (total) domination strategy, a vertex is deemed (totally) protected under if S is a (total) dominating set and there exists such that is a (total) dominating set. In such a case, in order to emphasise the role of vertex u, we say that v is (totally) protected by u under S. A set is said to be a secure (total) dominating set if every vertex in is (totally) protected under S.
For instance, let G be the graph shown in Figure 1, and suppose that an observer is stationed at vertex a and another one is stationed at b. In such a case, the graph is under the control of the observers, as its vertices are (i.e., is a dominating set). Now, if the observer stationed at vertex a moves to any vertex in , then the graph is under the control of the observers as well. In this case, is a secure dominating set. Furthermore, if there are three observers and they are stationed at a, b, and c, then every vertex of the graph (including a, b, and c) is under the control of the observers, and this property is preserved if the observer stationed at c moves to d or e. Hence, is a secure total dominating set.
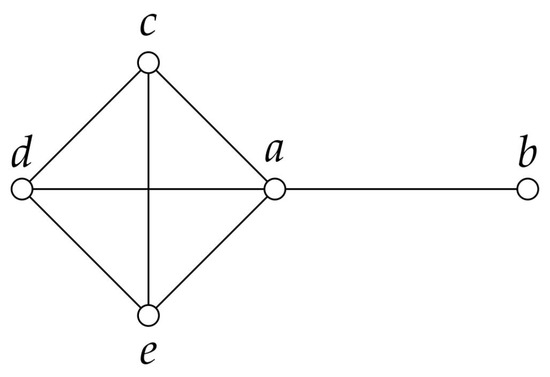
Figure 1.
In this case, is a dominating set, is a total dominating set and also a secure dominating set, while is a secure total dominating set.
The minimum cardinality among all secure dominating sets of G is the secure domination number of G, denoted by . This domination parameter was introduced by Cockayne et al. in [1] and studied further in a number of works including [12,13,14,15,16,17]. Now, the minimum cardinality among all secure total dominating sets of G is the secure total domination number of G, which is denoted by . This parameter was introduced by Benecke et al. in [2] and studied further in [3,4,16,18,19].
A secure total dominating set of cardinality will be called a -set. A similar agreement will be assumed when referring to optimal sets associated to other parameters used in the article.
The problem of computing is NP-hard [18], even when restricted to chordal bipartite graphs, planar bipartite graphs with arbitrary large girth and maximum degree three, split graphs and graphs of separability at most two. This suggests finding the secure total domination number for special classes of graphs or obtaining tight bounds on this invariant. This is precisely the aim of this article in which we study the case of rooted product graphs.
2. Some Notation and Tools
All graphs considered in this paper are finite and undirected, without loops or multiple edges. The minimum degree of a graph G will be denoted by , i.e., . As usual, the closed neighbourhood of a vertex is denoted by . We say that a vertex is a universal vertex if . By analogy with the notation used for vertices, the open neighbourhood of is the set , while the closed neighbourhood is the set .
A set is a double dominating set of G if for every . The double domination number of G, denoted by , is the minimum cardinality among all double dominating sets of G. The k-domination number of a graph G, denoted by , is the cardinality of a smallest set of vertices such that every vertex not in the set is adjacent to at least k vertices of the set. Such sets are called k-dominating sets.
Remark 1.
Every secure total dominating set is a double dominating set and every double dominating set is a 2-dominating set. Therefore, for any graph G with no isolated vertex, .
By Remark 1, for every secure total dominating set S and every vertex , the set is a dominating set. Therefore, the following remark holds.
Remark 2.
For every graph G with no isolated vertex, .
A leaf of G is a vertex of degree one. A support vertex of G is a vertex which is adjacent to a leaf and a strong support vertex is a support vertex which is adjacent to at least two leaves. A leaf is said to be a strong leaf if it is adjacent to a strong support vertex, otherwise it is called a weak leaf. The set of leaves, support vertices, strong leaves and weak leaves are denoted by , , , and , respectively.
Remark 3.
If D is a secure total dominating set of a graph G, then and no vertex of G is totally protected under D by vertices in .
If v is a vertex of a graph H, then the vertex-deletion subgraph is the subgraph of H induced by . In Section 3 we will show the importance of in the study of the secure total domination number of rooted product graphs. Now we proceed to state some basic tools.
Lemma 1.
Let H be a graph with no isolated vertex. If , then
Furthermore, if , then v belongs to every -set.
Proof.
Assume that and let D be a -set. Suppose that . If , then is a secure total dominating set of H of cardinality , which is a contradiction. Suppose that . If , then for every we have that is a secure total dominating set of H of cardinality , which is a contradiction. Now, if , then by Remark 3 we can conclude that is a secure total dominating set of H of cardinality , which is a contradiction again. Hence, .
On the other hand, if there exists a -set S such that , then S is a secure total dominating set of , and so . Therefore, if , then for every -set S. □
If v is a weak leaf of H, then it could be that . For instance, Figure 2 shows the existence of cases in which the gap is arbitrarily large. In Remark 4 we highlight this fact.
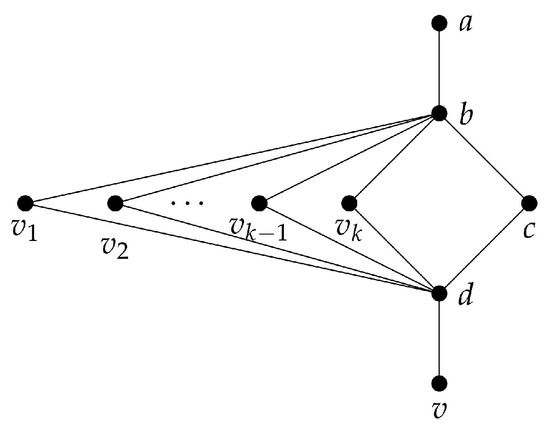
Figure 2.
A graph H where is the -set. Since forms a -set, we have that for every integer .
Remark 4.
For any integer there exists a graph H having a weak leaf vertex v such that .
In contrast to Remark 4, the following result shows the case where v is a strong leaf.
Lemma 2.
Let H be a graph with no isolated vertex. If , then
Proof.
Let D be a -set, and . By Remark 3 we deduce that is a secure total dominating set of and so . Now, let be a -set. Since , by Remark 3 we have that and no vertex of is totally protected by under , which implies that is a secure total dominating set of H and, as a result, . Therefore, □
Lemma 3.
For any graph H having a universal vertex v,
Proof.
Let D be a -set. Since v is a universal vertex of H, it is straightforward that is a secure total dominating set of H. Thus, .
From now on, suppose that and let S be a -set. We differentiate the following two cases.
Case 1. . In this case, as , we deduce that is not a dominating set of . Hence, there exists a vertex such that , which is a contradiction, as S is a 2-dominating set, by Remark 1.
Case 2. . In this case, S is a secure total dominating set of and so , which is a contradiction with Remark 2.
Therefore, the result follows. □
3. The Case of Rooted Product Graphs
Given a graph G of order and a graph H with root vertex v, the rooted product graph is defined as the graph obtained from G and H by taking one copy of G and copies of H and identifying the vertex of G with the root vertex v in the copy of H for every .
If H or G is a trivial graph, then is equal to G or H, respectively. In this sense, hereafter we will only consider graphs G and H of order greater than or equal to two.
For every , will denote the copy of H in containing x. The restriction of any set to will be denoted by , and the restriction to will be denoted by . Hence, and for every -set S we have that
Theorem 1.
For any graphs G and H with no isolated vertex and any ,
Furthermore, if , then
Proof.
Let D be a -set and such that is the subset of induced by D for every . Since S is a secure total dominating set of , we deduce that
Now, assume that . Let W be a -set and such that is the subset of induced by W for every . Since for any -set X, we have that is a secure total dominating set of , we deduce that . □
We now proceed to analyse three cases in which it is not difficult to give closed formulas for . Specifically, we consider the cases in which the root vertex v is a support vertex, a strong leaf, or a universal vertex.
Theorem 2.
The following statements hold for any graphs G and H with no isolated vertex.
- (i)
- If , then Furthermore, for every -set D and every .
- (ii)
- If is a universal vertex, then
- (iii)
- If , then
Proof.
Let D be a -set. Let us first consider the case where . Since for every , by Remark 3 we deduce that is a secure total dominating set of , and as a consequence for every . Hence, . Now, if for some , then , which contradicts Theorem 1. Therefore, (i) follows.
Let us now consider the case where is a universal vertex. Let . If , then is a secure total dominating set of and, as a result, . Now, if , then is a secure total dominating set of , and so Remark 2 and Lemma 3 lead to . Hence, and (ii) follows by Theorem 1.
From now on we assume that . Let be the support of x in for every . Since , we have that . Hence, by Remark 3 we deduce that is a secure total dominating set of , and by Lemma 2 we have that . Moreover, since for every , by Remark 1 it follows that every vertex in has to have a neighbour in , which implies that is a dominating set of G. Therefore,
It remains to show that To this end, let X be a -set, Y a -set, and such that is the subset of induced by Y for every . Notice that . In order to show that is a secure total dominating set of , we only need to observe that every vertex in is totally protected under S by any neighbour in X, while every is totally protected under S by some neighbour in . Thus, , and by Lemma 2 we deduce that . Therefore, (iii) follows. □
Given two graphs G and , the corona graph can be seen as a rooted product graph where H is the join (The join graph is the graph obtained from and by joining each vertex of to all vertices of ) graph and v is the vertex of . Therefore, Lemma 3 and Theorem 2 (ii) lead to the following result on corona graphs.
Theorem 3.
If G is a graph with no isolated vertex, then for every nontrivial graph ,
As we will see later, the behaviour of changes depending on whether the root vertex v is a weak leaf or not. First we proceed to consider the cases where the root vertex is not a weak leaf.
Lemma 4.
Let S be a -set and . If , then the following statements hold.
- .
- If , then .
Proof.
Let . Notice that every vertex in is totally protected under S by some vertex in . Now, suppose that and let . If , then is a secure total dominating set of of cardinality at most , which is a contradiction. Assume that . If , then and . Thus, by Remark 3 no vertex in is totally protected by y under S, and so is a secure total dominating set of of cardinality at most , which is a contradiction. Finally, if , then is a secure total dominating set of and, as above, we arrive to a contradiction. Therefore, .
Now, assume that . First, suppose that . Notice that if , then is a secure total dominating set of , which is a contradiction. Hence, there exists , and so is a secure total dominating set of and , which is a contradiction. Thus, . Now, suppose that . If there exists , then is a secure total dominating set of and , which is a contradiction. Now, if , then one can easily check that is a secure total dominating set of , which is a contradiction again, as . Therefore, . □
From Lemma 4 we deduce that if , then any -set S induces a partition of as follows.
The following corollary is a direct consequence of Theorem 2 (i).
Corollary 1.
Let S be a -set. If , then .
Lemma 5.
Let S be a -set, where . If , then
Proof.
By Lemma 4, if , then , which implies that is a secure total dominating set of of cardinality Hence, and . Notice that Lemma 2 leads to . Thus, by Lemma 1 we conclude that . Therefore, the result follows. □
The following result states the intervals in which the secure total domination number of a rooted product graph can be found.
Theorem 4.
Let G and H be two graphs with no isolated vertex. At least one of the following statements holds for every .
- (i)
- .
- (ii)
- .
- (iii)
- .
Proof.
Let S be a -set and consider the partition of defined above. We differentiate the following four cases.
Case 1. . In this case, for any we have that and, as a consequence, . Thus, Theorem 1 leads to (i).
Case 2. and . In this case, for any we have that and, as a result, .
In order to conclude the proof of (ii), we proceed to show that . To this end, we fix , , a -set D and define a subset W of vertices of as follows.
- (a)
- If , then for any we set and is induced by . It is readily seen that the set W constructed in this manner is a secure total dominating set of and so .
- (b)
- Assume that . If , then is induced by , while if , then is induced by . It is readily seen that the set W constructed in this manner is a secure total dominating set of and, as a result, .
Case 3. and . By Corollary 1, , and by Lemma 5 we have that . Hence, by Theorem 1 we conclude that .
From Lemma 4 we deduce that is a 2-dominating set of G. Hence, . Therefore, in this case (iii) holds.
Case 4. and . By Corollary 1, , and by Lemma 5, . Thus, by Theorem 1 we conclude that .
In order to conclude that in this case (iii) holds, let us define a double dominating set D of G such that . Set D has minimum cardinality among the sets satisfying that and for any , if , then there exists . Notice that every vertex in is dominated by at least one vertex in D and, by Lemma 4, every vertex in is dominated by at least two vertices in . Furthermore, if there exists one vertex such that , then is a secure total dominating set of , which is a contradiction, as . Hence, D is a double dominating set of G. Therefore, . □
The bounds given in the previous theorem are tight. To see this, we consider the following examples where and are the graphs shown in Figure 3.
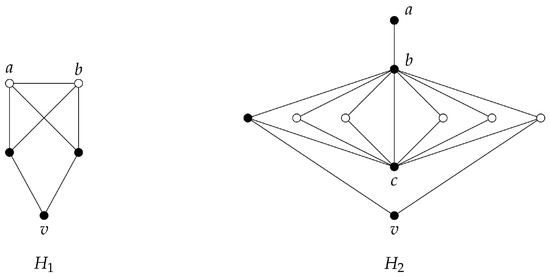
Figure 3.
The set of black-coloured vertices forms a -set for . The set is a -set, while is a -set.
- , where v is the central vertex of and G is a graph with .
- , where .
- Theorem 5 gives some conditions to achieve the equalities In this case we can take .
We now consider some particular cases in which we impose some additional restrictions on G and H. We begin with an immediate consequence of Theorem 4.
Theorem 5.
Let G and H be two graphs with no isolated vertex and . If and , then
Proof.
If , then and Theorem 1 leads to Thus, by Theorem 4 we conclude that if , then □
The following result considers the case in which .
Theorem 6.
Let G and H be two graphs with no isolated vertex and . If , then
Now, if and , then or .
Proof.
Let S be a -set and assume that . By Lemma 5 we have that , and so Lemma 4 leads to for every . Thus, . Therefore, Theorem 1 leads to
From now on we assume that and . Let us distinguish between two cases, according to whether or not .
Case 1. . We define a set as follows. For any we take as a -set, while for any we set . Notice that D is a secure total dominating set of . Now, if there exists a vertex , then the set is a secure total dominating set of . Hence, , and so , which is a contradiction. Thus, .
If for every , then Theorem 1 leads to Suppose that there exists a vertex such that . We define a set as follows. For every , the restriction of to is induced by . Notice that and, if , then every vertex in is totally protected under by some vertex in , which implies that is a secure total dominating set of . Therefore, , concluding that .
Case 2. . First, assume that . Since is a secure total dominating set of for every , we have that , and so Theorem 1 leads to .
Now, assume that there exists . Notice that Lemma 5 leads to . Hence, . If , we define a set as follows. For every , the restriction of to is induced by . As in Case 1, we deduce that is a secure total dominating set of and so we can conclude that Finally, if , then and by Theorem 1 we conclude that . □
Now, we consider a particular case in which .
Theorem 7.
Let G be a graph with no isolated vertex. Let H be a graph and such that . If for every -set S, then
Proof.
Assume that for every -set S. Notice that . Let D be a -set. By Lemma 5 we conclude that . Now, if , then by analogy to Case 1 in the proof of Theorem 4 it follows that .
Suppose that there exists a vertex . If , then is a secure total dominating set of , which implies that , which is a contradiction. Hence, . Now, if , then is a secure total dominating set of and so , which is a contradiction. Finally, if there exists , then is a secure total dominating set of of cardinality and , which is a contradiction again. Therefore, , and we are done. □
The Case in Which the Root Vertex Is a Weak Leaf
The first part of this section is devoted to the case in which the support vertex of the root v has degree greater than or equal to three. From Remark 4 we learned that if , and , then the gap could be arbitrarily large.
Remark 5.
Let H be a graph with no isolated vertex, and . If , then
Proof.
Let S be a -set. By Remark 3, we have that . If , then since , we deduce is a secure total dominating set of . Hence, . Now, if there exists , then is also a secure total dominating set of . Thus, . Therefore, the result follows. □
By Remarks 4 and 5, it seems reasonable to express in terms of rather than . To this end, we consider the following lemma.
Lemma 6.
Let S be a -set. If , and , then for every
Proof.
Let . Notice that every vertex in is totally protected under S by some vertex in . Now, suppose that and let . If , then is a secure total dominating set of , which is a contradiction as . Hence, . Now, if , then we set and otherwise we set for any . In both cases, is a secure total dominating set of and , which is a contradiction. Therefore, . □
By Theorem 1 and Lemma 6, we deduce the next result.
Theorem 8.
Let G and H be two graphs with no isolated vertex. If , and , then
The following result is an immediate consequence of the theorem above.
Corollary 2.
Let G and H be two graphs with no isolated vertex. Let and . If and , then
Theorem 9.
Let G be a graph with and H a graph with no isolated vertex. Let and . If and , then the following statements hold.
- (i)
- If for every -set D, then
- (ii)
- If there exists a -set D such that , then
Proof.
Let S be a -set such that is maximum. For any vertex , let . Let be the partition of defined as follows.
By Theorem 1 we have that Hence, in order to prove (i) we proceed to show that To this end, we need to estimate the gap . Obviously, if , then . Now, since , if , then is a secure total dominating set of , and so . By hypothesis of (i) we deduce that, if , then , while if , then . We now consider the case . By Lemma 6 we have that . If , then is a secure total dominating set of and , which contradicts the hypothesis of (i). Hence, leads to .
In summary, we can conclude that if , then , if , then , while if , then . We claim that there exists a secure total dominating set Z of G such that .
We define Z as a set of minimum cardinality satisfying that and for any with there exists . Notice that, by definition, Z is a double dominating set of G and, since , every vertex in has at least two neighbours in or one neighbour in . Let . Since , there exists such that x is totally protected under S by y. We claim that is a total dominating set of G. Since Z is a total dominating set of G, we have that every vertex in is dominated by some vertex in . Now, if there exists such that , then , and so , concluding that is a total dominating set of G. Hence, Z is a secure total dominating set of G, and as a consequence,
Therefore, proof of (i) is complete.
We now proceed to prove (ii). From Lemma 6 we can consider the partition of defined as follows.
By assumptions, there exists a -set D such that . Let such that is induced by D for every vertex .
If , then is a -set with , which is a contradiction. Hence, . If , then is a -set with , which is a contradiction. Hence, , and so . Now, by hypothesis of (ii), . Moreover, if , then is a secure total dominating set of , and so . Therefore, and .
Now, we suppose that there exists a vertex . Let such that is induced by for every vertex . Since we have that is a secure total dominating set of of cardinality . Therefore, and by Theorem 8, we deduce that .
From now on, we assume that . Hence, and . Let . As , we have that is a secure total dominating set of , and by hypothesis of (ii) we deduce that , which implies that . Hence, .
Since and , by Remark 1, any vertex in is dominated by at least one vertex in . Hence, is a dominating set of G and we differentiate the following two cases.
Case 1. There exists a -set D containing s, such that no vertex in is necessarily totally protected by s under D. Let such that is induced by D for every vertex . In this case, for every -set X we have that is a secure total dominating set of . Hence , and as a consequence, .
Case 2. For every -set D containing s, there exists a vertex in that is totally protected uniquely by s under D. In this case, any vertex in is dominated by another vertex in , which implies that is a total dominating set of G. As in Case 1, let such that is induced by D for every vertex . In this case, for every -set X we have that is a secure total dominating set of . Hence . Therefore, . □
From now on we consider the case in which the support vertex of the root v has degree two.
Lemma 7.
Let H be a graph with no isolated vertex. If , and , then
Proof.
Suppose that and let D be a -set. Since both s and its support vertex in are included in D, we have that is a secure total dominating set of H. Hence, , which is a contradiction. Therefore, , which completes the proof. □
Theorem 10.
Let S be a -set. If , and , then for any ,
Therefore, with the assumptions above,
Proof.
We first consider the case in which is a secure total dominating set of . Since we have that x belongs to every -set. So, .
Now, assume that is not a secure total dominating set of . Notice that every vertex in is totally protected under S by some vertex in . Since , we have that is a secure total dominating set of . Hence, . Now, if there exists such that , then for any -set D, we have that is a secure total dominating set of and , which is a contradiction. Therefore, for every , and since , the result follows. □
We now consider the particular case where . By Lemma 7 we only need to consider two cases according to whether or . These two cases are discussed in Theorems 11 and 12, respectively.
Theorem 11.
Let G be a graph with and H a graph with no isolated vertex. Let , and . If , then
Proof.
Let S be a -set such that . For any vertex , let and . By Theorem 10 there exists a vertex such that . If , then is a secure total dominating set of and so , which is a contradiction. Hence, .
We suppose that . Since , we deduce that . So, the set is a secure total dominating set of of cardinality , which is a contradiction. Hence, , and so .
Let such that is induced by , for any . Since , we deduce that W is a secure total dominating set of , and, as a result, . By Theorem 10 we obtain that , which completes the proof. □
Theorem 12.
Let G be a graph with and H a graph with no isolated vertex. Let , and . If , then
Proof.
By Theorem 10 we have that . Since , any -set D contains as a subset. Let such that is induced by D for every vertex . As for any -set X, the set is a secure total dominating set of , we deduce that .
Let S be a -set such that . For any vertex , let . By Theorem 10, we can conclude that the set is not empty. Since there exists a -set containing , we can assume, without loss of generality, that for every vertex . We claim that Z is a dominating set of G. Let and suppose that . In such a case, and we can define a set such that is induced by for every vertex . Notice that W is a secure total dominating set of and , which is a contradiction. Thus, , which implies that Z is a dominating set of G and so , which completes the proof. □
Theorem 13.
Let G be a graph such that and H a graph with no isolated vertex. If , , and , then
Proof.
For any vertex , let and notice that any -set satisfies that and is a secure total dominating set of . Since , we have that is a secure total dominating set of . Hence, . By Theorem 10 we obtain that , which completes the proof. □
4. Concluding Remarks
It is well-known that the problem of finding the secure total domination number of a graph is NP-hard. This suggests the challenge of finding closed formulas or giving tight bounds for this parameter. In this paper we develop the theory for the class of rooted product graph. The study shows that if the root vertex is strong leaf, a support, or a universal vertex, then there exists a formula for the secure total domination number of the rooted product graph. In the remaining cases, two different behaviours are observed depending on whether the root vertex is a weak leaf or not. Although in a different way, in both cases we were able to give the intervals to which the parameter belongs. The endpoints of these intervals are expressed in terms of other domination parameters of the graphs G and H involved in the product, which allows us to obtain closed formulas when certain conditions are imposed on G or H.
Author Contributions
All authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cockayne, E.J.; Grobler, P.J.P.; Gründlingh, W.R.; Munganga, J.; Van Vuuren, J.H. Protection of a graph. Util. Math. 2005, 67, 19–32. [Google Scholar]
- Benecke, S.; Cockayne, E.J.; Mynhardt, C.M. Secure total domination in graphs. Util. Math. 2007, 74, 247–259. [Google Scholar]
- Cabrera Martínez, A.; Montejano, L.P.; Rodríguez-Velázquez, J.A. On the secure total domination number of graphs. Symmetry 2019, 11, 1165. [Google Scholar] [CrossRef]
- Cabrera Martínez, A.; Montejano, L.P.; Rodríguez-Velázquez, J.A. Total weak Roman domination in graphs. Symmetry 2019, 11, 831. [Google Scholar] [CrossRef]
- Henning, M.A.; Hedetniemi, S.T. Defending the Roman Empire—A new strategy. Discrete Math. 2003, 266, 239–251. [Google Scholar] [CrossRef]
- Cockayne, E.J.; Dreyer, P.A., Jr.; Hedetniemi, S.M.; Hedetniemi, S.T. Roman domination in graphs. Discrete Math. 2004, 278, 11–22. [Google Scholar] [CrossRef]
- Stewart, I. Defend the Roman Empire! Scientific American: New York, NY, USA, 1999; Volume 281, pp. 136–138. [Google Scholar]
- Haynes, T.W.; Hedetniemi, S.T.; Slater, P.J. Domination in Graphs: Advanced Topics; Chapman and Hall/CRC Pure and Applied Mathematics Series; Marcel Dekker, Inc.: New York, NY, USA, 1998. [Google Scholar]
- Haynes, T.W.; Hedetniemi, S.T.; Slater, P.J. Fundamentals of Domination in Graphs; Chapman and Hall/CRC Pure and Applied Mathematics Series; Marcel Dekker, Inc.: New York, NY, USA, 1998. [Google Scholar]
- Henning, M.; Yeo, A. Total Domination in Graphs. Springer Monographs in Mathematics; Springer: New York, NY, USA, 2013. [Google Scholar]
- Chellali, M.; Haynes, T.W.; Hedetniemi, S.T.; McRae, A.A. Roman 2-domination. Discrete Appl. Math. 2016, 204, 22–28. [Google Scholar] [CrossRef]
- Boumediene Merouane, H.; Chellali, M. On secure domination in graphs. Inform. Process. Lett. 2015, 115, 786–790. [Google Scholar] [CrossRef]
- Burger, A.P.; Henning, M.A.; Van Vuuren, J.H. Vertex covers and secure domination in graphs. Quaest. Math. 2008, 31, 163–171. [Google Scholar] [CrossRef]
- Chellali, M.; Haynes, T.W.; Hedetniemi, S.T. Bounds on weak Roman and 2-rainbow domination numbers. Discrete Appl. Math. 2014, 178, 27–32. [Google Scholar] [CrossRef]
- Cockayne, E.J.; Favaron, O.; Mynhardt, C.M. Secure domination, weak Roman domination and forbidden subgraphs. Bull. Inst. Combin. Appl. 2003, 39, 87–100. [Google Scholar]
- Klostermeyer, W.F.; Mynhardt, C.M. Secure domination and secure total domination in graphs. Discuss. Math. Graph Theory 2008, 28, 267–284. [Google Scholar] [CrossRef]
- Valveny, M.; Rodríguez-Velázquez, J.A. Protection of graphs with emphasis on Cartesian product graphs. Filomat 2019, 33, 319–333. [Google Scholar] [CrossRef]
- Duginov, O. Secure total domination in graphs: Bounds and complexity. Discrete Appl. Math. 2017, 222, 97–108. [Google Scholar] [CrossRef]
- Kulli, V.R.; Chaluvaraju, B.; Kumara, M. Graphs with equal secure total domination and inverse secure total domination numbers. J. Inf. Optim. Sci. 2018, 39, 467–473. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).