Efficient Open Domination in Digraph Products

Abstract

A digraph D is an efficient open domination digraph if there exists a subset S of $V\left(D\right)$ for which the open out-neighborhoods centered in the vertices of S form a partition of $V\left(D\right)$. In this work we deal with the efficient open domination digraphs among four standard products of digraphs. We present a method for constructing the efficient open domination Cartesian product of digraphs with one fixed factor. In particular, we characterize those for which the first factor has an underlying graph that is a path, a cycle or a star. We also characterize the efficient open domination strong product of digraphs that have factors whose underlying graphs are uni-cyclic graphs. The full characterizations of the efficient open domination direct and lexicographic product of digraphs are also given.

1. Introduction

In this work we join two natural concepts. The first one is operations on digraphs (under some rules) that result in a bigger digraph than the starting ones. The second one is partitions of sets. There exist many digraph products for which the vertex set is the Cartesian product of vertex sets of its factors (there are also several operations which have (di)graph product in their name, but the vertex set is defined in a different manner). They differ by the definitions of the edge sets. Among them, four are called standard products. These are the Cartesian product, the strong product, the direct product and the lexicographic product. One can find a rich bibliography about them (see [1]). One standard approach of studying the digraph products is to study their structure and how to recognize them. Another approach is to deduce the properties of (di)graph products with respect to some properties of their factors. The later is also the topic of this work.

Partitions of objects are always interesting and useful as a mathematical concept, as every partition yields an equivalence relation. This further enables a factor structure of starting objects, which often brings simplification and deeper insight. Therefore, it is natural to study different kinds of partitions and the existence of them. Unfortunately, we are often not in the position to describe the mentioned relation with the properties of the investigated objects. This often disables further studies.

Graph theory offers a wide range of possibilities for partitions, one of them being the partitions of vertices. Open neighborhoods are a natural example for partitioning the set of vertices. Among graphs this was initiated in 1993 by Cockayne et al. in [2], where such partitions were named total perfect codes. The terminology efficient open domination graphs was introduced by Gavlas and Schultz in 2002 (see [3]). The study of efficient open domination of Cayley graphs can be found in [4]. Grid graphs, that is Cartesian products of two paths, were investigated in [5,6,7] and direct products of graphs with such a partition were characterized in [8]. Characterizations of efficient open domination graphs among lexicographic, strong and disjunctive product of two graphs can be found in [9]. In the same paper [9] the Cartesian products of some known families of graphs with respect to efficient open domination were also investigated. Later, in [10], one factor of a Cartesian product was fixed while the other factor was characterized in such a way that its Cartesian product is an efficient open domination graph.

Existence of a partition of vertices of a graph into closed neighborhoods was initiated even earlier by Biggs in 1976 (see [11]) under the name 1-perfect graphs. The name efficient (closed) domination graphs was proposed later by Bange et al. in [12]. This subject became quite popular and throughout the years several combinatorial and computational results were presented. One of the latest results of this type is that the problem of efficient closed domination is solvable in polynomial time for the class of $P_6$-free graphs, as shown in [13] and independently in [14]. This was further investigated in [15] for some subclasses of $P_6$-free graphs. The authors use the maximum weight independent set problem of a square graph $G^2$ to which the efficient closed domination of G can be reduced. Among products the strong product was treated in [16] and the direct product of (an arbitrary number of) cycles was covered in a series of papers [17,18,19]. For the lexicographic product the topic was covered in [20], while Mollard deals with the efficient closed domination Cartesian product in [21]. Recently, graphs that are both efficient open and efficient closed domination at the same time were considered in [22].

In the case of digraphs one can also distinguish between in- and out-neighborhoods besides open and closed neighborhoods. However, this dilemma is artificial because if we reverse the orientation of the digraph, then in-neighborhoods become out-neighborhoods and vice versa. Hence, we can deal with efficient open and efficient closed domination digraphs. Efficient open domination digraphs were introduced in [23] and studied further in [24,25,26,27]. In [28] Schaudt presented a useful characterization under the name of efficient total domination digraphs. See also [29] for more recent results. As in the case of graphs, there is more literature concerning efficient closed domination digraphs than that of efficient open domination digraphs. Here we mention only [30], a recent work that brings the results on the efficient closed domination among standard products of digraphs.

The paper is organized as follows. In the coming section we first settle the terminology. A section with several results on efficient open domination Cartesian products of digraphs follows. There we present a method for constructing an efficient open domination Cartesian product of digraphs with one fixed factor. Section four is devoted to the efficient open domination strong products of digraphs. We characterize those for which the factors have uni-cyclic graphs as their underlying graphs. Moreover, we conjecture that these are the only efficient open domination digraphs among strong products. The last section brings characterizations of the efficient open domination direct and lexicographic products of digraphs.

2. Preliminaries

The terminology and basic definitions in this section are summarized from [30] where the authors present the results on the efficient closed domination among standard products of digraphs.

Let D be a digraph with the vertex set $V\left(D\right)$ and the arc set $A\left(D\right)$. For any two vertices $u,v\in V\left(D\right)$, we write $(u,v)$ as the arc with direction or orientation from u to v, and say u is adjacent to v, or v is adjacent from u. For an arc $(u,v)$ we also say that u is the in-neighbor of v and that v is the out-neighbor of u. For a vertex $v\in V\left(D\right)$, the open out-neighborhood of v (open in-neighborhood of v) is $N_D^{+}\left(v\right)=\{u\in V\left(D\right):(v,u)\in A\left(D\right)\}$ ($N_D^{-}\left(v\right)=\{u\in V\left(D\right):(u,v)\in A\left(D\right)\}$). The in-degree of v is ${\delta }_D^{-}\left(v\right)=\left|N_D^{-}\left(v\right)\right|$, the out-degree of v is ${\delta }_D^{+}\left(v\right)=\left|N_D^{+}\left(v\right)\right|$ and the degree of v is ${\delta }_D\left(v\right)={\delta }_D^{-}\left(v\right)+{\delta }_D^{+}\left(v\right)$. Moreover, $N_D^{-}\left[v\right]=N_D^{-}\left(v\right)\cup \left\{v\right\}$ is the closed in-neighborhood of v ($N_D^{+}\left[v\right]=N_D^{+}\left(v\right)\cup \left\{v\right\}$ is the closed out-neighborhood of v). In the above notation we omit D if there is no ambiguity with respect to the digraph D. We similarly proceed with any other notation which uses such a style of subscripts. Throughout the paper we use $\left[k\right]=\{1,\dots ,k\}$.

A vertex v of D with ${\delta }^{+}\left(v\right)=\left|V\left(D\right)\right|-1$ is called an out-universal vertex, and if ${\delta }^{-}\left(v\right)=\left|V\left(D\right)\right|-1$, then v is called an in-universal vertex. A vertex v of D with ${\delta }^{+}\left(v\right)=0$ is called a sink, and if ${\delta }^{-}\left(v\right)=0$, then v is called a source. If $\delta \left(v\right)=0$, then v is an isolated vertex or a singleton. An arc of the form $(v,v)$ is called a loop and can be considered as a directed cycle of length one. A vertex v with $\delta \left(v\right)=1$ is called a leaf and is either a sink (if ${\delta }^{+}\left(v\right)=0$) or a source (if ${\delta }^{-}\left(v\right)=0$). Clearly, any vertex u with $\delta \left(u\right)=2$ is either a sink, or a source, or ${\delta }^{-}\left(u\right)=1={\delta }^{+}\left(u\right)$.

The underlying graph of a digraph D is a graph $G_D$ with $V\left(G_D\right)=V\left(D\right)$ and for every arc $(u,v)$ from D we have an edge $uv$ in $E\left(G_D\right)$. If $(u,v)$ and $(v,u)$ are both arcs, then we have two edges between u and v in the underlying graph. A directed path is a digraph $D\cong P_n$ with one source and one sink where its underlying graph is isomorphic to a path $P_n$. Similarly, a directed cycle is a digraph $D\cong C_n$ without sinks and sources with a cycle $C_n$ as its underlying graph. We also consider a loop as a directed cycle $C_1$ of length one and double arc with different orientation as a directed cycle $C_2$ of length two. The distance $d_D(u,v)$ between two vertices u and v is the minimum number of arcs on a directed path from u to v or ∞ if such a directed path does not exist. For $A\subseteq V\left(D\right)$ we denote by $D-A$ a digraph obtained from D by deleting all vertices from A. By $D\left[A\right]$ we denote the subdigraph of D that is induced on the vertices from A.

Let D be a digraph and let $S\subseteq V\left(D\right)$. The set S is called a total dominating set of D if the open out-neighborhoods centered in vertices of S cover $V\left(D\right)$, that is $V\left(D\right)={\bigcup }_{v\in S}{N}_D^{+}\left(v\right)$. Let S be a total dominating set of D. If $N_D^{+}\left(v\right)\cap N_D^{+}\left(u\right)=\varnothing$ for every two different vertices $u,v\in S$, then the set $\{N_D^{+}\left(v\right):v\in S\}$ not only covers $V\left(D\right)$ but also partitions $V\left(D\right)$. In this case we say that S is an efficient open dominating set (or an EOD set for short) of D. If there exists an EOD set S for the digraph D, then D is called an efficient open domination digraph (or an EOD digraph for short). For $A\subseteq V\left(D\right)$ we say that $S_A\subseteq V\left(D\right)$ is efficient open domination set only (or an EOD set only for short) for a digraph $D-A$ if every vertex from $V\left(D\right)-A$ has exactly one in-neighbor in $S_A$ and in addition $A\cap N_D^{+}\left(S_A\right)=\varnothing$.

Let D and F be digraphs. Different products of digraphs D and F have, similarly as in graphs, their set of vertices equal to $V\left(D\right)\times V\left(F\right)$. We roughly and briefly discuss the four standard products of digraphs: the Cartesian product $D\square F$, the direct product $D\times F$, the strong product $D⊠F$ and the lexicographic product $D\circ F$ (sometimes also denoted $D\left[F\right]$). Adjacency in different products is defined as follows.

• In the Cartesian product $D\square F$ there exists an arc from vertex $(d,f)$ to vertex $(d^{\prime },f^{\prime })$ if there exists an arc from d to $d^{\prime }$ in D and $f=f^{\prime }$ or $d=d^{\prime }$ and there exists an arc from f to $f^{\prime }$ in F.
• If there is an arc from d to $d^{\prime }$ in D and an arc from f to $f^{\prime }$ in F, then there exists an arc from $(d,f)$ to $(f^{\prime },d^{\prime })$ in the direct product $D\times F$.
• In the strong product we have $((d,f),(d^{\prime },f^{\prime }))\in A(D⊠F)$ if ($(d,d^{\prime })\in A\left(D\right)$ and $f=f^{\prime }$) or ($d=d^{\prime }$ and $(f,f^{\prime })\in A\left(F\right)$) or ($(d,d^{\prime })\in A\left(D\right)$ and $(f,f^{\prime })\in A\left(F\right)$).
• There is an arc in the lexicographic product $D\circ F$ from a vertex $(d,f)$ to a vertex $(d^{\prime },f^{\prime })$, whenever $(d,d^{\prime })\in A\left(D\right)$ or ($d=d^{\prime }$ and $(f,f^{\prime })\in A\left(F\right)$).

Some examples of the above mentioned products appear in Figure 1.

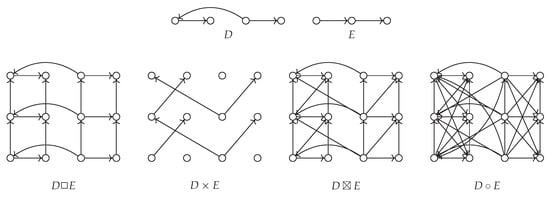
Figure 1. The digraphs D and E, and their Cartesian, direct, strong and lexicographic products.

Let $\ast \in \{\square ,\times ,⊠,\circ \}$. The map $p_D:V(D\ast F)\to V\left(D\right)$ defined by $p_D\left((d,f)\right)=d$ is called the projection map onto D. Similarly, we define $p_F$ as the projection map onto F. Projections are defined as maps between vertices, but frequently it is more convenient to see them as maps between digraphs. In this case we observe the subdigraphs induced by $B\subseteq V(D\circ F)$ and $p_X\left(B\right)$ for $X\in \{D,F\}$. Notice that in the Cartesian and in the strong product the arcs project either to arcs (with the same orientation) or to a vertex. In the case of the direct product arcs always project to arcs (with the same orientation). In the lexicographic product $D\circ F$ the projection $p_D$ maps arcs into arcs (with the same orientation) or into vertices. In the same product the projection $p_F$ maps arcs into vertices, into arcs with the same orientation, into arcs with different orientation or into two vertices without an arc between them.

For a fixed $f\in V\left(F\right)$ we call set $D^f=\{(d,f)\in V(D\ast F):d\in V\left(D\right)\}$ a D-layer through f in $D\ast F$, where $\ast \in \{\square ,\times ,⊠,\circ \}$. Symmetrically, an F-layer $F^d$ through d is defined for a fixed $d\in V\left(D\right)$. Notice that for the Cartesian product, for the strong product and for the lexicographic product, $(D\ast F)\left[D^f\right]$ is isomorphic to D and $(D\ast F)\left[F^d\right]$ is isomorphic to F, respectively. In the case of the direct product loops play an important role. If there are no loops in f and in d, then the subdigraphs $(D\ast F)\left[F^d\right]$ and $(D\ast F)\left[D^f\right]$ are isomorphic to an empty digraph on $\left|V\right(F\left)\right|$ and $\left|V\right(D\left)\right|$ vertices, respectively. If we have $(d,d)\in A\left(D\right)$ and $(f,f)\in A\left(F\right)$, then $(D\ast F)\left[F^d\right]$ and $(D\ast F)\left[D^f\right]$ are isomorphic to F and D, respectively.

It is easy to see that open out-neighborhoods in the direct product of digraphs satisfy

$$N_{D\times F}^{+}\left((d,f)\right)=N_D^{+}\left(d\right)\times N_F^{+}\left(f\right)$$

(1)

and for the lexicographic product of digraphs it holds that

$$N_{D\circ F}^{+}\left((d,f)\right)=\left(N_D^{+}\left(d\right)\times V\left(F\right)\right)\cup \left(\left\{d\right\}\times N_F^{+}\left(f\right)\right).$$

(2)

Using these two equalities a complete characterization of the EOD digraphs among the direct and the lexicographic product is presented in the last section.

3. The Cartesian Product

Definition 1.

Let F be a digraph and let$S_1,\dots ,S_k\subseteq V\left(F\right)$. If$S_i$is an EOD set only for$F-S_{i-1}$,$i\in \left[k\right]$, where$S_0=\varnothing$, then we say that F is a k-EOD path divisible. Similarly, if$S_i$is an EOD set only for$F-S_{i-1}$,$i\in \left[k\right]$, where$S_0=S_k$, then we say that F is a k-EOD cycle divisible. We say that sets$S_1,\dots ,S_k$are k-EOD path or k-EOD cycle divisible sets of F.

Notice that every k-EOD path divisible digraph is also an EOD digraph, because $S_1$ is an EOD set only for $F-S_0=F$. Therefore, an EOD digraph F with an EOD set $S_1$ is 1-EOD path divisible. Also if F is n-EOD path divisible, then it is also m-EOD path divisible for every $m\le n$. In particular, let F be a directed cycle, that is F is an EOD digraph with the EOD set $S=V\left(F\right)$. If we set $S_{2i-1}=V\left(F\right)$ and $S_{2i}=\varnothing$, then F is k-EOD path divisible for every positive integer k. If F is k-EOD path divisible, then it can happen that $S_i\cap S_j\ne \varnothing$. See an example of this on Figure 2.

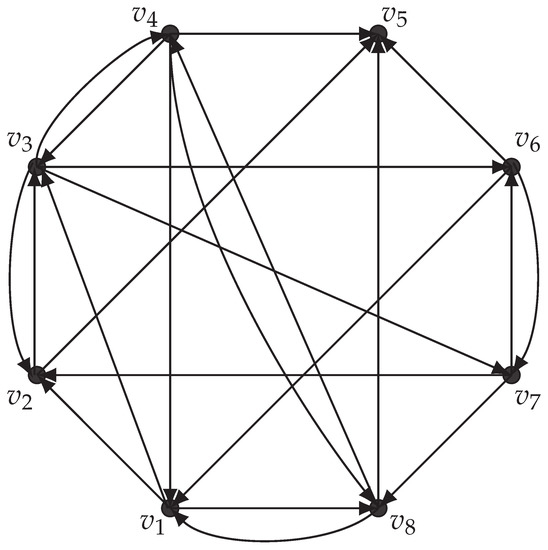
Figure 2. 4-EOD path divisible digraph with $S_1=\{v_3,v_4\},S_2=\{v_6,v_7\},S_3=\{v_1,v_8\},S_4=\{v_2,v_3\}$ and with $S_1\cap S_4=\left\{v_3\right\}$.

With the following example we underline the rich structure of n-EOD path (or cycle) divisible digraphs. We will show that every digraph can be an induced digraph of an n-EOD path (or cycle) divisible digraph. A complete digraph $K_n$ contains an arc in both directions between all different vertices of $K_n$. Let $V\left(K_n\right)=\{v_1,\dots ,v_n\}$. Digraph $K_n^{-}$ is obtained from $K_n$ by deleting all arcs $(v_{i+1},v_i)$, $i\in [n-1]$. For a digraph F we construct an n-EOD path divisible digraph $F^{+}$ in the folowing way. We take one copy of F and two copies of $K_n^{-}$, the first copy containing the vertices $V_1=\{v_1,\dots ,v_n\}$ and the second copy containing the vertices $V_2=\{v_1^{\prime },\dots ,v_n^{\prime }\}$. The arc set of $F^{+}$ contains $A\left(F\right)$, all arcs from both copies of $K_n^{-}$, the set $\{(v_i,v_i^{\prime }),(v_i^{\prime },v_i):i\in \left[n\right]\}$, all arcs from the set $\{(v_i,f):v_i\in V_1,f\in V\left(F\right)\}$ and an arbitrary subset of $\{(f,v_i),(f,v_i^{\prime }):f\in V\left(F\right),v_i\in V_1,v_i^{\prime }\in V_2\}$. It is not hard to see that $F^{+}$ is an n-EOD path divisible digraph with n-EOD path divisible sets $S_i=\{v_i,v_i^{\prime }\}$ for every $i\in \left[n\right]$.

Similar construction can be done to get an n-EOD cycle divisible digraph. We only need to delete arcs $(v_1,v_n)$ and $(v_1^{\prime },v_n^{\prime })$ from $F^{+}$. Also if F is an n-EOD cycle divisible digraph, then F is also an $kn$-EOD cycle divisible digraph, where $kn$-EOD cycle divisible sets are repeated cyclically k times.

Next we show that n-EOD path divisibility of F is essential for the Cartesian product $P_n\square F$ to be an EOD digraph, where $P_n$ is a directed path.

Theorem 1.

Let$P_n$be a directed path and let F be a digraph. The Cartesian product$P_n\square F$is an EOD digraph if and only if F is an n-EOD path divisible digraph.

Proof. 

Let $P_n=v_1\dots v_n$ be a directed path where $v_1$ is the source and $v_n$ is the sink and let F be an arbitrary digraph.

First assume that F is an n-EOD path divisible digraph. Denote by $S_1,\dots ,S_n$ the subsets of $V\left(F\right)$ that correspond with n-EOD path divisibility. We will show that $S={\cup }_{i=1}^n\left\{v_i\right\}\times S_i$ is an EOD set of $P_n\square F$, meaning that $|N^{-}(v_i,u)\cap S|=1$ for every $i\in \left[n\right]$ and $u\in V\left(F\right)$. For every $(v_1,u)$ it holds that $|N^{-}(v_1,u)\cap S|\ge 1$ because $S_1$ is an EOD set of F and therefore $\left\{v_1\right\}\times S_1$ is an EOD set for $(P_n\square F)\left[F^{v_1}\right]\cong F$. Since $v_1$ is a source of $P_n$, there do not exist any other in-neighbors of vertices in $F^{v_1}$ except those already in $F^{v_1}$, so $|N^{-}(v_1,u)\cap S|=1$. Next we observe $(v_i,u)$ for $2\le i\le n$ and $u\in V\left(F\right)$. If $u\in S_{i-1}$, then $(v_i,u)$ has an in-neighbor in $\left\{v_{i-1}\right\}\times S_{i-1}\subset S$ and if $u\in V\left(F\right)-S_{i-1}$, then $(v_i,u)$ has an in-neighbor in $\left\{v_i\right\}\times S_i\subset S$. On the other hand these neighbors are unique in S, because $N_F^{+}\left(S_i\right)\cap S_{i-1}=\varnothing$ and $S_i$ is an EOD set only for $F-S_{i-1}$. Hence, S is an EOD set of $P_n\square F$, which is therefore an EOD digraph.

Now assume that $P_n\square F$ is an EOD digraph and let S be its EOD set. Let $S_i=p_F(S\cap F^{v_i})$ for $i\in \left[n\right]$ and let $S_0=\varnothing$. Clearly, every vertex from $F^{v_1}$ must have exactly one in-neighbor in $\left\{v_1\right\}\times S_1$ because $v_1$ is a source of $P_n$. Therefore, $S_1$ is an EOD set of $F-S_0=F$ and $N_F^{+}\left(S_1\right)\cap S_0=\varnothing$. Now let $i>1$. Vertices from $\left\{v_i\right\}\times S_{i-1}$ have in-neighbors in $\left\{v_{i-1}\right\}\times S_{i-1}$ and therefore do not have in-neighbors in $\left\{v_i\right\}\times S_i$, meaning that $N_F^{+}\left(S_i\right)\cap S_{i-1}=\varnothing$. On the other hand all other vertices in $F^{v_i}$ must have an in-neighbor in $\left\{v_i\right\}\times S_i$, because S is an EOD set of $P_n\square F$. Thus, $S_i$ is an EOD set only for $F-S_{i-1}$. Therefore, $S_1,\dots ,S_n$ yield that F is an n-EOD path divisible digraph. □

With n-EOD cycle divisibility one can describe all EOD digraphs among $C_n\square F$ where $C_n$ is a directed cycle. The proof is very similar to the proof of Theorem 1 and is therefore omitted. The main difference is that we do not need to treat layer $F^{v_1}$ separately since everything follows from the general step.

Theorem 2.

Let$C_n$be a directed cycle and let F be a digraph. The Cartesian product$C_n\square F$is an EOD digraph if and only if F is an n-EOD cycle divisible digraph.

We continue with a path that is oriented in such a way, that it has exactly one source of degree two.

Theorem 3.

Let D be a digraph with an underlying graph$P_n=v_1\dots v_n$with such an orientation that$v_k$,$1<k<n$, is the only source, let$m=max\{k,n-k+1\}$and let F be a digraph. The Cartesian product$D\square F$is an EOD digraph if and only if F is an m-EOD path divisible digraph.

Proof. 

Let $v_k$ be the only source of D. Thus $P^{\prime }=v_k{v}_{k-1}\dots v_1$ is a directed path on k vertices, where $v_k$ is the source and $v_1$ is the sink, and $P^{″}=v_k{v}_{k+1}\dots v_n$ is a directed path on $n-k+1$ vertices, where $v_k$ is the source and $v_n$ is the sink. Let $m=max\{k,n-k+1\}$. If F is m-EOD path divisible with sets $S_i$, $i\in \left[m\right]$, then F is k-EOD path divisible with sets $S_i$, $i\in \left[k\right]$ and also $(n-k+1)$-EOD path divisible with sets $S_i$, $i\in [n-k+1]$. As shown in the proof of Theorem 1, sets $S\left(k\right)=({\cup }_{i=1}^k\left\{v_i\right\}\times S_{k-i+1})$ and $S(n-k+1)=({\cup }_{i=k}^n\left\{v_i\right\}\times S_i)$ are EOD sets for $P^{\prime }\square F$ and $P^{″}\square F$, respectively. Clearly, $S=S\left(k\right)\cup S(n-k+1)$ is an EOD set of $D\square F$ because $F^{v_k}\cap S\left(k\right)=F^{v_k}\cap S(n-k+1)$ and $D\square F$ is an EOD digraph.

Now assume that $D\square F$ is an EOD digraph and let S be its EOD set. Since $v_k$ is a source, $P^{\prime }\square F$ and $P^{″}\square F$ are also EOD digraphs. By Theorem 1 F is a k-EOD path divisible digraph and an $(n-k+1)$-EOD path divisible digraph. Hence, F is also m-EOD path divisible for $m=max\{k,n-k+1\}$. □

Before we deal with a path that is oriented in such a way, that it has exactly one sink of degree two, we need the following definition.

Definition 2.

Let F be a k-EOD and an ℓ-EOD path divisible digraph. We say that F is$k,\ell$-sink friendly if there exist k-EOD path divisible sets$S_1,\dots ,S_k$and ℓ-EOD path divisible sets$S_1^{\prime },\dots ,S_{\ell }^{\prime }$such that$S_k\cap S_{\ell }^{\prime }=\varnothing$and there exists a set$S_0\subseteq V\left(F\right)$, which is an EOD set only for$F-(S_k\cup S_{\ell }^{\prime })$.

Theorem 4.

Let D be a digraph with an underlying graph$P_n=v_1\dots v_n$with such an orientation that$v_k$,$1<k<n$, is the only sink and let F be a digraph. The Cartesian product$D\square F$is an EOD digraph if and only if F is$(k-1),(n-k)$-sink friendly.

Proof. 

Let F be digraph and let D be a digraph with an underlying graph $P_n=v_1\dots v_n$ where $v_k$, $1<k<n$, is the only sink. This means that $v_1$ and $v_n$ are the only sources of D.

First assume that F is $(k-1),(n-k)$-sink friendly. This means that there exist sets $S_1,\dots ,S_{k-1}$ that yield $(k-1)$-EOD path divisibility of F and sets $S_n,S_{n-1}\dots ,S_{k+1}$ that yield $(n-k)$-EOD path divisibility of F. In addition, $S_{k-1}\cap S_{k+1}=\varnothing$ and there exists a set $S_k\subseteq V\left(F\right)$ which is an EOD set only for $F-(S_{k-1}\cup S_{k+1})$. Let $A={\cup }_{i=1}^{k-1}(\left\{v_i\right\}\times S_i)$ and $B={\cup }_{j=k+1}^n(\left\{v_j\right\}\times S_j)$. We will show that $S=A\cup B\cup (\left\{v_k\right\}\times S_k)$ is an EOD set of $D\square F$. Let $Q=v_1\dots v_{k-1}$ and $R=v_n{v}_{n-1}\dots v_{k+1}$ be directed subpaths of D. By Theorem 1, $Q\square F$ and $R\square F$ are EOD digraphs with EOD sets A and B, respectively. No vertex from $F^{v_k}$ is an in-neighbor of vertices from $Q\square F$ and $R\square F$, because $v_k$ is a sink. Therefore, there exists exactly one in-neighbor in S for every vertex from $Q\square F$ and $R\square F$. So, we only need to check $(v_k,f)$ for every $f\in V\left(F\right)$. If $f\in S_{k-1}$, then $(v_{k-1},f)\in S$ is the in-neighbor of $(v_k,f)$. On the other hand this is the only neighbor of $(v_k,f)$ from S because $(v_{k+1},f)\notin S$ as $S_{k-1}\cap S_{k+1}=\varnothing$ and because $S_k$ is an EOD set only for $F-(S_{k-1}\cup S_{k+1})$. By symmetry we can see that $(v_k,f)$ has also exactly one in-neighbor in S whenever $f\in S_{k+1}$. So let $f\in V\left(F\right)-(S_{k-1}\cap S_{k+1})$. Clearly $(v_k,f)$ has no in-neighbor from S in $F^{v_{k-1}}$ and in $F^{v_{k+1}}$. Since $S_k$ is an EOD set only for $F-(S_{k-1}\cup S_{k+1})$, there exists exactly one in-neighbor x of f in $S_k$ and $(v_k,x)$ is therefore the only neighbor of $(v_k,f)$ from S. Hence, S is an EOD set of $D\square F$ which is therefore an EOD digraph.

Now assume that $D\square F$ is an EOD digraph and let S be its EOD set. Again, for directed paths $Q=v_1\dots v_{k-1}$ and $R=v_n{v}_{n-1}\dots v_{k+1}$, $Q\square F$ and $R\square F$ are EOD digraphs with no influence from $F^{v_k}$ in a product $D\square F$. Sets $S_i=p_F(S\cap F^{v_i})$ for $i\in [k-1]$ are $(k-1)$-EOD path divisible sets by Theorem 1 and sets $S_j=p_F(S\cap F^{v_j})$ for $j\in \{k+1,\dots ,n\}$ (in reversed order) are $(n-k)$-EOD path divisible sets by the same theorem. If $f\in S_{k-1}\cap S_{k+1}$, then $(v_k,f)$ has two in-neighbors $(v_{k-1},f)$ and $(v_{k+1},f)$ in S, a contradiction. Therefore, we have $S_{k-1}\cap S_{k+1}=\varnothing$. Let $S_k=p_F(S\cap F^{v_k})$ and let f be an arbitrary vertex from $\in V\left(F\right)-(S_{k-1}\cup S_{k+1})$. Clearly, $(v_k,f)$ has exactly one in-neighbor in $\left\{v_k\right\}\times S_k$ because S is an EOD set. Also $(v_k,f^{\prime })$, $f^{\prime }\in S_{k-1}\cup S_{k+1}$, has no in-neighbor in $\left\{v_k\right\}\times S_k$ as it has its unique in-neighbor either in S, in $\left\{v_{k-1}\right\}\times S_{k-1}$ or in $\left\{v_{k+1}\right\}\times S_{k+1}$. Hence, $S_k$ is an EOD set only for $V\left(F\right)-(S_{k-1}\cup S_{k+1})$ and F is $(k-1),(n-k)$-sink friendly. □

The next challenge considering digraphs with an underlying graph isomorphic to a path or to a cycle is when we have more sinks and sources of degree two. Clearly, after every sink there comes a source and after each source there is a sink. In the case of a sink v of degree two digraph F must be $k,\ell$-sink friendly by Theorem 4, where $k+1$ and $\ell +1$ are the distances to the sources that are closest to v. However this is not always enough. Let x and y be two sinks and let u be a source between them. By Theorem 4 digraph F must be $k_1,{\ell }_1$-sink friendly and $k_2,{\ell }_2$-sink friendly where $k_1+1$ and $k_2+1$ are the distances between u and x and u and y, respectively. We say that F is $k_1,k_2$-source friendly if $S_1=S_1^{\prime }$. Here, sets $S_1,\dots ,S_{k_1}$ and $S_1^{\prime },\dots ,S_{k_2}^{\prime }$ are appropriate $k_1$- and $k_2$-EOD path divisible sets from $k_1,{\ell }_1$-sink friendly and $k_2,{\ell }_2$-sink friendly constellation, respectively. Now, if we can assure sink friendliness for each sink, and also source friendliness for each source of a digraph F, then this is characteristic for $D\square F$ to be an EOD digraph. Here, the underlying graph of D is either $P_k$ or $C_k$ with more than one source or sink of degree two. Because the proof is very similar and the formal statement is problematic (it depends on the status of vertices of degree one in D), we omit the proof of this.

We end this section with another fixed factor which this time has a star $K_{1,n}$ as its underlying graph. Vertex of degree n is the source and all the others are sinks.

Theorem 5.

Let D be a digraph with an underlying graph$K_{1,n}$with the set of vertices$\{v_0,v_1,\dots ,v_n\}$, where${\delta }_D^{+}\left(v_0\right)=n$and let F be an arbitrary digraph. The Cartesian product$D\square F$is an EOD digraph if and only if F is a 2-EOD path divisible digraph.

Proof. 

Let D be a digraph with an underlying graph $K_{1,n}$ with the set of vertices $\{v_0,v_1,\dots v_n\}$, where ${\delta }_D^{+}\left(v_0\right)=n$, which means that $v_0$ is the source. Clearly, ${\delta }_D^{-}\left(v_i\right)=1$ and $v_i$ is a sink for every $i\in \left[n\right]$. Let F be an arbitrary digraph. Denote by A the set of vertices of $D\square F$.

First assume that F is 2-EOD path divisible with sets $S_1$ and $S_2$. We will show that $S=(\left\{v_0\right\}\times S_1)\cup ({\cup }_{i=1}^n\left\{v_i\right\}\times S_2)$ is an EOD set for $D\square F$, meaning that $|N^{-}\left((e,f)\right)\cap S|=1$ for every $(e,f)\in A$. For every $(v_0,f)\in A$ it holds that $|N^{-}\left((v_0,f)\right)\cap S|\ge 1$ since $S_1$ is an EOD set for F and therefore $\left\{v_0\right\}\times S_1$ is an EOD set for $(D\square F)\left[F^{v_0}\right]\cong F$. Since $v_0$ is a source, there do not exist any other in-neighbors of vertices $F^{v_0}$ except those from $F^{v_0}$, so $|N^{-}\left((v_0,f)\right)\cap S|=1$. Now let $(v_i,f)\in A$, $i\in \left[n\right]$. Vertices from $\left\{v_0\right\}\times S_1$ are the in-neighbors of all of the vertices from $\left\{v_i\right\}\times S_1$ and, since F is 2-EOD path divisible, vertices from $\left\{v_i\right\}\times S_2$ are the in-neighbors of all of the vertices from $\left\{v_i\right\}\times (V\left(F\right)-S_1)$. So $|N^{-}\left((v_i,f)\right)\cap S|\ge 1$. By the definition of 2-EOD path divisibility it holds that $|N^{+}(\left\{v_i\right\}\times S_2)\cap (\left\{v_i\right\}\times S_1)|=0$, meaning that $|N^{-}\left((v_i,f)\right)\cap S|=1$.

Now assume that $D\square F$ is an EOD digraph and let S be its EOD set. Let $v_i$ be an arbitrary vertex of the star D different from $v_0$. Vertices from $S\cap F^{v_0}$ are in-neighbors of some (or all) of the vertices of $F^{v_i}$. Denote the set of those vertices by $F_{v_i}$. Vertices from $F^{v_i}-F_{v_i}$ have to have in-neighbors in $S\cap F^{v_i}$, since they do not have in-neighbors in $S\cap F^{v_0}$. Vertices from $S\cap F^{v_i}$ are not in-neighbors of any of the vertices from $F_{v_i}$, since that would mean that there exists $(v_i,f)\in F_{v_i}$ for which $|N^{-}(v_i,f)\cap S|>1$, a contradiction with S being an EOD set of $D\square F$. Let $S_1:=p_H(S\cap F^{s_0})$ and $S_2:=p_H(S\cap F^{s_1})$. Clearly, $S_1$ is an EOD set of F and $S_2$ is an EOD set only for $F-S_1$. Hence, F is a 2-EOD path divisible digraph. □

4. The Strong Product

In this section we first characterize all EOD strong product digraphs $D⊠F$, such that the underlying graphs of D and F are cycles $C_m$ and $C_n$, respectively. Then we extend this result to a characterization of all EOD digraphs $D⊠F$ where D and F have uni-cyclic graphs as their underlying graphs. We also conjecture that there are no more EOD digraphs among the strong product of digraphs. We start with several lemmas that come in handy later.

Lemma 1.

Let D and F be two digraphs without isolated vertices. If one of them has a source, then$D⊠F$is not an EOD digraph.

Proof. 

Let D and F be two digraphs. If D has a source u and F has a source v, then vertex $(u,v)$ is a source in $D⊠F$ and it has no in-neighbor. Hence, there does not exist an EOD set for $D⊠F$. Without loss of generality let D have a source u and let F be an arbitrary digraph without a source. We will try to construct an EOD set S for $D⊠F$. Since u is a source, vertex $(u,y),y\in V\left(F\right),$ has in-neighbors only in $D^u$, and since F does not have a source at least one in-neighbor of $(u,y)$ exists. Let $(u,y^{\prime })\in S$ be the in-neighbor of $(u,y)$. Again, since u is a source and F has no source, there exists an in-neighbor $(u,y^{″})\in S$ of $(u,y^{\prime })\in D^u$. Denote by $u^{\prime }$ an out-neighbor of u in D. It exists since D contains no isolated vertices. By the definition of the strong product of two digraphs, both $(u,y^{\prime })$ and $(u,y^{″})$ are in-neighbors of $(u^{\prime },y^{\prime })$ and since $(u,y^{\prime }),(u,y^{″})\in S$ vertex $(u^{\prime },y^{\prime })$ has two different in-neighbors in S. Meaning that S is not an EOD-set, so $D⊠F$ is not an EOD digraph. □

In the rest of this section we use the following notation and orientation for directed cycles $C_m=c_1{c}_2\dots c_m$ and $C_n=d_n{d}_{n-1}\dots d_1$ on m and n vertices, respectively, see Figure 3, and with $(c_i,d_j)$ we denote a vertex of a strong product of those two cycles. All operations on the first index i are via $\left(\mathrm{mod}\mathrm{m}\right)$ and on the second index j are via $\left(\mathrm{mod}\mathrm{n}\right)$. We also partition $V(C_m⊠C_n)$ into sets

$$\begin{array}{cc}\hfill A& =\{(c_i,d_j);i+j=3q+1,q\in \mathbb{N}\},\hfill \\ \hfill B& =\{(c_i,d_j);i+j=3q+2,q\in \mathbb{N}\}\mathrm{and}\hfill \\ \hfill C& =\{(c_i,d_j);i+j=3q,q\in \mathbb{N}\}.\hfill \end{array}$$

(3)

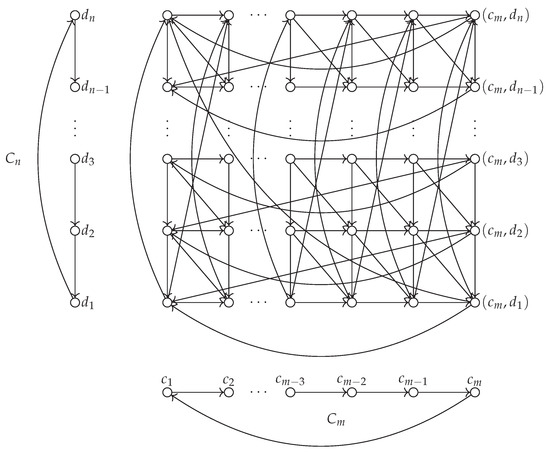
Figure 3. The strong product of two directed cycles $C_m$ and $C_n$.

Lemma 2.

If there exists an EOD set S for$C_m⊠C_n$,$m,n\ge 3$, and$(c_i,d_j)\in S$, then$(c_{i-1},d_{j+1})\in S$.

Proof. 

Let $C_m⊠C_n$, $m,n\ge 3$, be an EOD digraph, let S be its EOD set and let $(c_i,d_j)\in S$. The vertex $(c_i,d_j)$ is an in-neighbor of $(c_{i+1},d_j),(c_i,d_{j-1})$ and $(c_{i+1},d_{j-1})$. On the other hand $(c_i,d_j)$ must also have an in-neighbor in S. The only in-neighbors of $(c_i,d_j)$ are $(c_{i-1},d_j),(c_i,d_{j+1})$ and $(c_{i-1},d_{j+1})$. If $(c_{i-1},d_j)\in S$, then $(c_i,d_j)$ and $(c_{i-1},d_j)$ are both in-neighbors of $(c_i,d_{j-1})$, a contradiction. Similarly, if $(c_i,d_{j+1})\in S$, then $(c_i,d_j)$ and $(c_i,d_{j+1})$ are both in-neighbors of $(c_{i+1},d_j)$, a contradiction again. Hence, $(c_{i-1},d_{j+1})$ must be in S. □

Lemma 3.

If there exists an EOD set S for$C_m⊠C_n$,$m,n\ge 3$, and$(c_i,d_j)\in S$, then$(c_i,d_{j+3}),(c_{i-3},d_j)\in S$.

Proof. 

Let $C_m⊠C_n$, $m,n\ge 3$, be an EOD digraph and let S be its EOD set. With possible change of notation let $(c_m,d_1)\in S$. A vertex $(c_m,d_1)$ is an in-neighbor of the vertices $(c_1,d_1)$, $(c_m,d_n)$ and $(c_1,d_n)$. Vertex $(c_{m-1},d_2)$ belongs to S by Lemma 2. Clearly, $(c_{m-1},d_2)$ is also the in-neighbor of vertices $(c_{m-1},d_1)$ and $(c_m,d_2)$. So $(c_m,d_2)\notin S$ because otherwise $(c_m,d_1)$ has two in-neighbors in S. If $(c_m,d_3)\in S$, then $(c_m,d_2)$ has two in-neighbors in S again. So $(c_m,d_3)\notin S$.

Vertex $(c_{m-2},d_3)\in S$ by Lemma 2 since $(c_{m-1},d_2)\in S$ and $(c_{m-2},d_3)$ is an in-neighbor of $(c_{m-2},d_2)$ and $(c_{m-1},d_3)$. One of the in-neighbors $(c_{m-1},d_3)$, $(c_m,d_4)$ or $(c_{m-1},d_4)$ of the vertex $(c_m,d_3)$ must be in S. If $(c_{m-1},d_3)\in S$, then $(c_m,d_2)$ has two in-neighbors in S. Similarly, if $(c_{m-1},d_4)\in S$, then $(c_{m-1},d_3)$ has two in-neighbors in S. Hence, $(c_m,d_4)\in S$.

We can exchange the role of factors and by symmetric arguments get that $(c_{i-3},d_j)$ also belongs to S. □

Now we can characterize all EOD digraphs among strong product digraphs of two cycles.

Theorem 6.

Let D and F be digraphs with underlying graphs$C_m$and$C_n$, respectively. The strong product$D⊠F$is an EOD digraph if and only if both D and F are directed cycles,$m=3\ell$and$n=3k$for some$k,\ell \in \mathbb{N}$.

Proof. 

First, let $m=3\ell$ and $n=3k$, $k,\ell \in \mathbb{N}$, and let $D\cong C_m$ and $F\cong C_n$ be two directed cycles. Recall the sets $A,B$ and C from (3). We will show that A is an EOD set of $C_m⊠C_n$. The in-neighbor of a vertex $(c_i,d_j)\in B$, $i+j=3q+2$, that is in A is $(c_{i-1},d_j)$, since $(i-1)+j=(i+j)-1=(3q+2)-1=3q+1$. The in-neighbor of a vertex $(c_i,d_j)\in C$, $i+j=3q$, that is in A is $(c_i,d_{j+1})$, since $i+(j+1)=(i+j)+1=3q+1$. The in-neighbor of a vertex $(c_i,d_j)\in A$, $i+j=3q+1$, that is in A is $(c_{i-1},d_{j+1})$, since $(i-1)+(j+1)=i+j=3q+1$. So every vertex v from $V(C_m⊠C_n)$ is efficiently dominated by A. Moreover v has exactly one in-neighbor in A since exactly one in-neighbor of v has the sum of indices equal to $3q+1$.

To prove the contrary let D and F be two digraphs with underlying graphs $C_m$ and $C_n$, respectively, such that $D⊠F$ is an EOD digraph with an EOD set S. If one of the cycles is not directed, then it has a source. By Lemma 1 the strong product $D⊠F$ is not an EOD digraph. So we may assume that both D and F are directed cycles. With possible change of notation we may assume that $(c_m,d_1)\in S$. By consecutive use of Lemma 3 we get that $\{(c_m,d_{3k+1}):k\in [\lfloor n/3\rfloor \left]\right\}\subseteq S$ and that $\{(c_{m-3\ell },d_1):\ell \in [\lfloor m/3\rfloor \left]\right\}\subseteq S$. If $n=3k$, then $(c_m,d_{n-2})\in S$ and $(c_m,d_{n+1})\in S$ by Lemma 3 again where $(c_m,d_{n+1})=(c_m,d_1)$. If $n=3k+1$, then $(c_m,d_n)\in S$ and $(c_m,d_{n+3})\in S$ by Lemma 3 again where $(c_m,d_{n+3})=(c_m,d_3)$. Hence, $(c_m,d_3),(c_m,d_4)\in S$ and they are both the in-neighbors of $(c_1,d_3)$, a contradiction. If $n=3k+2$, then $(c_m,d_{n-1})\in S$ and $(c_m,d_{n+2})\in S$ by Lemma 3 again where $(c_m,d_{n+2})=(c_m,d_2)$. Hence, $(c_m,d_1),(c_m,d_2)\in S$ and they are both the in-neighbors of $(c_1,d_1)$, a contradiction again. Therefore, $n=3k$. By symmetric arguments we also get that $m=3\ell$ and the proof is completed. □

Next we expand Theorem 6 and present a bigger class of EOD strong product digraphs. For this let $T_1,\dots ,T_m$ be arbitrary trees with roots $r_1,\dots ,r_m$, respectively. We define an underlying graph $C_m^{+}$ such that we identify root $r_i$ with vertex $c_i$ of a cycle $C_m$ for every $i\in \left[m\right]$. Clearly, $C_m^{+}$ is exactly a uni-cyclic graph, but we need the before mentioned structure. Notice that $C_m^{+}\cong C_m$ if every tree $T_i$ is a one vertex tree. We say that a digraph with the underlying graph $C_m^{+}$ is well oriented if $C_m$ is a directed cycle and every edge from $T_i$ is oriented away from the root $r_i$ for every $i\in \left[m\right]$. We use the same notation $C_m^{+}$ for a digraph with the underlying graph $C_m^{+}$.

Theorem 7.

Let$m,n\ge 3$be two positive integers. The strong product$C_m^{+}⊠C_n^{+}$is an EOD digraph if and only if both$C_m^{+}$and$C_n^{+}$are well oriented,$m=3\ell$and$n=3k$for some$k,\ell \in \mathbb{N}$.

Proof. 

First, let $m=3\ell$ and $n=3k$, $k,\ell \in \mathbb{N}$, and let $C_m^{+}$ and $C_n^{+}$ be well oriented. We show this direction in two steps. First let $C_n^{+}\cong C_n$ and we show that $C_m^{+}⊠C_n$ is an EOD digraph. By Theorem 6$C_m⊠C_n$ is an EOD digraph with an EOD set A from (3). We extend set A to set $A^{+}$ for which we then show that it is an EOD set of $C_m^{+}⊠C_n$. First we choose the notation for all the vertices from $(C_m^{+}⊠C_n)-V(C_m⊠C_n)$. With $v_i$ we denote all the vertices from $C_m^{+}-V\left(C_m\right)$ with $d_{C_m^{+}}(c_m,v_i)=i$. Notice that different vertices from $C_m^{+}$ can have the same notation. Vertices from $(C_m^{+}⊠C_n)-V(C_m⊠C_n)$ are then denoted as usual by $(v_i,d_j)$. Furthermore, we denote sets $A^{\prime }=\{(v_i,d_j):i+j=3q+1,q\in \mathbb{N}\}$, $B^{\prime }=\{(v_i,d_j):i+j=3q+2,q\in \mathbb{N}\}$ and $C^{\prime }=\{(v_i,d_j):i+j=3q,q\in \mathbb{N}\}$. Now we partition $V(C_m^{+}⊠C_n)$ into sets $A^{+}=A\cup A^{\prime }$, $B^{+}=B\cup B^{\prime }$ and $C^{+}=C\cup C^{\prime }$, where $A,B$ and C are from (3). We will show that $A^{+}$ is an EOD set of $C_m^{+}⊠C_n$.

By Theorem 6 each vertex from A, B and C has exactly one in-neighbor in A. The in-neighbor of a vertex $(v_i,d_j)\in B^{\prime }$, $i+j=3q+2$, that is in $A^{+}$ is either $(v_{i-1},d_j)$ or $(c_{i-1},d_j)$, since $(i-1)+j=(i+j)-1=(3q+2)-1=3q+1$. The in-neighbor of a vertex $(v_i,d_j)\in C^{\prime }$, $i+j=3q$, that is in $A^{+}$ is $(v_i,d_{j+1})$, since $i+(j+1)=(i+j)+1=3q+1$. The in-neighbor of a vertex $(v_i,d_j)\in A^{\prime }$, $i+j=3q+1$, that is in $A^{+}$ is either $(v_{i-1},d_{j+1})$ or $(c_{i-1},d_{j+1})$, since $(i-1)+(j+1)=i+j=3q+1$. So every vertex x from $V(C_m^{+}⊠C_n)$ has an in-neighbor in $A^{+}$. Moreover x has exactly one in-neighbor in $A^{+}$ since exactly one in-neighbor of x has the sum of indices equal to $3q+1$.

By symmetric arguments we can show that $C_m^{+}⊠C_n^{+}$ is an EOD digraph whenever $C_m^{+}\cong C_m$. So, we can assume that $C_m^{+}\ncong C_m$ and $C_n^{+}\ncong C_n$. We know by the above arguments that $C_m^{+}⊠C_n$ is an EOD digraph with an EOD set $A^{+}$. Since there is no arc from vertices of $D=(C_m^{+}⊠C_n^{+})-V(C_m^{+}⊠C_n)$ to vertices of $(C_m^{+}⊠C_n)$ we will use the set $A^{+}$ for $C_m^{+}⊠C_n$ and enlarge it to $A^{\ast }$ that will be an EOD set of $C_m^{+}⊠C_n^{+}$. For this we first need to present the following notation for vertices of D. By $(c_i,u_k^j)$ we denote all the vertices from D that belong to layers ${\left(C_m^{+}\right)}^{d_j}$ and ${\left(C_n^{+}\right)}^{c_i}$ and are at the distance k from $(c_i,d_j)$. Similarly, we use $(v_i,u_k^j)$ for all the vertices from D that belong to layers ${\left(C_m^{+}\right)}^{d_j}$ and ${\left(C_n^{+}\right)}^{v_i}$ and are at the distance k from $(v_i,d_j)$. Notice that different vertices from D can have the same notation. Beside $A^{+}$ we put $(c_i,u_k^j)$ and $(v_i,u_k^j)$ in $A^{\ast }$ if ($i+j=3q+1$ and $k=3p$) or ($i+j=3q+2$ and $k=3p-2$) or ($i+j=3q$ and $k=3p-1$) for some $p,q\in \mathbb{N}$.

We will show that $A^{\ast }$ is an EOD set of $C_m^{+}⊠C_n^{+}$. We already know that $A^{+}\subseteq A^{\ast }$ is an EOD set of $C_m^{+}⊠C_n$ and we need to show that every vertex from D has exactly one in-neighbor in $A^{\ast }$. Notice that every $(x_i,u_k^j)$, where $x\in \{c,v\}$, has exactly three in-neighbors $(x_{i-1},u_k^j),(x_{i-1},u_{k-1}^j)$ and $(x_i,u_{k-1}^j)$. (If $k=1$, then we put $u_0^j=d_j$.) We need to consider nine cases. They are presented in the following Table 1.

Table 1. Nine cases considered that show that every vertex from D has exactly one in-neighbor in $A^{\ast }$.

$\mathit{i}+\mathit{j}$	k	Neighbor in ${\mathit{A}}^{\ast }$
$3q$	$3p$	$(x_i,u_{k-1}^j)$	$i+j=3q$	$k-1=3p-1$
$3q$	$3p-2$	$(x_{i-1},u_k^j)$	$i-1+j=3q-1$	$k=3p-2$
$3q$	$3p-1$	$(x_{i-1},u_{k-1}^j)$	$i-1+j=3q-1$	$k-1=3p-2$
$3q+1$	$3p$	$(x_{i-1},u_{k-1}^j)$	$i-1+j=3q$	$k-1=3p-1$
$3q+1$	$3p-2$	$(x_i,u_{k-1}^j)$	$i+j=3q+1$	$k-1=3p-3$
$3q+1$	$3p-1$	$(x_{i-1},u_k^j)$	$i-1+j=3q$	$k=3p-1$
$3q+2$	$3p$	$(x_{i-1},u_k^j)$	$i-1+j=3q+1$	$k=3p$
$3q+2$	$3p-2$	$(x_{i-1},u_{k-1}^j)$	$i-1+j=3q+1$	$k-1=3p-3$
$3q+2$	$3p-1$	$(x_i,u_{k-1}^j)$	$i+j=3q+2$	$k-1=3p-2$

In the first two columns we present all nine options. The middle column contains the in-neighbor of $(x_i,u_k^j)$ from $A^{\ast }$ and the last two columns show why this is the in-neighbor of $(x_i,u_k^j)$ in $A^{\ast }$. Finally, we show that only one of the three in-neighbors of $(x_i,u_k^j)$ is in $A^{\ast }$. If $(x_{i-1},u_{k-1}^j)\in A^{\ast }$, then exactly one index of the other two in-neighbors differs by 1 from the same index of $(x_{i-1},u_{k-1}^j)$ and they are therefore not in $A^{\ast }$. By symmetry $(x_{i-1},u_{k-1}^j)$ is also not in $A^{\ast }$ whenever either $(x_{i-1},u_k^j)$ or $(x_i,u_{k-1}^j)$ is in $A^{\ast }$. So let $(x_i,u_{k-1}^j)\in A^{\ast }$. In this case we can build a similar table as before, only that this table shows that $(x_{i-1},u_k^j)$ is not in $A^{\ast }$. Similarly, also $(x_i,u_{k-1}^j)\notin A^{\ast }$ when $(x_{i-1},u_k^j)\in A^{\ast }$.

To prove the contrary let $C_m^{+}⊠C_n^{+}$ be an EOD digraph with an EOD set S. If there exists an arc in a tree $T_i$ that is not oriented away from the root, then we have a source in $T_i$ and with that a contradiction with Lemma 1. Hence, all arcs of trees from $C_m^{+}$ are oriented away from the root. If cycle $C_m$ is not a directed cycle, then we have a source $c_j$ on $C_m$ for some $j\in \left[m\right]$. Because all arcs of $T_j$ are oriented away from the root $r_j=c_j$, we have a source $c_j$ in $C_m^{+}$ as well, a contradiction with Lemma 1 again. Hence, $C_m^{+}$ is well oriented. Also, $C_n^{+}$ must be well oriented by the same arguments. Next we observe a subdigraph $C_m⊠C_n$ of $C_m^{+}⊠C_n^{+}$. By the orientation of all arcs of all the trees, we see that there does not exist an arc from vertices of $(C_m^{+}⊠C_n^{+})-V(C_m⊠C_n)$ to vertices of $C_m⊠C_n$. Therefore, $C_m⊠C_n$ is an EOD digraph as well and by Theorem 6 we get $m=3\ell$ and $n=3k$ for some positive integers ℓ and k. □

The above results give rise to the following conjecture. We believe that it is true, but the proof is a challenge.

Conjecture 1.

The strong product$D⊠F$is an EOD digraph if and only if$D\cong C_m^{+}$and$F\cong C_n^{+}$are well oriented,$m=3\ell$and$n=3k$for some$k,\ell \in \mathbb{N}$.

5. The Direct and the Lexicographic Product

We conclude this paper with characterizations of the EOD digraphs among the direct and the lexicographic product. They follow from (1) and (2), respectively, and are no surprise. The following result for the direct product is an analogue of the result for the EOD graphs from [8] (under the name of total perfect codes).

Theorem 8.

Let D and F be digraphs. The direct product$D\times F$is an EOD digraph if and only if D and F are EOD digraphs.

Proof. 

Let D and F be EOD digraphs with EOD sets $S_D$ and $S_F$, respectively. We will show that $S_D\times S_F$ is an EOD set of $D\times F$. By (1) it holds that

$$V(D\times F)\subseteq \bigcup _{(d,f)\in S_D\times S_F}{N}_{D\times F}^{+}\left((d,f)\right).$$

Suppose there exists a vertex $(d_0,f_0)$ that has two different in-neighbors $(d,f)$ and $(d^{\prime },f^{\prime })$ in $S_D\times S_F$. If $d=d^{\prime }$, then $f\ne f^{\prime }$, and by (1) we have

$$N_{D\times F}^{+}\left((d,f)\right)\cap N_{D\times F}^{+}\left((d^{\prime },f^{\prime })\right)=\left(N_D^{+}\left(d\right)\times N_F^{+}\left(f\right)\right)\cap \left(N_D^{+}\left(d\right)\times N_F^{+}\left(f^{\prime }\right)\right)=N_D^{+}\left(d\right)\times \left(N_F^{+}\left(f\right)\cap N_F^{+}\left(f^{\prime }\right)\right).$$

Thus, $f_0$ has two different in-neighbors f and $f^{\prime }$ in $S_F$. That is a contradiction since $S_F$ in an EOD set of F. If $f=f^{\prime }$, then $d\ne d^{\prime }$ and we obtain a contradiction by symmetric arguments. Meaning that $d\ne d^{\prime }$ and $f\ne f^{\prime }$. Again by (1) the vertex $d_0$ has two different in-neighbors d and $d^{\prime }$ in $S_D$ and $f_0$ has two different in-neighbors f and $f^{\prime }$ in $S_F$, a contradiction with $S_D$ and $S_F$ being EOD sets of D and F, respectively. Therefore, no two vertices from $S_D\times S_F$ have a common out-neighbor, meaning that $D\times F$ is an EOD digraph.

Now let $D\times F$ be an EOD digraph and S be its EOD set. Let $f\in F$ be an arbitrary vertex. Every vertex from $D^f$ has exactly one in-neighbor in S. Denote with $S_f$ the set of all those vertices. We will show that $p_D\left(S_f\right)$ is an EOD set of D. Let d and $d^{\prime }$ be two different vertices from $p_D\left(S_f\right)$. Choose $f^{\prime },f^{″}\in V\left(F\right)$ such that $(d,f^{\prime }),(d^{\prime },f^{″})\in S_f$. If there exists $d_0$ such that d and $d^{\prime }$ are its in-neighbors, then $(d_0,f)$ has two in-neighbors $(d,f^{\prime })$ and $(d^{\prime },f^{″})$ in S, a contradiction with S being an EOD set of $D\times F$. By (1) and because S is an EOD set of $D\times F$ it also holds that $V\left(D\right)\subseteq {\bigcup }_{d\in p_D\left(S_f\right)}{N}_D^{+}\left(d\right)$. Therefore, $p_D\left(S_f\right)$ is an EOD set of D, meaning that D is an EOD digraph. By symmetric arguments F is also an EOD digraph and with that the proof is completed. □

The result for EOD digraphs among the lexicographic product of digraphs is an analogue to the graph version from [9].

Theorem 9.

Let D and F be digraphs. The lexicographic product$D\circ F$is an EOD digraph if and only if

(i) 

D is a digraph without arcs and F is an EOD digraph, or

(ii) 

D is an EOD digraph and F contains a sink.

Proof. 

Let D be a digraph on n vertices without edges and F be an EOD digraph. Then $D\circ F$ is isomorphic to n copies of F and since F is an EOD digraph, n copies of F also form an EOD digraph.

Now, let D be an EOD digraph, let $S_D$ be its EOD set and let $f_0$ be a sink in F. We will show that $S_D\times \{f_0\}$ is an EOD set of $D\circ F$. By (2) it holds that $N_{D\circ F}^{+}((d,f_0))=N_D^{+}\left(d\right)\times V\left(F\right)$ since $f_0$ is a sink in F. So ${\bigcup }_{d\in S_D}{N}_{D\circ F}^{+}((d,f_0))$ equals $V(D\times F)$. If for $d,d^{\prime }\in S_D$ and $d\ne d^{\prime }$ there exists a vertex in $D\circ F$ which in-neighbors are both $(d,f_0)$ and $(d^{\prime },f_0)$, then there also exists a vertex in D which in-neighbors are both d and $d^{\prime }$. A contradiction with $S_D$ being an EOD set of D. Therefore, $D\circ F$ is an EOD digraph.

Conversely, let $D\circ F$ be an EOD digraph, S its EOD set and $(d,f)\in S$ an arbitrary vertex. If f is not a sink in F, then there exists a vertex $f^{\prime }\in F^d$, such that $(d,f)$ is an in-neighbor of $(d,f^{\prime })$. Denote with $(d_1,f_1)$ the unique in-neighbor of $(d,f)$ from S. If $d_1\ne d$, then $(d,f^{\prime })$ has both $(d,f)$ and $(d_1,f_1)$ as its in-neighbors, which is not possible. Hence, $d_1=d$. If d has any out-neighbors, then for every out-neighbor $d^{\prime }$ of d a vertex $(d^{\prime },f)$ has both $(d,f)$ and $(d_1,f_1)$ as its in-neighbors, a contradiction. So no d such that $(d,f)\in S$ has any out-neighbors. Since every vertex $(d^{″},f^{″})\in V(D\circ F)$ has exactly one in-neighbor $(d,f)\in S$, we conclude that $d^{″}\ne d$ yields that d has at least one out-neighbor, which is not possible. Therefore, $d^{″}=d$ and no $d^{″}\in V\left(D\right)$ has any out-neighbors. Meaning that D is a digraph without arcs. To prove that F is an EOD digraph choose an arbitrary F-layer $F^d$ (which always induces a digraph isomorphic to F). Clearly, the vertices in $F^d$ that are also in S form an EOD set of $(D\circ F)\left[F^d\right]\cong F$. So F is an EOD digraph and $\left(i\right)$ follows.

Now assume f is a sink. Notice that in this case $F^d$ is a subset of all out-neighbors of $(d_0,f)$, where $d_0$ is an in-neighbor of d. We will prove that $p_D\left(S\right)$ is an EOD set of D. Suppose it is not. Then there exist $d,d^{\prime }\in p_D\left(S\right)$ with a common out-neighbor. With this and (2) we have a contradiction with S being an EOD set of $D\circ F$. Meaning that $p_D\left(S\right)$ is an EOD set of D and $\left(ii\right)$ follows. □

6. Conclusions

In this work we treated the four standard products of digraphs (the Cartesian, the strong, the direct and the lexicographic) with respect to the efficient open domination. The idea is to describe which digraphs among these products are efficient open domination digraphs and to describe them with the properties of their factors. We completely characterized such digraphs among the direct product (Theorem 8) and among the lexicographic product (Theorem 9). For the efficient open domination Cartesian product digraphs the characterizations are given for those for which the first factor has an underlying graph that is a path (Theorems 1, 3 and 4), a cycle (Theorem 2) or a star (Theorem 5). This yields an idea on how to deal with the Cartesian product of digraphs with one fixed factor and an arbitrary second one. Among the efficient open domination strong product of digraphs we characterized those in which both factors have uni-cyclic graphs as their underlying graphs (Theorems 6 and 7). We also conjecture that this are the only strong product digraphs that are the efficient open domination digraphs.