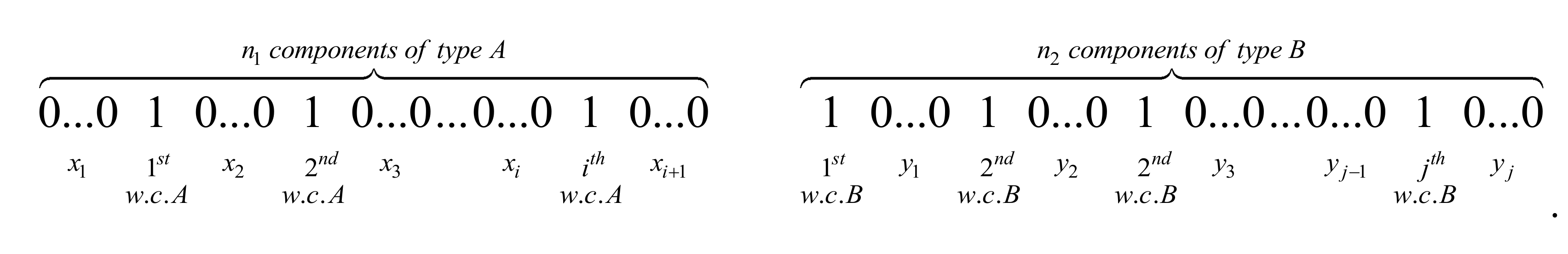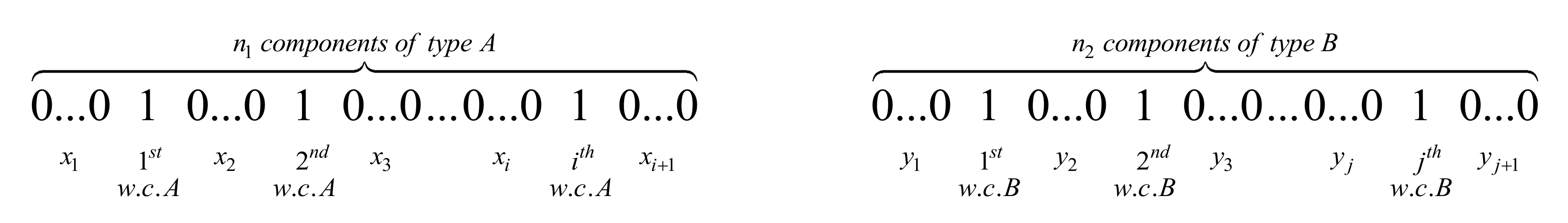m-Consecutive-k-out-of-n: F Structures with a Single Change Point

Abstract

In the present article, we introduce the m-consecutive-k-out-of-n: F structures with a single change point. The aforementioned system consists of n independent components, of which the first n₁ units are identically distributed with common reliability p₁, while the remaining ones share a different functioning probability p₂. The general setup of the proposed reliability structures is presented in detail, while an explicit expression for determining the number of its path sets of a given size is derived. Additionally, closed formulae for the reliability function and mean time to failure of the aforementioned models are also provided. For illustration purposes, several numerical results and comparisons are presented in order to shed light on the performance of the proposed structure.

1. Introduction

In the field of Reliability Engineering, an enthralling quest calls for the design of appropriate structures, which are related to real-life applications or existing devices and contrivances. A particular group of reliability models, which have seemed to reel in scientists during the last few decades, is the family of consecutive-type systems. Due to the abundance of their applications in Engineering and Statistical Modeling, the so-called consecutive-type structures comprise an engrossing scope of research activity.

The general framework of constructing a consecutive-type system requires n linearly or circularly ordered components. The resulting system fails, whenever a pre-specified condition (or even more) is satisfied. A great variety of structures have been already introduced in the literature. For example, a consecutive-k-out-of-n: F system consists of n linearly ordered components and fails if and only if at least k consecutive units fail (see, e.g., [1,2]). Additionally, the so-called m−consecutive-k-out-of-n: F system seems to be a direct generalization of the traditional m-out-of-n: F system and the consecutive-k-out-of-n: F structure; it consists of n linearly ordered components such that the system stops its operation if and only if there are at least m non-overlapping runs of k consecutive failed units (see, e.g., [3,4,5]). A quite different modification of the common consecutive-k-out-of-n: F system is known as an r-within-consecutive k-out-of-n: F structure. The particular system was established in [6] and fails if and only if there exist k consecutive components, which include among them include at least r failed units (see also [3,7,8,9]). For some recent contributions to the field of consecutive-type structures, the interested reader is referred to [10,11,12].

On the other hand, some applications are related to two different criteria, and several appropriate reliability structures have been established and studied in the literature. For instance, the $(n,f,k)$ structure proposed in [13] fails if, and only if, there exist at least f failed units or at least k consecutive failed units. Several reliability characteristics of the so-called $(n,f,k)$ systems are studied in detail [14,15]. Among others, the $<n,f,k>$ structure (see, e.g., [16,17]) and the constrained (k, d)-out-of-n: F system (see, e.g., [18] or [19]) are well-known consecutive-type reliability systems with two failure criteria. For a detailed and up-to-date survey on the consecutive-type systems, we refer to the detailed reviews offered by [20,21] and the well-documented monographs devised by [22,23]. A survey of reliability approaches in various fields of Engineering and Physical Sciences is also provided in [24].

Throughout the lines of the present paper, we focus on structures with a single change point, e.g., we study reliability systems consisting of two different types of components (see, e.g., [25]). More precisely, the m-consecutive-k-out-of-n: F structure with a single change point is introduced. The paper follows the standard structure in the sense that at the beginning, there exists an introductory section, the next two sections provide the theory and methods, while the last two sections offer some numerical results and a detailed discussion respectively. More specifically, in Section 2, the general setup of the proposed structure is presented in detail, while explicit expressions for computing some reliability characteristics of it are proven in Section 3. An extensive numerical experimentation is carried out in Section 4 in order to shed light on the performance of the proposed reliability structure. Finally, the Discussion section summarizes the contribution of the present manuscript, while some interesting conclusions based on previous sections are also highlighted.

2. The General Setup of m-Consecutive-k-out-of-n: F Structures with a Single Change Point

Let us first introduce the basic notions and notations for an m-consecutive-k-out-of-n: Fail (or simpler F) system consisting of n independent and linearly ordered components with a single change point. Among its components, n₁ of them have the probability to function at a specific time point t equal to p₁, while for the remaining ones, the corresponding probability equals p₂. Denoting by $X_1,X_2,\dots ,X_{n_1}$ ($X_{n_1+1},X_{n_1+2},\dots ,X_n$) the lifetimes of the first (last) $n_1(n_2=n-n_1)$ components, the probabilities $p_1,p_2$, which are known as the components’ reliabilities, are defined as

$$p_1=P(X_i>t), \mathrm{for} i=1,2,\dots ,n_1$$

and

$$p_2=P(X_i>t), \mathrm{for} i=n_1+1,n_1+2,\dots ,n.$$

It is evident that the random variable of interest is actually the lifetime (or failure time) T of the m-consecutive-k-out-of-n: F structure. For the whole system, the probability that it functions at a specific time point t is called reliability R and corresponds simply to the probability that the lifetime T of the system exceeds t, namely $R(t)=P(T>t)$. It is straightforward that the complement of the last probability coincides with the failure probability of the system and corresponds to the distribution function of random variable T.

Needless to say, the reliability of the system depends not only on the probabilities p₁, p₂ but also on the design parameters m, n, k. Consequently, the reliability of the m-consecutive-k-out-of-n: F system consisting of n = n₁ + n₂ independent and linearly ordered components with a single change point shall be denoted by $R_{n_1,n_2,m,k}(p_1,p_2)$. It is evident that the parameters m, k are related to the failure criterion of the proposed structure, while the parameter n corresponds to the total number of its components. Moreover, the number of path sets of the proposed structure, namely the number of all sets consisting of those working components which guarantee that the system functions properly, are denoted by $r_{n_1,n_2,m,k}$.

Generally speaking, the reliability study of consecutive-type systems is closely related to the Theory of Runs. Let us first consider an m-consecutive-k-out-of-n: F system consisting of n independent and linearly ordered components. As already mentioned, the particular structure fails if and only if at least m non-overlapping runs of k consecutive units fail. It is worth mentioning that the reliability of an m-consecutive-k-out-of-n: F system is connected with the total number of non-overlapping runs of 1s of length k in a binary sequence (see, e.g., [26]). Some recent contributions to the field of runs distributions for sequences of binary trials and related combinatorial topics are provided by [27,28].

We next assume that the first n₁ components of the m-consecutive-k-out-of-n: F system share a common reliability p₁ (components of Type A, hereafter), while the remaining ones, namely the rest of the $n_2=n-n_1$ units, have a common reliability p₂ (components of Type B, hereafter), where $p_2\ne p_1$. The location of the $(n_1+1)-th$ component could be considered as a change point of the system, and consequently, the structure described above is called an m-consecutive-k-out-of-n: F system with a single change point. It is straightforward that in case of $p_2=p_1=p$, the aforementioned structure reduces to the traditional m-consecutive-k-out-of-n: F system introduced by [3]. The proposed setup seems to be more flexible and realistic in comparison with the structure having the same failure criterion but consisting of identical components with common reliability. It is worth mentioning that structures with one or more change points have been already introduced in the literature (see, e.g., [25,29]).

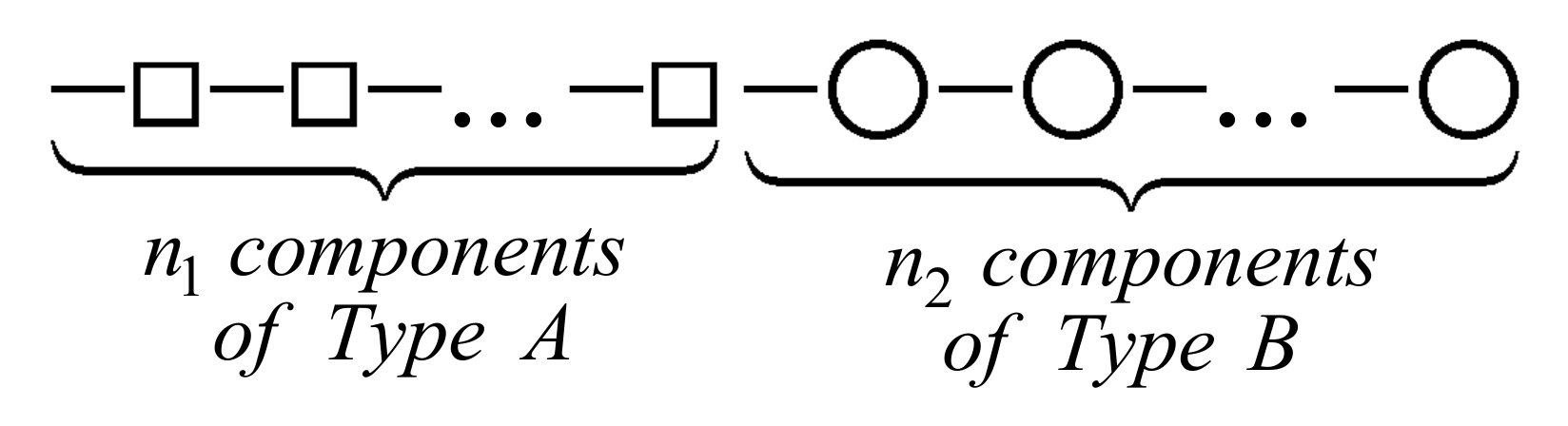
Figure 1 represents the proposed m-consecutive-k-out-of-n: F system with a single change point.

The components of type A are represented by the symbol $\square$ and share a common reliability p₁, while the remaining components of type B appear as $◯$ and have reliability p₂. The resulting structure fails whenever at least m non-overlapping runs of k consecutive components fail. Note that the above-mentioned runs could be formed by components either exclusively of type A or B or even of both types.

3. Reliability Characteristics of m-Consecutive-k-out-of-n: F Structures with a Single Change Point

In the present section, we investigate the performance of the m-consecutive-k-out-of-n: F structures with a single change point. Explicit formulae for calculating the number of path sets of the structure including i components of type A and j components of type B are established. Moreover, the reliability function and the mean time to failure of the above-mentioned systems are also studied.

The following proposition offers explicit expressions for the quantities $r_{n_1,n_2,m,k}(i,j)$ under two different schemes. The differentiation between these scenarios depends exclusively on the status of the first component of the group of components of type B. More precisely, according to the first scenario (Scenario 1, hereafter), the first component of type B, e.g., the first $◯$ that appears in the structure line, is assumed to be in a functioning state. In other words, if we denote by 0 and 1, the failure and functioning state of each component respectively, a typical sequence of n binary elements (under Scenario 1), including i working components of type A (w.c.A) and j working components of type B (w.c.B), appears at Figure 2.

Note that $x_r, r=2,3,\dots ,i$ corresponds to the amount of 0s that appear between two successive 1s throughout the components of type A, while $x_1$ denotes simply the component failures of type A that occurred before the appearance of the first working component of the same type. In other words, the quantity $x_r, r=2,3,\dots ,i$ expresses the length of run of 0s in each urn between successive 1s throughout the first n₁ components, while $x_1$ indicates the length of the first run of 0s. It is straightforward that the quantities $x_r, r=2,3,\dots ,i$ satisfy the following conditions:

$$0\le x_r\le n_1, r=1,2,\dots ,i \mathrm{and} {\displaystyle \sum _{r=1}^i{x}_r}=n_1-i.$$

(1)

Similarly, $y_s, s=1,2,\dots ,j$ represents the amount of 0s between successive 1s throughout the components of type B, namely the quantity $y_s, s=1,2,\dots ,j$ corresponds to the length of run of 0s in each run between successive 1s throughout the n₂ components of type B. It goes without saying that the following restrictions hold true

$$0\le y_s\le n_2, s=1,2,\dots ,j \mathrm{and} {\displaystyle \sum _{s=1}^j{y}_s}=n_2-j.$$

(2)

On the contrary, under the second scenario (Scenario 2, hereafter), the first component of type B that appeared in the structure line is considered to be in failure state. Consequently, a binary sequence of n elements (under Scenario 2), including i working components of type A (w.c.A) and j working components of type B (w.c.B), is displayed in Figure 3.

Note that once again, the quantities $x_r, r=1,2,\dots ,i,i+1$ and $y_s, s=1,2,\dots ,j,j+1$ are related to the length of runs of 0s in the corresponding urn. Clearly, the above-mentioned variables satisfy the following set of conditions (under Scenario 2)

$$0\le x_r\le n_1, r=1,2,\dots ,i,i+1, {\displaystyle \sum _{r=1}^{i+1}{x}_r}=n_1-i-1$$

and

$$0\le y_s\le n_2, s=1,2,\dots ,j,j+1,{\displaystyle \sum _{s=1}^{j+1}{y}_s}=n_2-j-1.$$

(3)

Proposition 1.

Let us consider an m-consecutive-k-out-of-n: F structure with a single change point, consisting of n₁ (n₂) components of type A (B) with common reliability p₁ (p₂). The number of path sets of the structure including i components of type A and j components of type B is given as

$$\begin{array}{c}{r}_{n_1,n_2,m,k}(i,j)={\displaystyle \sum _{\psi =0}^{m-1}{\displaystyle \sum _{\xi =0}^{m-\psi -1}\left(\begin{array}{l} i+1\\ i+1-\xi \end{array}\right)}}\left(\begin{array}{l} j\\ j-\psi \end{array}\right)C_{\xi ,\psi }(i,j,n_1,n_2)\hfill \\ +{\displaystyle \sum _{x=0}^{n_1-i}{\displaystyle \sum _{y=\max (k-x,1)}^{n_2-j}{\displaystyle \sum _{\psi =0}^{m-2}{\displaystyle \sum _{\xi =0}^{m-\psi -2}\left(\begin{array}{l} i\\ \xi \end{array}\right)}}\left(\begin{array}{l}j\\ \psi \end{array}\right)D_{\xi ,\psi }(i,j,n_1,n_2)}}\hfill \\ +{\displaystyle \sum _{x=0}^{k-2}{\displaystyle \sum _{y=1}^{k-1-x}{\displaystyle \sum _{\psi =0}^{m-1}{\displaystyle \sum _{\xi =0}^{m-\psi -1}\left(\begin{array}{l} i\\ \xi \end{array}\right)}}\left(\begin{array}{l}j\\ \psi \end{array}\right)D_{\xi ,\psi }(i,j,n_1,n_2)}},\hfill \end{array}$$

(4)

where

$$\begin{array}{l}{C}_{\xi ,\psi }(i,j,n_1,n_2)\\ ={\displaystyle \sum _{a_1=0}^{n_1-i}{\displaystyle \sum _{b_1=0}^{n_2-j}{c}_k(i+1-\xi ,a_1)}}{c}_{n_1-i-k+1}(\xi ,n_1-i-a_1-\xi k)c_k(j-\psi ,b_1)c_{n_2-j-k+1}(\psi ,n_2-j-b_1-\psi k)\end{array}$$

(5)

$$\begin{array}{l}{D}_{\xi ,\psi }(i,j,n_1,n_2)\\ ={\displaystyle \sum _{a_3=0}^{n_1-i-x}{\displaystyle \sum _{b_3=0}^{n_2-j-y}{c}_{n_1-i-x-k+1}(\xi ,a_3-\xi k)}}{c}_k(i-\xi ,n_1-i-x-a_3)c_{n_2-j-y-k+1}(\psi ,b_3-\psi k)c_k(j-\psi ,n_2-j-y-b_3),\end{array}$$

(6)

and

$$c_h(a,b)={\displaystyle \sum _{g=0}^{\min (a,[b/h])}{(-1)}^g\left(\begin{array}{l}a\\ g\end{array}\right)\left(\begin{array}{l}a+b-gh-1\\ a-1\end{array}\right)}, a>0,b\ge 0.$$

(7)

Proof.

Let us first consider that the m-consecutive-k-out-of-n: F structure with a single change point operates under Scenario 1 (see Figure 2); namely, the first component of type B, which appears in the structure line, is assumed to be in a functioning state. We next assume that ξ $x^{\prime }s$ (say $x_{(1)},x_{(2)},\dots ,x_{(\xi )}$) range from k to $n_1-i$, while the remaining $(i+1-\xi )$ ones (say $x_{(\xi +1)},x_{(\zeta +2)},\dots ,x_{(i+1)}$) are not greater than $k-1$, where $\xi =0,1,\dots ,i+1$. The number of binary sequences of the components of type A under Scenario 1 equal the number of integer solutions of the following linear equations

$$x_{(1)}+x_{(2)}+\dots +x_{(\xi )}=a_2$$

(8)

and

$$x_{(\xi +1)}+x_{(\zeta +2)}+\dots +x_{(i+1)}=a_1$$

(9)

such that

$$k\le x_{(\lambda )}\le n_1-i, \mathrm{for} \lambda =1,2,\dots ,\xi$$

and

$$0\le x_{(\lambda )}\le k-1, \mathrm{for} \lambda =\xi +1,\xi +2,\dots ,i+1,$$

while $a_1+a_2=n_1-i$. The number of integer solutions of the linear Equations (8) and (9) is given by (see, e.g., [30], p. 138)

$$Q=\left(\begin{array}{c}\xi +a_2-\xi k-1\\ \xi -1\end{array}\right)+{\displaystyle \sum _{r=1}^{\xi }{(-1)}^r{\displaystyle \sum \left(\begin{array}{c}\xi +a_2-\xi k-r(n_1-i-k+1)-1\\ \xi -1\end{array}\right)}}$$

(10)

and

$$V=\left(\begin{array}{c}i-\xi +a_1\\ i-\xi \end{array}\right)+{\displaystyle \sum _{r=1}^{i-\xi +1}{(-1)}^r{\displaystyle \sum \left(\begin{array}{c}i-\xi +a_1-rk\\ i-\xi \end{array}\right)}},$$

(11)

respectively. Note that in the inner sum appeared in Equations (10) and (11), the summation is extended over all r-combinations of the available indices. □

Moreover, let us next assume that ψ $y^{\prime }s$ (say $y_{(1)},y_{(2)},\dots ,y_{(\psi )}$) range from k to $n_2-j$, while the remaining $(j-\psi )$ ones (say $y_{(\psi +1)},y_{(\psi +2)},\dots ,y_{(j)}$) are not greater than $k-1$, where $\psi =0,1,\dots ,j$. The number of binary sequences of the components of type B under Scenario 1 equals to the number of integer solutions of the following linear equations

$$y_{(1)}+y_{(2)}+\dots +y_{(\psi )}=b_2$$

(12)

and

$$y_{(\psi +1)}+y_{(\psi +2)}+\dots +y_{(j)}=b_1$$

(13)

such that

$$k\le y_{(\theta )}\le n_2-j, \mathrm{for} \theta =1,2,\dots ,\psi$$

and

$$0\le y_{(\theta )}\le k-1, \mathrm{for} \theta =\psi +1,\psi +2,\dots ,j,$$

while $b_1+b_2=n_2-j$. The number of integer solutions of the linear Equations (8) and (9) is given by (see, e.g., [30], p. 138)

$$W=\left(\begin{array}{c}\psi +b_2-\psi k-1\\ \psi -1\end{array}\right)+{\displaystyle \sum _{r=1}^{\psi }{(-1)}^r{\displaystyle \sum \left(\begin{array}{c}\psi +b_2-\psi k-r(n_2-j-k+1)-1\\ \psi -1\end{array}\right)}}$$

(14)

and

$$Z=\left(\begin{array}{c}j-\psi +b_1-1\\ j-\psi -1\end{array}\right)+{\displaystyle \sum _{r=1}^{j-\psi }{(-1)}^r{\displaystyle \sum \left(\begin{array}{c}j-\psi +b_1-rk-1\\ j-\psi -1\end{array}\right)}},$$

(15)

respectively. Note once again that in the inner sum that appeared in Equations (14) and (15), the summation is extended over all r-combinations of the available indices.

Employing analogous arguments to those mentioned previously, we shall next deal with the so-called Scenario 2. We first assume that ξ $x^{\prime }s$ (say $x_{(1)},x_{(2)},\dots ,x_{(\xi )}$) range from k to $n_1-i-x_{i+1}$, while the remaining $(i-\xi )$ ones (say $x_{(\xi +1)},x_{(\zeta +2)},\dots ,x_{(i)}$) are not greater than $k-1$, where $\xi =0,1,\dots ,i$. Indeed, the number of binary sequences under Scenario 2 of the components of type A equals the number of integer solutions of the following linear equations

$$x_{(1)}+x_{(2)}+\dots +x_{(\xi )}=a_3$$

(16)

and

$$x_{(\xi +1)}+x_{(\zeta +2)}+\dots +x_{(i)}=a_4$$

(17)

such that

$$k\le x_{(\lambda )}\le n_1-i-x_{i+1}, \mathrm{for} \lambda =1,2,\dots ,\xi$$

and

$$0\le x_{(\lambda )}\le k-1, \mathrm{for} \lambda =\xi +1,\xi +2,\dots ,i,$$

while $a_3+a_4=n_1-i-x_{i+1}$. The number of integer solutions of the linear Equations (16) and (17) is given by (see, e.g., [30], p. 138)

$$T=\left(\begin{array}{c}\xi +a_3-\xi k-1\\ \xi -1\end{array}\right)+{\displaystyle \sum _{r=1}^{\xi }{(-1)}^r{\displaystyle \sum \left(\begin{array}{c}\xi +a_3-\xi k-r(n_1-i-x_{i+1}-k+1)-1\\ \xi -1\end{array}\right)}}$$

(18)

and

$$S=\left(\begin{array}{c}i-\xi +a_4-1\\ i-\xi -1\end{array}\right)+{\displaystyle \sum _{r=1}^{i-\xi }{(-1)}^r{\displaystyle \sum \left(\begin{array}{c}i-\xi +a_4-rk-1\\ i-\xi -1\end{array}\right)}}.$$

(19)

Let us next assume that ψ $y^{\prime }s$ (say $y_{(1)},y_{(2)},\dots ,y_{(\psi )}$) range from k to $n_2-j-y_1$, while the remaining $(j-\psi )$ ones (say $y_{(\psi +1)},y_{(\psi +2)},\dots ,y_{(j)}$) are not greater than $k-1$, where $\psi =0,1,\dots ,j$. Needless to say, the corresponding result for the components of type B under Scenario 2 is related to the following equations

$$y_{(1)}+y_{(2)}+\dots +y_{(\psi )}=b_3$$

(20)

and

$$y_{(\psi +1)}+y_{(\psi +2)}+\dots +y_{(j)}=b_4$$

(21)

such that

$$k\le y_{(\theta )}\le n_2-j-y_1, \mathrm{for} \theta =1,2,\dots ,\psi$$

and

$$0\le y_{(\theta )}\le k-1, \mathrm{for} \theta =\psi +1,\psi +2,\dots ,j,$$

while $b_1+b_2=n_2-j-y_1$. Consequently, the number of integer solutions of the linear Equations (20) and (21) is given by (see, e.g., [30], p. 138)

$$E=\left(\begin{array}{c}\psi +b_3-\psi k-1\\ \psi -1\end{array}\right)+{\displaystyle \sum _{r=1}^{\psi }{(-1)}^r{\displaystyle \sum \left(\begin{array}{c}\psi +b_3-\psi k-r(n_2-j-y_1-k+1)-1\\ \psi -1\end{array}\right)}}$$

(22)

and

$$G=\left(\begin{array}{c}j-\psi +b_4-1\\ j-\psi -1\end{array}\right)+{\displaystyle \sum _{r=1}^{j-\psi }{(-1)}^r{\displaystyle \sum \left(\begin{array}{c}j-\psi +b_4-rk-1\\ j-\psi -1\end{array}\right)}}.$$

(23)

Note once again that in the inner sum that appeared in Equations (18), (19), (22), and (23), the summation is extended over all r-combinations of the available indices.

By combining Equations (10), (11), (14), (15), (18), (19), (22), and (23), we next recall Equations (5) and (7) mentioned above, and the proof is complete after some straightforward maneuvering.

In words, Proposition 1 offers an explicit expression for determining the number of path sets of the proposed m-consecutive-k-out-of-n: F system with a single change point.

It is straightforward that for m = 1, the m-consecutive-k-out-of-n: F structure with a single change point reduces to the consecutive-k-out-of-n: F system with a change point, which has been already established by [27]. It is noteworthy that for the special case m = 1, Proposition 1 of the present manuscript leads to the corresponding result offered by [27] for determining the number of path sets including i (j) components from the first (second) group. Indeed, under the assumption that m = 1, each one of the three double summations of the right-hand side of Equation (4) coincides to the terms $C_{0,0}(i,j,n_1,n_2)$, 0, and ${\displaystyle \sum _{x=0}^{k-2}{\displaystyle \sum _{y=1}^{k-1-x}{D}_{0,0}(i,j,n_1,n_2)}}$ respectively. Moreover, for $\xi =0,\psi =0$, we easily observe that $a_2=0,b_2=0$ (or equivalently $a_1=n_1-i,b_1=n_2-j$) and $a_3=0,b_3=0$. Consequently, the following holds true

$$C_{0,0}(i,j,n_1,n_2)=c_k(i+1,n_1-i)c_k(j,n_2-j)$$

and

$$D_{0,0}(i,j,n_1,n_2)=c_k(i,n_1-i-x)c_k(j,n_2-j-y).$$

Based on the above-mentioned equations, we readily reach the same formula (as a special case of our Proposition 1) with the one appeared in [27] (see Equation (8) therein) for calculating the number of path sets, including i and j components from each separate group of the consecutive-k-out-of-n: F system with a change point.

Having at hand the result offered by Proposition 1, we could readily provide explicit expressions for determining the reliability and the mean time to failure of the m-consecutive-k-out-of-n: F structure with a single change point. In order to deliver the above-mentioned formulae, we should first clarify whether the number of components of each type is pre-specified or randomly chosen in the resulting system. The next corollaries cover both cases.

Corollary 1.

Let us consider an m-consecutive-k-out-of-n: F structure with a single change point, consisting of n₁ (n₂) components of type A (B) with common reliability p₁ (p₂). Under the assumption that the number of components of each type is fixed, the following ensue:

(i)

The reliability of the m-consecutive-k-out-of-n: F system with a single change point is expressed as

$$R_{n_1,n_2,m,k}(p_1,p_2)={\displaystyle \sum _{i=0}^{n_1}{\displaystyle \sum _{j=0}^{n_2}{r}_{n_1,n_2,m,k}(i,j)p_1^i{(1-p_1)}^{n_1-i}{p}_2^j{(1-p_2)}^{n_2-j}}},$$

(24)

where$r_{n_1,n_2,m,k}(i,j)$represents the number of path sets of the structure including i components of type A and j components of type B.

(ii)

The mean time to failure of the m-consecutive-k-out-of-n: F system with a single change point, namely the expected time until the system no longer operates, can be expressed as

$$MTT{F}_{n_1,n_2,m,k}(F_1,F_2)={\displaystyle \sum _{i=0}^{n_1}{\displaystyle \sum _{j=0}^{n_2}{r}_{n_1,n_2,m,k}(i,j){\displaystyle {\int }_0^{\infty }{\overline{F}}_1^i(t)F_1{}^{n_1-i}(t){\overline{F}}_2^j(t)F_2{}^{n_2-j}(t)dt}}},$$

(25)

where${\overline{F}}_1(t)=1-F_1(t)$and${\overline{F}}_2(t)=1-F_2(t)$correspond to the reliability function of the components of type A and type B respectively, while$F_1(t),F_2(t)$denotes the distribution functions of random lifetimes of the components ($X_1,X_2,\dots ,X_{n_1}$) and ($X_{n_1+1},X_{n_1+2},\dots ,X_n$), respectively.

On the other hand, if the number of components of each type is random, then the reliability of the underlying system could be approached by applying appropriate conditioning arguments. More precisely, we define the random variable N₁, which corresponds to the number of components of type A ($0\le N_1\le n$), while $f(n_1)=P(N_1=n_1)$ expresses its probability mass function.

Corollary 2.

Let us consider an m-consecutive-k-out-of-n: F structure with a single change point, consisting of n₁ (n₂) components of type A (B) with common reliability p₁ (p₂). Under the assumption that the number of components of each type is random, the following ensue:

(i)

The reliability of the m-consecutive-k-out-of-n: F system with a single change point is expressed as

$$R_{n,m,k}(p_1,p_2)={\displaystyle \sum _{n_1=0}^n{R}_{n_1,n-n_1,m,k}(p_1,p_2)f(n_1)}.$$

(26)

(ii)

The mean time to failure of the m-consecutive-k-out-of-n: F system with a single change point, namely the expected time until the system does no longer operates, can be expressed as

$$MTT{F}_{n,m,k}(F_1,F_2)={\displaystyle \sum _{n_1=0}^{n}MTT{F}_{n_1,n-n_1,m,k}(F_1,F_2)f(n_1)}.$$

(27)

4. Numerical Results

In the present section, we shall provide several numerical results, which illustrate the performance of the m-consecutive-k-out-of-n: F systems with a single change point. All numerical outcomes and graphical representations, which are presented throughout the lines of the present section, have been produced by the aid of the theoretical results, which have been proved previously. By the aid of Proposition 1, we first determine the number of path sets of the proposed structure, and then, its reliability is computed by recalling Equation (24). We next carry out a detailed numerical experimentation referring to the reliability of the proposed structure. More precisely, we present the reliability values of the m-consecutive-k-out-of-n: F systems with a single change point for several values of the parameters p₁, p₂, m, n, k. 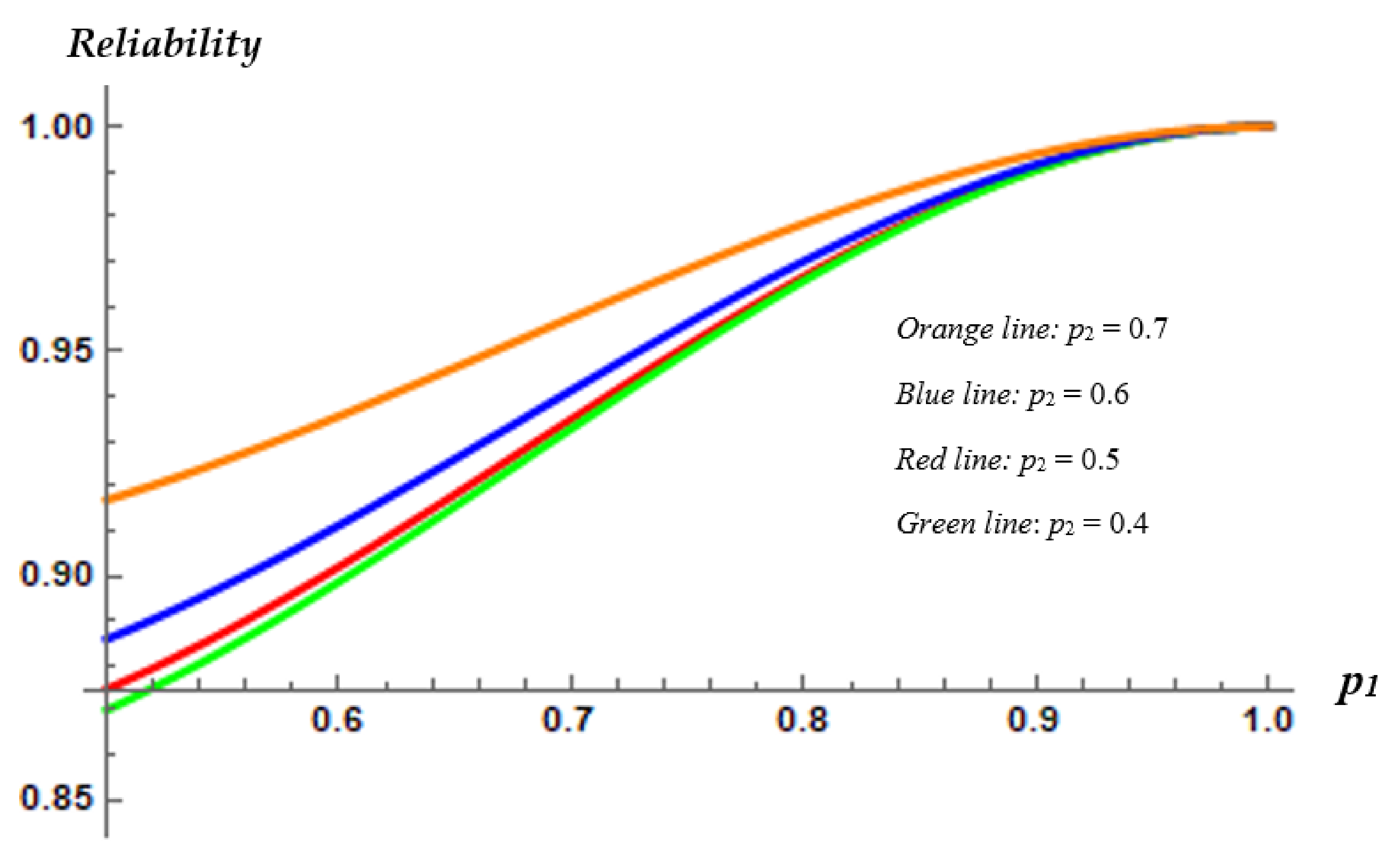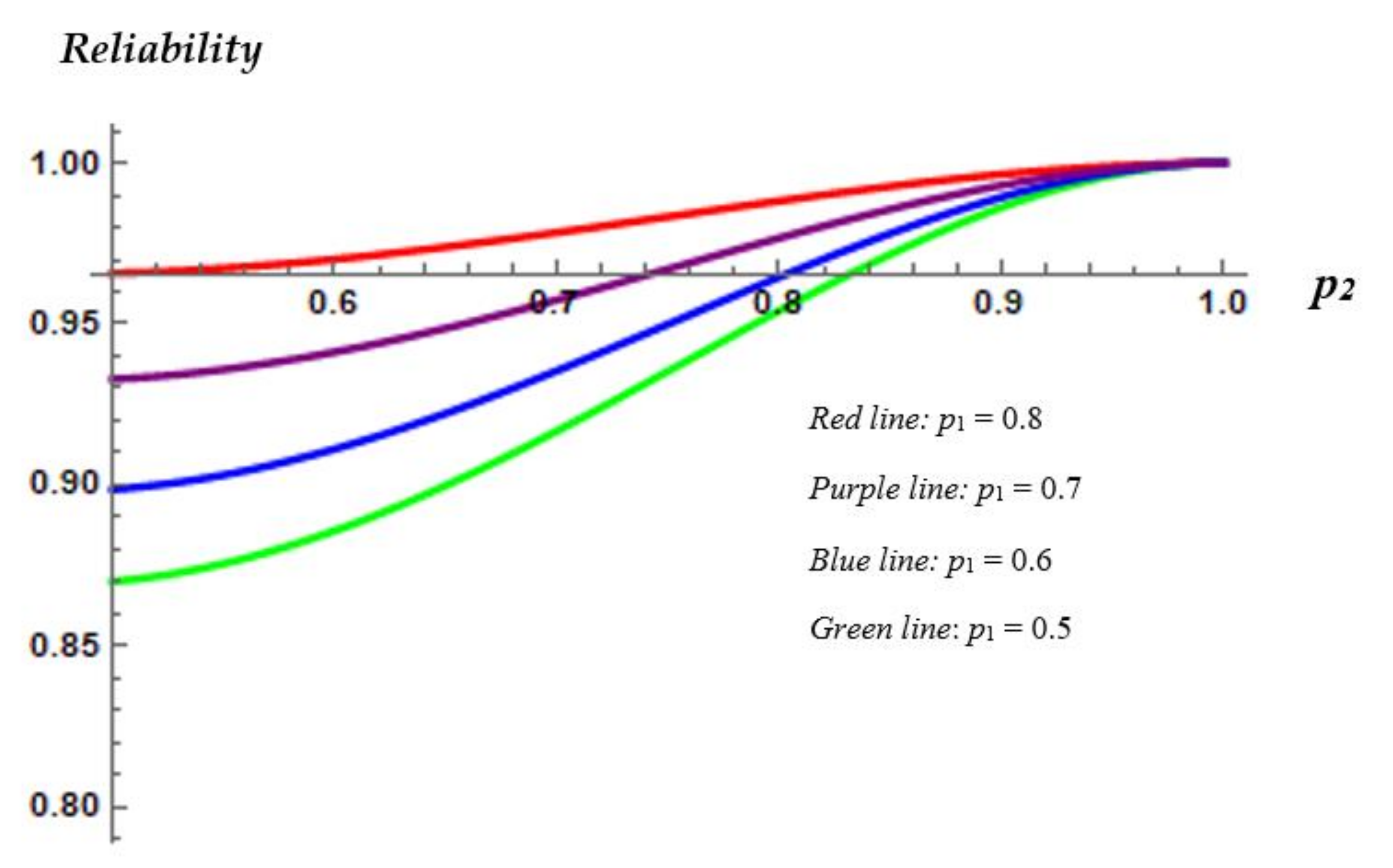Figure 4 displays the reliability of the underlying system versus the probability p₁ under different choices of the parameter p₂.

As it easily observed, Figure 4 illustrates the reliability values of the proposed structure under four different choices of parameter p₂, namely p₂ = 0.7 (Orange line), p₂ = 0.6 (Blue line), p₂ = 0.5 (Red line), and p₂ = 0.4 (Green line). Please note that the design parameters m, n, and k remain stable for all structures displayed in Figure 4 (m = 3, n = 10, k = 2). In other words, Figure 4 depicts the 3-consecutive-2-out-of-10: F system with a single change point for four different choices of the probability p₂. Based on Figure 4, we readily deduce that the reliability of the m-consecutive-k-out-of-n: F system with a single change point increases with respect to p₂.

A similar argumentation could be developed for the behavior of the reliability of the proposed structure in terms of probability p₁. Figure 5 illustrates the reliability values of the proposed structure under four different choices of parameter p₁, namely p₁ = 0.8 (Red line), p₁ = 0.7 (Purple line), p₁ = 0.6 (Blue line), and p₁ = 0.5 (Green line).

Based on Figure 5, we easily observe that the reliability of the m-consecutive-k-out-of-n: F system with a single change point increases with respect to p₁.

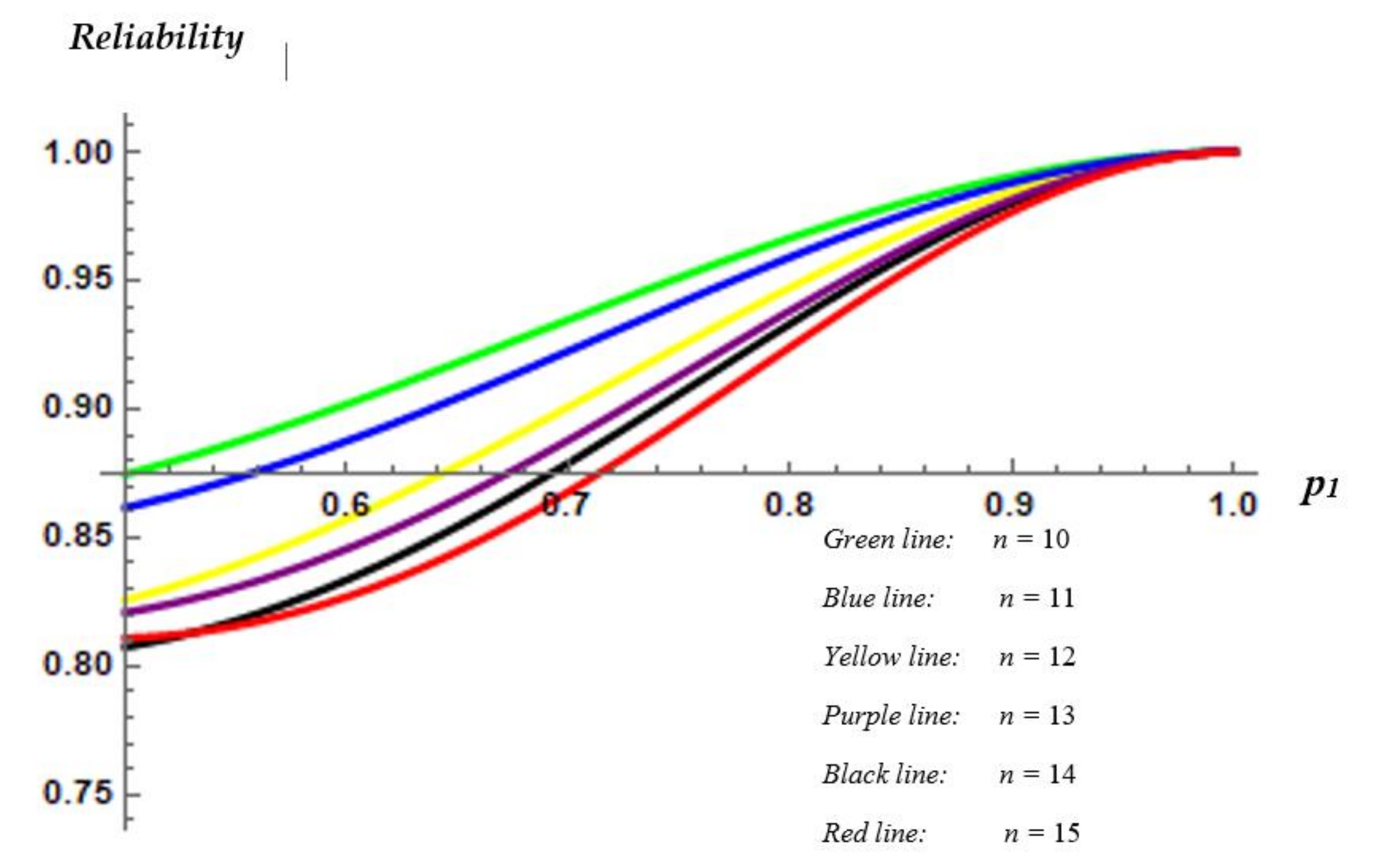
The next two figures shed light on the performance of the proposed structure with respect to the parameters n and k, respectively. Figure 6 illustrates the reliability of the m-consecutive-k-out-of-n: F system with a single change point for different values of n. In other words, we first determine the parameters m, k, p₂ as m = 3, k = 2, p₂ = 0.4, and we next compare the reliability values of the resulting structures for different choices of n.

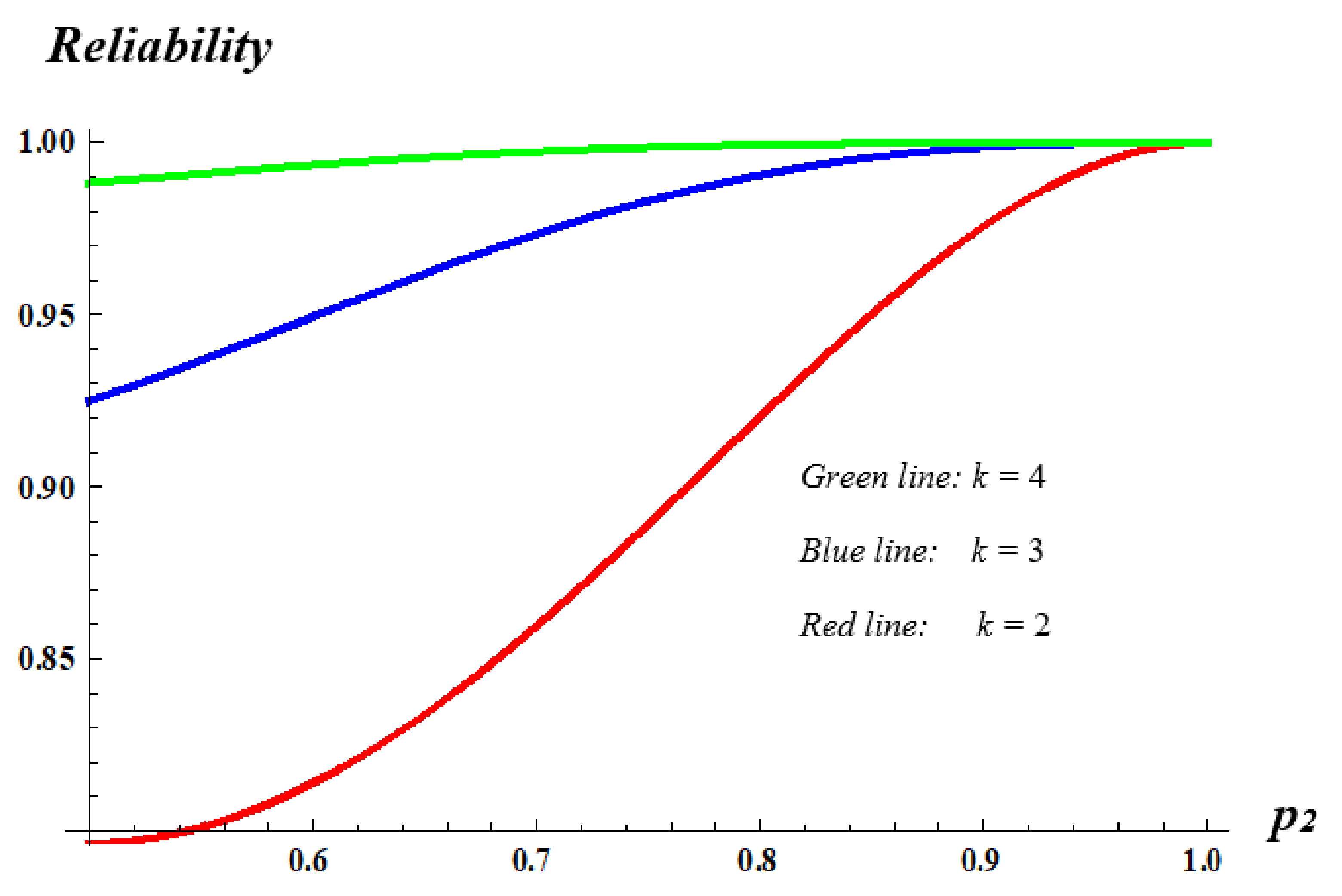
Based on Figure 6, it is straightforward that as the parameter n increases, the reliability of the resulting m-consecutive-k-out-of-n: F system with a single change point decreases. Consequently, the performance of the proposed structure strengthens as the total number of its components gets smaller. On the other hand, it is of some interest to investigate the behavior of the m-consecutive-k-out-of-n: F system with a single change point in terms of parameter k.

Based on Figure 7, we deduce that as the parameter k increases, the reliability of the resulting m-consecutive-k-out-of-n: F system with a single change point increases, too. Consequently, the performance of the proposed structure becomes better as the parameter k gets bigger.

We next compare numerically the performance of the m-consecutive-k-out-of-n: F system with a single change point against the consecutive-k-out-of-n: F structure with a single change point proposed in [25]. In order to provide fair comparisons, we consider for both systems the same design parameters p₁, p₂, n₁, n₂, k, and we evaluate the corresponding reliability values.

Based on the numerical comparisons displayed in

Table 1. Numerical comparisons between m-consecutive-k-out-of-n: F with a change point system and consecutive-k-out-of-n: F with a change point system.

			Consecutive-k-out-of-n: F with a Change Point		m-Consecutive-k-out-of-n: F with a Change Point
n1	n2	(p1, p2)	(n, k)	Reliability	(n, m, k)	Reliability
5	5	(0.8, 0.7)	(10, 2) (10, 3)	0.60236 0.89714	(10, 3, 2) (10, 3, 3)	0.97846 0.99946
		(0.9, 0.8)	(10, 2) (10, 3)	0.82023 0.97187	(10, 3, 2) (10, 3, 3)	0.99673 0.99997
7	5	(0.8, 0.7)	(12, 2) (12, 3)	0.56174 0.88552	(12, 3, 2) (12, 3, 3)	0.96951 0.99911
		(0.9, 0.8)	(12, 2) (12, 3)	0.80526 0.97011	(12, 3, 2) (12, 3, 3)	0.99516 0.99995
8	7	(0.8, 0.7)	(15, 2) (15, 3)	0.60236 0.89714	(15, 3, 2) (15, 3, 3)	0.94613 0.99722
		(0.9, 0.8)	(15, 2) (15, 3)	0.82023 0.97187	(15, 3, 2) (15, 3, 3)	0.99961 0.99986
10	8	(0.8, 0.7)	(18, 2) (18, 3)	0.60236 0.89714	(18, 3, 2) (18, 3, 3)	0.92696 0.99542
		(0.9, 0.8)	(18, 2) (18, 3)	0.82023 0.97187	(18, 3, 2) (18, 3, 3)	0.98668 0.99977

, we readily deduce that the m-consecutive-k-out-of-n: F system with a single change point provides bigger reliability values and consequently performs better compared to the corresponding consecutive-k-out-of-n: F system with a single change point. For instance, let us consider the special case p₁ = 0.8, p₂ = 0.7, n₁ = 10, n₂ = 8, k = 3. As it is easily observed, the resulting 3-consecutive-3-out-of-18: F system with a single change point achieves a reliability value equal to 99.542%, while the corresponding value for the competitive consecutive-3-out-of-18: F system with a single change point is equal to 89.714%.

Finally, it is of some interest to provide a numerical illustration for the behavior of the proposed reliability structure under the assumption that the number of components of each type is random. In other words, we assume that the random variable N₁, which is defined in Section 3, follows the well-known binomial distribution, and consequently, the corresponding probability mass function of N₁ is given by

$$f(n_1)=\left(\begin{array}{l}n\\ n_1\end{array}\right){\xi }^{n_1}{(1-\xi )}^{n-n_1}, n_1=0,1,\dots ,n,$$

where $0\le \xi \le 1$. We next apply Equation (26) in order to compute numerically the reliability values of the m-consecutive-k-out-of-n: F system with a single change point for several designs. The numerical results are displayed in

Table 2. Reliability values of the m-consecutive-k-out-of-n: F with a change point system.

	m-Consecutive-k-out-of-n: F with a Change Point
(p1, p2)	(n, m, k, ξ)	Reliability
(0.6, 0.5)	(11, 4, 2, 0.5) (11, 4, 2, 0.6)	0.90219 0.92399
(0.7, 0.5)	(11, 4, 2, 0.5) (11, 4, 2, 0.6)	0.93493 0.94932
(0.8, 0.5)	(11, 4, 2, 0.5) (11, 4, 2, 0.6)	0.96672 0.97406
(0.7, 0.6)	(11, 4, 2, 0.5) (11, 4, 2, 0.6)	0.94283 0.95538
(0.8, 0.6)	(11, 4, 2, 0.5) (11, 4, 2, 0.6)	0.97086 0.97721
(0.8, 0.7)	(11, 4, 2, 0.5) (11, 4, 2, 0.6)	0.97882 0.98338

.

For example, the 4-consecutive-2-out-of-11: F system with a single change point (p₁ = 0.6, p₂ = 0.5) achieves reliability values equal to 90.219% and 92.399%, when ξ equals 0.5 and 0.6, respectively.

5. Discussion

In the present paper, the m-consecutive-k-out-of-n: F structure with a single change point is introduced. Some reliability characteristics of the proposed system are studied, and the corresponding explicit expressions for determining them are also deduced. The proposed reliability model seems to fit well not only in applications of Industrial Engineering, but also in other fields, such as Biomedicine or Biology, where a computational study of biological sequences or DNA sequence recognition could be accomplished by the aid of consecutive-type structures. The main contribution of the manuscript refers to the determination of the number of path sets of a given size for the proposed reliability structure. Based on the above-mentioned result, one may readily reach closed formulae for the computation of the corresponding reliability function and mean time to failure of the system. The proposed m-consecutive-k-out-of-n: F structure with a single change point generalizes the well-known consecutive-k-out-of-n: F line with a single change point, which has been introduced in [25]. The aforementioned argument holds true, since for m = 1, the proposed structure reduces to the one established in [25]. Finally, an analogous reliability study of structures with two common failure criteria and a single change point and maintenance policy (see, e.g., [31,32]) could be an interesting topic for future research.