Immersed Boundary Method for Simulating Interfacial Problems
Abstract
1. Introduction
2. Mathematical Formulations
3. Discretization
4. Numerical Results
4.1. Code and Simulation





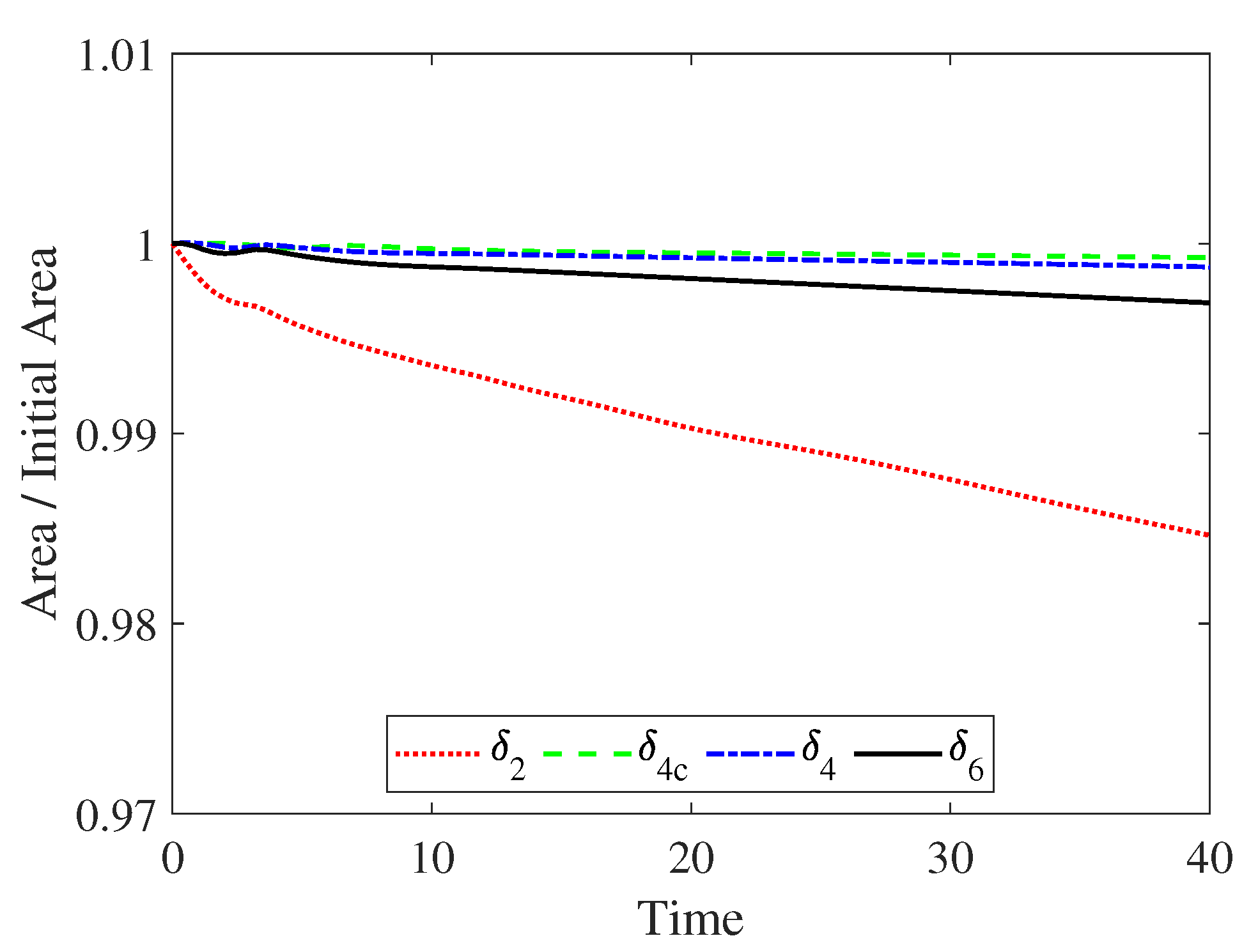
4.2. Discrete Delta Function
- is continuous,
- for ,
- for all r,
- for all r, and
- for all r.
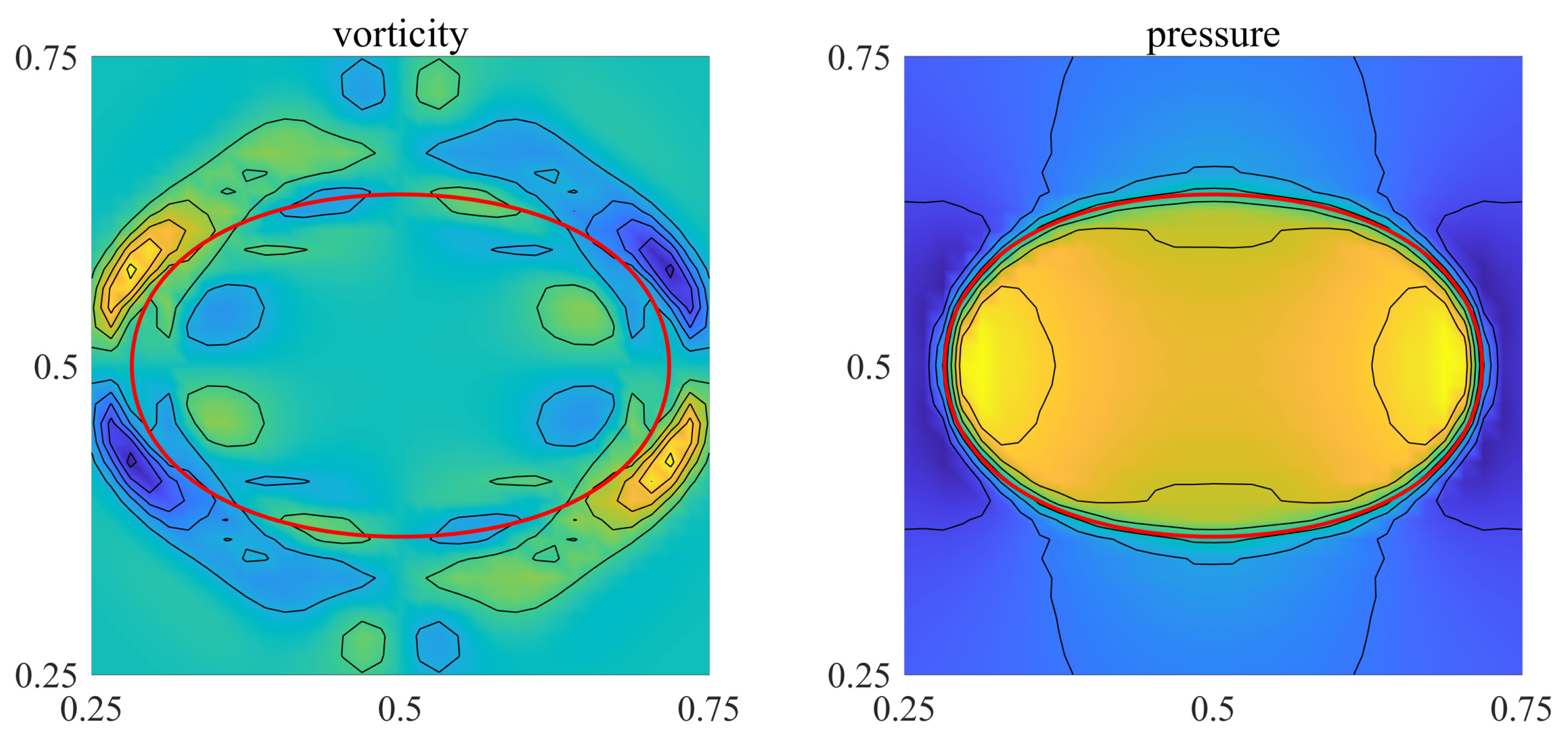
4.3. Effect of the Reynolds Number
- , regime of unseparated flow,
- , a fixed pair of Föppl vortices in the wake of the cylinder,
- , periodic the von Karman vortex street, and
- , transition to turbulence in vortex street.
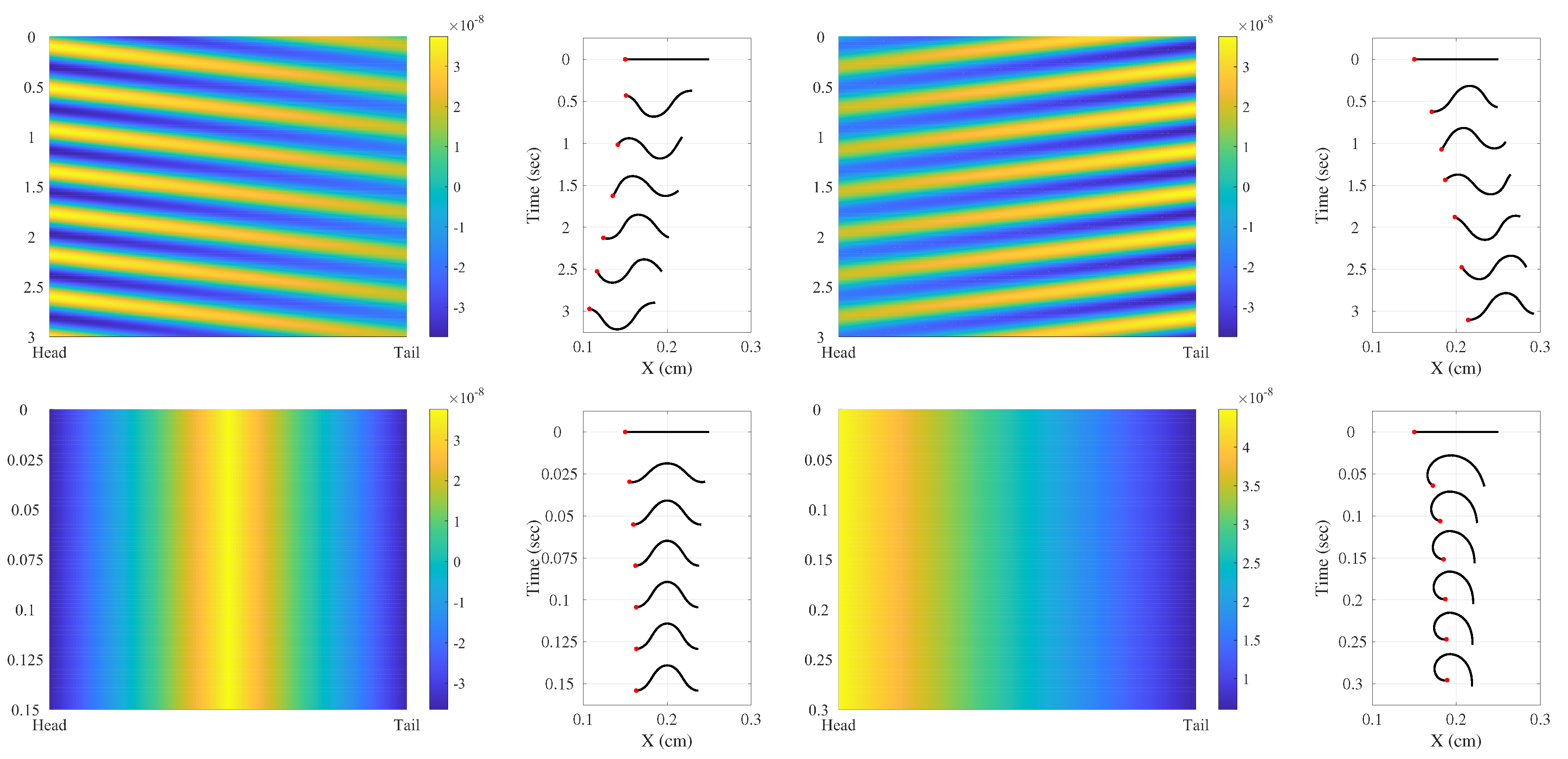
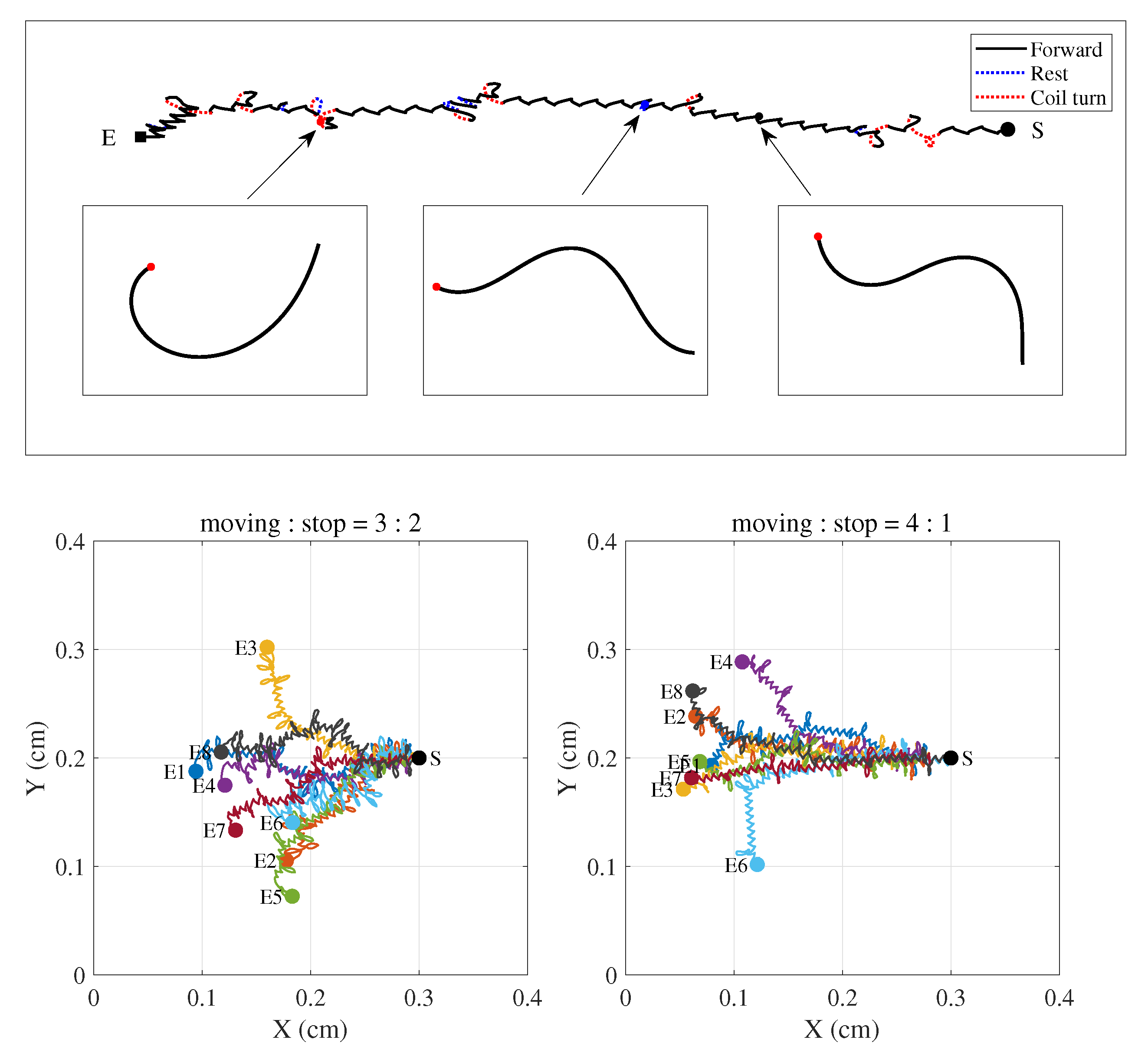
4.4. Biological Problem
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| IB | immersed boundary |
| NS | Navier–Stokes |
Appendix A. Code Structure

- main_IB2D.m: main code, including animation code for vorticity and pressure.
- initialization.m: setting parameters, including the domain and grid sizes, Reynolds and Weber numbers, and the initial boundary configuration
- spread.m: spreading out the boundary force density to the fluid force density using the Dirac-delta function
- NSsolver.m: updating the fluid velocity and pressure by using fast Fourier transformation
- Interp.m: getting the velocity on the elastic IB boundary from the fluid velocity
- phi1.m: setting the Dirac-delta function along the x-direction
- phi2.m: setting the Dirac-delta function along the y-direction
References
- Donea, J.; Giuliani, S.; Halleux, J. An arbitrary Lagrangian-Eulerian finite element method for transient dynamic fluid-structure interactions. Comput. Methods Appl. Mech. Eng. 1982, 33, 689–723. [Google Scholar] [CrossRef]
- Gibou, F.; Min, C. Efficient symmetric positive definite second-order accurate monolithic solver for fluid/solid interactions. J. Comput. Phys. 2012, 231, 3246–3263. [Google Scholar] [CrossRef]
- Jamalabadi, M. Analytical solution of sloshing in a cylindrical tank with an elastic cover. Mathematics 2019, 7, 1070. [Google Scholar] [CrossRef]
- Jamalabadi, M. Optimal design of isothermal sloshing vessels by entropy generation minimization method. Mathematics 2019, 7, 380. [Google Scholar] [CrossRef]
- Lee, S.; Li, Y.; Shin, J.; Kim, J. Phase-field simulations of crystal growth in a two-dimensional cavity flow. Comput. Phys. Commun. 2017, 216, 84–94. [Google Scholar] [CrossRef]
- Peskin, C.S. Flow patterns around heart valves: A numerical method. J. Comput. Phys. 1972, 10, 252–271. [Google Scholar] [CrossRef]
- Peskin, C.S. The immersed boundary method. Acta Numer. 2002, 11, 497–517. [Google Scholar] [CrossRef]
- Iaccarino, G.; Verzicco, R. Immersed boundary technique for turbulent flow simulations. Appl. Mech. Rev. 2003, 56, 331–347. [Google Scholar] [CrossRef]
- James, N.; Maitre, E.; Mortazavi, I. Immersed boundary methods for the numerical simulation of incompressible aerodynamics and fluid-structure interactions. Ann. Mathématiques Blaise Pascal 2013, 20, 139–173. [Google Scholar] [CrossRef][Green Version]
- Bächer, C.; Gekle, S. Computational modeling of active deformable membranes embedded in three-dimensional flows. Phys. Rev. E 2019, 99, 062418. [Google Scholar] [CrossRef]
- Lee, S. Mathematical model of contractile ring-driven cytokinesis in a three-dimensional domain. Bull. Math. Biol. 2018, 80, 583–597. [Google Scholar] [CrossRef] [PubMed]
- Lee, W.; Lim, S.; Kim, Y. The role of myosin II in glioma invasion: A mathematical model. PLoS ONE 2017, 12, e0171312. [Google Scholar] [CrossRef]
- Fauci, L.J. A computational model of the fluid dynamics of undulatory and flagellar swimming. Am. Zool. 1996, 26, 599–607. [Google Scholar] [CrossRef]
- Kim, Y.; Peskin, C.S. Penalty immersed boundary method for an elastic boundary with mass. Phys. Fluids 2007, 19, 053103. [Google Scholar] [CrossRef]
- Kim, Y.; Peskin, C.S. A penalty immersed boundary method for a rigid body in fluid. Phys. Fluids 2016, 28, 033603. [Google Scholar] [CrossRef]
- Lee, K.; Yang, K. Large Eddy simulation of turbulent flow past a circular cylinder in the subcritical and critical regimes. J. Mech. Sci. Technol. 2017, 31, 1729–1737. [Google Scholar] [CrossRef]
- Posa, A.; Vanella, M.; Balaras, E. An adaptive reconstruction for Lagrangian, direct-forcing, immersed-boundary methods. J. Comput. Phys. 2017, 351, 422–436. [Google Scholar] [CrossRef]
- Kang, S. An improved near-wall modelling for large-eddy simulation using immersed boundary methods. Int. J. Numer. Methods Fluids 2015, 78, 76–88. [Google Scholar] [CrossRef]
- Yang, X.; Sadique, J.; Mittal, R.; Meneveau, C. Integral wall model for large eddy simulations of wall-bounded turbulent flows. Phys. Fluids 2015, 27, 025112. [Google Scholar] [CrossRef]
- Peskin, C.S.; McQueen, D.M. Fluid Dynamics of the Heart and its Valves. In Case Studies in Mathematical Modeling: Ecology, Physiology, and Cell Biology; Othmer, H.G., Adler, F.R., Lewis, M.A., Dallon, J.C., Eds.; Prentice-Hall: Englewood Cliffs, NJ, USA, 1996. [Google Scholar]
- Chorin, A. Numerical solution of the Navier–Stokes equations. Math. Comput. 1968, 22, 745–762. [Google Scholar] [CrossRef]
- Liu, Y.; Mori, Y. Properties of discrete delta functions and local convergence of the immersed boundary method. SIAM J. Numer. Anal. 2012, 50, 2986–3015. [Google Scholar] [CrossRef]
- Stockie, J.M. Analysis and Computation of iMmersed Boundaries, with Application to Pulp Fibres. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 1997. [Google Scholar]
- Braza, M.; Chassaing, P.; Minh, H.H. Numerical study and physical analysis of the pressure and velocity fields in the near wake of a circular cylinder. J. Fluid Mech. 1986, 165, 79–130. [Google Scholar] [CrossRef]
- Ding, H.; Shu, C.; Yeo, K.S.; Xu, D. Numerical simulation of flows around two circular cylinders by mesh-free least square-based finite difference methods. Int. J. Numer. Methods Fluids 2007, 53, 305–332. [Google Scholar] [CrossRef]
- Harichandan, A.B.; Roy, A. Numerical investigation of low Reynolds number flow past two and three circular cylinders using unstructured grid CFR scheme. Int. J. Heat Fluid Flow 2010, 31, 154–171. [Google Scholar] [CrossRef]

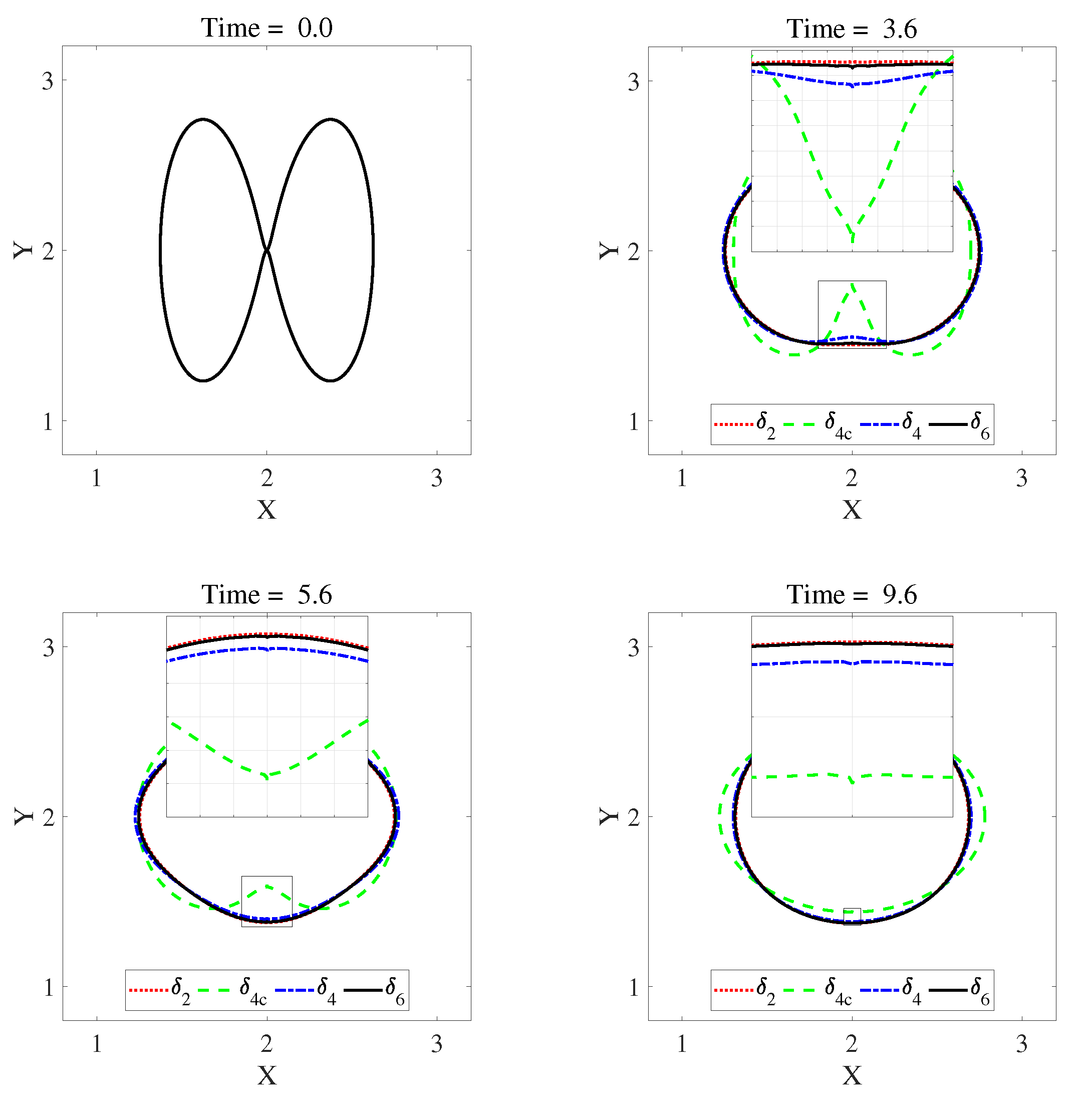
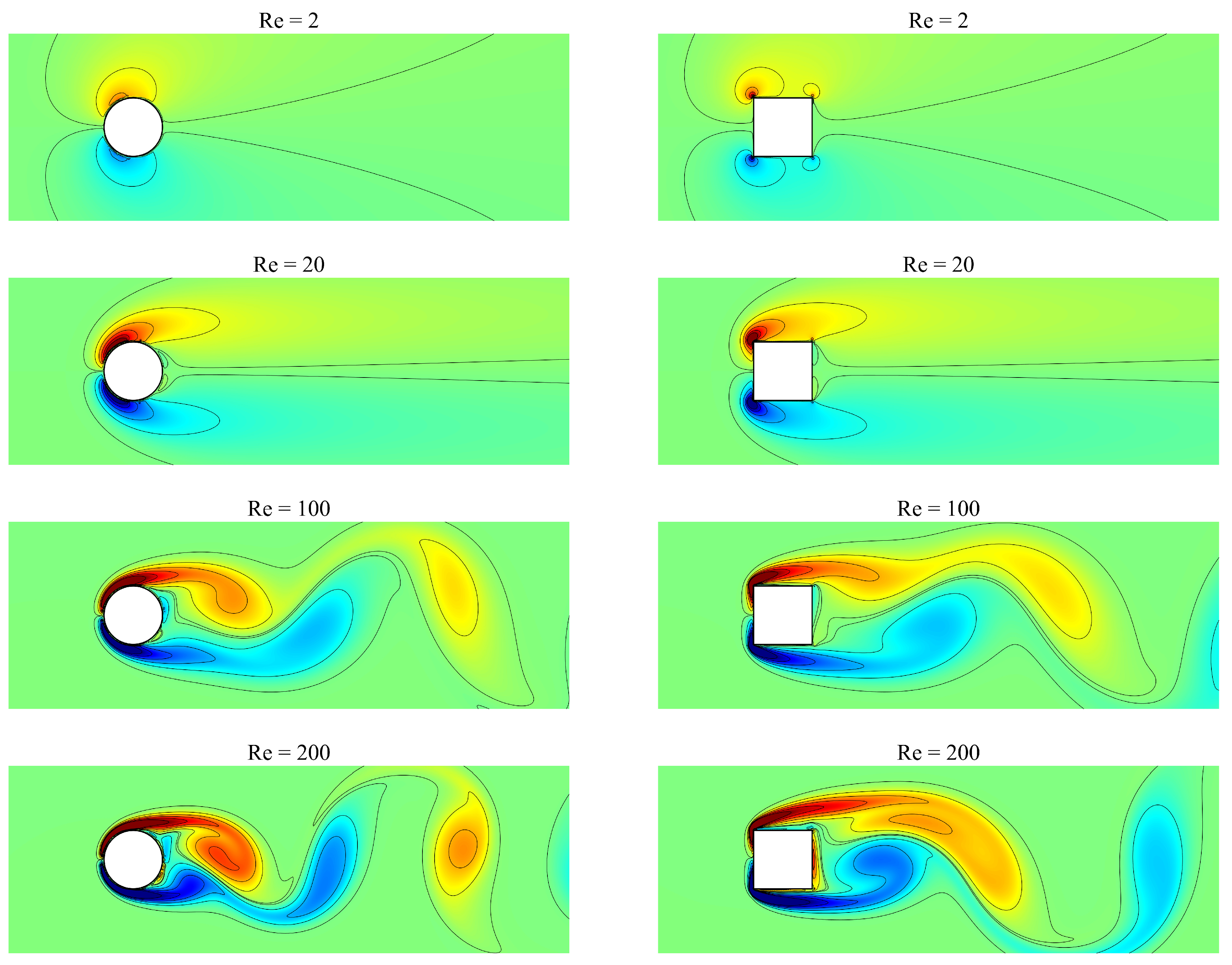
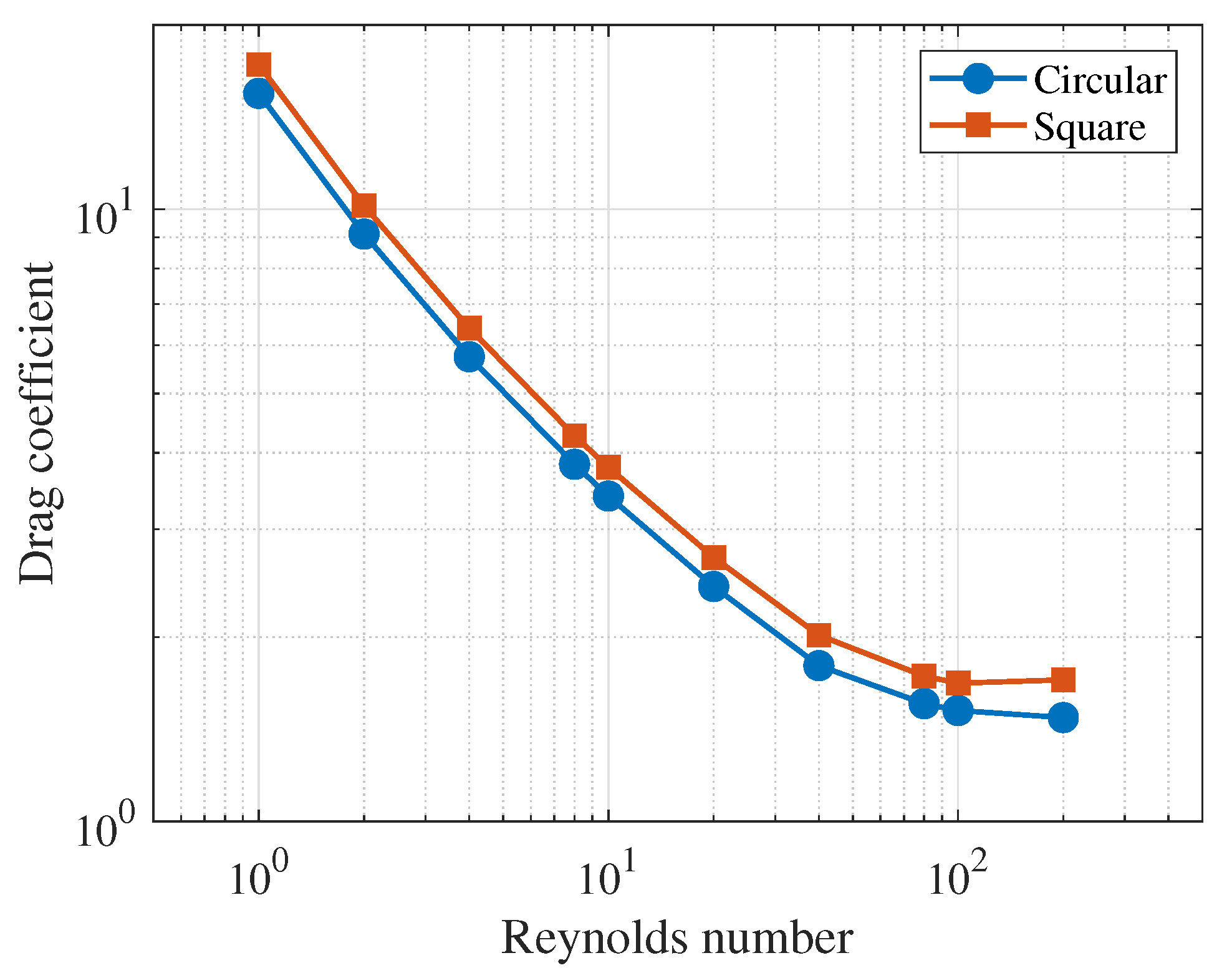
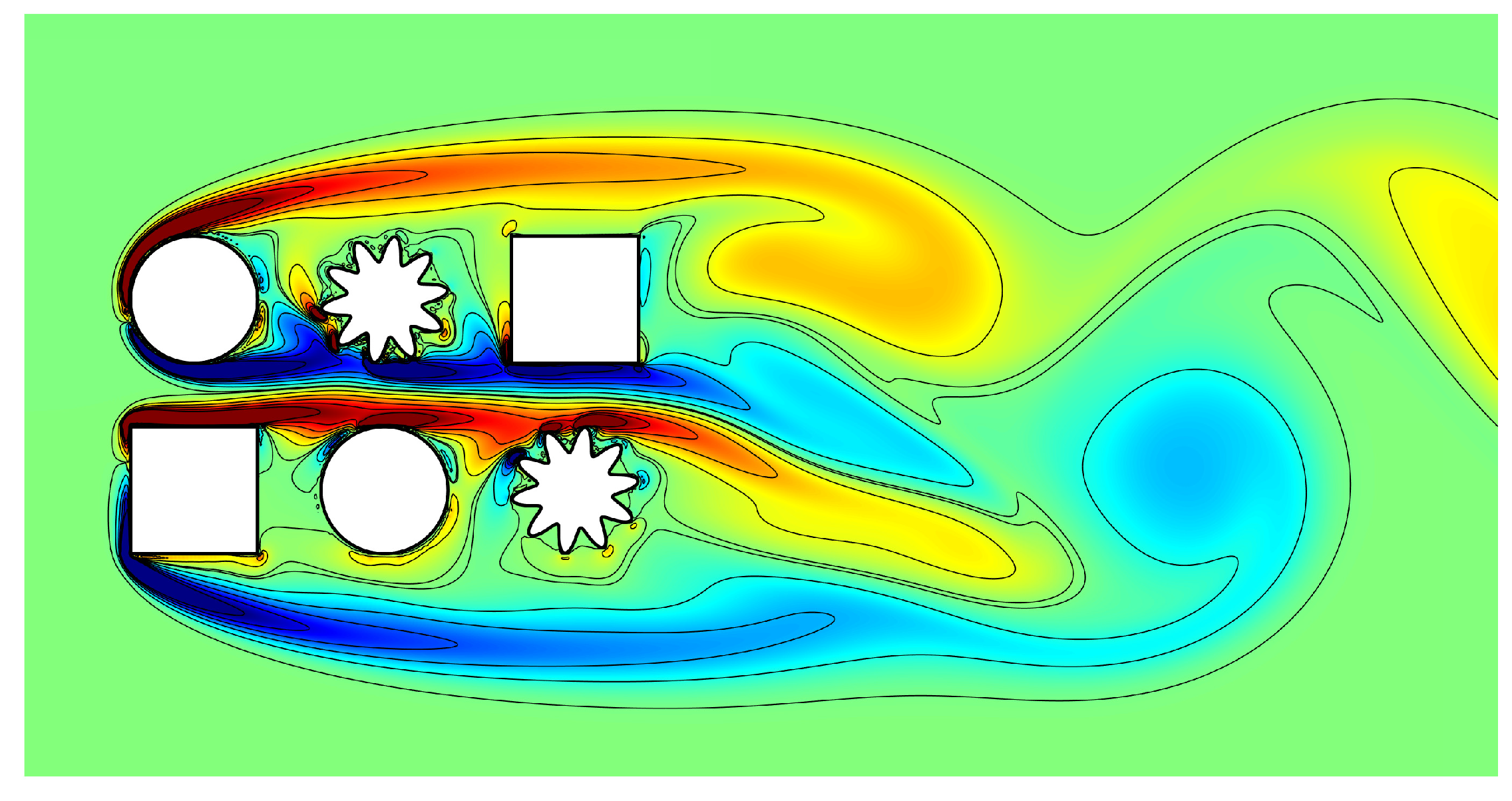
| Lift Coefficient (CL) | Drag Coefficient (CD) | Reference | |||
|---|---|---|---|---|---|
| Re 100 | Re 200 | Re 100 | Re 200 | ||
| Braza et al. (1986) | [24] | ||||
| Ding et al. (2007) | [25] | ||||
| Harichandan et al. (2010) | [26] | ||||
| Present result | tw | ||||
| Present result (Square) | tw | ||||
| Motion Ratio 3:2 | Motion Ratio 4:1 | |||
|---|---|---|---|---|
| mean | std | mean | std | |
| moving distance (cm) | 0.1755 | 0.0169 | 0.2223 | 0.0120 |
| turn angle () | 22.8487 | 17.1738 | 11.3732 | 10.5050 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, W.; Lee, S. Immersed Boundary Method for Simulating Interfacial Problems. Mathematics 2020, 8, 1982. https://doi.org/10.3390/math8111982
Lee W, Lee S. Immersed Boundary Method for Simulating Interfacial Problems. Mathematics. 2020; 8(11):1982. https://doi.org/10.3390/math8111982
Chicago/Turabian StyleLee, Wanho, and Seunggyu Lee. 2020. "Immersed Boundary Method for Simulating Interfacial Problems" Mathematics 8, no. 11: 1982. https://doi.org/10.3390/math8111982
APA StyleLee, W., & Lee, S. (2020). Immersed Boundary Method for Simulating Interfacial Problems. Mathematics, 8(11), 1982. https://doi.org/10.3390/math8111982





