Scale Mixture of Rayleigh Distribution

Abstract

In this paper, the scale mixture of Rayleigh (SMR) distribution is introduced. It is proven that this new model, initially defined as the quotient of two independent random variables, can be expressed as a scale mixture of a Rayleigh and a particular Generalized Gamma distribution. Closed expressions are obtained for its pdf, cdf, moments, asymmetry and kurtosis coefficients. Its lifetime analysis, properties and Rényi entropy are studied. Inference based on moments and maximum likelihood (ML) is proposed. An Expectation-Maximization (EM) algorithm is implemented to estimate the parameters via ML. This algorithm is also used in a simulation study, which illustrates the good performance of our proposal. Two real datasets are considered in which it is shown that the SMR model provides a good fit and it is more flexible, especially as for kurtosis, than other competitor models, such as the slashed Rayleigh distribution.

1. Introduction

Rayleigh distribution is a continuous and positive distribution named after Lord Rayleigh (J.W. Strutt 1880–1919), who introduced it in connection with a problem in acoustics. Since then, it has been widely used in different fields of science and technology and has become one of the most popular models for describing skewed positive data. Siddiqui [1] discussed the relationship of certain problems with the Rayleigh distribution. Miller [2] worked with this distribution for modeling the length of a vector in an N-dimensional euclidean space, whose components are independent and normally distributed according to a $N(0,{\sigma }^2)$ distribution. Polovko [3], in the field of reliability, highlight that the hazard function of a Rayleigh distribution is an increasing linear function of time. Hirano [4] provides us the history and relevant properties of this model. Results on unbiased minimum variance estimation in this model can be seen in Lopez-Blazquez et al. [5]. Bayesian analysis has been carried out by Ahmed et al. [6], who discussed and compared classical and Bayesian methods by using the mean squared error. As for applications of interest in the fields of Engineering and Physics, Sarti et al. [7], Kalaiselvi et al. [8] and Dhaundiyal and Singh [9] can be cited, among others. All these references illustrate the potential interest of this model from a theoretical and applied point of view.

Recall that a continuous random variable (RV) X follows a Rayleigh (R) distribution with scale parameter $\sigma >0$, denoted as $X\sim R\left(\sigma \right)$, if its probability density function (pdf) is

$$\begin{array}{c}\hfill f_X\left(x\right)=\frac{x}{\sigma }{e}^{-\frac{x^2}{2\sigma }},x,\sigma >0.\end{array}$$

(1)

An extension of (1), named slashed Rayleigh (SR), was proposed by Iriarte et al. [10]. The SR model, $T\sim SR(\sigma ,q)$, is defined as

$$\begin{array}{c}\hfill T={\displaystyle \frac{X}{U^{\frac{1}{q}}}},\end{array}$$

where X and U are independent RVs, $X\sim R\left(\sigma \right)$, U follows an uniform distribution on $(0$,$1)$, $U\sim U(0,1)$ and $q>0$ is a scalar. The pdf of T is

$$\begin{array}{ccc}\hfill f_T(t;\sigma ,q)& =& {\displaystyle \frac{q{\left(2\sigma \right)}^{\frac{q}{2}}}{t^{q+1}}}\Gamma \left({\displaystyle \frac{q+2}{2}}\right)F\left({\displaystyle \frac{t^2}{2\sigma }};{\displaystyle \frac{q+2}{2}};1\right),t>0,\hfill \end{array}$$

where $\Gamma (·)$ denotes the gamma function, and $F(·;a;b)$ the cdf of a gamma distribution with shape and rate parameters a and b, respectively.

In this paper, an extension of the R distribution is introduced following the general method to obtain distributions with a higher kurtosis coefficient than the slash version of the Rayleigh model proposed by Iriarte et al. [10], and applied successfully by other authors: Reyes et al. [11] to obtain the Generalized Modified slash model, Reyes et al. [12] to get a generalization of Birnbaum–Saunders, Iriarte et al. [13] and Segovia [14] to extend the quasi-gamma and power Maxwell distributions, respectively. It will be proven that our proposal admits a representation as a scale mixture of a Rayleigh and a Generalized Gamma distribution. Throughout the different sections in this paper, it will be shown that the SMR distribution can be used for modeling positive, right skew data with a heavy right tail.

The outline of this paper is as follows. Section 2 is devoted to the study of the SMR model; the property of mixture is presented and closed expressions are given for its pdf, cdf, moments, asymmetry and kurtosis coefficient. In Section 3, results of interest in survival analysis and reliability are given. These are the survival and hazard function, mean residual life and order statistics. We highlight that, in contrast to the Rayleigh distribution, whose hazard function is increasing and linear, the hazard function of the SMR model is unimodal. In Section 4, the Rényi entropy is obtained. Section 5 is devoted to moment and ML estimation of parameters. An EM type algorithm is given, which has closed expressions in all the stages, and therefore it allows us to estimate the parameters in a computationally efficient way. In Section 6, a simulation study is carried out, which suggests the consistency of estimators even for moderate sample sizes. In Section 7, two real applications from the fields of survival analysis and engineering are provided. Plots and criteria are considered that show that the SMR model fits better than R and SR models, especially on the right tail of the datasets. The simulation study and applications have been carried out by using R programming language. Some final conclusions can be seen in Section 8.

2. Definition and Properties

In this section, a new extension of R distribution is introduced. Simple expressions (which can be computed easily in many softwares) for its pdf and cdf are obtained, along with its moments, skewness and kurtosis coefficients. It is also proved that this model can be expressed as a scale mixture of distributions. This result is the basis to apply the EM algorithm in Section 5.

Our proposal is based on the Generalized Gamma (GG) distribution introduced by Stacy [15] and whose pdf is given in Definition 1.

Definition 1.

An RV Z follows a three-parameter GG distribution, proposed by Stacy [15], if its pdf is

$$\begin{array}{ccc}\hfill f(z;a,d,p)& =& \frac{p{a}^d}{\Gamma \left(\frac{d}{p}\right)}{z}^{d-1}{e}^{-{\left(az\right)}^p},a,d,p,z>0.\hfill \end{array}$$

(2)

We denote as $Z\sim GG(a,d,p)$.

Next, the new model is introduced.

Definition 2.

An RV T follows an SMR distribution with parameters $\sigma >0$ and $q>0$, if T can be expressed as the ratio of two independent RVs

$$\begin{array}{c}\hfill T={\displaystyle \frac{X}{Y}},\end{array}$$

(3)

with $X\sim R\left(\sigma \right)$ and $Y\sim GG(1,q,2)$. We use the notation $T\sim SMR(\sigma ,q)$.

Next, the pdf of T is given.

Proposition 1.

Let $T\sim SMR(\sigma ,q)$ with $\sigma >0$ and $q>0$. Then the pdf of T is

$$\begin{array}{c}\hfill f_T(t;\sigma ,q)={\displaystyle \frac{qt}{2\sigma {\left(\frac{t^2}{2\sigma }+1\right)}^{\frac{q}{2}+1}}},t>0.\end{array}$$

(4)

Proof. 

Taking into account (3) with $X\sim R\left(\sigma \right)$ independent of $Y\sim GG(1,q,2)$, with $\sigma ,q>0$ and whose pdfs are given in (1) and (2), respectively. By applying the Jacobian method (see Casella and Berger [16], Section 4.3) to $X=TZ$ and $Y=Z$, the joint pdf of $(T,Z)$, $f_{T,Z}$, is

$$\begin{array}{ccc}\hfill f_{T,Z}(t,z)& =& {\displaystyle \frac{2t}{\sigma \Gamma (q/2)}}{z}^{q+1}exp\left\{-z^2\left({\displaystyle \frac{t^2}{2\sigma }}+1\right)\right\},t>0,z>0.\hfill \end{array}$$

The marginal pdf of T is

$$\begin{array}{ccc}\hfill f_T(t;\sigma ,q)& =& {\displaystyle \frac{2t}{\sigma \Gamma (q/2)}}{\int }_0^{\infty }{z}^{(q+2)-1}exp\left\{-\left({\displaystyle \frac{t^2}{2\sigma }}+1\right)z^2\right\}dz,t>0.\hfill \end{array}$$

(5)

Note that the integrand in (5) is related to the pdf of a $GG\left({\left(1+\frac{t^2}{2\sigma }\right)}^{1/2},q+2,2\right)$ distribution, except for a constant. Therefore,

$$\begin{array}{ccc}\hfill f_T(t;\sigma ,q)& =& {\displaystyle \frac{qt}{2\sigma {\left(1+\frac{t^2}{2\sigma }\right)}^{\frac{q}{2}+1}}},t>0.\hfill \end{array}$$

□

Remark 1.

A $GG(1,q,2)$ model has been proposed for Y in (3) in order to get a closed expression for the pdf of T given in (4).

Next, the cumulative distribution function (cdf) of T is obtained.

Proposition 2.

Let $T\sim SMR(\sigma ,q)$ with $\sigma >0$ and $q>0$. Then the cdf of T is

$$\begin{array}{ccc}\hfill F_T\left(t\right)& =& 1-{\displaystyle \frac{1}{{\left(\frac{t^2}{2\sigma }+1\right)}^{\frac{q}{2}}}},t>0.\hfill \end{array}$$

(6)

Proof. 

Taking into account (4) and the change of variable $u={\displaystyle \frac{x^2}{2\sigma }}+1$, the result is obtained. □

Plots of (4) and (6) are given in Figure 1 for $\sigma =1$ and several values of q.

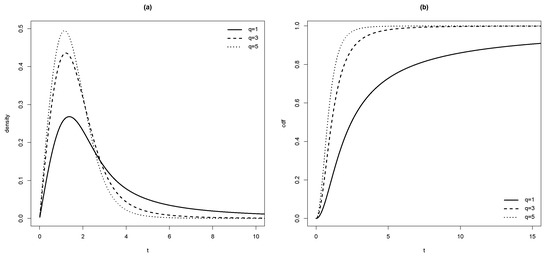
Figure 1. (a) pdf and (b) cdf in SMR model for $\sigma =1$ and different values of q.

It will be seen that $\sqrt{\sigma }>0$ is a scale parameter and $q>0$ is a shape parameter since it affects the skewness and kurtosis coefficients in this model.

The next proposition shows that the SMR model can be expressed as a scale mixture of distributions.

Proposition 3.

Let $T|V=v\sim R\left({\displaystyle \frac{\sigma }{v^2}}\right)$ and $V\sim GG(1,q,2)$ with σ and $q>0$. Then $T\sim SMR(\sigma ,q)$.

Proof. 

Recall that the joint pdf of $(T,V)$ is $f(t,v)=f_{t|v}\left(t\right)f_v\left(v\right)$. Then $f_T\left(t\right)$ is given by

$$\begin{array}{ccc}\hfill f_T(t;\sigma ,q)& =& {\int }_0^{\infty }f(t,v)dv\hfill \\ & =& {\displaystyle \frac{qt}{2\sigma {\left(1+\frac{t^2}{2\sigma }\right)}^{(q+2)/2}}}{\int }_0^{\infty }{\displaystyle \frac{2v^{(q+2)-1}}{{\left(1+\frac{t^2}{2\sigma }\right)}^{-(q+2)/2}\frac{q}{2}\Gamma \left(\frac{q}{2}\right)}}exp\left(-{\left[\frac{v}{{\left(1+\frac{t^2}{2\sigma }\right)}^{-1/2}}\right]}^2\right)dv.\hfill \end{array}$$

Note that the last integrand corresponds to the pdf of an RV with $GG\left({\left(1+\frac{t^2}{2\sigma }\right)}^{1/2},q+2,2\right)$ distribution. Therefore, such integral is 1 and then

$$\begin{array}{ccc}\hfill f_T(t;\sigma ,q)& =& {\displaystyle \frac{qt}{2\sigma {\left(1+\frac{t^2}{2\sigma }\right)}^{(q+2)/2}}},t>0,\hfill \end{array}$$

that is $T\sim SMR(\sigma ,q)$. □

Remark 2.

Proposition 3 is a key result in this paper since it allows us to generate random samples of SMR model. It will be also useful for the application of EM algorithm, simulation studies and computation of ML estimators.

Moments

In this subsection, the moments of SMR distribution are obtained. For this, the next lemma will be useful.

Lemma 1.

Let $Y\sim GG(1,q,2)$ with $q>0$. For $r>0$, $\mathbb{E}\left[Y^{-r}\right]$ exists if and only if $r<q$ and in this case

$$\begin{array}{ccc}\hfill \mathbb{E}\left[Y^{-r}\right]& =& {\displaystyle \frac{\Gamma \left(\frac{q-r}{2}\right)}{\Gamma \left(\frac{q}{2}\right)}}.\hfill \end{array}$$

(7)

Proof. 

By definition,

$$\mathbb{E}\left[Y^{-r}\right]=\frac{2}{\Gamma (q/2)}{\int }_0^{\infty }{y}^{-r+q-1}{e}^{-y^2}dy.$$

By making the change of variable $u=y^2$, the result is immediate. □

In Proposition 4, the noncentral moments of an SMR model are given.

Proposition 4.

Let $T\sim SMR(\sigma ,q)$ with σ and $q>0$. For $r>0$, $\mathbb{E}\left[T^r\right]$ exists if and only if $r<q$ and in this case

$$\begin{array}{ccc}\hfill \mathbb{E}\left[T^r\right]& =& {\left(2\sigma \right)}^{r/2}\Gamma \left(\frac{r+2}{2}\right)\frac{\Gamma \left(\frac{q-r}{2}\right)}{\Gamma \left(\frac{q}{2}\right)}.\hfill \end{array}$$

(8)

Proof. 

By using the representation given in (3) and the independence of X and Y

$$\begin{array}{ccc}\hfill \mathbb{E}\left[T^r\right]& =& E\left[{\left(\frac{X}{Y}\right)}^r\right]=\mathbb{E}\left[X^r\right]\mathbb{E}\left[Y^{-r}\right]\hfill \\ & =& {\left(2\sigma \right)}^{r/2}\Gamma \left(\frac{r+2}{2}\right)\frac{\Gamma \left(\frac{q-r}{2}\right)}{\Gamma \left(\frac{q}{2}\right)}\hfill \end{array}$$

where $\mathbb{E}\left[X^r\right]={\left(2\sigma \right)}^{r/2}\Gamma \left(\frac{r+2}{2}\right)$ is the rth-moment of a $R\left(\sigma \right)$ distribution and $E\left[Y^{-r}\right]$ was given in (7). □

From Proposition 4, the explicit expression of the noncentral moments, ${\mu }_r=\mathbb{E}\left[T^r\right]$, for $r=1,2,3,4$ and the variance of $T\sim SMR(\sigma ,q)$, $V\left(T\right)$ follow.

Corollary 1.

Let $T\sim SMR(\sigma ,q)$ with $\sigma ,q>0$. From (8), the first four noncentral moments and the variance of T, say $\mathbb{V}\left(T\right)$, are given by

$$\begin{array}{ccc}& & {\mu }_1=\sqrt{\frac{\pi \sigma }{2}}\frac{\Gamma \left(\frac{q-1}{2}\right)}{\Gamma \left(\frac{q}{2}\right)},q>1,{\mu }_2=2\sigma \frac{\Gamma \left(\frac{q-2}{2}\right)}{\Gamma \left(\frac{q}{2}\right)},q>2,\hfill \\ \\ & & {\mu }_3=3\sqrt{\frac{\pi {\sigma }^3}{2}}\frac{\Gamma \left(\frac{q-3}{2}\right)}{\Gamma \left(\frac{q}{2}\right)},q>3,{\mu }_4=8{\sigma }^2\frac{\Gamma \left(\frac{q-4}{2}\right)}{\Gamma \left(\frac{q}{2}\right)},q>4,\hfill \end{array}$$

$$\begin{array}{ccc}& & \mathbb{V}\left(T\right)=\frac{\sigma \left[4\Gamma \left(\frac{q-2}{2}\right)\Gamma \left(\frac{q}{2}\right)-\pi {\left[\Gamma \left(\frac{q-1}{2}\right)\right]}^2\right]}{2{\left[\Gamma \left(\frac{q}{2}\right)\right]}^2},q>2.\hfill \end{array}$$

Remark 3.

From Corollary 1, it follows that $\sqrt{\sigma }$ is a scale parameter, that is, if $T\sim SMR(\sigma ,q)$ then $\frac{T}{\sqrt{\sigma }}\sim SMR(1,q)$. In addition, note that the coefficient of variation, $c.v\left(T\right)=\frac{\mathbb{V}{\left(T\right)}^{1/2}}{{\mu }_1}$, does not depend on σ.

The next proposition gives us the asymmetry coefficient, $\sqrt{{\beta }_1}$, of an $SMR(\sigma ,q)$ model.

Proposition 5.

Let $T\sim SMR(\sigma ,q)$ with $\sigma >0$ and $q>3$. Then the asymmetry coefficient of T is

$$\begin{array}{ccc}\hfill \sqrt{{\beta }_1}& =& {\displaystyle \frac{2\sqrt{\pi }\left[3a_{31}{a}_{02}-6a_{11}{a}_{21}{a}_{01}+\pi a_{13}\right]}{{\left[64a_{23}{a}_{03}-48\pi a_{12}{a}_{22}{a}_{02}+12{\pi }^2{a}_{21}{a}_{01}{a}_{14}-{\pi }^3{a}_{16}\right]}^{1/2}}},\hfill \end{array}$$

(9)

where $a_{ij}={\left[\Gamma \left(\frac{q-i}{2}\right)\right]}^j$.

Proof. 

Recall that

$$\begin{array}{c}\hfill \sqrt{{\beta }_1}={\displaystyle \frac{\mathbb{E}\left[{(T-\mathbb{E}\left(T\right))}^3\right]}{{\left(\mathbb{V}\left(T\right)\right)}^{3/2}}}={\displaystyle \frac{{\mu }_3-3{\mu }_1{\mu }_2+2{\mu }_1^3}{{({\mu }_2-{\mu }_1^2)}^{3/2}}},\end{array}$$

where ${\mu }_1$, ${\mu }_2$ and ${\mu }_3$ were given in Corollary 1. Then

$$\begin{array}{ccc}\hfill \sqrt{{\beta }_1}& =& {\displaystyle \frac{2\sqrt{\pi }\left[3a_{31}{a}_{02}-6a_{11}{a}_{21}{a}_{01}+\pi a_{13}\right]}{{\left[64a_{23}{a}_{03}-48\pi a_{12}{a}_{22}{a}_{02}+12{\pi }^2{a}_{21}{a}_{01}{a}_{14}-{\pi }^3{a}_{16}\right]}^{1/2}}}.\hfill \end{array}$$

□

The next proposition gives us the kurtosis coefficient, ${\beta }_2$, of an $SMR(\sigma ,q)$ model.

Proposition 6.

Let $T\sim SMR(\sigma ,q)$ with $\sigma >0$ and $q>4$. Then the kurtosis coefficient of T is

$$\begin{array}{ccc}\hfill {\beta }_2& =& {\displaystyle \frac{\left[32a_{41}{a}_{03}-24\pi a_{31}{a}_{11}{a}_{02}+24\pi a_{12}{a}_{21}{a}_{01}-3{\pi }^2{a}_{14}\right]}{\left[16a_{22}{a}_{02}-8\pi a_{01}{a}_{21}{a}_{12}+{\pi }^2{a}_{14}\right]}}.\hfill \end{array}$$

(10)

Proof. 

Recall that

$$\begin{array}{c}\hfill {\beta }_2={\displaystyle \frac{\mathbb{E}\left[{(T-\mathbb{E}\left(T\right))}^4\right]}{{\left(\mathbb{V}\left(T\right)\right)}^2}}={\displaystyle \frac{{\mu }_4-4{\mu }_1{\mu }_3+6{\mu }_1^2{\mu }_2-3{\mu }_1^4}{{({\mu }_2-{\mu }_1^2)}^2}},\end{array}$$

where ${\mu }_1$, ${\mu }_2$, ${\mu }_3$ and ${\mu }_4$ were given in Corollary 1. Then

$$\begin{array}{ccc}\hfill {\beta }_2& =& {\displaystyle \frac{\left[32a_{41}{a}_{03}-24\pi a_{31}{a}_{11}{a}_{02}+24\pi a_{12}{a}_{21}{a}_{01}-3{\pi }^2{a}_{14}\right]}{\left[16a_{22}{a}_{02}-8\pi a_{01}{a}_{21}{a}_{12}+{\pi }^2{a}_{14}\right]}}.\hfill \end{array}$$

□

Note that the asymmetry and kurtosis coefficients only depend on the parameter q. Therefore q is a shape parameter since it determines the asymmetry and kurtosis coefficients of this model. In addition, it is of interest to compare both coefficients to other models, such as SR distribution, introduced in Iriarte et al. [10].

Figure 2 shows the plots for the asymmetry, (a), and kurtosis, (b), coefficients for SMR and SR models. We highlight that both coefficients are much higher for the SMR distribution than the ones for the SR model. That means that SMR distribution is more flexible with respect to the asymmetry and kurtosis than SR model.

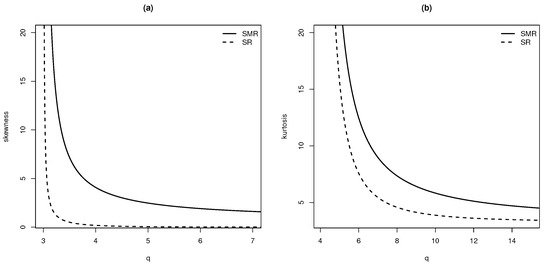
Figure 2. (a) Asymmetry and (b) kurtosis coefficients for the SMR and SR distribution.

To conclude, note that (9) and plot (a) in Figure 2 suggest that $\sqrt{{\beta }_1}$ takes values in $[0.68$; $+\infty )$. On the other hand, (10) and plot (b) in Figure 2 suggest that ${\beta }_2$ approximately takes values in $[3.36$; $+\infty )$. That is, we are dealing with a skew right model, (the right tail is long relative to the left one), with positive kurtosis, i.e., heavy tails.

3. Lifetime Analysis

Since the SMR distribution is nonnegative and asymmetric, it can be used to model survival time data. In this section, the main features of interest in this field are studied. First the survival and hazard function for an SMR model are given.

Proposition 7.

Let $T\sim SMR(\sigma ,q)$ with σ and $q>0$. Then

 1.

The survival function is $S(t;\sigma ,q)={\left(\frac{t^2}{2\sigma }+1\right)}^{-\frac{q}{2}}$, $t>0$.

 2.

The hazard function is

$$\begin{array}{ccc}\hfill h(t;\sigma ,q)& =& {\displaystyle \frac{qt}{t^2+2\sigma }},t>0.\hfill \end{array}$$

(11)

Proof. 

Straightforward from $S\left(t\right)=1-F\left(t\right)$ and $h\left(t\right)=f\left(t\right)/S\left(t\right)$. □

Remark 4.

From (11), it follows that for an $SMR(\sigma ,q)$ model the hazard function $h(t;\sigma ,q)$ is monotone increasing for $t\in (0,\sqrt{2\sigma })$, monotone decreasing for $t\in (\sqrt{2\sigma },+\infty )$ and reaches its maximum at $t=\sqrt{2\sigma }$. Moroever,

$$0<h(t;\sigma ,q)\le \frac{q}{2\sqrt{2\sigma }},t>0.$$

Note that the intervals where $h(t;\sigma ,q)$ is monotone only depend on the parameter σ, they do not depend on q.

Plots of $h(t;\sigma ,q)$ are given in Figure 3 for $\sigma =1$ and $q<1$ in (a) and $q>1$ in (b). In both settings, we note that the peak increases with q.

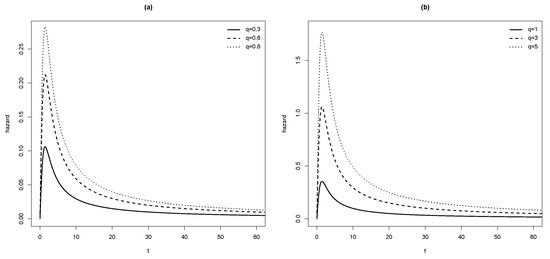
Figure 3. Hazard function $SMR(1,q)$ model with (a) $q<1$ and (b) $q>1$.

Remark 5.

For $\lambda >0$, the survival function of the SMR model satisfies that

$$\underset{t\to +\infty }{lim}\frac{S(\lambda t;\sigma ,q)}{S(t;\sigma ,q)}=\underset{t\to +\infty }{lim}\frac{{\left(\frac{t^2}{2\sigma }+1\right)}^{-\frac{q}{2}}}{{\left(\frac{{\left(\lambda t\right)}^2}{2\sigma }+1\right)}^{-\frac{q}{2}}}=\underset{t\to +\infty }{lim}{\left(\frac{{\lambda }^2+2\sigma /t^2}{1+2\sigma /t^2}\right)}^{-q/2}={\lambda }^{-q}\ne 1.$$

Therefore, the survival function of the SMR distribution is regularly varying.

Mean Residual Life

Next the mean residual life is studied. Recall that for a nonnegative RV T, its mean residual life is defined as $m\left(t\right)=\mathbb{E}(T-t|T>t)$ for $t>0$. $m\left(t\right)$ can be obtained as

$$m\left(t\right)=\mathbb{E}(T-t|T>t)={\int }_t^{\infty }{\displaystyle \frac{S\left(z\right)}{S\left(t\right)}}dz$$

(12)

with $S(·)$ the survival function of T.

It will be proved that this characteristic can be expressed in terms of the survival function of a Pearson Type VII (PTVII) distribution.

Definition 3.

An RV W follows a PTVII distribution with parameters m, c and ξ (see Johnson et al. [17]) if its pdf is given by

$$\begin{array}{ccc}\hfill f(w;m,c,\xi )& =& \frac{c^{2m-1}\Gamma \left(m\right)}{\sqrt{\pi }\Gamma \left(m-\frac{1}{2}\right)}{\left(c^2+{(w-\xi )}^2\right)}^{-m},\hfill \end{array}$$

(13)

with $w\in \mathbb{R}$, $m>1/2$, $c>0$ and $\xi \in \mathbb{R}$. We denote as $W\sim PTVII\left(m,c,\xi \right)$.

Proposition 8.

The mean residual life of $T\sim SMR(\sigma ,q)$, $q>1$, can be obtained as

$$\begin{array}{ccc}\hfill m(t;\sigma ,q)& =& {\displaystyle \frac{\sqrt{2\pi \sigma }\Gamma \left(\frac{q-1}{2}\right)}{\Gamma \left(\frac{q}{2}\right)}}{\left(\frac{t^2}{2\sigma }+1\right)}^{\frac{q}{2}}{S}_W\left(t\right),t>0\hfill \end{array}$$

(14)

where $S_W$ denotes the survival function of an RV $W\sim PTVII\left(\frac{q}{2},\sqrt{2\sigma },0\right)$.

Proof. 

Recall that

$$\begin{array}{ccc}\hfill m(t;\sigma ,q)& =& \mathbb{E}(T-t|T>t)={\int }_t^{\infty }{\displaystyle \frac{S(z;\sigma ,q)}{S(t;\sigma ,q)}}dz\hfill \\ & =& {\left(\frac{t^2}{2\sigma }+1\right)}^{\frac{q}{2}}{\int }_t^{\infty }{\displaystyle \frac{1}{{\left(\frac{z^2}{2\sigma }+1\right)}^{\frac{q}{2}}}}dz.\hfill \end{array}$$

(15)

Note that the integrand in previous expression is, up to a constant, the pdf of a $PTVII\left(\frac{q}{2},\sqrt{2\sigma },0\right)$ distribution. Therefore we can write

$$\begin{array}{ccc}\hfill m(t;\sigma ,q)& =& {\displaystyle \frac{\sqrt{2\pi \sigma }\Gamma \left(\frac{q-1}{2}\right)}{\Gamma \left(\frac{q}{2}\right)}}{\left(\frac{t^2}{2\sigma }+1\right)}^{\frac{q}{2}}{S}_W\left(t\right)\hfill \end{array}$$

with $S_W$ the survival function of $W\sim PTVII\left(\frac{q}{2},\sqrt{2\sigma },0\right)$, $q>1$. □

In Proposition 9, an explicit expression for (14) is given in terms of the regularized incomplete beta function, defined as

$$I_x(a,b)={\displaystyle \frac{B(x;a,b)}{B(a,b)}},\mathrm{with}B(x;a,b)={\int }_0^x{t}^{a-1}{(1-t)}^{b-1}dt\mathrm{and}B(a,b)=B(1,a,b).$$

This expression is useful from a computational point of view.

Proposition 9.

For $q>1$, the mean residual life of $T\sim SMR(\sigma ,q)$ can be obtained as

$$m(t;\sigma ,q)={\left(\frac{t^2}{2\sigma }+1\right)}^{\frac{q}{2}}{\displaystyle \frac{\sqrt{\pi \sigma }\Gamma \left(\frac{q-1}{2}\right)}{\sqrt{2}\Gamma \left(\frac{q}{2}\right)}}\left[1-I_{\frac{t^2}{2\sigma +t^2}}\left({\displaystyle \frac{1}{2}},{\displaystyle \frac{q-1}{2}}\right)\right],t>0.$$

(16)

Proof. 

Let us consider the integral in (15) and the change of variable $u={\displaystyle \frac{z^2}{2\sigma }}$

$$\begin{array}{ccc}\hfill {\int }_t^{\infty }{\displaystyle \frac{1}{{\left(\frac{z^2}{2\sigma }+1\right)}^{\frac{q}{2}}}}dz& =& {\displaystyle \frac{\sqrt{\sigma }}{\sqrt{2}}}{\int }_{\frac{t^2}{2\sigma }}^{\infty }{\displaystyle \frac{u^{-1/2}}{{(1+u)}^{q/2}}}du\hfill \\ & =& {\displaystyle \frac{\sqrt{\sigma }}{\sqrt{2}}}\left[B\left({\displaystyle \frac{1}{2}},{\displaystyle \frac{q-1}{2}}\right)-{\int }_0^{\frac{t^2}{2\sigma }}{\displaystyle \frac{u^{-1/2}}{{(1+u)}^{q/2}}}du\right]\hfill \\ & =& {\displaystyle \frac{\sqrt{\sigma }}{\sqrt{2}}}B\left({\displaystyle \frac{1}{2}},{\displaystyle \frac{q-1}{2}}\right)\left[1-I_{\frac{t^2}{2\sigma +t^2}}\left({\displaystyle \frac{1}{2}},{\displaystyle \frac{q-1}{2}}\right)\right].\hfill \end{array}$$

(17)

By using the relationship

$$B(a,b)={\displaystyle \frac{\Gamma \left(a\right)\Gamma \left(b\right)}{\Gamma (a+b)}}$$

and $\Gamma (1/2)=\sqrt{\pi }$, from (16) and (17) is obtained. □

Order Statistics

Given a random sample of size n of $T\sim SMR(\sigma ,q)$, let us denote by $T_{\left(j\right)}$ the $jth-$order statistics, $j\in \{1,\dots ,n\}$.

Proposition 10.

The pdf of $T_{\left(j\right)}$ is

$$\begin{array}{ccc}\hfill f_{T_{\left(j\right)}}\left(t\right)& =& {\displaystyle \frac{n!}{(j-1)!(n-j)!}}{\displaystyle \frac{qt}{2\sigma }}{\left[1-{\left({\displaystyle \frac{t^2}{2\sigma }}+1\right)}^{-\frac{q}{2}}\right]}^{j-1}{\left[{\displaystyle \frac{t^2}{2\sigma }}+1\right]}^{-\frac{q}{2}(n-j+1)-1},t>0.\hfill \end{array}$$

In particular, the pdf of the minimum, $T_{\left(1\right)}$, is

$$f_{T_{\left(1\right)}}\left(t\right)={\displaystyle \frac{nqt}{2\sigma }}{\left[{\displaystyle \frac{t^2}{2\sigma }}+1\right]}^{-\frac{qn}{2}-1},t>0.$$

(18)

and the pdf of the maximum, $T_{\left(n\right)}$, is

$$f_{T_{\left(n\right)}}\left(t\right)={\displaystyle \frac{nqt}{2\sigma }}{\left[1-{\left({\displaystyle \frac{t^2}{2\sigma }}+1\right)}^{-\frac{q}{2}}\right]}^{n-1}{\left[{\displaystyle \frac{t^2}{2\sigma }}+1\right]}^{-\frac{q}{2}-1},t>0.$$

Proof. 

Since we are dealing with an absolutely continuous model, the pdf of the $jth-$order statistics is obtained by applying

$$\begin{array}{ccc}\hfill f_{T_{\left(j\right)}}\left(t\right)& =& {\displaystyle \frac{n!}{(j-1)!(n-j)!}}f\left(t\right){\left[F\left(t\right)\right]}^{j-1}{[1-F\left(t\right)]}^{n-j},j\in \{1,\dots ,n\}\hfill \end{array}$$

where F and f denote the cdf and pdf of the parent distribution, $T\sim SMR(\sigma ,q)$ in this case. □

Remark 6.

From (18), note that $T_{\left(1\right)}\sim SMR(\sigma ,qn)$. That is, when sampling from an $SMR(\sigma ,q)$ distribution then the minimum is also distributed according to an SMR model.

4. Entropy

In this section Rényi entropy is obtained for the SMR model. Given T an RV and $\gamma \in (0,1)\bigcup (1,\infty )$, the Rényi entropy of T is given by

$$E_R\left(\gamma \right)={\displaystyle \frac{1}{1-\gamma }}log\left\{{\int }_0^{\infty }{\left[f_T\left(t\right)\right]}^{\gamma }dt\right\},$$

(19)

where $log={log}_e$ denotes the Naperian logarithm.

Proposition 11.

Let $T\sim SMR(\sigma ,q)$ and $\gamma \in (0,1)\bigcup (1,\infty )$. Then the Rényi entropy of T is

$$E_R\left(\gamma \right)={\displaystyle \frac{log\left(\sigma \right)}{2}}+{\displaystyle \frac{1}{1-\gamma }}\left[-\frac{(\gamma +1)}{2}log\left(2\right)+\gamma log\left(q\right)+logB\left({\displaystyle \frac{\gamma +1}{2}},{\displaystyle \frac{\gamma (q+1)-1}{2}}\right)\right]$$

(20)

Proof. 

By proceeding similarly to Proposition 9, it can be proved that

$${\int }_0^{\infty }{\left[f_T\left(t\right)\right]}^{\gamma }dt=2^{-\left(\frac{\gamma +1}{2}\right)}{q}^{\gamma }{\sigma }^{-\left(\frac{\gamma -1}{2}\right)}B\left({\displaystyle \frac{\gamma +1}{2}},{\displaystyle \frac{\gamma (q+1)-1}{2}}\right)$$

(21)

By applying (19), from (20) and (21) is obtained. □

5. Inference

In this section, moment and ML estimation methods are studied.

5.1. Moment Method Estimators

Let $T_1,\dots ,T_n$ be a random sample from $T\sim SMR(\sigma ,q)$. Let us consider the first and second sample moments, denoted by $\overline{T}=\frac{{\sum }_{i=1}^n{T}_i}{n}$ and $\overline{T^2}=\frac{{\sum }_{i=1}^n{T}_i^2}{n}$, respectively.

Proposition 12.

Given $T_1,\dots ,T_n$ a random sample from $T\sim SMR(\sigma ,q)$ with $q>2$, the moment method estimators of σ and q are

$$\begin{array}{c}{\widehat{\sigma }}_m={\displaystyle \frac{2}{\pi }}{\left({\displaystyle \frac{\overline{T}\Gamma \left(\frac{{\widehat{q}}_m}{2}\right)}{\Gamma \left(\frac{{\widehat{q}}_m-1}{2}\right)}}\right)}^2\hfill \end{array}$$

(22)

$$\begin{array}{ccc}& & 4{\overline{T}}^2\Gamma \left(\frac{{\widehat{q}}_m}{2}\right)\Gamma \left(\frac{{\widehat{q}}_m-2}{2}\right)-\pi \overline{T^2}\Gamma {\left(\frac{{\widehat{q}}_m-1}{2}\right)}^2=0,\hfill \end{array}$$

(23)

where (23) must be solved numerically to obtain ${\widehat{q}}_m$. Later, ${\widehat{q}}_m$ must be replaced in (22) to get ${\widehat{\sigma }}_m$.

Proof. 

Consider the moment method equations

$$\begin{array}{ccc}\hfill {\mu }_1& =& \overline{T}\hfill \end{array}$$

(24)

$$\begin{array}{ccc}\hfill {\mu }_2& =& \overline{T^2}\hfill \end{array}$$

(25)

with ${\mu }_i$ the noncentral moments of T given in Corollary 1 for $i=1,2$.

${\widehat{\sigma }}_m$ given in (22) is obtained from (24). From (22) and (25), we have

$$\begin{array}{ccc}\hfill {\displaystyle \frac{2}{\pi }}·\frac{{\overline{T}}^2\Gamma {\left(\frac{q}{2}\right)}^2}{\Gamma {\left(\frac{q-1}{2}\right)}^2}& =& \frac{\overline{T^2}\Gamma \left(\frac{q}{2}\right)}{2\Gamma \left(\frac{q-2}{2}\right)},\hfill \end{array}$$

which can be rewritten as (23) and must be solved numerically to obtain ${\widehat{q}}_m$. □

5.2. ML Estimation

Let $T_1,\dots ,T_n$ be a random sample from $T\sim SMR(\sigma ,q)$. Then the log-likelihood function is

$$\begin{array}{ccc}\hfill l(\sigma ,q)& =& nln\left(q\right)+\sum _{i=1}^{n}ln\left(t_i\right)-nln\left(2\right)-nln\left(\sigma \right)-\left(\frac{q}{2}+1\right)\sum _{i=1}^{n}ln\left(\frac{t_i^2}{2\sigma }+1\right)\hfill \end{array}$$

Taking partial derivatives in $l(\sigma ,q)$ with respect to $\sigma$ and q and setting them equal to zero, we get

$$\begin{array}{ccc}& & -n+\left(1+\frac{n}{{\displaystyle \sum _{i=1}^{n}ln\left(\frac{t_i^2}{2\widehat{\sigma }}+1\right)}}\right)\sum _{i=1}^n{\displaystyle \frac{t_i^2}{\left(t_i^2+2\widehat{\sigma }\right)}}=0\hfill \\ \hfill \end{array}$$

(26)

$$\begin{array}{c}\widehat{q}=\frac{2n}{{\displaystyle \sum _{i=1}^{n}ln\left(\frac{t_i^2}{2\widehat{\sigma }}+1\right)}},\hfill \end{array}$$

(27)

where (26) must be solved numerically to get $\widehat{\sigma }$, which must be substituted into (27) to obtain $\widehat{q}$. Since we do not have explicit expressions for ML estimators, EM algorithm can be implemented to get these estimates. The next section is devoted to reach this aim.

5.3. ML Estimation Using EM-Algorithm

The EM-algorithm (Dempster et al. [18]) enables the computationally efficient determination of the ML estimates when iterative procedures are required. Next, details about the implementation of this algorithm for the SMR model are given. The method is based on Proposition 3 and Lemma 2.

Lemma 2.

Let $X\sim Gamma(k,\beta )$ with $k>0$ shape parameter and $\beta >0$ rate parameter, that is its pdf is $f_X\left(x\right)={\displaystyle \frac{1}{\Gamma \left(k\right)}}{\beta }^k{x}^{k-1}{e}^{-\beta x}$, $x>0$. Then

 1.

$X^m\sim GG\left({\beta }^m,\frac{k}{m},\frac{1}{m}\right)$, $m>0$, with pdf given in (2).

 2.

$\mathbb{E}[log(X\left)\right]=\Psi \left(k\right)-log\left(\beta \right)$ where $\Psi (·)$ denotes the digamma function.

Let $T\sim SMR(\sigma ,q)$, by applying the hierarchical representation given in Proposition 3, we can write $T|Y=y\sim R(\sigma /y^2)$ and $Y\sim GG(1,q,2)$. The joint pdf of $(T,Y)$ is

$$\begin{array}{ccc}\hfill f(t,y|\theta )& =& f_T\left(t\right|y,\theta )·f_Y\left(y\right|\theta )\hfill \\ & =& {\displaystyle \frac{2t{y}^{q+1}}{\sigma \Gamma (q/2)}}exp\left\{-y^2\left(1+\frac{t^2}{2\sigma }\right)\right\},\hfill \end{array}$$

(28)

where Y is a latent variable and the parameter vector is $\theta ={(\sigma ,q)}^T$, $\theta \in {\mathbb{R}}^{+}\times {\mathbb{R}}^{+}$.

Given $T_1,\dots ,T_n$, a random sample of size n from $T\sim SMR(\sigma ,q)$, let us denote by $\mathbf{t}={[t_1,\dots ,t_n]}^{\top }$ the observed data, $\mathbf{y}={[y_1,\dots ,y_n]}^{\top }$ the unobserved data and ${\mathbf{t}}_c={[{\mathbf{t}}^{\top },{\mathbf{y}}^{\top }]}^{\top }$ the complete data, that is, the original data $\mathbf{t}$ augmented by $\mathbf{y}$.

Let $l_c\left(\theta \right|{\mathbf{t}}_c)$ and $Q\left(\theta \right|\widehat{\theta })=\mathbb{E}\left[l_c\left(\theta \right|{\mathbf{t}}_c)\right|\mathbf{t},\widehat{\theta }]$ the complete log-likelihood function associated with ${\mathbf{t}}_c$ and its expected value, respectively. From (28), $l_c\left(\theta \right|{\mathbf{t}}_c)$ is

$$\begin{array}{ccc}\hfill l_c\left(\theta \right|{\mathbf{t}}_c)& =& \sum _{i=1}^{n}logf(t_i,y_i|\left(\theta \right)\hfill \\ \\ & =& (q+1)\sum _{i=1}^{n}log\left(y_i\right)-nlog\left(\sigma \right)-nlog(\Gamma (q/2))-\sum _{i=1}^n{y}_i^2\left(1+\frac{t_i^2}{2\sigma }\right)+c,\hfill \end{array}$$

where c is a constant, which does not depend on $\theta$.

In order to get $Q\left(\theta \right|\widehat{\theta })$ and apply EM-algorithm, we need to calculate $\mathbb{E}\left[y_i^2\right|t_i,\theta ]$ and $\mathbb{E}[log\left(y_i\right)|t_i,\theta ]$. From (28) and (2)

$$\begin{array}{ccc}\hfill f\left(y_i\right|t_i,\theta )& =& C\times y_i^{q+1}exp\left\{-y_i^2\left(1+\frac{t_i^2}{2\sigma }\right)\right\}\hfill \\ & =& C\times y_i^{(q+2)-1}exp\left\{-{\left[y_i{\left(1+\frac{t_i^2}{2\sigma }\right)}^{1/2}\right]}^2\right\},\hfill \end{array}$$

(29)

where C is a constant that does not depend on $y_i$. As (29) is related to the pdf of a Generalized Gamma distribution, specifically,

$$Y_i|t_i,\theta \sim GG\left({\left(1+\frac{t_i^2}{2\sigma }\right)}^{1/2},q+2,2\right).$$

(30)

Then

$$\begin{array}{ccc}\hfill \mathbb{E}\left[Y_i^2\right|t_i,\theta ]& =& {\left[{\left(1+\frac{t_i^2}{2\sigma }\right)}^{-1/2}\right]}^2{\displaystyle \frac{\Gamma \left(\frac{(q+2)+2}{2}\right)}{\Gamma \left(\frac{q+2}{2}\right)}}={\displaystyle \frac{\sigma (q+2)}{2\sigma +t_i^2}}\hfill \end{array}$$

(31)

On the other hand, Lemma 2 can be applied to (30) with

$$\begin{array}{c}\hfill \beta =1+\frac{t_i^2}{2\sigma },k=\frac{q+2}{2}\mathrm{and}m=\frac{1}{2}.\end{array}$$

Taking into account that

$$\begin{array}{ccc}\hfill \mathbb{E}[log\left(X^m\right)]& =& \mathbb{E}[m·log(X\left)\right]=m[\Psi (k)-log(\beta \left)\right]\hfill \end{array}$$

we have

$$\begin{array}{ccc}\hfill \mathbb{E}[log\left(Y_i\right)|t_i,\theta ]& =& \frac{1}{2}\Psi \left(\frac{q+2}{2}\right)-\frac{1}{2}log\left(1+\frac{t_i^2}{2\sigma }\right).\hfill \end{array}$$

(32)

Let $Q\left(\theta \right|\widehat{\theta })=\mathbb{E}\left[l_c\left(\theta \right|{\mathbf{t}}_c)\right|\mathbf{t},\widehat{\theta }]$ be the conditional expectation of the complete log-likelihood function. We have

$$\begin{array}{ccc}\hfill Q\left(\theta \right|\widehat{\theta })& =& (q+1)\sum _{i=1}^n\widehat{log{y}_i}-nlog\left(\sigma \right)-nlog\left(\Gamma \left(\frac{q}{2}\right)\right)-\sum _{i=1}^n\widehat{y_i^2}\left(1+\frac{t_i^2}{2\sigma }\right),\hfill \end{array}$$

with $\widehat{y_i^2}=\mathbb{E}\left[Y_i^2\right|t_i,\theta =\widehat{\theta }]$ and $\widehat{log{y}_i}=\mathbb{E}[log\left(Y_i\right)|t_i,\theta =\widehat{\theta }]$ given in (31) and (32), respectively. Taking first partial derivative with respect to $\sigma$, the estimate of $\sigma$ is given by

$$\begin{array}{ccc}\hfill \widehat{\sigma }& =& {\displaystyle {\displaystyle \frac{1}{2}}·\overline{t^2\widehat{y^2}}}\hfill \end{array}$$

where $\overline{t^2\widehat{y^2}}$ is the mean of $t_i^2\widehat{y_i^2}$. By proceeding similarly, the estimate of q is

$$\begin{array}{ccc}\hfill \widehat{q}& =& 2{\Psi }^{-1}\left(2·\overline{\widehat{log\left(y\right)}}\right)\hfill \end{array}$$

where $\overline{\widehat{log\left(y\right)}}$ is the mean of $\widehat{log\left(y_i\right)}$ and ${\Psi }^{-1}(·)$ is the inverse of the digamma function. Therefore, the EM algorithm is

• E-step: For $i=1,\dots ,n$ compute

  $$\begin{array}{cc}\hfill {\widehat{y_i^2}}^{(k+1)}={\displaystyle \frac{{\sigma }^{\left(k\right)}(q^{\left(k\right)}+2)}{2{\sigma }^{\left(k\right)}+t_i^2}},& {\widehat{log\left(y_i\right)}}^{(k+1)}=\frac{1}{2}\left[\Psi \left(\frac{q^{\left(k\right)}+2}{2}\right)-log\left(1+\frac{t_i^2}{2{\sigma }^{\left(k\right)}}\right)\right]\end{array}$$
• M-step: Update the vector of parameters $\theta =(\sigma ,q)$

  $$\begin{array}{cc}\hfill {\displaystyle {\widehat{\sigma }}^{(k+1)}={\displaystyle \frac{1}{2}}\overline{t^2{\widehat{y^2}}^{(k+1)}},}& {\widehat{q}}^{(k+1)}=2{\Psi }^{-1}\left(2\overline{{\widehat{log\left(y\right)}}^{(k+1)}}\right).\end{array}$$
• E and M steps are repeated until a suitable convergence is reached.

EM algorithm implementation was carried out by using R software. Three functions were implemented. In the function used in E step, estimates of ${y_i^2}^{(k+1)}$ and ${log\left(y_i\right)}^{(k+1)}$ were generated. In the function used in M step, estimates of $\sigma$ and q were obtained. Later, these steps were repeated by using a function with the convergence criterion. The criterion was to stop when the difference between the successive values obtained is less than a a value fixed in advance, specifically it was

$$\begin{array}{c}\hfill max\left(\left|{\sigma }^{\left(k\right)}-{\sigma }^{(k-1)}\right|,\left|q^{\left(k\right)}-q^{(k-1)}\right|\right)<ϵ\mathrm{with}ϵ={10}^{-4}.\end{array}$$

6. Simulation Study

In this section, the performance of ML estimates for finite sample sizes is studied. It is empirically checked if the proposed estimators satisfy desirable properties, such as asymtotic unbiasedness, asymptotic efficiency, asymptotic normality. Values of the Rayleigh and the Generalized Gamma distributions were generated to get values of the SMR distribution introduced in (4). The EM algorithm was used to compute the estimates of parameters in the SMR model, and their standard errors. This procedure was carried out 10,000 times with sample sizes $n=\{30,40,\dots ,190,200\}$, and taking as values of the parameters $\sigma =$ 1 and 10; $q=$ 1, 1.5, 2 and 3.

As summaries of these simulations, the average of estimates, average of standard errors of estimates, average bias, squared root of mean squared error (RMSE) and the empirical coverage probability of confidence intervals for the parameters (with confidence level 0.95) were calculated. From Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11, average bias, RMSE and empirical coverage probability (in percentages) are plotted for n varying in $\{30,40,\dots ,190,200\}$. It is observed that if the sample size increases then bias and RMSE decrease, this fact suggests that the estimators are consistent. In addition, we note that the empirical coverage probability (in percentage) approaches to the nominal level (95%) when the sample size increases.

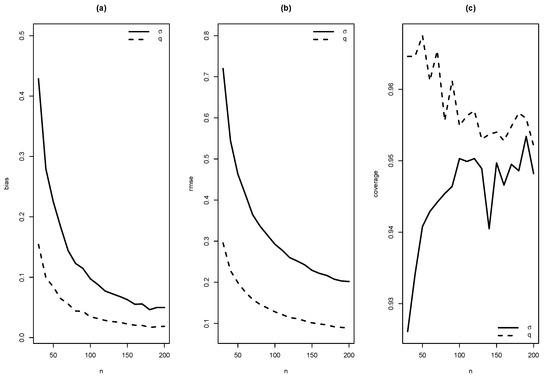
Figure 4. Graphics of (a) bias, (b) RMSE and (c) coverage of simulation for $\sigma =1$, $q=1$ with $n=30,\dots ,200$.

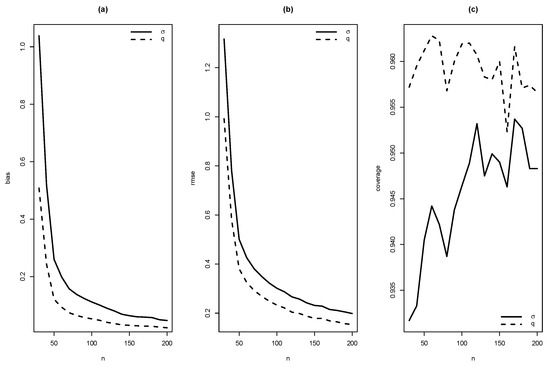
Figure 5. Graphics of (a) bias, (b) RMSE and (c) coverage of simulation for $\sigma =1$, $q=$1.5 with $n=30,\dots ,200$.

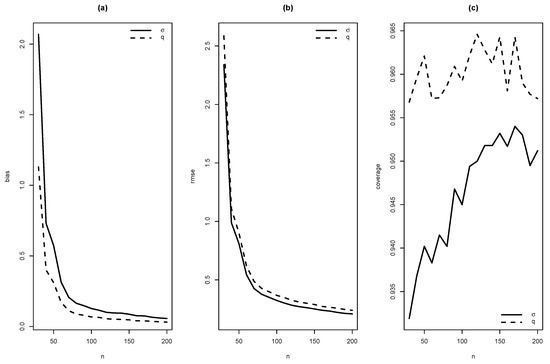
Figure 6. Graphics of (a) bias, (b) RMSE and (c) coverage of simulation for $\sigma =1$, $q=2$ with $n=30,\dots ,200$.

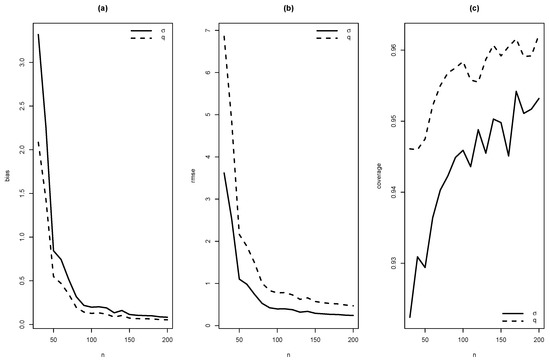
Figure 7. Graphics of (a) bias, (b) RMSE and (c) coverage of simulation for $\sigma =1$, $q=3$ with $n=30,\dots ,200$.

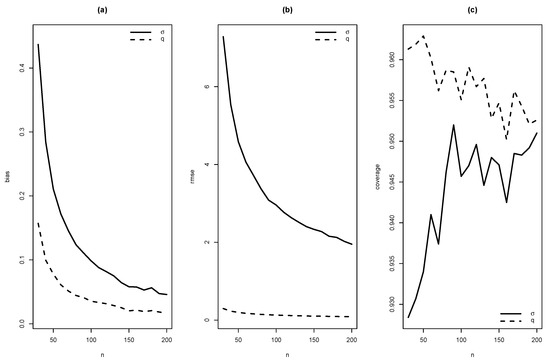
Figure 8. Graphics of (a) bias, (b) RMSE and (c) coverage of simulation for $\sigma =10$, $q=1$ with $n=30,\dots ,200$.

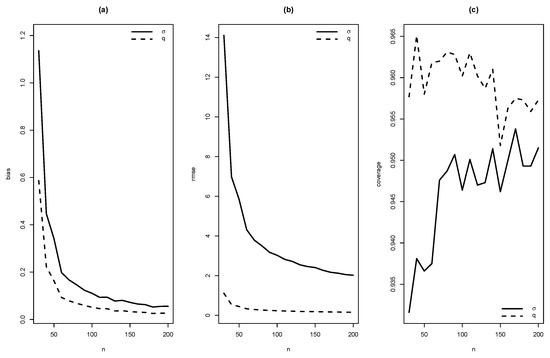
Figure 9. Graphics of (a) bias, (b) RMSE and (c) coverage of simulation for $\sigma =10$, $q=$1.5 with $n=30,\dots ,200$.

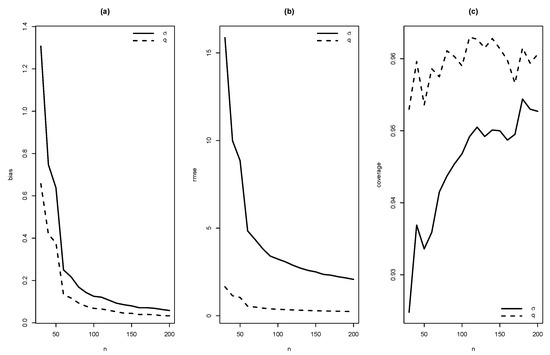
Figure 10. Graphics of (a) bias, (b) RMSE and (c) coverage of simulation for $\sigma =10$, $q=2$ with $n=30,\dots ,200$.

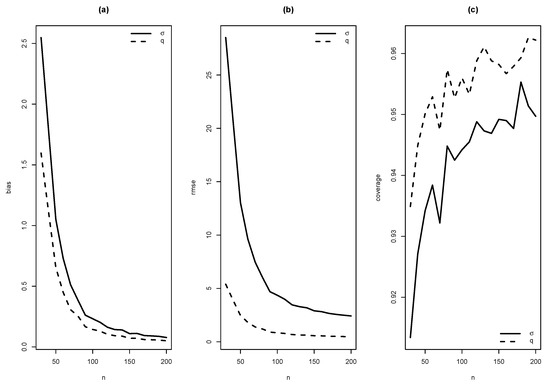
Figure 11. Graphics of (a) bias, (b) RMSE and (c) coverage of simulation for $\sigma =10$, $q=3$ with $n=30,\dots ,200$.

7. Real Data Illustration

In this section, we present applications of SMR model in two real datasets from the fields of lifetime analysis and reliability. To illustrate its good performance, our proposal is compared to other competing models previously introduced in literature. These are R and SR distributions.

7.1. Application to Patients with Bladder Cancer

We consider a dataset corresponding to remission times (in months) of a random sample of 128 bladder cancer patients studied by Lee and Wang [19]. The $SMR(\sigma ,q)$ model is proposed to describe this dataset. The EM algorithm was used to estimate $\sigma$ and q. Their corresponding standard errors were obtained by using the inverse of the hessian matrix.

Table 1 provides the descriptive summaries. These are: the sample size n, the sample mean $\overline{T}$, the standard deviation S, the sample asymmetry coefficient $\sqrt{b_1}$, the sample kurtosis coefficient $b_2$, the sample minimum $min\left(T\right)$ and the sample maximum $max\left(T\right)$. We highlight that we are dealing with positive, positive skewed data with a really high kurtosis, $b_2=18.483$.

Table 1. Descriptive statistics for the remission times of patients with bladder cancer.

n	$\overline{\mathit{T}}$	S	$\sqrt{{\mathit{b}}_1}$	${\mathit{b}}_2$	$min\left(\mathit{T}\right)$	$max\left(\mathit{T}\right)$
128	9.366	10.508	3.287	18.483	0.08	79.05

Table 2 provides the ML estimates of parameters and their standard errors in parentheses for SMR, R and SR models. These models are compared by using the Akaike Information Criterion (AIC), Akaike [20] and the Bayesian Information Criterion (BIC), introduced in Schwarz [21]. Both criteria reveal that the SMR model provides a better fit to this data since their values are less than the others.

Table 2. Estimates, standard errors (SE) in parenthesis, log-likelihood, AIC and BIC values for the remission times of patients with bladder cancer.

Estimaciones	R (SE)	SR (SE)	SMR (SE)
$\widehat{\sigma }$	98.639 (8.718)	8.647 (2.051)	15.369 (5.108)
$\widehat{q}$	-	1.424 (0.224)	1.772 (0.318)
log-likelihood	−491.266	−415.815	−413.339
AIC	984.531	835.631	830.677
BIC	987.383	841.335	836.381

Figure 12 depicts the histogram of this dataset along with the estimated pdf for R, SR and SMR distributions. Moreover, Figure 13 provides the corresponding QQ-plots for these models. Note that the QQ-plots for R and SR models show that these distributions does not provide a good fit on the right tail of these data. However the QQ-plot for the SMR distribution does not exhibit this drawback.

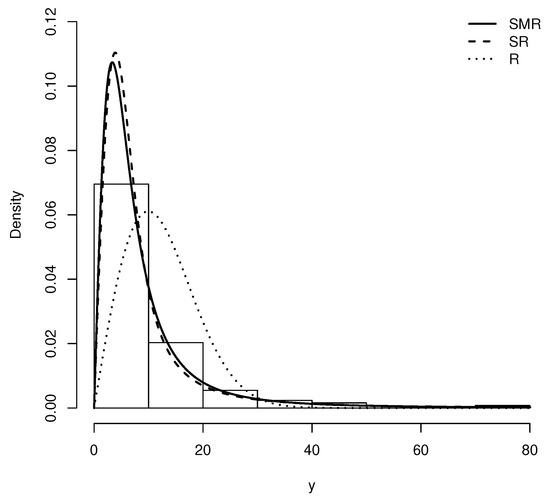
Figure 12. Density adjusted for the remission times of patients with bladder cancer in the R, SR and SMR distributions.

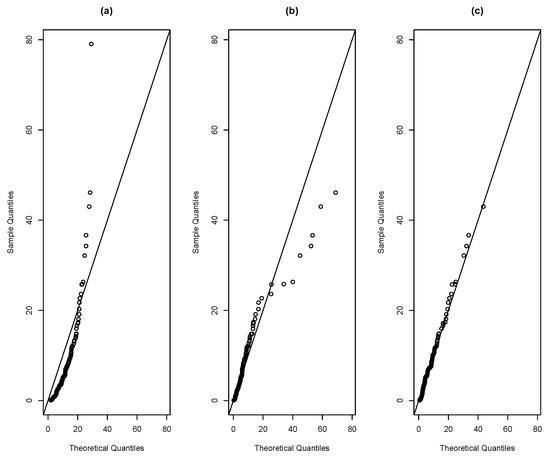
Figure 13. QQ-plot for distributions (a) R, (b) SR, (c) SMR for the remission times of patients with bladder cancer.

All these plots and summaries suggest that the SMR model provides a better fit to this dataset than the other models under consideration.

7.2. Application to Number of Failures of an Air Conditioning System

The second dataset under consideration was reported by Proschan [22]. This dataset consists of the times between failures of the air-conditioning equipment in 13 Boeing 720 aircrafts. A similar outline to that given in previous applications has been followed. Table 3 shows the basic statistical summaries. We highlight that, again, a high value of kurtosis is observed $b_2=8.023$.

Table 3. Descriptive statistics for number of failures of an air conditioning system.

n	$\overline{\mathit{T}}$	S	$\sqrt{{\mathit{b}}_1}$	${\mathit{b}}_2$	$min\left(\mathit{T}\right)$	$max\left(\mathit{T}\right)$
188	92.074	107.916	2.139	8.023	1	603

In Table 4, results related to the fit of R, SR and SMR models are given. Note that the SMR model provides a better fit over the others since its AIC and BIC values are less than those in R and SR models.

Table 4. Estimates, SE in parenthesis, log-likelihood, AIC and BIC values for the number of failures of an air conditioning system.

Estimaciones	R (SE)	SR (SE)	SMR (SE)
$\widehat{\sigma }$	10,030.83 (730.135)	264.611 (68.021)	382.761 (113.843)
$\widehat{q}$	-	0.902 (0.107)	1.069 (0.136)
log-likelihood	−1191.275	−1053.503	−1046.549
AIC	2384.550	2111.006	2097.097
BIC	2387.787	2117.479	2103.570

In Figure 14, the histogram and the estimated pdfs are given. Figure 15 provides the corresponding QQ-plots. Note that the SMR model provides a better fit, especially for the right tail of the dataset.

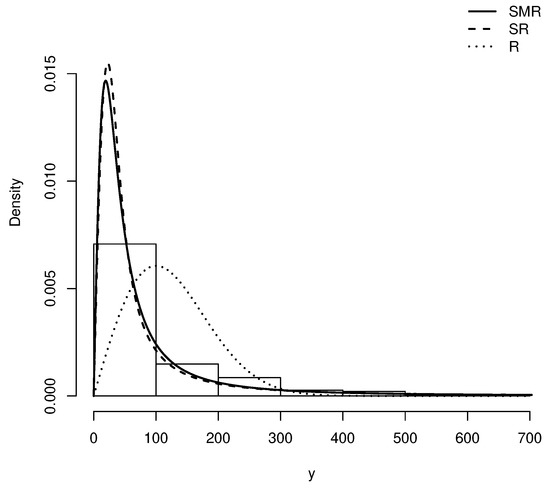
Figure 14. Density adjusted for the number of failures of an air conditioning system in the R, SR and SMR distributions.

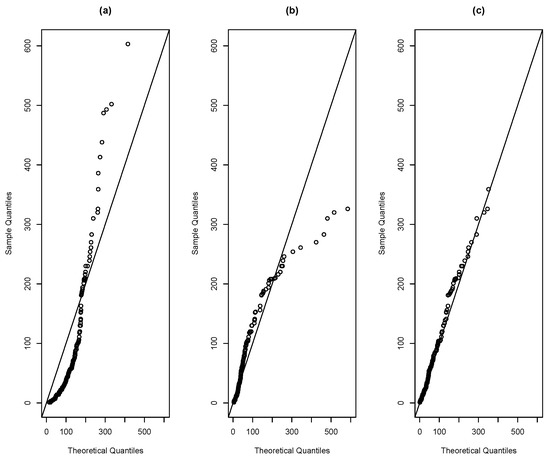
Figure 15. QQ-plot for distributions (a) R, (b) SR, (c) SMR for the number of failures of an air conditioning system.

8. Conclusions

In this paper, the SMR distribution is introduced. As strengths of our proposal, we highlight that it is more flexible as for its kurtosis coefficient and hazard function than the Rayleigh and slashed Rayleigh distribution. Closed expressions are given for its main characteristics: pdf, cdf, moments and related coefficients. Since we are dealing with a positive and skew right model, it can be of interest for modeling survival time and reliability data. For this reason, features of interest in this field such as the hazard function, mean residual life and order statistics are studied. A closed expression is obtained for the Rényi entropy. The special interest is the EM estimation algorithm based on the hierarchical representation proposed for this model. A simulation study is included, which suggests that the ML estimators are consistent even for moderate sample sizes. Two real applications are included, in which AIC, BIC and QQ-plots show that our proposal provides a better fit than R and SR distributions, especially on the right tail of these datasets.