Abstract
A characterizing property of Zenga (1984) inequality curve is exploited in order to develop an estimator for the extreme value index of a distribution with regularly varying tail. The approach proposed here has a nice graphical interpretation which provides a powerful method for the analysis of the tail of a distribution. The properties of the proposed estimation strategy are analysed theoretically and by means of simulations. The usefulness of the method will be tested also on real data sets.
1. Introduction
A distribution function F with survivor function is regularly varying (RV) at infinity with index , if there exists an such that
in this case we say that . In the extreme value (EV) literature it is typical to refer to the EV index with . Informally, we will say that the distribution has a Pareto tail or that the distribution is of the power-law type. Note that the case (or ) entails distributions with infinite variance and finite mean while the case (or entails distributions with finite mean and variance.
Precision in the analysis of the tail of a distribution allows to, for example, perform proper risk evaluation in finance, correcting empirical income distributions for various top-income measurement problems, or individuating a proper growth theory in economics or the biological sciences. For further examples of applications and deeper discussion see Clauset et al. [1], Jenkins [2] and Hlasny [3] with specific references to applications in income distributions and an overview of available models; see also Heyde and Kou [4] for a deep discussion of graphical methods for tail analysis.
The present paper will concentrate on estimation of the EV index . Probably the most well-known estimator of the EV index is the Hill [5] estimator, which exploits the k upper order statistics of a random sample through the formula
where denotes the i-th order statistics from a sample of size n and diverges to ∞ in an appropriate way. The Hill estimator has been thoroughly studied in the literature and several generalizations have been proposed. For a recent review of estimation procedures for the EV (or tail) index of a distribution see Gomes and Guillou [6].
Some recent approaches in tail or EV index estimation we would like to mention here are those of Brilhante et al. [7] which define a moment of order p estimator which reduces to the Hill estimator for and Beran et al. [8] which define a harmonic moment tail index estimator. Recently Paulauskas and Vaičiulis [9] and Paulauskas and Vaičiulis [10] have connected in an interesting way some of the above approaches by defining parametric families of functions of the order statistics. Reduced bias (RB) versions of the above estimators have appeared in the literature, see for example Caeiro et al. [11], Gomes et al. [12] and Gomes et al. [13].
The main contribution of this paper consists in a new estimation procedure for EV index of a distribution satisfying (1) which relies on Zenga’s inequality curve , (Zenga [14]).
The curve has the property of being constant for the Pareto Type I distribution, it has an intuitive graphical interpretation, it does not depend on location and it shows a nice regular behaviour when estimated. These properties will be discussed, analysed and extended in order to define our inferential strategies. Also it is important to point out that an inequality curve is defined for positive observations and hence we will implicitly assume that the right tail of a distribution is analysed. This is not really a restriction since if one wishes to consider the left tail it is enough to change sign to the data. Also, if the distribution is over the real line, tails can be considered separately and, under the symmetry assumption, absolute values of the data could be considered. The approach to estimation proposed here, directly connected to the inequality curve , has a nice and effective graphical interpretation which greatly helps in the analysis. Other graph-based methods are to be found in Kratz and Resnick [15], which exploit properties of the QQ-plot, and Grahovac et al. [16] which discuss an approach based on the asymptotic properties of the partition function, a moment statistic generally employed in the analysis of multi-fractality; see also Jia et al. [17] which analyse graphically and analytically the real part of the characteristic function at the origin.
We would like to point out here that the curve discussed by Zenga [14] does not coincide with the Zenga [18] curve originally indicated by the author with , (more details in the next Section).
The paper is organized as follows: Section 2 introduces the curve and discusses its properties; Section 3 analyses the proposed estimation strategy and discusses some practical issues in applications. Finite sample performances are analysed in Section 4 and Section 5 where applications with simulated and real data are considered. Proofs are postponed to the last Section.
2. The Proposed Estimator for the EV Index
Let X be a positive random variable with finite mean , distribution function F, and probability density f. The inequality curve has been first defined in Zenga [14]; with original notation:
where is the generalized inverse of F and is the first incomplete moment. Q can be defined as a function of p via the Lorenz curve
See further Zenga [19] Arcagni and Porro [20] for a general introduction and analysis of for different distributions. It is worth to mention that the curve should not be confused with the inequality curve defined in Zenga [18], originally indicated as
The curve has many nice properties and has been heavily studied in some recent literature; it is now commonly known as the Zenga curve . For the sake of completeness in Zenga [14] the notation was originally used for another inequality curve based on quantiles, that is,
where and . As pointed out in Zenga [14] (without providing if and only if results) the curve is constant in p for type-I Pareto distributions, while the curve Z, as defined in Equation (6), is constant in p for Log-normal distributions. On the contrary, the curve I, as defined in (5), is not constant for any distribution, see Zenga [14] and Zenga [18] for further details. Turning back the attention to the curve , note that for a Pareto Type I distribution with
under the condition that , the Lorenz curve has the form
it follows that in this case , , that is is constant in p. This is actually an if-and-only-if result, which we formalize in the following lemma (see Section 7 for its proof).
Lemma 1.
Lemma 1 could be exploited to derive a new approach to the estimation of the EV index for the Pareto distribution. In order to define an estimator for the more general case where satisfies (1) it is worth to analyse in more detail what is the behaviour of the Lorenz curve under the framework defined by (1). This will be done by considering the truncated random variable with , . If G and g denote respectively the distribution function and the density of Y, note that and . Furthermore, setting and inverting we have . A formal result on the Lorenz curve for Y is given in the next lemma.
Lemma 2.
Consider the random variable X with distribution function and absolutely continuous density f; define , , and let the Lorenz curve of Y. Then
Remark 1.
Lemma 2 implies that the curve , for the truncated random variable , with distribution satisfying (1), will be constant with value γ for all if the truncation level s will be large enough. This fact can be exploited to derive a general estimator for the EV index for all distributions in the class (1) as long as .
Before arriving at a formal definition of the estimator, some preliminary quantities need to be defined. Let be the order statistics of a random sample of size n from a distribution satisfying (1). Let and as . Define the estimator of the conditional Lorenz curve as
After defining
the proposed estimator of is
Remark 2.
The estimator defined in (12), based on a Lorenz curve computed on upper order statistics (defined by k), puts into practice the results of Lemma 1 and Lemma 2. Below we will discuss conditions under which (12) provides a consistent estimator of γ for the class of distributions satisfying (1). Guidance in the choice of k will be also discussed.
Letting denote the indicator function of the event A the above estimators are based on the non-parametric estimators
Under the Glivenko-Cantelli theorem it holds that almost surely and uniformly in ; under the assumption that , it holds that almost surely and uniformly in (Goldie [21]). and are both step functions with jumps at . The jumps of are of size while the jumps of are of size where .
Letting , we note that since and that for we have the representation
Exploiting the above representation and the results of Goldie [21], uniform consistency of can be claimed. As far as uniform consistency of we state the following lemma, which is proven in Section 7.
Lemma 3.
For from a distribution F with ; then
Following Lemma 2, graphical inspection of the tail of a distribution satisfying (1) can be carried out by analysing a graph with coordinates , which will show a flat line with intercept around the value . Apart from the case of the Pareto distribution, for distributions satisfying (1), to observe a constant line with intercept close to it is necessary to truncate the sample, that is, using only the upper order statistics when estimating .
As an example, Figure 1 reports the empirical curve as a function of for some cases of interest at different truncation thresholds. There appear two distributions with tail satisfying (1), namely Pareto as defined by (7) and Fréchet (more formally defined below), both with tail index . There appear also two distributions which do not satisfy (1), namely Log-normal with null location and standard deviation equal to 2 and Exponential with unit scale. Note that for Log-normal distribution the curve does not depend on location, while it does not depend on scale for the exponential distribution (Zenga [14]).
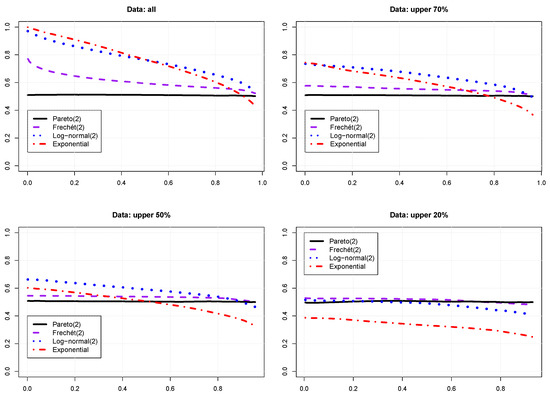
Figure 1.
Plot of (y-axis) as a function of (x-axis), , for Pareto, Fréchet, Log-normal and Exponential distributions at various levels of truncation. Sample size .
Inspection of the graphs reveals a remarkably regular behaviour of the curves; the Pareto case is constant (with some slight variations) for all level of truncation, while the Fréchet one becomes more and more constant with increasing levels of truncation. The Log-normal and Exponential cases show a slope in the curve at all levels of truncation.
3. Asymptotic Properties of
3.1. Consistency
Exploiting some theoretical results given Section 7 (see the proof Lemma 2 for details), one can write
where is a slowly varying function, that is, it holds that for any .
To analyze in more detail the second term on the r.h.s. of the above equation we assume a second order condition which is quite common in the EV theory (Caeiro et al. [11] and Gomes et al. [13]), that is,
where , , , , . To evaluate the r.h.s. of (16), as , set from which . Then, an asymptotic evaluation requires to evaluate the expression
Note that the asymptotic behaviour of the sum in (18) is governed by . Expanding in Taylor series the numerator and using as ,
which is as if , with . For example if then one can choose in order to have an asymptotically bias free estimator. There exists valid estimation methods for and implemented also in R (see Section 4 for details).
Lemma 4.
Under the conditions of Lemma 3 and condition (17), with ,
3.2. Asymptotic Distribution
To provide an operational distributional result, we exploit a result of Csorgo and Mason [22]. Given i.i.d. with , , let , where ’s are i.i.d. Exponential with unit scale parameter (Exp(1)) random variables; then, for fixed k,
Note that and that if then Y has a Generalized Inverse Gamma (GIG) distribution with density
Compare with Mead [23] setting , , , . Using this general result, a simple and fast parametric bootstrap procedure can be implemented in order to obtain the full asymptotic distribution of and from it estimates of the standard error and confidence intervals.
Remark 3.
Since is consistent, the above procedure is consistent for the asymptotic distribution of the estimator (12).
Once the bootstrap distribution is available it can be used for variance and confidence intervals estimation. Simulations show that the approximation works quite well already for small sample sizes and for different k values. Clearly the precision depends on a good preliminary estimator of which is the only parameter needed in determining the distribution; this is however a typical feature of asymptotic results for estimators.
Figure 2, considering different sample sizes () from a Fréchet(2) distribution, shows the histograms of true distribution of (obtained by the Montecarlo method with 2000 iterations) and the bootstrap distribution obtained by Algorithm 1. The value of used in Algorithm 1 has been randomly selected from the 1000 central values estimated in the connected Montecarlo experiment. Sampling of has been done independently in each of the 4 experiments in the graph.
| Algorithm 1 Bootstrap for the asymptotic distribution of . |
|
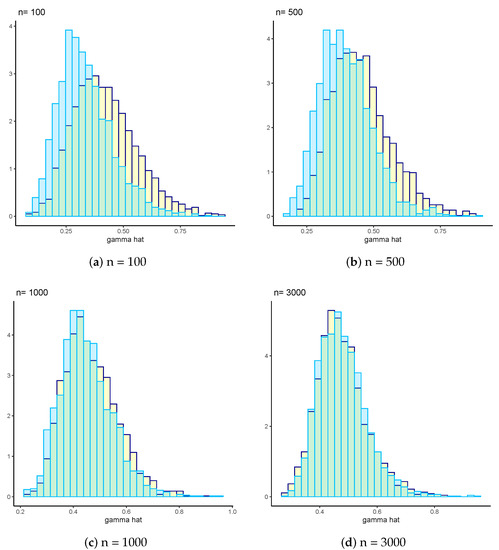
Figure 2.
Histograms of the empirical distribution of for selected sample sizes; ; data samples are generated from a Fréchet(2) distribution. Yellow: values obtained by Montecarlo simulations (2000 iterations); blue: values obtained by Algorithm 1 (2000 iterations). The value of used has been selected randomly from a pool of estimated values.
3.3. Selecting k
The estimator , like many tail estimators, requires the choice of k, the number of upper order statistics to be used in estimation. Lemma 4 provides some indication on how to do so; estimation of the required parameters governing the second order conditions can be carried on quite straightforwardly (see discussion in the next section).
In order to arrive at a data-driven procedure to define the fraction of upper order statistics for estimation of the EV index, consider the linear equation
From Lemmas 1 and 2, it follows that for a type-I Pareto distribution and for for a truncated random variable satisfying (1), as is large enough, distribution F satisfying (7) with , in the above equation one has and . Considering a sample version of (23): given a random sample , using the notation established in the previous Section, write
where . Note that the proposed estimator (12) can be interpreted as the intercept estimate in model (24) exploiting the information that . More formally, using ordinary least squares, define the estimators
where is the mean of the ’s and , . Lemma 3 implies
Proposition 1.
Under the conditions of Lemma 4 it holds that .
Following this reasoning, one can define a procedure based on the graph of for different levels of truncation: we observe the fraction of upper order statistics which gets the smallest, in absolute value, regression coefficient from the regression (25).
| Algorithm 2 Data-driven estimator . |
|
In the next two Sections, the performance of the proposed estimation strategy is analysed on simulated and real data.
4. Numerical Comparisons
In this section we will evaluate the performance of with respect to some alternative estimators of the EV (or tail) index. As far as the estimator for is concerned, beyond considering the estimator , the estimator with different levels of truncation of the data is considered. In the tables, indicates the estimator , with indicating the fraction of upper order statistics used in estimation; the notation indicates the case where all the sample data are used in estimation.
Numerical comparisons will be carried out with respect to some reduced bias (RB) competitors (Caeiro et al. [11], Gomes et al. [12]) based on Hill (Hill [5]), generalized Hill (Beirlant et al. [24]), moment (Dekkers et al. [25]) and moment of order p (Gomes et al. [13]) estimators; optimized with respect to the choice of k as discussed in Gomes et al. [13].
RB estimation of for the above mentioned alternative estimators is based on external estimation of additional parameters (refer to Gomes et al. [26] and Gomes et al. [13] for further details). In our comparisons the following RB-versions are used:
- (1)
- (2)
- RB-Moment estimator, denoted by MM in the tables,withand , .
- (3)
- RB-Generalized Hill estimator, , denoted GH in the tables, with the same bias correction as in (27) applied towith .
- (4)
- RB-MOP (moment of order p) estimator, for (the case reduces to the Hill estimator) defined bywith , , , . Denoted by in the tables. In this case p is a tuning parameter which will be set, in our simulations, equal to and 1. For an estimated optimal value of p based on a preliminary estimator of see Gomes et al. [13].
Computations of the above estimators have been performed using the package evt0 (Manjunat and Caeiro [27]) in R. More precisely, and are obtained using the function other.EVI() respectively with the options GH and MO. Estimation of the parameters for the bias correction terms can be obtained from the function mop(). RB-Hill and RB-MOP estimates are directly obtained by the function mop() by appropriately specifying a value of p and the option RB-MOP. In order to optimize the choice of k we used the formula [13]
where is the integer part of x and . For the comparisons, the following distributions are used:
- (1)
- Pareto distribution, as defined in (7). Random numbers from this distribution are simply generated in R using the function runif() and inversion of F.
- (2)
- Fréchet distribution with , , denote by Fréchet. This distribution is simulated in R using the function rfrechet() from the package evd (Stephenson [28]) with shape parameter set equal to .
- (3)
- Burr distribution with , indicated with Burr. This distribution is simulated in R using the function rburr() from the package actuar (Dutang et al. [29]) with the parameter shape1 set to 1 and shape2 set equal to .
- (4)
- Symmetric stable distribution with index of stability , , indicated with Stable:= Stable; where , and indicate, respectively, asymmetry, location and scale. This distribution is simulated in R using the function rstable() from the package stabledist (Wuertz et al. [30]). For this distribution only the positive observed data are used in estimation.
Table 1, Table 2, Table 3, Table 4, Table 5, Table 6, Table 7 and Table 8 contain the empirical RMSE (Root-MSE) and the relative RMSE, with respect to , of the estimators, that is, for any of the evaluated estimators, say , then

Table 1.
RMSE of the estimators for the Pareto(4) distribution; 1000 Montecarlo replications.

Table 2.
Relative RMSE of the estimators for the Pareto(4) distribution; 1000 Montecarlo replications.

Table 3.
RMSE of the estimators for the Fréchet(1.5) distribution; 1000 Montecarlo replications.

Table 4.
Relative RMSE of the estimators for the Fréchet(1.5) distribution; 1000 Montecarlo replications.

Table 5.
RMSE of the estimators for the Burr(2) distribution; 1000 Montecarlo replications.

Table 6.
Relative RMSE of the estimators for the Burr(2) distribution; 1000 Montecarlo replications.

Table 7.
RMSE of the estimators for the Stable(1.1) distribution; 1000 Montecarlo replications.

Table 8.
Relative RMSE of the estimators for the Stable(1.1) distribution; 1000 Montecarlo replications.
Note that a Rel-RMSE greater than one implies a worse performance of the estimator with respect to . denotes the empirical expected value, that is, the mean over the Montecarlo experiments. For each sample size , 300, 500, and 1000; 1000 Montecarlo replicates were generated. Computations have been carried out with R version 3.5.1 and each experiment, that is, given a chosen distribution and a chosen n, has been initialized using set.seed(3). Numerical results representative for each distribution are reported in the tables. More tables with other choices of parameters can be found in the on-line Supplementary Materials accompanying this paper.
Trying to summarize the results we note the general good performance of the estimators based on the curve defined in this paper for which the gain in efficiency can be substantial. We note also the actual usefulness of for practical applications since it is able to individuate appropriate levels of truncation for different distributions although an actual knowledge of the optimal level of truncation would obtain higher efficiency.
Turning to the single cases, one can note that the outperforms all the other estimators for the Pareto distribution where relative efficiency (see Table 2), is always greater than 4. For the case of the Pareto distribution, would be the most efficient choice, as expected.
In the case of the Fréchet distribution is always more efficient than all competitors test for smaller sample sizes (see Table 4); as sample size increases the gain in efficiency decreases and maybe slightly lower in some cases.
The performance of in the case of the Burr distribution is comparable to that of the competitors, with relative RMSE (see Table 6) slightly smaller or greater than one depending on the case considered.
In the case of the Symmetric stable distribution, the performance of is slightly better than all alternative estimators in all cases (see Table 8). The MM estimator turns out to be quite efficient for the stable distribution with closer to 2 (see the on-line Supplementary Materials).
We note that the MM and GH estimators, computed with the package evt0, has shown some illogical results in some instances with extremely high values of the RMSE, typically for some specific sample sizes, after several checks, we could not figure out the reason of such results.
5. Examples
Here we concentrate on six real data examples that have been used in the literature to discuss methods to detect a power-law in the tail of the underlying distribution. These data have all been thoroughly analysed, for example, in Clauset et al. [1]. The following data sets are analysed here:
- 1.
- The frequency of occurrence of unique words in the novel Moby Dick by Herman Melville (Newman [31]).
- 2.
- The severity of terrorist attacks worldwide from February 1968 to June 2006, measured as the number of deaths directly resulting (Clauset et al. [32]).
- 3.
- The sizes in acres of wildfires occurring on U.S. federal land between 1986 and 1996 (Newman [31]).
- 4.
- The intensities of earthquakes occurring in California between 1910 and 1992, measured as the maximum amplitude of motion during the quake (Newman [31]).
- 5.
- The frequencies of occurrence of U.S. family names in the 1990 U.S. Census (Clauset et al. [1]).
- 6.
- Peak gamma-ray intensity of solar flares between 1980 and 1989 (Newman [31]).
Figure 3 provides the estimated curves for the six examples, either considering the whole data and selected percentages of the upper order statistics. The range of may vary in the graphs in order to have a better detail of the path of the curves.
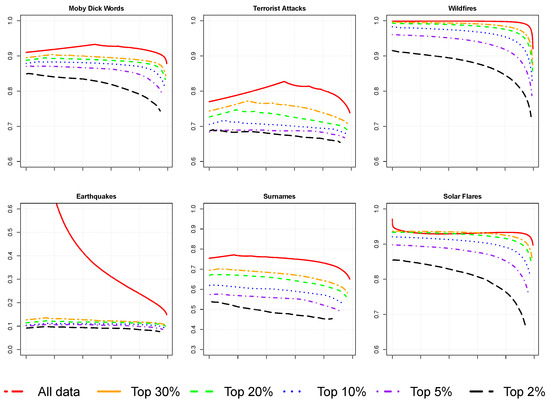
Figure 3.
Plot of the estimated curves for the six dataset: all data and selected percentages of upper order statistics.
On each of the data-set we apply Algorithm 2 in order to select the optimal number of k in computing ; with the given estimate we apply Algorithm 1 in order to compute a 95% confidence interval for the estimate.
Next we apply a testing procedure to evaluate if the graphs in Figure 3, for the k chosen by Algorithm 1, can be considered “enough flat” in order to support the hypothesis that the data come from a distribution within the class (1). A bootstrap test setting in model (24) has been developed in Taufer et al. [33].
For comparison we apply also the testing procedure for the power-law hypothesis developed by Clauset et al. [1].
Table 9 reports analytical results on estimated values, 95% confidence intervals, the fraction of upper order statistics used and the p-values of the testing procedures.

Table 9.
Sample size, estimated and 95% confidence intervals for the six data-sets. Fraction of upper order statistics used and p-values of the testing procedures defined in Taufer et al. [33] (Sig) and Clauset et al. [1] (Sig). Asterisk indicates significant p-values.
Trying to summarize briefly the results we would say that the conclusions about the presence of a Pareto-type tail in the distributions coincide fully with the conclusions of Clauset et al. [1], that is: clear evidence of a power law distribution fitting the data is for the Moby Dick and Terrorism data-sets. For the others there is no convincing evidence. We point out that for the contrasting p-values for the Solar Flares data, Clauset et al. [1] suggest a power tail with an exponential cut-off at a certain point. Given the characteristics of the graphs based on the curve this feature cannot be noticed in our analysis.
As far as the estimated values of , the values of the estimators obtained here are substantially lower with respect to those obtained by Clauset et al. [1] (which uses the Hill estimator). Given the good performance in the simulations of in comparison to the Hill estimator, the values in Table 9, at least for the Moby Dick and Terrorism data-set can be considered reliable.
For the other data-sets, since the null hypotheses of a power law has significant p-values, the estimated should be discarded and it becomes of interest to select an alternative model by using, for example a likelihood ratio test as discussed in Clauset et al. [1] to which the interested reader is referred.
6. Conclusions
An estimation strategy for the tail index of a distribution in class (1) has been defined starting from a characterizing property of Zenga’s inequality curve . On the basis of the theoretical properties of the estimator two simple bootstrap procedures have been obtained: the first provides a general result for the asymptotic distribution of and the second gives a data-driven procedure to determine the optimal value of k. Simulations show the good performance of and the implementation algorithm.
The data-driven optimized estimator often outperforms optimized (with respect to bias) competing estimation strategies. The gain in efficiency is substantial in the case of Pareto distributions.
The graph of the curve associated with the estimator provides a valid support in the analysis of real data.
7. Proofs
Proof of Lemma 1.
It is trivially verified that if F satisfies (7) then . Suppose now that , , where k is some constant. Then it must hold that or equivalently, after some algebraic manipulation,
Taking derivatives on both sides we have that
which gets
from which, setting , which implies , it follows that, after some further elementary manipulations,
Setting , properly normalized, the above F follows (7). □
Proof of Lemma 2.
Let G and g denote respectively the distribution function and the density of and note that and . Setting and inverting we have . Note that
also, setting ,
Consider the Lorenz curve for Y, and , let and . Then
Consider first the numerator of the above expression
after setting . Next, to link to the function , set ; the above term, as , by Karamata’s theorem (see De Haan and Ferreira [34], p. 363), becomes
since as , . is a slowly varying function. Next consider the denominator; similar computations bring to
which, as , converges to
Finally, putting together the results one has
since as , by the properties of slowly varying functions. □
Proof of Lemma 3.
Note that and that p lies in a compact interval. is continuous transformation of ; it follows that for fixed , .
To prove uniform consistency of we need to show it is equicontinuous. For this note that depends on p stochastically only through , which is uniformly continuous. Hence for any such that , it is possible to find an , not depending on such that for , , one has
□
Proof of Lemma 4.
We have
by using Lemma 3 and condition (17) with , . □
Supplementary Materials
The following are available online at https://www.mdpi.com/2227-7390/8/10/1834/s1.
Author Contributions
Conceptualization, E.T.; Data curation, P.L.N.I., G.E. and M.M.D.; Investigation, E.T., F.S. and P.L.N.I.; Methodology, E.T. and F.S.; Project administration, G.E.; Supervision, E.T.; Writing, review and editing, E.T., P.L.N.I. and M.M.D. All authors have read and agree to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors would like to than two anonymous referees whose comments lead to an improved version of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Clauset, A.; Shalizi, C.R.; Newman, M.E. Power-law distributions in empirical data. SIAM Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef]
- Jenkins, S.P. Pareto Distributions, Top Incomes, and Recent Trends in UK Income Inequality. Economica 2016. Available online: https//www.econstor.eu/bitstream/10419/145258/1/dp10124.pdf (accessed on 30 September 2020).
- Hlasny, V. Parametric Representation of the Top of Income Distributions: Options, Historical Evidence and Model Selection (No. 90); Department of Economics, Tulane University: New Orleans, LA, USA, 2020. [Google Scholar]
- Heyde, C.C.; Kou, S.G. On the controversy over tailweight of distributions. Oper. Res. Lett. 2004, 32, 399–408. [Google Scholar] [CrossRef]
- Hill, B.M. A simple general approach to inference about the tail of a distribution. Ann. Stat. 1975, 3, 1163–1174. [Google Scholar] [CrossRef]
- Gomes, M.I.; Guillou, A. Extreme value theory and statistics of univariate extremes: A review. Int. Stat. Rev. 2015, 83, 263–292. [Google Scholar] [CrossRef]
- Brilhante, M.F.; Gomes, M.I.; Pestana, D. A simple generalisation of the Hill estimator. Comput. Stat. Data Anal. 2013, 57, 518–535. [Google Scholar] [CrossRef]
- Beran, J.; Schell, D.; Stehlík, M. The harmonic moment tail index estimator: Asymptotic distribution and robustness. Ann. Inst. Stat. Math. 2014, 66, 193–220. [Google Scholar] [CrossRef]
- Paulauskas, V.; Vaičiulis, M. A class of new tail index estimators. Ann. Inst. Stat. Math. 2017, 69, 461–487. [Google Scholar] [CrossRef]
- Paulauskas, V.; Vaičiulis, M. On an improvement of Hill and some other estimators. Lith. Math. J. 2013, 53, 336–355. [Google Scholar] [CrossRef]
- Caeiro, F.; Gomes, M.I.; Pestana, D. Direct reduction of bias of the classical Hill estimator. Revstat 2005, 3, 111–136. [Google Scholar]
- Gomes, M.I.; de Haan, L.; Henriques-Rodrigues, L. Tail index estimation for heavy tailed models: Accomodation of bias in weighted log-excesses. J. R. Stat. Soc. B 2008, 70, 31–52. [Google Scholar]
- Gomes, M.I.; Brilhante, M.F.; Pestana, D. New reduced-bias estimators of a positive extreme value index. Commun. Stat.-Simul. Comput. 2016, 45, 833–862. [Google Scholar] [CrossRef]
- Zenga, M. Proposta per un indice di concentrazione basato sui rapporti fra quantili di popolazione e quantili di reddito. Giornale degli Economisti e Annali di Economia 1984, 5, 301–326. [Google Scholar]
- Kratz, M.F.; Resnick, S.I. The QQ-estimator and heavy tails. Commun. Stat. Stoch. Model. 1996, 12, 699–724. [Google Scholar] [CrossRef]
- Grahovac, D.; Jia, M.; Leonenko, N.N.; Taufer, E. Asymptotic properties of the partition function and applications in tail index inference of heavy-tailed data. Stat. J. Theor. Appl. Stat. 2015, 49, 1221–1242. [Google Scholar] [CrossRef][Green Version]
- Jia, M.; Taufer, E.; Dickson, M. Semi-parametric regression estimation of the tail index. Electron. J. Stat. 2018, 12, 224–248. [Google Scholar] [CrossRef]
- Zenga, M. Inequality curve and inequality index based on the ratios between lower and upper arithmetic means. Stat. Appl. 2007, 1, 3–27. [Google Scholar]
- Zenga, M. Concentration curves and Concentration indexes derived from them. In Income and Wealth Distribution, Inequality and Poverty; Dagum, C., Zenga, M., Eds.; Springer: Berlin/Heidelberg, Germany, 1990; pp. 94–110. [Google Scholar]
- Arcagni, A.; Porro, F. A comparison of income distributions models through inequality curves. Stat. Appl. 2016, XIV, 123–144. [Google Scholar]
- Goldie, C.M. Convergence theorems for empirical Lorenz curves and their inverses. Adv. Appl. Probab. 1977, 9, 765–791. [Google Scholar] [CrossRef]
- Csorgo, S.; Mason, D.M. The asymptotic distribution of sums of extreme values from a regularly varying distribution. Ann. Probab. 1986, 14, 974–983. [Google Scholar] [CrossRef]
- Mead, M.E. Generalized Inverse Gamma Distribution and its Application in Reliability. Commun. Stat. Theory Methods 2015, 44, 1426–1435. [Google Scholar] [CrossRef]
- Beirlant, J.; Vynckier, P.; Teugels, J.L. Excess functions and estimation of the extreme-value index. Bernoulli 1996, 2, 293–318. [Google Scholar] [CrossRef]
- Dekkers, A.L.M.; Einmahl, J.H.J.; de Haan, L. A moment estimator for the index of an extreme-value distribution. Ann. Stat. 1989, 17, 1833–1855. [Google Scholar] [CrossRef]
- Gomes, M.I.; Figueiredo, F.; Neves, M.M. Adaptive estimation of heavy right tails: Resampling-based methods in action. Extremes 2012, 15, 463–489. [Google Scholar] [CrossRef]
- Manjunath, B.G.; Caeiro, F. evt0:Mean of Order p, Peaks over Random Threshold Hill and High Quantile Estimates R Package Version 1.1-3. Available online: https://cran.r-project.org/web/packages/evt0 (accessed on 31 August 2020).
- Stephenson, A.G. evd: Extreme Value Distributions. R News 2002, 2, 31–32. Available online: https://CRAN.R-project.org/doc/Rnews/ (accessed on 31 August 2020).
- Dutang, C.; Goulet, V.; Pigeon, M. actuar: An R Package for Actuarial Science. J. Stat. Softw. 2008, 25, 1–37. Available online: http://www.jstatsoft.org/v25/i07 (accessed on 31 August 2020).
- Wuertz, D.; Maechler, M.; Rmetrics Core Team Members. Stabledist: Stable Distribution Functions. R Package Version 0.7-1. 2016. Available online: https://CRAN.R-project.org/package=stabledist (accessed on 31 August 2020).
- Newman, M.E. Power laws, Pareto distributions and Zipf’s law. Contemp. Phys. 2005, 46, 323–351. [Google Scholar] [CrossRef]
- Clauset, A.; Young, M.; Gleditsch, K.S. On the frequency of severe terrorist events. J. Confl. Resolut. 2007, 51, 58–87. [Google Scholar] [CrossRef]
- Taufer, E.; Santi, F.; Espa, G.; Dickson, M.M. Goodness-of-fit test for Pareto and Log-normal distributions based on inequality curves. 2020. Unpublished. [Google Scholar]
- De Haan, L.; Ferreira, A. Extreme Value Theory: An Introduction; Springer Science & Business Media: New York, NY, USA, 2007. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).