Abstract
In this work, the new model of photothermal and elastic waves, with and without energy dissipation, under a hyperbolic two-temperature model, is used to compute the displacement, carrier density, thermodynamic temperature, conductive temperature and stress in a semiconductor medium. The medium is considered in the presence of the coupling of plasma and thermoelastic waves. To get the complete analytical expressions of the main physical fields, Laplace transforms and the eigenvalue scheme are used. The outcomes are presented graphically to display the differences between the classical two-temperature theory and the new hyperbolic two-temperature theory, with and without energy dissipation. Based on the numerical results, the hyperbolic two-temperature thermoelastic theory offers a finite speed of mechanical waves and propagation of thermal waves.
1. Introduction
Most previous studies considering the thermal and elastic properties of semiconducting elastic medium are isotropic and homogeneous. However, plasma, thermal and elastic wave equations are partially coupled, and the coupling between them has also been neglected. Solving the system with the coupling of plasma, thermal and elastic equations is very complex. However, analysis with partially coupled equations is enough in most experimental studies that neglect the coupling between plasma, thermal and elastic waves. In particular cases, the problems of thermoelastic and electronic distortion were taken into account. The effect of coupling was studied in terms of approximately quantitative analysis. Studying the excitations of short elastic pulses by photothermal means is important for physicists and engineers because it is applied in many areas, such as the formation of images by thermal waves, determination of the parameters of thermoelastic materials, monitoring of laser drilling, laser annealing and fusion phenomena, and in photoacoustic microscopes. The different influences of thermoelastic and electronic deformations in semiconductor mediums have been analyzed without taking into account the coupling between the plasma and the thermoelastic equations. Todorovic [1,2] investigated photothermal and elastic waves in a semiconductor medium. The change in the propagation of photothermal and elastic waves going back to the linear coupling between heat and mass transport (i.e., thermodiffusion) was included.
The thermoelastic (TE) machining of elastic waves is explained as a result of the propagation of an elastic perturbation toward the surface of the material subjected to the heating waves in that material. Song et al. [3,4] studied thermoelastic vibrations due to optically excited semiconductor microcantilevers. Complementing that, the reflections of plane waves in a semiconducting material upon photothermal theories [5,6] were also explored. Lotfy [7] investigated elastic wave propagation for a photothermoelastic medium under the influence of an internal heat source and gravitational field upon the dual-phase-lag (DPL) model. Hobiny and Abbas [8] studied photothermal and elastic waves in an unbounded semiconductor medium with a cylindrical hole.
The thermoelastic model under two classical temperatures was established by Chen and Gurtin [9], Chen et al. [10] and Williams and Gurtin [11]. When another model is used, depending on the classic two-temperature model (thermodynamic temperature and conductivity temperature ), the classical Clausius–Duhem inequality is replaced. The first is subjected to an inherent mechanical process, and the second is subjected to a thermal process through the particles and the elastic material layer. Ezzat et al. [12] studied the effect of the two-temperature parameter with fractional order in magneto-thermoelasticity under the dual-phase-lag model. Abbas and Youssef [13] applied a finite element approach to investigate the generalized thermoelasticity problem under a two-temperature model. Youssef and El-Bary [14] investigated thermoelastic interaction with hyperbolic two-temperature models with one relaxation time. Kumar et al. [15] studied the thermoelastic interaction on hyperbolic two-temperature generalized thermoelasticity in an unbounded medium with a cylindrical cavity. Prasad and Kumar [16] investigated the characterizations and stability of a plane wave under hyperbolic two-temperature generalized thermoelasticity. Ezzat [17] studied hyperbolic thermal-plasma wave propagation in a semiconductor of organic materials. Alzahrani and Abbas [18] solved the two-dimensional semiconductor problem under the photothermoelastic model without energy dissipation. Hobiny and Abbas [19] investigated the photothermoelastic interaction in a 2D semiconducting medium under the Green and Naghdi model with energy dissipation (GN III) model. Lotfy et al. [20] investigated the electromagnetic and Thomson effect under a photothermoelastic model in a rotator semiconductor medium. Ali et al. [21] investigated the reflections of a wave in a rotating semiconductor nanostructure material under torsion-free boundary conditions. Alzahrani and Abbas [22] applied the hyperbolic two-temperature theory to study photothermoelastic interactions in semiconductor medium with a spherical cavity. Lotfy et al. [23] investigated the impacts of variable thermal conduction of a semiconductor hole under fractional-order photothermal with magnetic field models. Several authors [24,25,26,27,28,29,30,31,32] have obtained the numerical and analytical solution of many thermoelastic problems. Abd-Elaziz et al. [33] studied the effects of Thomson and initial stresses in a thermal porous elastic material under the Green–Naghdi electromagnetic model. Itu et al. [34] studied the improvement of the rigidity of composite circular plates through radial ribs. Vlase et al. [35] investigated the equation of motion for a flexible one-dimension element used in the dynamic analysis of a multibody system. Abbas and Marin [36] investigated the analytical solutions of thermoelastic interactions in a plate due to pulsed laser heating. In fact, without any assumed restriction on the factual physical fields, the eigenvalue scheme gives the analytical solution in the Laplace domain.
In this article, we applied the Green and Naghdi model (type III) to deal with the photothermal interaction in a semiconductor medium under a new hyperbolic two-temperature model. Laplace transforms and numerical Laplace inverses were used to solve the problem. Silicon (Si) material was used to make a simulation and obtain the numerical results. The outcomes are presented graphically to depict the differences between the new hyperbolic two-temperature theory and the classical two-temperature theory with and without energy dissipation.
2. Basic Equations
For a homogeneous, isotropic semiconductor material, the governing equations for the photothermal waves, with and without energy dissipation, under a new hyperbolic two-temperature model in the absence of thermal sources and body forces are presented by [14,37]:
where is the two-temperature parameter, is the reference temperature, , is the displacement component, are the Lamé constants, is the thermal conductivity, is the specific heat at constant strain, is the characteristic material constant of the model, is the stress component, , is the electronic deformation coefficient, , is the coefficient of linear thermal expansion, , is the conductive temperature increment, , is the increment of thermodynamic temperature, is the density of the medium, , is the carrier concentration at equilibrium, is the coefficient of carrier diffusion, is the lifetime of the photogenerated carrier, is the time and is the thermal activation coupling parameter [38]. An unbounded semiconductor medium is considered, which mean that the medium depends on and only, as in Figure 1. Subsequently, the Equations (1)–(5) are expressed as:
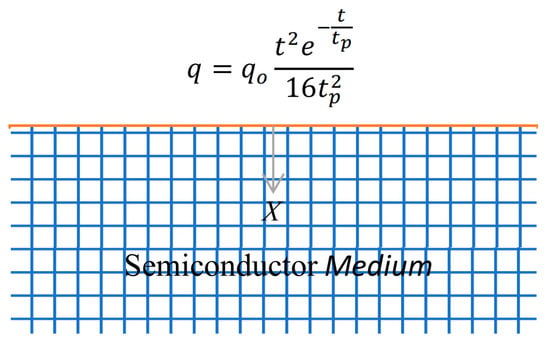
Figure 1.
Schematic of the problem.
3. Application
The problem initial conditions are assumed to be homogeneous and the boundary conditions are expressed as:
where is a constant, is the velocity of recombination on the surface and is the characteristic time of pulsing heat flux. It is convenient to write the basic equations in their nondimensional forms. Thus, the nondimensional parameters are given by:
where and .
The non-dimensional forms of variables (14) are substituted in the basic equations, which can be rewritten as follows (the stars have been ignored for convenience):
where
The function Laplace transform is given by:
where is the Laplace transform parameter. Therefore, the governing equations can be given by the following forms:
The solutions of Equations (22)–(24) with (27) are obtained by using the eigenvalue approach as in [39,40]. By substituting Equations (22)–(25), they can be obtained the following forms:
where
Therefore, the vector-matrix form of Equations (28)–(30) can be written as:
where
Thus, the characteristic equation of matrix is expressed as:
where
The solutions of Equation (31) are the eigenvalues of matrix , which have the forms . Then, the eigenvector corresponding to eigenvalue is calculated as:
By using Equation (33), the eigenvectors corresponding to eigenvalues are computed. The solution of Equation (31) takes the following form:
Due to the regularity condition of the solution, the increasing exponential nature of the spatial variable is eliminated to infinity, so the general solutions of Equation (31) can be written in the form:
where the constants and are calculated using the presented problem boundary conditions. From Equation (35) in (31), the general solutions of the physical fields with respect to and can be expressed by:
Now, the numerical inverse approach is adopted for the general solutions of the carrier density, displacement, thermodynamic temperature, conductive temperature and the stress distribution. The Stehfest [41] numerical inversion approach is taken. In this approach, the inverse Laplace transform for is approximated by:
where
where is the number of terms.
4. Numerical Result and Discussion
Numerical examples for the computation purpose similar to silicon (Si) media are considered with the physical parameters as in [4]:
Based on the values of physical constants as in Table 1, the computation of physical fields along the distance under the new hyperbolic two-temperature model and the classical two-temperature model (see Abbas and Hobiny [42]) are given in Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6. Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 depict the variations of physical fields along the distance at . The conductive and the thermodynamic temperature, stress distributions, carrier density and the displacement with respect to the x-direction in the context of the photothermoelastic model without energy dissipation (Type II) and with energy dissipation (Type III) are computed numerically. Figure 2 shows the variation of displacement along for various types. It is shown that the displacement starts from zero, with the appropriate boundary condition of the problem. After that, it increases up to the maximum value in a particular place near the surface. Figure 3 shows the variation of thermodynamic temperature along the distance . It is observed that it has maximum values at the boundary condition , and after that, it reduces gradually with the rising of to come to the reference temperature . Figure 4 depicts the variation of conductive temperature with respect to the distance . It is observed that it has the maximum value at the boundary condition , and after that, it gradually reduces with the rising of to reach to the reference temperature . Figure 5 displays the variation of carrier density along the distance x for various types. It is noticed that it starts with its maximum values at , and after that, it progressively decreases with the rising until it comes to the equilibrium carrier concentration . Figure 6 shows the distribution of stress along the distances for various types. It is clear that the magnitudes of stress always begin from its ultimate values and then decrease with the increasing to come to zero. Finally, in comparisons between the solutions, one can conclude that the coupled photothermoelastic models in the context of the photothermoelastic model without energy dissipation (Type II) and with energy dissipation (Type III) under the new hyperbolic two-temperature model are major phenomena and have a great effect on the distributions of field quantities. The values of the conductive and the thermodynamic temperature, stress distributions, carrier density and displacement are evidently smaller with the inclusion of GN II when compared to that GN III. Based on the numerical results, the hyperbolic two-temperature thermoelastic theory offers a finite speed of mechanical waves and propagation of thermal waves.

Table 1.
The values of physical parameters.
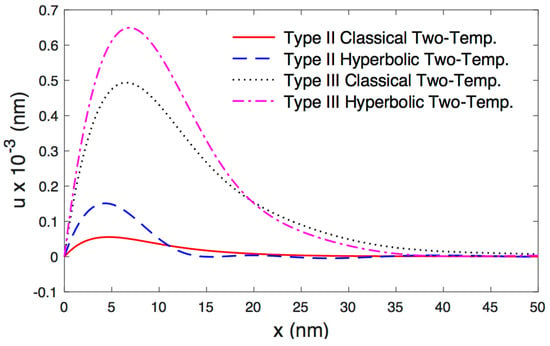
Figure 2.
The variation of displacement versus the distance.
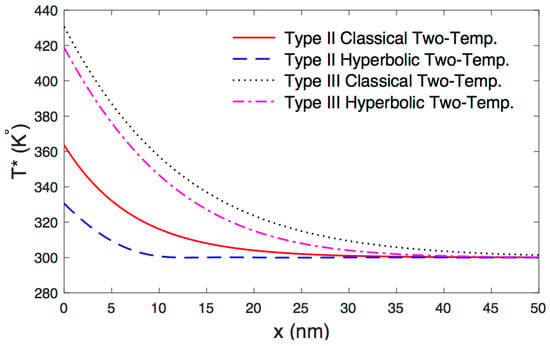
Figure 3.
The variation of thermodynamic temperature with respect to the distance.
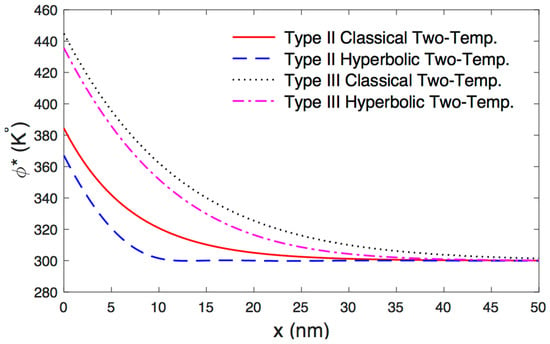
Figure 4.
The variation of conductive temperature versus the distance.
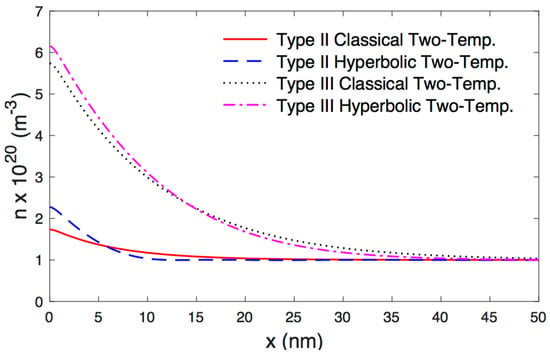
Figure 5.
The variation of carrier density with respect to the distance.
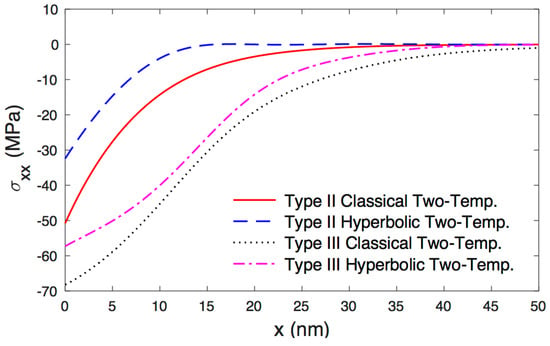
Figure 6.
The variation of stress with respect the distance.
5. Conclusions
In the present work, the coupled thermal, plasma and elastic waves in a semiconducting material were studied under a new hyperbolic two-temperature model. Analytical expressions for carrier density, temperature, displacement and stress in the material were obtained. It was found to be an important phenomenon, with a great effect on the distribution of field quantities. Based on the numerical results, the hyperbolic two-temperature thermoelastic theory offers a finite speed of mechanical wave and propagation of thermal waves. The results obtained in this study are advantageous to analysts involved in material science, engineering, physicists, rock mechanics and geophysics, in addition to people active in the area of continuum mechanics and construction of semiconductor elements to fulfill exceptional engineering needs.
Author Contributions
The two authors conceived the framework and structured the whole manuscript, checked the results, and completed the revision of the paper. The authors have equally contributed to the elaboration of this manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
The Deanship of Scientific Research (DSR) at King Abdulaziz University, Jeddah, Saudi Arabia funded this project, under grant no. (FP-156-42).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Todorović, D. Plasma, thermal, and elastic waves in semiconductors. Rev. Sci. Instrum. 2003, 74, 582–585. [Google Scholar] [CrossRef]
- Todorović, D. Photothermal and electronic elastic effects in microelectromechanical structures. Rev. Sci. Instrum. 2003, 74, 578–581. [Google Scholar] [CrossRef]
- Song, Y.; Todorovic, D.M.; Cretin, B.; Vairac, P. Study on the generalized thermoelastic vibration of the optically excited semiconducting microcantilevers. Int. J. Solids Struct. 2010, 47, 1871–1875. [Google Scholar] [CrossRef]
- Song, Y.; Todorovic, D.M.; Cretin, B.; Vairac, P.; Xu, J.; Bai, J. Bending of Semiconducting Cantilevers under Photothermal Excitation. Int. J. Thermophys. 2014, 35, 305–319. [Google Scholar] [CrossRef]
- Song, Y.; Bai, J.; Ren, Z. Reflection of Plane Waves in a Semiconducting Medium under Photothermal Theory. Int. J. Thermophys. 2012, 33, 1270–1287. [Google Scholar] [CrossRef]
- Song, Y.; Bai, J.; Ren, Z. Study on the reflection of photothermal waves in a semiconducting medium under generalized thermoelastic theory. Acta Mech. 2012, 223, 1545–1557. [Google Scholar] [CrossRef]
- Lotfy, K. The elastic wave motions for a photothermal medium of a dual-phase-lag model with an internal heat source and gravitational field. Can. J. Phys. 2016, 94, 400–409. [Google Scholar] [CrossRef]
- Hobiny, A.D.; Abbas, I.A. A study on photothermal waves in an unbounded semiconductor medium with cylindrical cavity. Mech. Time-Depend. Mater. 2017, 21, 61–72. [Google Scholar] [CrossRef]
- Chen, P.J.; Gurtin, M.E. On a theory of heat conduction involving two temperatures. Z. Angew. Math. Phys. 1968, 19, 614–627. [Google Scholar] [CrossRef]
- Chen, P.J.; Gurtin, M.E.; Williams, W.O. On the thermodynamics of non-simple elastic materials with two temperatures. Z. Angew. Math. Phys. 1969, 20, 107–112. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Williams, W.O. An axiomatic foundation for continuum thermodynamics. Arch. Ration. Mech. Anal. 1967, 26, 83–117. [Google Scholar] [CrossRef]
- Ezzat, M.A.; El-Karamany, A.S.; Ezzat, S.M. Two-temperature theory in magneto-thermoelasticity with fractional order dual-phase-lag heat transfer. Nucl. Eng. Des. 2012, 252, 267–277. [Google Scholar] [CrossRef]
- Abbas, I.A.; Youssef, H.M. Two-temperature generalized thermoelasticity under ramp-type heating by finite element method. Meccanica 2013, 48, 331–339. [Google Scholar] [CrossRef]
- Youssef, H.M.; El-Bary, A.A. Theory of hyperbolic two-temperature generalized thermoelasticity. Mater. Phys. Mech. 2018, 40, 158–171. [Google Scholar]
- Kumar, R.; Prasad, R.; Kumar, R. Thermoelastic interactions on hyperbolic two-temperature generalized thermoelasticity in an infinite medium with a cylindrical cavity. Eur. J. Mech.-A/Solids 2020, 82, 104007. [Google Scholar] [CrossRef]
- Prasad, R.; Kumar, R. On the characterization and stability of plane waves under hyperbolic two-temperature generalized thermoelasticity. J. Therm. Stress. 2020, 1–18. [Google Scholar] [CrossRef]
- Ezzat, M.A. Hyperbolic thermal-plasma wave propagation in semiconductor of organic material. Waves Random Complex Media 2020, 1–25. [Google Scholar] [CrossRef]
- Alzahrani, F.S.; Abbas, I.A. Photo-thermo-elastic interactions without energy dissipation in a semiconductor half-space. Results Phys. 2019, 15, 102805. [Google Scholar] [CrossRef]
- Hobiny, A.; Abbas, I. A GN model on photothermal interactions in a two-dimensions semiconductor half space. Results Phys. 2019, 15, 102588. [Google Scholar] [CrossRef]
- Lotfy, K.; El-Bary, A.; Hassan, W.; Alharbi, A.; Almatrafi, M. Electromagnetic and Thomson effects during photothermal transport process of a rotator semiconductor medium under hydrostatic initial stress. Results Phys. 2020, 16, 102983. [Google Scholar] [CrossRef]
- Ali, H.; Jahangir, A.; Khan, A. Reflection of waves in a rotating semiconductor nanostructure medium through torsion-free boundary condition. Indian J. Phys. 2019, 1–9. [Google Scholar] [CrossRef]
- Alzahrani, F.S.; Abbas, I.A. Photo-Thermal Interactions in a Semiconducting Media with a Spherical Cavity under Hyperbolic Two-Temperature Model. Mathematics 2020, 8, 585. [Google Scholar] [CrossRef]
- Lotfy, K.; El-Bary, A.; Tantawi, R. Effects of variable thermal conductivity of a small semiconductor cavity through the fractional order heat-magneto-photothermal theory. Eur. Phys. J. Plus 2019, 134, 280. [Google Scholar] [CrossRef]
- Bera, M.B.; Das, N.C.; Lahiri, A. Eigenvalue approach to two-temperature generalized thermoelastic interactions in an annular disk. J. Therm. Stress. 2015, 38, 1310–1324. [Google Scholar] [CrossRef]
- Santra, S.; Lahiri, A.; Das, N.C. Eigenvalue approach on thermoelastic interactions in an infinite elastic solid with voids. J. Therm. Stress. 2014, 37, 440–454. [Google Scholar] [CrossRef]
- Kumar, R.; Abbas, I.A. Deformation due to thermal source in micropolar thermoelastic media with thermal and conductive temperatures. J. Comput. Theor. Nanosci. 2013, 10, 2241–2247. [Google Scholar] [CrossRef]
- Marin, M.; Nicaise, S. Existence and stability results for thermoelastic dipolar bodies with double porosity. Contin. Mech. Thermodyn. 2016, 28, 1645–1657. [Google Scholar] [CrossRef]
- Marin, M.; Ellahi, R.; Chirilă, A. On solutions of Saint-Venant’s problem for elastic dipolar bodies with voids. Carpath. J. Math. 2017, 33, 219–232. [Google Scholar]
- Mondal, S.; Sur, A. Photo-thermo-elastic wave propagation in an orthotropic semiconductor with a spherical cavity and memory responses. Waves Random Complex Media 2020, 1–24. [Google Scholar] [CrossRef]
- Marin, M.; Vlase, S.; Ellahi, R.; Bhatti, M. On the partition of energies for the backward in time problem of thermoelastic materials with a dipolar structure. Symmetry 2019, 11, 863. [Google Scholar] [CrossRef]
- Marin, M.; Craciun, E.-M.; Pop, N. Considerations on mixed initial-boundary value problems for micropolar porous bodies. Dyn. Syst. Appl. 2016, 25, 175–196. [Google Scholar]
- Hobiny, A. Effect of the hyperbolic two-temperature model without energy dissipation on Photo-thermal interaction in a semi-conducting medium. Results Phys. 2020, 18, 103167. [Google Scholar] [CrossRef]
- Abd-Elaziz, E.M.; Marin, M.; Othman, M.I. On the effect of Thomson and initial stress in a thermo-porous elastic solid under GN electromagnetic theory. Symmetry 2019, 11, 413. [Google Scholar] [CrossRef]
- Itu, C.; Öchsner, A.; Vlase, S.; Marin, M.I. Improved rigidity of composite circular plates through radial ribs. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2019, 233, 1585–1593. [Google Scholar] [CrossRef]
- Vlase, S.; Marin, M.; Öchsner, A.; Scutaru, M. Motion equation for a flexible one-dimensional element used in the dynamical analysis of a multibody system. Contin. Mech. Thermodyn. 2019, 31, 715–724. [Google Scholar] [CrossRef]
- Abbas, I.A.; Marin, M. Analytical solution of thermoelastic interaction in a half-space by pulsed laser heating. Phys. E Low-Dimens. Syst. Nanostruct. 2017, 87, 254–260. [Google Scholar] [CrossRef]
- Hobiny, A.; Abbas, I.A. Analytical solutions of photo-thermo-elastic waves in a nonhomogenous semiconducting material. Results Phys. 2018, 10, 385–390. [Google Scholar] [CrossRef]
- Mandelis, A.; Nestoros, M.; Christofides, C. Thermoelectronic-wave coupling in laser photothermal theory of semiconductors at elevated temperatures. Opt. Eng. 1997, 36, 459–468. [Google Scholar] [CrossRef]
- Abbas, I.A. A dual phase lag model on thermoelastic interaction in an infinite fiber-reinforced anisotropic medium with a circular hole. Mech. Based Des. Struct. Mach. 2015, 43, 501–513. [Google Scholar] [CrossRef]
- Abbas, I.A. The effects of relaxation times and a moving heat source on a two-temperature generalized thermoelastic thin slim strip. Can. J. Phys. 2015, 93, 585–590. [Google Scholar] [CrossRef]
- Stehfest, H. Algorithm 368: Numerical inversion of Laplace transforms [D5]. Commun. ACM 1970, 13, 47–49. [Google Scholar] [CrossRef]
- Abbas, I.A.; Hobiny, A. A two-temperature photothermal interaction in a semiconductor medium containing a cylindrical hole. Int. J. Thermophys. 2018, 39, 17. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).