1. Introduction
The product form of the stationary distribution greatly simplifies the analysis of complex queueing systems. In such systems, the stationary distribution of the network can be written as the product of the distributions of its nodes with the arrival rates modified to reflect the routing of customers in the network. Jackson [
1] showed that a specific class of open queueing networks has a product-form stationary distribution. Gordon and Newell [
2] introduced product-form Markovian models for closed queueing networks. Kobayashi [
3] and Towsley [
4] developed forms of state-dependent routing in a queueing network, allowing a product-form solution. Baskett et al. [
5] found product-form solutions for open, closed or mixed queueing networks with multiple classes of customers and various service disciplines and service time distributions. Surveys by Disney and König [
6], Nelson [
7] and Balsamo [
8], as well as books by Kelly [
9], Ross [
10], Whittle [
11] and Walrand [
12] cover various aspects of product-form solutions for conventional queueing networks.
Gelenbe [
13,
14] proposed models of a queueing network with positive and negative customers: the G-networks. These models, which include G-networks with signals [
15], resets [
16], and multiple customer classes [
17], radically extend the class of Markovian queueing systems with the product-form stationary distributions. The complexity of such systems continues to increase, with the introduction of new extensions of G-networks being an essential area of research [
18,
19].
In conventional queueing networks, each node in isolation can be represented by a birth and death process. Nodes in a Markov network [
20] are Markovian queueing systems whose behavior can be represented by general discrete-state Markov processes. The details of the nodes’ internal structure can be ignored. Each node of a Markov network can have three types of state changes: arrival, departure and internal transitions, which are distinguished only by the rates or probabilities at which they occur. A transition of the network as a whole involves changes at only one or two nodes. The former case corresponds to a network transition consisting of an internal change at one node. The latter consists of a departure transition at one node that triggers an arrival transition at another node determined by a routing probability.
Naumov [
21] obtained the necessary and sufficient conditions for a product-form solution for a Markov network consisting of two nodes, the first of which generates a Markovian arrival process (MAP) of customers arriving to the second node. Chao et al. [
20] obtained the necessary and sufficient conditions for a general Markov network to be of product form. Chao and Miyazawa [
22] extended the notion of quasi-reversibility to Markov networks and applied it to the study of networks with triggered movements and positive and negative signals. In [
23], Chao provided an overview of product-form Markov networks.
The procedure for establishing the existence of a product-form stationary distribution for Markov networks includes a solution of a system of nonlinear equations [
20]. The objective of this paper is to simplify this procedure for some Markov networks so that it can be easily applied in practice. We consider two-node Markov networks and multi-class Markovian arrival processes (MMAP). In
Section 2, we formulate the basic properties of MMAP. In
Section 3, we derive a matrix formulation of the product-form conditions and develop a simple procedure to check whether a Markov network with two customer classes is of product form. Examples given in
Section 4 illustrate the theory developed in the paper.
The following notation conventions are used throughout the article. Bold lowercase letters denote vectors and bold capitalized letters denote matrices. Inequality represents for all vectors and ; if and otherwise; denotes the identity matrix; is the column vector of all ones; the i-th component of vector is equal to one, and the others are equal to zero.
2. Multi-Class Markovian Arrival Process
Consider a multi-class arrival process
, where
are the arrival times and
is the class of the
n-th customer. Denote
the number of class
customers arrived during time t and
. The process
is a MMAP if for some random process
with a finite set of states
the process
is a homogeneous Markov process and the following conditions are satisfied:
for all
,
, and for all nonnegative integer vectors
of length
k [
24]. In this case, the probability of more than one arrival in the interval of length
is
and the process
is a Markov process that is homogeneous in time and in the second component [
25]. That is, for all
,
and
we have:
The phase process
is a time-homogeneous Markov chain with a matrix of transition probabilities:
where
[
25]. It follows from (1) that matrices
,
,
, which characterize MMAP, have the following properties [
26,
27]:
Matrix has non-negative off-diagonal elements.
Matrices , are non-negative.
The matrix
is the generator of the phase process.
Transition probability matrices
can be calculated by the recursion [
27]
If matrices
are known, the joint probability distribution of the number of arrivals in disjoint intervals can be calculated as:
where
is a row vector of the initial probability distribution of the phase process,
.
Consider the MAP of class
v customers. It is characterized by transition probability matrices
which satisfy the following recursion:
The joint probability distribution of the number of class
arrivals in disjoint intervals can be calculated as:
If
is the stationary vector of
and satisfies
, it follows from (3) that
It follows from (4) that, in this case, the arrival process of class
customers is Poisson with rate
. Similarly, if matrix
satisfies
, it follows from (3) that
and the arrival process of class
customers is Poisson with rate
(see also [
28]). We next show that the property
is important for the existence of product-form distribution, in contrast to the property
, although in both cases the arrival processes are Poisson.
3. Interacting Markovian Queueing Systems
We consider a Markov network with two nodes having state spaces
and
. The first node generates MMAP defined by non-zero matrices
,
,
, and the second node generates MMAP defined by non-zero matrices
,
,
. If the nodes are operated in isolation, the first node could be represented by a homogeneous Markov process with a generator:
Also, the second could be represented by a homogeneous Markov process with a generator:
When a class
customer arrives from the first node to the second, the state of the second node changes according to a stochastic matrix
,
,
. When a class
customer arrives from the second node to the first, the state of the first node changes according to a stochastic matrix
,
,
. The behavior of the system can be represented by a homogeneous Markov process
, with the finite state space
and the generator
where
denotes the Kronecker product.
Further, we assume that the generator
is irreducible. Therefore, the stationary distribution
,
,
, of the process
is the unique solution to the system of the following steady-state equations:
which satisfy the normalizing condition:
We next derive the conditions under which the stationary distribution has the product form:
First, however, we need the following auxiliary result.
Theorem 1. The generatorsare irreducible for any ,, and,.
Note that matrix is the generator of a Markov process representing the behavior of the first node with a multi-class Poisson arrival process with rates , Matrix is the generator of a Markov process representing the behavior of the second node with a multi-class Poisson arrival process with rates , . Therefore, Theorem 1 states that if the MMAP arriving to each network node is replaced by a multi-class Poisson arrival process, then the generators of the Markov processes representing each node in isolation are irreducible.
Theorem 2. For the stationary distribution of the processto have the product form (10), it is necessary and sufficient that vectorsandsatisfy the following equations: Hence, components
and
of the product form (10) can be found as the stationary distributions of the nodes with Poisson arrival processes. However, this is not an easy task because the systems of Equations (13) and (14) must be solved together with the conditions (16), and therefore the problem of finding vectors
and
that satisfy the conditions of the theorem is nonlinear. In the next section, we consider particular cases for which this problem can be simplified. The proofs of Theorems 1 and 2 are provided in
Appendix A.
Corollary 1. Let,, vectorbe the solution of equations,, and vectorbe the solution of equations,, where. Then, for the product form of the stationary distribution of the process, it is necessary and sufficient that eitheror.
Proof. Indeed, according to Theorem 2, for the product-form stationary distribution
it is required that for any
which is equivalent to either
or
.
It was shown in
Section 2 that if the condition
is fulfilled, then, in the stationary mode, the MAP generated by the first node is Poisson with rate
(see also [
9,
23]). Because of the PASTA property (Poisson Arrivals See Time Averages) of the Poisson process, the stationary distribution of the second node is equal to the stationary distribution of the Markov chain embedded at times before the customer arrivals. However, then vector
is the stationary distribution of the Markov chain embedded at times after the customer arrivals. Thus, the condition
implies that, for the second node with Poisson arrivals, the Markov chains embedded before and after customer arrivals have the same stationary distributions. □
Corollary 2. Let,, vectorbe the solution of equations,, where, and vectorbe the solution of equations,, where. Then for the product-form stationary distribution of the process, it is necessary and sufficient that at least one of the following conditions is satisfied: There exists a constantsuch thatfor all with, andfor allwith.
Proof. According to Theorem 2, for the product-form stationary distribution
, it is required that for any
the following holds:
The sufficiency of each of the five conditions given above for the product-form stationary distribution is obvious. Let us prove that at least one of them is necessary for the stationary distribution to be of product form.
Suppose that the stationary distribution
has the product form. From (23), it follows that if one of the vectors
,
,
,
is a zero vector then there is another zero vector in this group such that one of the conditions (17)–(20) is fulfilled. It remains to consider the case when all these vectors are non-zero. Let
be a set of
such that
, and let
be a set of
such that
. Then, the following holds for all
and
:
Since the left-hand side of this equation does not depend on r, and the right-hand side does not depend on j, then for and they are both equal to some constant and therefore (21) and (22) are satisfied. Since vectors and are non-zero, it follows from (24) that for each the relationships and are both true or both false. Then, for all in (21), and therefore .□
The proof of the following Corollary 3 is similar to the proof of Corollary 2.
Corollary 3. Let,, vectorbe the solution of the linear system,, and vectorbe the solution of the linear system,, where. Then for the product-form stationary distribution of the process, it is necessary and sufficient that at least one of the following conditions is satisfied: There exists a constantsuch thatfor all with, andfor allwith.
4. Examples
To demonstrate the applicability of the results obtained, let us consider several examples. Examples 1 and 2 illustrate the product-form conditions for and .
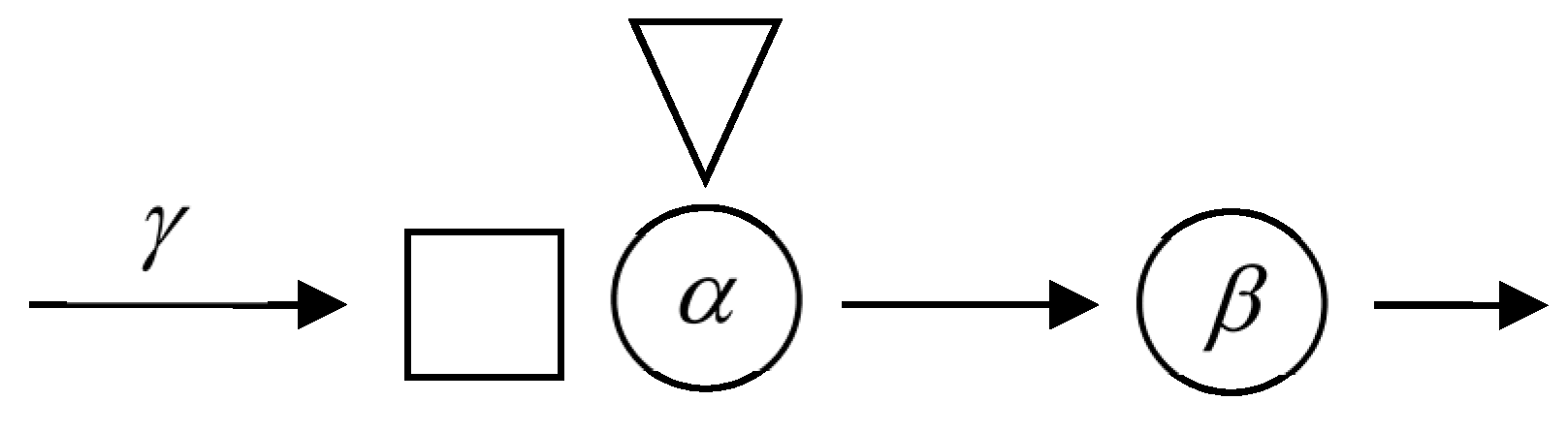
Example 1. Consider a system with the first node consisting of a bunker with waiting space for one customer and one server (Figure 1). There are always customers in the bunker. They arrive to the first node’s server, bypassing the queue, only when the server and the waiting space are empty. In addition to the customers from the bunker, there are customers from an external source forming a Poisson process with rate. An external customer waits if, at the time of the customer’s arrival, the server is busy. If the waiting space is occupied, the arriving customer is lost. All customers served by the first node arrive to the second node, consisting of one server, without waiting space. The service times are exponentially distributed with parametersandfor the first and second servers, respectively. Because the first server is always busy, the departure process of the first node is Poisson with rate. The state of the first node can berepresented by the number of customers in the queue, and the state of the second node by the number of customers in service. We here show that the stationary probability distribution of the network is not of product form. This system is characterized by matrices
and the solutions of the linear systems (13) and (14) are given by
where
. The steady-state equations for the stationary distribution of the process
are as follows:
It is easy to verify that the normalized solution of these equations is given by
It is clear that Thus, although the second node has a Poisson arrival process, this is not enough for the stationary distribution to have the product form. The product-form condition of Corollary 1 does not hold since neither nor .
Example 2. Let the second node havewaiting spaces and no servers. An arriving customer takes one of the free waiting spaces, if there are any. If all waiting spaces are occupied at the instant of arrival, then the arriving customer and all those in the queue are considered served and leave the system.
Such a system with a Poisson arrival process can be represented by a Markov process with the state set . This process has a uniform stationary distribution , , and obviously satisfies the condition According to Corollary 1, the stationary distribution has the product form.
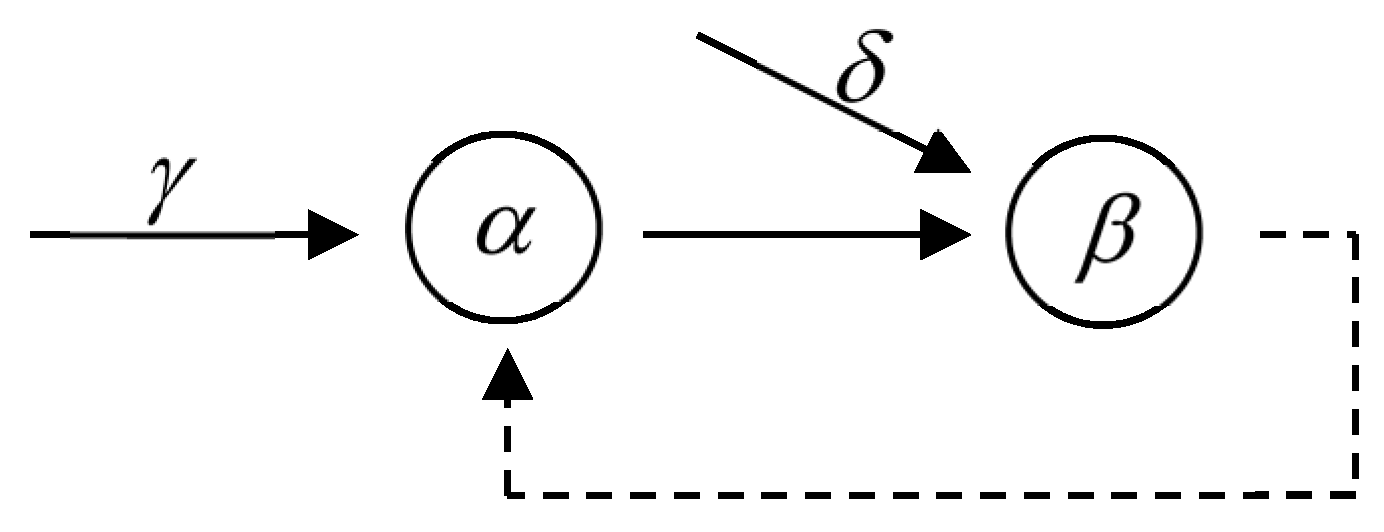
Example 3. Now, to illustrate Corollary 2, consider a system with positive and negative customers. Each node consists of one server without waiting space (Figure 2). The service times at the first and second servers are exponentially distributed with parametersand, respectively. External Poisson processes of positive customers arrive to the servers with ratesand, respectively. A customer departing from the first server arrives to the second server as a positive customer. Arriving positive customers are lost if the servers are busy. A customer leaving the second server comes to the first server as a negative customer and—if the first server is busy—deletes the customer in service.
The matrices that specify the interaction of the nodes are as follows:
and the solutions of the system of Equations (13) and (14) are given by the formulae
where
To check the conditions of Corollary 2, we first calculate the vectors that appear in them:
It is clear that the first four conditions of Corollary 2 are not satisfied for any positive parameters
In the particular case of , , the system of Equations (31) and (32) has the unique solution , and the parameter from the fifth condition of Corollary 2 is Thus, in this case, the stationary distribution has the product form.
5. Conclusions
In this paper, we have studied a Markov network consisting of two nodes of arbitrary structure, where each node generates a MMAP of customers arriving to the other node. We have derived the necessary and sufficient conditions for the product-form stationary distribution of the network. Simple criteria to check whether a Markov network with one and two customer classes is of product form have been developed. Unlike the existing product-form criteria for Markov networks, the criteria obtained in this article are readily applicable to establish the existence of a product-form stationary distribution for specific Markovian queueing systems. The extension of the developed theory to networks with more than two classes of customers is the subject of our future research.