1. Introduction
Consider a queueing system with an infinite number of waiting places which may be modeled by a Quasi-Birth-and-Death (QBD) process
on a state space
where
and
,
. Here
l represents the number of customers in the queue and
represents the internal state of the system. The generator of the process
has the block tri-diagonal form
where
is a square matrix of order
n, the matrices
,
,
and
are square of order
m, and the matrices
and
are rectangular of appropriate dimensions. We denote by
the stationary probability vector associated with
and we partition it as
, where
is an
n-vector, and
,
, are
m-vectors. We also define the generator
.
According to [
1], the positive recurrent Markov chain
has a modified matrix-geometric stationary probability vector,
where
, which is called the rate matrix, has the spectral radius
and is the minimal nonnegative solution of the matrix equation
Once
is known, vectors
and
are obtained by solving the linear system
with the normalizing condition
where
is the column vector of all ones of appropriate size.
The rate matrix
is usually computed via iterative algorithms [
1,
2,
3,
4] among which the fastest is the logarithmic reduction algorithm [
2]. Available methods for computation of the rate matrix are effective only for relatively small values of
m. Exceptions are processes with off-diagonal blocks of a special type. If matrices
or
have rank one [
5,
6], or matrix
is triangular [
7,
8], it is possible to find an explicit solution of Equation (3).
Now, consider a queueing system with
waiting places, that can be modeled by a Markov chain
on a state space
with a generator of the block tri-diagonal form
The change in the lower diagonal block is due to the fact that if an arriving customer finds all waiting places occupied it is lost, but the internal state of the system changes in the same manner as if the customer were not lost.
We partition the stationary probability vector
associated with
as
, where
is an
n-vector, and
,
are
m-vectors. Solving finite QBD processes is more complicated than solving infinite processes [
9,
10,
11]. If for some number
s matrices
,
,
satisfy
then the stationary probability vector
can be expressed using two matrix-geometric terms as [
12]
which require computation of the minimal nonnegative solutions of two matrix equations
The vectors
,
and
can be found by solving the linear system
and normalizing vector
. The condition
holds, for example, if the generator
is irreducible and
, where
is the stationary probability vector of
[
13].
The stationary probability vector
of the generator (Equation (1)) satisfies the equation
for all
. In the finite case the stationary probability vector
also satisfies the equation
for all
, but the boundary equation is different
It is clear that if the rate matrix satisfies then the stationary distribution of can be obtained by the truncation of the matrix-geometric stationary distribution (Equation (2)) of at the level of . In turn, this is enough to fulfill the condition for some In this paper we study the properties of QBD processes with rate matrix satisfying . If it is so, then for any L the stationary distribution of the process can be obtained by truncation of the stationary distribution of .
In the next section we show when the rate matrix
satisfies
. In
Section 3, we analyze the stationary distributions of infinite and finite QBD processes. In
Section 4, we use the obtained results for solving a semi-open network in which customers from an external queue may only arrive to the node from which a departed customer left the system. We assume the process
to be positive recurrent.
The following notation conventions are used throughout the article. Bold lowercase letters denote vectors, and bold capitalized letters denote matrices, if and otherwise; is the identity matrix; the ith component of vector is equal to one and the others are zero.
3. Truncation of the Stationary Distribution
Consider a queueing system with waiting places that can be modeled by a Markov chain with a generator of the form (7) with the block-diagonal matrices , , as in Equation (17). We partition the stationary probability vector corresponding to as , where is an n-vector, and is partitioned as , with -vectors , .
Theorem 2. Let a generatorbe irreducible, matrices,,have the block-diagonal form (Equation (17)),be an irreducible generator with the stationary probability vectorthe matricesbe given by Equations (19) and (20) respectively, and vectorsandsatisfy the linear system Then the stationary probability vector of is given bywhere is the normalization constant, Proof. Since the matrices
and
are given by Equations (19) and (20), under the Corollary 1 of Theorem 1, matrix (18) is the solution of Equation (3) and satisfies
. It implies that vectors
and
given by Equation (25) satisfy the following relations:
It follows that
is the stationary probability vector of the generator
Power
of the matrix
is given by
Using this formula and equality (Equation (24)) we obtain the normalization constant (Equation (26)). This completes the proof of the theorem. □
Note that the vector in Equations (22)–(24) gives the stationary distribution of the Markov chain which models a queueing system without waiting places, and the stationary distribution of the Markov chain depends on the number of waiting places L only via the normalizing constant . Similar results are valid for the infinite QBD process with generator of the form (1).
Theorem 3. Let generatorbe irreducible, matrices,,have the block-diagonal form (17),be an irreducible generator with stationary probability vectormatricesbe given by (19) and (20) respectively, and vectorsandsatisfy the linear system (22)–(24). Then processis positive recurrent if and only iffor allIn this case the stationary probability vector ofis given bywhereis the normalization constant, Proof. The proof of Equations (27) and (28) is similar to the proof of Equations (25) and (26). The spectral radius of the rate matrix is the maximum of the spectral radii if its diagonal blocks are given by Equation (21). Therefore, the process is positive recurrent if and only if for all . □
The following result is a direct consequence of Equation (25) for the stationary distribution of the processes and of Equation (27) for the stationary distribution of the process .
Corollary 2. If the conditions of Theorem 2 hold andfor allthen the stationary distributions of the processescan be obtained by truncation of the stationary distribution of the process.
4. Semi-Open Networks with Replacement
Since the first papers [
14,
15] on semi-open networks appeared, the use of these models has become increasingly widespread [
16,
17,
18]. However, the exact analysis even of the simplest network, with two exponential single-server nodes, Poisson arrival process, and an infinite queue, remains a difficult task [
15]. The semi-open networks with external queue are mainly analyzed by approximate methods and the matrix-geometric method [
19,
20,
21,
22,
23].
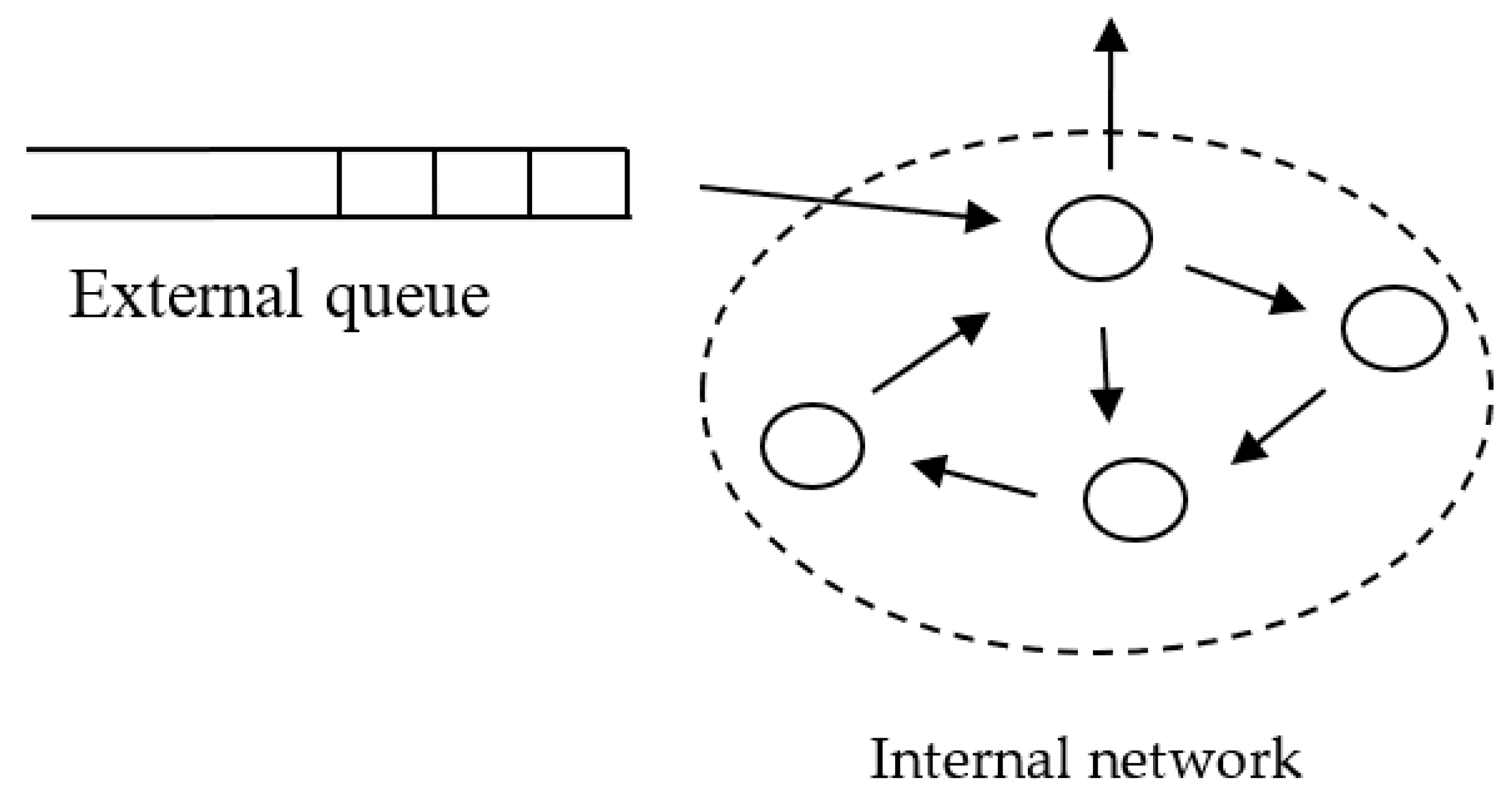
Consider a semi-open network consisting of an internal network with v nodes and an external queue. The number of customers in the internal network cannot exceed N. If an arriving customer finds the internal network busy it waits in the external queue or is lost if the number of customers in the queue has reached its maximum value . Such a network can be considered as a queuing system with N resource units. If all N resource units are occupied, the arriving customer waits in the external queue until a resource unit becomes available. Upon completion of its service in the internal network, the customer releases the occupied resource unit.
We consider semi-open networks in which the customers waiting in the external queue select a node for entering the internal network according to the following rule, which we call the replacement. If a customer leaves the system upon completing service at node
i, then a customer from the external queue will start service also at node
i, thus “replacing” the leaving customer. As a result, the number of customers in the external queue will decrease by one, but the number of customers at each node of the internal network remains unchanged. An example of a system in which only the replacement of customers leaving the system is possible is shown in
Figure 1. It is a semi-open network with only one node where customers can complete service and through which waiting customers can enter the internal network.
Let the arrival process be Poisson with rate
. The service rate
at node
i depends on the number
of customers at this node:
and
for
A customer entering the internal network is sent to node
i with probability
,
. A customer completing service at node
i will either require service at node
j with a probability
or leave the system with probability
. The visit ratios
can be found as a solution of the linear system
and the nodes’ throughputs are given by
,
. Summing both sides of Equation (1) over
j, we obtain a useful relation
A semi-open network can be modeled by a Markov chain
where
represents the number of customers in the system at time
t, and
,
, represent the number of customers at node
j of the internal network. The process
has a state space
with
where
We assume that all states of the process communicate and denote its stationary distribution as , , .
The generator of the process
has the block tri-diagonal form (Equation (18)) with the following nonzero transition rates
where
In Equation (8) the matrices , , are diagonal with elements , , respectively. Therefore, the stationary distributions for the finite and infinite semi-open networks with replacement can be found using Theorems 2 and 3.
For a semi-open network without an external queue the closed form solution can be easily derived because there exists an equivalent closed network of capacity
N. The equivalent network can be obtained by adding a single-server node 0 with an infinite queue and exponentially distributed service times with parameter
to the original network. Node 0 plays the role of the external environment of the original network. When a customer arrives to or departs from the original network, it departs from or arrives to node 0 in the equivalent network. The stationary distribution
,
,
of closed queueing networks with state-dependent service rates have a product form [
24] and the solution
and
of the linear system (Equations (19)–(21)) is given by
For closed queueing networks, there are several effective methods for computation of the normalization constant
[
25].
By virtue of Theorem 2 for semi-open network with replacement and a finite external queue, the stationary distribution of the process
is given by
where
It follows from Theorem 3 that a semi-open network with replacement and an infinite external queue is stable if and only if
for all states
. In this case, the stationary distribution of
is given by
Similarly, it is possible to analyze semi-open queuing networks partitioned into subnetworks. Each such subnetwork consists of a subset of nodes of the internal network. If a customer leaves the system, then a customer from the external queue will proceed with a certain probability to a node in the same subnetwork in which the customer leaving the system was served. The generator of the related QBD process has the matrices of the form of Equation (17). The results of this paper can be used if the diagonal blocks of satisfy relation (19).