1. Introduction
The guaranteed minimum death benefit (GMDB) is a common rider embedded in variable annuity products that promises a minimum payout upon the death of the insured. In this product, policyholders first pay premiums to the insurance company, and then, investment accounts are established for capital investment. When the insured dies, a payment shall be given to the designated beneficiary, and the payout amount depends on the performance of the policyholder’s account. This mechanism not only provides insurance guarantee for policyholders, but also has the opportunity to benefit from the financial market, which appeals to customers.
For
, let
denote the price of a stock fund or mutual fund at time
t. For a person currently aged
x, let
denote the remaining lifetime, called the time-until-death random variable hereafter. Moreover, we assume
is independent with the asset price process
throughout this paper. Consider a GMDB rider that guarantees a payment of
to the beneficiary when the insured dies, where
is an equity-linked death benefit function. For a constant force of interest
, we are interested in valuing the following expectation:
which represents a fair price for an equity-linked life-contingent payment at
. Since most contracts have a finite expiry date, we can modify (
1) by introducing an expiry date
T and consider:
where
denotes the indicator function of event
A.
We are also interested in the case when the death benefit amount depends on two stocks (or stock funds). Let
denote the price process of two stocks, and let:
In the sequel, it is also assumed that
is independent with both
and
. Accordingly, we are interested in evaluating the following expectations:
Recently, the valuation of the GMDB product has drawn many researchers’ attention. Under an exponential mortality law, Milevsky and Posner [
1] proposed a risk-neutral framework to derive valuation equations for GMDB contracts. Besides, they conducted a numerical study under the Gompertz-Makeham law. Later, in Bauer et al. [
2], they supposed that the death should only occur at the policy anniversary date, which facilitates a discrete numerical valuation approach for fairly valuing varieties of guaranteed riders, including GMDB. Gerber et al. [
3] proposed a discounted density approach to value GMDB in a Brownian motion risk model, and their results were extended by Gerber et al. [
4] and Siu et al. [
5] to the jump diffusion model and the regime-switching jump diffusion model, respectively. Based on the fact that the combination of exponential distributions is weakly dense on the set of probability functions defined on
(see Dufresne [
6] and Ko and Ng [
7]), we notice that the density function of the time-until-death random variable was approximated by a linear combination of exponential distributions in Gerber et al. [
3,
4] and Siu et al. [
5]. More recently, Zhang and Yong [
8] and Zhang et al. [
9] used two different methods to value GMDB products. Recent related literature can be found in Dai et al. [
10], Bélanger et al. [
11], Kang and Ziveyi [
12], Asmussen et al. [
13], and Zhou and Wu [
14].
When the density function of the time-until-death random variable is approximated by a linear sum of exponential distributions, Gerber et al. [
3,
4,
15] derived explicit valuation equations for GMDB contracts under various payoffs. The simplicity of using a combination of exponential distributions is excellent, but they are not representative of reality. A direct way to calibrate this is to use life table data. In Ulm [
16,
17], he emphasized the valuation of GMDB products under mortality laws, such as the De Moivre law of mortality and the Makeham law of mortality. A similar consideration could be found in Liang et al. [
18]. They novelly introduced the piecewise constant forces of the mortality assumption to describe the time-until-death variable, then decomposed the valuation problem and presented explicit valuation equations for GMDB.
Except the aforementioned assumptions on the time-until-death random variable, the modeling of the asset process has attracted the attention of scholars. Brownian motion was widely used to model the log-asset price process, which was adopted in Milevsky and Posner [
1], Bauer et al. [
2] (
Section 4), Gerber et al. [
3], and Liang et al. [
18]. In the field of financial markets, this case is basically a Black-Scholes framework. However, more processes could be also implemented. In Gerber et al. [
4], Kou’s jump model was used as the log-asset process. A counterpart study of Gerber et al. [
3] was referred to by Gerber et al. [
15], in which a random walk exponentially generates the price process. To study the valuation issue in a different perspective, scholars turned to the regime-switching model, which was used to investigate the performance of an object subject to the economic changes in financial markets. In the literature, interest readers can refer to Fan et al. [
19], Siu et al. [
5], Ignatieva et al. [
20], and Hieber [
21].
In Fang and Oosterlee [
22], a highly-efficient option pricing method was proposed to price European options. The method was based on the Fourier cosine series expansions, and it is now called the cosine series expansion (COS) method in the literature. The COS method is quite easy to implement to approximate an integrable function as long as the objective function has a closed-form Fourier transform. The one-dimensional COS (1D COS) method in [
22] was extended to the two-dimensional COS method (2D COS) by Ruijter and Oosterlee [
23] to price financial options in two-dimensional asset price processes. Leitao et al. [
24] proposed a data-driven COS method. Except for option pricing, this method has been adopted in insurance ruin theory. For example, Chau et al. [
25,
26] used the 1D COS method to compute the ruin probability and the expected discounted penalty function; Zhang [
27] approximated the density function of the time to ruin by both 1D and 2D COS methods; Yang et al. [
28] proposed a nonparametric estimator for the deficit at ruin by the 2D COS method; Wang et al. [
29] and Huang et al. [
30] used the 1D COS method to estimate the expected discounted penalty function under some risk models with stochastic premium income. The COS method has also been used by some authors to value variable annuities. For example, Deng et al. [
31] used the 1D COS method for equity-indexed annuity products under general exponential Lévy models; Alonso-García et al. [
32] extended the 1D COS method to the pricing and hedging of variable annuities embedded with guaranteed minimum withdraw benefit riders. The latest research on Fourier transform was given by Zhang et al. [
33], Chan [
34], Zhang and Liu [
35], Have and Oosterlee [
36], Shimizu and Zhang [
37], Tour [
38], Zhang [
39], and Wang et al. [
40].
The discounted density method proposed by Gerber et al. [
3,
4] can be successfully used to value GMDB products when the log-return process is the Brownian motion or Kou’s jump diffusion model. Under these two models, the density functions have some closed-form expressions. However, in practice, we cannot obtain the closed-from expression for the discounted density function. In this paper, we use the COS method to approximate the discounted density function, which is applicable since most of the widely-used Lévy processes have explicit characteristic functions. To the best of our knowledge, this is the first paper exploring the COS method on numerical valuation of the GMDB product under the general exponential Lévy models. In particular, there are few papers on GMDB valuation dependent on two stock prices in the literature, and this is the first paper dealing with this problem.
This paper aims to value the GMDB contracts in a risk-neutral framework, mainly by numerically solving Equations (
1) and (
2). In subsequent sections, we first briefly recall the COS method in Fang and Oosterlee [
22], then adopt the method to approximate
and
in the one-dimensional framework. We define auxiliary functions to simplify deductions and display equations under different payoffs in
Section 2. Motivated by Gerber et al. [
3], we consider the situation where the density function of
is approximated by a linear combination of exponential distributions, and calculate cosine coefficients in
Section 4.1. Under the multi-dimensional case, we shed light on a two-dimensional framework in
Section 3. Finally, numerical examples are presented in
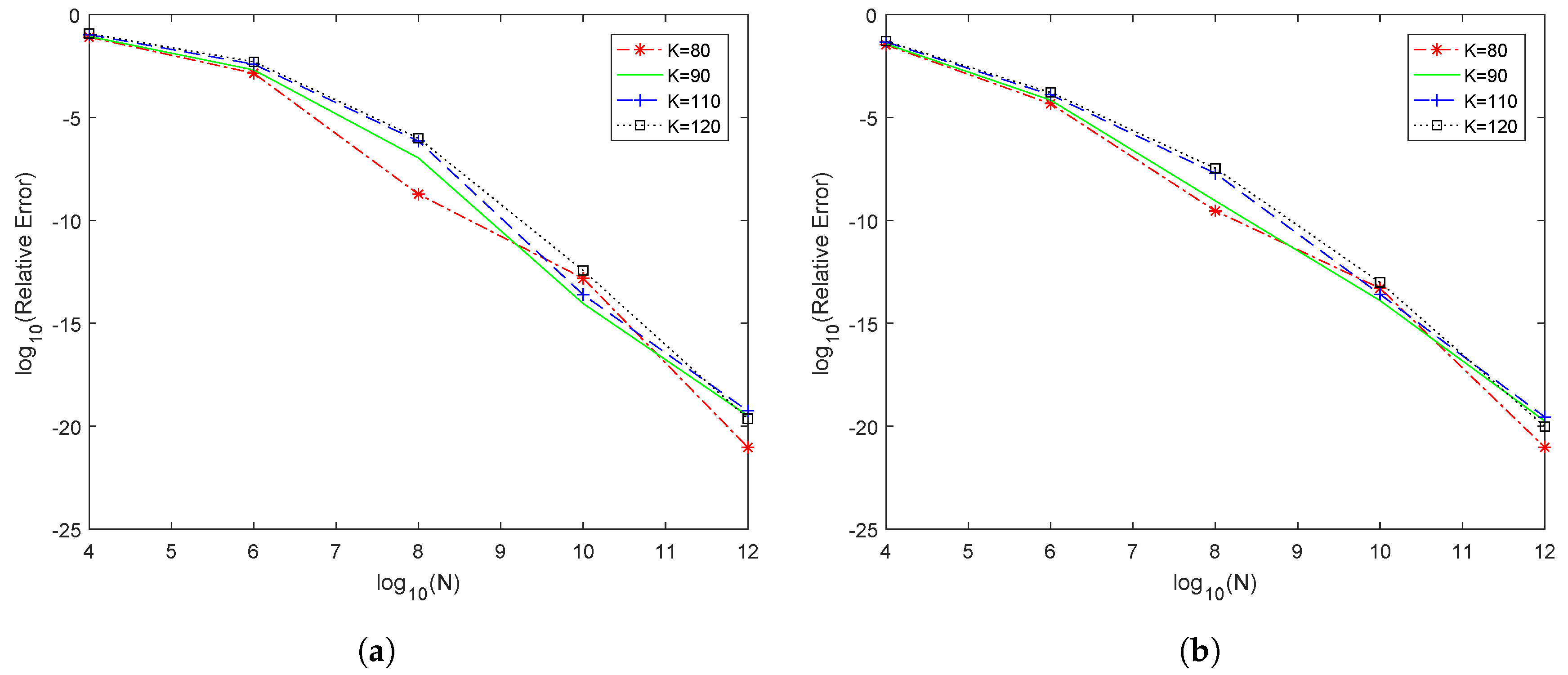
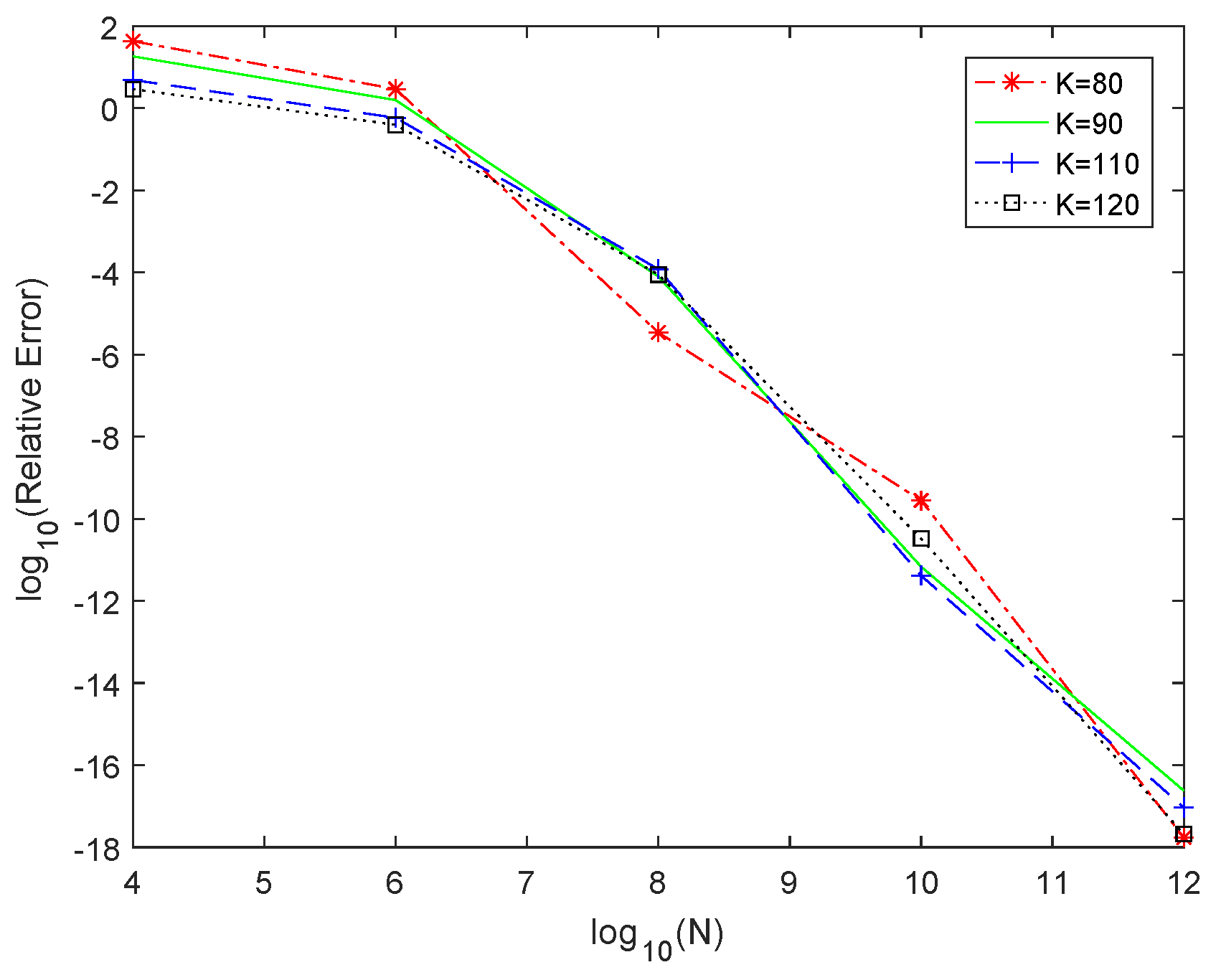
Section 4, in which we display tables and figures to illustrate the performance of our proposed approach.
2. 1D COS Approximation
In the section, we shall use the 1D COS method to compute
and
. The idea of the 1D COS method is that every absolutely integrable function
f can be approximated on a truncated domain
by a truncated Fourier cosine series with
N terms,
where
means that the first term in the summation has half weight, and the cosine coefficients are given by:
Here, , , is the Fourier transform of f, and means taking the real part.
Let
denote the probability density function of
, and for
, let
be the probability density function of
. By changing the order of integrals, we can obtain:
where:
is the discounted density function of the random variable
. Similarly, for the
T-year life-contingent option, we have:
where:
We shall implement the 1D COS method to compute the integrals in (
5) and (
7). Instead of expanding the discounted densities
and
via Fourier cosine series, we shall consider the following auxiliary functions:
Suppose that both
and
belong to
, then by Equations (
3) and (
4), we have:
and:
Remark 1. The cosine coefficients and can be explicitly computed when is a Lévy process and is a combination of exponential density function. To this end, it suffices to specify the Fourier transforms and . Suppose that (with ) is a Lévy process with characteristic function:where is called the characteristic exponent. Furthermore, suppose that:where and . Under these assumptions, one easily obtains:and: In the sequel, we shall consider three payoff functions.
Case 1. .
In this case, Equations (
5) and (
7) become:
For small number
and large number
, using Equation (
9), we can approximate
as follows,
where:
Similarly,
can be approximated as follows,
Case 2. with and .
Here, the positive constant
K denotes the strike price. Put
. It follows from Equation (
5) that:
Then, using the 1D COS method, we obtain for large number ,
Similarly, for
, we have:
Remark 2. For the call option, the payoff is given by: By applying Equations (
5)
and (
17)
, we obtain: For the T-year life-contingent option, we have: Case 3. with and .
By Equation (
5) and the 1D COS method, we have for small number
,
Similarly, for
, we have:
Remark 3. For the put option, the payoff function is given by:which together with Equations (
21)
and (
22)
gives:and: 3. 2D COS Approximation
In this section, we use the 2D COS method to compute
and
. For a bivariate integrable function
f, we denote its Fourier transform by:
It follows from Ruijter and Oosterlee [
23] that
f can be approximated on a truncated domain
by truncated Fourier cosine series expansions with
terms,
where the cosine coefficients are given by:
with:
For
, we denote the joint probability density function of
by
, and for
, define the following discounted density functions:
For
, by changing the order of integrals, we have:
As in
Section 2, we shall pay attention to the following auxiliary functions,
Suppose that both
and
are absolutely integrable. Then, by Equation (
25), we obtain:
and:
To calculate cosine coefficients in Equations (
29) and (
30), we suppose
is a two-dimensional Lévy process with
. The characteristic exponent is defined by:
Furthermore, suppose that
is a combination of the exponential density function given by Equation (
12). By Fubini theorem, we have:
and:
In the sequel, we study the numerical approximation of the value of life-contingent two-asset options. We shall consider the Margrabe option, maximum/minimum option, and geometric option. First, the contingent Margrabe option, also called the exchange option, is considered. Note that its payoff function is:
Then, we have:
where
denotes the region
. Set
. Utilizing Equation (
29), we obtain the following approximation formula:
where the double integrals in both summations can be analytically computed.
What follows next are the approximation procedures for maximum/minimum options. The payoff functions for maximum and minimum options are given by:
With a trivial mathematical change, we can turn them into the following forms:
Hence, the valuation equations can be obtained by taking discounted expectations on both sides of the above equations,
which imply that we can take advantage of the deductions of exchange option and basic option taking the form
to compute the above expectations.
Finally, we pay attention to the geometric option. The payoff function with strike price
K is given by:
When condition
holds, we can develop the following approximation.
where
denotes the region
. Set
. Then, Equation (
34) can be approximated by:
where analytical expressions of the double integrals in both summations exist.
Remark 4. When we study , the approximation Equations are similar to those of , and the only modification is replacing by .